私たちの心は「価値」と「確率」を正しく把握できない。
「人は合理的ではなく、心の世界で生きている」
そんな当たり前の答えをあらわした2つの関数を分かりやすく簡単に解説!
価値関数とは?

価値関数とは
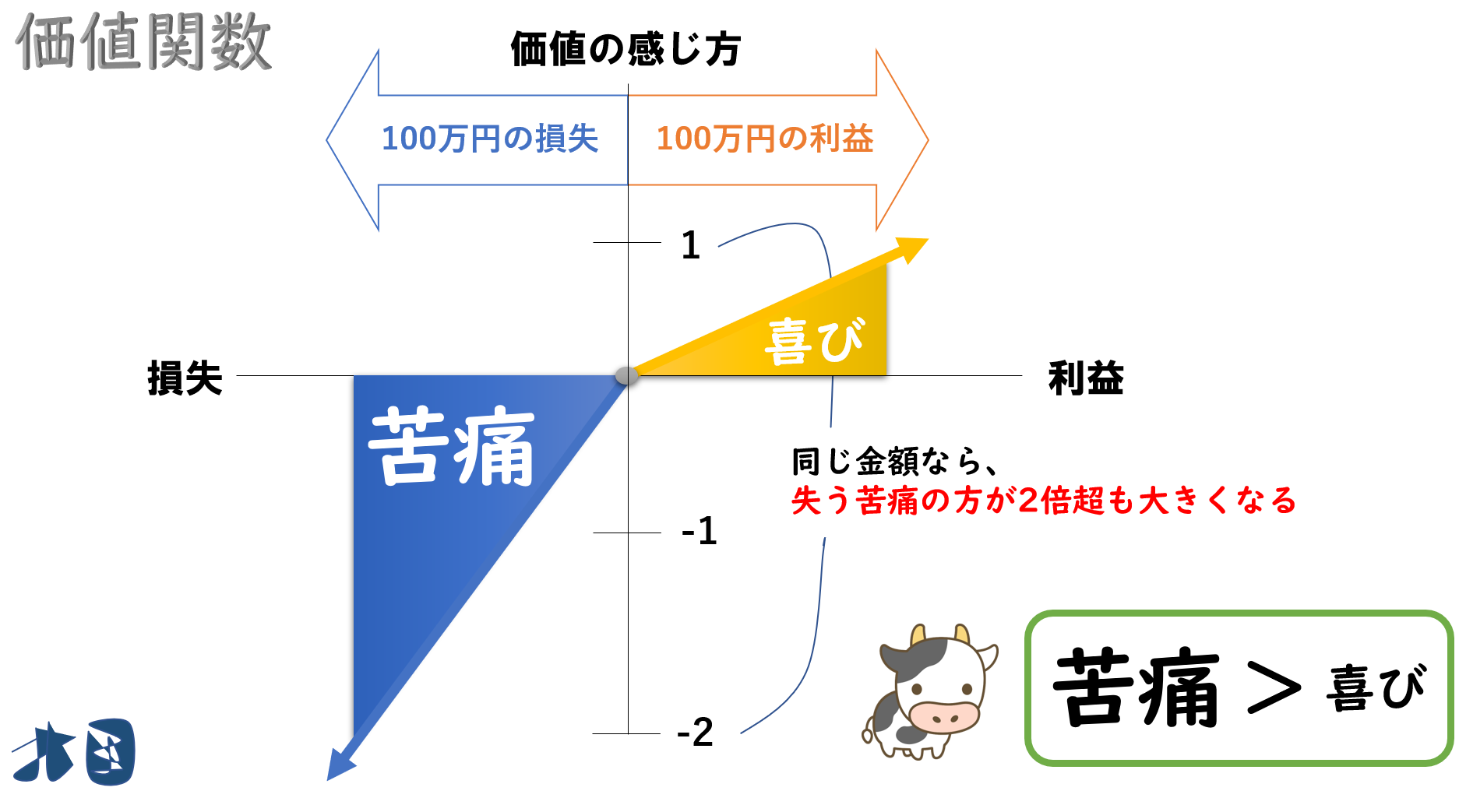
ある物事に対して感じる主観的な価値をあらわした関数のこと。


これまでの経済学
ひとは「利益でも損失でも、金額の通りの価値を感じる」と考えていました。
しかし、この考えは間違っています。
行動経済学を知っている人なら分かる通り「ひとは1円の価値を1円とは認識しません」。置かれた状況によって、1円以下にも1円以上にも価値を感じることがあります。
どうして間違っているのか?
私たちは、何をするにも心の影響を受けるからです。ロボット的に数字を計算して・・という価値の感じかたはしていません。
つまり、人の心を分析することが重要なわけですが、とくに価値関数の話で重要な心理現象があります。
重要なのがコレ
-

-
【損失回避性とは?】絶対に知るべき行動経済学で登場する心理学
あなたが「失う」ことを嫌うのは何故か。 行動経済学の理論の多くが「損失回避の法則」と関係しています。 必ず知るべき「人の ...
続きを見る
損失回避性とは
「損をする」ことに対して過剰に恐怖を覚える人の性質のこと。同じ金額ならば、利益を得る喜びよりも損をする苦痛の方が2倍以上大きく感じるのです。
人の心は「損」というものに過剰に反応するように出来ています。
ポイント
ひとの心には、本能的なものが残っています。
野生の世界で、食べ物を失っては命にかかわります。つまり「損失回避」というのは、生命に深く刻まれた、人が生き残るための心理現象なのです。


この「損失回避性(損失忌避)」という心理ですが、実は他にも影響を及ぼします。
人がギャンブラーになる時
損を嫌うことは分かってもらえたかと思いますが
「損をしている時」はどうなるのでしょうか?
じつは、人が損をしている時も「損失回避性」が働きます。
損を避ける・嫌うのが「損失回避性」でしたが
損をしている状態だと「損から逃れよう」とします。


損失回避性の影響で、損をしていると危険な賭けに出やすくなることが分かっています。
フレーミング効果でも登場する「アジア疾病問題」の1つを見てみましょう!
アジアで流行している病気の対策案が2つあります。
対策案①:400人が死ぬ
対策案②:1/3の確率で誰も死なないけど2/3の確率で600人が死ぬ
どちらの対策案が好まれるでしょうか?(期待値はどちらも同じ)
結果は・・
多くの人が②を選ぶことが分かっています。
「400人が100%死ぬ」という損失を避けたいあまり、②のギャンブル要素満載な対策案が好まれるようになるのです。
さらに詳しく
損失を抱えている状態でリスクのある行動を取りやすくなることを、行動経済学では「リスク志向的」と言います。


誰もが安心を求める
逆に利益がある状態だとどうなるのでしょうか?
- 損している⇒損から逃れようとする
- 得している⇒そのまま逃げ切りたい
こんな心理になりませんか?この心理から「得られる利益は確実に得たい」という気持ちが高くなります。
さきほどの「アジア疾病問題」で確認しましょう。
アジアで流行している病気の対策案が2つあります。
対策案①: 200人が助かる
対策案②: 1/3の確率で600人が助かるけど 2/3の確率で誰も助からない
どちらの対策案が好まれるでしょうか?期待値はどちらも同じ
結果は・・
多くの人が①を選ぶことが分かっています。
「200人が100%助かる」という確実性のある選択肢が好まれるのです。
さらに詳しく
利益がある状態では、リスクを避けて行動しやすくなることを、行動経済学では「リスク回避的」と言います。


価値の感じ方のまとめ
-
得よりも損の方が2倍以上嫌な気持ちになる
-
損していると損を取り戻そうとする⇒目先の利益の価値が高くなる
-
得しているとそのまま逃げ切りたい⇒手元の利益の価値が高くなる・目先の利益にそこまでの価値を見出さなくなる
上記の3つ特徴をまとめたグラフが「価値関数」となります。
まとめ!
「損失の苦痛のほうが2倍以上も感じる」というのはグラフから見て取れるかと思います。
グラフの見方
損失を抱えている状態(グラフの ‐2)を想定してみましょう。
ちょっとの利益で苦痛が一気に減ります。
なので目先の利益に価値を感じるようになります。
一方で、利益がある状態(グラフの 1)なら、利益を得ても喜びが緩やかにしか増えません。なので手元の利益を失わないようにする意識の方が強くなるのです。
確率加重関数とは?
確率加重関数とは
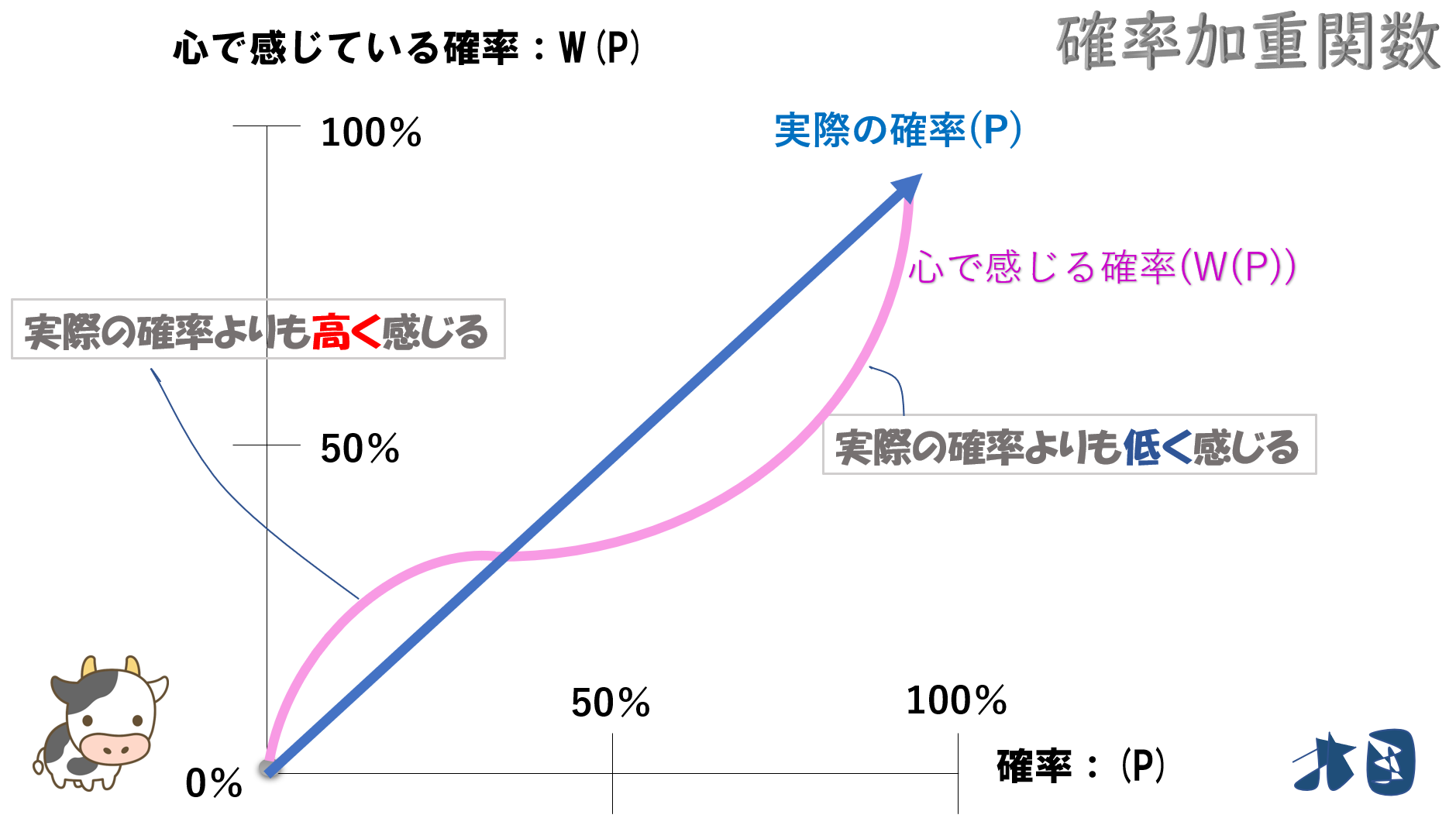
人の心が感じる確率を表した関数のこと。
人は「低い確率」と「高い確率」を目の前にすると、心のなかで確率を歪めて認識してしまう。
経済学者のモーリス・アレが、こんなパラドックスを提示します。

(モーリス・アレ Wikipediaより)
モーリス・アレは、フランス出身の経済学者。1988年にノーベル経済学賞を受賞している。
アレのパラドックス
- 2つの宝くじに関する質問
【1回目のくじ】
選択肢A:確実に1,000ドルがもらえる。
選択肢B:10%の確率で2,500ドル・89%で1,000ドル・1%は賞金なし。
【2回目のくじ】
選択肢A:11%の確率で1,000ドル・89%は賞金なし。
選択肢B:10%の確率で2,500ドル・90%は賞金なし。
それぞれどちらの宝くじを選びますか?
ちなみに、1,000ドルは日本円で1万1,000円くらい。2,500ドルは2万7,000円くらい
ここでパラドックスが生まれました。
多くの人が
- 1回目のくじでは「期待値の低い方を選択」
- 2回目のくじでは「期待値が高い方を選択」
この結果を、従来の経済学では説明することが出来なかったのが始まりです。
詳しくはこちら
-

-
【アレのパラドックスと日常例】なぜ私たちは確率を計算できないのか
あなたの心は確率を正しく認識していません。 「ほぼ0%」や「ほぼ100%」なのに、その確率を信じることが出来ないのは何故 ...
続きを見る


ココがポイント
私たちは確率を正しく認識していない。50%と言われても、心の中では50%だとは感じていないのです。
心の中では確率をどのように感じているのか?という問題ですが、これを研究して答えを出した人物がいます。
それがダニエル・カーネマン教授です。
-

-
【ダニエル・カーネマン】行動経済学の権威が語る人間の科学
ノーベル経済学賞を受賞したダニエル・カーネマンが語る「人間の科学」 行動経済学の第一人者であるカーネマン教授から学ぶ「人 ...
続きを見る
行動経済学の権威と言われている人物です。
カーネマン教授は、心と確率の関係を見つけました。
低い確率を高く感じる
例えば、1%で1億円が当たる宝くじがあります。
微妙に当たるかもしれない感じがしませんか?
人は、小さな確率を目の前にすると、その確率よりも高く評価してしまう。
「もしかしたら・・・」という気持ちが湧き上がる。
事故や通り魔のニュースを見て危険を感じて「もしかしたら私にも危険が・・」と感じるときのあの感覚です。
こうした心理は、宝くじの購入や保険の加入などのビジネスの世界にも表れています。
高い確率を低く感じる
例えば、90%で手術が成功しますと言われました。
微妙に失敗するんじゃないかって心配になりませんか?
人は、高い確率を目の前にすると、その確率よりも低く評価してしまう。
「もしかしたら・・・」という気持ちが湧き上がる。
高確率で成功するって分かっても一歩踏み出せなかったりする、あの心理です。


確率加重関数
- 「P」が実際の確率
- 「W(p)」が主観確率(心の中の感じ方)


35%はあくまで目安なので、人それぞれです。
「価値関数」と「確率加重関数」の2つを見てきました。
価値も確率も、心の影響を受けて感じ方が変わっているって面白いですよね。
どちらも プロスペクト理論の中核をなす話なので、行動経済学の勉強をしている人はしっかりとしておきましょう!