長期費用曲線は大きく3つあります。
- 長期総費用(LTC)
- 長期平均費用(LAC)
- 長期限界費用(LMC)
この3つの長期費用曲線について簡単に要点をまとめています。
長期費用曲線の概要
長期費用曲線(LC)
通常の費用曲線と異なり、固定的な生産要素も、すべて調整できる(=可変的)と考える費用曲線のこと。次の3つがある。
- 長期総費用曲線(LTC)
- 長期平均費用曲線(LAC)
- 長期限界費用曲線(LMC)
固定費用・可変費用の区別を付けないのが長期費用曲線の特徴の1つです。
短期の費用曲線について理解していれば簡単です。
ポイント
固定費用を考えないことで短期費用曲線と長期費用曲線にどのような違いが表れるかを押さえる。


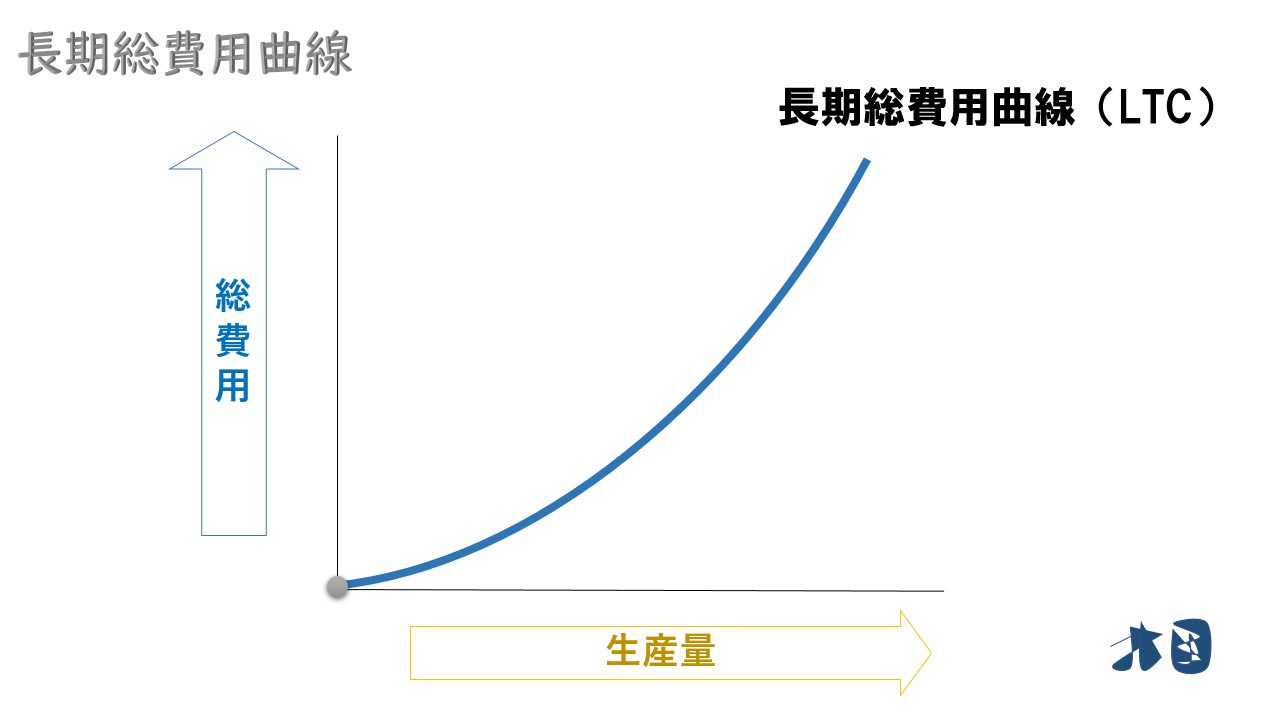
長期総費用曲線(LTC)
長期総費用曲線(LTC)
企業の長期的な総費用曲線。通常の総費用曲線(短期総費用曲線)と異なり、固定費用も可変的なものとして扱うのが特徴の1つ。


ポイントは2つ
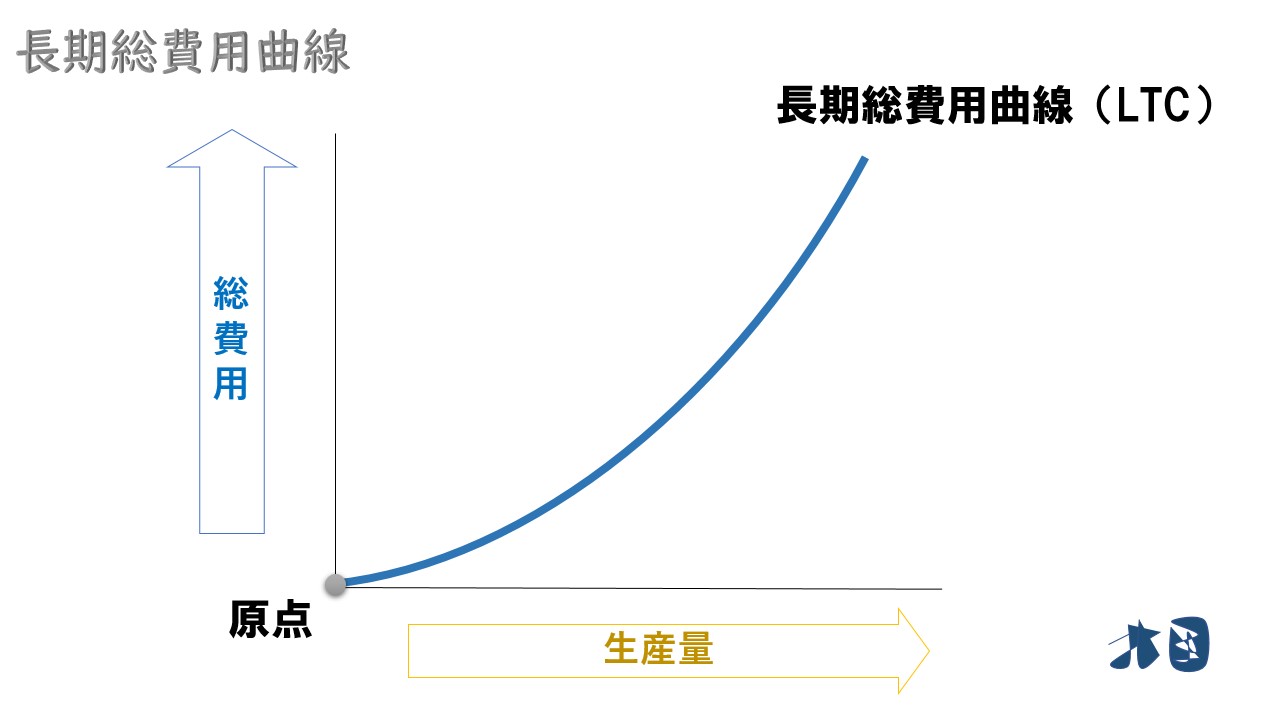
- 長期総費用曲線は原点を通る
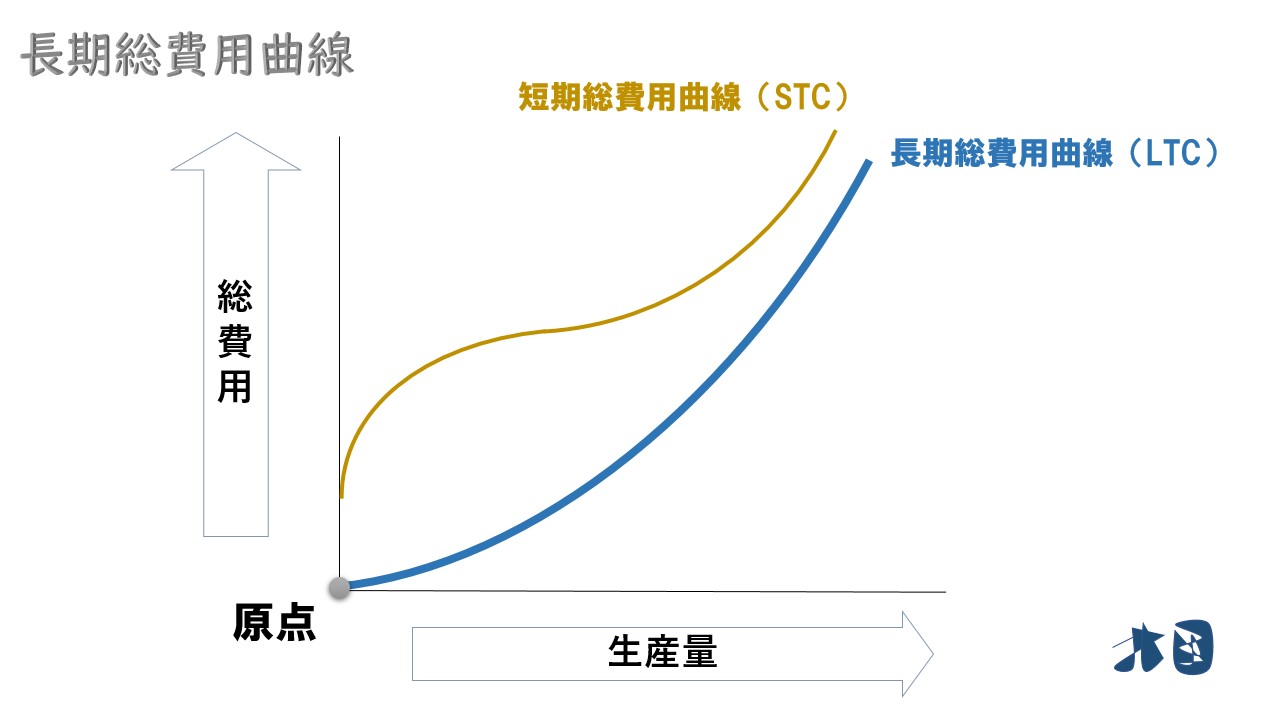
- 長期総費用は短期総費用より小さくなる(もしくは同じ)
原点を通る
ポイント
長期費用では、固定的な生産要素をすべて調整可能と考えるため「総費用=可変費用」となる。
短期費用では、工場の地代などは固定費用(FC)として扱っていました。
しかし
長いスパンで考えると、企業は工場の所在地を変更できる。

企業は「生産に有利な場所(地代が安い等)」に工場を移転していきます。つまり、長期的には工場の地代は固定費用(FC)ではなく、可変費用(VC)として考えることが出来ます。


- 短期総費用曲線(STC)は原点を通らないが、長期総費用曲線(LTC)は原点を通る。
- 長期総費用曲線は逆S字型で書かれることも、通常の右上がりの曲線として書かれることもあります。ここでは通常の右上がりの曲線として書いています。
包路線(長期総≦短期総)
ポイント
企業は長期的には固定費用の最適化も実現できるため、短期費用より長期費用の方が小さくなると考える。「長期総費用≦短期総費用」
再確認
長期総費用曲線(LTC)は原点を通るでも説明しましたが、長いスパンで考えると企業は「生産に有利な場所(地代が安い等)」に工場を移転していきます。

すると、短期で考えるよりも長期的には生産が最適化されます。
生産が最適化されると、短期よりも長期の方が費用対効果がよくなるはずなので、短期総費用よりも長期総費用の方が小さい、もしくは同じになります。
グラフで考える
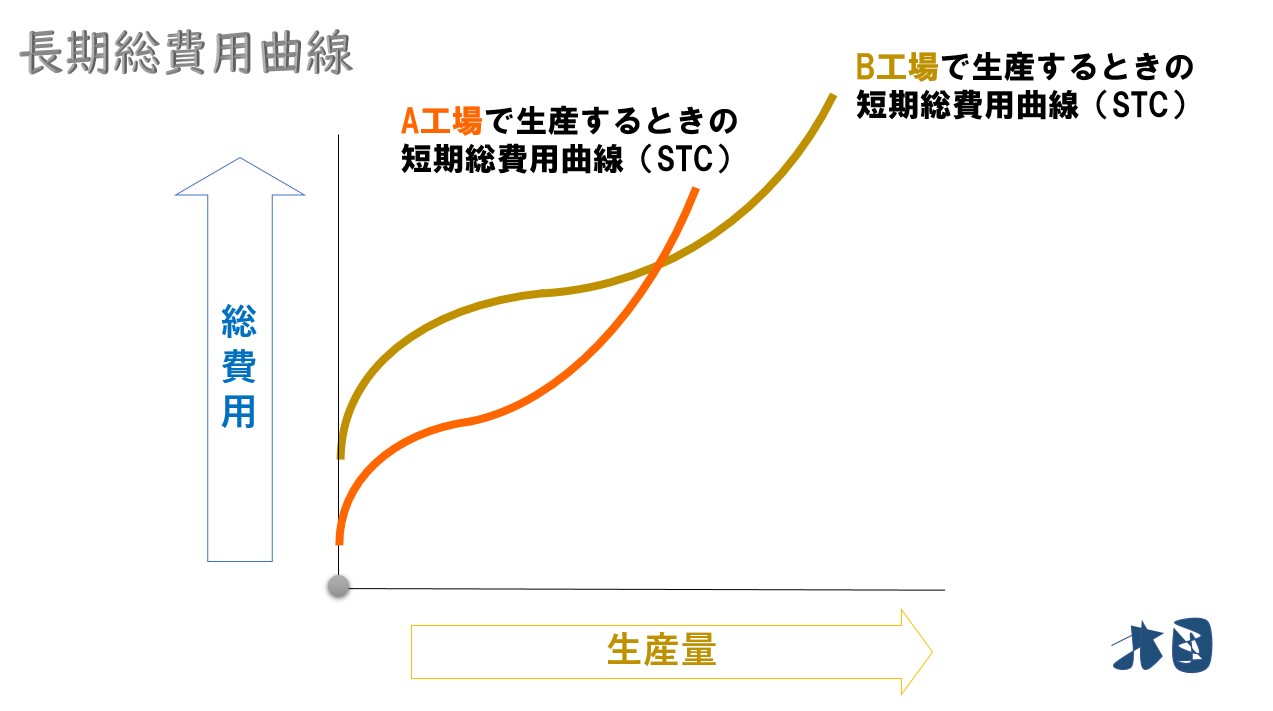
- 2つの工場のどちらかで生産を行う
- A工場は少量生産向け
- B工場は大量生産向け
ここで
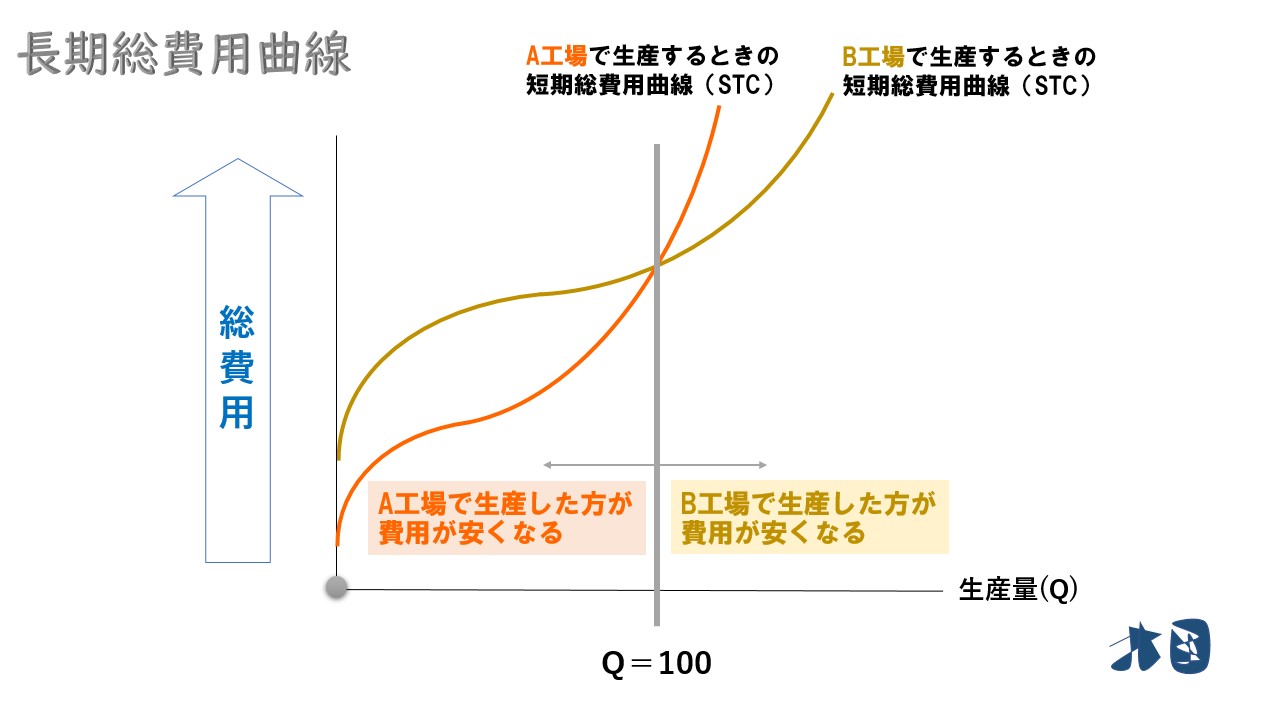
- 生産量が100までなら、A工場で製造したほうが費用が安くなります
- 生産量が101を超えるならB工場で製造したほうが費用が安くなります
このとき
企業は、長期的にA工場・B工場のどちらで製造を行うか意思決定を行います
長期的に生産量が100以下ならA工場を選択して、100を超える生産を行うならB工場を選択します。
つまり
ポイント
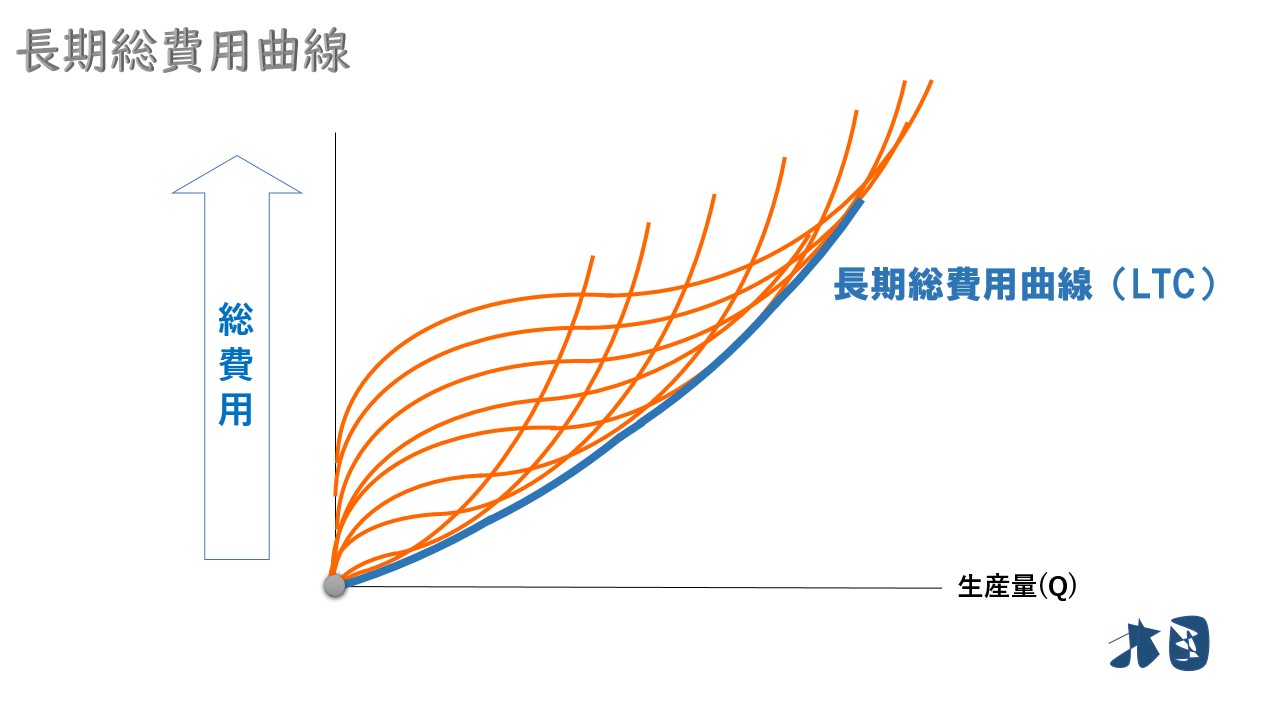
長期総費用曲線は、2つの短期費用曲線の接する曲線となる。


一般化する
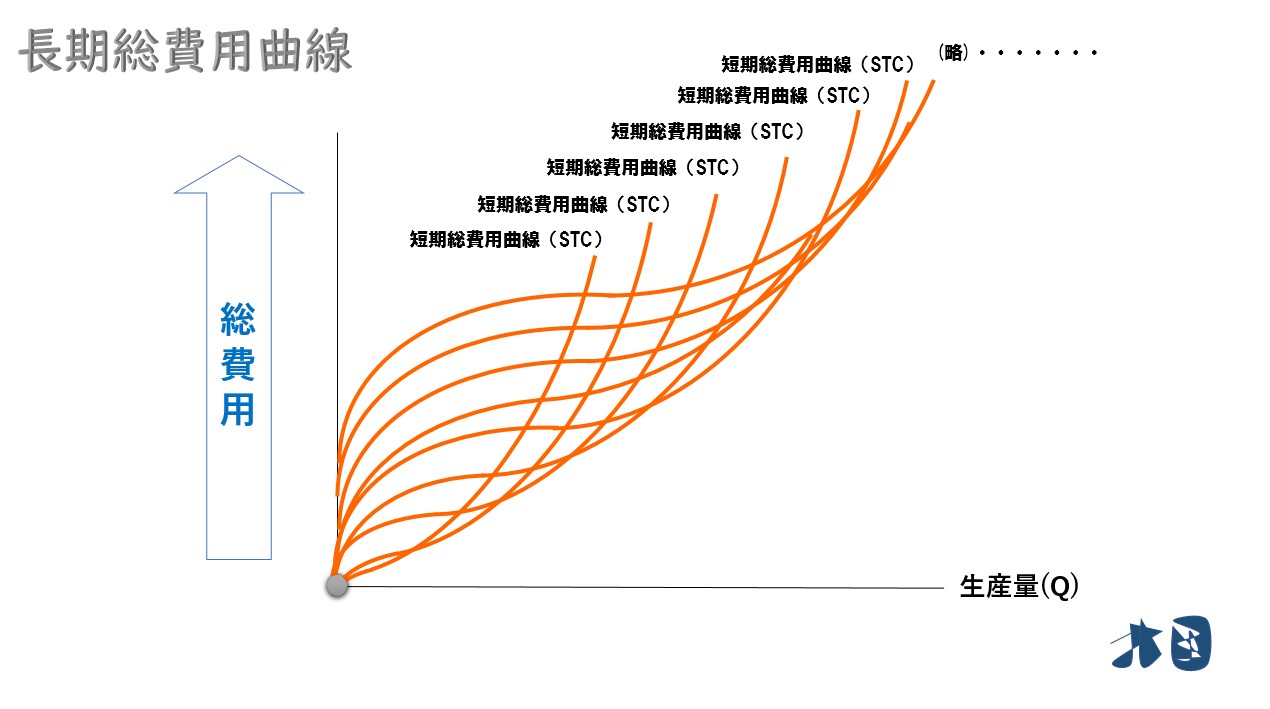
- 2つの工場(A工場・B工場)で考えましたが、世の中には無数に工場があります
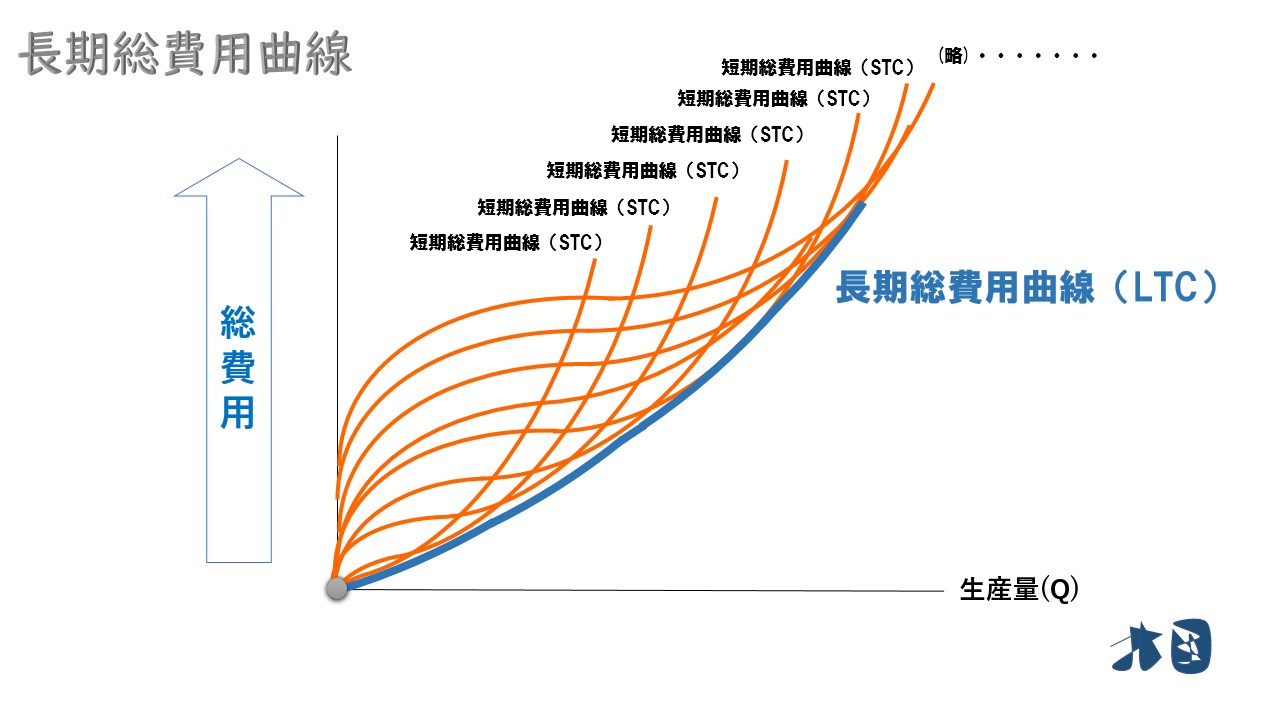
次に短期総費用曲線(SMC)と接する曲線を描く
これこそが長期総費用曲線(LTC)のグラフになります。また、グラフから分かる通り「長期総費用≦短期総費用」となります。
さらに詳しく
無数の短期総費用曲線に接する曲線となり「長期総費用曲線は、短期総費用曲線の包路線となる」と言われます。包路線は数学で登場する用語で、物理学にも応用される有名な考え方です。
※包路線=与えられた全ての曲線群に接する曲線のこと
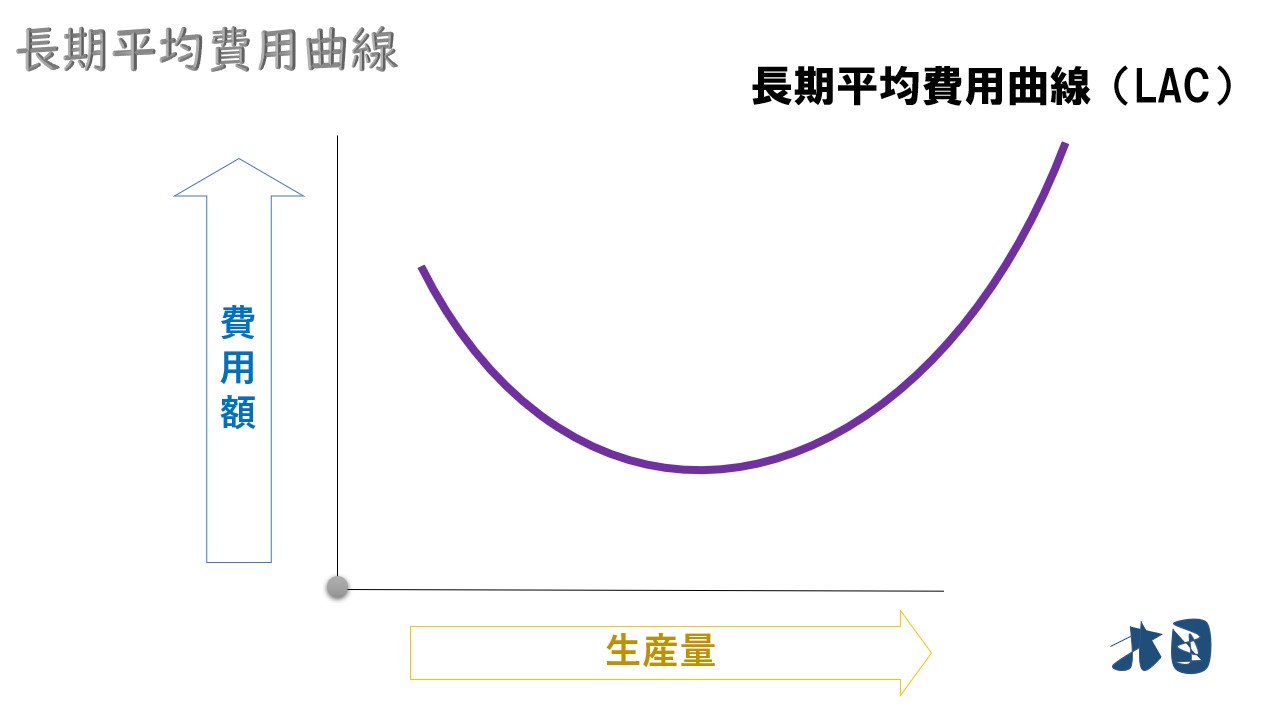
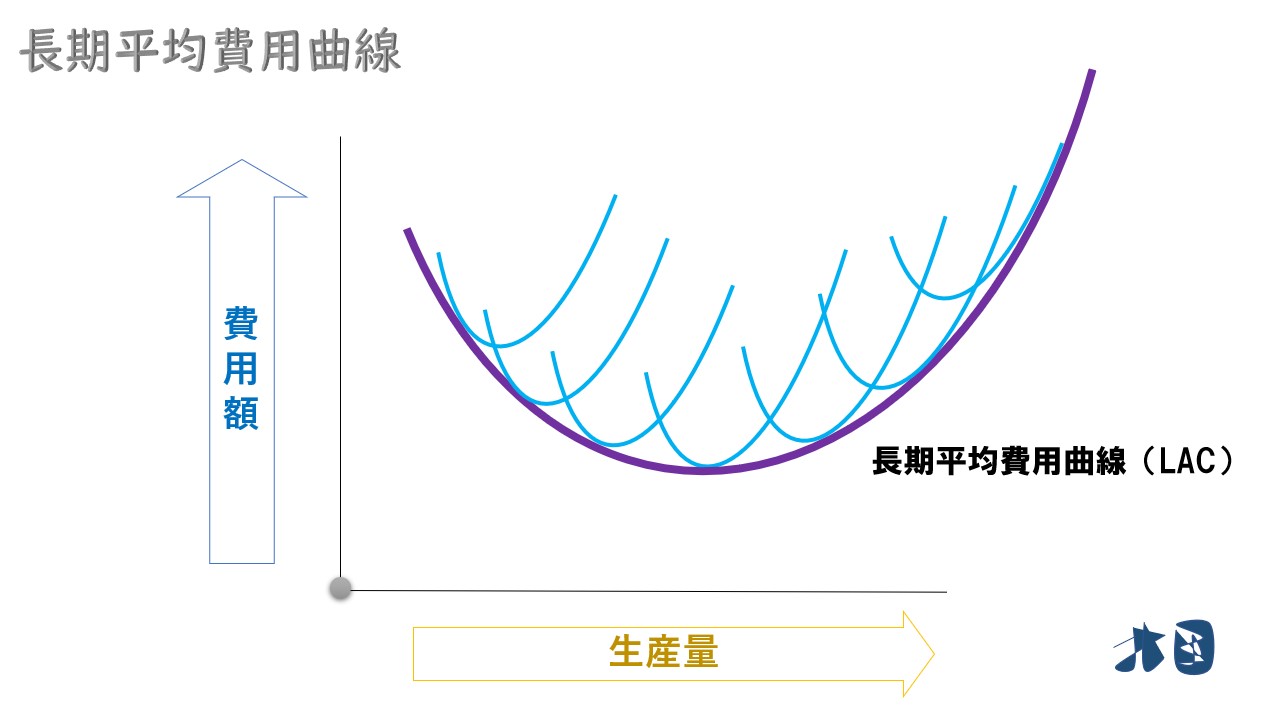
長期平均費用曲線(LAC)
長期平均費用曲線(LAC)
企業の長期的な平均費用曲線。通常の平均費用曲線(短期平均費用曲線)と異なり、固定費用も可変的なものとして扱うのが特徴の1つ。そのため短期の場合と異なり、平均費用・平均可変費用の区別はしない。
※長期では固定費用が存在しないため「長期平均費用=長期平均可変費用」となり「長期平均費用」という表現で統一されている。


ポイントは2つ
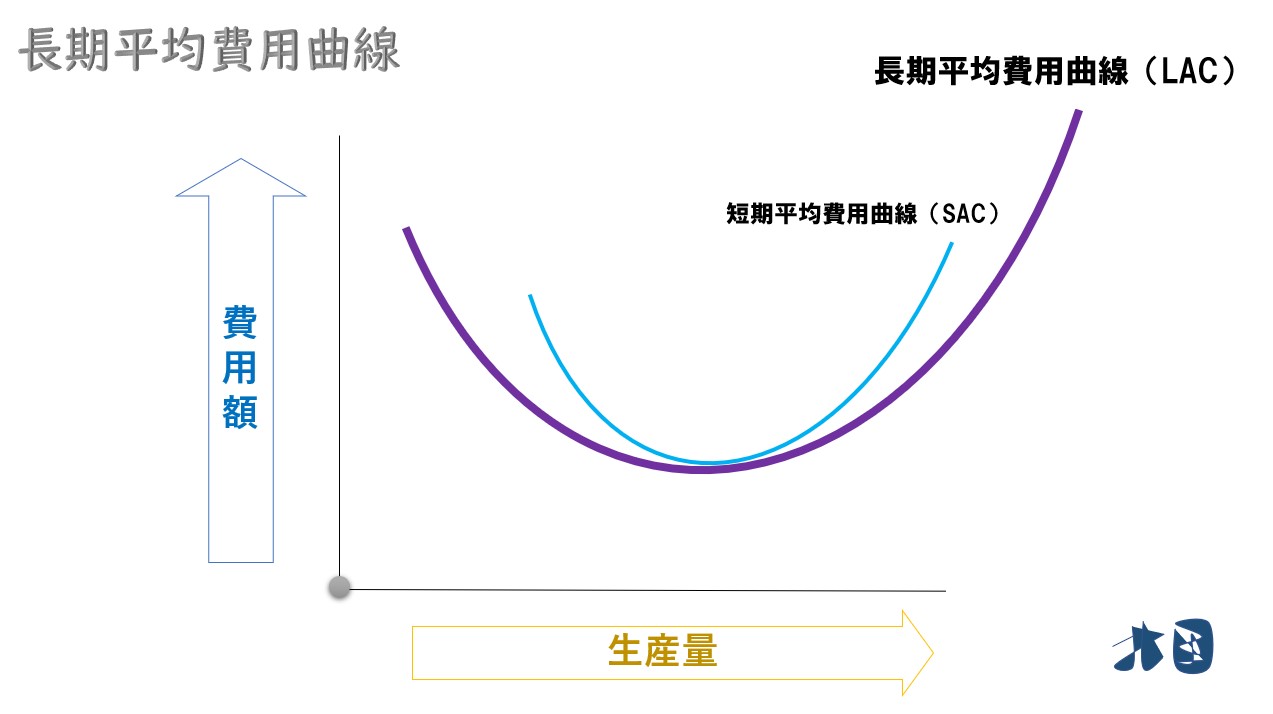
- 長期平均費用曲線は短期平均費用曲線よりも平らなU字になる
- 長期平均費用は短期平均費用より小さくなる(もしくは同じ)
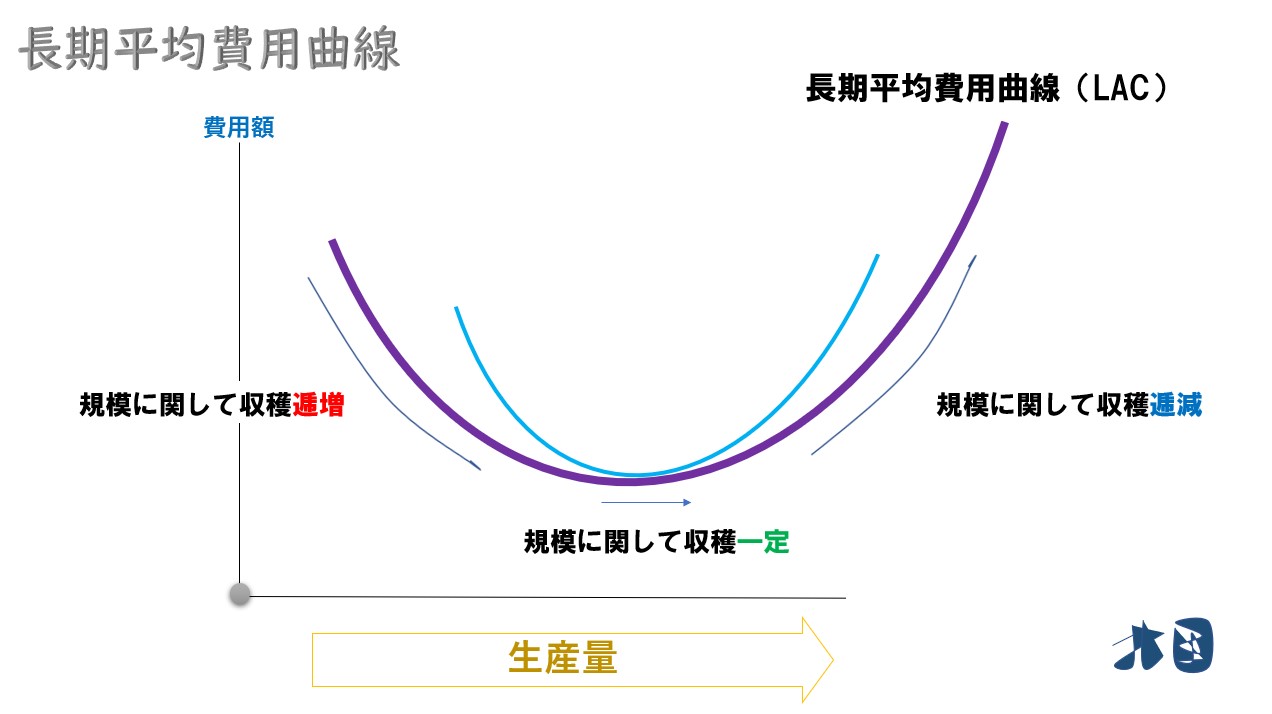
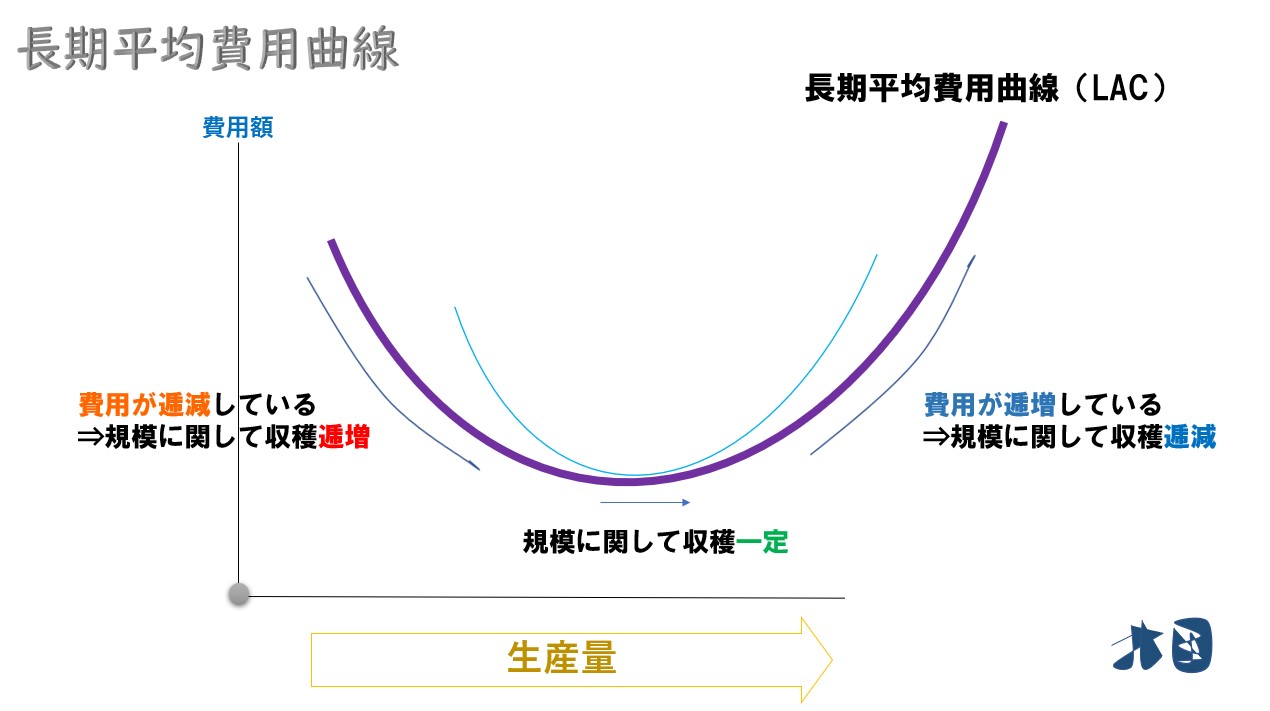
平らなU字・規模に関する収穫
ポイント
長期平均費用曲線は短期平均費用曲線よりも平らなU字になる。
おさらい
短期費用では、工場の地代などは固定費用(FC)として扱っていました。
しかし
長いスパンで考えると、企業は工場の所在地を変更できる。

企業は「生産に有利な場所(地代が安い等)」に工場を移転していきます。つまり、長期的には工場の地代は固定費用(FC)ではなく、可変費用(VC)として考えることが出来ます。
そのため
長期的には固定費用もすべて調整できるため、最も効率的な生産が実現される。そのため、固定費用を調整できない短期費用よりも、長期費用のほうが低費用を実現できる。
ポイント
以上より、長期平均費用(LAC)は、全ての短期平均費用曲線よりも下方に位置する。


おまけで
規模に関する収穫
長期平均費用のグラフから「規模に関して収穫逓減・一定・逓増」なのかを判断できます。
まとめ
- 長期平均費用曲線(LAC)は短期平均費用曲線(SAC)よりも平らなU字になる。
- U字のグラフから「規模に関して収穫逓減・一定・逓増」を判断できる。
包路線(長期平均≦短期平均)
ポイント
企業は長期的には固定費用の最適化も実現できるため、短期平均費用より長期平均費用の方が小さくなると考える。「長期平均費用≦短期平均費用」
再確認
- 考え方は長期総費用(LTC)と同じ!
総費用で「長期総費用≦短期総費用」となるので、平均費用も同様に「長期平均費用≦短期平均費用」となります。
基本的に総費用曲線のときと同じ考え方ですが、注意点が2つあります。
注意ポイント
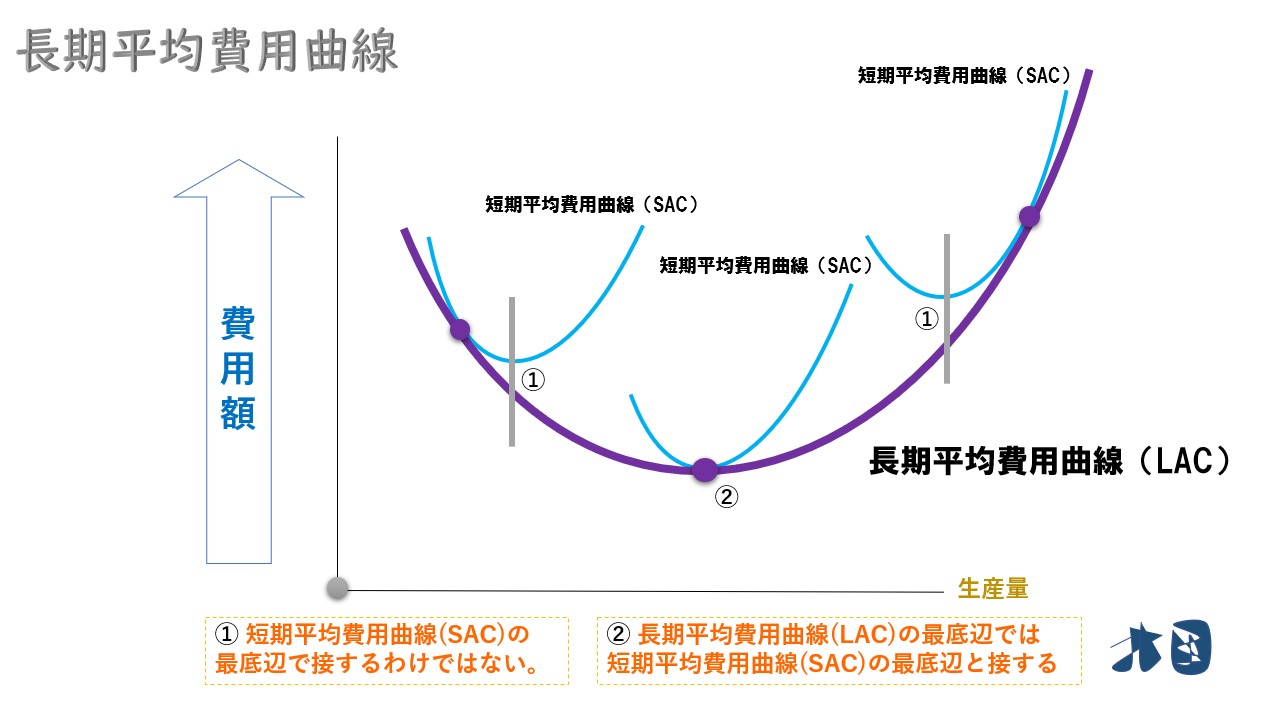
- 全ての短期平均費用曲線の最底辺を通っているわけではない
- 長期平均費用の最底辺は、短期平均費用曲線の最底辺の接線
グラフで確認する


まとめとして、長期平均費用曲線が描かれるまでの話を一般化します。
一般化する
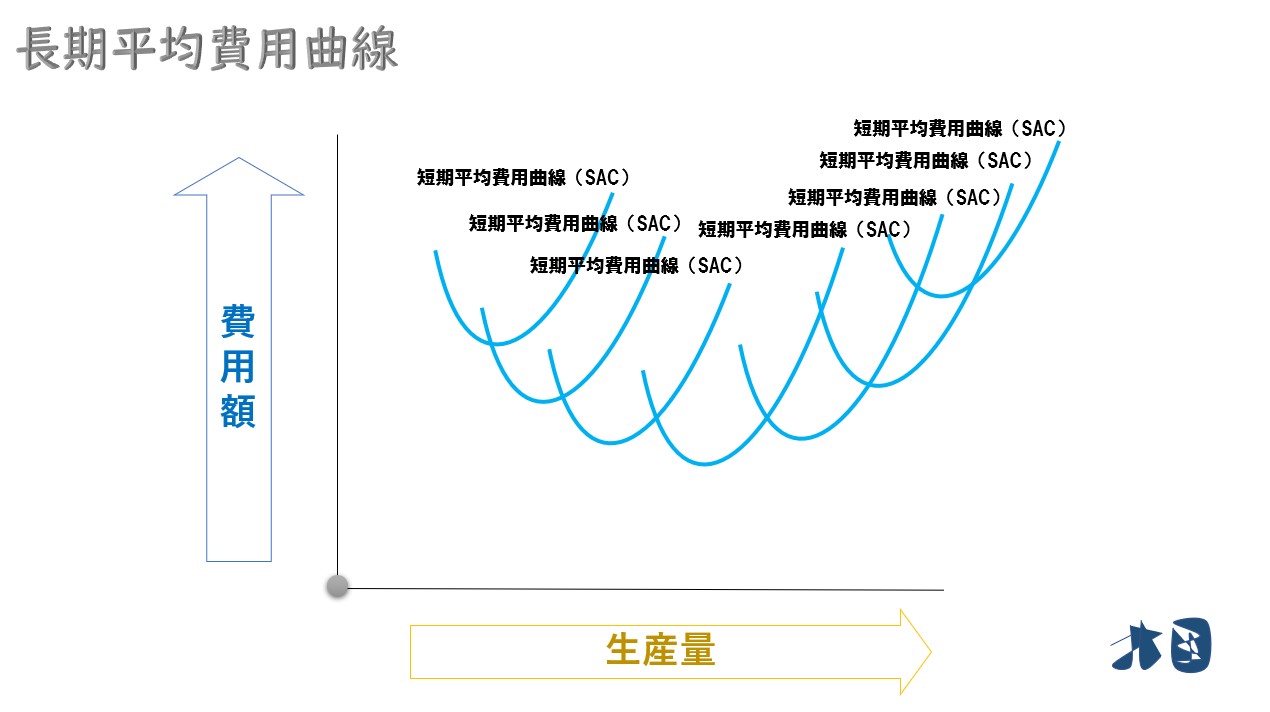
短期の総費用曲線は無数に存在します。
この短期総費用曲線に対応した短期の平均費用曲線も存在します。
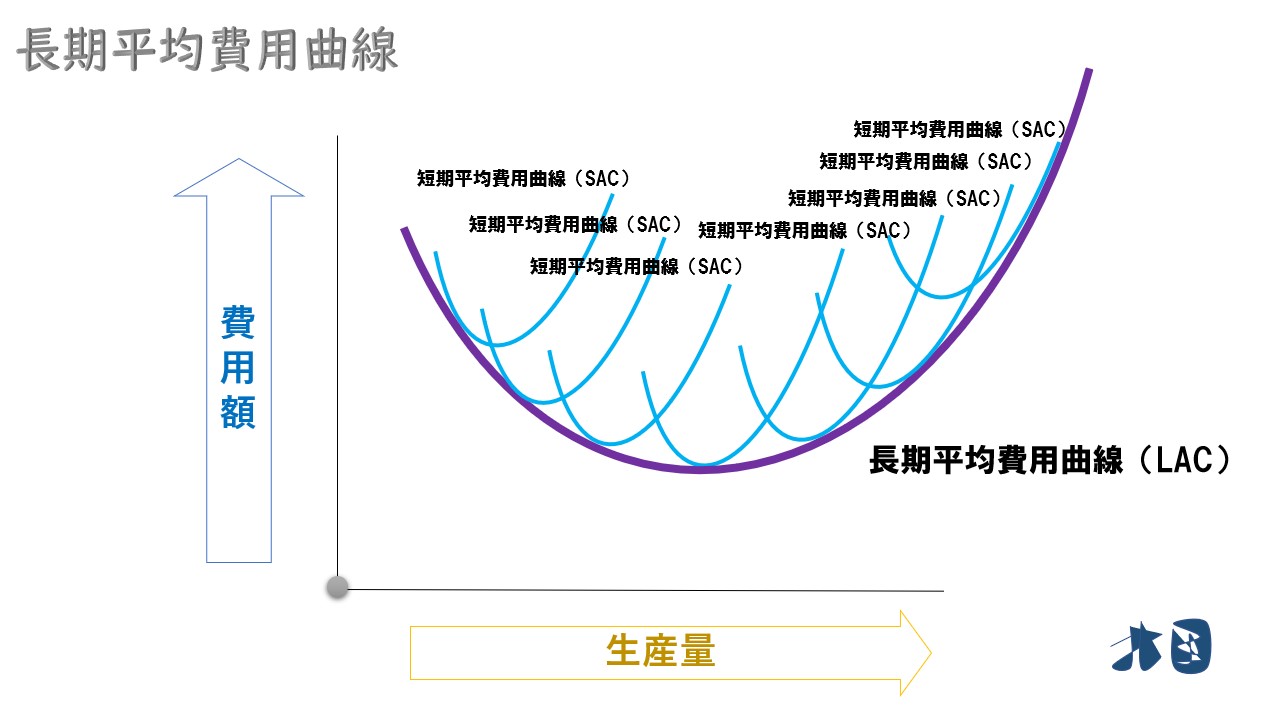
この無数の短期平均費用曲線に合わせて、長期平均費用曲線が描かれます。
これが長期平均費用曲線(LAC)のグラフになります。また、グラフから分かる通り「長期平均費用≦短期平均費用」となります。
さらに詳しく
総費用曲線と同じく、無数の短期平均費用曲線に接する曲線となり「長期平均費用曲線は、短期平均費用曲線の包路線となる」と言われます。包路線は数学で登場する用語で、物理学にも応用される有名な考え方です。
※包路線=与えられた全ての曲線群に接する曲線のこと
長期限界費用曲線(LMC)
長期限界費用曲線(LMC)
企業の長期的な限界費用曲線。


ポイントは2つ
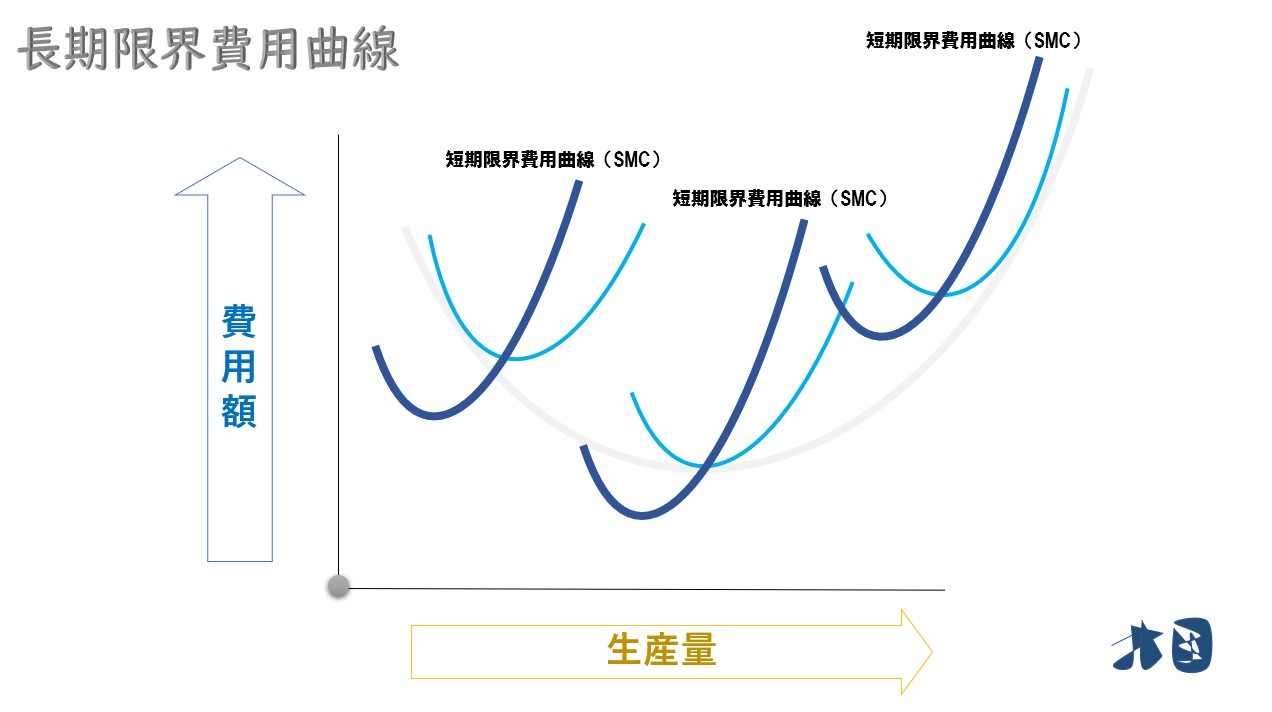
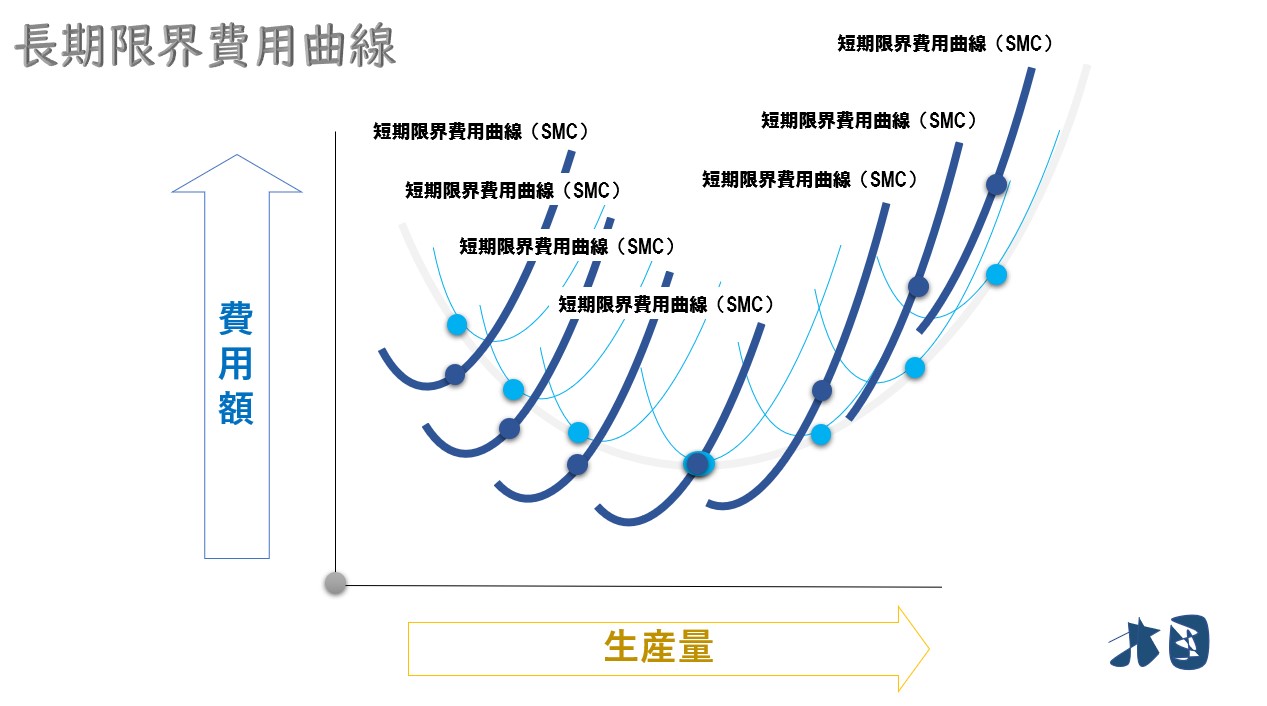
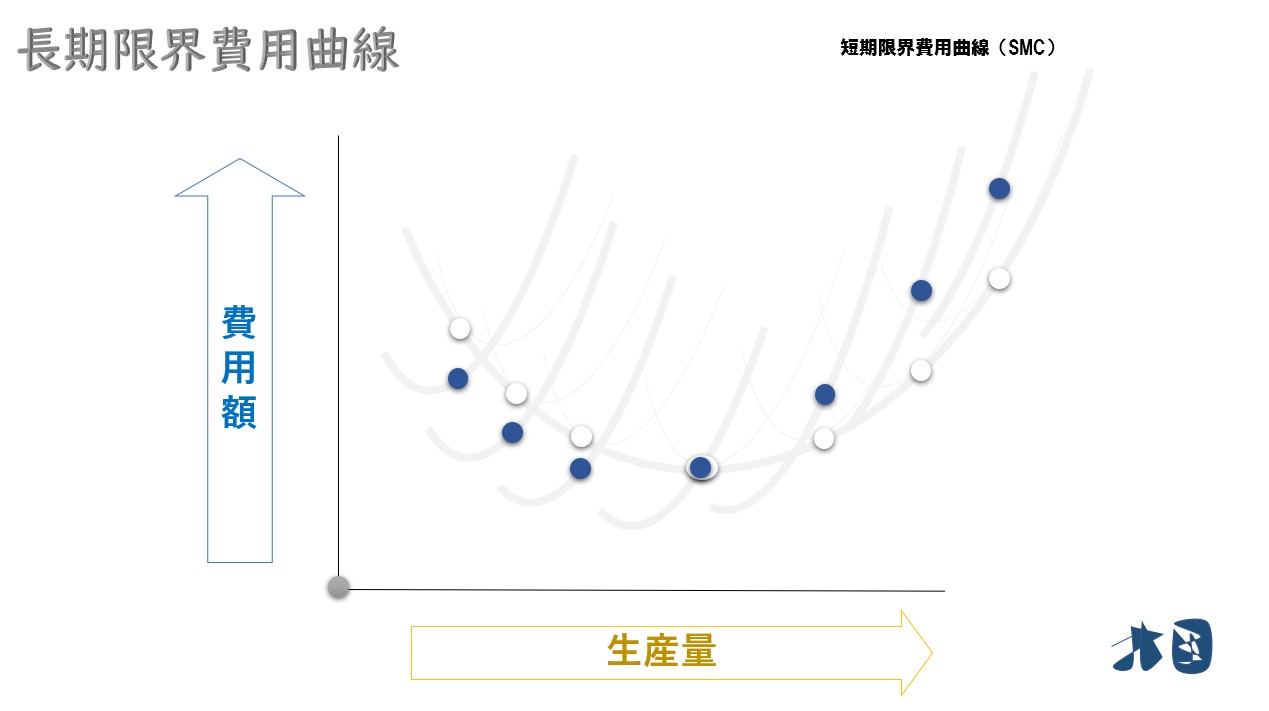
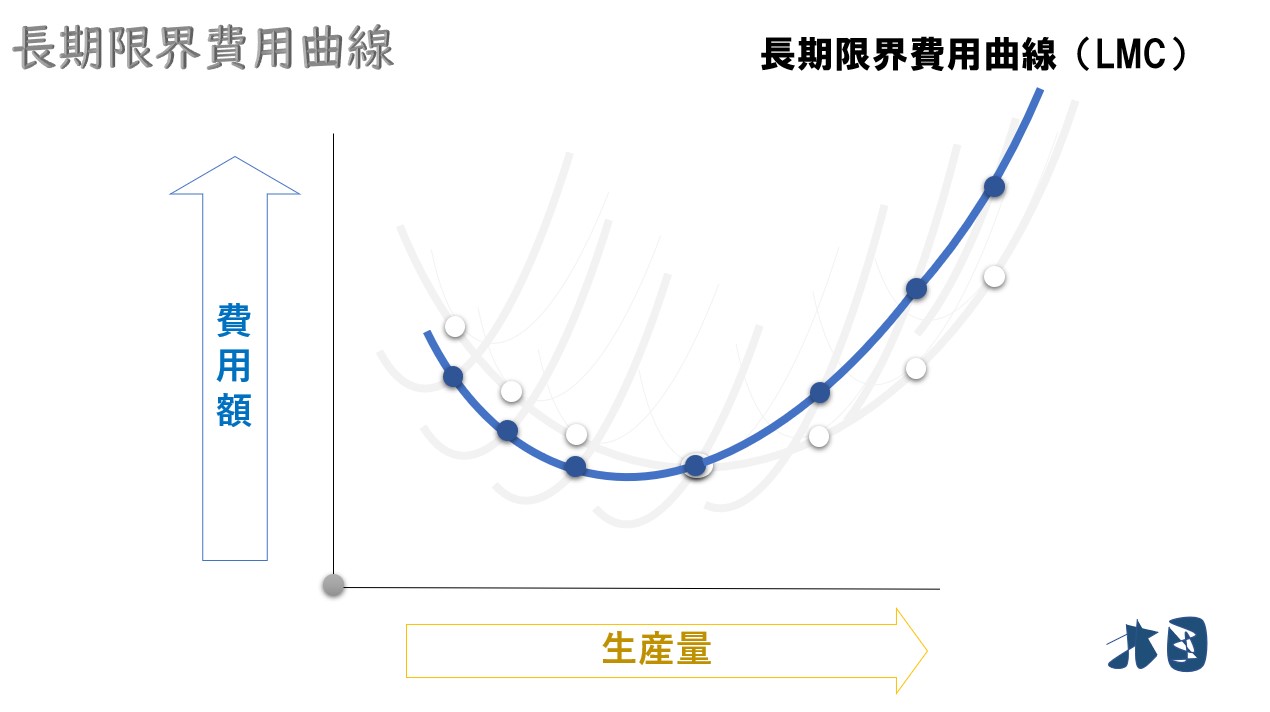
- 長期限界費用曲線は短期限界費用曲線の軌跡になる
- 長期限界費用曲線は長期平均費用曲線の最下点を通る
- 長期限界費用から長期供給曲線が得られる
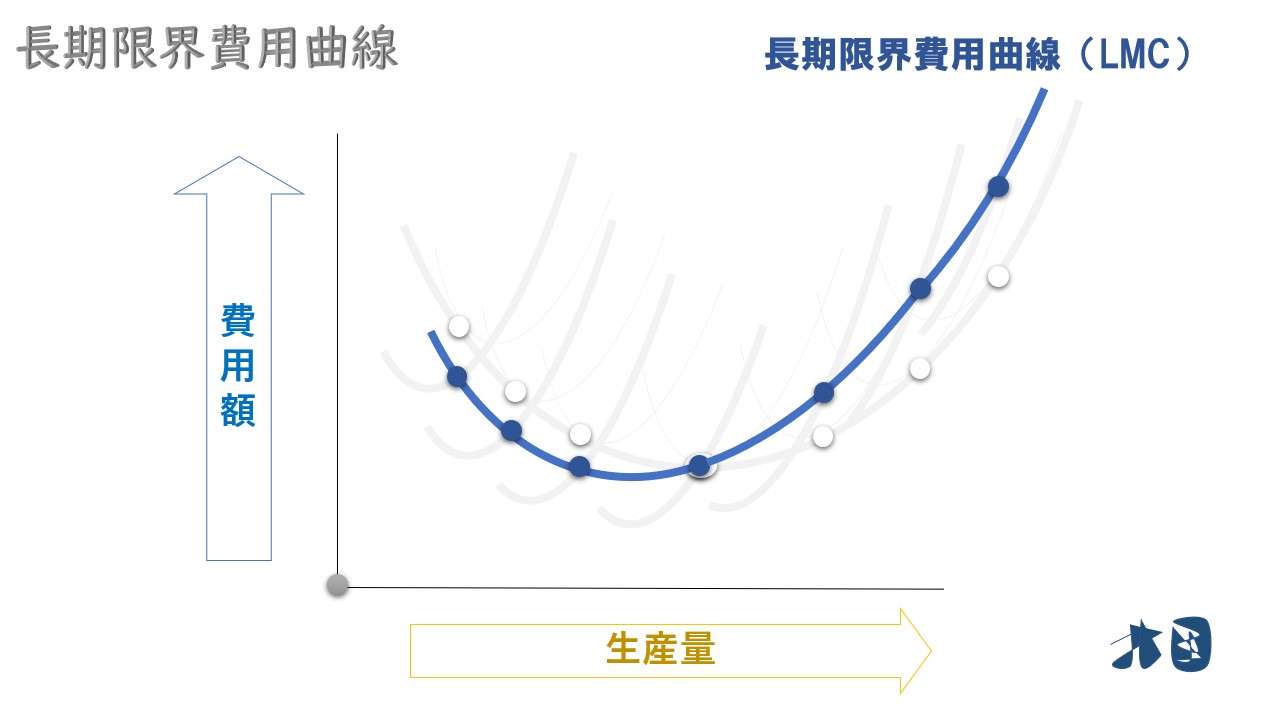
短期限界費用の軌跡・長期総費用の接線
ポイント
長期限界費用曲線は、短期限界費用の点を結ぶ(=軌跡)と求められる。
まずは
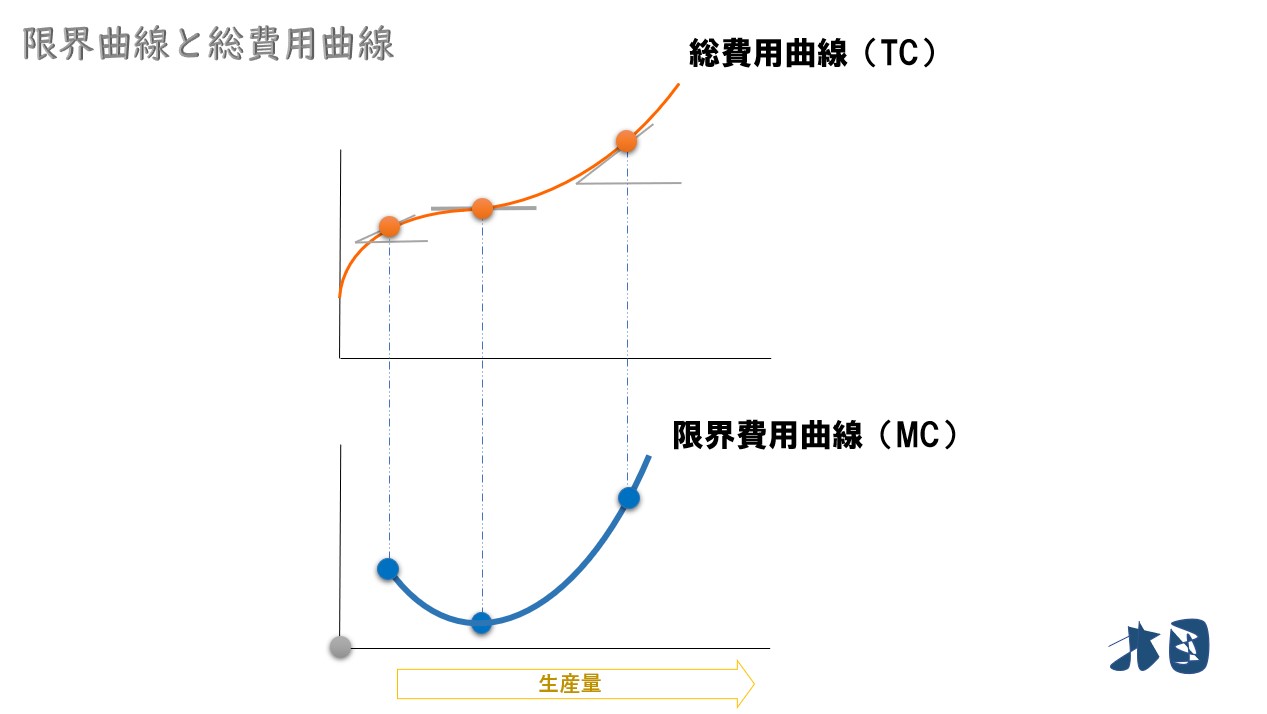
- 短期限界費用を思い出す
①総費用曲線の接線の傾き
②短期平均費用の最下点を通る


こちらで確認する⇒【費用曲線の要点を分かりやすく】総費用・固定・可変・平均可変・限界
次に
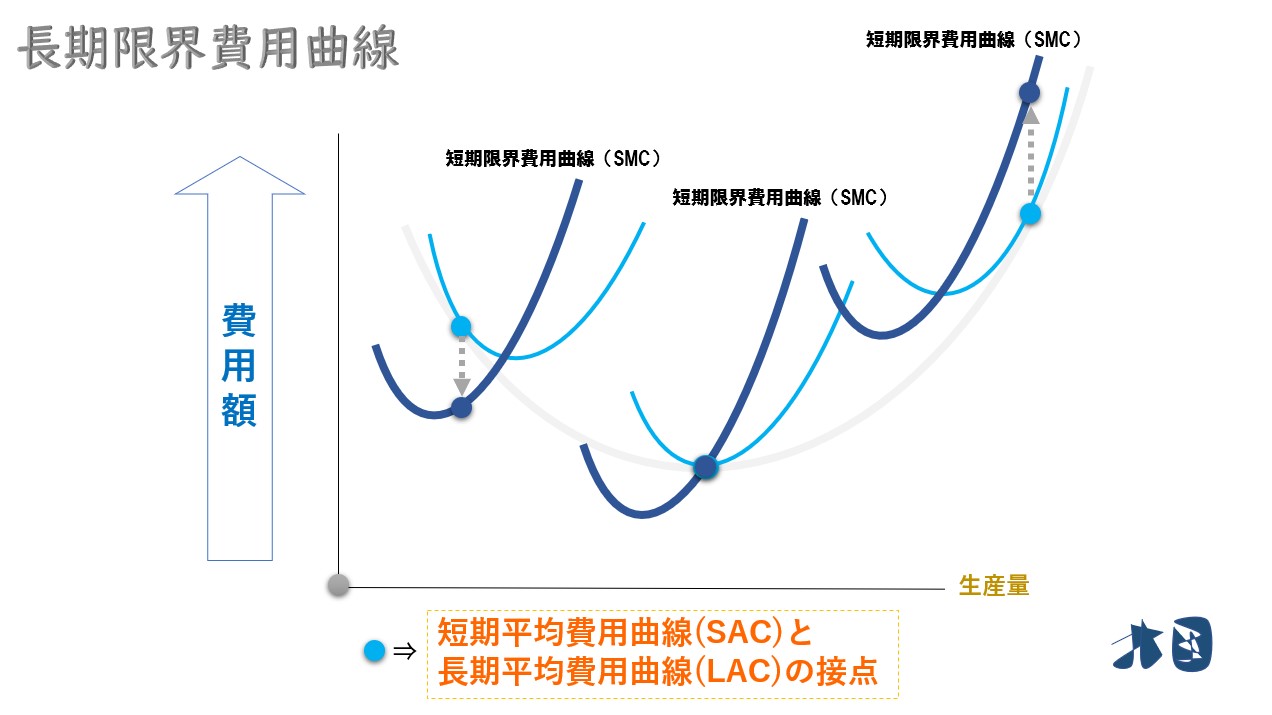
①短期平均費用曲線の最下点を通る短期限界費用曲線に注目する
②短期平均費用曲線(SAC)と長期平均費用曲線(LAC)の接点(=生産量)と対応する、短期限界費用曲線(SMC)の点に注目する
③ ②の短期限界費用曲線(SMC)の点を結ぶ
これが長期限界費用曲線(LMC)のグラフになります。
知っておく
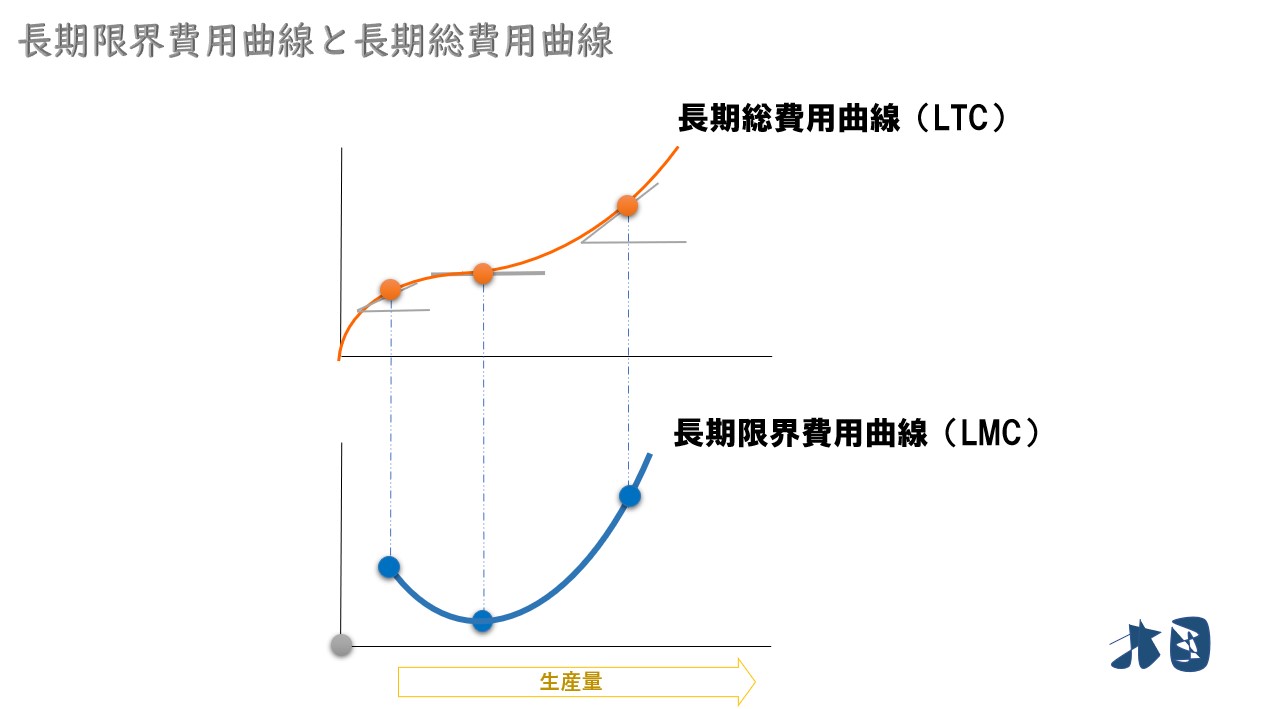
短期費用の場合と同じく、長期総費用曲線(LTC)の接線の傾きを求めることで長期限界費用曲線(LMC)を求めることも可能です。
「総費用曲線の接線の傾き=限界費用曲線」が分からない人は確認する⇒【費用曲線の要点を分かりやすく】総費用・固定・可変・平均可変・限界
逆S字型の長期総費用曲線の場合
右上がりの長期総費用曲線の場合
長期総費用曲線の形状によって、長期限界費用曲線はU字型・右上がり型のどちらの形状もあり得ます。教科書ではU字で描かれていることが多いです。
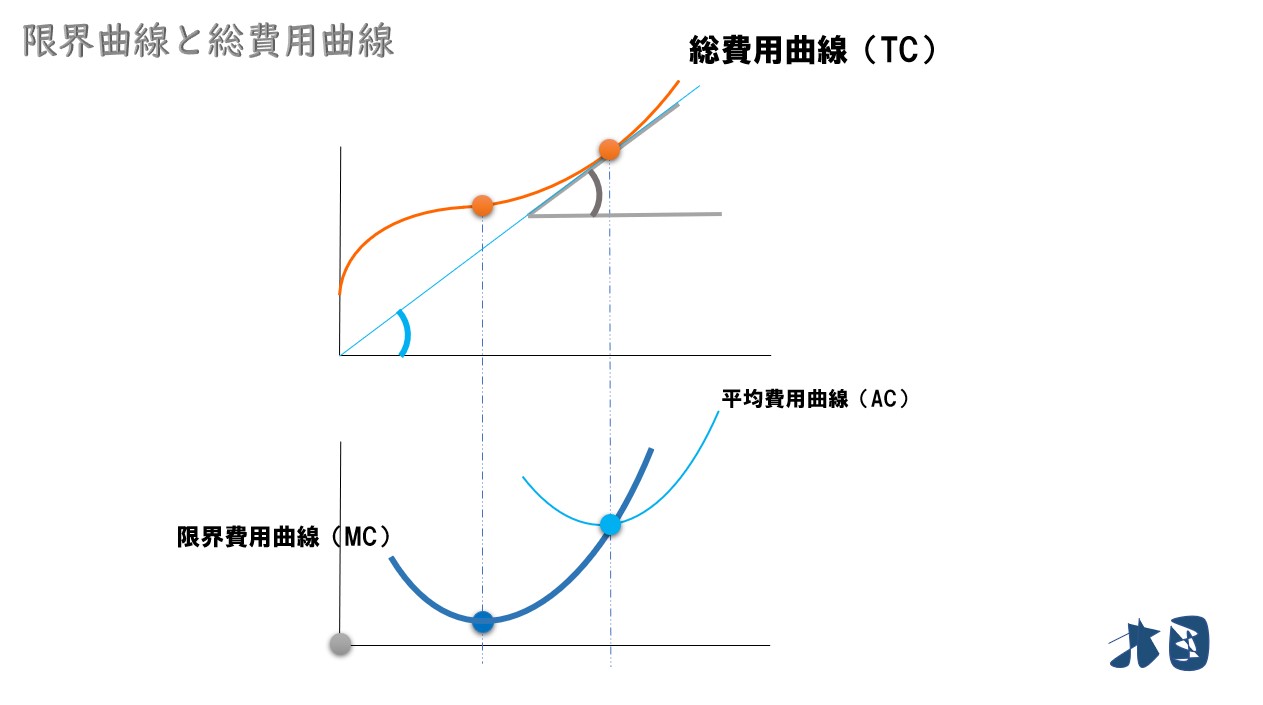
長期平均費用曲線の最下点を通る
ポイント
長期限界費用曲線は、長期平均費用曲線の最下点を通る(短期平均曲線・短期限界費用曲線の関係と同じ)。
長期限界費用曲線(LMC)が長期平均費用曲線(LAC)の最下点を通る理由は、短期費用と同じ理屈になります。
(短期)限界費用曲線の部分を読んでください。⇒【費用曲線の要点を分かりやすく】総費用・固定・可変・平均可変・限界
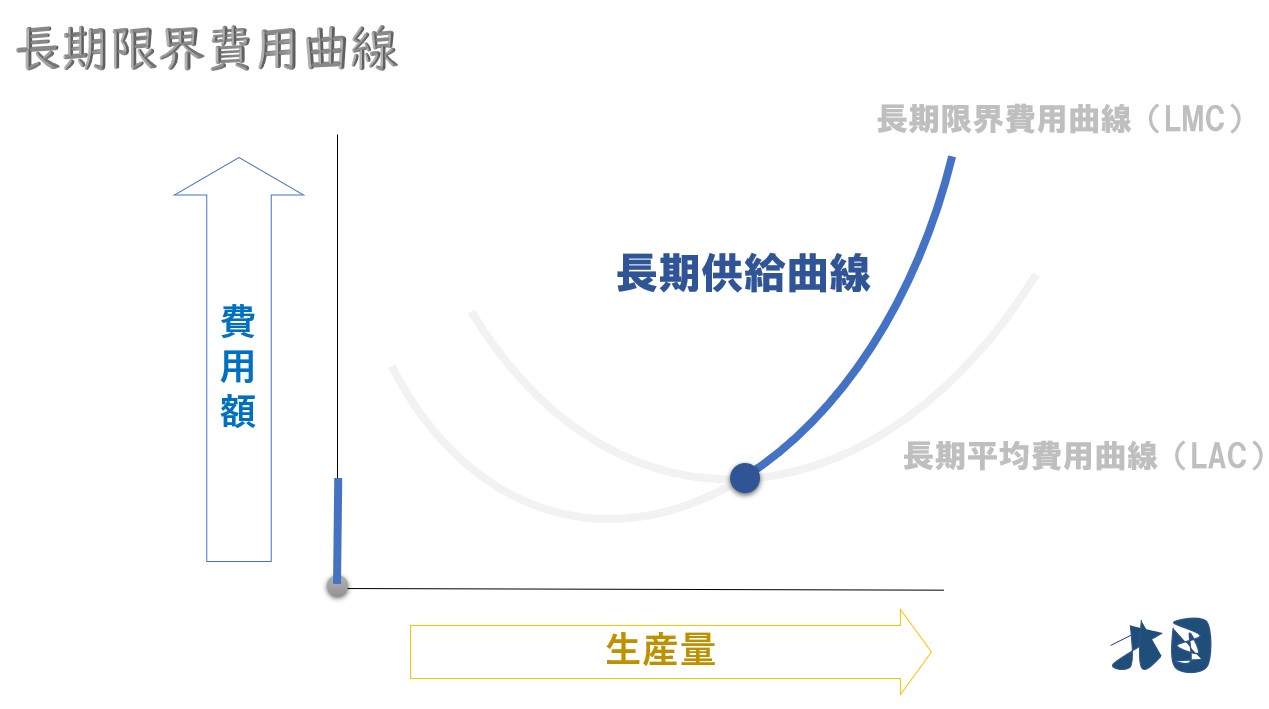
長期供給曲線
ポイント
長期限界費用曲線は、長期平均費用曲線の最下点より右上部分が長期供給曲線となる(短期平均曲線・短期限界費用曲線の関係と同じ)。
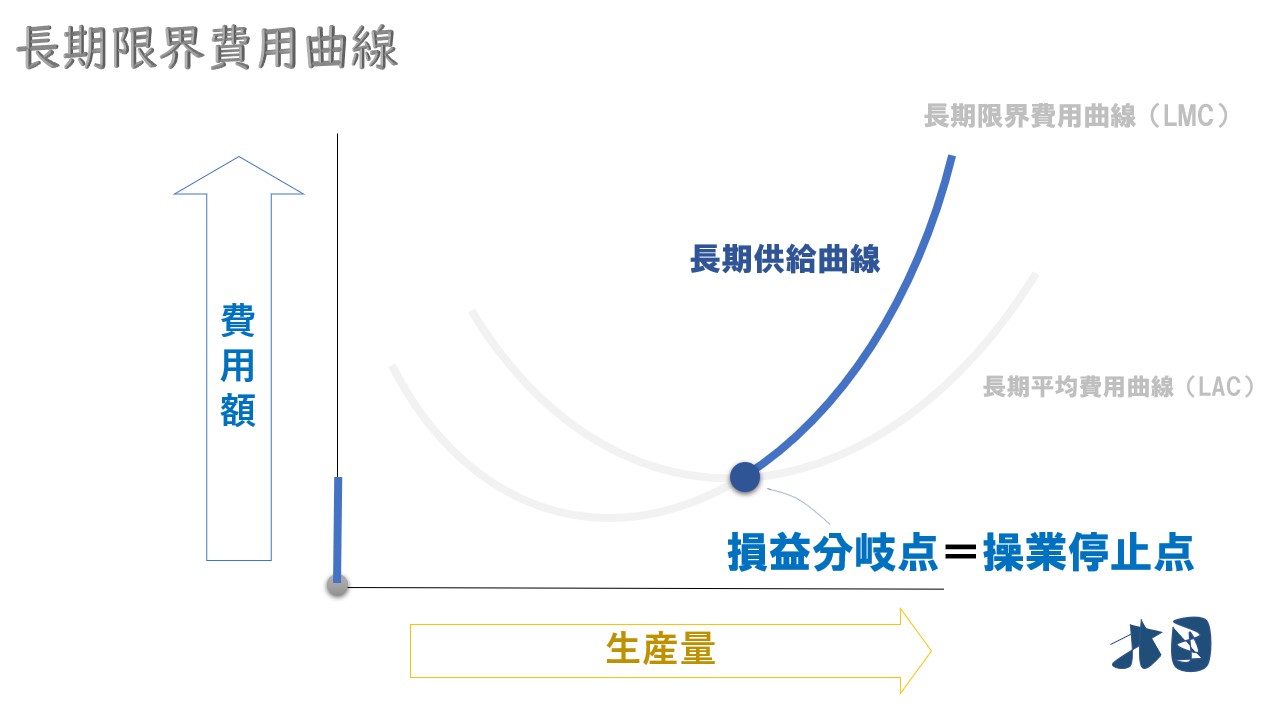
短期との違い
長期供給曲線の場合は、損益分岐点=操業停止点になります。
短期では平均費用曲線・平均可変費用曲線が分かれているため、損益分岐点・操業停止点が分かれます(確認する)。しかし、長期では固定費用を考えないため平均費用曲線=平均可変費用曲線なので、損益分岐点・操業停止点が一致します。