通常の需要曲線から所得効果を除いた「補償需要曲線」
- ヒックスの補償需要曲線とは?
- 補償需要曲線の形
- 補償需要関数の求め方・計算方法
通常の需要曲線との違いがよく分からない人に向けて、分かりやすく簡単にまとめています。
ヒックスの補償需要曲線とは?

(Wikipediaより・ジョン・ヒックス)
ヒックスの補償需要曲線とは?
効用の値が一定だと仮定して描かれる需要曲線のこと。縦軸に価格(P)・横軸に財の消費量を取って、代替効果のみを抽出した曲線になる。
通常の需要曲線は、所得が一定という仮定で描かれている。一方で補償需要曲線は、所得の制限がなく「所得が補償されている」と想定しているのが特徴。
ヒックスは、マクロ経済学で有名な「IS-LM理論」を数学的に定式化した人物で、消費者理論を別の視点で捉え直し、社会の望ましい在り方を考察した(補償原理やヒックス基準)。その過程で補償需要関数などが登場する。ちなみにスルツキー分解を行って代替効果・所得効果を提唱したのもヒックスです。一連の業績でノーベル経済学賞を受賞。
ヒックスは望ましい社会変化は何か?という疑問を経済学で解くために補償という考えを持ち出しました。補償需要曲線はその過程の産物です。本来なら、等価変分・補償変分を使った分析が続きます。
過程の補償需要曲線だけが登場するので「だから何?」という感じで終わってしまいますが、続きの分析が難しいレベルなので触れられないことが多いだけです。


はじめに
「通常の需要曲線」と「補償需要曲線」がどの情報を使っているかを確認しましょう。
- ①効用の大きさ(U)
- ②所得(M)
- ③価格(P)
- ④X財の消費量(X)
- 通常の需要曲線=②は一定で③④を抽出してグラフを描く
- ヒックスの需要曲線=①は一定で③④を抽出してグラフを描く


次に
イメージを掴みやすくするために「通常の需要曲線」と「ヒックスの需要曲線」のグラフの形状を確認します。
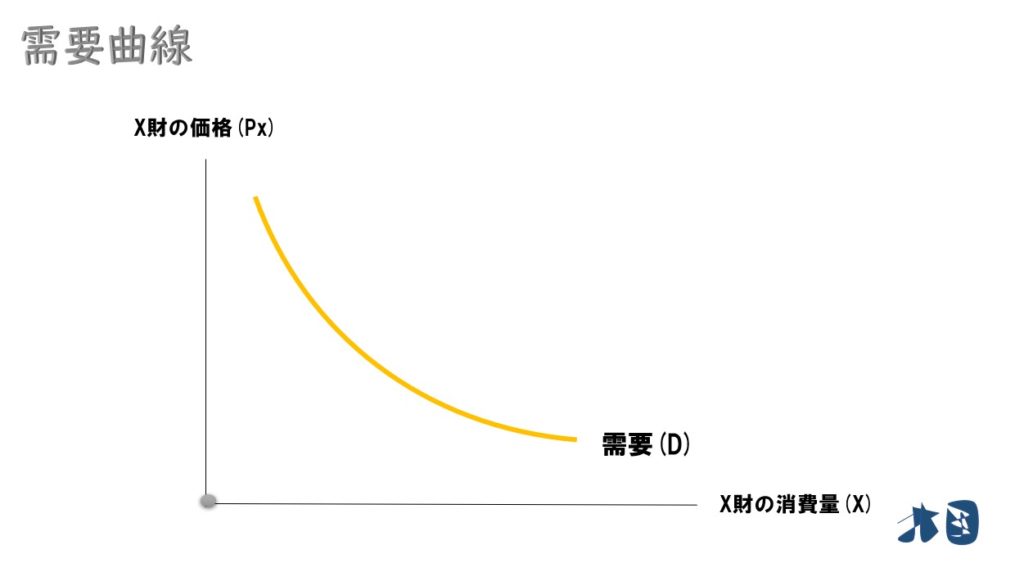
通常の需要曲線
最初に書いた通り、通常の需要曲線は所得が変化しないと仮定して「縦軸に価格(P)」「横軸に財の消費量(X)」を取ってグラフを描いています。
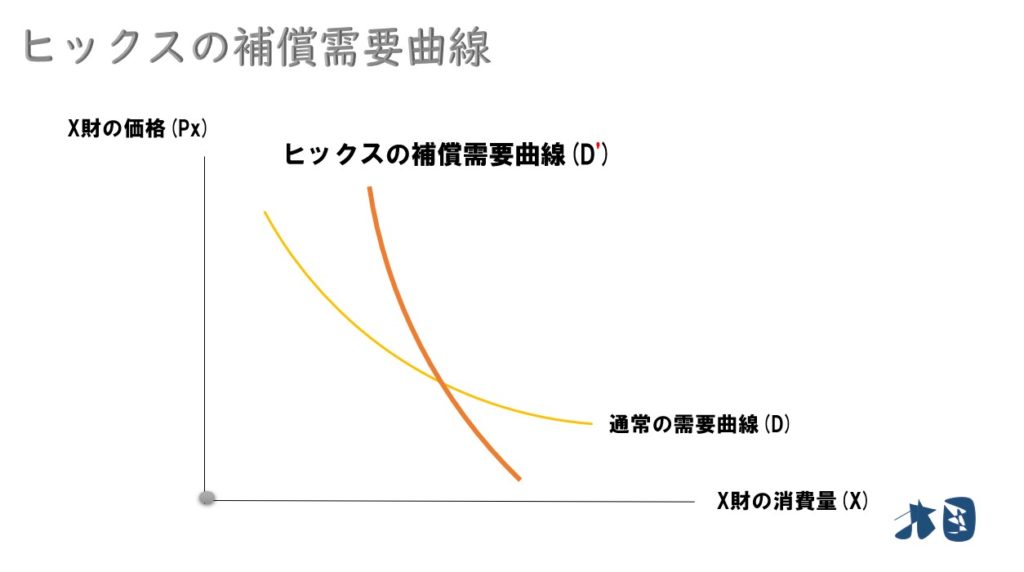
一方で
ヒックスの補償需要曲線は、所得効果を考慮していないため傾きが急になる。
上級財の場合で考えていきます。下級財の場合は補償需要曲線の方が緩やかになります。
ヒックスの補償需要曲線では、所得に制限はなく(いくらでも使える状態)を想定しているため、所得効果が打ち消されます。その影響で、通常の需要曲線よりも傾きが急になるのです。
所得効果は、全部効果(価格効果と所得効果)で登場する話です。詳しくはこちら⇒【代替効果・所得効果】グラフで視覚的に理解する
例えば
- X財の価格が上がったとします。
① 他の財の方が相対的に安くなるのでX財を買う気持ちが小さくなり、X財の消費量は減少します(代替効果)。
② それに加えて、お財布事情も苦しくなります。これは実質的に所得(手持ちのお金)が減少したと言えるので、これもX財の消費量減少させる要因になります(所得効果)。
ポイント
X財の価格が上がったことで買うのを止めたりする理由は、①代替効果・②所得効果の2つの理由があるとミクロ経済学では考えています。
補償需要曲線は、①②のうち、②の所得効果を考慮しない需要曲線というわけです。
価格が上昇しても、②所得効果が働かない分、ヒックスの補償需要曲線の方がX財の消費量の減少幅が小さくなるため、グラフが急な傾きになっている。
更に
ヒックスの補償需要曲線は、代替効果だけに注目しているため、効用水準(U)が一定だと言えます。
ポイント
無差別曲線を使って代替効果を分析すると、代替効果は同じ無差別曲線上で表現できます。同じ無差別曲線上なので、効用水準(U)が変わっていない(一定である)ことが分かります。
詳しくはこちら
代替効果を測定する時に、同じ無差別曲線上で最適消費点を動かしていることに注目!


ちなみに
代替効果だけで考えると、財の種類(上級財・下級財・ギッフェン財)を問わずに必ず負の方向に働きます(X財の価格が上がる⇒X財の需要は下がる)。
そのため、代替効果だけを考慮しているヒックスの需要曲線は右下がりになります。
通常の需要曲線は、ギッフェン財のときだけ右上がりになりますが、ヒックスの需要曲線ではそれもありません。
補償需要関数の求め方

補償需要関数の求め方は簡単です。
「効用関数(U)」が与えられていれば、自分で価格(P)を設定して計算します。
普通の効用最大化や需要関数を求める問題では、所得(I)がいくらかが決まっています。しかし、補償需要曲線は、所得は補償されている(所得効果は除いている)という前提があったので、所得の情報は不要です。
考え方
補償需要曲線は、所得の影響は考えないという前提がある一方で「効用水準が一定」という前提もあります。⇒ 戻って確認する
例えば、効用水準(U)・財の価格を次のようにします。
- 効用水準(U)を100で固定する
- 財の価格は10円
この時、補償需要関数は「効用水準(U)=100を達成するためには、価格10円の財をいくつ消費する必要があるか?」を表す数式になることが分かります。
ここで
所得は考えないので、無限に価格10円の財を消費することが出来ますが、効用水準(U)=100を達成するだけ消費すれば十分です。
仮に価格10円の財を1つ消費すれば50の効用(U)が得られるなら、所得が無限にあろうが2個消費すれば十分です。
ポイント
3個も4個も消費出来る中で、2個消費すれば十分ということは「支出を最小にして目標を達成するには?」という問題に置き換えて考えることが出来ます。
なので、補償需要関数を求める時は、問題文にある効用関数(U)から、支出(費用)最小化問題として計算する事になります。


超ポイント
「支出を最小にして目標を達成するには?」という支出(費用)最小化問題は、最適消費点を求める効用最大化問題と同じ要領で解くことが出来ます。
これを双対性と言います。証明は長くなるので飛ばします。
計算方法
「効用水準(U)」は、ふつう数式が与えられているので、それを使います。価格はないことが多いので、自分でPx・Pyなどと置きます。
例えば
- 「U(x, y)=xy」のとき、補償需要関数を求める
はじめに・・
- X財の価格=Px
- Y財の価格=Py
- X財の消費量=x
- Y財の消費量=y
支出額(E)は「(X財の消費量×X財の価格)+(Y財の消費量×Y財の価格)」で決まるので「xPx + yPy」と置けます。
以上より「支出額(E)= xPx + yPy」です。
まとめると
効用関数「U(x, y)=xy」と支出額「E=xPx + yPy」を使って、支出(費用)最小化問題を解けばいいことが分かります。
難しく次のように表現することがあります。
- s.t.(Subject to) U(x, y)=xy
- min xPx + yPy
双対性があるので効用最大化問題として計算することが出来ます。
計算
ここでは1番オーソドックスな「予算制約線の傾き=限界代替率(MRS)」を使って計算します。
ここからは効用最大化問題の解き方を知っている前提で話を進めていきます。分からない人はこちらで確認!⇒【最適消費・効用最大化】求め方をグラフを使って分かりやすく
① 予算制約線の傾きを求める
E=xPx+yPyより
- E=xPx+yPy
- y=-(xPx/Py)+E
- y=-(Px/Py)x+E/Py
② 効用関数から限界代替率を求める
「U=xy」から「y=U/x」へ変形後に微分します。
- 「y=U/x」⇒「U/xの2乗(=U・xの-2乗)」
- 「U/xの2乗」に「U=xy」を代入
- 「U(=xy)/xの2乗」⇒「xy/xの2乗」=「y/x」
③ 予算制約線の傾き=限界代替率で効用最大化(最適消費点)を求める
「-(Px/Py)」=「-y/x」
- x=(Py/Px) y
- y=(Px/Py) x
補足
- X財についての補償需要関数なら「x=(Py/Px)y」
- Y財についての補償需要関数なら「y=(Px/Py)x」