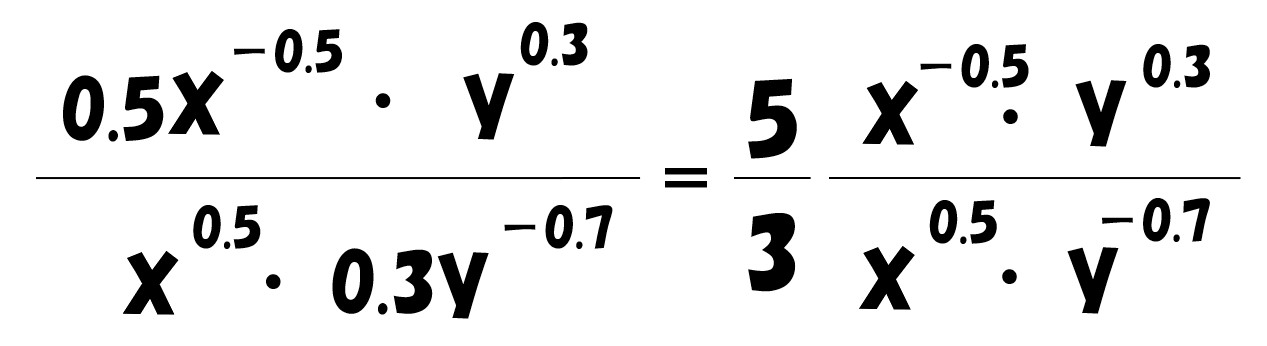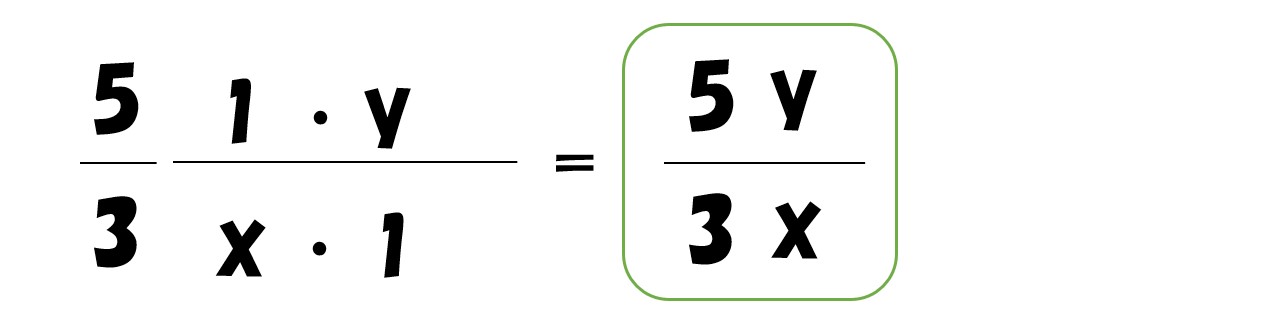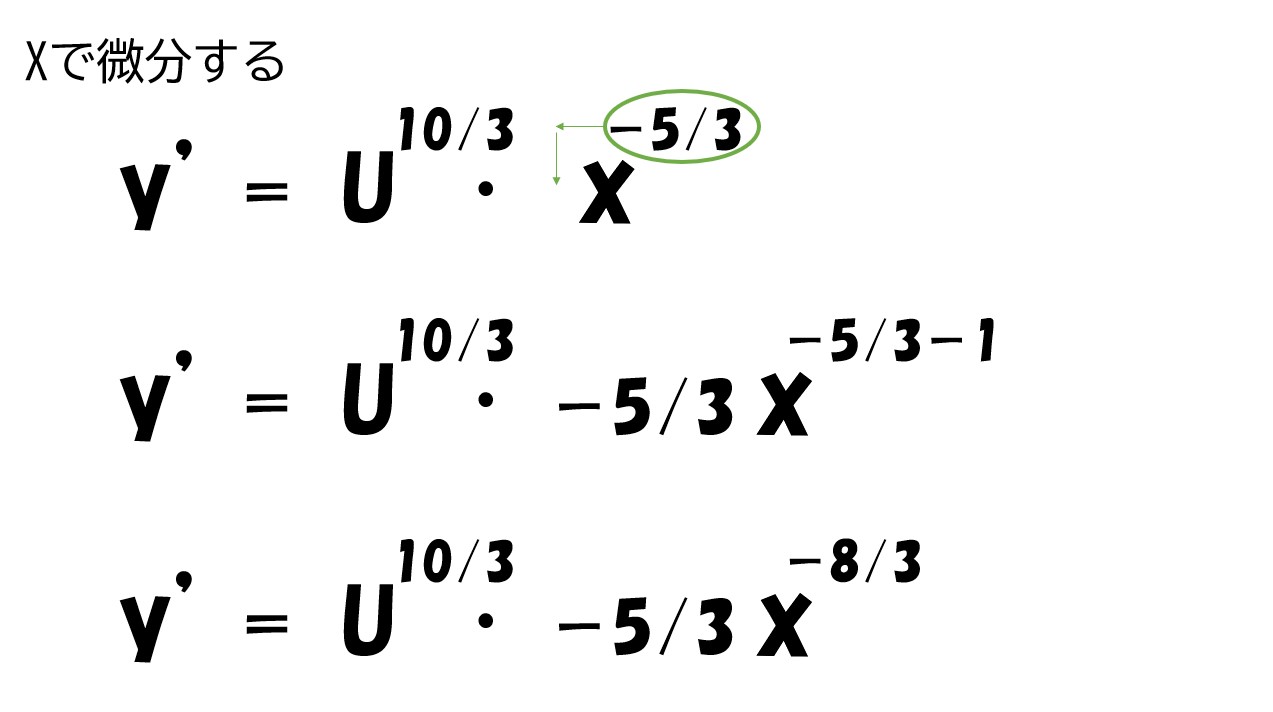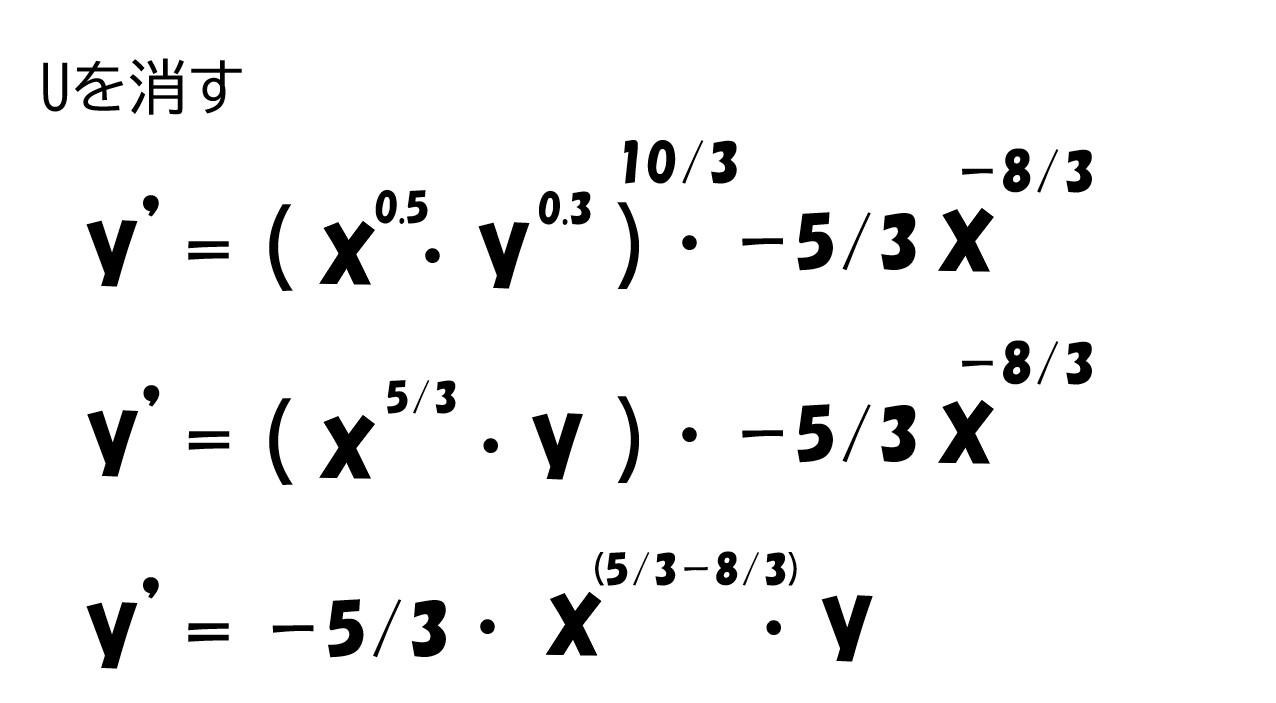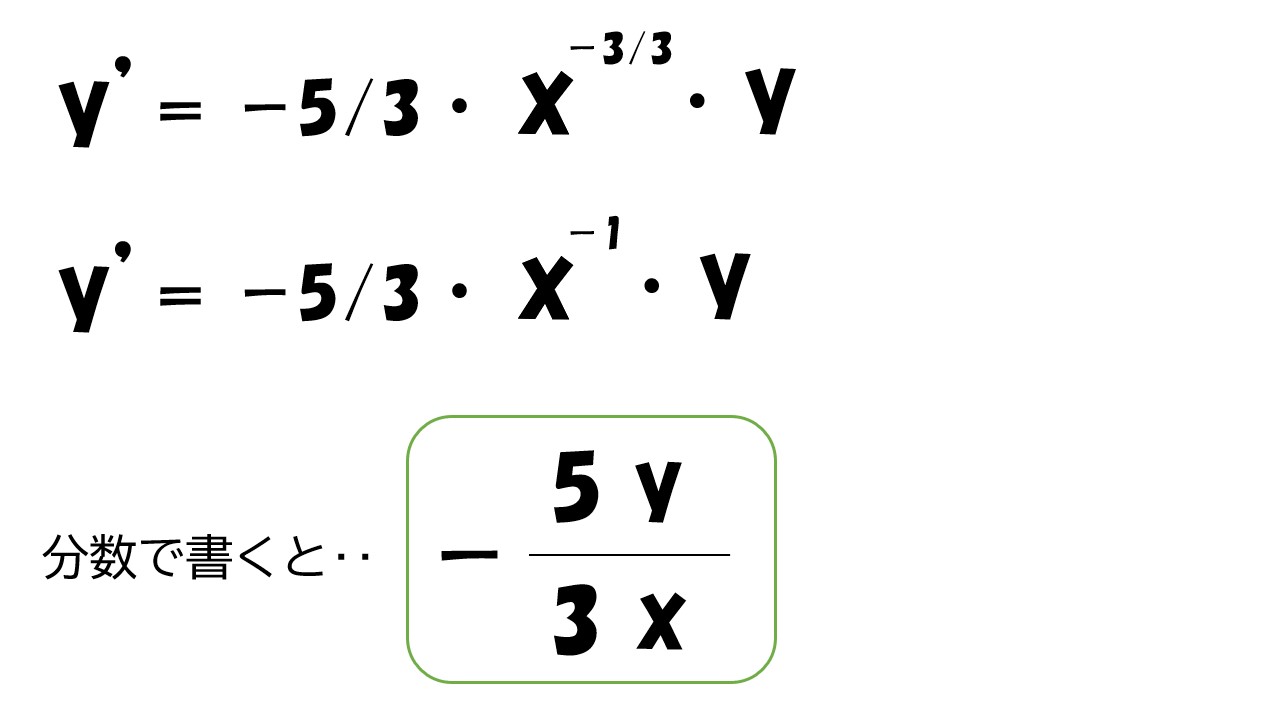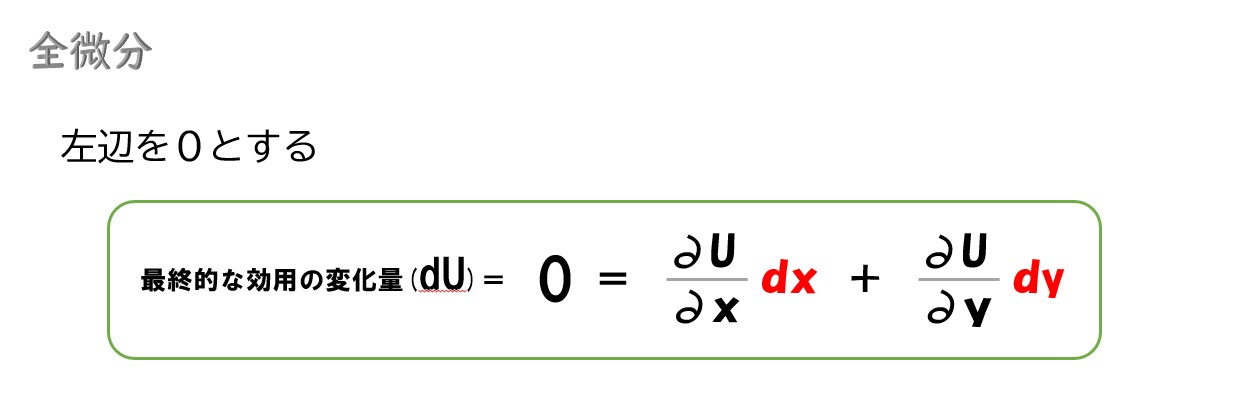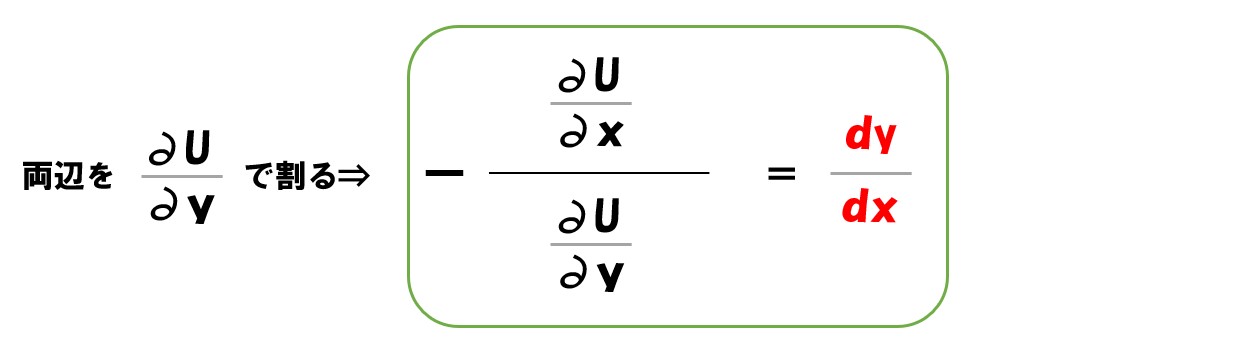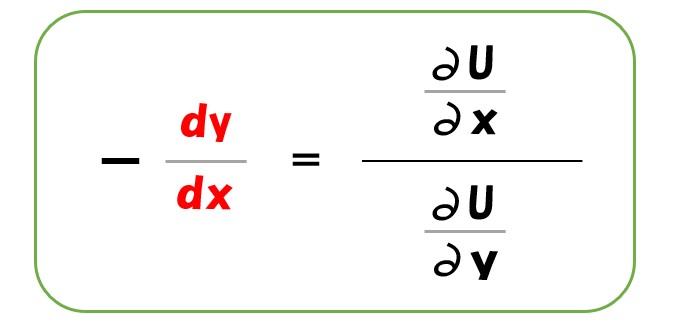無差別曲線の傾きや限界効用の比を求める「限界代替率」
限界代替率の意味が分からずに苦労する人も多いです。
- 限界代替率とは?
- 限界代替率逓減の法則とは?
- 計算の方法・求め方
- 限界代替率と無差別曲線の傾き
- 限界代替率と2財の限界効用の比
- 2財の限界効用の比率と全微分
限界代替率について、イマイチ理解できない人向けに簡単にまとめています。
限界代替率・限界代替率逓減の法則とは?
限界代替率とは
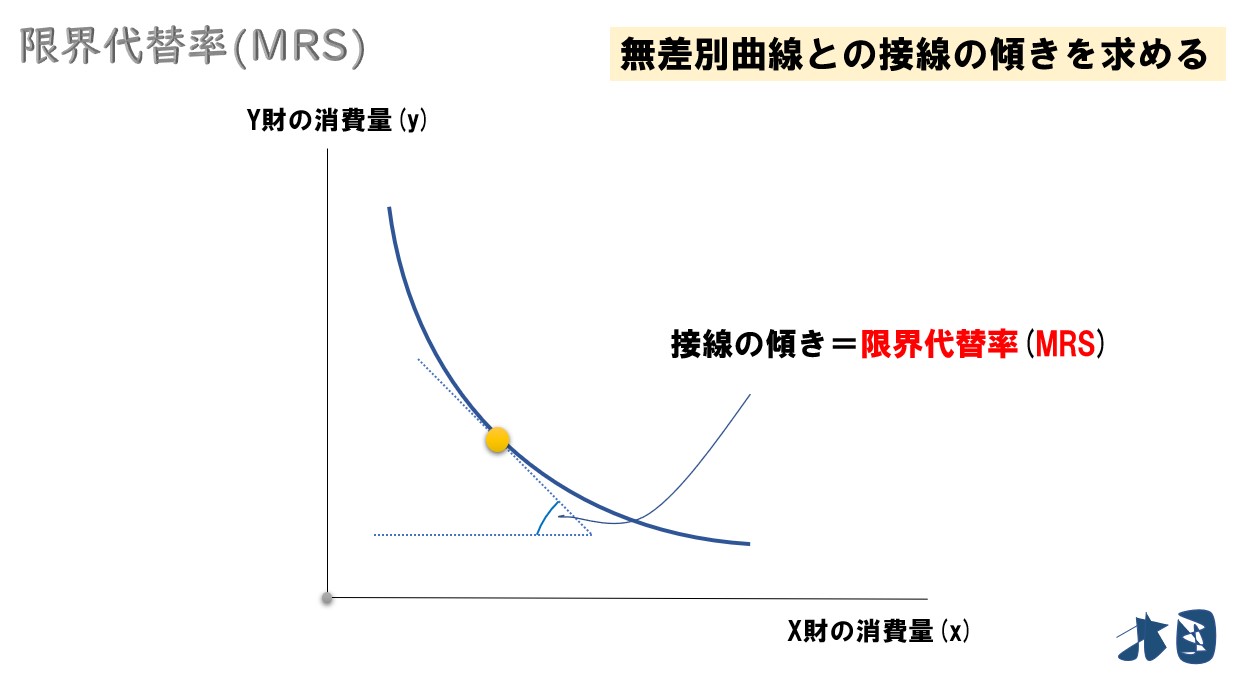
同じ効用水準を維持するための2財の交換比率。
ある財の消費量を増やすとき、もう片方の財の消費量をどれくらい減らせば、同じ効用を維持できるかを表している。無差別曲線の接線の傾きになる。


例えば
紅茶とコーヒーを飲みます。


紅茶・コーヒー、どちらを飲んでも10の効用を得られるとします。
ここで
「効用=10」を維持することを考えてみます。


ポイント
10の効用を維持するためには「紅茶を1杯飲んで、コーヒーを飲まない」「紅茶を飲まずに、コーヒーを1杯飲む」のどちらかです。
つまり、どちらの場合でも、財を1単位消費するときに、もう片方の財を1単位減らす(諦める)必要があります。この交換比率を限界代替率と言います。
※紅茶とコーヒーの例では、限界代替率は「1」となります。
限界代替率逓減の法則について
限界代替率には「X財の消費量を1つ増やすほど、減らすY財の消費量は小さくなる」という特徴がある。


例えば
紅茶とパンケーキを食べます。


今度は、紅茶を全然飲めずに、パンケーキばかりを食べているとします。
甘党
そろそろ、飲み物が欲しいな・・


ポイント
もし紅茶を飲めずに、パンケーキを5個食べていると、紅茶の価値は凄く高くなります。「パンケーキ6枚目< 紅茶1杯」と感じる。
このように「2つの財があったとき、片方の財を消費し続けると、次第にもう片方の財の価値(得られる効用)が高まる状態のこと」を限界代替率逓減の法則と言います。
仮に
- 紅茶とパンケーキを食べて、100の効用を得ようとします。
最初にパンケーキを食べて効用が50になりました。次の紅茶を1杯飲めばもう50の効用を得られそうです。
しかし
紅茶を飲まずに、パンケーキをもう1枚食べたとします。残念ながら、お腹いっぱいで+30の効用にしかなりませんでした。
もう1枚パンケーキを食べれば+20の効用で、合計100の効用になります。
ポイント
追加的な1単位の消費から得られる効用
- 2枚目のパンケーキ=30の効用
- 3名目のパンケーキ=20の効用
- 紅茶1杯=50の効用
パンケーキを追加で1枚消費するにつれて、紅茶の相対的な価値が高まっています。これを、パンケーキの効用を基準に考えてみます。
2枚目のパンケーキ
- 2枚目のパンケーキ=30の効用
- 紅茶1杯=50の効用
30÷50=0.6
つまり、2枚目のパンケーキは「紅茶0.6杯分」に相当します。
3枚目のパンケーキ
- 3枚目のパンケーキ=20の効用
- 紅茶1杯=50の効用
20÷50=0.4
つまり、3枚目のパンケーキは「紅茶0.4杯分」に相当します。
ココがポイント
「パンケーキの消費量」を1枚増やすにつれて、同じ効用を得るために必要な「紅茶の消費量」が減っているのが分かります。この特徴こそが「X財の消費量を1つ増やすほど、減らすY財の消費量は小さくなる」という限界代替率逓減の法則の意味になります。
補足
- 2枚目のパンケーキと同じ効用を得るために必要な「紅茶の消費量」は0.6杯
- 3枚目のパンケーキと同じ効用を得るために必要な「紅茶の消費量」は0.4杯
「片方の財の消費量」を1単位増やすほど、同じ効用を得るために必要な「もう片方の財の消費量」が減っていることが分かります(0.6杯 → 0.4杯)。
まとめ
限界代替率は「X財の消費量を1つ増やしたとき、同じ効用を維持するために、どれくらいY財の消費量を減らす必要があるか」を表している。限界代替率には「X財の消費量を1つ増やすほど、減らすY財の消費量は小さくなる」という特徴がある。これを「限界代替率逓減の法則」という。
限界代替率の求め方・計算方法

ポイント
基本的には、無差別曲線の傾きを求めることで「限界代替率」が分かります。
無差別曲線についてはこちら⇒【無差別曲線】意味や性質・効用関数との関係を簡単に理解する
グラフで見ると


この先は
次の項目が続きます。
①「無差別曲線の傾き=限界代替率の理由」で考え方を理解します。
②「計算式」で限界代替率=「dy/dx」になる理由を理解します。
③「2財の限界効用の比」で計算問題を解くときに重要となる考え方「dy/dx」=「MUx/MUy」を理解します。
④「例題」を解きます。
そもそも、限界代替率の求め方が良くわからない人は、順番に読んでいくと理解が深まると思います。
ある程度理解できている人は、例題を先に読んで、理解できない部分を勉強するとかが効率が良いかもしれません。
無差別曲線の傾き=限界代替率の理由
まずは
- 無差別曲線が直線だった場合を考えてみる
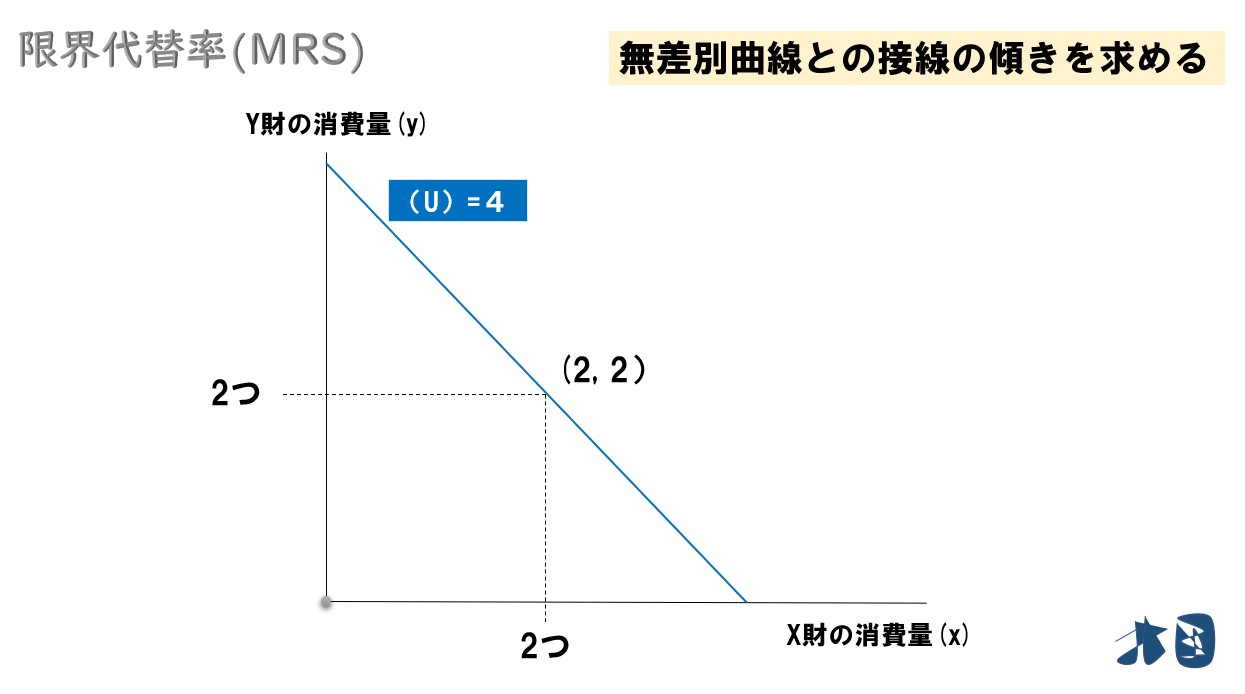
この直線(無差別曲線)は、4の効用を得られる消費の組合わせを結んでいます。
- X財の消費量=2
- Y財の消費量=2 という状態になっています。
次に
限界代替率の定義を思い出してください。
ある財の消費量を増やすとき、同じ効用を維持するために、もう片方の財の消費量をどれくらい減らす必要があるのか(交換比率)を表したもの。
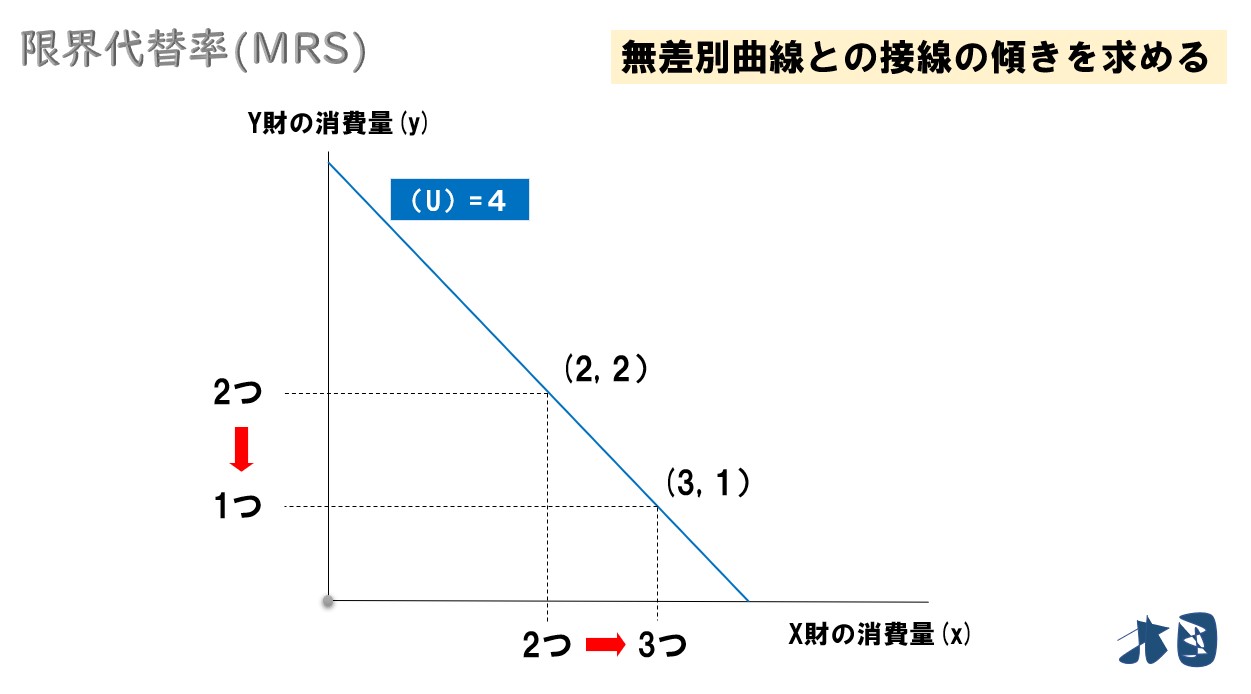
X財の消費量を1単位増やしてみる
この時、同じ効用水準(4)を維持するために Y財の消費量を1減らす必要があるとします。
同じ効用水準(4)を維持するためには
- X財の消費量を1増やす
- Y財の消費量を1減らす
つまり、限界代替率(MRS)=1となります。X財を1つ多く消費したら、Y財を1つ少なくしないと同じ効用が保てない⇒ 交換比率=1:1(1分の1)となっている状態。


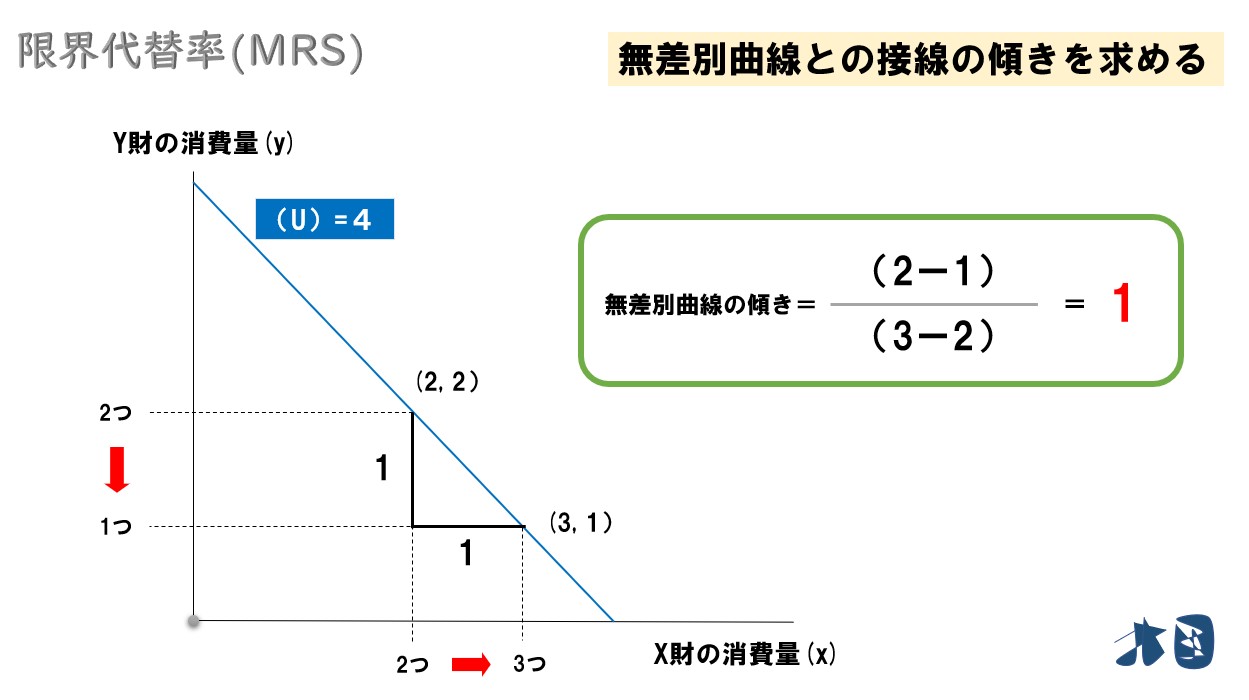
この無差別曲線の傾きを考えてみる
つまり
この無差別曲線(直線)の傾きは、1となります。


ポイント
限界代替率(MRS)は「X財を1つ消化したとき、同じ効用を維持するためにY財の消費量をどれくらい減少させるか」を計算することになる。
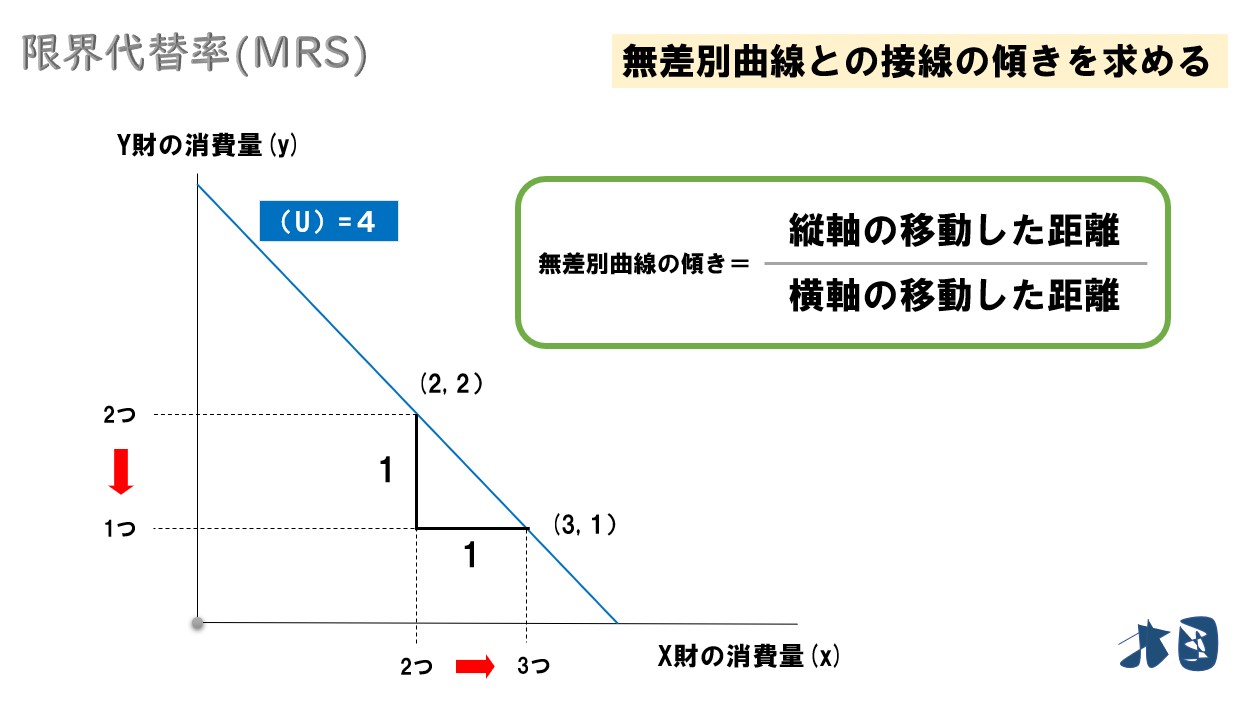
グラフ的に見れば
- X財を1つ消化したとき=横軸の移動距離
- Y財をどれくらい減少させるか=縦軸の移動距離
となるため、数学的には、無差別曲線の傾きを求めるのと同じになる。
限界代替率の計算式
先ほどの「無差別曲線の傾き=限界代替率の理由」を理解していれば簡単です。
確認する⇒無差別曲線の傾き=限界代替率の理由
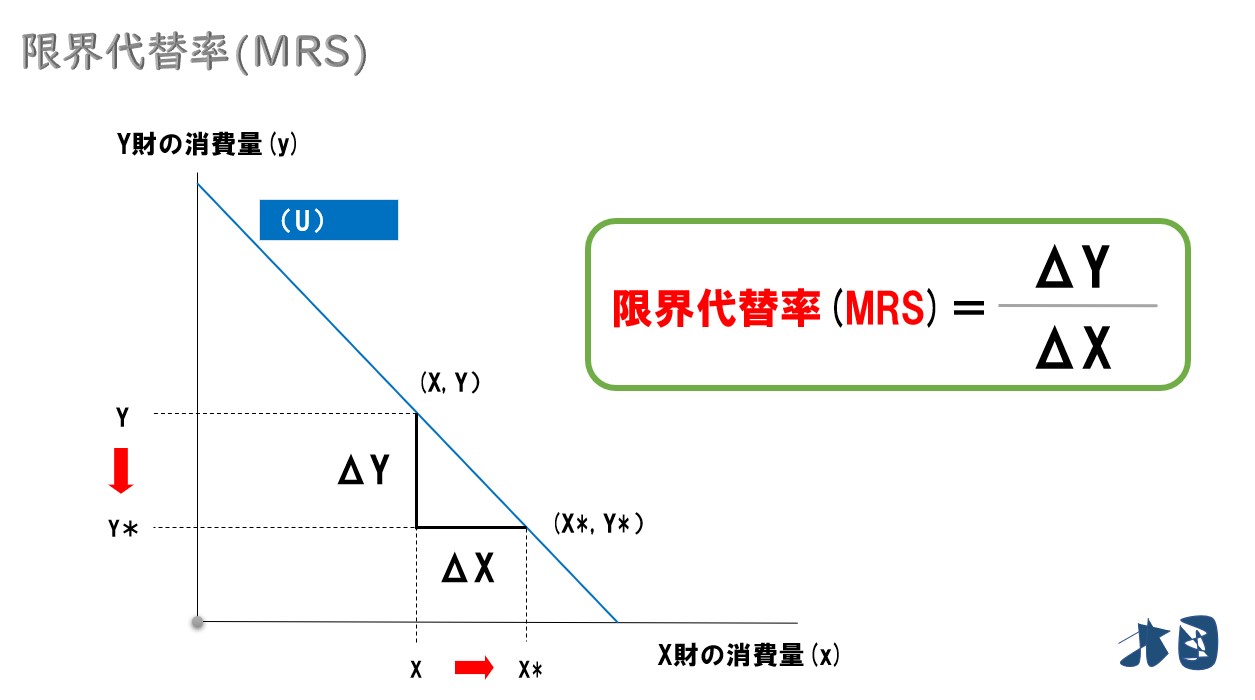
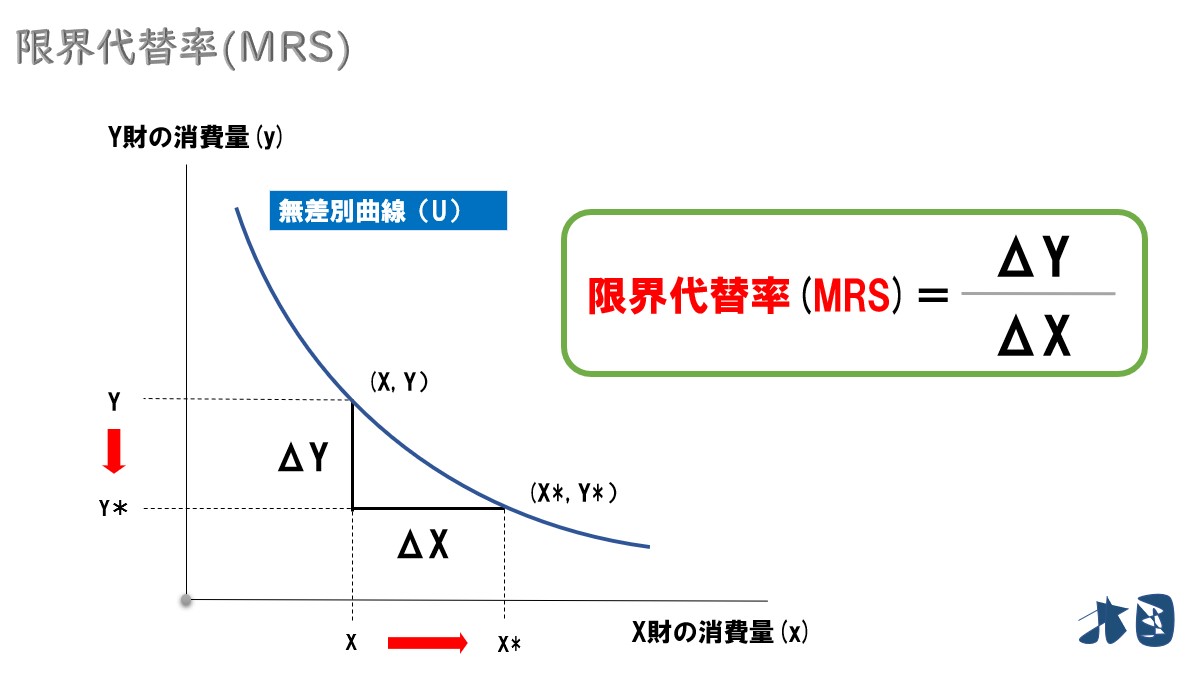
変化量をΔとする
- X財の消費量の増加分=ΔX
- Y財の消費量の減少分=ΔY
普通の無差別曲線でも同じ


限界代替率は2財の限界効用の比になる
ポイント
限界代替率(MRS)は、2財の限界効用から求めることも出来る。(限界代替率は「X財の限界効用」と「Y財の限界効用」の比率で表すことができる。)


はじめに
1つ前の段落で「限界代替率=Δy/Δx」と書きましたが、ここから「限界代替率=Δy/Δx=MUx/MUy」と式が続きます。
「Δ」と「d」は同じ意味です。
限界効用(MU)が登場する理由
先ほどまでは「横軸に移動した距離」「縦軸に移動した距離」という表現を使って、限界代替率(無差別曲線の傾き)を求めました。実は、この移動距離が限界効用(MU)に当たります。
ポイント
限界代替率(MRS)は「X財を1つ消化したとき、同じ効用を維持するためにY財の消費量をどれくらい減少させるか」を計算することになる。
グラフ的に見れば
- X財を1つ消化したとき=横軸の移動距離
- Y財をどれくらい減少させるか=縦軸の移動距離
限界代替率(MRS)=「縦軸に移動した距離」/「横軸に移動した距離」
ここで
限界効用(MU)は、「財を追加的に1単位消費したときの、効用の増加分」です。
限界効用(MU)の「財を追加的に1単位消費」の部分が、グラフ上の横軸・縦軸の移動距離にあたります。


ポイント
そもそも同じ無差別曲線上では、効用の大きさは一定です。つまり、同じ無差別曲線上の移動なので「X財の効用が増加した分」と「Y財の効用が減少した分」は、足し引き=0になります。
つまり
- X財の限界効用 ⇒「横軸に移動した距離・それに伴って変化した効用の大きさ」
- Y財の限界効用 ⇒「縦軸に移動した距離・それに伴って変化した効用の大きさ」
「それに伴って変化した効用の大きさ」は、どちらも同じになります。
- X財の限界効用 ⇒「横軸に移動した距離
・それに伴って変化した効用の大きさ」 - Y財の限界効用 ⇒「縦軸に移動した距離
・それに伴って変化した効用の大きさ」
このようになるので「限界代替率(MRS)(無差別曲線の傾き)」を求めるときに、2財の限界効用(MU)の比率を使うことが出来きます。
上の説明は、効用関数(U)を全微分を行う過程で「dU=0となる」という過程を言葉で説明したつもりです。説明を考えながら書いてみて分かりましたが、数学的に処理する方が簡単です(汗)→最後の段落を確認する。


考えると分けわからなくなります。ひとまず「2財の限界効用(MU)の比率で限界代替率(MRS)が求められる」という点を覚えておきましょう。
まとめ
例題

ここまでの話を使って、簡単な例題を解いてみましょう。
次の条件のとき、X財のY財に対する限界代替率を求めよ。
- 第1財(X財)の消費量=x
- 第2財(Y財)の消費量=y
- 効用関数(U)=√x・yの0.3乗
「X財のY財に対する~」などの表記で混乱する人も多いかと思いますが、深く考えると迷宮に突入するので初めは無視してください。
step
1効用関数の形を確認する
はじめに、与えられている効用関数がレオンチェフ型の効用関数になっていないことを確認します。
- レオンチェフ型の効用関数「U=min{x,y}」
minは、xとyの小さい方の値を取るという意味(片方の財の消費量が増えても、もう片方の財の消費量が増えないと、効用が増えない)で2財が完全補完財のときに現れます。
効用関数がレオンチェフ型になっていないことを確認したら計算に移ります。
ちなみに
レオンチェフ型の効用関数(完全補完財)のときは限界代替率は0もしくは無限大になります。そもそも代替できない完全補完財なので、値が0か無限大になるというイメージです。
レオンチェフ型では無差別曲線がL字になりますが、x軸をグラフの横軸と考えるとき、限界代替率は次のようになります。
- x軸に垂直な部分(L字の垂直部分)では限界代替率=0
- x軸に平行な部分(L字の水平部分)では限界代替率=∞
step
2X財・Y財の限界効用(MU)を求める
限界代替率(MRS)は、2財の限界効用(MU)の比から求めることが出来ます。なので、X財・Y財のそれぞれの限界効用(MU)を求めます。
限界効用(MU)を求めるには、X・Yそれぞれで偏微分すればOKです。
偏微分の意味が分からなくても、計算は直ぐにできるので続きを読んでください。
ポイント
微分は乗数を手前に持ってきて、乗数をマイナス1します。
まず
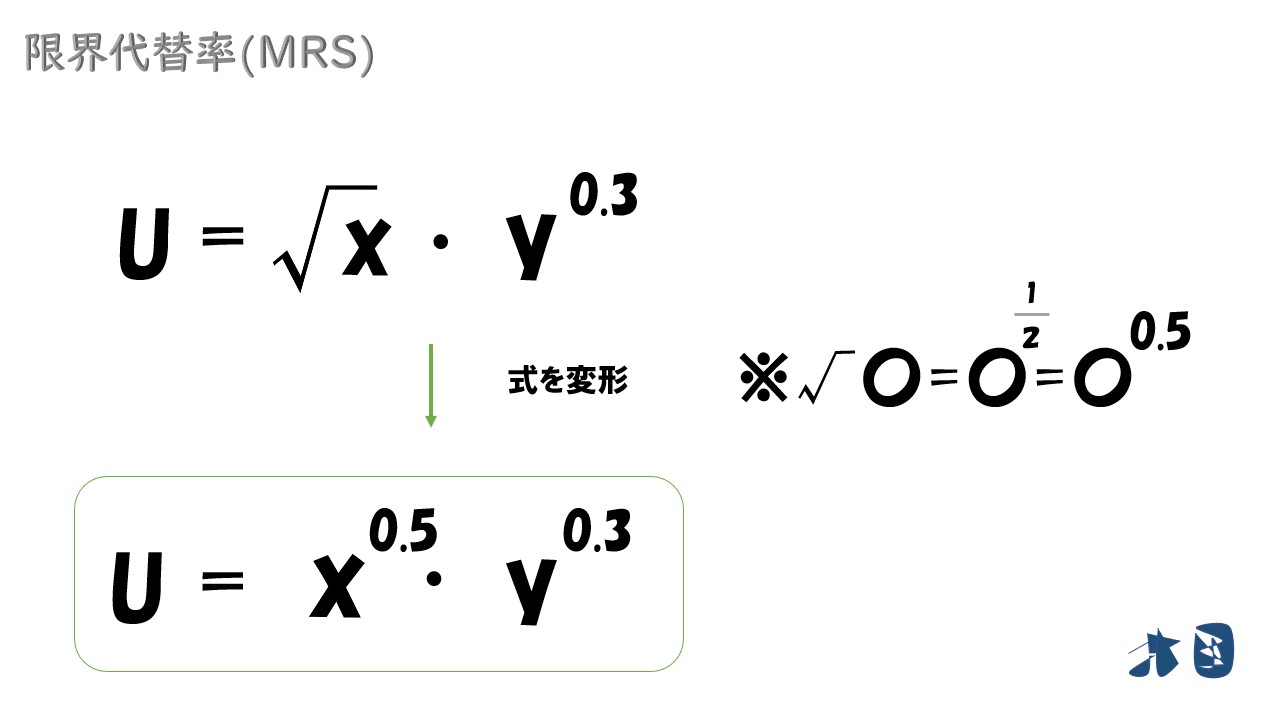
- 偏微分をする前に、効用関数の表記を変えます
「√」は「0.5乗(=2分の1乗)」と表記できます。「√」の微分方法でつまづく人がいるので、確認しましょう。
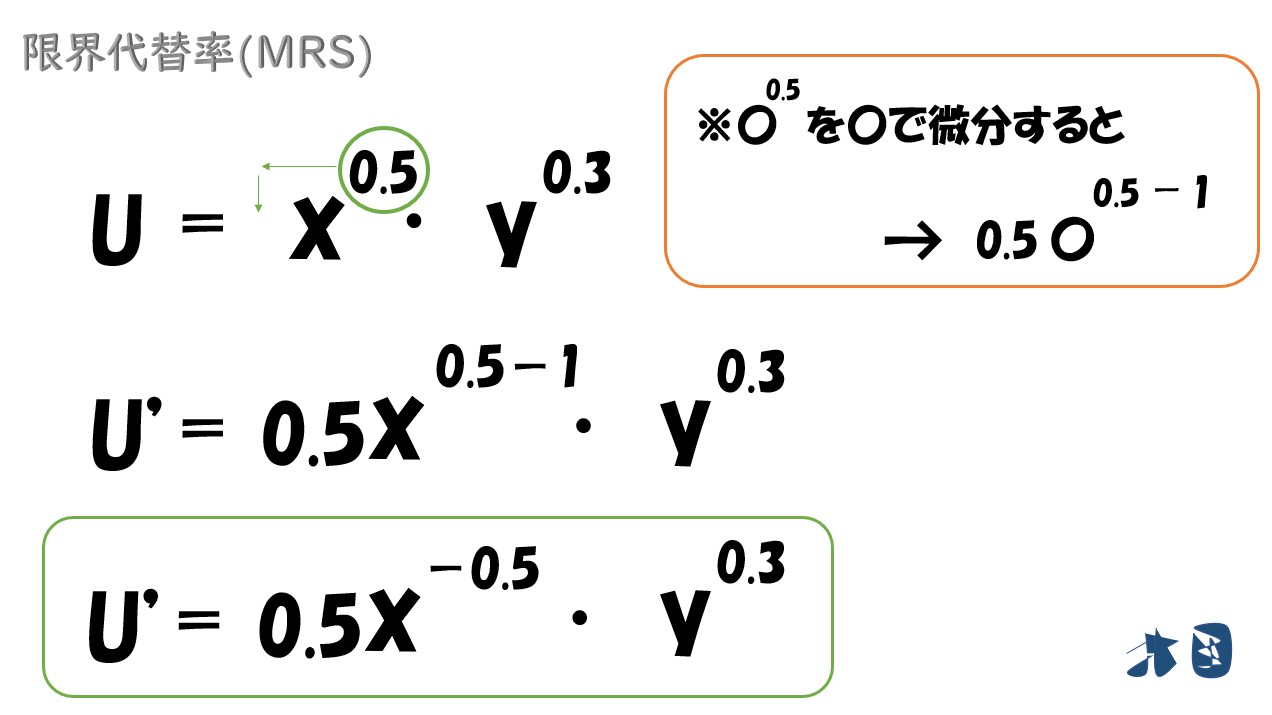
- ①X財の限界効用(MUx)を求める
X財の限界効用(MUx)を求めるためには、効用関数を「x」で偏微分すればOKです。実際に計算しましょう。
以上より、X財の限界効用(MUx)=「0.5xの-0.5乗・yの0.3乗」
- ②Y財の限界効用(MUy)を求める
Y財の限界効用(MUy)を求めるためには、効用関数を「y」で偏微分すればOKです。
以上より、Y財の限界効用(MUy)=「xの0.5乗・0.3yの-0.7乗」
- ③限界代替率を求める
①②より、2財の限界効用の比を使って限界代替率を求めます。
0.5や0.3が邪魔なので分母分子を10倍して整数にします。
次に、乗数の小数点を消していきます。
(1)まずは、xの乗数を綺麗にします
(2)そのまま、yの乗数も綺麗にします
ここで
0乗は「1」となるので「xの0乗」と「yの0乗」は1です。また、1乗はわざわざ表記する必要はないので消します。
(答え)限界代替率(MRSxy)=5y/3x
別解
- dy/dx(無差別曲線の傾き)を直接求める
さきほどの計算では「限界代替率=dy/dx=2財の限界効用(MU)の比」という関係を使って計算しましたが、別解として「限界代替率=無差別曲線の傾き(dy/dx)」を使った計算をします。
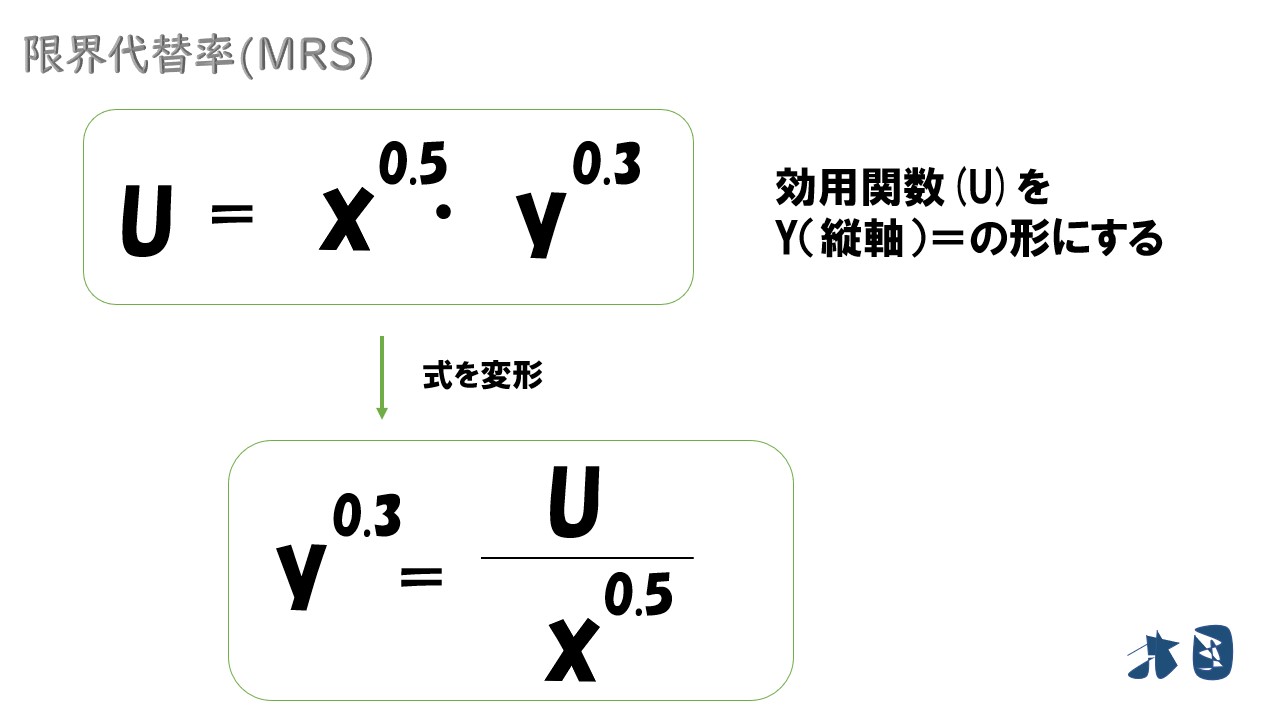
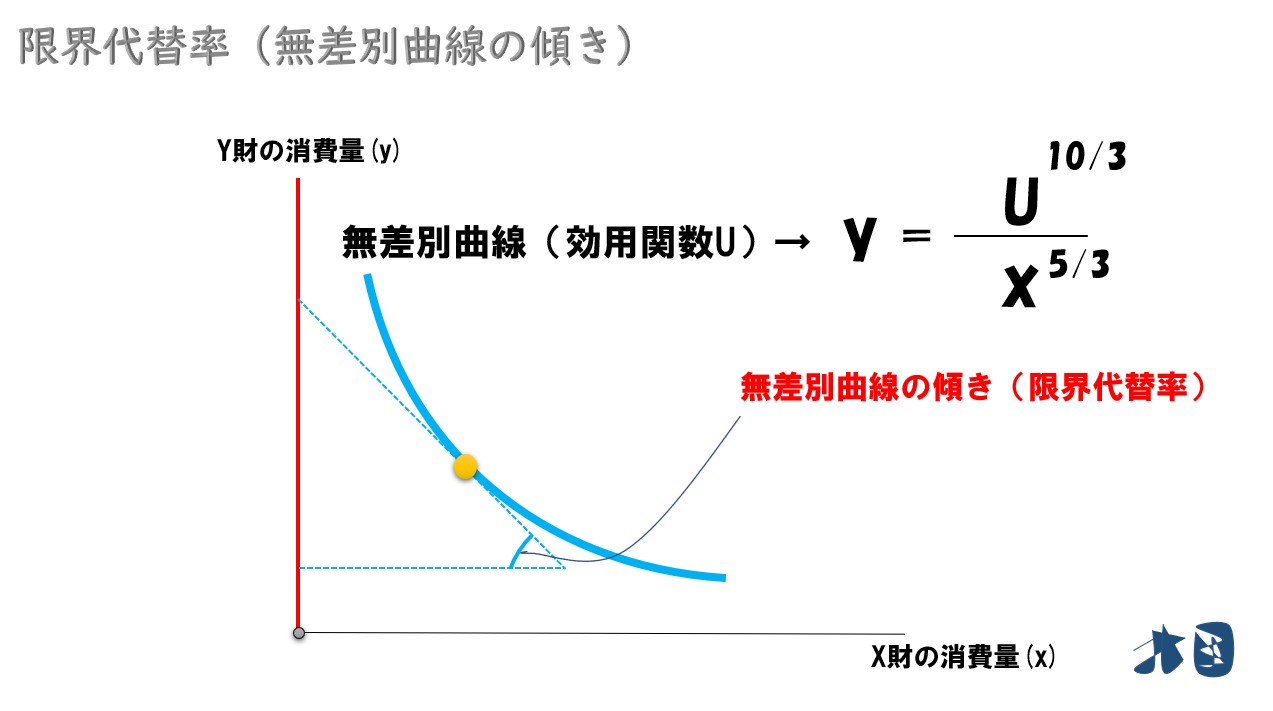
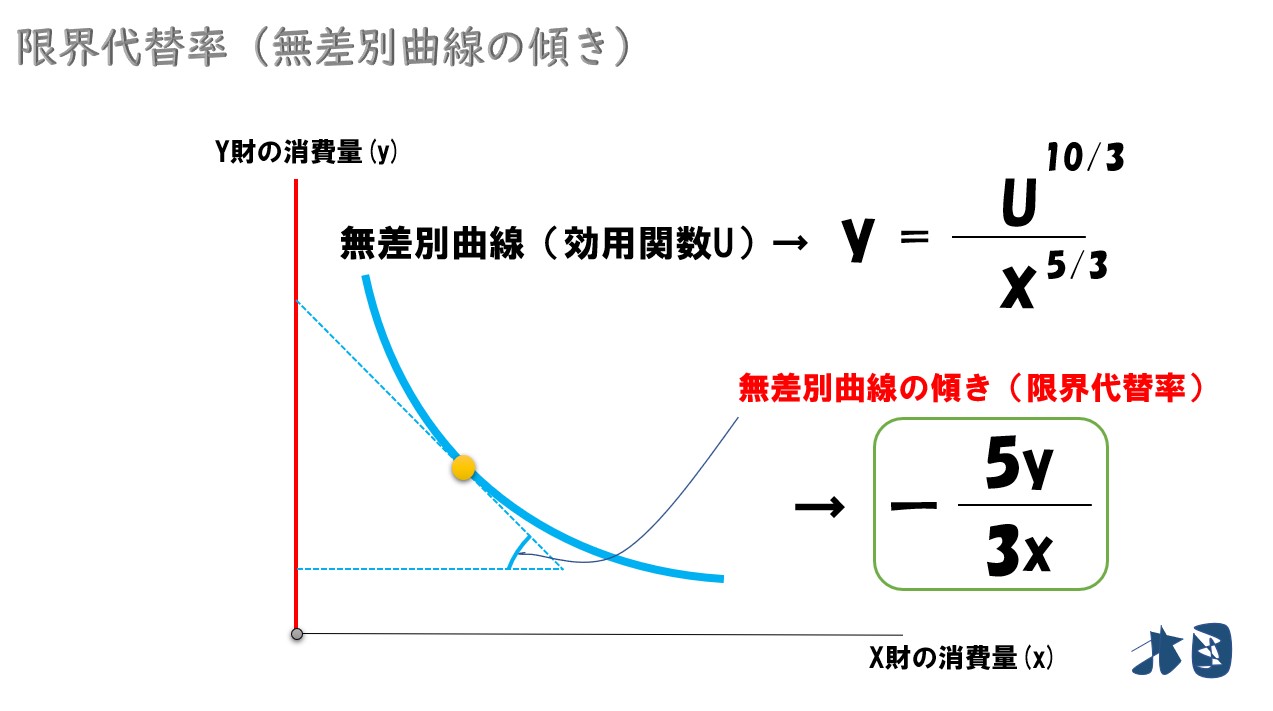
はじめに、効用関数(U)を「縦軸(y)=~」の形にします。
yの0.3乗を「y=」となるように乗数を消します。
0.3乗=(3/10)乗を消すために、両辺を(10/3)乗します。
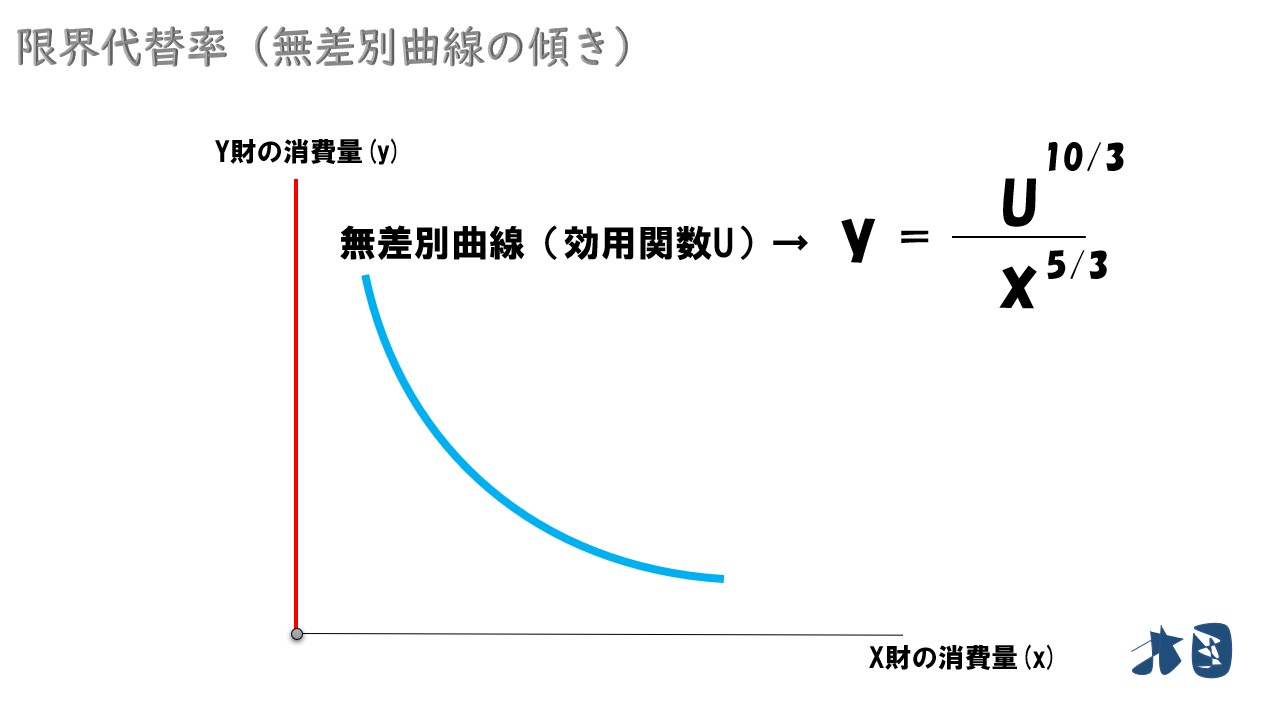
Y=の綺麗な形になりました。これがグラフの無差別曲線(効用関数・水色の曲線)を表しています。
限界代替率を求めるには、この曲線の傾きを求めればOKです。
傾きを求めるために、横軸であるX財の消費量「x」で微分します。
微分は、接線の傾きを求めることが出来る計算方法です。無差別曲線はカーブを描いているため、接線を引いて傾きを求めると考えて微分をします。
分数を微分する時は注意が必要です。
ポイント
分数は「-1乗」です。「1/2」なら「2の-1乗」と表記できます。
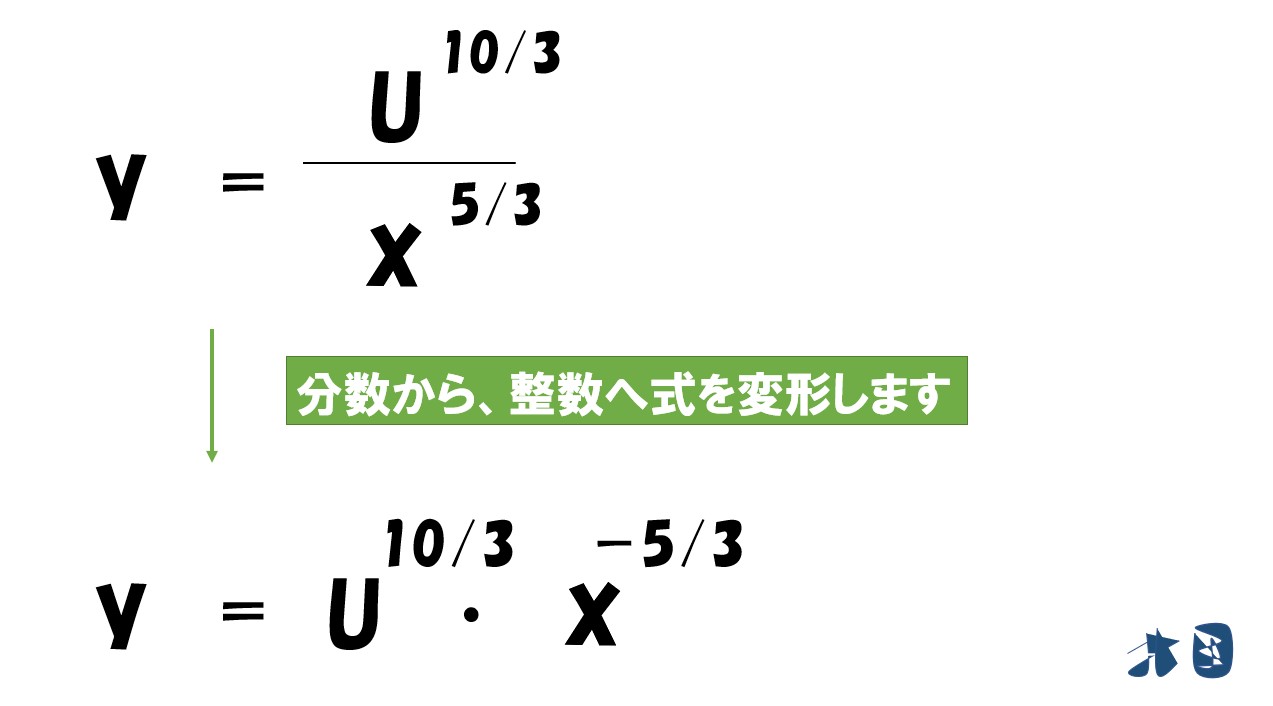
式を整数に直してから微分する
ここで、Uという文字が邪魔くさいので消します。
「効用関数(U)=√x・yの0.3乗=xの0.5乗・yの0.3乗」より
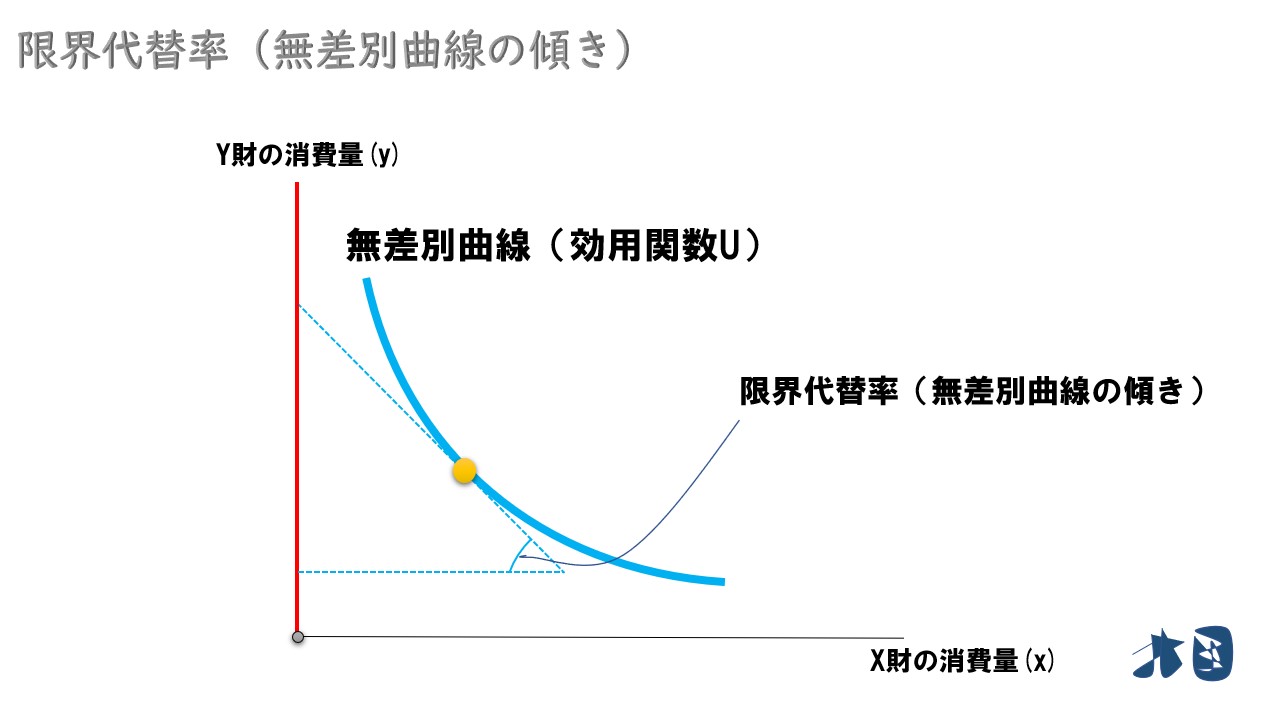
グラフで確認すると‥
また、限界代替率を答える時は、マイナスは不要です。
厳密に言えば、限界代替率は「無差別曲線の傾き(dy/dx)にマイナスを付けたもの」であるため、マイナスの傾きにマイナスを付けてプラスになるという理屈です。
(答え)限界代替率(MRSxy)=5y/3x


2財の限界効用の比になる数学的な説明(全微分)

おまけで「限界代替率(MRS)=2財の限界効用の比」となる理由を、全微分をして、数学的に求めてみます。
数学的な説明
- 効用関数(U)=U(x, y)がある
- 「U」は「効用の大きさ」
- 「x」は「X財の消費量」
- 「y」は「Y財の消費量」
つまり「X財の消費量」「Y財の消費量」から、どれくらいの効用(U)が得られるのか?を数式化したもの。
そもそも無差別曲線は、効用関数(U)から求められるものです。その辺りの話が分からない人はこちらで確認⇒【無差別曲線】意味や性質・効用関数との関係をわかりやすく※よくある疑問の「無差別曲線と効用関数はイコールじゃない」を参照
確認
「効用関数(U)=U(x, y) 」の「U(x, y)」は次の意味があります。
効用関数(U)=「〇x」×「〇y」
- 効用関数(U)=x × y
- 効用関数(U)=5x × 5y
- 効用関数(U)=100x × 200y
このような数式を意味しています。通常「〇x」×「〇y」の「〇」にどんな数字が入るかは問題文に書いています。ここでは、〇の部分(定数)は不要なので省略します。
ここで
- 「効用関数(U)=U(x, y)」を全微分する
ここでの全微分の意味は、効用関数(U)=「〇x」×「〇y」の「x」「y」の大きさが変化した時に、効用(U)の大きさがどんな変化をするか?を知るためです。
具体的な数字が分かれば計算できますが、文字だけで表現するとどうなるか?という感じです。
それぞれを文字に置き換える
- 「x (X財の消費量)」の変化量を「dx」
- 「y (Y財の消費量)」の変化量を「dy」
- 最終的な効用(U)の変化量を「dU」
「d」は「ディー」などと呼びます。


ポイント
全微分した後に登場する「∂U/∂x」「∂U/∂y」は限界効用(MU)と同じ。
2財のときの限界効用(MU)を求めると
- X財を消費した時の限界効用(MUx)=「∂U/∂x」
- Y財を消費した時の限界効用(MUy)=「∂U/∂y」
という風になります。
2財の限界効用(MU)を求める話は、こちらで確認できます⇒ 限界効用・限界効用逓減の法則とは?求め方も含めて簡単にわかりやすく※「財が2つの場合」を参照
つまり
全微分した後の数式の意味は、次のようになります。


あらためて
ここまでの話は「限界代替率(MRS)を求める」=「無差別曲線の傾きを求める」と進んできていました

ポイント
ここで、同じ無差別曲線上なら、どの点でも効用の大きさは同じです。
先ほどの「効用関数(U)=U(x, y)」で「x」「y」の大きさがどう変わろうと、効用の大きさは常に同じ値になります。
つまり
- 全微分した式の左辺が=0になる
全微分した式は、X財・Y財の消費量を変化させた結果、最終的な効用がどれくらい変化するかを表しています。無差別曲線上の変化を考えると、効用はどの点でも同じになるので効用の変化量は「0」になります。
ここで
- 「x (X財の消費量)」の変化量を「dx」
- 「y (Y財の消費量)」の変化量を「dy」
とおいていたので、次のように言えます。
- 「dx」が「横軸に移動する距離」
- 「dy」が「縦軸に移動する距離」
「縦軸に移動する距離=dx」/「横軸に移動する距離=dy」
ポイント
限界代替率(MRS)=「dy/dx」になる。


限界代替率(MRS)=「dy/dx」になることは重要なポイントです。
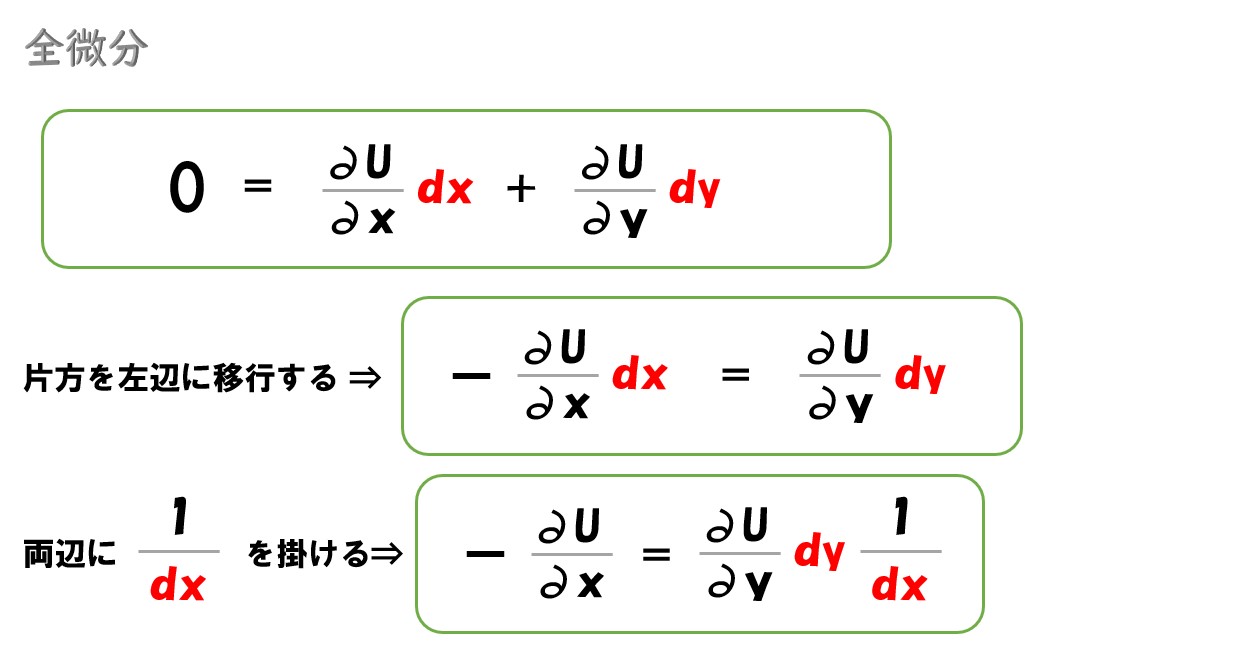
先ほどの全微分した式を見てください。
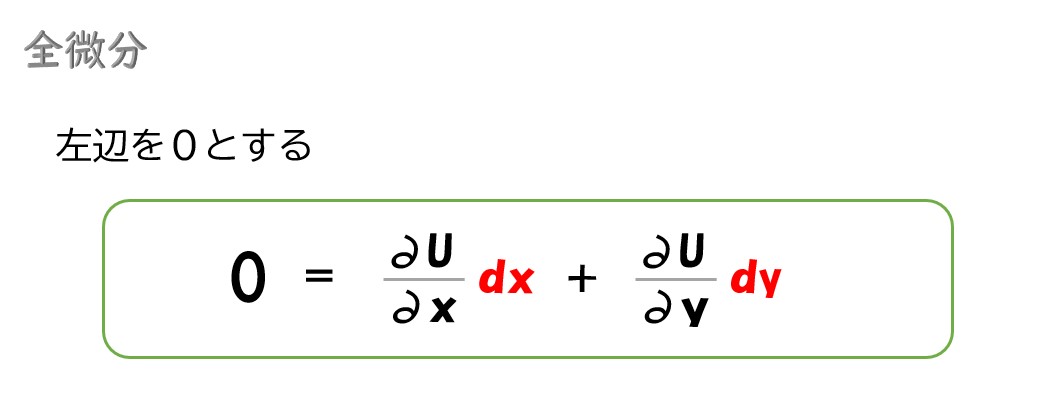
この式は、ここから限界代替率(MRS)=「dy/dx」を導出することが出来ます。


一般的には、限界代替率(MRS)の方をマイナスにして表記します。
ポイント
効用関数(U)=U(x, y)を全微分した式は、左辺が限界代替率(MRS)=「-(dy/dx)」になる。


途中でも書きましたが、2財の限界効用は次のようになります。
- X財を消費した時の限界効用(MUx)=「∂U/∂x」
- Y財を消費した時の限界効用(MUy)=「∂U/∂y」
2財の限界効用(MU)を求める話は、こちらで確認できます⇒ 限界効用・限界効用逓減の法則とは?求め方も含めて簡単にわかりやすく※「財が2つの場合」を参照
つまり
「X財の限界効用(MUx)」/「Y財の限界効用(MUy)」となっていますが、これは比率を表しています。
例えば「縦軸(y)=5:横軸(x)=2」なら比率は「2/5」と分数表記できます。
まとめ
- 限界代替率(MRSxy)=「X財の限界効用(MUx)」/「Y財の限界効用(MUy)」
※限界代替率(MRSxy)の「xy」部分は、xyの限界代替率という意味合い。
効用関数(U)を全微分した式から上記が求められる。つまり、限界代替率(MRS)は2財の限界効用(MU)の比になることが言える。