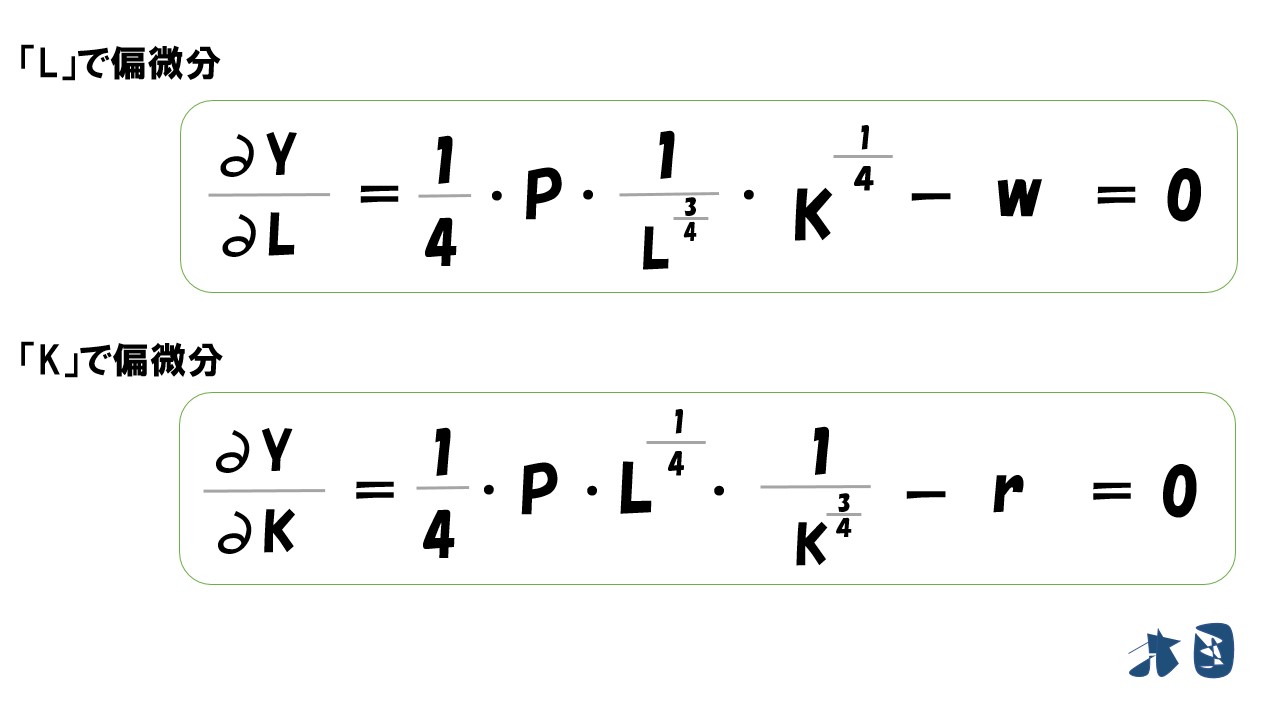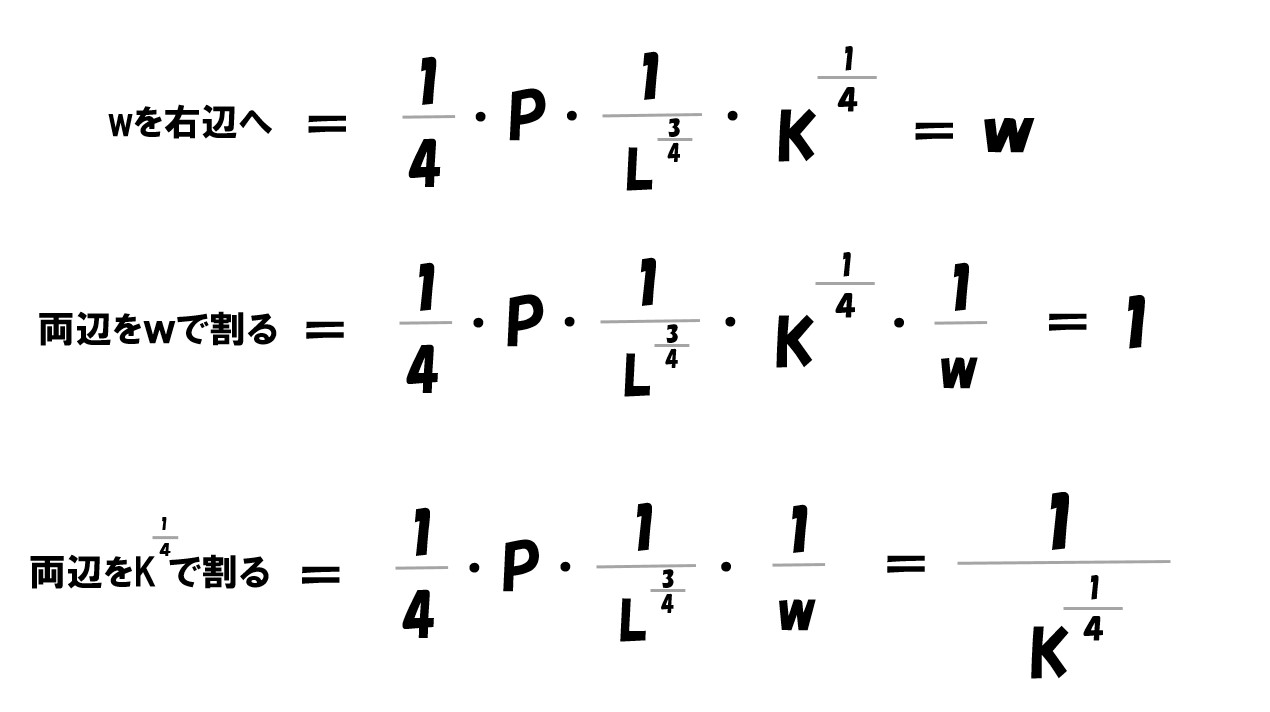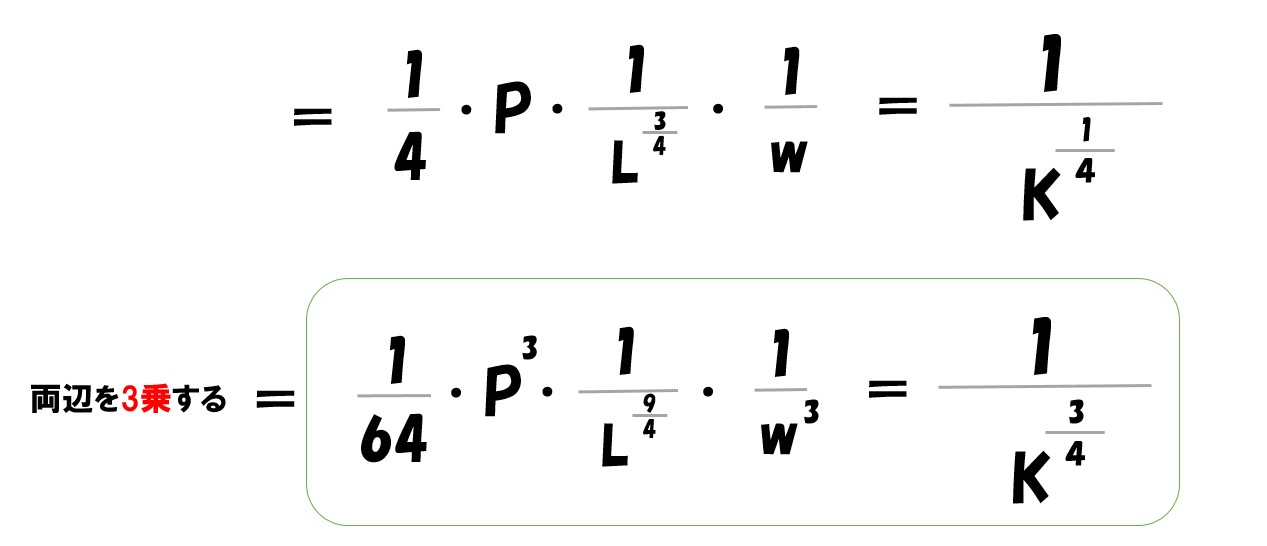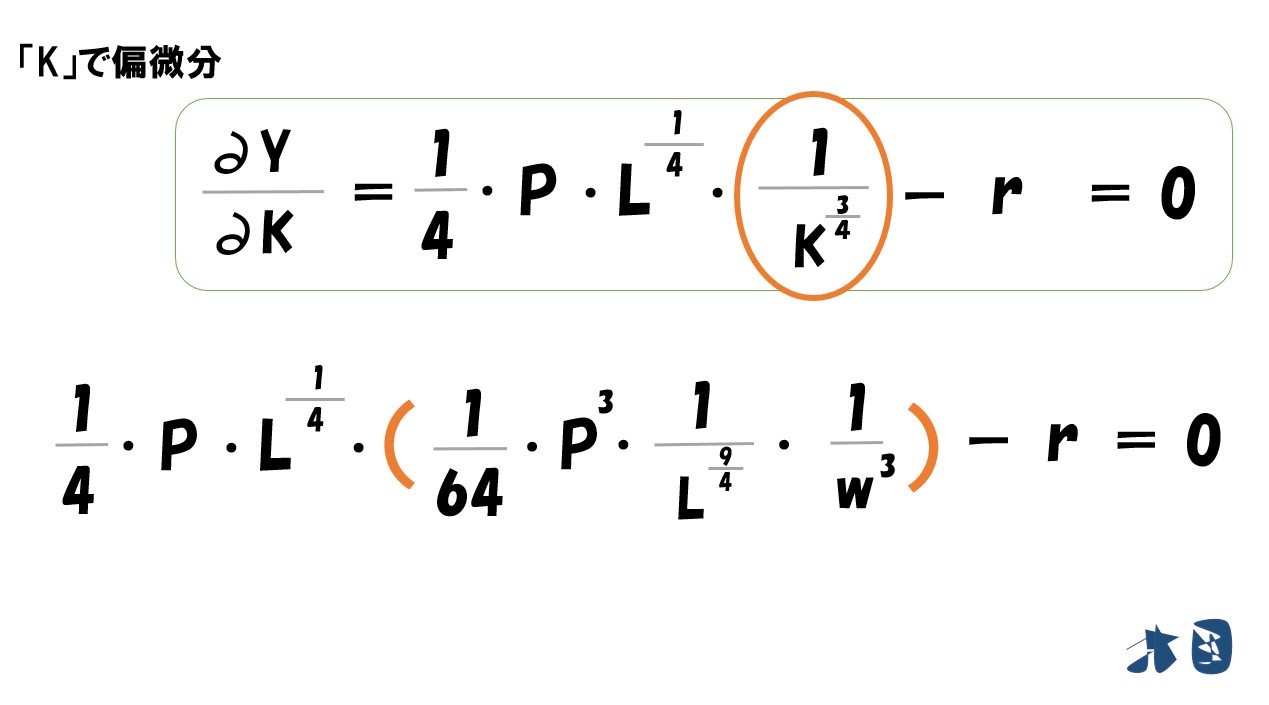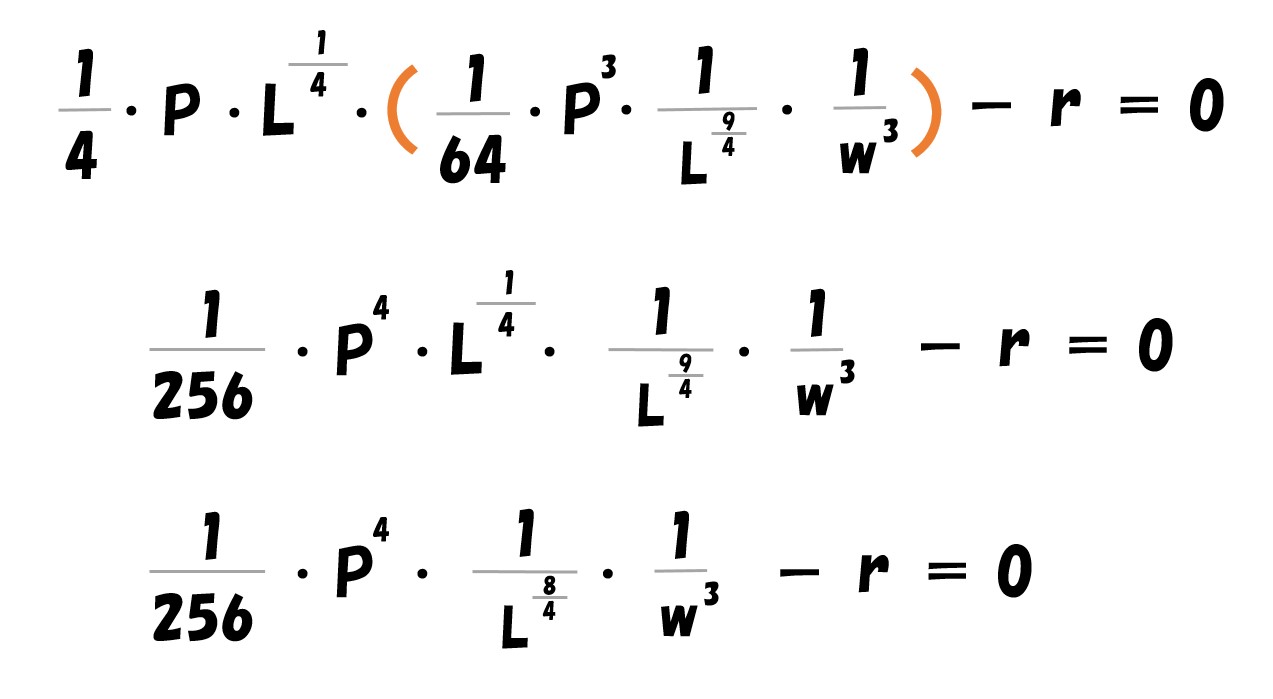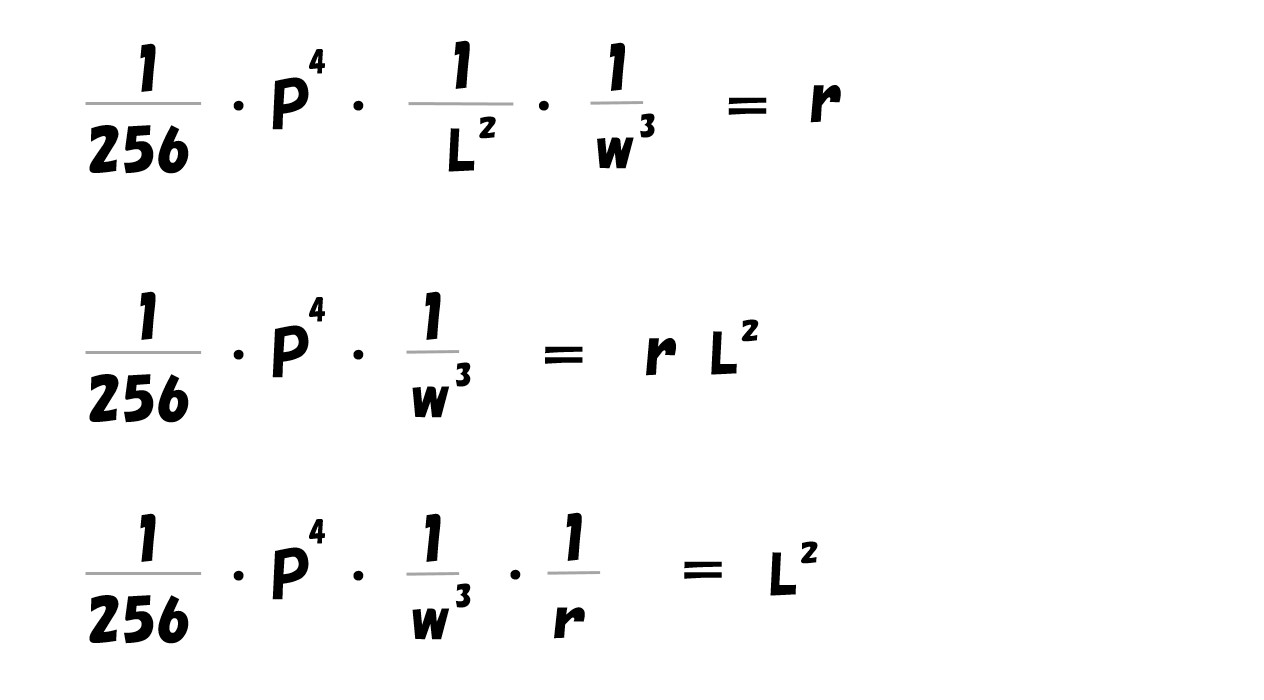「要素需要関数」は、企業の利潤最大化が実現するとき、生産要素はどれくらい必要か(需要量)を表しています。
- 要素需要関数とは?
- 要素需要関数の求め方
利潤最大化問題に関連して登場するため、突然「需要」という言葉が出てきて混乱する人もいます。そんな人向けに「要素需要関数」について簡単にまとめました。
要素需要関数とは?

要素需要関数とは
生産物の価格(P)・生産量(Y)が与えられているとき、利潤最大化が実現する生産要素の投入量(L・K)を「(生産物の)価格(P)・生産要素の価格(r・w)」で表した関数のこと。
ちなみに費用最小化が実現するとき、生産要素の投入量(L・K)を「(生産物の)生産量(Y)・生産要素の価格(r・w)」で表した関数を「制約付き要素需要関数」というものがあるので違いに気を付けましょう。


この関数を求めるためには企業の利潤最大化に関する知識がいるため、関連する知識が定着しているかを知るために出題されることもあります。
どうして「需要関数」なの?
要素需要関数は「利潤最大化が実現するときに、どれくらい生産要素(労働・資本)が必要なのか」を表した関数と言えます。
ポイント
つまり、利潤が最大化するとき企業の生産要素の需要がどれくらいあるのか?を表していると言えるので、需要関数という表現をします。
「需要」と言うと消費者側の視点を考えてしまいますが、ここでは企業側がどれくらい生産要素を必要としているか(=需要)と考えています。
さらに詳しく
利潤最大化問題を解くと「企業の最適な供給量(生産量)」が求まります。ここから供給関数が求められます。
一方で、生産を行うために生産要素(労働・資本)が必要です。「最適な生産を行うためには生産要素がどれくらい必要か」を表したのが要素需要関数です。
つまり、利潤最大化問題を解くと次の2つの式が得られます。
- 供給関数
- 要素需要関数
ここでは、2つのうち要素需要関数に焦点を当てています。
要素需要関数の求め方・計算

ポイント
最終的に「労働の投入量(L)=●●」「資本の投入量(K)=●●」という関数を求めます。
例題
あるプライステイカーの企業の生産関数が次のように与えられているとき
![]()
- 生産物の販売価格=P
- 生産量=Y
- 賃金=w
- 労働の投入量=L
- レンタル料=r
- 資本の投入量=K
要素需要関数(=利潤最大化する生産要素の需要関数)を求める。
利潤最大化を求める
利潤最大化問題の解き方を知っている前提で計算を進めるので、分からない人はこちらで確認⇒【完全競争・利潤最大化】条件や求め方・計算方法をグラフを使って理解する
ポイント
「利潤(π)=総収入ー総費用」なので
- 総収入=価格(P)×生産量(Y)
- 総費用=賃金(w)×労働量(L)+レンタル料(r)×資本量(K)
したがって「利潤(π)=(PY)-(wL+rK)」と考える。
はじめに
利潤最大化条件「∂π/∂L=0,∂π/∂K=0」に当てはめるために「利潤(π)=(PY)-(wL+rK)」を変形する
![]()
より
- 利潤(π)=(PY)-(wL+rK)
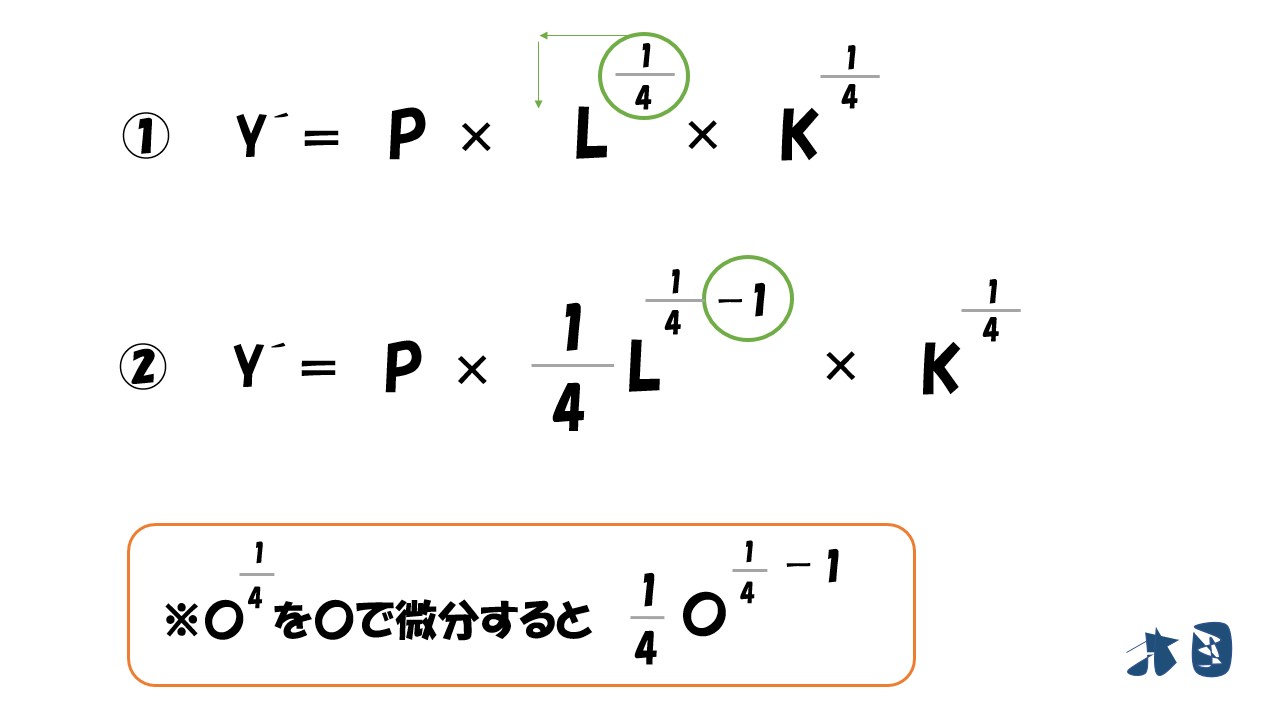
- 利潤(π)=(P・L^0.25・K^0.25)-(wL+rK)
⇒「利潤(π)=(P・L^0.25・K^0.25)-(wL+rK)」とする。
1/4=0.25。念のためですが「L^0.25」は「Lの0.25乗」を表しています。「Lの4分の1乗」と同じです。
この「利潤(π)=(P・L^0.25・K^0.25)-(wL+rK)」を「L」「K」で偏微分して「=0」と置きます。
微分する理由が分からない人はこちらで確認してください⇒【完全競争・利潤最大化】条件や求め方・計算方法をグラフを使って理解する
知っておく
偏微分をするときは
- 乗数を手前に持ってくる
- 乗数を「1」マイナスする
知っておく②
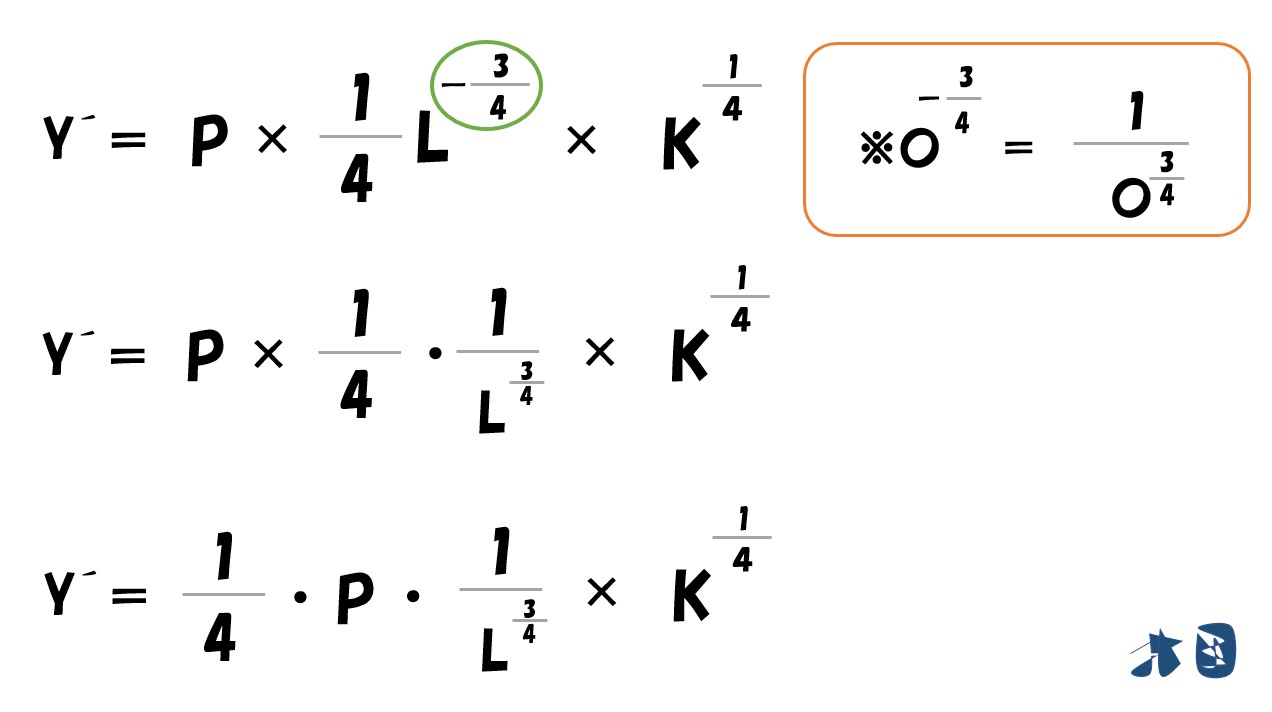
「乗数がマイナス」のときは「分数になる」
というわけで
「利潤(π)=(P・L^0.25・K^0.25)-(wL+rK)」を「L」で偏微分すると‥
- (P・L^0.25・K^0.25)は上で説明した通りで微分できます。
- (wL+rK)は(Lの1乗)なので微分すると(1×Lの0乗)=1になります。よって「w×1=w」
「L」で偏微分するなら「L」という文字がついていない部分は無視されます。※あくまで微分は変化量(Lという数量が変化したら式の答えがどう変化するか?)を見るため。
最終的にL・Kで偏微分すると
ここで
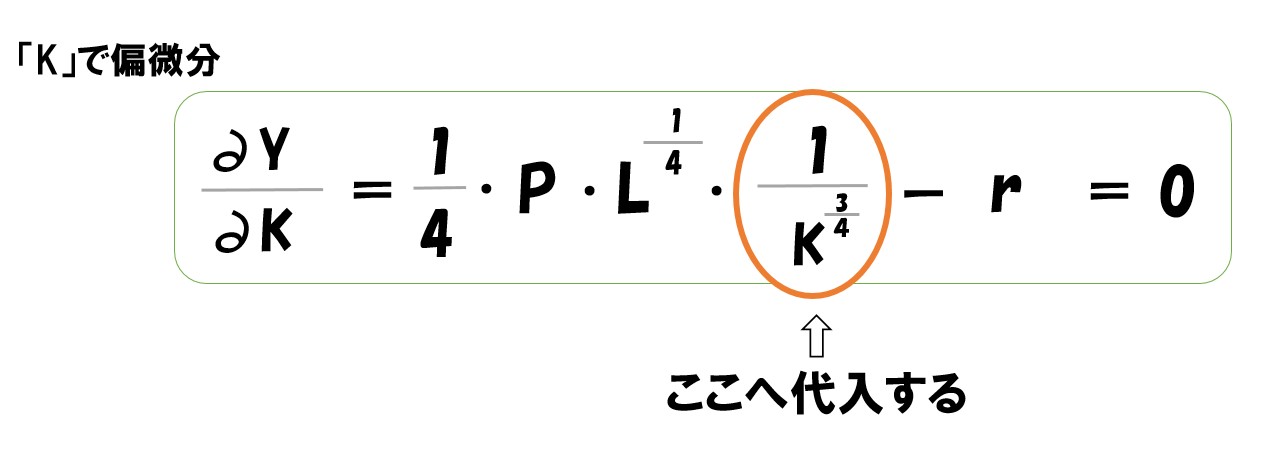
Lで偏微分した式を「K=●●」の形にする
(計算のポイント)
「K=●●」とした上記の式は、次のステップで「Kで偏微分した方の式」に代入します。
そこで、先ほどの式を代入しやすいように変形します
ここで、上記の式を「Kで偏微分した式」に代入します。
後はこれを計算して「L=●●」の形にすれば、労働の要素需要関数となります。
計算過程をざっと
今さらですが、わざわざ分数に直さなくても乗数でマイナス●乗として計算したほうが楽です。数学が苦手な人向けに分数に直して計算しています。
資本の要素需要関数も同様の手順で計算できます(省略)
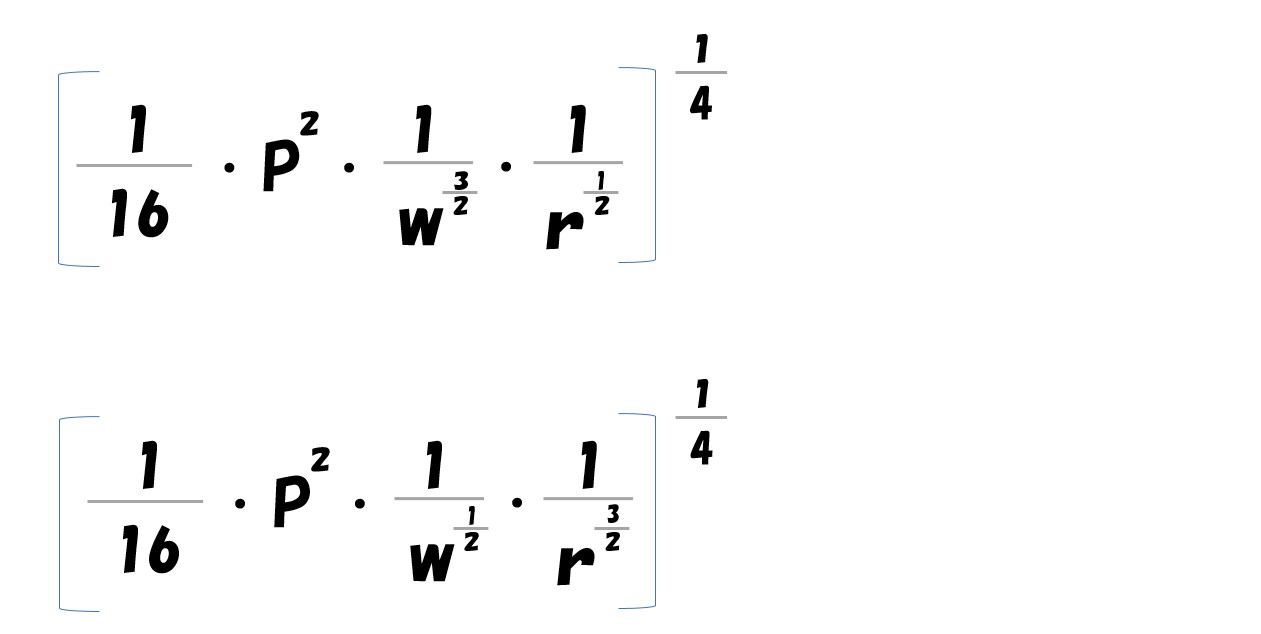
答え
ちなみに
- 労働の要素需要関数
- 資本の要素需要関数
2つを生産関数(Y)へ代入して「Y=●●」の形にすれば供給関数になります。
![]() より
より