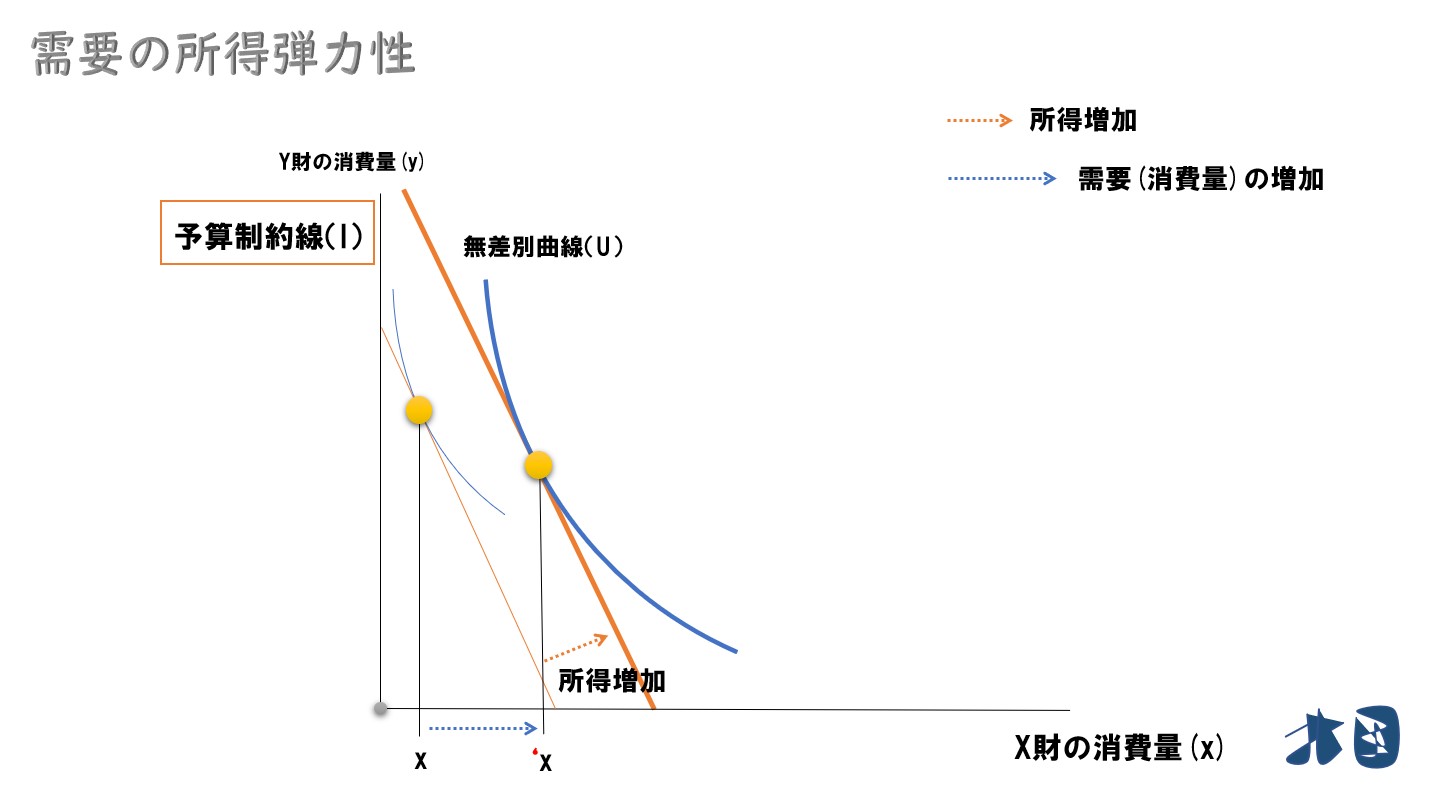
「需要の所得弾力性」は、財の種類を判別したり、計算問題でよく登場します。
- 需要の所得弾力性とは?
- 所得弾力性の大きさと財の種類
- 所得弾力性の計算方法
需要の所得弾力性に関わる話を、このページに簡単にまとめました。
需要の所得弾力性とは?
需要の所得弾力性
所得が変化するとき、どれくらい需要が変化するかを数値化したもの。
需要の所得弾力性は次の式で表されます。
需要の所得弾力性(ε)の式
需要の所得弾力性(ε)=需要の変化率(%)/所得の変化率(%)
※ε=イプシロン
(Em)や(Ei)と表記することもあります。
E=Elasticity(弾力性)
m=Money income/i=Incomeの頭文字


需要の所得弾力性(ε)の大きさが
- 1以上
- 1~0
- 0
- 0より小さい
という基準で財の分類が出来ます。
まずは、それぞれで何が言えるのかを見ていきます。
上級財(奢侈品)の場合(ε≧1)
所得弾力性(ε)が1以上の大きさ(ε ≧1)なら
この財は上級財(正常財)の中でも奢侈品である。
「奢侈品(ぜいたく品)」は次のような特徴があります。
- 所得が少し増えれば、一気に需要が増える
- 所得が少し減れば、一気に需要が減る
例えば
高級ステーキ(肉)

所得が増えれば、少し高級なお肉を食べよう!と考える人が増えます。逆に、所得が減ったのに、高級な肉を食べよう!と思う人は一般にいません。
つまり、所得が増えた時に、一気に需要が増える高級肉などは、奢侈品(ぜいたく品)に分類されます。
高級ステーキ(肉)は「需要の所得弾力性が1以上になる(はず)」なので奢侈品(ぜいたく品)だと言えます。
上級財(必需品)の場合(1>ε>0)
所得弾力性(ε)が1よりも小さく0よりも大きい(1>ε>0)なら
この財は上級財(正常財)の中でも必需品である。
「必需品」は次のような特徴があります。
- 所得が少し増えれば、少しだけ需要が増える
- 所得が少し減れば、少しだけ需要が減る
例えば
ペットボトルのお茶

日本人の国民的飲料物のお茶ですが、お金に余裕が出てくると、コンビニでペットボトルのお茶を買うことに抵抗がなくなります。
逆に所得が減り始めると、少しずつマイボトルにお茶を入れて、節約しようと思い始めます。
ただし、高級肉とは違って、所得が増えた(減った)からと言って、「ペットボトルのお茶をたくさん買う(全く買わない)」という程ではないです。
つまり、所得が増えた時に、少しだけ需要が増える一方で、所得が減ったときに、少しだけ需要が減るペットボトルのお茶は、必需品に分類されます。
ペットボトルのお茶は「需要の所得弾力性が1より小さく、0よりも大きくなる(はず)」なので必需品だと言えます。
中級財の場合(ε=0)
所得弾力性(ε)が0に等しい(ε =0)なら
この財は中級財(中立財)である。
「中級財(中立財)」は次のような特徴があります。
- 所得が増えても(減っても)、需要は変わらない
例えば
持病の薬などが中級財に近いです。
所得が増えようと減ろうと、飲む薬の量は変わりません。
ただし、所得が減ると飲む薬の量を減らそうとする人もいるので、完ぺきに中級財と言えるわけではありません。このように考えると、完ぺきに中級財となる財は基本はないと考えて良いです。
下級財の場合(ε<0)
所得弾力性(ε)が0よりも小さい(ε< 0)なら
この財は下級財(劣等財)である。
「下級品(劣等財)」は次のような特徴があります。
- 所得が増えれば、需要が減る
- 所得が減れば、需要が増える
例えば
カップ麺

お金に余裕が出てくると、カップ麺などを食べる機会が減ります。逆に所得が減り始めると、カップ麺で済ませてしまおうと思う人が増えてきます。
つまり、所得が増えた時に、需要が減る一方で、所得が減ったときは、需要が増えるカップ麺は、下級財(劣等財)に分類されます。
カップ麺は「需要の所得弾力性が0より小さくなる(はず)」なので下級財だと言えます。
さらに詳しく
ちなみにですが、上級財や下級財は、相対的なものです。どの財も状況により、上級財にも下級財にもなります。
- カップ麺とステーキが並べば「カップ麺は下級財」「ステーキは上級財」になります。
- しかし、カップ麺とパンの耳が並べば「カップ麺は上級財」「パンの耳は下級財」になります。
このように、上級財や下級財の分類は置かれた状況によって変化するので、柔軟に考えることが必要です。
「需要の所得弾力性」の求め方(計算)

計算問題では需要の所得弾力性の式を使います。
需要の所得弾力性(ε)の式
需要の所得弾力性(ε)=需要の変化率(%)/所得の変化率(%)
=「ΔD/D」/「ΔM/M」
※Δ= (変化後の数字)-(変化前の数字)で求められます。ただし、微分が必要なときは微分して求めます。
所得弾力性を求める問題は大きく2つのパターンがあります。
- 1つは、所得・消費量の変化前後の数字が分かっているパターン
- もう1つは需要関数から求めるパターン
順番に見ていきましょう。
通常の計算で求める

普通に計算できるのは、変化前と変化後の数値が分かる場合です。
例えば
- 所得が1,000円で、消費量(需要量)が10の財がある
- 所得が1,100円になり、消費量が20となった
需要の所得弾力性を求めて、この財が奢侈品か必需品かを判断する。
計算方法
変化前と変化後の数値が分かるため、微分をせずに普通に計算します。
- 所得変化:(1,100-1,000)/1,000=0.1
- 需要変化:(20-10/10)=1
「需要の変化率=1」/「所得の変化率=0.1」=10
需要の所得弾力性が、1よりも大きいため、この財は奢侈品である。


需要関数から求める(微分)

例えば
- 効用関数「U(x, y)= x・y」
- 所得(M)=90
- X財の価格が1
- Y財の価格が3
このとき、消費者均衡点におけるX財の需要の所得弾力性はいくらか?
まず
消費者均衡点は、最適消費点のこと
なので最適消費点(効用最大化)を求めるところから始める。
ここからは、最適消費点の求め方を知っている前提で計算していきます。もし分からない所が出てきたら、最適消費点の求め方で確認してください。
ここでは「予算制約線の傾き=限界代替率」で最適消費点を求めます
① 予算制約線の傾きを求める
- 「予算制約線(M)=(X財価格×X財の消費量)+(Y財価格×Y財の消費量)」
「X財の消費量=x」「Y財の消費量=y」として「予算制約線:90=1x+3y」とします。
- 90=1x+3y
- 3y=-1x+90
- y=-(1/3)x+30
② 効用関数から限界代替率を求める
「U=xy」から「y=U/x」へ変形後に微分します。
- 「y=U/x」を微分する※と‥
- 「-U/xの2乗(=-U・xの-2乗)」
- 「-U/xの2乗」に「U=xy」を代入
- 「-U(=xy)/xの2乗」⇒「-xy/xの2乗」=「-y/x」
※分数は「マイナス○乗」と表記されることに注意する。そのため「1/x」は「xの-1乗」と表記できます。この状態から微分する。微分は「乗数を1減らして手前に持ってくる」ので、「xの-1乗」の乗数を1減らすと「xの-2乗」となります。-1を手前に持ってくるので「-1・xの-2乗」です。以上より「-1・xの-2乗」ですが、分数で表記すると「-1/xの2乗」となります。
③ 予算制約線の傾き=限界代替率で最適消費点を求める
「-1/3」=「-y/x」
- y= (1/3)x
- x=3y
「予算制約線:M=90=1x+3y」より
M=1x+3(1/3x)
M=1x+1x
M=2x(①と②へ)
① M=90より
x=45(X財の最適消費点)
② x=(1/2)M(X財の需要関数)
最適消費点を求めた後、X財の需要関数が必要になるので、x=○○Mの形にした式(需要関数)も計算してください。
- M=90
- x=45
- x=(1/2)M(X財の需要関数)
ここで
需要の所得弾力性(ε)の式を変形します。
需要の所得弾力性(ε)の式
需要の所得弾力性(ε)=需要の変化率(%)/所得の変化率(%)
=「ΔD/D」/「ΔM/M」
⇒「ΔD/ΔM」×「M/D」
「需要の変化量(ΔD)/所得の変化量(ΔM)」×「元の所得(M)/元の需要量(D)」
「ΔD/ΔM」の部分が、まだ求められていません。
そこで「x=(1/2)M(X財の需要関数)」をMで微分します。
- (Δx/ΔM)=(1/2)となります
微分は乗数を1つ減らして手前に持ってくる計算です。(1/2)Mは「(1/2)・Mの1乗」です。「Mの1乗」の1を手前に持ってきて「(1/2)×1=(1/2)」とします。また、Mの0乗になりますが「0乗=1」なのでM=1でMが消えます。
- M=90
- x=45
- Δx/ΔM=1/2
全ての情報がそろったので、先ほどの式に当てはめます。
「ΔD/ΔM」×「M/D」
「需要の変化量(ΔD)/所得の変化量(ΔM)」×「元の所得(M)/元の需要量(D)」
※ちなみに「需要量(D)=X財の消費量(x)」なので「D=x」です。
X財の所得弾力性は・・
所得弾力性(ε)=(1/2)・(90/45)=1 となります。


ちなみに、最適消費点までの計算は、ラグランジュ未定乗数法や、その他の計算方法がたくさんあるので、自分がやり易い方法を使ってください。