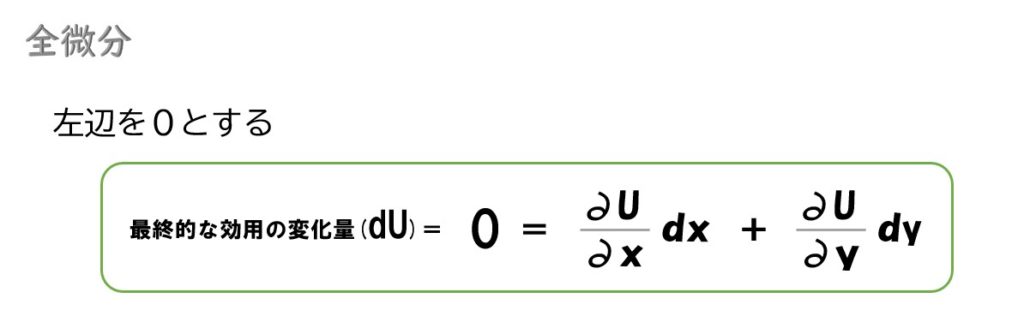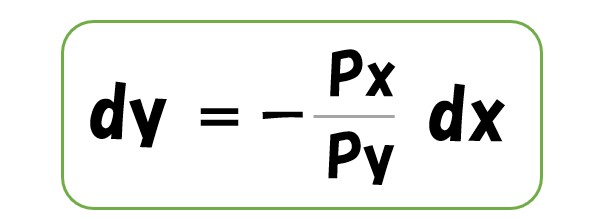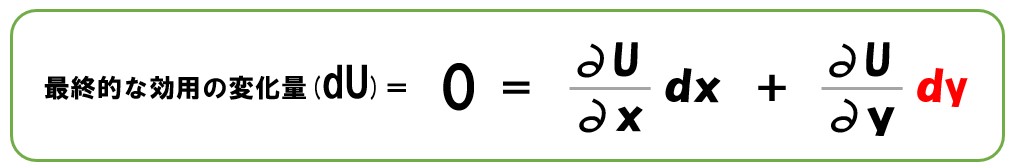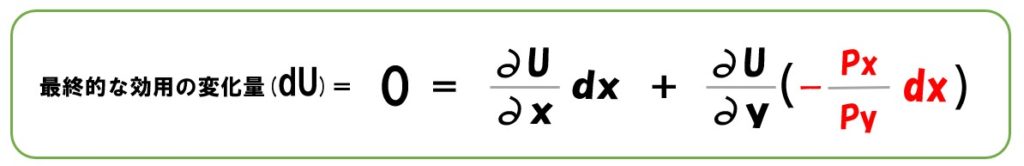いきなり教科書で登場してきて、イメージもしづらい「限界効用均等の法則」
- (加重)限界効用均等の法則とは?
- (加重)限界効用均等の法則の公式
- (加重)限界効用均等の法則の証明
- 公式を使って最適消費点(効用最大化)を求める
「限界効用均等の法則」で分かりづらいポイントを、念入りにまとめています。
限界効用均等の法則・加重限界効用均等の法則

(加重)限界効用均等の法則
最適消費量(効用最大化)が実現する2財の消費の組合わせでは、1円当たりの2財の限界効用が等しく(均等に)なることを「限界効用均等の法則」と呼ぶ。
また、1円当たりの限界効用を「加重限界効用」と呼ぶため「加重限界効用均等の法則」と呼ばれることが多い。
限界効用逓減の法則をゴッセンの第一法則と呼ぶのに対して、ゴッセンの第二法則とも呼ばれる。


例えば
- 白米と鮭

「(加重)限界効用均等の法則」の説明のときに、よく登場するのがご飯とおかずです。
ご飯を食べていると「白米」「鮭」を交互に食べていきます。
白米を食べていると、途中で鮭を食べたくなります。これは、白米を食べ続けると「限界効用逓減の法則」により、1口あたりの得られる限界効用が減少していくためです。
「白米」の限界効用が減少するため、途中から「鮭」を食べた時の限界効用の方が高くなります。


ここで
食事が終わる直前を考えてみましょう。
私たちは「白米⇒鮭」「鮭⇒白米」という風に、食べるものを途中で変えます。これは、限界効用逓減の法則によって、同じものを食べ続けると得られる限界効用(満足度)が減少していくためです。
しかし、お腹が膨れてきて「白米」「鮭」どちらを食べても限界効用(満足度)が得られなくなっていきます。言い換えれば「どっちも、もう要らない」です。
最終的に、お腹がいっぱいになれば「白米」「鮭」もどちらも食べられなくなります。つまり、1口で得られる限界効用が、どちらも(等しく)「0」になっていると言えます。
仮に、白米の限界効用が「1」あるなら、まだ白米を食べ続けているはずです。つまり、もう食べられない=白米・鮭のどちらからも満足度が得られない状態なので「白米の限界効用(0)=鮭の限界効用(0)」と言えます。※分かりやすいように、どちらも限界効用=0になると考えています。
ポイント
「お腹がいっぱい」というのは、満足度がマックスで幸せな状態です。この状態を最適消費点(効用最大化)と考えれば、「最適消費点(効用最大化)では2財の限界効用は等しくなる」と言えます。
究極的には「白米1円分」「鮭1円分」のレベルで限界効用が等しくなると考えたのが「(加重)限界効用均等の法則」です。


さらに詳しく
「(加重)限界効用均等の法則」がゴッセンの第二法則と呼ばれる理由。
ゴッセンは「限界効用逓減の法則」「(加重)限界効用均等の法則」を唱えた経済学者です。
限界効用は初めが一番大きく次第に減少していく法則=「限界効用逓減の法則」をゴッセンの第一法則と呼びます。
「白米と鮭」の例で説明したように、最初に「限界効用逓減の法則」が表れて、最後に「(加重)限界効用均等の法則」が出現するという流れがあります。
つまり「限界効用逓減の法則(第一法則)」⇒「(加重)限界効用均等の法則(第二法則)」という関係になっています。
公式の数学的な証明
ポイント
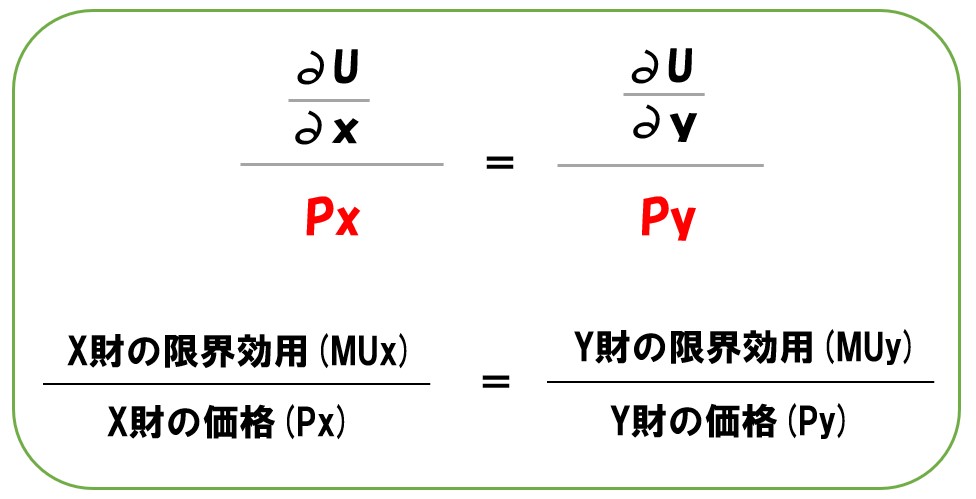
「最適消費量(効用最大化)が実現する2財の消費の組合わせでは、1円当たりの2財の限界効用が等しく(均等に)なる」ことを式で表すと次の通りになる。
「MUx/Px」=「MUy/Py」
「X財の限界効用/X財の価格」=「Y財の限界効用/Y財の価格」
※X・Yどちらも財1単位当たりの限界効用・価格です。「X財1つを消化した時の限界効用」と「X財1つ当たりの価格」を意味しています。
「(加重)限界効用均等の法則」の公式的なものは上の通りです。
どうしてこうなるのか?を考えてみましょう。
ここで
- 効用関数=U(x, y)
- X財の価格=Px
- Y財の価格=Py
- X財の消費量=x
- Y財の消費量=y
この時、最適消費点ならば、X財・Y財の限界効用が等しくなることを証明する。
まずは「効用関数=U(x, y)」からX財・Y財の限界効用を求めます。
全微分する
- 「効用関数=U(x, y)」を全微分します。
ポイント
ここでの全微分の意味は、効用関数(U)=「〇x」×「〇y」の「x」「y」の大きさが変化した時に、効用(U)の大きさがどんな変化をするか?を知るためです。
⇒「x」「y」の変化量(消費量)に対して、効用がどう増減するか=限界効用を求めることになります。
全微分の意味が分からなければ、「効用関数=U(x, y)」を全微分をすると「全体の効用の変化量=X財の限界効用×変化量 + Y財の限界効用×変化量」という式に変形できると解釈してください。
それぞれを文字に置き換える
- 「x (X財の消費量)」の変化量を「dx」
- 「y (Y財の消費量)」の変化量を「dy」
- 最終的な効用(U)の変化量を「dU」
「d」は「ディー」などと呼びます。
- 「∂U/∂x」=X財を消費した時の限界効用(MUx)
- 「∂U/∂y」=Y財を消費した時の限界効用(MUy)
※「∂U/∂x」「∂U/∂y」が限界効用(MU)を表している理由はこちらで確認できます⇒ 限界効用・限界効用逓減の法則とは?求め方も含めて簡単にわかりやすく※「財が2つの場合」を参照
ポイント①
- 左辺を「dU=0」とする


「限界効用=0」は、限界効用が変化しないことを表す。
限界効用には「財を消費すればするほど次第に増加する効用も小さくなる」という限界効用逓減の法則があります。
経済学では、消費者は与えられた条件の中で「財を消費しても限界効用が増えない状態=0」まで財を消費すると考えています。
仮に、ある財を好きなだけ消費できると考えた場合、効用が得られる限り、消費者はその財を消費し続けます。そして、いずれ財を消費しても効用が得られない状態(限界効用=0)に到達します。
また、限界効用が「1」得られるなら、財をもう1つ消費する方が合計の効用が高くなります。つまり「限界効用=0になるまで消費を続ければ、自然と消費者の満足度が最大」になります。
この状態は、X財・Y財の2つでも同じです。通常は、X財・Y財も「限界効用=0」になるまで消費を続けると考えます。
ポイント
限界効用(MU)が最も効率的な場合、最終的な効用の変化量(dU)は「0」となる。
そのため、効用関数を全微分した式(左辺)を「dU=0」と考える。
ちなみに数学では、偏微分可能な2変数関数が(a, b)で極値をとる場合「(∂U/∂x)(a, b)」=「(∂U/∂y)(a, b)」=「0」になるという話があります。それと理屈は同じです。この証明をすると長くなるので置いておきます。
先ほどの式で見ると
ポイント②
- 上の式に予算制約線の式を代入する
ここで予算額を「I」とします。
※予算=「(X財の消費量)×(X財の価格)」+「(Y財の消費量)×(Y財の価格)」となります。
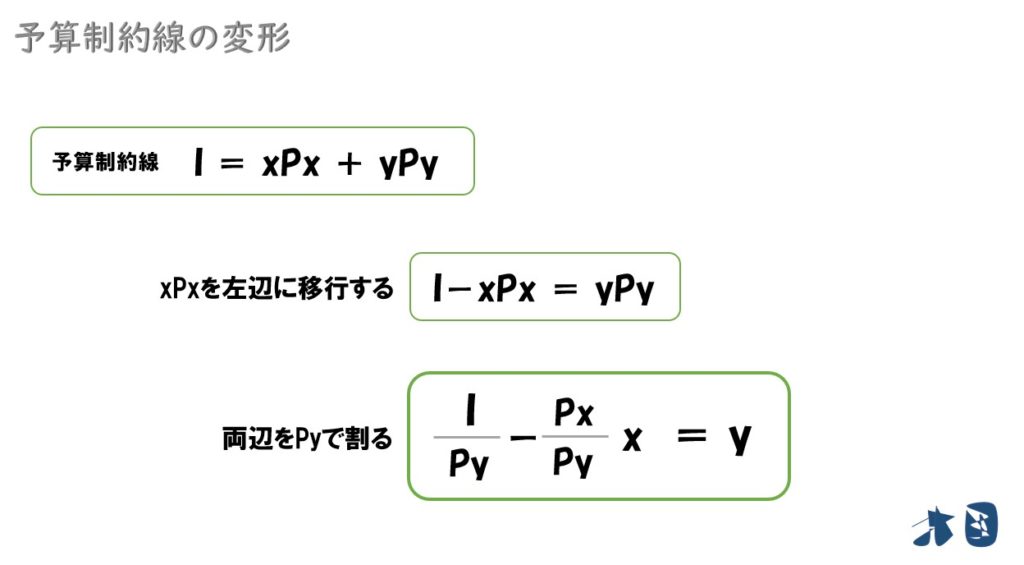
- 予算制約線「I=xPx+yPy」
予算制約線を「y=」の形にする
ここで、先ほどの式は変化量を見ていた式なので、予算制約線も同じことをします。
それぞれを文字に置き換える
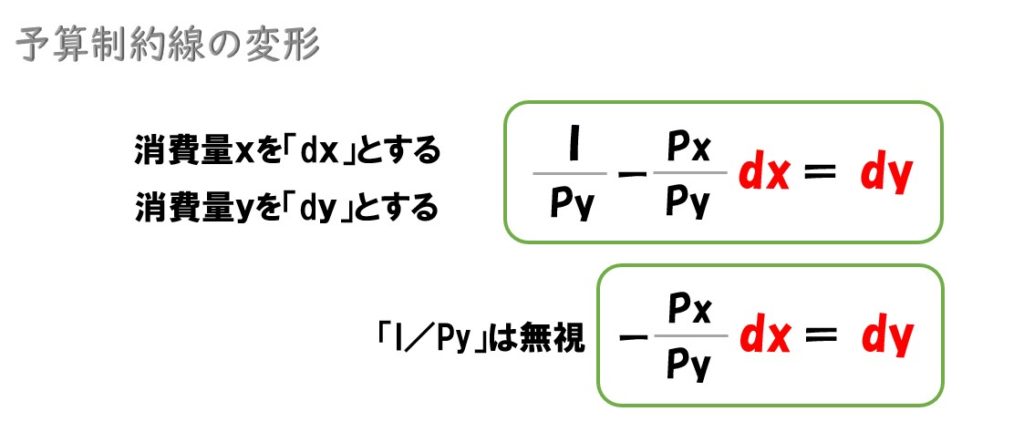
- 「x (X財の消費量)」の変化量を「dx」
- 「y (Y財の消費量)」の変化量を「dy」
注意ポイント
予算制約線の「y=I/Py-(Px/Py)x」ですが、変化量を見たい場合は「I/Py」は無視されます。
※「I/Py」は切片なので「y」「x」の消費量が変化しても、数字が変わりません。変化するのは下記の「消費量x・消費量y」のみで、「x」「y」が含まれていない「I/Py」は無視できる。
- X財の価格=Px
- Y財の価格=Py
- X財の消費量=x
- Y財の消費量=y
ちなみに「X財の消費量=x」を「dx」と置いたのは、変化量で考えているためです。
通常は「x=10」ならば「x財の消費量=10」という意味です。
しかし、変化量の場合は「dx(変化量)=40⇒消費量が10から50に変化した時」という意味合いになります。
最終的にコレ
上の式を、先ほどの式に代入します。
「dy」に代入する
あとは計算するだけです。ひとまず、ここまでの流れをまとめましょう!
ここまでの流れ
- 与えられた条件から限界効用を求めるために効用関数=U(x, y)を全微分する
- 全微分後の式で左辺を「dU=0」とする
- 予算制約線から「y=」の式を求める
- 1.で求めた式に合わせるために、3.の式にある「x・y」を「dx・dy」とする
- 1.の式に4.の式を代入して計算する


実際に計算する
途中でも書きましたが「∂U/∂x」「∂U/∂y」は限界効用を意味します。
- 「∂U/∂x」=X財の限界効用(MUx)
- 「∂U/∂y」=Y財の限界効用(MUy)
※限界効用についてはこちらで確認できます⇒ 限界効用・限界効用逓減の法則とは?求め方も含めて簡単にわかりやすく※「財が2つの場合」を参照
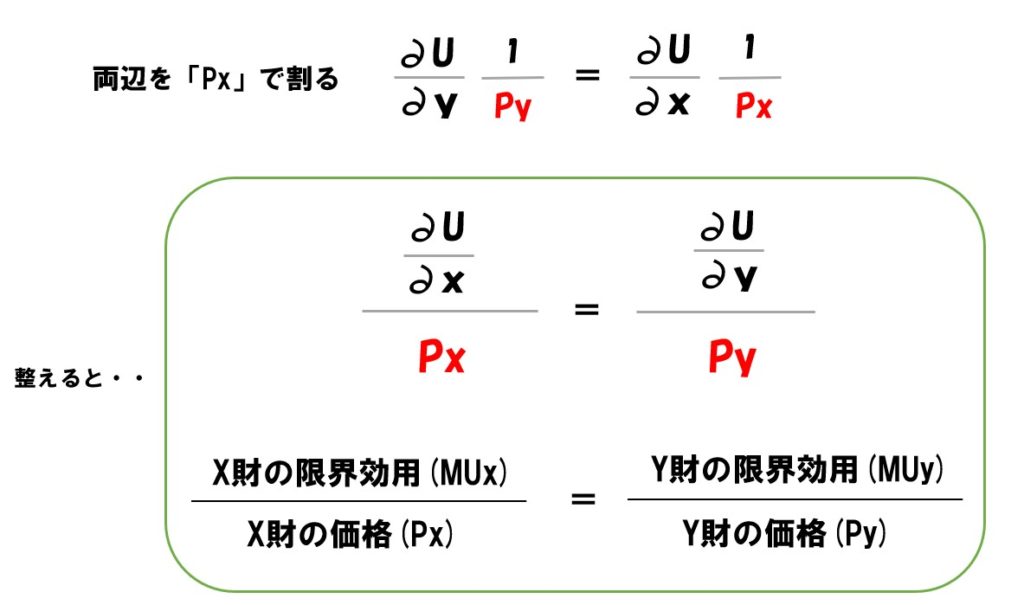
上記の式から、最適消費点では2財の1円当たりの限界効用は等しくなったことが分かる。


(加重)限界効用均等の法則
「MUx/Px」=「MUy/Py」
「X財の限界効用/X財の価格」=「Y財の限界効用/Y財の価格」
上の式は「MUx:MUy」=「Px:Py」と変形できる※ので、次のようにも言えます。
※「A/B=C/D」の両辺に「B/C」を掛けると「A/C=B/D」と出来ます。「A/C=A:C」です。
「X財の限界効用:Y財の限界効用」=「X財の価格:Y財の価格」
最適消費点の求め方

加重限界効用均等の法則は、効用最大化(最適消費を求める)問題で登場することが多いです。
例題を使って計算方法を見ていきましょう!
例えば
- 効用関数U(x, y)=xy
- X財の価格 (Px)=10
- Y財の価格 (Py)=30
- 予算=600
この時の最適消費量(効用最大化)を「加重限界効用均等の法則」を使って求める。
「MUx/Px」=「MUy/Py」
「X財の限界効用/X財の価格」=「Y財の限界効用/Y財の価格」
初めに
- 「X財の限界効用」と「Y財の限界効用」を求める。
限界効用を求めるためには「効用関数U(x, y)=xy」を微分する必要があります。公式を求めるときは全微分をしましたが、実際の数字を計算する時は、xとyでそれぞれ偏微分をする事になります。
X財の限界効用(MUx)
「xy」をxで偏微分すると「1×y」なので「y」になります。
「xy」をxで偏微分する場合は「x」だけを微分すればOKです。「y」はそのままになります。ちなみに「x」は「x=(xの1乗)」なので、微分すると「1xの0乗」となり「1」となります。微分は「乗数を1減らして手前に持ってくる」という作業です。「0乗=1」になることも覚えておきましょう。
Y財の限界効用(MUy)
「xy」をyで偏微分すると「x×1」なので「x」になります。
以上より
- X財の限界効用(MUx)=y
- Y財の限界効用(MUy)=x
ポイント
「MUx/Px」=「MUy/Py」より「y/10」=「x/30」
最初に、X財の価格 (Px)=10・Y財の価格 (Py)=30と与えられていることを忘れずに。
両辺に30を掛けると「3y=x」
次に
予算制約線の式を求めます。
与えられた条件から「600=10x+30y」と式を作れます。
最初に、予算=600と与えられているので忘れずに。
「y=」の式にする
- 30y=-10x+600
- y=-(1/3)x+20
予算制約線の式に「3y=x」を代入する。
- y=-(1/3)・3y+20
- y=-y+20
- 2y=20
- y=10
最後に
今度は「y=10」を予算制約線の式に代入する
- 10=-(1/3)x+20
- (1/3)x=10
- x=30
したがって最適消費点は「x=30」「y=10」※(x, y)=(30, 10)とも表記できる。