消費者理論で頻出の「最適消費・効用最大化」
- 最適消費・効用最大化とは
- 最適消費の求め方
- 効用最大化条件・計算方法
- 効用最大化問題の解き方
最適消費(効用最大化)を求める問題の意味が分からない人、解き方が分からなくなる人に向けて、簡単にまとめています。
最適消費と効用最大化
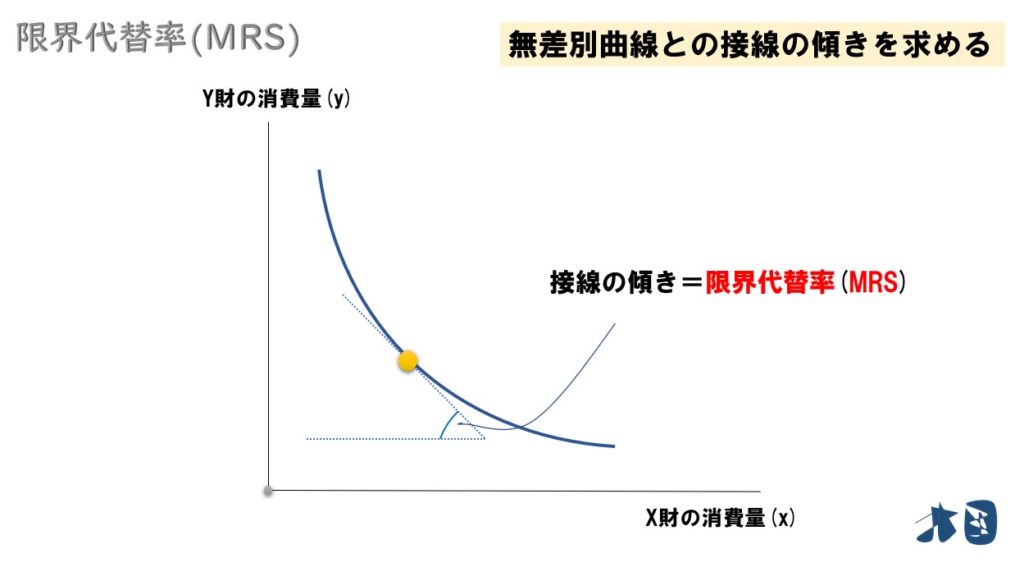
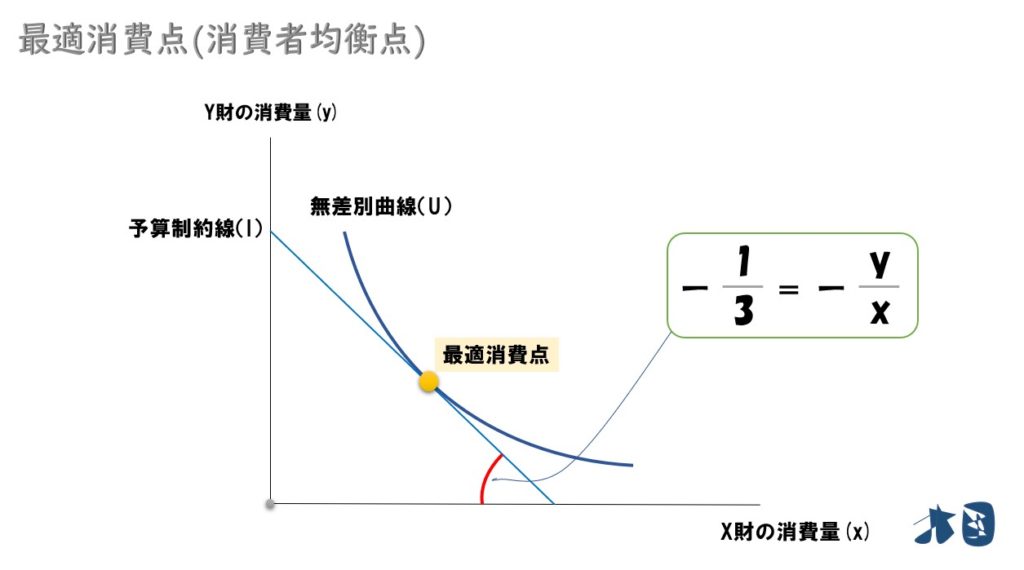
最適消費とは?
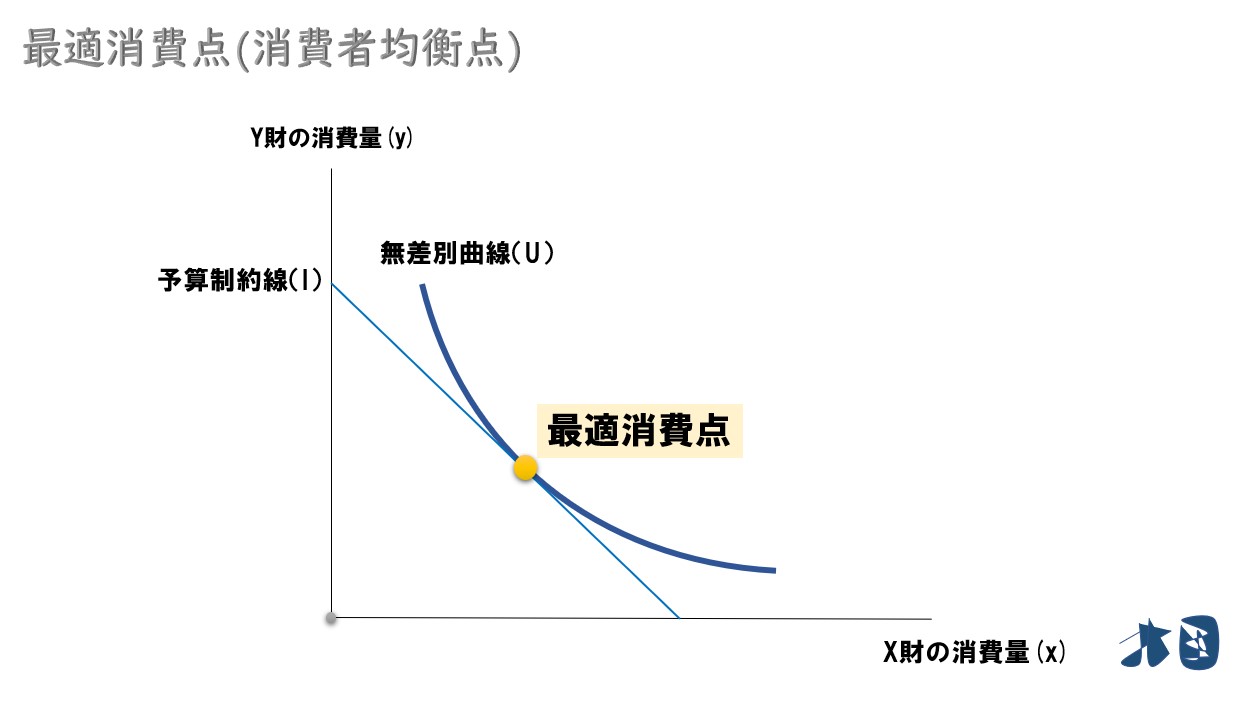
一定の予算制約のもとで、消費者の効用(効用水準)が最大化する消費の組合わせを最適消費(最適消費点・最適消費量・消費者均衡点・最適消費計画)という。その最適消費を求める問題を「効用最大化問題」と呼ぶ。
※問題を解くときは、予算制約線に接する無差別曲線上の財の組合わせ(=点)を求めるため、最適消費点(消費者均衡点)という言葉で表されることが多いイメージです。


ポイント
ミクロ経済学では、消費者は限られた所得(予算制約)のなかで、自身の効用を最大化させるために行動すると考えています。
この分野では
- 「効用関数」
- 「無差別曲線」
- 「予算制約線」
などが出てきましたが、これらを使って消費者の行動を分析するのが目標です。
最適消費点(消費者均衡点)の求め方

最適消費点・最適消費量・消費者均衡点・最適消費計画などと言いますが、ここでは最適消費点と呼びます。
最適消費点を求める際に重要となる「考え方」「計算式」「計算方法」を順番に見ていきましょう。
考え方

① 財をたくさん消費した方が効用が高まるので、予算を全部使ってたくさん財を消費する方が効用が高くなるはず。「予算を全部使う」=「予算制約線上」
② 消費の組合わせは「無差別曲線」で表されているため「予算制約線上」にある「無差別曲線上」の消費の組合わせが一番効用が高い。「予算制約線」=「無差別曲線」
③ このとき、数学的に考えると予算制約線と無差別曲線の傾きが等しい。
④ 無差別曲線の傾きは限界代替率なので「予算制約線=限界代替率」となる。
ポイント
最適消費点を求める時は「予算制約線=限界代替率」となる消費の組合わせを求める。


確認しよう!
グラフで見ると
式で考える(効用最大化条件)

1つ前の段落で紹介した「考え方」を理解している前提で話を進めます。
ポイント
消費者の効用最大化が実現するとき、次の2つが一致する。
- 予算制約線の傾き
- 限界代替率(無差別曲線の傾き)
この2つの条件を数式で「予算制約線の傾き=限界代替率」と表現したものを効用最大化条件と呼ぶ。問題を解くときは、この関係を使って計算するので数式でも理解できるように頑張ろう。
step
1予算制約線の傾き
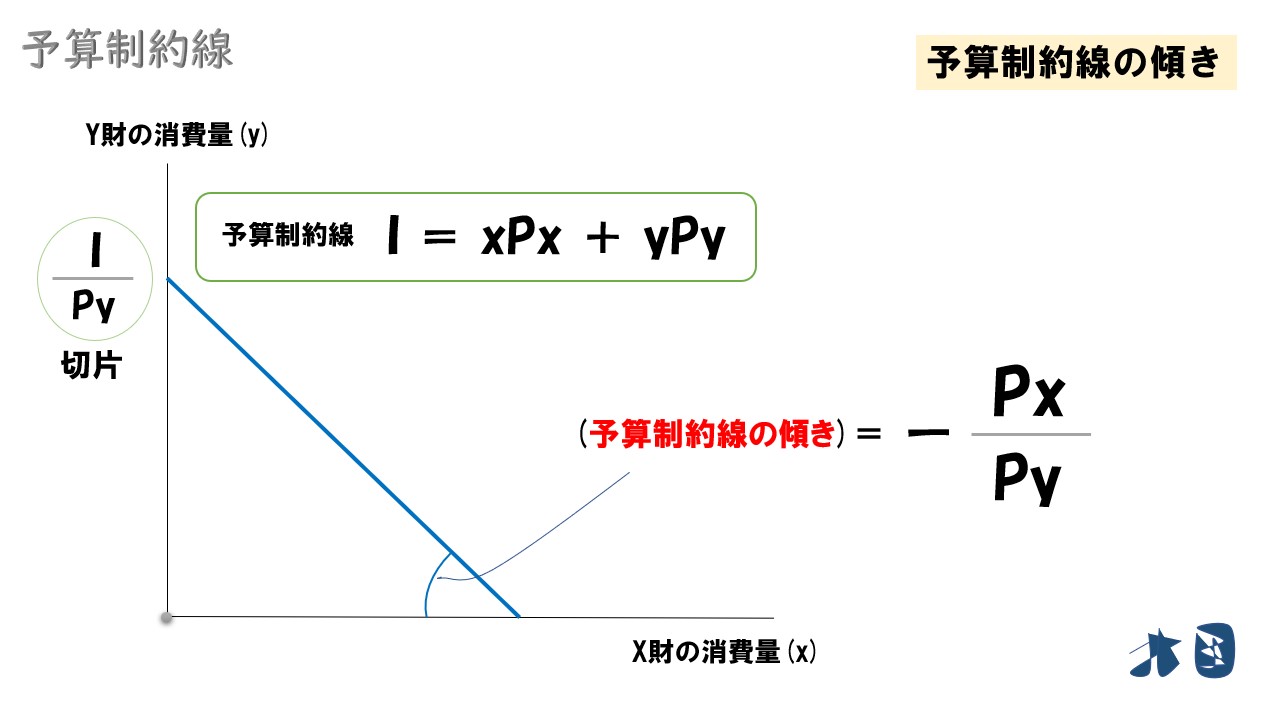
予算制約線を「I=xPx+yPy」とする
- X財の消費量=x
- X財の価格=Px
- Y財の消費量=y
- Y財の価格=Py
- 予算=I(income[所得]の頭文字を取っている)
このとき
「予算制約線の傾き」とはグラフの部分を指す。
予算制約線の傾き
予算制約線「I=xPx+yPy」の傾き⇒「-(Px/Py)」
※予算制約線の傾きは、2財の価格比(相対価格)になっている。
計算過程
・I=xPx+yPy
・yPy=I-xPx
・y=(I-xPx)/Py
・y=I/Py-xPx/Py
・y=I/Py-(Px/Py)x
・y=-(Px/Py)x+I/Py
step
2限界代替率(無差別曲線の傾き)
「限界代替率(無差別曲線の傾き)」とはグラフの部分を指す。
限界代替率
限界代替率(無差別曲線の傾き)⇒「-(dy/dx)」
この「dy」「dx」は、微分したことを意味しています。というのも、予算制約線は直線だったため、簡単に傾きを求めることが出来ましたが、無差別曲線はカーブを描いているため、普通の計算では傾きを求めることが出来ません。そこで微分をするわけですが、「d」は無差別曲線を微分したことを意味した記号です。ここでは「-(dy/dx)」を「無差別曲線を微分して傾きを求めたもの=限界代替率」と考えてください。具体的な数字や計算は、次の段落の「計算方法」で紹介します。
step
3(おまけ)2財の限界効用の比
初めはステップ2まで理解していればOKですが、おまけで紹介しておきます。
2財の限界効用の比
2財の限界効用の比⇒「MUx/MUy」
数学的な話なので、無理な人は飛ばして大丈夫です。
無差別曲線の傾きを求める過程で効用関数(U)を微分して「=0」と置きます(効用関数=無差別曲線と考えて差し支えありません)。
ここから、限界代替率(無差別曲線の傾き)⇒「-(dy/dx)」が求められるのですが、式には続きがあり「-(dy/dx)=(MUx/MUy)」と求められます。それぞれ「X財から得られる限界効用(MUx)」と「Y財から得られる限界効用(MUy)」を意味しており、この関係から2財の限界効用の比と表現します。
step
4step1~3をまとめる
効用最大化条件
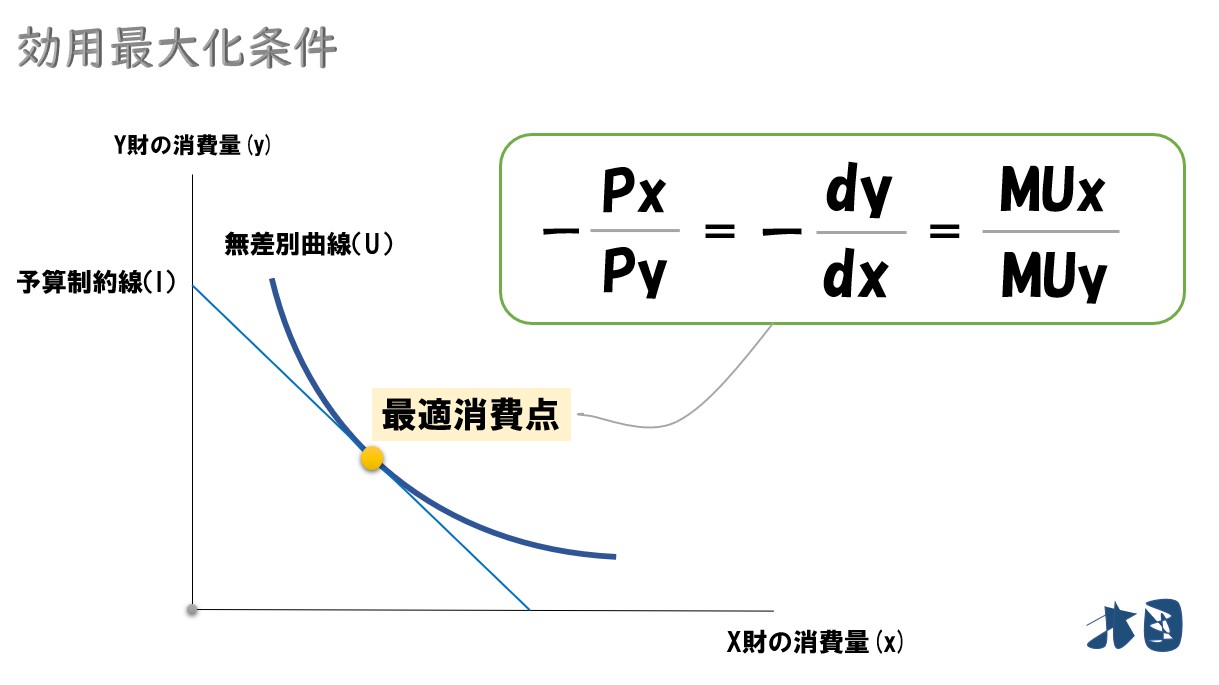
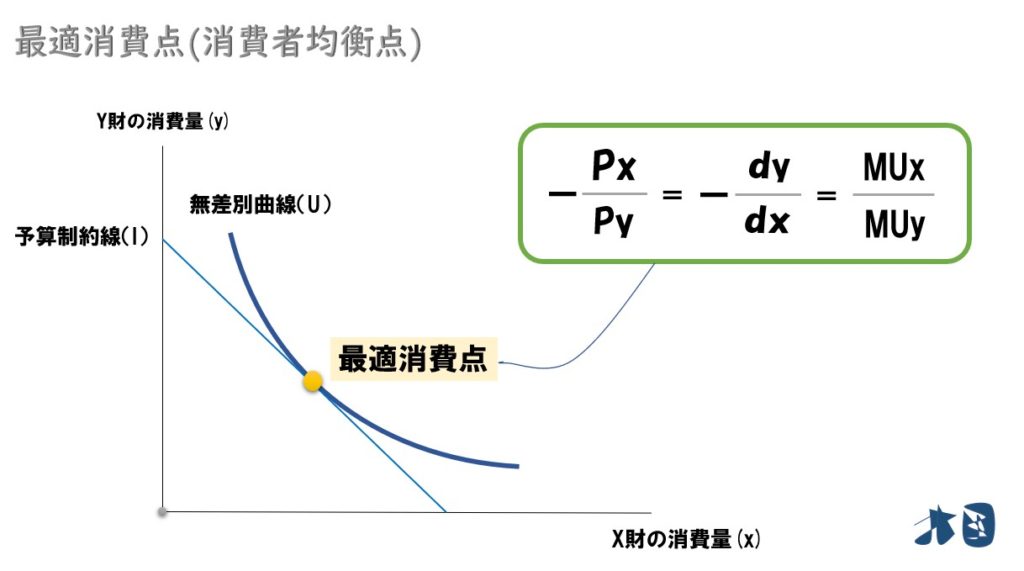
3つの話をまとめると最適消費点では次の数式が成り立つ。
「-(Px/Py)」=「-(dy/dx)」=「MUx/MUy」
「価格比(相対価格)=限界代替率=2財の限界効用の比」これを「効用最大化条件」と呼びます。最適消費点では、上記の効用最大化条件が成立することを使って計算問題を解くので、しっかりと理解しましょう。次の段落で例題を解きます。


確認する
予算制約線の傾きが「-(Px/Py)」になる理由が分からない人
⇒【予算制約線】式の意味・傾きと相対価格について分かりやすく
限界代替率「-(dy/dx)」と2財の限界効用の比「MUx/MUy」が分からない人
⇒【限界代替率】求め方・計算方法を確認する
計算方法

最適消費点
最適消費点では次の式が成り立つ。
「-(Px/Py)」=「-(dy/dx)」=「MUx/MUy」
「価格比(相対価格)=限界代替率=2財の限界効用の比」
計算問題は「最適消費点では上の式が成立する」ことを使って解いていきます。
よくあるパターン
- 効用最大化が実現する最適消費点を求める
- 効用水準が最大となる2財の消費の組合わせを求める
- 消費者の最適消費計画を求める
- 合理的な消費者だった場合の最適消費量を求める
- ある家計の消費者均衡点を求める
最適消費点という言葉が入っていなくても、最終的に求めるものは同じです。
例題
次の条件のとき、最適消費点を求める
- 効用関数「U(x, y)= x・y」
- 所得(I)が300
- X財の価格が10
- Y財の価格が30
step
1予算制約線の式に数字を入れる
- 「所得(I)=(X財価格×X財消費量)+(Y財価格×Y財消費量)」
⇒「300=10x+30y」
効用関数が「U(x, y)= x・y」と与えられているので「x=X財の消費量」「y=Y財の消費量」と考える。
step
2「予算制約線の傾き」を求める
- [Step1]で予算制約線「300=10x+30y」と分かったので傾きを求めます。
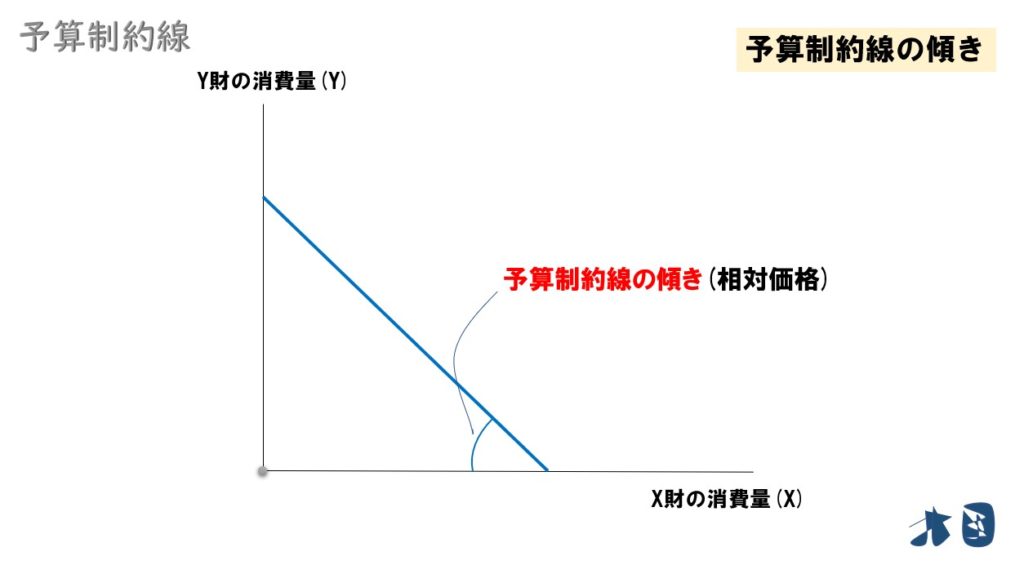
予算制約線の傾きは「価格比(相対価格)」とも表現されます。
今から求めるのはコレ
ポイント
グラフの傾き部分を求めるために予算制約線を「縦軸(y)=●●x」の形に変形します。
計算すると
- 300=10x+30y
- 30y=-10x+300
- y=-(1/3)x+10
傾きは「-1/3」
step
3限界代替率(MRS)を求める
- 効用関数(無差別曲線)から「限界代替率」を求めます。
ポイント
効用関数(無差別曲線)から限界代替率(MRS)を求める方法は2つあります。
- 無差別曲線の傾きを直接求める(-dy/dx)
- 2財の限界効用(MU)を求める(MUx/MUy)
ちなみに②の求め方が教科書に載っていることが多いです。
ここからは①の無差別曲線の傾きを計算することで限界代替率(MRS)を求めます。その後に、別解として②の2財の限界効用(MU)を求める方法で限界代替率(MRS)を求めます。
この問題に関しては②の方が計算は簡単ですが、いかんせんイメージしづらいので①から説明します。
そもそも限界代替率(MRS)の計算を初めてするという人は、次の記事で計算方法や考え方を理解しておくと良いかもしれません⇒【限界代替率・限界代替率逓減の法則】意味や求め方・計算方法を分かりやすく理解する
①
- 無差別曲線の傾きを求めることで限界代替率(MRS)を求める
⇒まず、無差別曲線の傾きを求めるために効用関数(無差別曲線)を微分します。
効用関数(無差別曲線)を微分する理由
効用関数(無差別曲線)は緩やかなカーブを描いているため、普通の計算では傾きを求めることは出来ません。
そのため、効用関数(無差別曲線)上に、ある特定の点に接線を引いて「接線の傾き」を求めます。微分は文字通り、グラフを細かく分けて1つの点として処理する方法なので、微分をすることで効用関数(無差別曲線)の傾きを求められます。
今から求めるのはコレ
なので
「効用関数:U=xy」を微分して傾きを求めます。
「効用関数U(x, y)= x・y」は「U=xy」という意味です。
計算方法
はじめに効用関数を「y=●●x」の形にする
なぜ「y=●●x」にするかというと、”グラフの傾き”を求めることと関係しています。グラフを見ると分かる通り、グラフの傾きは縦軸を基準にして考えています(予算制約線の傾きを求める時と同じ)。そのため、数式も「縦軸(y)=」とします(中学校の数学で「y=ax」と勉強するのと同じイメージです)。
- 「U=xy」から「y=U/x」とする
「y=U/x」を微分します。
注意ポイント
「1/x」を微分するときは注意です。誤って「1/1」と計算してしまう人がいます。
「1/x」は微分すると「-1/xの2乗」となります。
※分数は「マイナス○乗」と表記されることに注意する。そのため「1/x」は「xの-1乗」と表記できます。この状態から微分しましょう。
微分は「乗数を1減らして手前に持ってくる」ので、「xの-1乗」の乗数を1減らすと「xの-2乗」となります。-1を手前に持ってくるので「-1・xの-2乗」です。
以上より「-1・xの-2乗」ですが、分数で表記すると「-1/xの2乗」となります。
- 話を戻して「y=U/x」を微分します。
「y=U/x」⇒「-U/xの2乗(=-U・xの-2乗)」となります。
ここで
「U」という文字が邪魔なので、Uを「xとy」に置き換えます。
「U=xy」を「-U/xの2乗」に代入します。
「-U(=xy)/xの2乗」⇒「-xy/xの2乗」=「-y/x」
グラフのまさにコレを求めたことになる
②(別解)
- 2財の限界効用(MU)を求めることで限界代替率(MRS)を求める
効用関数(無差別曲線)から限界効用(MU)を求めるためには、それぞれの消費量(x・y)で偏微分すればOKです。
偏微分する理由は省略します。上記に限界効用(MU)の別記事を載せておきますので、分からない人は確認してください。
xで偏微分する(X財の限界効用)
・U=xy
・U’=y
微分は「乗数を1減らして手前に持ってくる計算方法」です。「xy」はそれぞれ「xの1乗・yの1乗」という意味です。xで微分するとき、乗数を1減らすと「xの0乗」となります。1を手前に持ってくるので「1・xの0乗・yの1乗」です。
ここで「0乗」は「1」とイコールです。以上より「1・1・yの1乗」で「yの1乗」だけが残るので、X財の限界効用(MUx)は「y」です。
yで偏微分する(Y財の限界効用)
・U=xy
・U’=x
※計算方法はxで偏微分するときの説明を参考にしてください。
以上より
・MUx=y
・MUy=x
また、冒頭で記載した通り、最適消費点では「-(Px/Py)」=「-(dy/dx)」=「MUx/MUy」が成り立つため、計算結果を当てはめる。
- MUx/MUy=y/x
あとの計算と合わせるため「-y/x」とします。
①②どちらの方法で限界代替率(MRS)を求めても「-y/x」となります。
step
4「予算制約線の傾き=限界代替率」でxとyを求める
- 予算制約線の傾き「-1/3」
- 限界代替率「-y/x」
今はこの状態
「-1/3」=「-y/x」
① 両辺にxを掛ける
y= (1/3)x
最後に
- 予算制約線「300=10x+30y」に「y= (1/3)x 」を代入します
300=10x+30 (1/3x)
=10x+10x
=20x
x=300/20=15
- 今度は予算制約線にx=15を代入して計算します
300=10×15+30y =150+30y
300-150 =30y
30y=150
y=5
したがって最適消費点は「x=15」「y=5」※(x, y)=(15, 5)とも表記できる。


最適消費点を求める問題は「効用最大化問題」という言葉で表現されます。
最後に「効用最大化問題」の解法パターンを紹介して、それぞれでどんな計算方法があるのかを紹介していきます。
効用最大化問題の解法パターン

ここでは有名な解法を4つ紹介します。
順番に見ていきましょう!
予算制約線・限界代替率を使った解法

一番オーソドックスな解き方です。
「予算制約線の傾き(価格比・相対価格)」=「限界代替率」という関係を使って計算します。
計算方法は先ほど記載した通りです。
戻って確認してみる
⇒確認する
予算制約式の代入法

この方法は、予算制約線を効用関数(U)に直接代入して計算する方法です。
先ほどの例をもとに計算をしてみます。
- 効用関数「U(x, y)= x・y」
- 所得(I)が300
- X財の価格が10
- Y財の価格が30
※予算制約線=300=10x+30y
予算制約線の式を「y=」の形にする
- 30y=-10x+300 ⇒ y=-(1/3)x+10
ポイント
この予算制約線を、効用関数「U=xy」に代入します。
U=「x・(-(1/3)x+10)」 = 「-(1/3)xの2乗+10x」
この式では「y」がなくなり「x」だけの式になったため、財が1つと考えて計算できます。
ポイント
もともと「与えられた予算の中で、効用が最大化するような2財の消費の組合わせ」を求めていました。
この式では、財が1つの状態として計算できるので、そのまま「X財の限界効用を使って効用が最大化する消費量」を求めれば良いことになります。
ちなみに
「効用が最大化するような2財の消費の組み合わせ」を求めるのに、どうして限界効用が登場するのか?と疑問に思った人のために、簡単に補足です。
「効用最大化」を別の言い方で表すと「もうこれ以上、効用を増やすことが出来ない」です。
「限界効用」は、財を1つ追加で消化したときの効用の増加分です。つまり、財を追加で消費しても、これ以上効用を増やすことが出来ない(限界効用が0)という状態を求めれば良いことになります。
ポイント
予算(所得や価格)に関する情報を効用関数に代入しました ⇒ 予算が与えられた効用関数から、効用を最大化させるX財の消費量を求めます。
そのためには、この効用関数から「①限界効用を求める」「②これ以上は効用が増えない状態(限界効用(追加的な効用の増加分)が0)を求める」
※最初に予算制約線を代入しているので、あくまで予算の範囲内でX財の効率的な消費量が求まります。
つまり
- ①限界効用を求めるため、xで微分
- ②更に「=0」とします
U =「-(1/3)xの2乗+10x」
⇒ 「-(2/3)x +10=0」
限界効用を求めるときに微分する意味などが分からない人はこちらで確認⇒【限界効用】求め方も含めて簡単にわかりやすく
計算すると
- 「-(2/3)x +10=0」⇒「2/3x =10」
両辺に(3/2)を掛ける
x=30/2=15
次に「x=15」を予算制約線に代入します。
予算制約線=300=10x+30y
300=10×15+30y =150+30y
300-150 =30y
30y=150
y=5
したがって最適消費点は「x=15」「y=5」※(x, y)=(15, 5)とも表記できる。


加重限界効用均等の法則

この方法は、よく試験問題を解くときに使われることが多い印象です。
ポイント
効用が最大化する2財の消費の組合わせでは「2財の1円当たりの限界効用が一致する性質」を使って問題を解いていきます。
数学的に解いていくため簡単に解くことが出来ますが、この法則をちゃんと理解できない人も多いです。(効用最大化問題は、数学的には数理計画問題に該当しており、線形計画法で解くことが出来る。)
※これだけで1ページ分の解説が必要になりそうなので別で解説します。
詳しくはこちら
-

-
【限界効用均等の法則・加重限界効用均等の法則】意味・例や公式を分かりやすく解説
いきなり教科書で登場してきて、イメージもしづらい「限界効用均等の法則」 (加重)限界効用均等の法則とは? (加重)限界効 ...
続きを見る
ラグランジュの未定乗数法

与えられた条件からラグランジュ関数を作って解く方法です。
ポイント
ラグランジュ未定乗数法は、「制約条件がある関数」の極値を求めることが出来る計算方法のことです。
最適消費点(効用最大化)の問題は、まさに「制約条件がある関数の極値」を求めていることになるので応用されます。
※これだけで1ページ分の解説が必要になりそうなので別で解説します。
詳しくはこちら
-

-
ラグランジュ未定乗数法でミクロ経済学の効用最大化問題を解く
効用最大化問題を解くときに登場する「ラグランジュ未定乗数法」 そもそも数学的な解法なので「数学が分からない!」という人に ...
続きを見る