ミクロ経済学の壁の1つと言われる「無差別曲線」
- 無差別曲線の意味
- 無差別曲線の性質と証明
- 無差別曲線のよくある疑問
無差別曲線は、最終的に需要曲線へつながります。
そのため非常に重要な項目ですが、意外と理解しづらい。
そんな無差別曲線をわかりやすく解説していきます。
無差別曲線とは?
無差別曲線とは
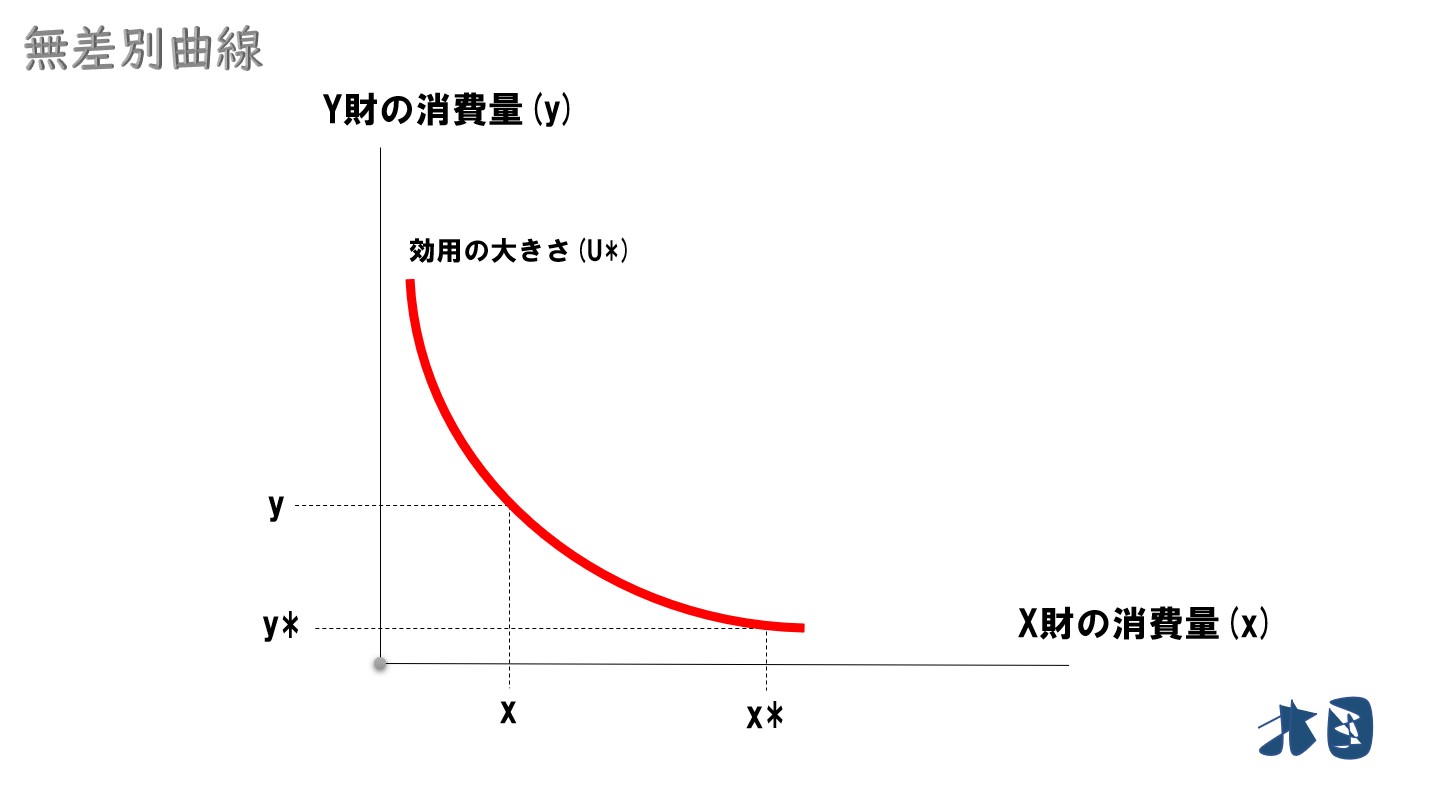
消費者が同じ満足度を得られる消費の組み合わせを結んだ曲線のこと。同じ無差別曲線上ならば、どの点でも同じ満足度を得られる。等効用線ともいう。
ちなみに
無差別は「同一のものとして扱うこと」を意味します。
同じ曲線状なら、どの点を選んでも同じ効用(満足度)になるため「無差別曲線」と呼んでいる。


例えば
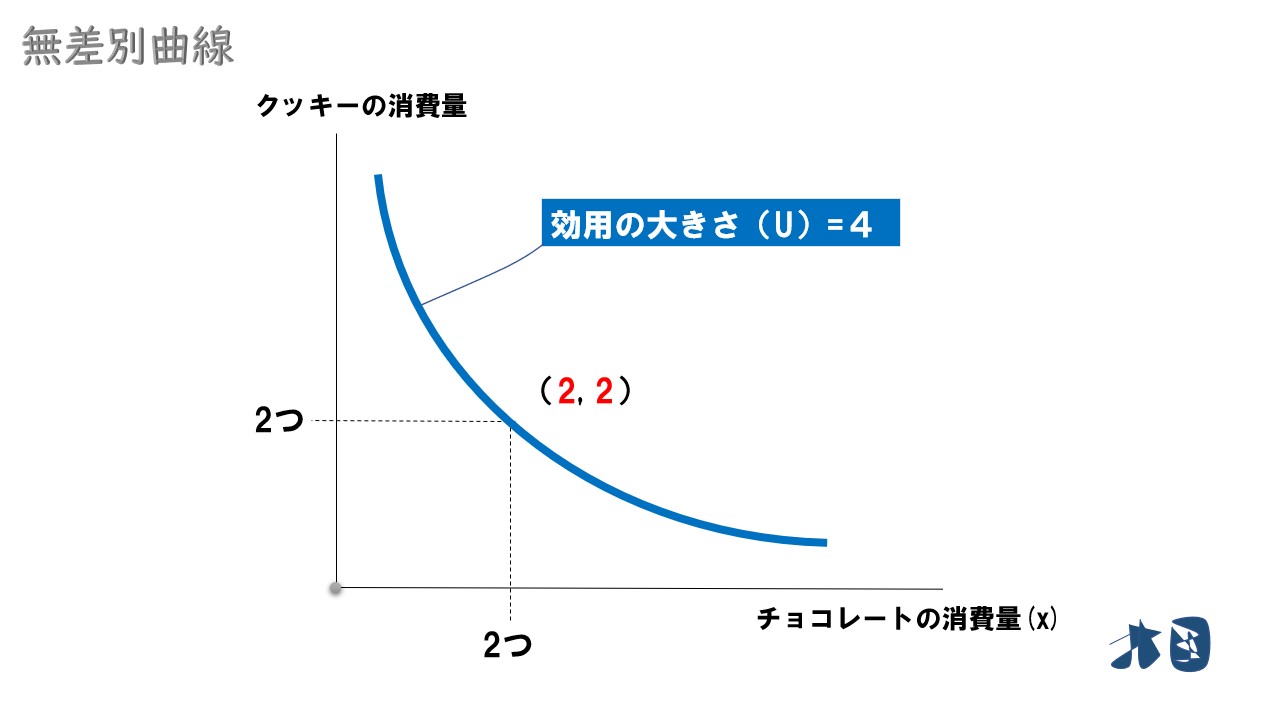
- チョコレート2枚とクッキー2枚を食べた時の効用が4だったとします。
グラフで見ると
ポイント
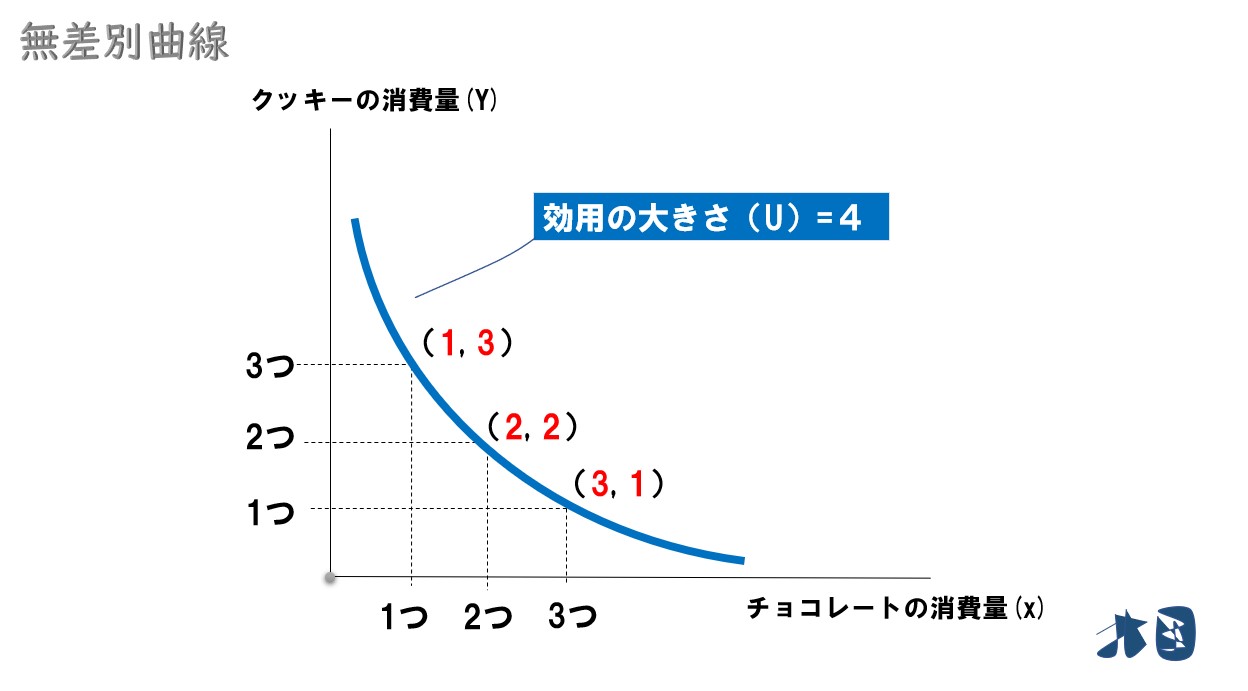
このように、同じ効用水準になる「X財の消費量(X)」と「Y財の消費量(Y)」の組み合わせを結んだ線が無差別曲線です (曲線は直線を含みます)。
無差別曲線の性質

無差別曲線には大きく4つの性質があります。
無差別曲線は
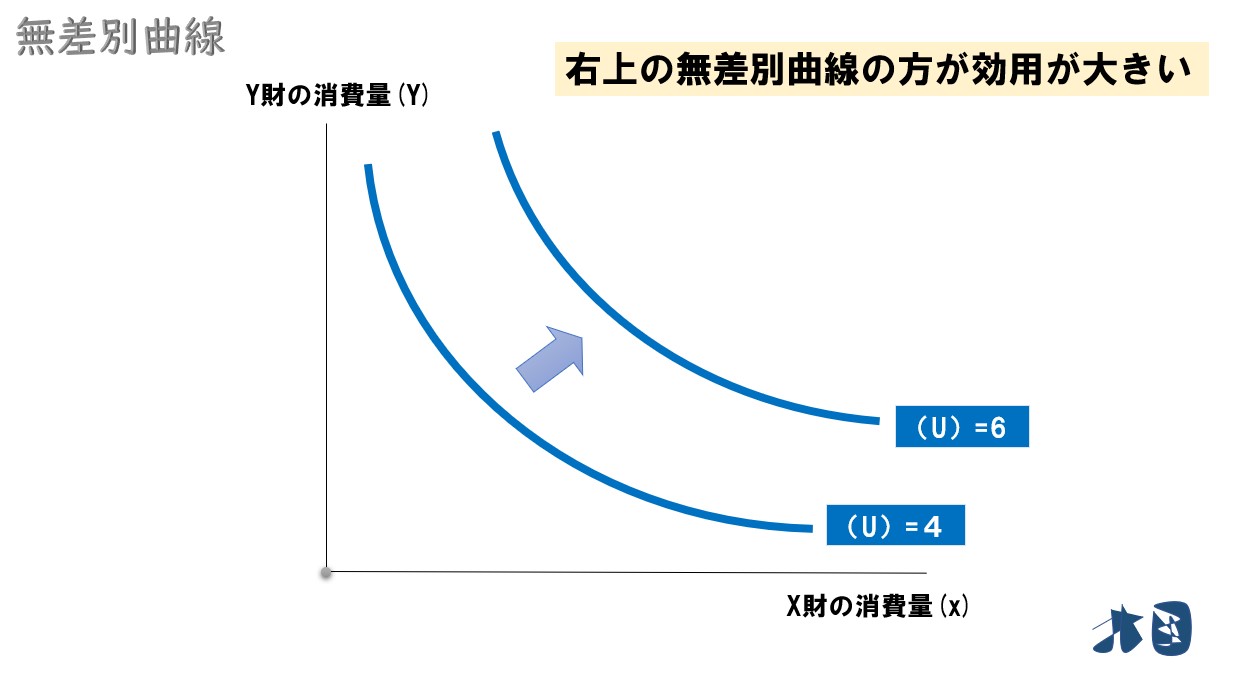
- 右上に行くほど効用が高い
- 右下がり
- 交わらない
- 原点から見て内側に膨らむ
① 右上に行くほど効用が高い
厳密に言うと「上方の無差別曲線上の点は、下方の無差別曲線上の点よりも効用が高い」
例えば
- 無差別曲線上の点(1, 3)
- 無差別曲線上の点(4, 2)
点(3, 1)よりも点(4, 2)の方が右上の無差別曲線(U=6)上に存在している。
そのため、点(4, 2)の方が効用が大きい。
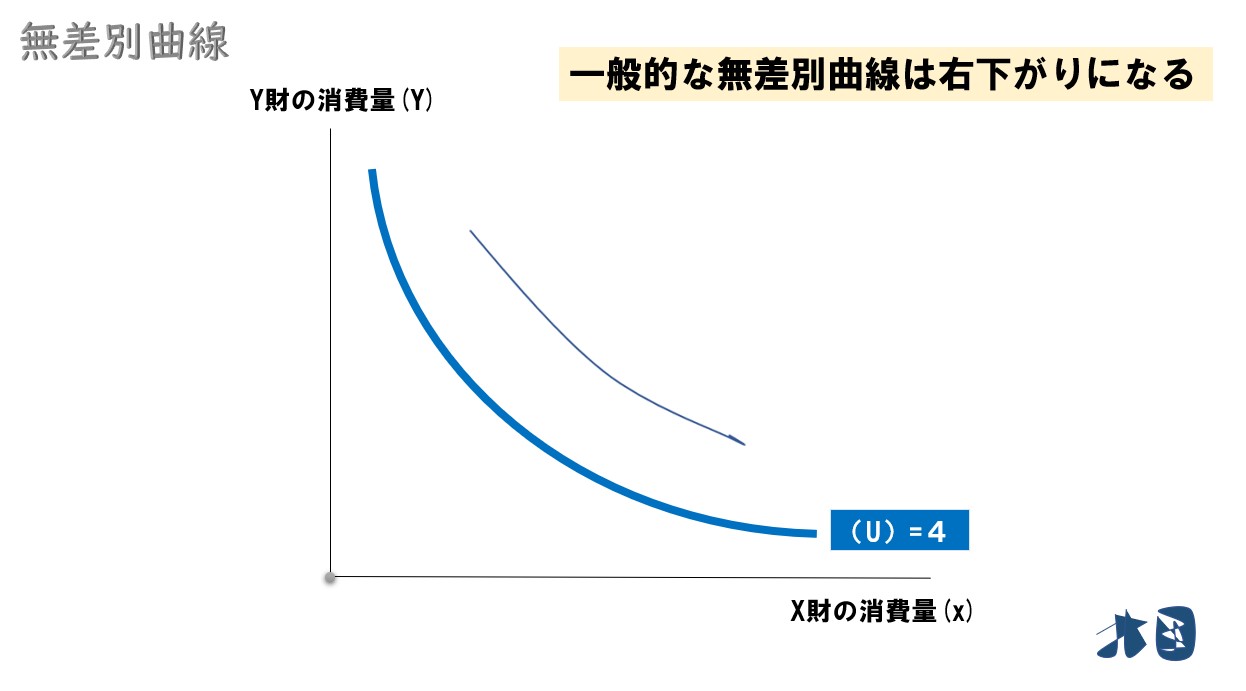
② 右下がりになる
経済学で登場する無差別曲線は、基本的には右下がりになる。
大学などで初めて無差別曲線を学習する段階なら、基本的に無差別曲線は右下がりのものが登場します。
ココに注意
基本的には右下がりですが、L字型の無差別曲線や、右上がりの無差別曲線も存在します。こうした特殊な形状の無差別曲線は応用的な話になります。
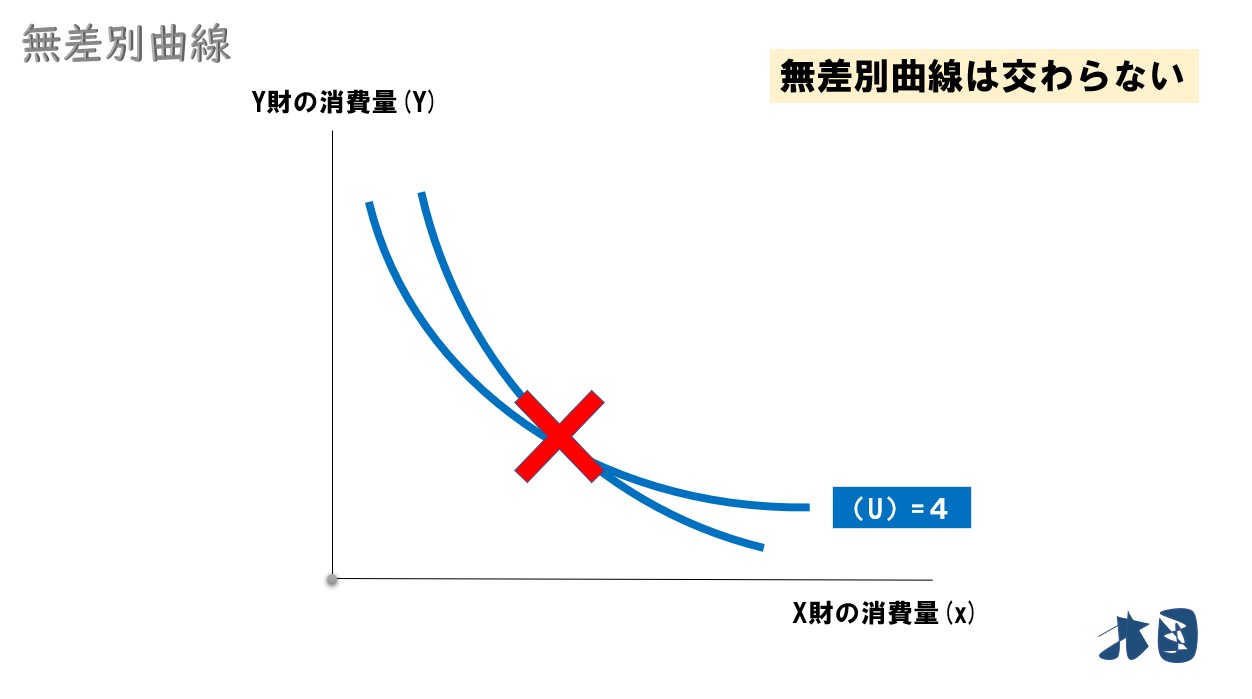
③ 交わらない
異なる2本の無差別曲線は、お互い決して交わりません。
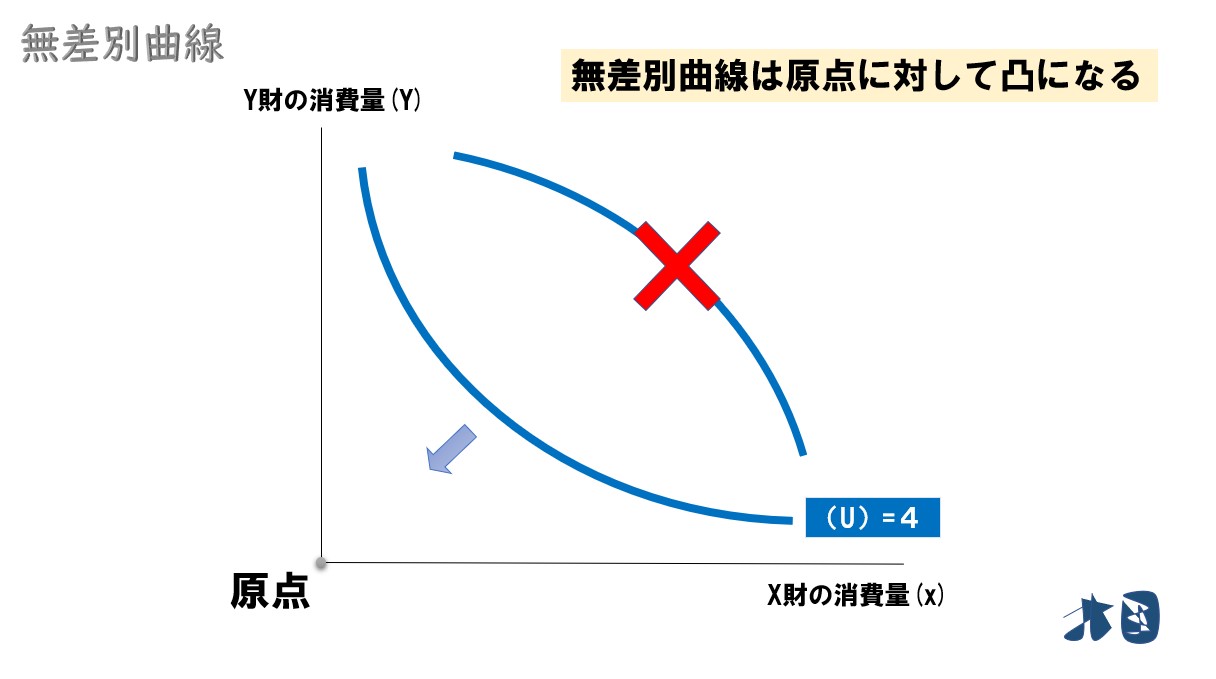
④ 原点から見て内側に膨らむ
一般的な無差別曲線は、原点に向かって内側に膨らんだ曲線になります。原点に対して凸とも表現されます。
限界代替率逓減の法則により、無差別曲線は原点に対して凸になります。
ココに注意
基本的には原点に対して凸ですが、例外があります。消費すればするほど、不快になる(効用が下がる)場合は、原点に向かって凹んだ形状になります。他にも消費しても効用が変化しない中立財なども凸になりません。
無差別曲線の性質①~④の証明

無差別曲線の性質を証明する問題が出題されることもあります。
- 右上に行くほど効用が高い
- 右下がり
- 交わらない
- 原点から見て内側に膨らむ
事前に出題されることが分かっているなら勉強しておけばいいかと思います。そうではないなら飛ばして大丈夫です。
一般的な無差別曲線は次の条件を満たしていることが前提になっている
- 単調性(非飽和性)
- 推移性
上の前提をもとに証明することが多いです。
詳しくはこちら!
無差別曲線のよくある疑問

無差別曲線のよくある疑問をまとめています。
特に
計算問題をしていると、よく分からないことが出てきます。ここでは、よく分からなくなるけど、検索してもあまり答えが出てこないものをまとめました。
①無差別曲線と効用関数はイコールじゃない
そもそも「無差別曲線=効用関数」ではありません。
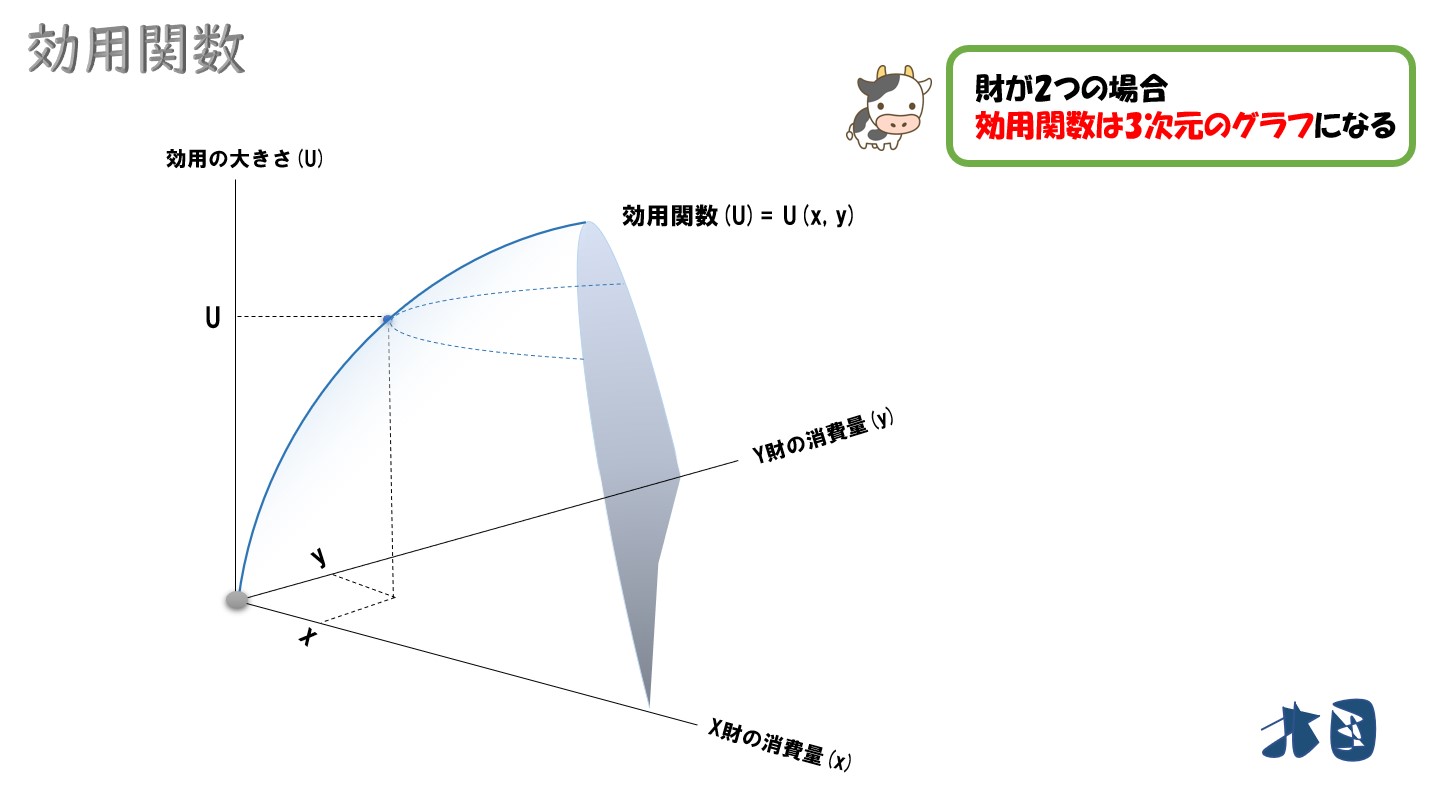
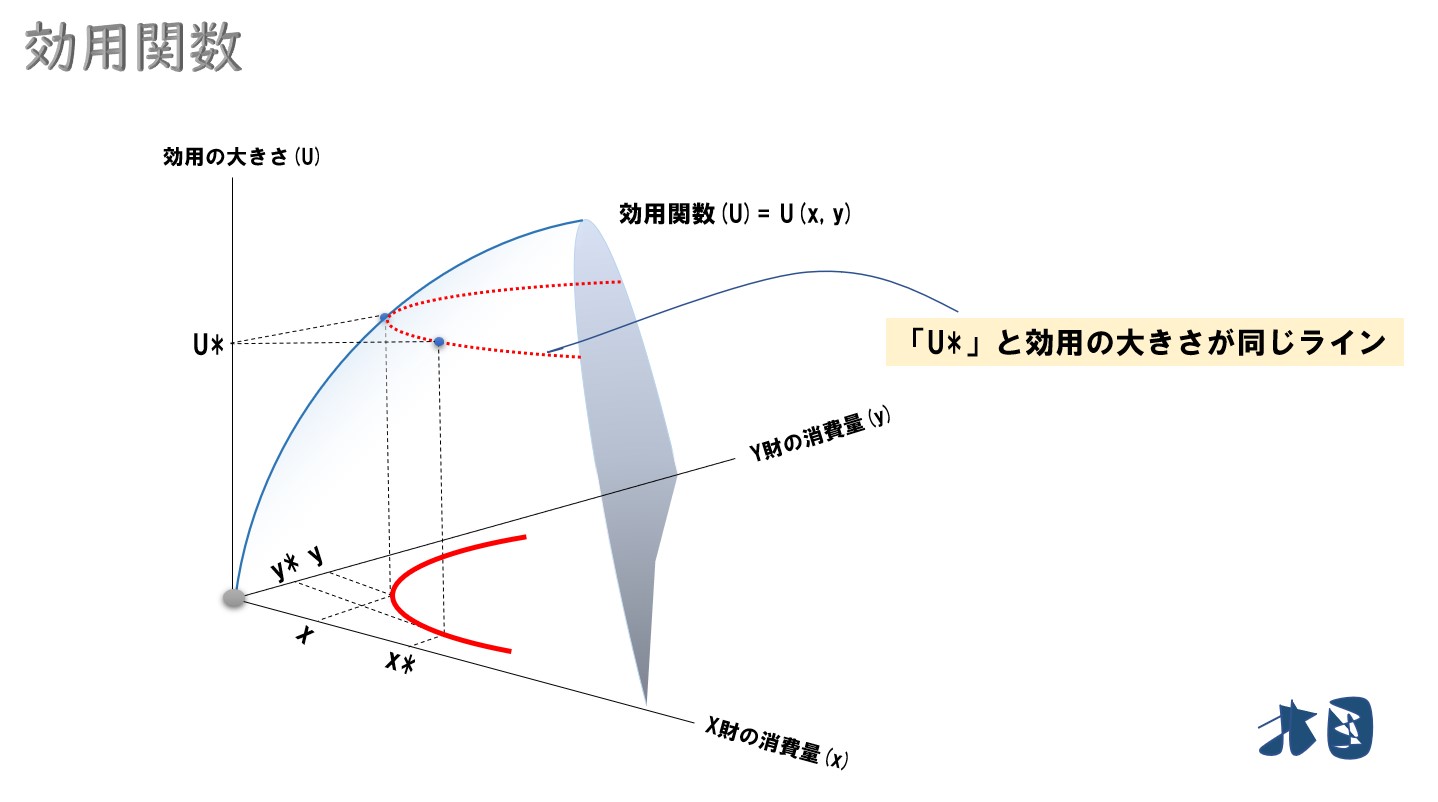
上のグラフは、財が2つの時の効用関数(U)です。


ここまでは、なんとなくのイメージで理解してもらって大丈夫です。重要なのは次です。
注目
「X財の消費量(x)」「Y財の消費量(y)」の組み合わせ次第で、同じ効用が得られます。
例えば
「チョコを1つ食べて、紅茶を2杯飲んだ時」と「チョコを2つ食べて、紅茶を1杯の飲んだ時」の効用の大きさが同じ状態です。


2次元に落とし込む
無差別曲線が登場


ポイント
財が2つの場合、効用関数のグラフは3次元になる。また、縦軸は効用の大きさを表している。
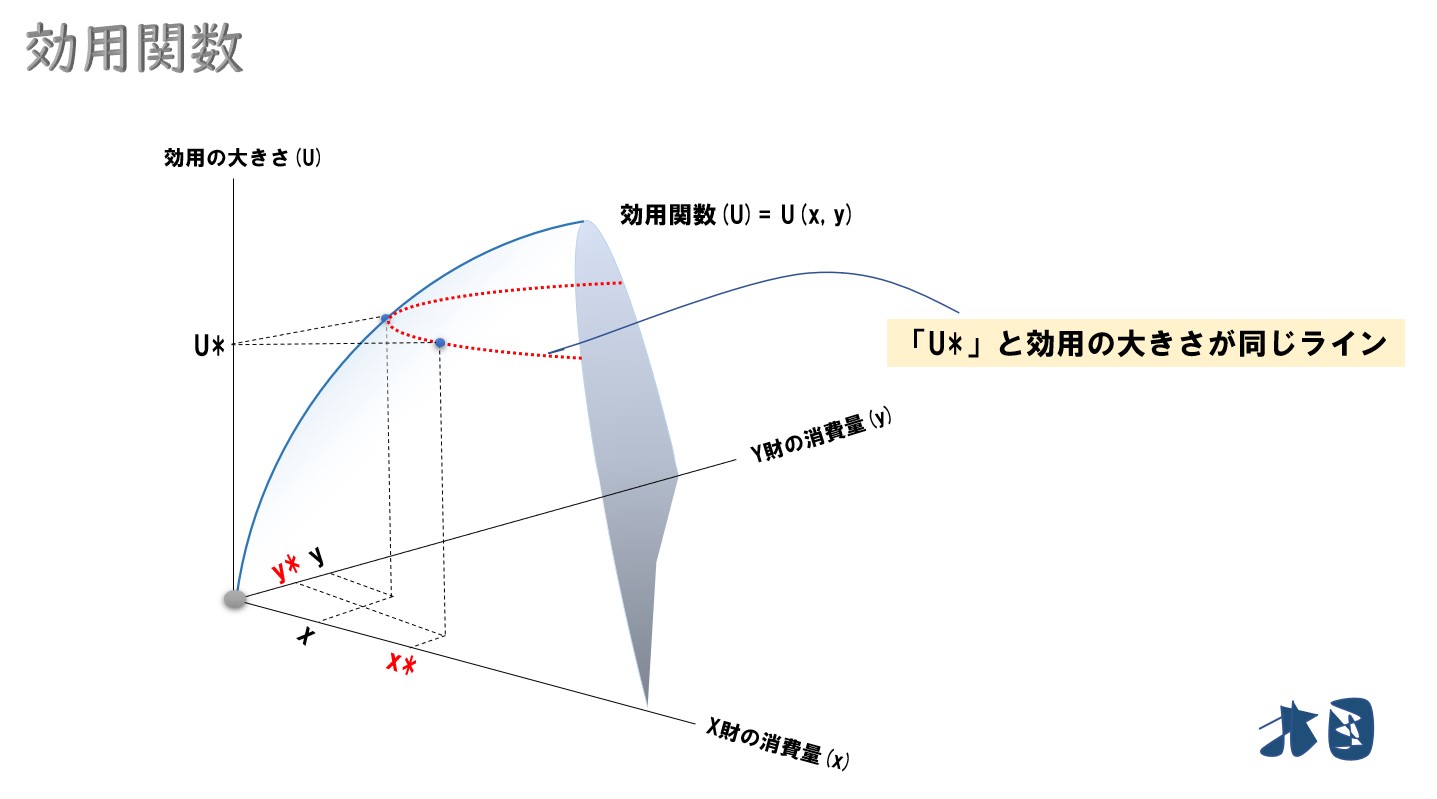
同じ効用水準のラインを線で結び、2次元に落とし込むと平面上に無差別曲線が描ける。経済学で登場する無差別曲線は、この過程を省き、最終的に平面で描かれたものを扱っていることに注意する。
つまり
「効用関数=無差別曲線」ではなく、効用関数によって求められた3次元のグラフから、同じ効用のラインを結び、平面に落とし込んだ曲線が無差別曲線となる。
まとめ
効用関数(U)が「U(x, y)」という2変数関数のとき「U(x, y)」の等高線を無差別曲線という。
②効用関数(無差別曲線)「U(x, y)=xy」の意味

「効用関数(U)=U(x, y)」というのがあった時に、無差別曲線を「U=xy」になると考える人がいますが、注意してください。
「効用関数(U)=U(x, y)」は、X財の消費量を「x」・Y財の消費量を「y」とした時の、効用水準を表す2変数関数を意味している。
効用関数「U(x, y)」の「(x, y)」は変数です。
効用関数U=「〇x」×「〇y」となりますが、〇の部分は「効用関数(U)=U(x, y)」の情報だけでは分かりません。
色々と考えられる
- 効用関数U=「x」×「y」
- 効用関数U=「10x」×「10y」
- 効用関数U=「1/2 x」×「1/2 y」
なので、効用関数U (x, y)というのがあった時に、必ずしも「U=xy」にはなりません。
通常、問題文の中に「効用関数 U(x, y)=2x × 2y」とする、などの記載があります。もしくは、この式が求められるような情報があるはずです。
ポイント
「効用関数(U)=U(x, y)」で「U(x, y)=xy」の時、という記載(又はそう判断できる情報)があることを確認してから「U=xy」と認識するようにしましょう。
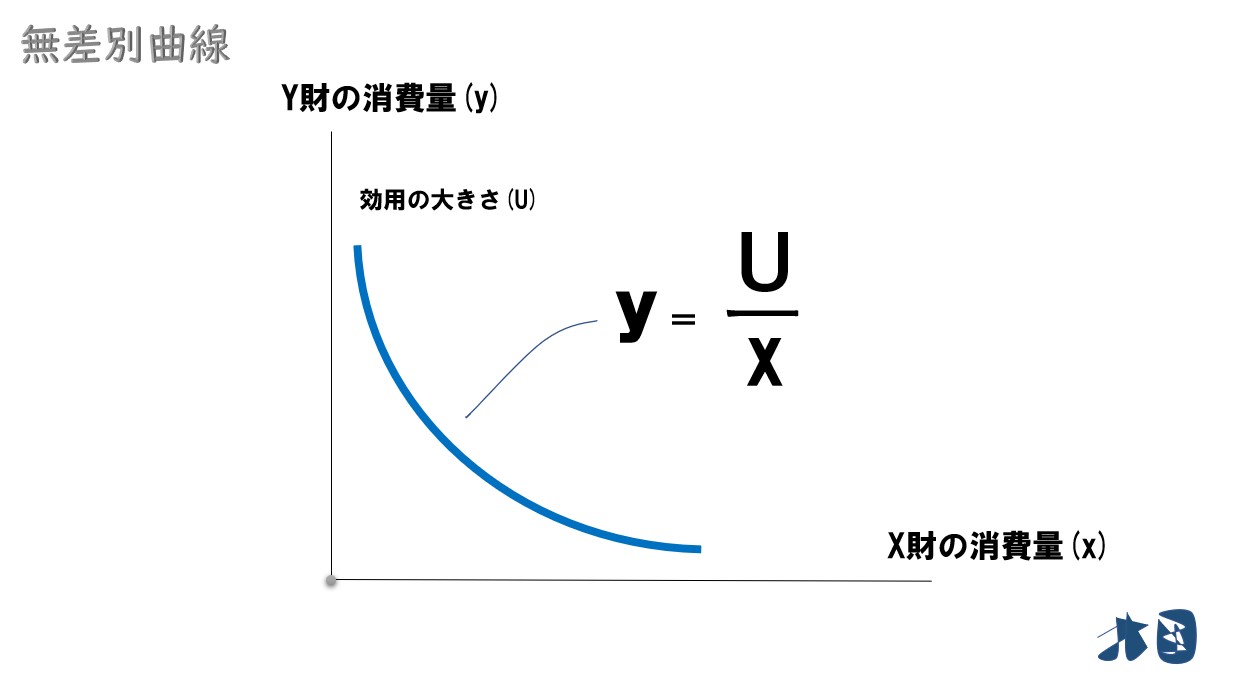
③無差別曲線の関数「y=U/x」について
ポイント
効用関数が「U(x, y)=xy」だった場合、無差別曲線を「y= U/x」という関数で表すことが出来ます。


無差別曲線は
- (2, 2)(3, 1)(1, 3)を通る
- 効用関数(U)から求められた3次元のグラフから、同じ効用のラインを結び、平面に落とし込んだ曲線。
などと表現してきました。
つまり
これまでの説明では無差別曲線自体の関数(数式)は登場していません。
そこで、効用関数(U)を使って、無差別曲線を数式として表現したものが「無差別曲線の関数」になります。
例えば
- X財の消費量:?
- Y財の消費量:5
- 得られた効用:25
効用関数(U)がU(x, y)=xyのとき、X財の消費量を求める


ポイント(再)
効用関数が「U(x, y)=xy」だった場合、無差別曲線は「y= U/x」と表現出来ます。
上の関数に代入する
5(y)= 25(U)/ ?(x)
?=5
つまり、x財の消費量は5が正解になります。