生産者理論で登場する「シェファードの補題(シェパードの補題)」
消費者の理論でも応用されるため教科書で頻出しますが、それでは理解できない人向けに詳しい解説を加えて簡単な証明をしていきます。
シェファードの補題の簡単な証明
シェファードの補題とは
企業の費用関数(C)を生産要素の価格(w･r)で偏微分すると、制約(条件)付き要素需要関数(L･K)になることを証明したもの
※シェパードの補題とも言う
※消費者理論のマッケンジー･シェパードの補題はこちらで確認してください。⇒マッケンジー(シェパード)の補題の意味と偏微分して補償需要関数になる証明
実際にそうなるのか確認していきましょう～！
費用関数(C)を「生産要素の価格(w･r)」で偏微分
はじめに
- 費用＝C
- 賃金＝ｗ
- 労働の投入量＝L
- レンタル料＝ｒ
- 資本の投入量＝K
- 生産量＝Y
このとき「費用関数(C)＝wL＋rK」と表せます。
確認する
まずこの2つに注目します。
- 労働の投入量＝L
- 資本の投入量＝K
費用が最小化するときの「労働の投入量」「資本の投入量」は制約付き要素需要関数と言われています。
制約付き要素生産関数は、生産量(Y)･賃金(w)･レンタル料(r)の3つの文字で表記します。
すると
- 労働の投入量＝L(Y,w,r)
- 資本の投入量＝K(Y,w,r)
L･Kのカッコ内の（Y,w,r）は、生産量(Y)･賃金(w)･レンタル料(r)の3つの要素で構成される(置き換えることが出来る)という意味です。
ちなみに
- 賃金＝ｗ
- レンタル料＝ｒ
この2つは、市場価格を受け入れるのでそのままです。
まとめると
- 費用＝C
- 賃金＝ｗ
- 労働の投入量＝L(Y,w,r)
- レンタル料＝ｒ
- 資本の投入量＝K(Y,w,r)
- 生産量＝Y
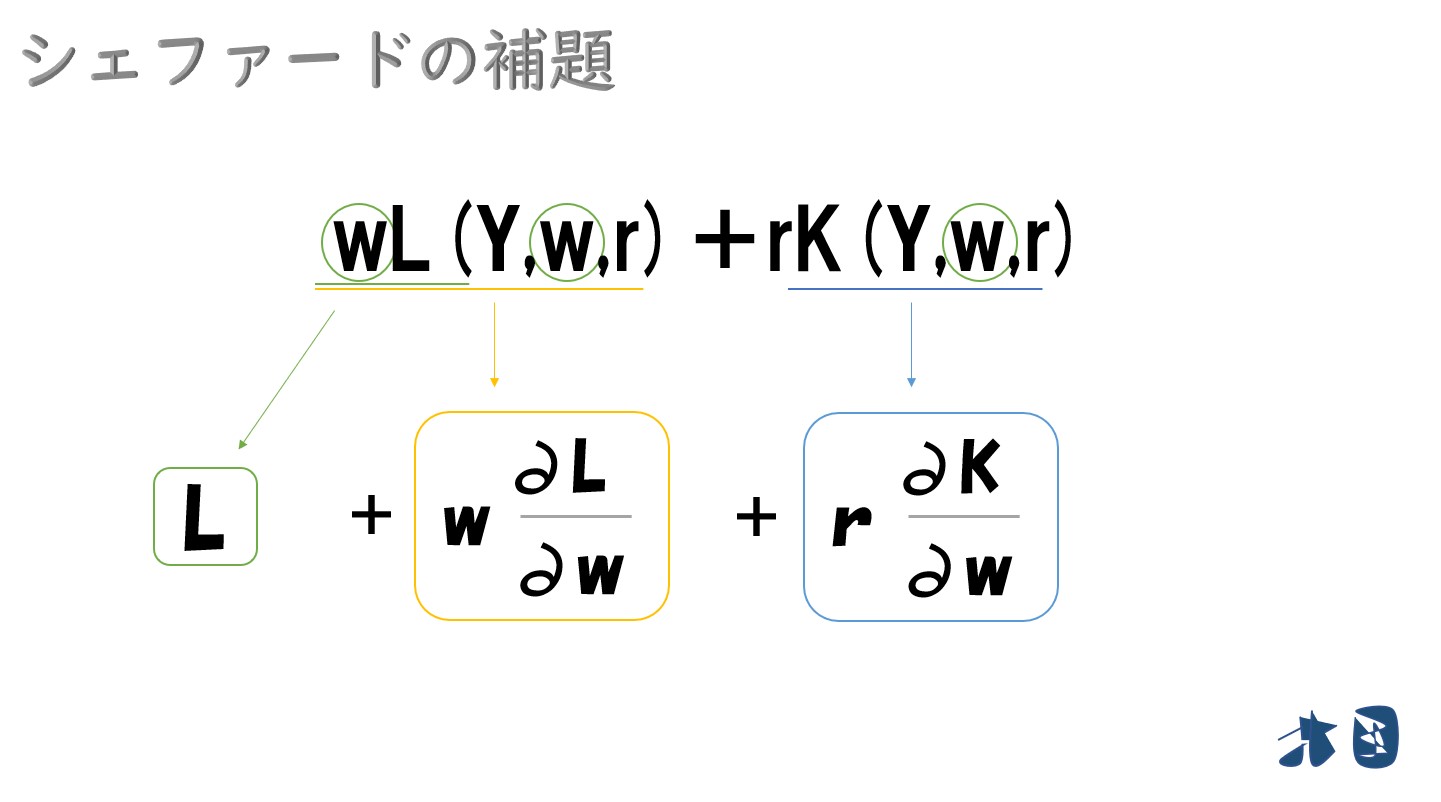
このとき、費用を「費用(C)＝(wL(Y,w,r)＋rK(Y,w,r))」と表せます。
証明
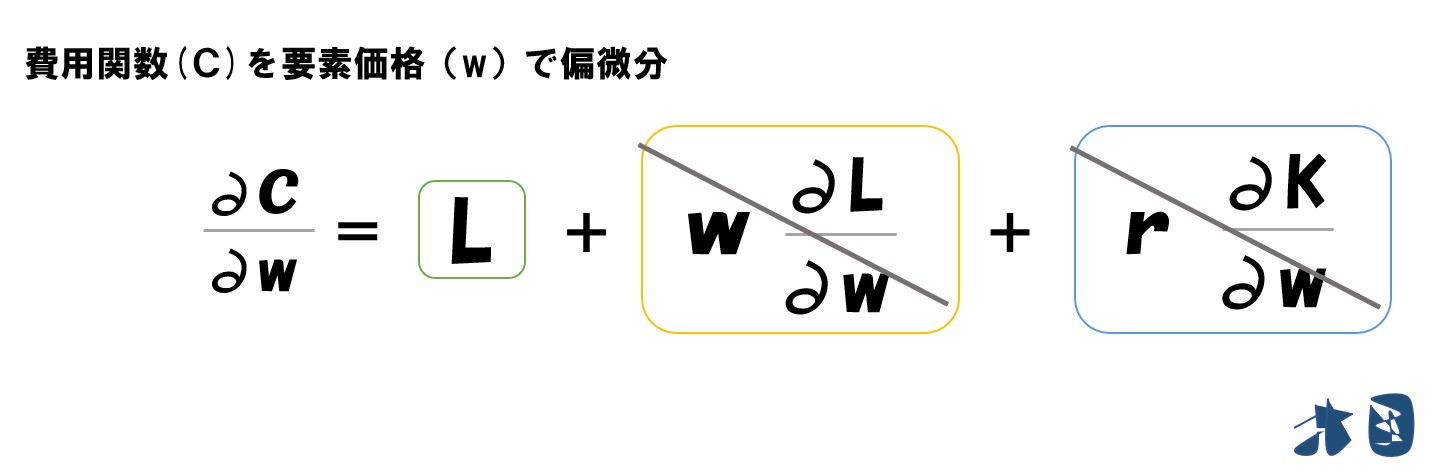
「費用(C)＝(wL(Y,w,r)＋rK(Y,w,r))」を要素価格(w･r)で偏微分して、制約付き要素需要関数になるかを確認する
注意点
微分のやり方に気を付けましょう
「費用(C)＝wL＋rK」なので、例えば要素価格(w)で微分して「費用(C)＝L」とすると話が終ってしまいます。
ここで思い出すのが‥
- 労働の投入量＝L(Y,w,r)
- 資本の投入量＝K(Y,w,r)
ポイント
L･Kを構成する要素にも要素価格(w･r)が含まれているため、それらも微分します。
ここからは「w」で偏微分してみます
ここに注目
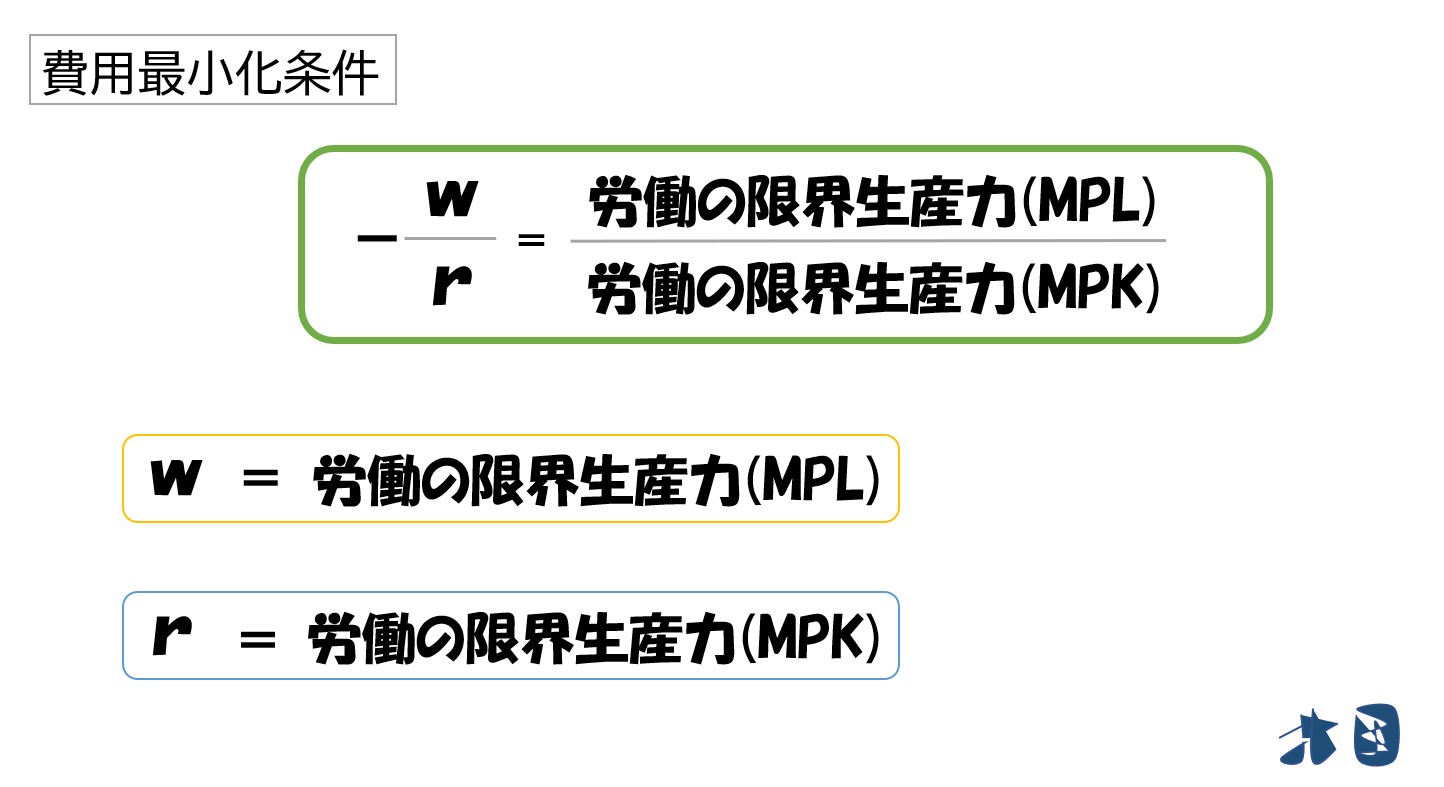
費用最小化についてはこちら⇒【費用最小化】考え方･条件式･求め方について分かりやすく解説※式で考える（費用最小化条件）を参照
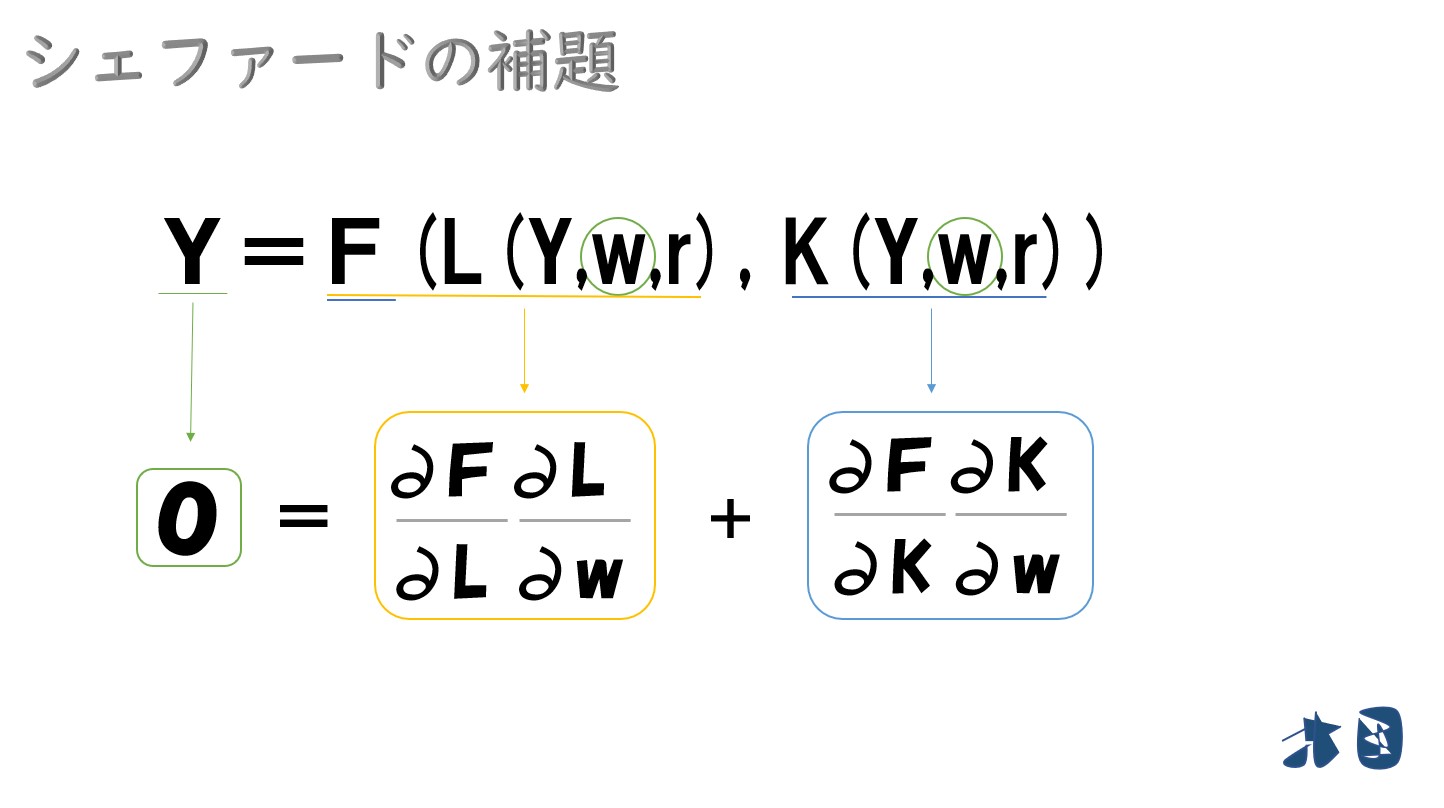
これを確認するために生産関数(F)も要素価格(w)で微分する
ここで、費用最小化が実現する生産量(Y)を決める生産関数(F)があると考える（問題で見かける「生産関数=L･K」というやつ）。
生産関数(F)は、労働の投入量(L)･資本の投入量(K)で産出量(Y)が決定する関数となっている。また、L･K･Yをそれぞれ次のように考えていた。
- 労働の投入量＝L(Y,w,r)
- 資本の投入量＝K(Y,w,r)
- 生産量＝Y
以上より、生産関数(F)を次のように表記する
Y＝生産関数F(L(Y,w,r), K(Y,w,r)）
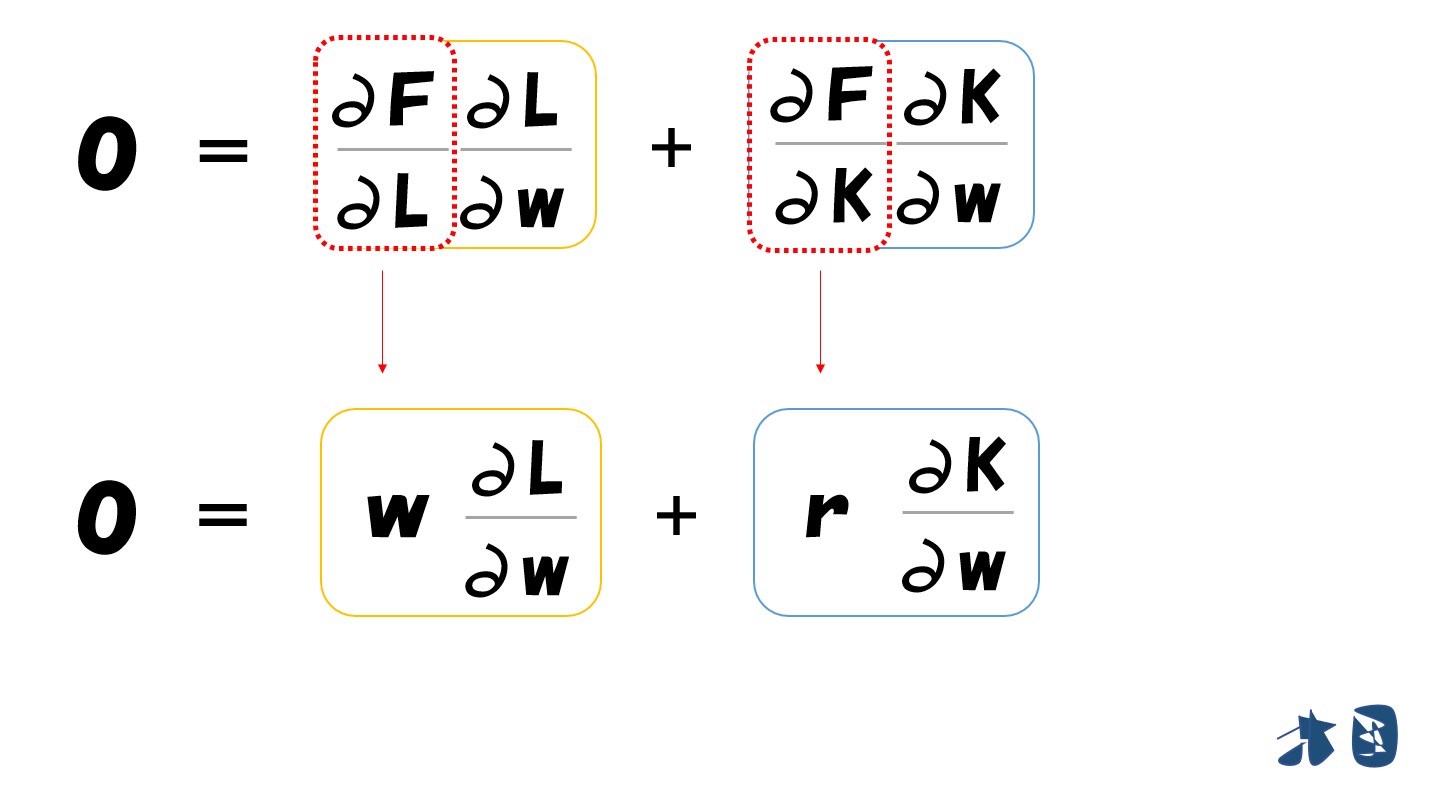
この両辺を要素価格(w)で微分します
- Y＝F(L(Y,w,r), K(Y,w,r)）
ここに注目
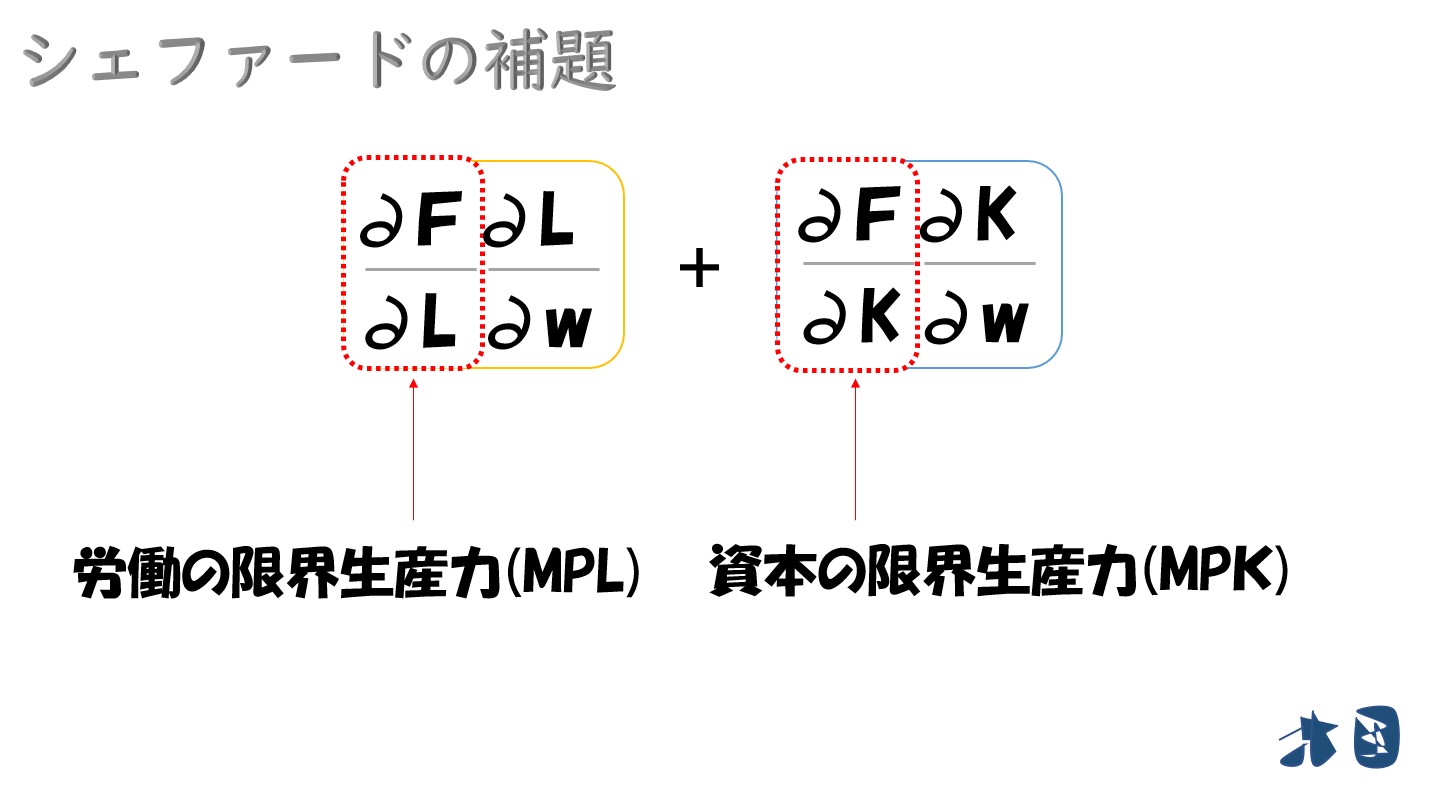
生産関数(F)を生産要素の投入量(L･K)で偏微分した部分を「限界生産力(MP)」と言いました。※限界生産力について確認する
費用最小化条件より
これらを踏まえると
以上より
黄色枠と青色枠の合計が0になるので消えます。
残ったのは・・
労働の投入量＝Lだけ！
この労働の投入量(L)は「L(Y,w,r)」と表記できます。
改めてですが「L(Y,w,r)」は労働の制約付き要素需要関数を表しています。
ちなみに
要素価格(レンタル料:r)でやっても同様の結果が得られます
その場合は「∂C/∂r＝K(Y,w,r)」となります。
以上で題意は示されたことになります。
」 消費者の理論でも応用されるため教科書で頻出しますが、それ ...){kind=link}