政府が数量規制を実施したときの例と余剰分析(余剰・死荷重)を見ていきます。
- 数量規制を行う理由
- 総余剰・死荷重の求め方
- 計算方法
数量規制を行う理由・メリット
政府の数量規制
政府は、商品・サービスに対して、供給量(数量)の上限を設定することがある。
ポイント①
- 政府が数量規制を行う理由
市場の均衡点で取引が行われると、生産者にとって不利益となる場合や、社会生活(または地球環境など)を維持する上で大きな問題が発生すると考えられる場合、その他国の政策上の問題から、政府は市場へ介入して数量規制を行う。
例えば
- ある商品を作るときに有害な物質が発生するとき
商品の需要量はたくさんある一方で、工場の近隣住民は有害物質に迷惑しており、国も環境上の問題から大量生産が行われるのを問題視していた。
このような場合に、国は商品の生産数を抑えるために商品の供給量に制限をかける。
ポイント②
- 政府が数量規制を行うと死荷重を発生する
数量規制により、市場では経済効率性が失われて総余剰が最大化しません。このとき発生した社会的な損失は死荷重(デッドウェイトロス)となります。


総余剰と死荷重の決まり方
ポイント
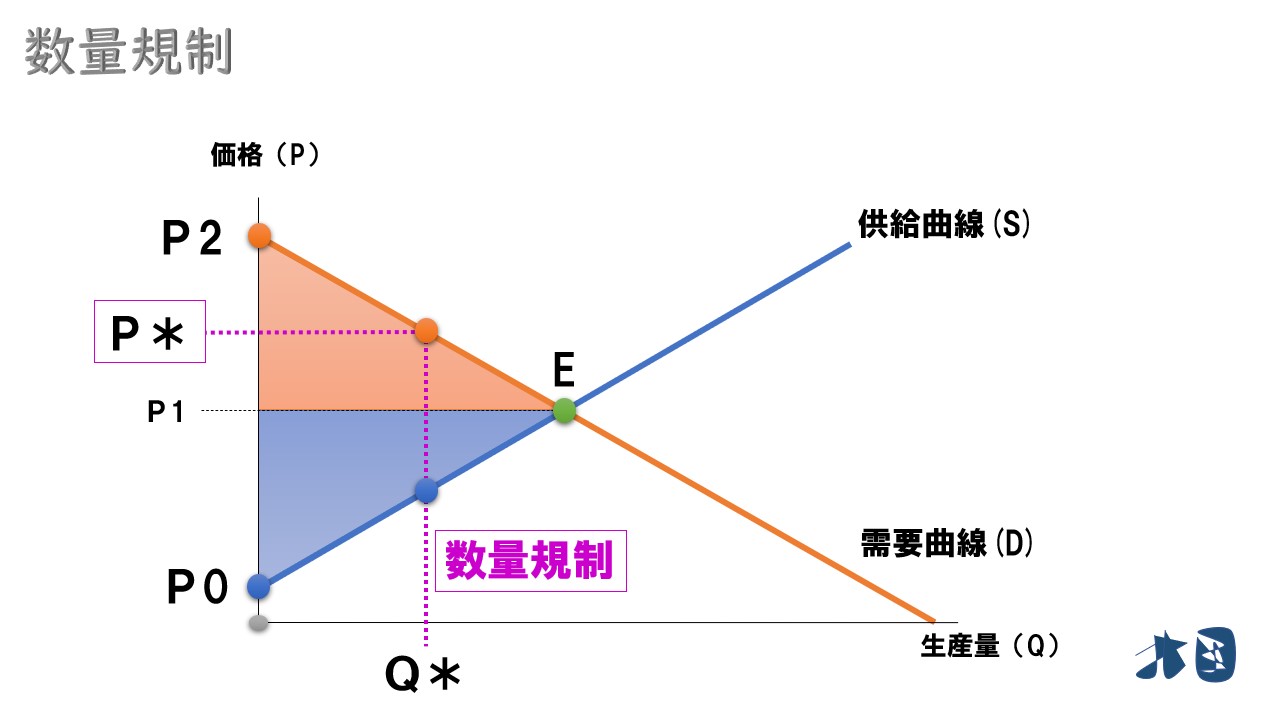
数量規制が行われると供給曲線が垂直になり、市場価格より高い値段で商品・サービスが取引される。
グラフで見ると
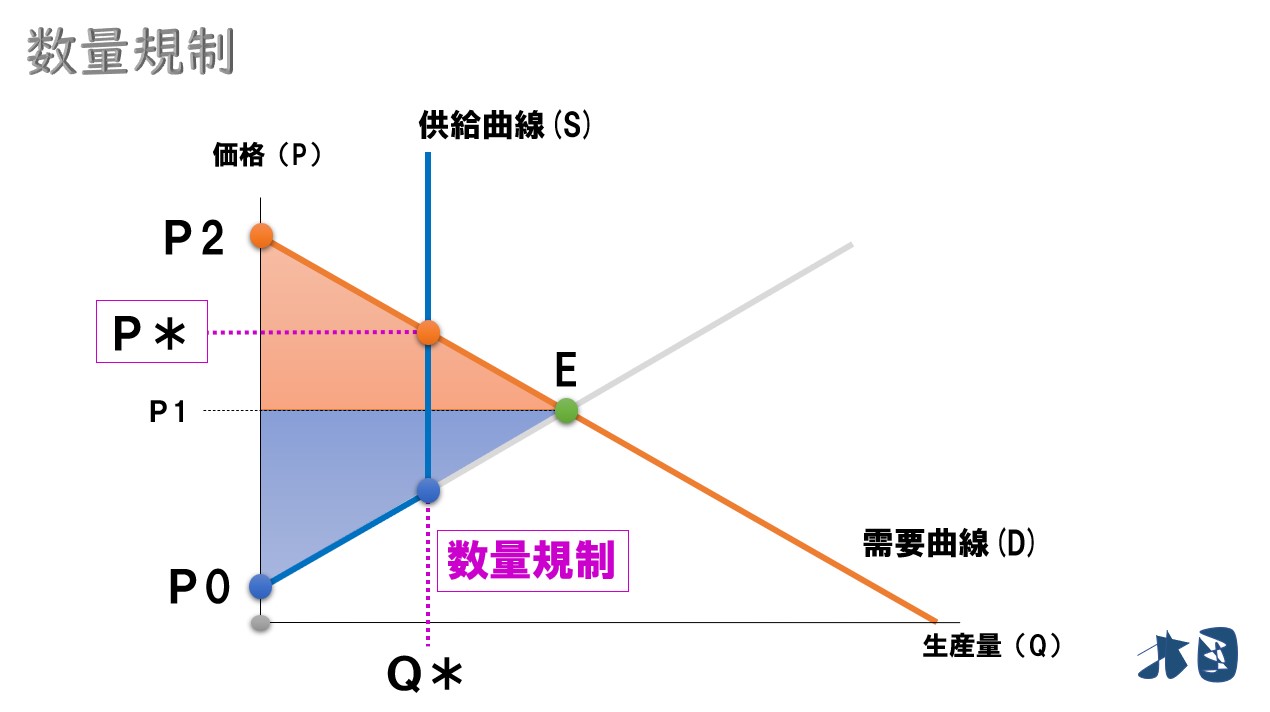
数量規制により、規制数量より右側の供給が消えます。その結果「Q*」で供給曲線が垂直となっています。
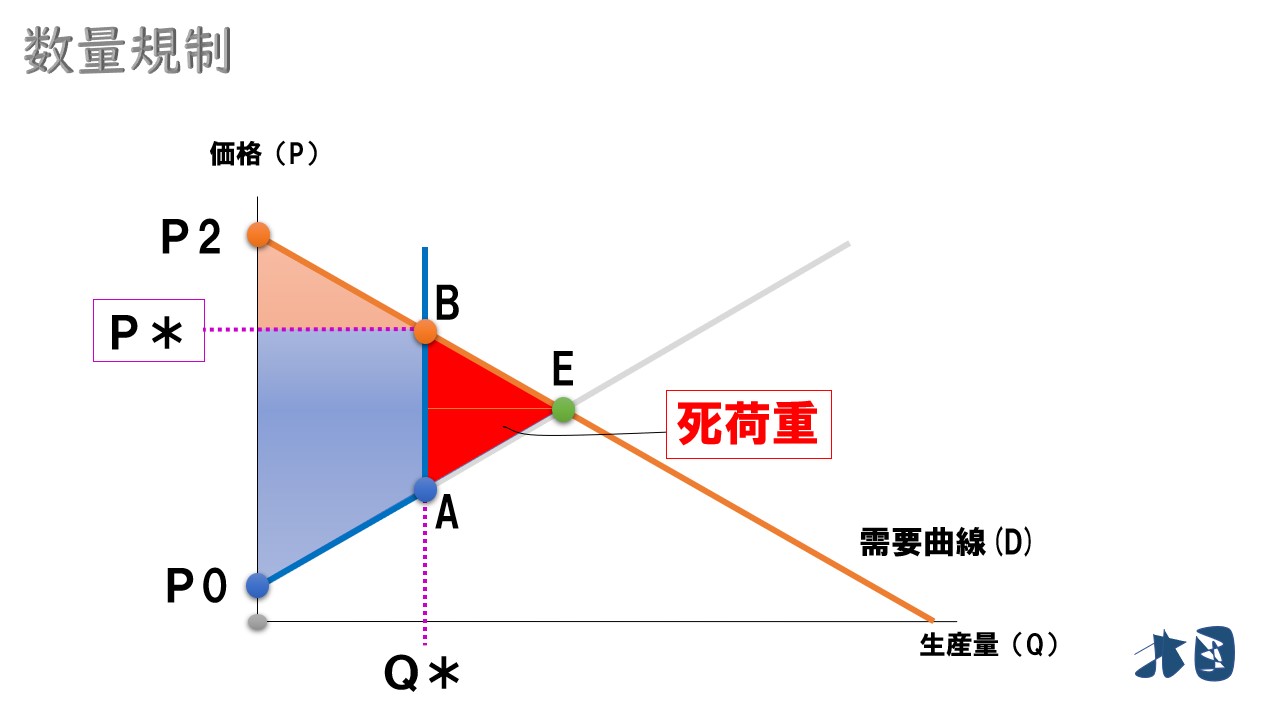
死荷重
数量規制によって市場均衡点から外れたところで価格と数量が決まるため死荷重が発生します。
- 点B
- 均衡点E
- 点A
この3つの点からなる三角形部分が死荷重(社会的損失)となります
社会的損失=「三角形B・E・A」
ポイント
数量規制によって、均衡取引量よりも少ない取引量しか実現しない(価格も高止まりする)ため死荷重が生まれ、経済的に非効率となることが分かる。
ちなみに
消費者余剰(CS)と生産者余剰(PS)は‥
消費者余剰は
次の三角形で囲まれた部分
- 点P2
- 点B
- 点P*
生産者余剰は
次の四角形で囲まれた部分
- 点P*
- 点B
- 点A
- 点P0
ポイント
市場価格よりも価格が高いところで取引されるので生産者が得をしている(生産者余剰が消費者余剰よりも大きい)。
実例

ここからは現実世界で実施されたことのある数量規制を紹介します。
数量規制の具体例
- 減反政策(お米の生産調整)
- 水産資源の漁獲量
- 計画停電
- 配給制

減反政策は、お米を生産している農家に対して作付面積の削減を要求する農業政策です。お米が大量に流通すると価格が下落してしまうため、農家を保護する目的で国が実施しました。減反政策によってお米の生産量は減少して、価格も少々高く設定されています。
ただし、お米の話は単純に生産量の調整をしている以外にも、補助金・貿易・価格調整など、複数の視点から分析が必要です。ここでは生産量を調整したという点にのみ焦点を当てて考えています。

資源保護の目的で、特定の魚の漁獲量には制限が設けられています。これは、世界的な流れであり、日本では水産庁が、魚の種類ごとに漁獲量の上限を決めて、各漁船に割り当てる方針を決めています。
漁獲量に制限がある以上、市場に出回る量も減るため、均衡取引量よりも少ない量で取引が行われています。逆に言えば、取れるだけ取りまくれば、もっと安く魚を食べられるはずです(水産庁HP)

計画停電(輪番停電)は、東日本大震災後に政府主導で行われた電力政策です。電力需要がひっ迫(電力供給を上回る電力需要が発生すると大規模な停電が発生)する可能性があったため、一部地域で電力供給を停止しました。計画停電の場合、価格が高止まりするということはありませんが、供給が制限されたことは数量規制に該当すると考えられます。また、電力などの費用逓減産業は需給のグラフが通常とは異なるため、分析の際には注意が必要です。

よく戦争中に見られる配給制も数量規制だと考えられます。
国が供給量をコントロールして国民に配るため、市場均衡点で取引が行われないことになります。ただし、計画停電と同じように、価格がどのようになるかは国の都合で決まります。
計算方法

例えば
- 財Aの需要曲線が「D=-20P+500」
- 財Aの供給曲線が「S=30P-150」
政府が、この財の供給量を均衡取引量の半分にすることを決定した場合の消費者余剰・生産者余剰・死荷重はいくらか?
はじめに市場均衡点を求めるために「D=S」として計算します。
- -20P+500=30P-150
次に均衡点における市場価格を計算します。
- 50P=650
- P=13
「S=30P-150」に市場価格のP=13を代入します。
- S=390-150=240
これで、市場均衡点における価格と供給量(生産量)が分かりました。
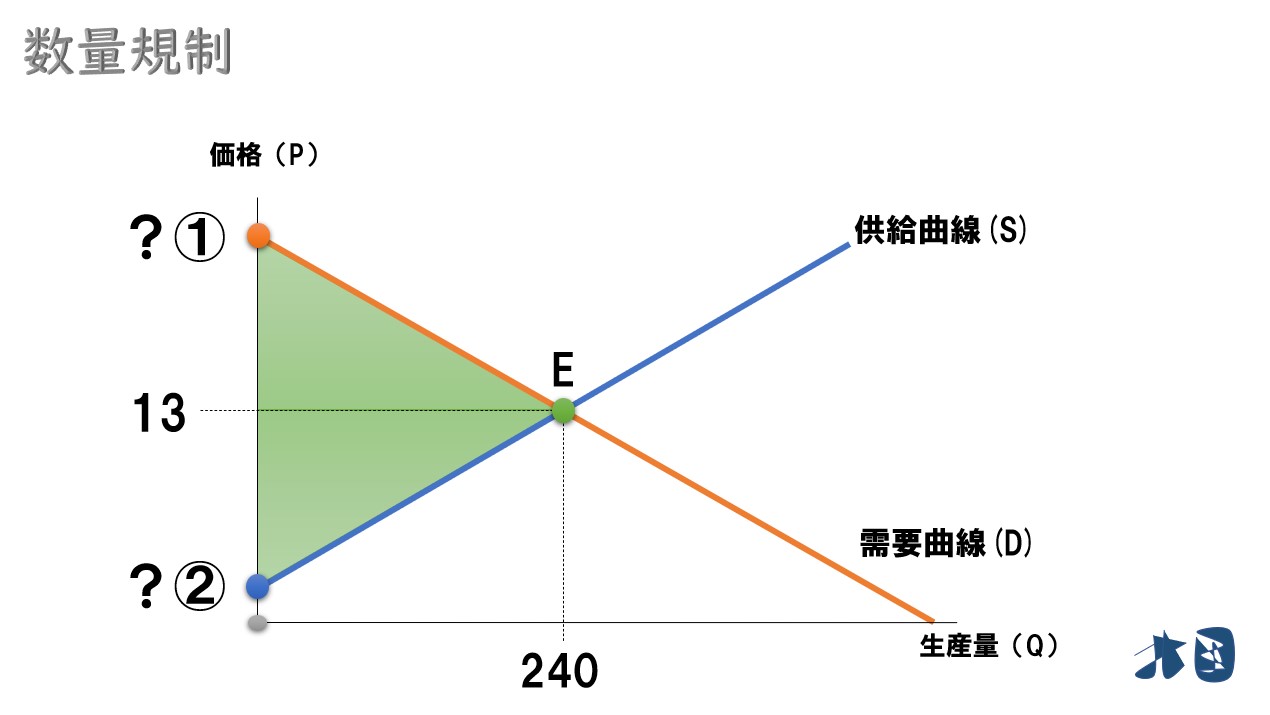
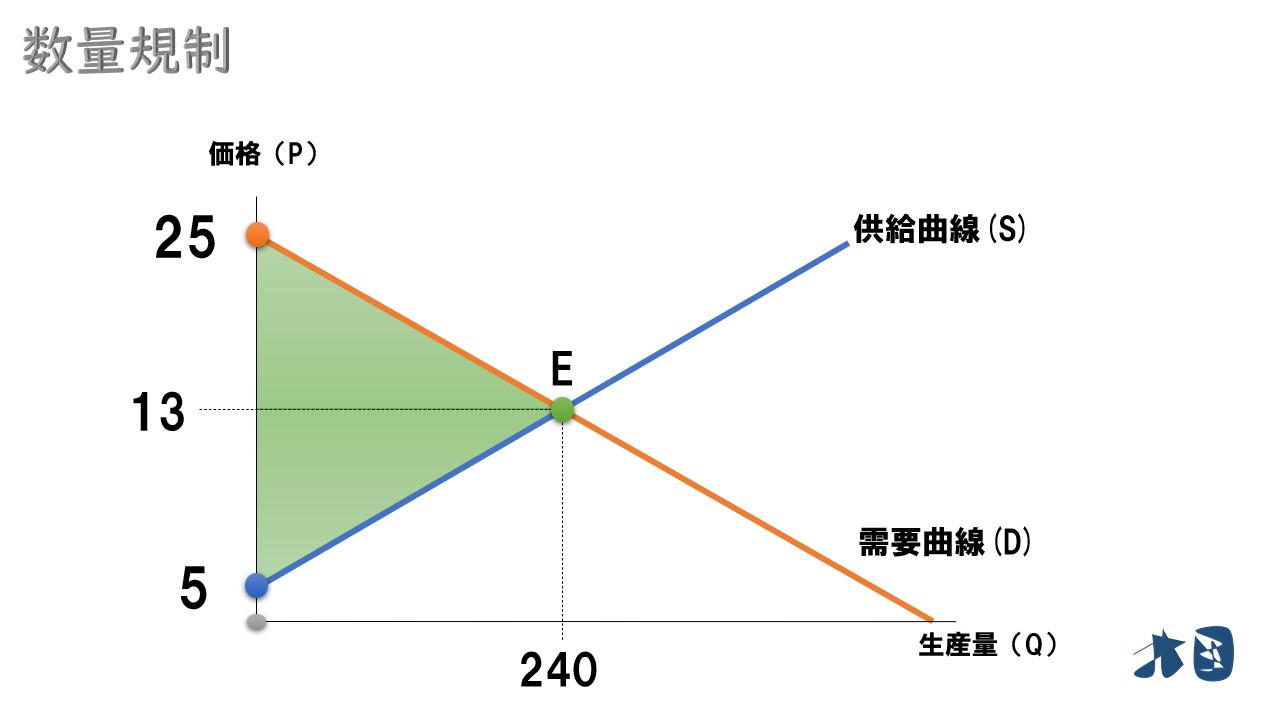
グラフで見ると
まずは2つの切片(?)の値が必要です。
- ①需要曲線「D=-20P+500」を「P=●●の形(逆需要関数)」にする
20P=-D+500
P=(-D+500)/20
切片なので横軸の需要量(D)は0となります
グラフの横軸は”生産量Q”という表記になっていますが、需要量(D)・供給量(S)と同じ意味です。
P=(-0+500)/20
P=(500)/20
P=25
- ②供給曲線「S=30P-150」を「P=●●の形(逆供給関数)」にする
30P=S+150
P=(S+150)/30
切片なので横軸の供給量(S)は0となります
グラフの横軸は”生産量Q”という表記になっていますが、需要量(D)・供給量(S)と同じ意味です。
P=(0+150)/30
P=(150)/30
P=5
以上より
次に
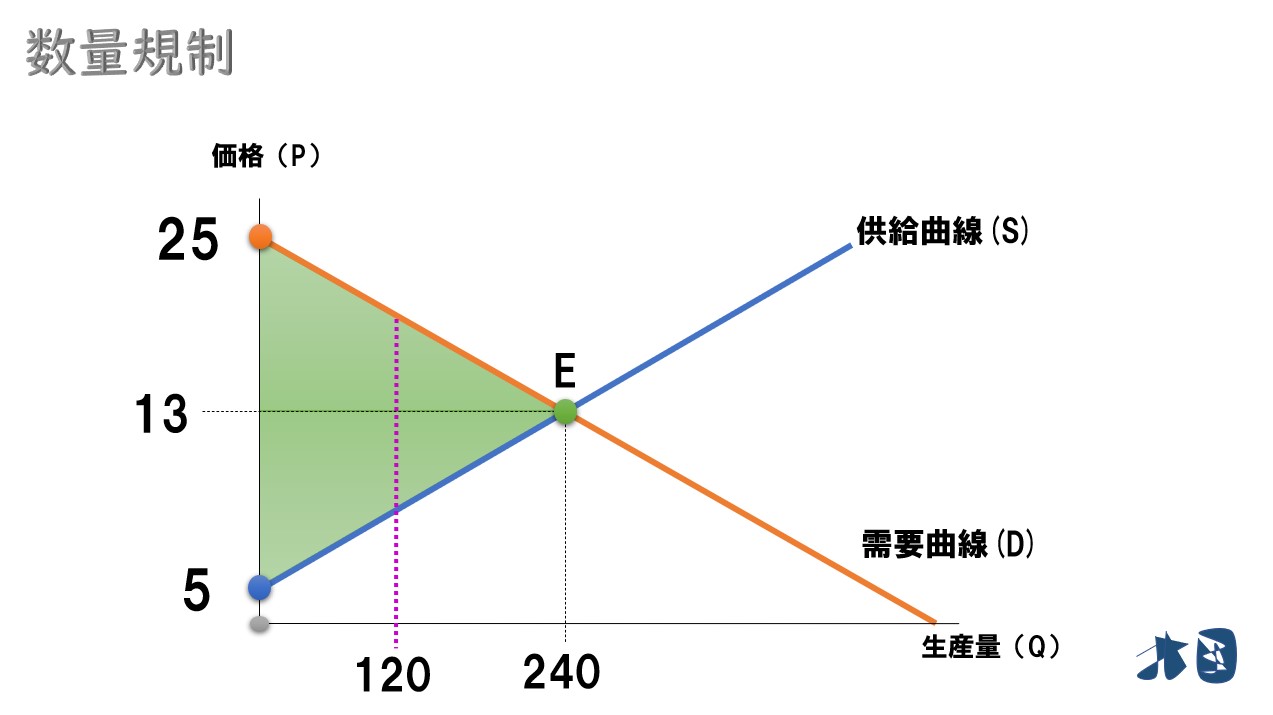
- 数量制限を考える
均衡取引量の半分まで規制するので、240の半分である120が供給量になる。
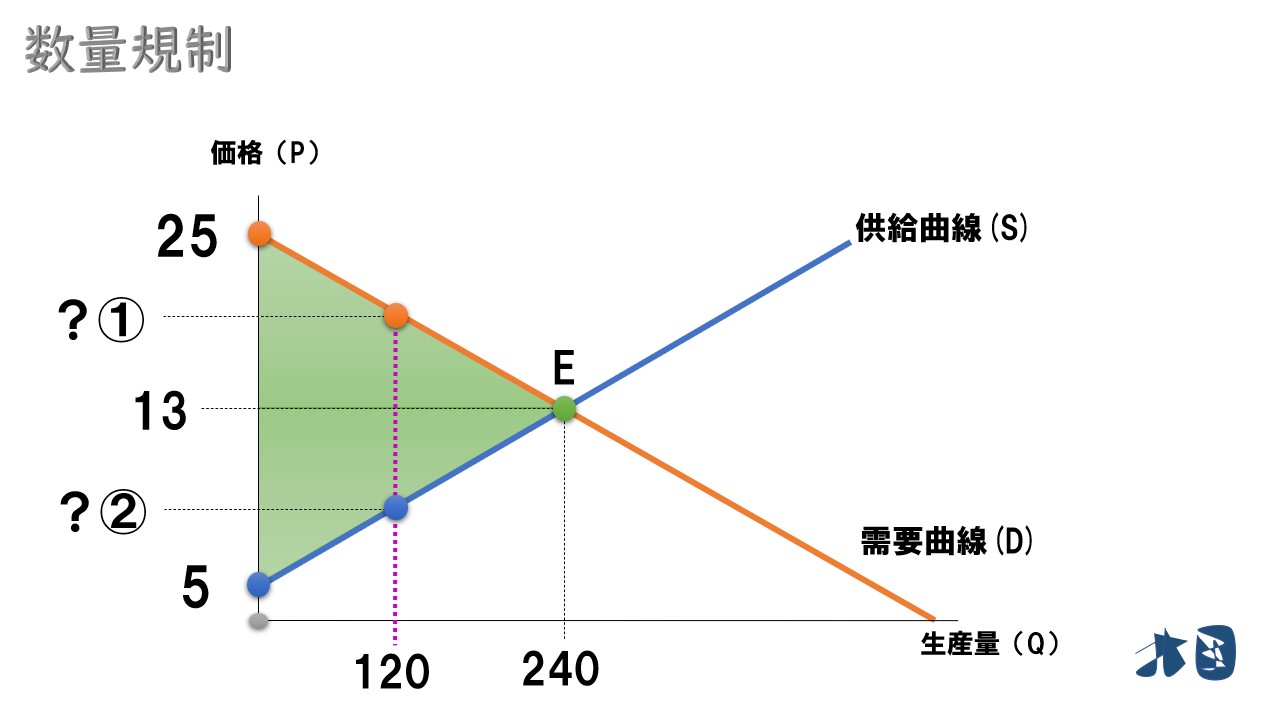
「?①」「?②」を求める
- ①数量120のときの需要者価格を求める
需要曲線「D=-20P+500」に「D(Q)=120」を代入する
生産量(Q)=需要量(D)・供給量(S)と同じ意味です。
120=-20P+500
20P=500-120
20P=380
P=19
- ①数量120のときの供給者価格を求める
供給曲線「S=30P-150」に「S(Q)=120」を代入する
生産量(Q)=需要量(D)・供給量(S)と同じ意味です。
120=30P-150
30P=270
P=9
以上より
ポイント
後は「消費者余剰」「生産者余剰」「死荷重」を求めるだけ。
- 消費者余剰=P25・点B・P19
- 生産者余剰=P19・点B・点A・P5
- 死荷重=点B・点E・点A
消費者余剰は三角形の面積を求めるだけ
- 縦=(25-19)=6
- 横=120
三角形の面積=(縦×横)÷2
(6×120)÷2==360
以上より、消費者余剰(CS)=360
生産者余剰は台形の面積を求めるだけ
- 縦①(下底)=(19-5)=14
- 縦②(上底)=(19-9)=10
- 横(高さ)=120
台形の面積=(上底+下底)×高さ÷2
(14+10)×120÷2=1440
以上より、生産者余剰(PS)=1440
死荷重は三角形の面積を求めるだけ
- 縦=(19-9)=10
- 横=(240-120)=120
(10×120)÷2=600
以上より、死荷重=600