フランスの経済学者クールノーが構築した「不完全競争市場における企業行動を分析したモデル」を1から簡単にまとめています。
- クールノーの(数量競争)モデル
- クールノー競争(例など)
- クールノー均衡(クールノー・ナッシュ均衡)
- 反応曲線
- 余剰分析
- 計算方法や求め方
この記事内では「クールノーモデル」は、このモデルが経済学の中でどのような位置かを説明するために、「クールノー競争」はモデルの具体的な説明をするために段落を分けています。一般的には細かく分けません。
クールノー・モデル

(英語版Wikipediaより・アントワーヌ・オーギュスタ・クールノー)
はてな
寡占市場(複占市場)の企業が、どのように生産量を決定するのかを分析した有名なモデル。クールノーモデルが生産量(数量)に注目しているのに対して、ベルトランモデルが価格に注目しているため、比較して語られることが多い。
クールノーモデルは「数量競争(生産量競争)」「クールノー競争」「クールノー・ゲーム」など状況に応じて様々な呼称がある。
寡占市場の企業戦略には3つの有名なモデルがあります。
- クールノー・モデル(数量)
- ベルトラン・モデル(価格)
- シュタッケルベルグ・モデル(先導・追随)
クールノーとベルトランは比較して語られることが多く、シュタッケルベルグは前提条件が2つとは異なるため別個に語られます。
ここで扱うクールノー・モデルは歴史が古く、1800年代中旬~後半に登場したモデルです。なので経済学で寡占市場の学習をすると初めに項目が出てきます。
どうでもいいですが、クールノーは、レオン・ワルラスに経済学を勧めて、それが間接的に一般均衡理論へと繋がっています。それくらい経済学の歴史的には古いモデルということです。


クールノー競争
はてな
ある寡占市場の企業は「ライバル他社の生産量が今後変化しない前提で、自社の生産量を決定する」と考えるとき、寡占市場の企業が利潤最大化のために生産量をどのように決定するか(どのような競争が行われるのか)の過程・結果を分析する。
価格よりも数量を調節しやすい場合はクールノー競争になりやすい。
クールノー競争は「寡占市場では各企業が生産量を通じて価格操作をしようとする」と考えているため「数量競争(生産量競争)」と呼ばれる理由になっている。一見すると完全競争市場と似ているが、不完全競争市場では企業が価格決定力を持っており、市場参加者が数社に限られる点が完全競争市場とは異なる。
例えば
 「石油」は、価格よりも産油量を調節することの方が多いです。これは市場価格を操作するよりも、産油量を調節する方が直ぐに需給への対応ができるためです。
「石油」は、価格よりも産油量を調節することの方が多いです。これは市場価格を操作するよりも、産油量を調節する方が直ぐに需給への対応ができるためです。
例えば、産油国Aが石油の減産を試みると、大体、サウジアラビアかロシアが増産を仕掛けてきます。クールノー競争に陥ると、産油国Aが石油を減産したときに、産油国Bは増産して市場のパイを奪うのが最適戦略だからです(これを「戦略的代替性」と呼びます)。
近年ではコロナ感染拡大により石油需要が減少しました。しかし、ライバル国が増産してパイを奪いに来る可能性(その他政治的な駆け引きも)あり、当初、各国は減産に踏み出せませんでした。
このように、クールノー競争によって石油需給のバランスが崩れないように「OPEC (石油産出国機構)」という組織が各国の利害を調節しています(最近は機能しているのか怪しいですが‥)。
他にも「半導体市場」が有名です。半導体は、とにかく需要がひっ迫すると増産しまくります。半導体不足になると「TSMC(台湾セミコンダクター)」という超有名企業が増産のための設備投資をしてニュースになります。これは、ライバルの供給量を見て、残りの需要量を自社で取り込もうとしているためです(つまり、価格競争ではなくクールノー競争(数量競争)をしている)。
前提
- 寡占市場の企業は、利潤最大化のために生産量を操作する。
- 自社と相手は同時に生産量を決定する(同時手番ゲーム)
- ライバルの生産量は変化しない
同時手番ゲームとは、ゲーム理論の考え方の1つ。(1)相手がどのような選択をするのかが分からない、(2)同時に意思決定をする、という条件で繰り広げられる戦略的状況のこと。
ゲームのモデル
- 独占的な企業が2社(A社・B社)存在する複占市場を考える‥①
- この2社は同質的な財を生産している‥②
①数社が独占的に市場を支配していると「寡占」になるが、その中で2社が独占的に支配しているケースを特別に「複占」と呼ぶ。②同質的な財というのは「同じジャンルの財」という意味。カップラーメンには細かな商品がたくさんありますが、全て「カップラーメン」というジャンルに属しています。ここでは、2社が「同じジャンルの財」を生産していると考えます。
いま
次の条件を考える
- x=生産量(需要量)
- P=価格
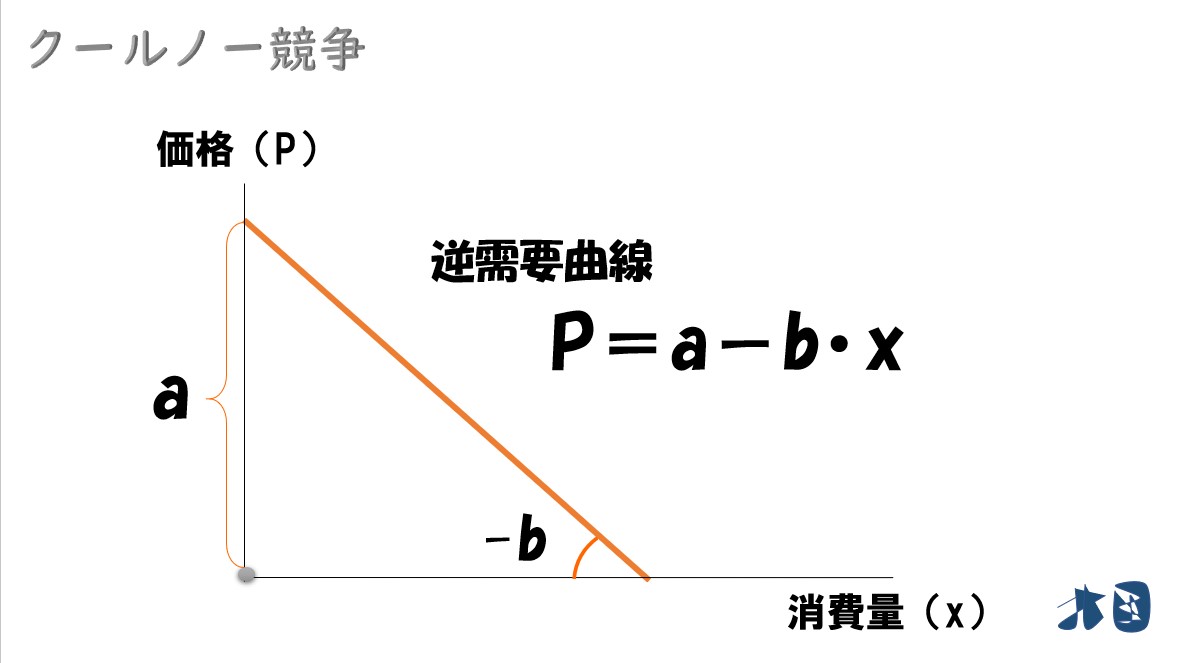
- 市場の逆需要関数(D)「P=a-b・x」‥①
- 2社の費用関数(C)「C・x」‥②
①逆需要関数というのは需要関数をP=の形にしたもの。②2社とも同質的な財を生産しているため、同じような費用関数になると考えています。
上記の条件のもとで、各社(今回のケースでは2社)が生産を行うと、最終的にどのような結果になるのかを考えます。
先に答えを書くと、最終的には「クールノー均衡」と呼ばれる状態にたどり着きます。
クールノー均衡(クールノー・ナッシュ均衡)
はてな
クールノー競争の結果たどり着く状態を「クールノー均衡(クールノー・ナッシュ均衡)」と呼びます。
ゲーム理論で登場する「ナッシュ均衡」とは何が違うのか?と疑問に思う人もいるかもしれませんが、クールノー競争のナッシュ均衡を特別に「クールノー均衡」と呼んでいるため「ナッシュ均衡=クールノー均衡」と考えて差し支えありません。
ここからは均衡にたどり着く過程を説明します。競争(モデル)の前提条件などは前の段落で確認してください。
step
1企業Aの視点で考える
企業A
ライバル企業Bは、1万個くらい生産してきそうだな‥
このとき、企業Aは次の行動を考える。
ポイント
この市場はA社とB社でシェアをおさえている(複占市場)
⇩
市場全体では3万個くらいは需要がありそう
⇩
B社が1万個作ってきそうなので、うちは2万個作ろう
step
2数式で考える
企業Aの利潤を次のように表記できる
- (企業Aの利潤)=(価格)×(企業Aの生産量)-(企業Aの費用)
仮に2万個作って100円で売るとき「100円(P)×2万個(x)」です。
費用が1個当たり20円かかるなら「20円(C)×2万個(x)」です。
よって企業Aの利潤「π=100×2万-20×2万」
文字式に置き換えると
π[a]=P・x[a]-C・x[a]
教科書などでは添え字で「a」とか「1」など掛かれていますが、表現しきれないので[a]とつけて、π[a]やx[a]で企業Aの利潤や生産量を表しています。
次に「価格P」に注目する
初めの方で、市場の逆需要関数(D)「P=a-b・x」と表現したので「価格(P)」は「a-b・x」と表現できます。
グラフで見ると‥
生産量が多ければ価格や安くなるし、生産量が減れば価格は上昇する。ごく一般的な需要曲線を文字式を使って表しています。
ポイント①
更に「x」は、市場全体の生産量を表しています。
A社とB社しかいない複占市場を考えていたので、市場全体の生産量は「企業Aの生産量(x[a])+企業Bの生産量(x[b])」です。
つまり「x=x[a]+x[b]」となるため「P=a-b (x[a]+x[b])」
ポイント②
企業Aは、企業Bの生産量を予想することは出来るが、実際の数値は不明。
⇒企業A側の視点では「x[b]」は予想値になる。
この予想値が的中して、かつ最適な消費量だったとして「x[b*]」とします。
以上より
価格は「P=a-b (x[a]+x[b*])」と表現できる。
上記の式を、企業Aの利潤を求める式「π[a]=P・x[a]-C・x[a]」に代入する。
⇒「π[a]=(a-b (x[a]+x[b*])・x[a]-C・x[a]」
全体を「x[a]」でくくる
⇒「π[a]=(a-b (x[a]+x[b*])-C)・x[a]」
カッコ内(-bの部分)を展開する
⇒「π[a]=(a-b・x[a]-b・x[b*]-C)・x[a]」


step
3企業Aの利潤をグラフで考える
式を展開すると「-b・x[a]の2乗」が登場するため「π[a]=(a-b・x[a]-b・x[b*]-C)・x[a]」は2次式です。中学校の数学を思い出してもらえればいいのですが、〇の2乗が登場する数式は放物線を描くようなグラフになります。
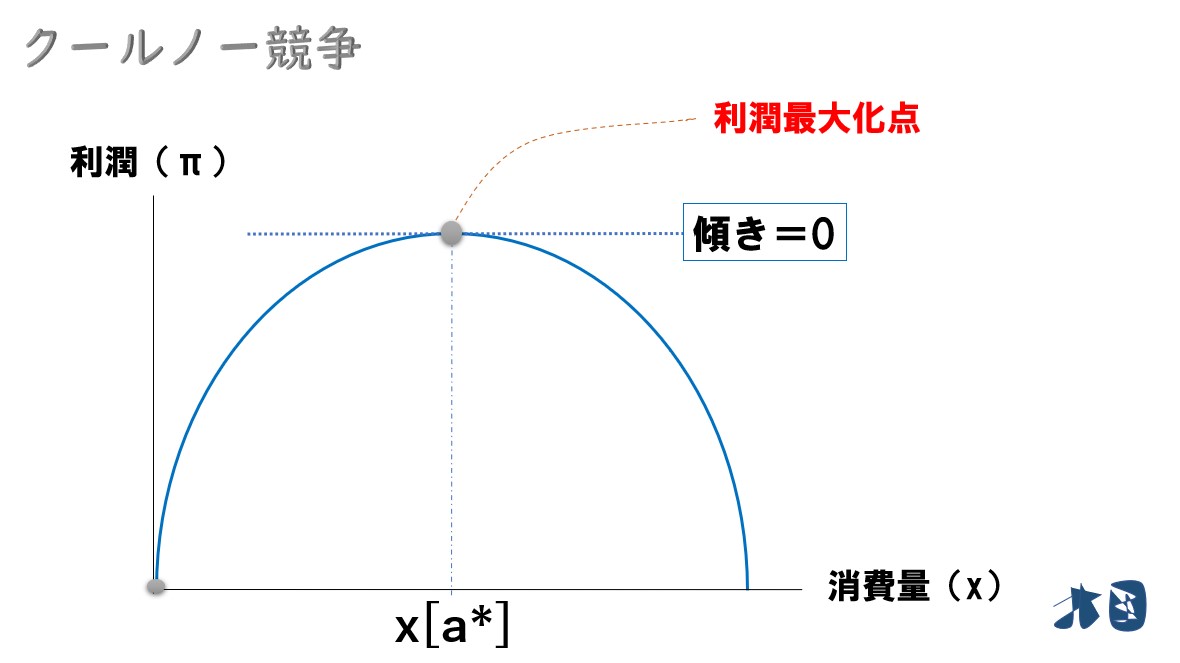
グラフの縦軸と横軸に注目
- 縦軸=企業Aの利潤の大きさ「π[a]」
- 横軸=企業Aの生産量「x[a]」
ポイント
このグラフは、企業Aが生産量(x)を増やすと利潤(π)がどのように変化するかを表している。グラフより、企業Aはグラフが頂点を描くときの生産量(x[a]*)にすれば利潤最大化を実現できることが分かる。
グラフの頂点では「傾きが0」になることにも注目する。
step
4企業Aの利潤最大化条件を計算する
先ほどのグラフより、グラフの傾きが0になるとき、企業Aの利潤が最大化します。
ポイント
- π[a]=(a-b・x[a]-b・x[b*]-C)・x[a]
↑この式の傾きが0になる瞬間を求めれば利潤最大化点が分かる。


数学的には「微分して、イコール0」にすればOKです!
微分の意味が分からない人向けに簡単に補足です。微分は、グラフを細分化して、その小さな点の傾きがどれくらいなのかを計算できます。つまり、グラフの放物線の傾きが0になる⇒「微分した結果がイコール0になるはず」というわけです。
以上より
- 企業Aの生産量(x[a])で微分します。
最後に=0で結びます。


step
5企業Bの視点で考える
(企業Aと同様の考え方です)
ポイント
複占市場で企業A・企業Bが利潤最大化を実現させるための条件が整いました(1階条件)。
step
62社の条件式を連立方程式として解く
「x[b*]」「x[a*]」も各企業の予想値と考えていましたが、それぞれ実際の消費量と予想が一致していると仮定して、「x[b*]=x[b]」「x[a*]=x[a]」と考えて連立方程式を解きます。
ポイント
わざわざ計算する必要があったのか不明ですが、対照的な連立方程式になっているので「x[a]=x[b]」となります。分かりづらくなるので「x[a]=x[b]=x*」と考えます。
企業Aの式で「x[a]=x[b]=x*」として計算する!
x[a]=x[b]=x*=(a-c)/3b


最後に
この計算結果を説明します。
複占市場の2社がどのような行動を取るのかを考えてきました
- x=生産量(需要量)
- P=価格
- 市場の逆需要関数(D)「P=a-b・x」‥①
- 2社の費用関数(C)「C・x」‥②
この条件のとき、A社とB社が利潤最大化を実現させるために取る行動は・・「x[a]=x[b]=x*=(a-c)/3b」と計算されました。
ポイント
複占市場で上記の条件のとき、2社とも利潤最大化を目指して相手がどれくらい生産を行うかを想像しながら自社の生産量を調整する。最終的に次の生産量に落ち着くことが分かった。
- 企業Aの生産量=(a-c)/3b
- 企業Bの生産量=(a-c)/3b
クールノー競争で最終的にたどり着く、上記の2社の生産量を「クールノー均衡(クールノー・ナッシュ均衡)※」と呼ぶ。ようは、複占市場で企業が利潤最大化を目指すと上記の生産量に落ち着く。その状態を「クールノー均衡」と呼んでいる。
※「需要曲線と供給曲線が交わるところで均衡が決まる」という従来の考え方とは、全く異なる考え方なので注意する。複占・寡占市場の「均衡」の考え方は基本的にゲーム理論と同じです。


と、その前にですが、クールノー均衡の重要な意味を把握するためにも、もう少し準備が必要になります(反応曲線に続く!)
最適反応曲線
はてな
相手の生産量に応じて自社の生産量をどれくらいにしたらよいかを表した曲線(もしくは関数)。「反応曲線」「最適反応関数」とも呼ばれる。
例えば
(先ほどの例)複占市場で企業Aが企業Bの生産量を1万と予想します。このとき、市場規模は3万なので、企業Aは「2万生産しよう」と考えます。
この関係を表したのが最適反応曲線です。
はじめに
グラフを描く前に、最適反応を表す式を求めます。
クールノー均衡を求めるときに登場した式を使います。どのような経緯でこの式が出てきたのか理解できない人は戻って確認してください。
2つの式は、企業Aと企業Bが複占市場で利潤最大化を実現するための条件式です(1階条件)
つまり、企業Aの最適な生産量(最適反応)を求めるには、この式を「生産量(x)=~」の形にすればOKです。
企業Aの式を変形してみる
ポイント
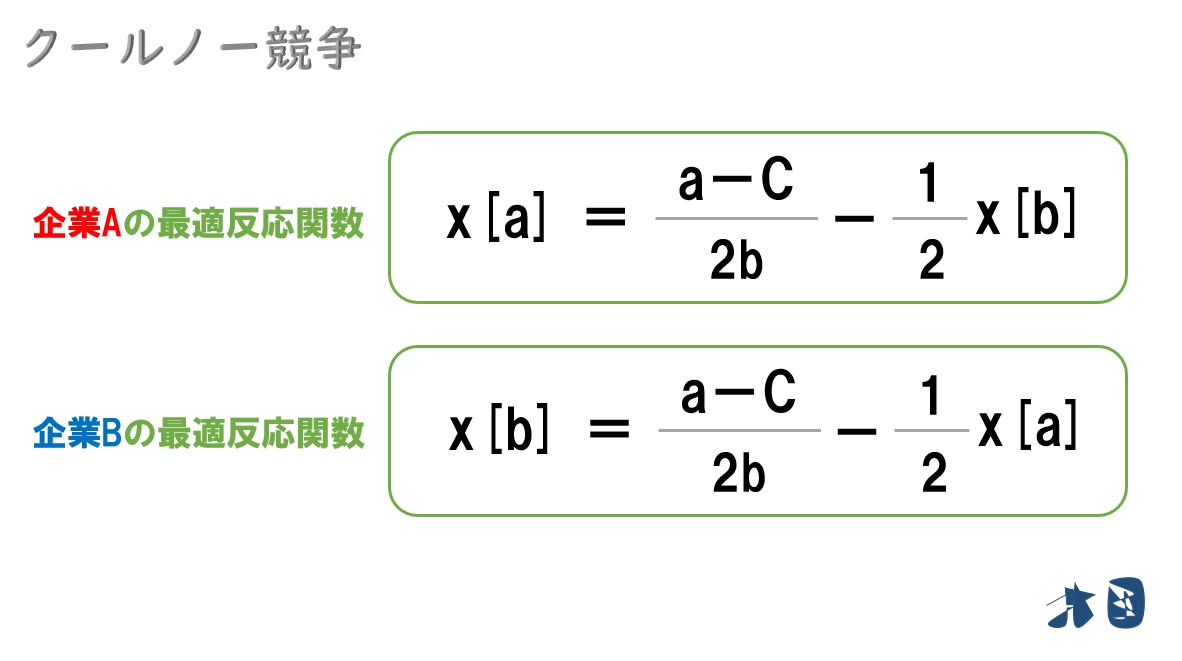
企業Aの最適反応関数=(a-c)/2b-1/2x[b]
よって、A社・B社の最適反応関数は‥


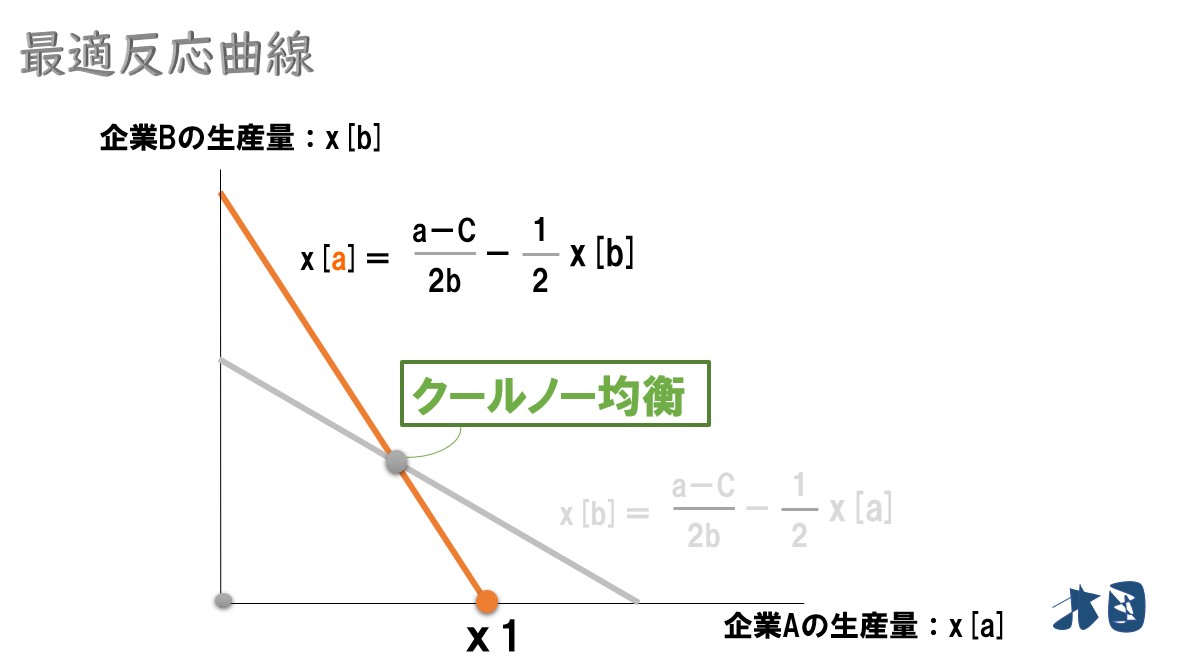
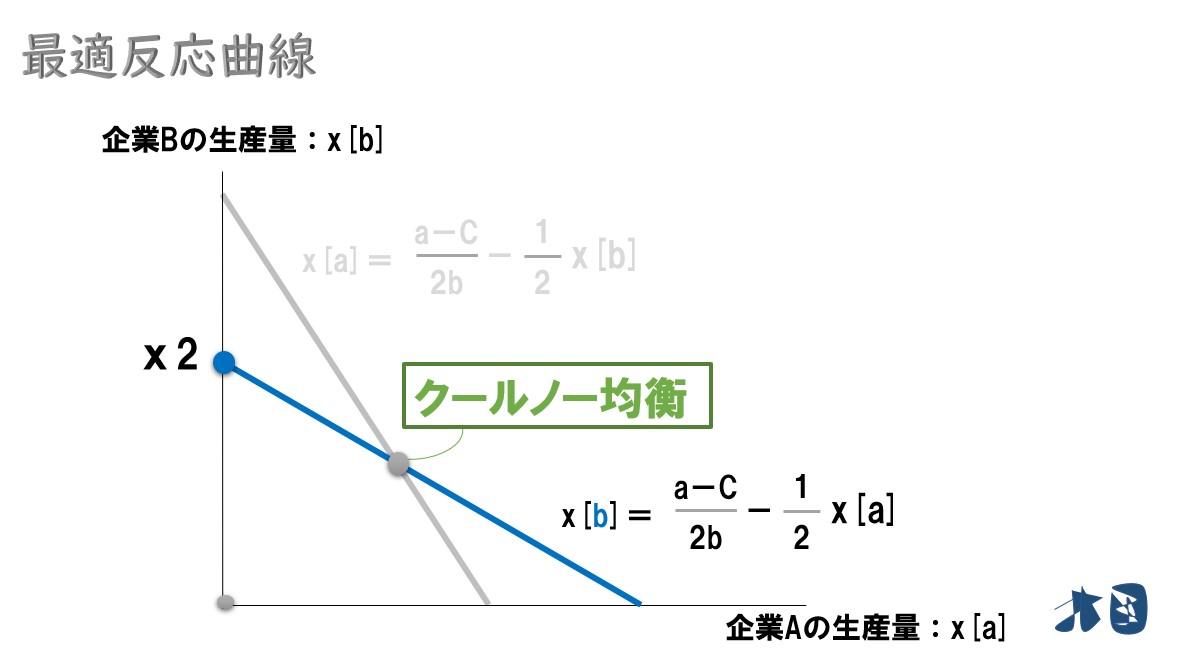
グラフにすると‥
初めて見る人は、グラフが少し分かりづらいかもしれません。ただ、2つの式が対照的でほとんど同じなので、グラフも似たような感じになっている程度でOKです。
ちなみに、2つの最適反応曲線が交わっている点はクールノー均衡です。
この点は、2社がそれぞれ最適な生産量を実現している点です(クールノー競争の結果、たどり着く2社の生産量を表しています)。クールノー均衡がグラフ上で確認できましたね。
それで、重要なのはここからです。
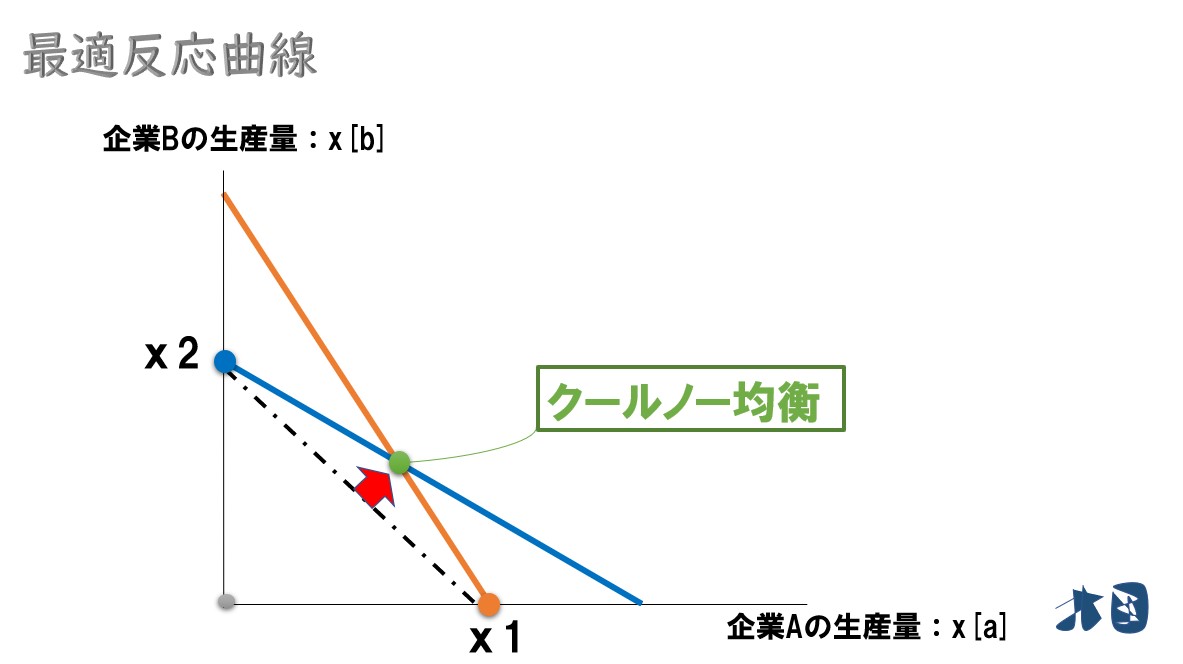
仮に
独占市場なら、どうなっていたか
独占市場を考えるには、B社の生産量が0だった場合を考えればOKです。複占市場でB社の生産量が0ならばA社が単独で生産します⇒実質的にA社が市場を独占する。
グラフより独占市場ならばA社は「x1」の生産量を実現させます。
B社が独占する場合も同様に考える。
以上より分かること
- 複占市場の方が生産量が多くなる
- 独占市場の生産量は「x1」もしくは「x2」
- 複占市場の生産量は緑点(クールノー均衡)
独占市場の生産量よりも、複占市場の生産量の方が多くなっていることが分かる。
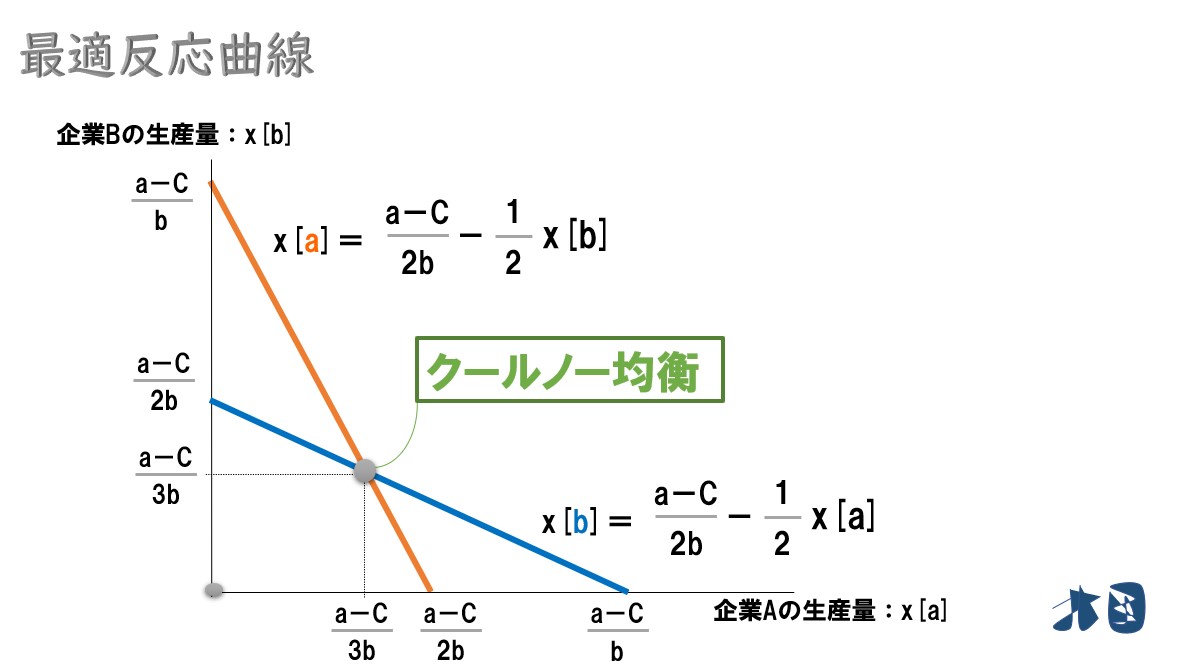
少し厳密にグラフを見る
先ほどの話を理解できればOKですが、念のため厳密な値も付け加えます(飛ばしてもOK)
企業Aの視点で考えます(オレンジ色の最適反応曲線)
- クールノー均衡=(a-c)/3b
- 企業Bが生産量0のとき=(a-c)/2b
- 企業Aが生産量0のとき=(a-c)/b
企業Bも同様の考えます(省略)。


ここまで分かれば、クールノー均衡が何を意味しているのかが分かってきます(続く)
クールノー均衡の意義
ポイント
クールノー均衡より「完全競争市場>複占市場(寡占市場)>独占市場」の順番で市場全体の生産量が多くなることが分かる。
以上より、複占市場では(独占市場ほどではないが)市場を支配する複数の企業が、生産量をおさえて価格を吊り上げている。よって、複占市場は非効率的な状態に陥っていることが分かる。
最適反応曲線から、独占市場よりも複占市場の方が生産量が多くなることが分かりました。
クールノー競争のモデルや均衡・反応曲線などを理解している前提で話を進めます。分からない人は戻って確認してください。
今度は
完全競争市場と比べると、どうなるのか
これはグラフを使わずに数式で直ぐに分かります。
- 市場の逆需要関数(D)「P=a-b・x」
- 費用関数(C)「C・x」
完全競争市場の利潤最大化条件「P=MC」より
- 「P=a-b・x=c」
限界費用(MC)は、費用関数を生産量(x)で微分すれば求められます。「C・x」をxで微分すると「C」になります。
市場全体の生産量(x)は‥
・a-b・x=c
・a-c=b・x
・x=(a-c)/b
ここで
クールノー均衡のとき、2社の生産量は‥
- 企業Aの生産量=(a-c)/3b
- 企業Bの生産量=(a-c)/3b
市場全体の生産量=「A社の生産量+B社の生産量」なので
「(a-c)/3b+(a-c)/3b=2/3・(a-c)/b」
以上より
- x=(a-c)/b(完全競争市場)
- x=2/3・(a-c)/b(複占市場)
市場全体の生産量は
完全競争市場(a-c)/b>複占市場2/3・(a-c)/b
よって、完全競争市場の方が市場全体の生産量が多くなる。
さらに詳しく
完全競争市場の方が、市場全体の生産量が多くなることが分かりました。これが何を意味しているのかを補足します。
ふつう、市場では生産量が多くなるほど、商品がたくさん流通するので価格が下落します。
つまり、複占市場の方が生産量が少ないということは、商品の流通量が減っているため、完全競争市場よりも価格が高止まりする傾向にあるわけです。
「クールノー均衡」は複占市場(寡占市場)の非効率性をあぶり出しています。
まとめ
(途中に記載したものと同じ)
クールノー均衡より「完全競争市場>複占市場(寡占市場)>独占市場」の順番で市場全体の生産量が多くなることが分かる。
以上より、複占市場では(独占市場ほどではないが)市場を支配する複数の企業が、生産量をおさえて価格を吊り上げている。よって、複占市場は非効率的な状態に陥っていることが分かる。


クールノー競争のモデルから、均衡や最適反応を順番に見ていくと、上記のような結果が導出できました。何となく学習すると、数式だらけで何をしているのかが分かりづらいですが、一連の分析から不完全競争市場が非効率的だということが客観的に示されたわけです。
おまけで、複占市場の余剰分析も付けておきますので興味があれば参考にしてください。
余剰分析
次の条件で複占市場を考える。
- 市場の逆需要関数(D)「P=a-b・x」
- 費用関数(C)「C・x」
限界費用(MC)は、費用関数を生産量(x)で微分すれば求められます。「C・x」をxで微分すると「C」になります。
クールノー均衡のとき、2社の生産量は次の通り。
- 企業Aの生産量=(a-c)/3b
- 企業Bの生産量=(a-c)/3b
市場全体の生産量=「A社の生産量+B社の生産量」なので
「(a-c)/3b+(a-c)/3b=2/3・(a-c)/b」
ここまではクールノー競争の話で登場しました。
次に
市場の逆需要曲線「P=a-b・x」なので「x=2/3・(a-c)/b」を代入して価格(P)を求める。
・P=a-b・x
・P=a-b・2/3・(a-c)/b
・P=a-2/3・(a-c)
・P=3/3・a-2/3・(a-c)
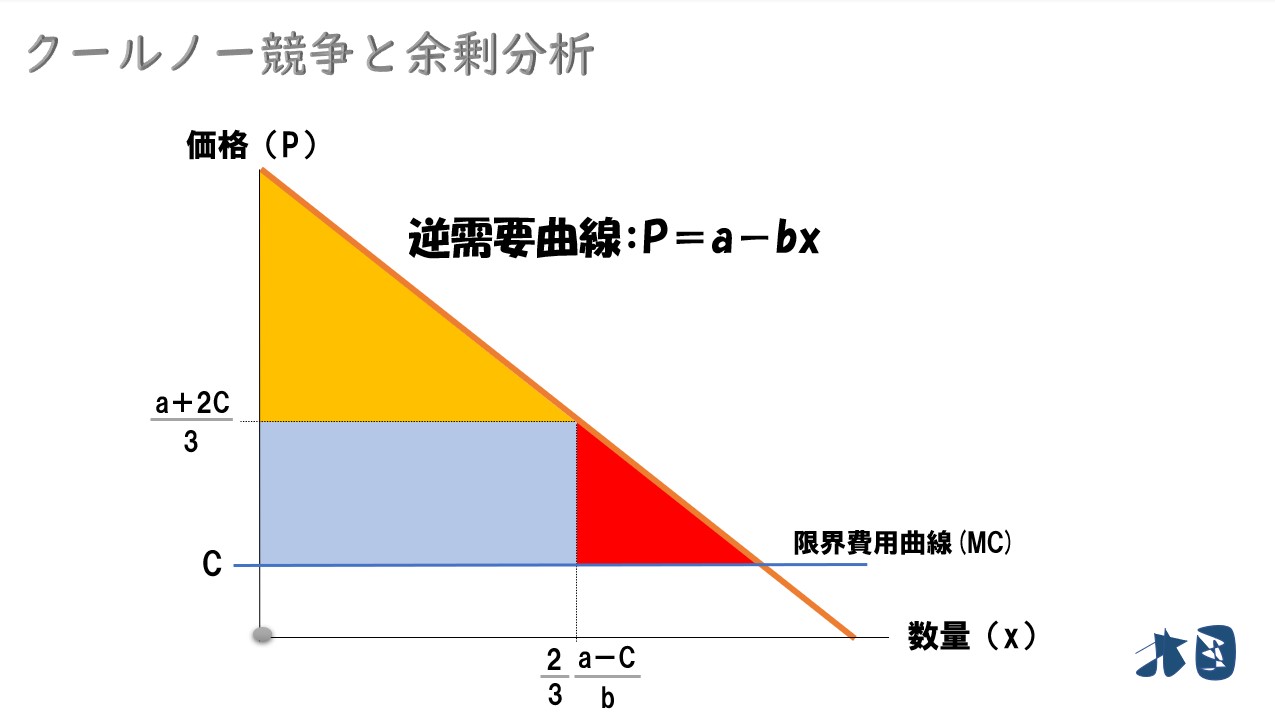
・P=(a+2c)/3
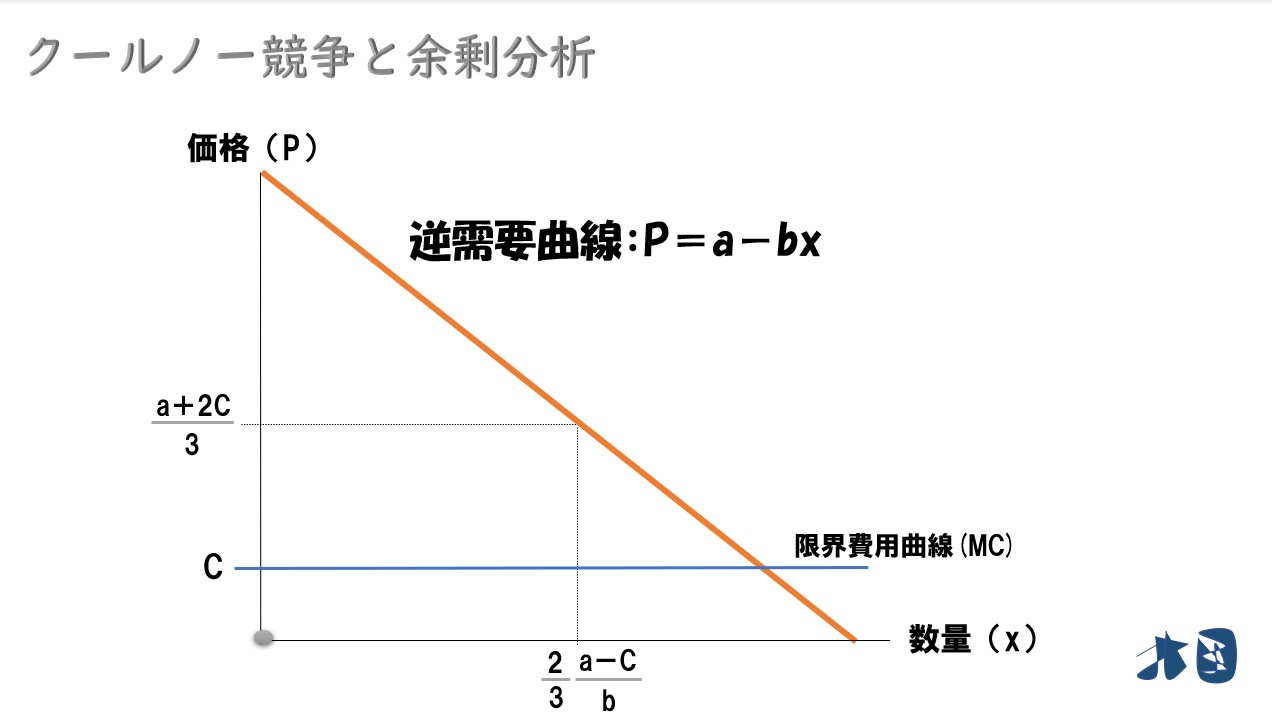
以上より
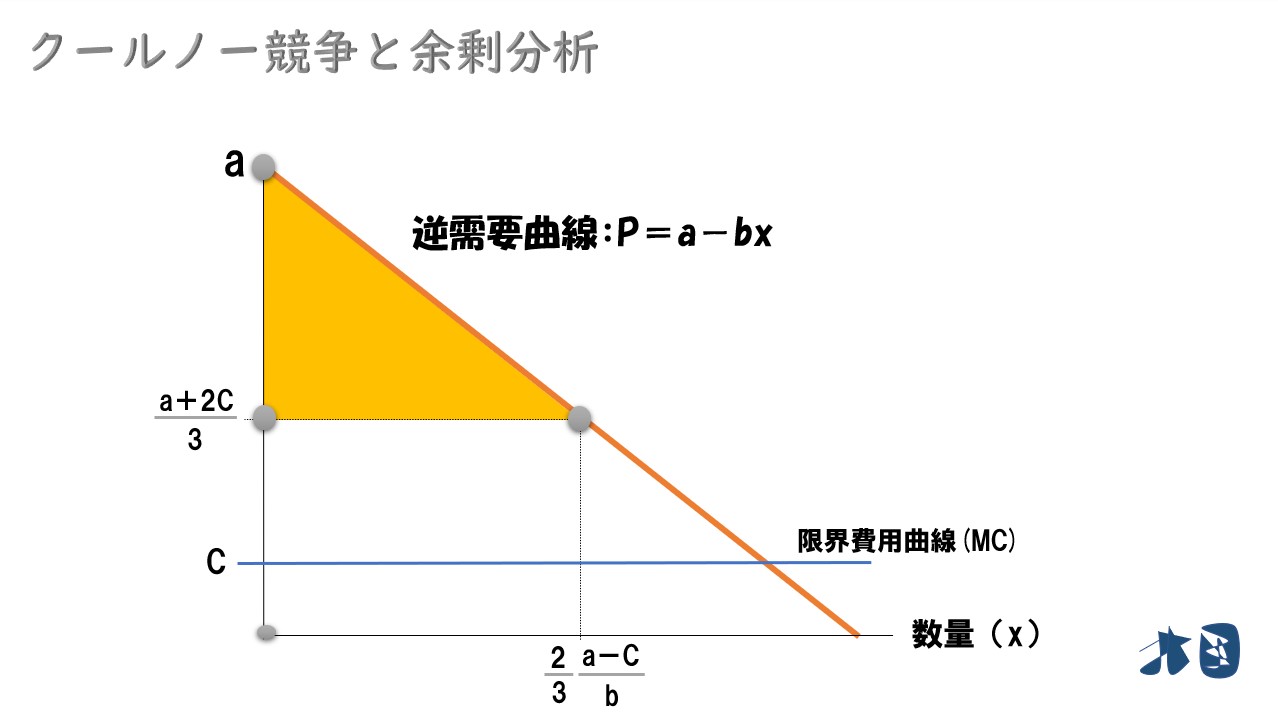
- 消費者余剰(CS)=黄色三角形
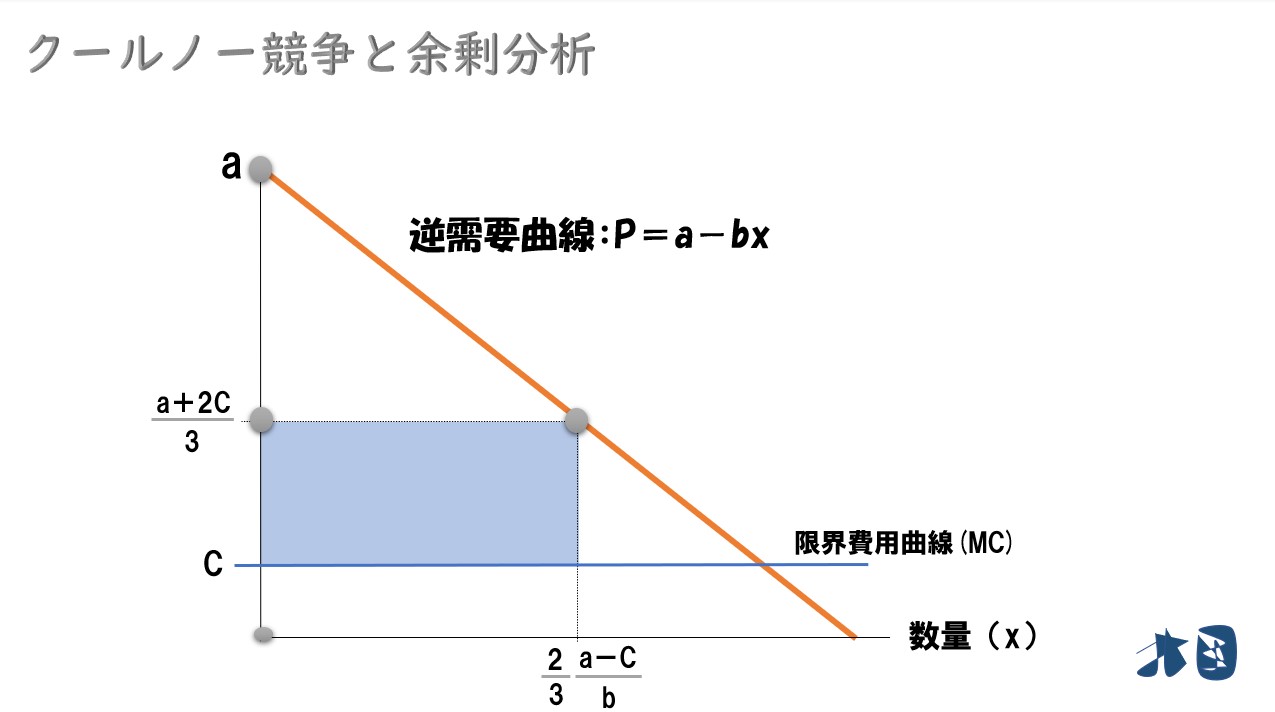
- 生産者余剰(PS)=青色四角形
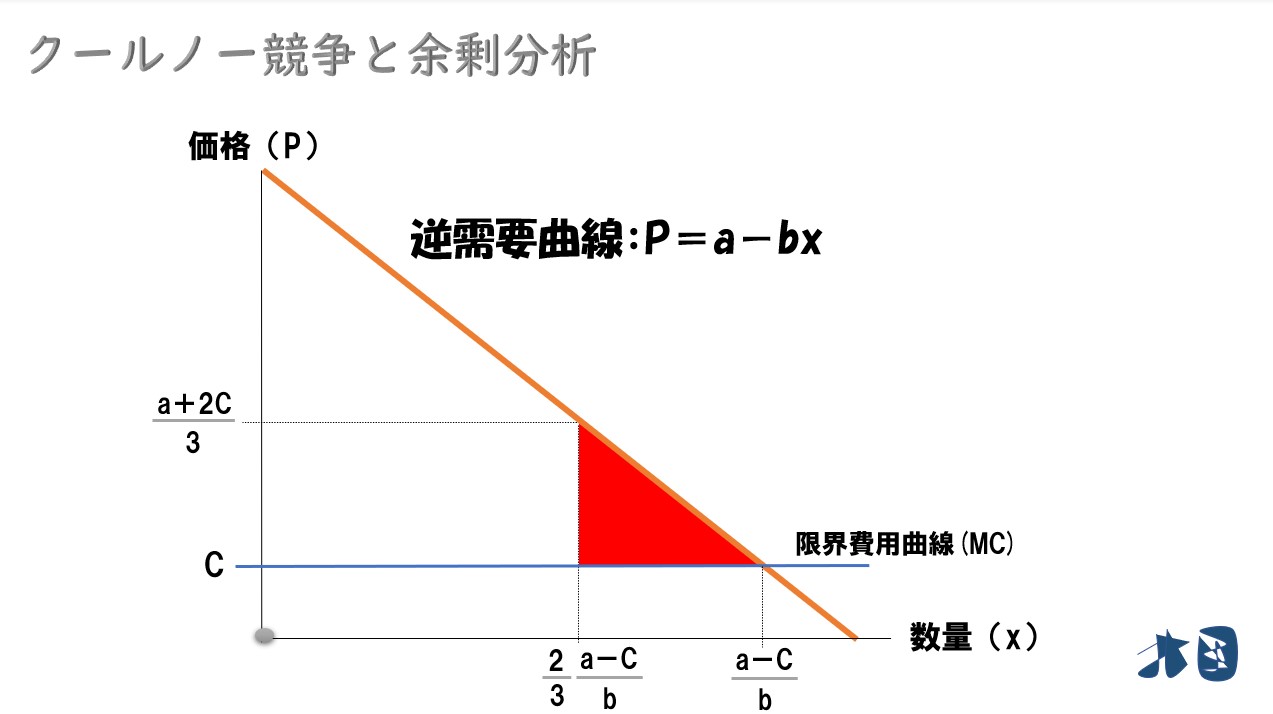
- 死荷重=赤色三角形
計算すると
- 消費者余剰(CS)
三角形の面積「1/2×縦×横」より
・CS=1/2・(a-(a+2c)/3)・2/3・(a-c)/b
・CS=1/2・(2a-2c)/3・2/3(a-c)/b
・CS=1/9・(2a-2c)(a-c)/b
・CS=1/9・2(a-c)(a-c)/b
・CS=1/9・2(a-c)^2/b
- 生産者余剰(PS)
四角形の面積「縦×横」より
・PS=((a+2c)/3-c)・2/3・(a-c)/b
・PS=(a-c)/3・2/3・(a-c)/b
・PS=1/9・2(a-c)(a-c)/b
・PS=1/9・2(a-c)^2/b
- 死荷重
三角形の面積「1/2×縦×横」より
・死荷重=1/2・((a+2c)/3-c)・2/3・(a-c)/b-(a-c)/b
・死荷重=1/2・(a-c)/3・-1/3・(a-c)/b
・死荷重=1/18・(a-c)(a-c)/b
・死荷重=1/18・(a-c)^2/b
以上より
計算問題

いま、企業Xと企業Yの2社が支配する複占市場を考える。2社は同質的な財を生産している。
- 需要関数:D=12-P
- X社の生産量=x
- Y社の生産量=y
- X社費用関数(Cx)=x
- Y社費用関数(Cy)=2y
このとき、クールノー均衡における下記2つを求めよ。
- 価格
- 2社の利潤
はじめに
2社が生産したものが需要されるため
- 需要(D)=「X社の生産量+Y社の生産量」
よって「12-P=x+y」
先に企業Xの利潤を考える。
- X社の利潤=「価格×生産量-費用」
- よって「πx=P・x-Cx」
「12-P=x+y」より「P=-x-y+12」‥①
X社費用関数(Cx)=x‥②
①②を代入する
・πx=P・x-Cx
・(-x-y+12)・x-x
・-xの2乗-xy+12x-x
・-xの2乗-xy+11x
・-xの2乗+(11-y)x
クールノー競争のとき、利潤の式を「微分して=0」とすれば利潤最大化を求められる。
「-xの2乗+(11-y)x」を「生産量=x」で微分する
「x」という文字がついている部分の乗数を減らして手前に持ってくる。また0乗になった部分は「1」となることに注意する。
Δπ/Δx=
・-2x+11-y=0
・2x=11-y
・x=5.5-0.5y
企業Yも同様に求められる(省略)
・y=5-0.5x
クールノー競争における、2社の利潤最大化を実現させる生産量は下記の通りだと分かった。
・x=5.5-0.5y
・y=5-0.5x
連立方程式or代入して解くと
・x=5.5-0.5(5-0.5x)
・x=5.5-2.5+0.25x
・0.75x=3
・x=3÷3/4
・x=3×4/3
・x=4
y=5-0.5xに代入して
・y=3
以上より、クールノー均衡は(x,y)=(4,3)である。
需要関数:D=12-Pより
市場全体の生産量=4+3=7なので「D=7」だと分かる
・7=12-P
・P=12-7
・P=5
(1)クールノー均衡における価格は「5」
- X社の利潤は「πx=P・x-x」なので
πx=5×4-4=16
- Y社の利潤は「πx=P・y-2y」なので
πy=5×3-2・3=9
(2)X社の利潤は「16」/Y社の利潤は「9」