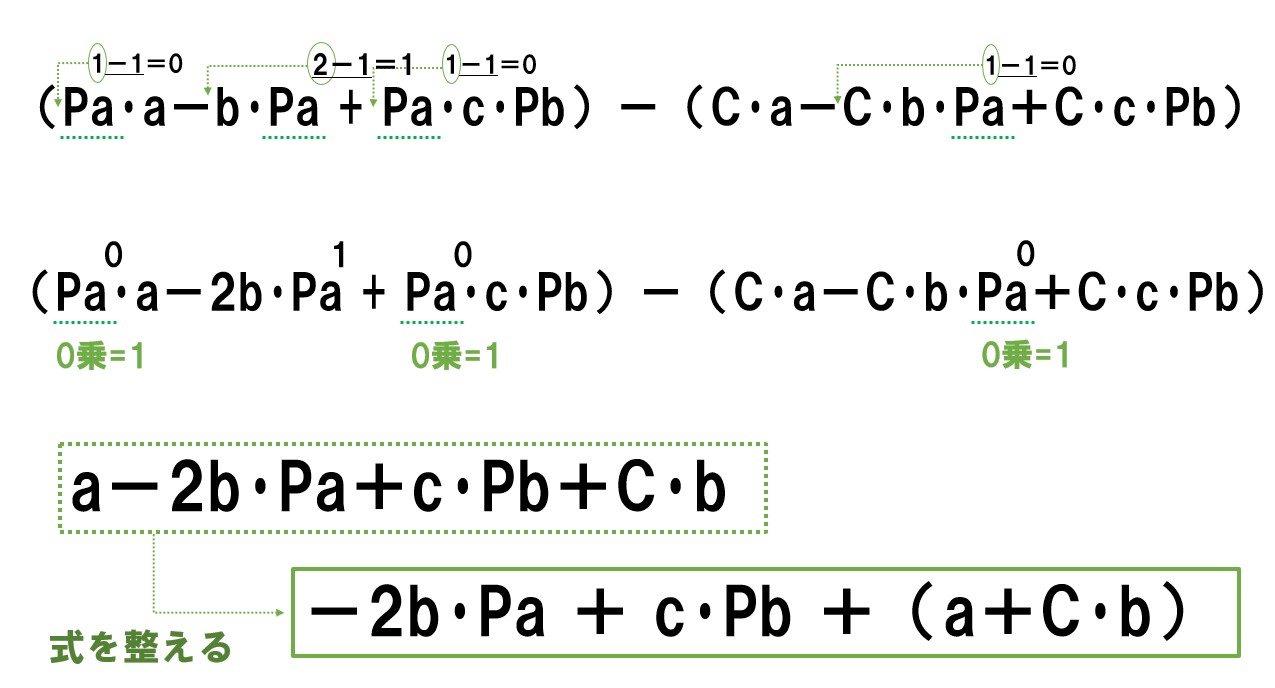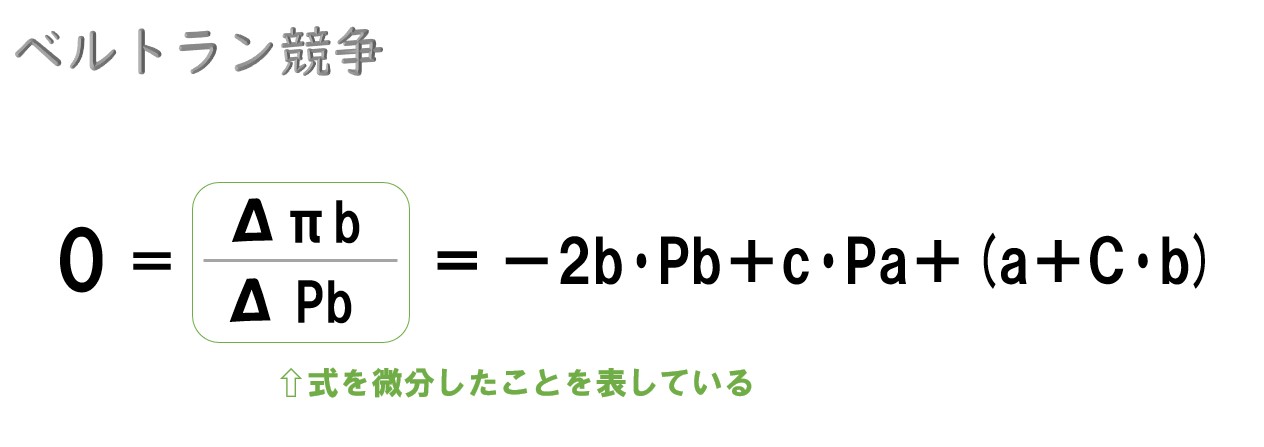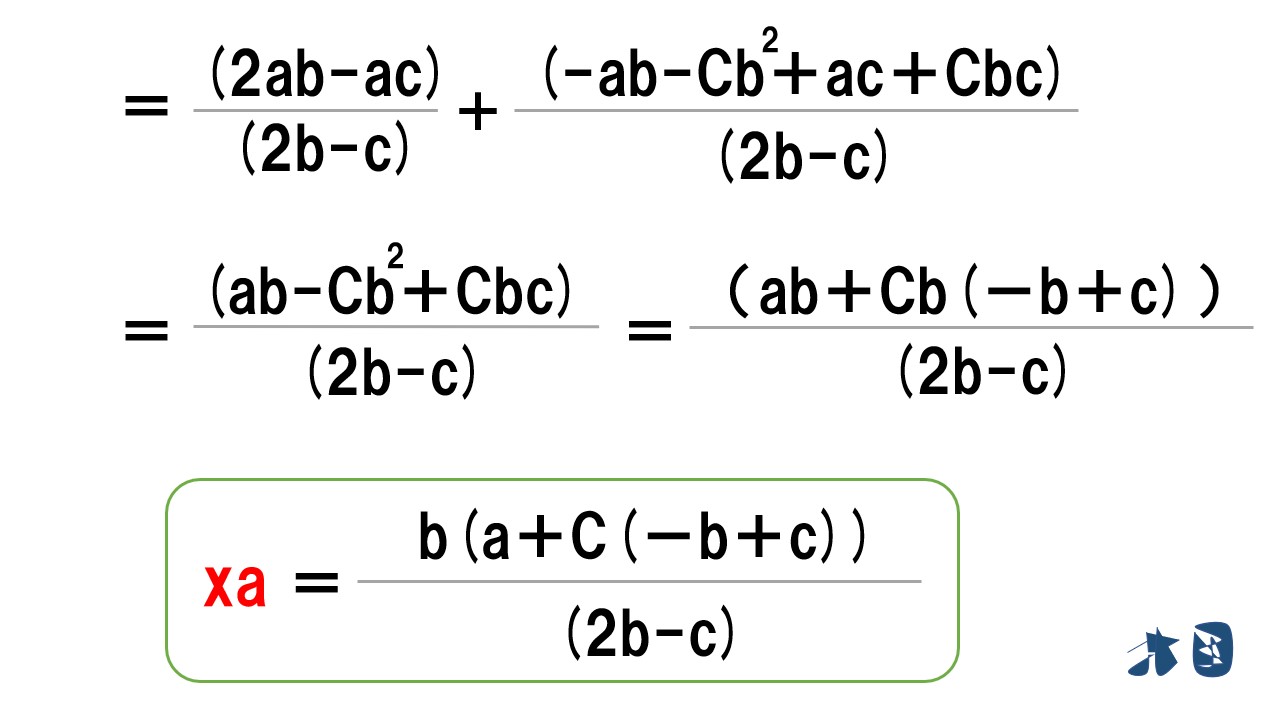フランスの数学者ベルトランが構築した「不完全競争市場における企業行動を分析したモデル」を1から簡単にまとめています。
- ベルトランの(価格競争)モデル
- ベルトラン競争(例など)
- ベルトラン均衡
- ベルトラン・パラドクス
- 製品差別化のあるベルトラン競争
- 反応曲線
- ベルトラン均衡の意義(独占)
- 余剰分析
- 戦略的補完
- 計算方法や求め方
この記事内では「ベルトランモデル」は、このモデルが経済学の中でどのような位置かを説明するために、「ベルトラン競争」はモデルの具体的な説明をするために段落を分けています。一般的には細かく分けません。
ベルトラン・モデル

(wikipediaより ジョゼフ・ルイ・フランソワ・ベルトラン)
はてな
寡占市場(複占市場)の企業が、どのように価格を決定するのかを分析したモデル。クールノーモデルが生産量(数量)に注目しているのに対して、ベルトランモデルが価格に注目しているため、比較して語られることが多い。
ベルトランモデルは「価格競争」「ベルトラン競争」「ベルトラン・ゲーム」など状況に応じて様々な呼称がある。
寡占市場の企業戦略には3つの有名なモデルがあります。
- クールノー・モデル(数量)
- ベルトラン・モデル(価格)
- シュタッケルベルグ・モデル(先導・追随)
クールノーとベルトランは比較して語られることが多く、シュタッケルベルグは前提条件が2つとは異なるため別個に語られます。
ここで扱うベルトラン・モデルは、クールノー・モデルを作り替えたモデルです。なので、経済学の教科書ではクールノー⇒ベルトランという順序で紹介されます。
ちなみに、ベルトランはクールノーの著書※1をレビューして、1883年にベルトランモデルのアイデアを構築しました。ざっくり言うと、ベルトランは、クールノーは寡占市場で「企業は数量を調整する」と考えたけど、本当は「企業は価格を調整する」と考えた方がいいんじゃない?と考えました。
具体的には、クールノーは「寡占市場で企業が生産量(数量)を調整すると、価格(P)が限界費用(MC)よりも高くなる(価格は競争市場よりも寡占市場のほうが高止まりする)。なので、競争市場よりも寡占市場のほうが企業は高い利潤を得ている」と考えていました。しかし、ベルトランは「それは、寡占市場で企業が生産量を調整すると考えたからだ。寡占市場で企業が価格を調整すると考えれば、寡占市場でも競争市場と同じように価格が高止まりすることはない(価格と限界費用(MC)が一致する)。」と考えました。
※1『Recherches sur les principes mathematiques de la theorie des richesses par Augustin Cournot(1838)』


ベルトラン競争
はてな
ある寡占市場の企業は「ライバル他社の価格が今後変化しない前提で、自社の価格を決定する」と考えるとき、寡占市場の企業が利潤最大化のために価格をどのように決定するか(どのような競争が行われるのか)の過程・結果を分析する。
数量よりも価格を調節しやすい場合はベルトラン競争になりやすい。
ベルトラン競争は「寡占市場では各企業が価格を調整して利潤最大化を目指す」と考えているため、「価格競争」と呼ばれる理由になっている。
例えば
 「航空券」や「宿泊関係」などは、数量を調節するよりも価格調節(繁忙期に値段が跳ね上がるやつ)の割合が大きいのでベルトラン競争に陥るリスクがあります(現状では程よい価格帯でキープされていますね)。
「航空券」や「宿泊関係」などは、数量を調節するよりも価格調節(繁忙期に値段が跳ね上がるやつ)の割合が大きいのでベルトラン競争に陥るリスクがあります(現状では程よい価格帯でキープされていますね)。

近年では「スマホの通信料」が良い例です。政府の圧力がトリガーになって、キャリア3社はベルトラン競争に陥ったと考えることも出来ます。国内の通信供給量を操作するのは難しく、価格競争っぽくなっています。

他には「牛丼の値下げ競争」はベルトラン競争の代表例として扱われます(この話は戦略的補完の段落で触れます)。
前提
- 寡占市場の企業は、利潤最大化のために価格を操作する。
- 自社と相手は同時に価格を決定する(同時手番ゲーム)
- ライバルの価格は変化しない
同時手番ゲームとは、ゲーム理論の考え方の1つ。(1)相手がどのような選択をするのかが分からない、(2)同時に意思決定をする、という条件で繰り広げられる戦略的状況のこと。
ゲームのモデル
- 独占的な企業が2社(A社・B社)存在する複占市場を考える‥①
- この2社は同質的な財を生産している‥②
①数社が独占的に市場を支配していると「寡占」になるが、その中で2社が独占的に支配しているケースを特別に「複占」と呼ぶ。②「同質的な財=似たような財」のこと。製品差別化がされるケースものちに紹介します。
先に答えを書くと、最終的には「ベルトラン均衡」と呼ばれる状態にたどり着きます。
ベルトラン均衡(ナッシュ均衡)
はてな
ベルトラン競争の結果たどり着く状態を「ベルトラン均衡」と呼びます。ベルトラン均衡は(弱い)ナッシュ均衡になっているため、たんにナッシュ均衡(もしくはベルトラン・ナッシュ均衡)と呼ぶこともあります。
ここからは均衡にたどり着く過程を説明します。競争(モデル)の前提条件などは前の段落で確認してください。
消費者の視点で考える
消費者
同じ商品なら一番安いところから買いたいな。
企業Aの視点で考える
企業A
B社よりも安い価格設定にして、消費者を囲い込もう!
もちろん、B社も、A社よりも安い価格にして消費者を囲い込もうと考えます。
ポイント
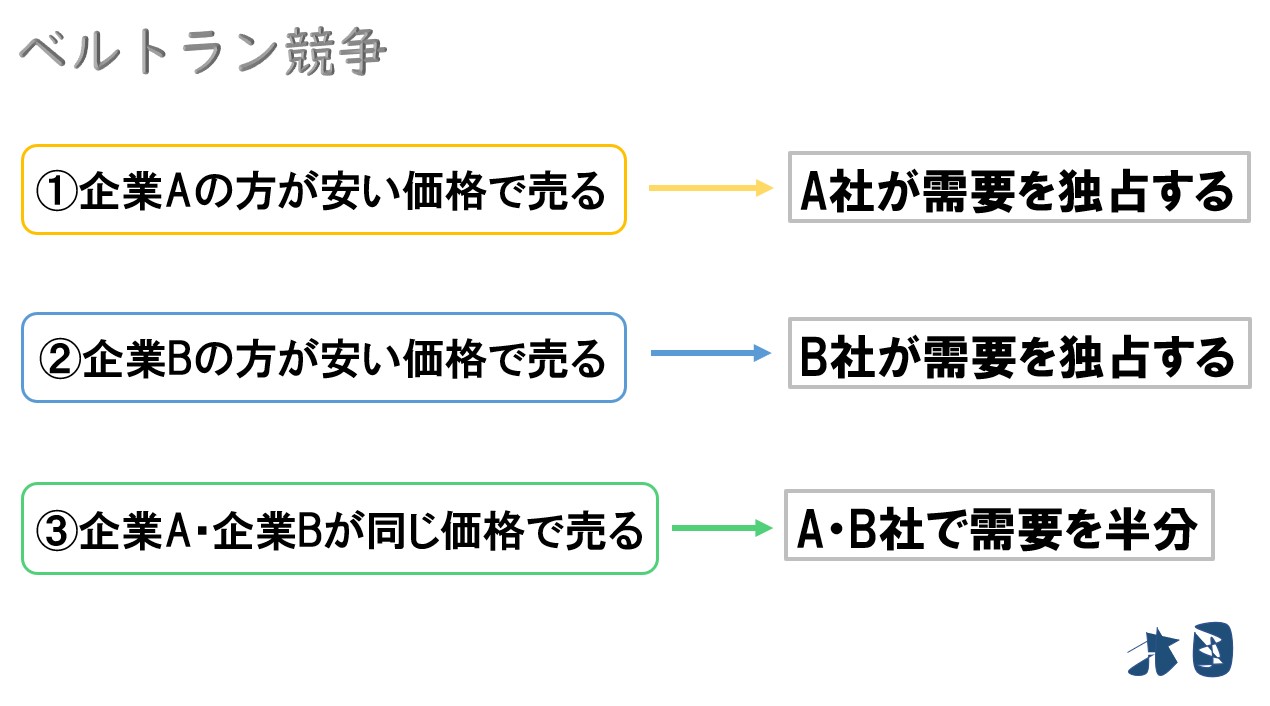
同じ財なので、とにかく安い価格で売った企業が、需要を独占する。
3つのケース


2社とも同じことを考える
- 利潤が出るギリギリまで安い価格設定を目指す
安い価格にしないとライバル企業に需要を持っていかれるので、企業は何としても他社より安い価格設定にしようとする。
ちなみに、赤字になるような価格設定はできないので、利潤が0になるところまでは値下げ競争が生まれます。つまり最終的に各企業は利潤が0になるギリギリの水準で価格設定をするはずなので、そこが均衡になる(ベルトラン均衡)!
数式でも考えてみましょう!(計算の結果がベルトラン均衡になります)
数式で考える
- A社の価格設定=Pa
- A社の生産量=xa
- B社の価格設定=Pb
- B社の生産量=xb
- 市場の逆需要関数(D)「P=a-b・x」‥①
- 2社の費用関数(C)「C・x」‥②
①逆需要関数というのは需要関数をP=の形にしたもの。②2社とも同じ財を生産しているため、同じ費用関数になると考えています。
上記の式をもとに、各社(今回のケースでは2社)が価格設定を行うと、最終的にどのような結果になるのかを考えます。
はじめに
各企業の利潤関数を考える
- 企業Aの利潤(πa)=価格(Pa)・生産量(xa)-費用(C)・生産量(xa)
- 企業Bの利潤(πb)=価格(Pb)・生産量(xb)-費用(C)・生産量(xb)
生産した商品を全て売ると考えて「価格×生産量」で各企業の総収入と考える。また、はじめに費用関数を「C・x」と設定していたので「費用×生産量」で各企業の総費用と考える。利潤は「総収入-総費用」で求められるので上記の式になる。
ここで
利潤関数を変形する(A社の利潤関数で見てみる)
- 利潤(πa)=価格(Pa)・生産量(xa)-費用(C)・生産量(xa)
- 利潤(πa)=(価格(Pa)-費用(C))×生産量(xa)
「各企業は利潤が0になるギリギリの水準で価格設定をするはず」と記載しましたが、数式で考えると「価格(P)-費用(C)」が0になる水準で価格が決まる。
ポイント
よって、各社の価格設定が「価格(P)=費用(C)」となるとき、ベルトラン競争の均衡になる。
- 企業Aの価格(Pa)=費用(C)
- 企業Bの価格(Pb)=費用(C)
以上より「企業Aの価格(Pa)=企業Bの価格(Pb)=費用(C)」となる価格設定を「ベルトラン均衡(ベルトラン・ナッシュ均衡)」と呼ぶ。


ココに注意
複占市場を考えたベルトラン競争の結果、価格競争が行われて企業が利潤0になるところで均衡するという話は、完全競争市場と同じ考え方になっている。
不完全競争市場を分析するために複占市場(寡占市場)を分析したのに、完全競争市場と同じ結果に辿り着いた。これを「ベルトラン・パラドックス(ベルトランの逆説)」と呼ぶ。


ベルトラン・パラドックスから「製品差別化」という話へ繋がります。
ベルトラン・パラドックス(製品差別化)
ポイント
複占市場(寡占市場)で価格競争(ベルトラン競争)が引き起こると、完全競争市場と同じ結果(ベルトラン均衡)に辿り着く。ベルトラン競争を想定した不完全競争市場と完全競争市場で同じ結果が得られることを「ベルトラン・パラドックス(ベルトランの逆説)」と呼ぶ。
そして、このパラドックスを解消するために製品差別化という考え方が登場する。
ちなみに、パラドックスの解消には他にも考え方がある。例えば、企業の生産量は有限なので理論通りにはならない(生産量の制約を考慮したクレップス=シャインクマンのモデルは有名)。他にも、現実では価格競争をせずに他社と歩調を合わせる(カルテル)等が考えられる。
流れを確認する
- 寡占市場でベルトラン競争が行われる
- すると一番安い価格設定にした企業が需要を独占することが分かる
- 各企業は価格競争を始める
⇒不完全競争市場(寡占市場)なのに、完全競争市場と同じような結果になる。
ここで
- 企業は生き残りのために色々と考えます
企業A
このまま値下げ競争をしてもジリ貧になるだけ。そうだ、うちの商品を改良して、他社と差別化を図ろう‥!
ポイント
ベルトラン競争の行き着く先には、製品差別化という未来が待っている。


ここからは
製品差別化が行われるベルトラン競争を分析します。
- 数式で状況を確認する(利潤最大化を考える)
- ベルトラン均衡を考える
- 最適反応曲線で均衡をグラフで見る
- ベルトラン均衡の意義
この4つを順番に見ていきましょう!
step
1数式で状況を整理する
企業Aの視点で考えてみましょう。
- 財Aの需要曲線(xa)=a-b・Pa+c・Pb
- 企業Aの費用関数(Ca)=C・xa
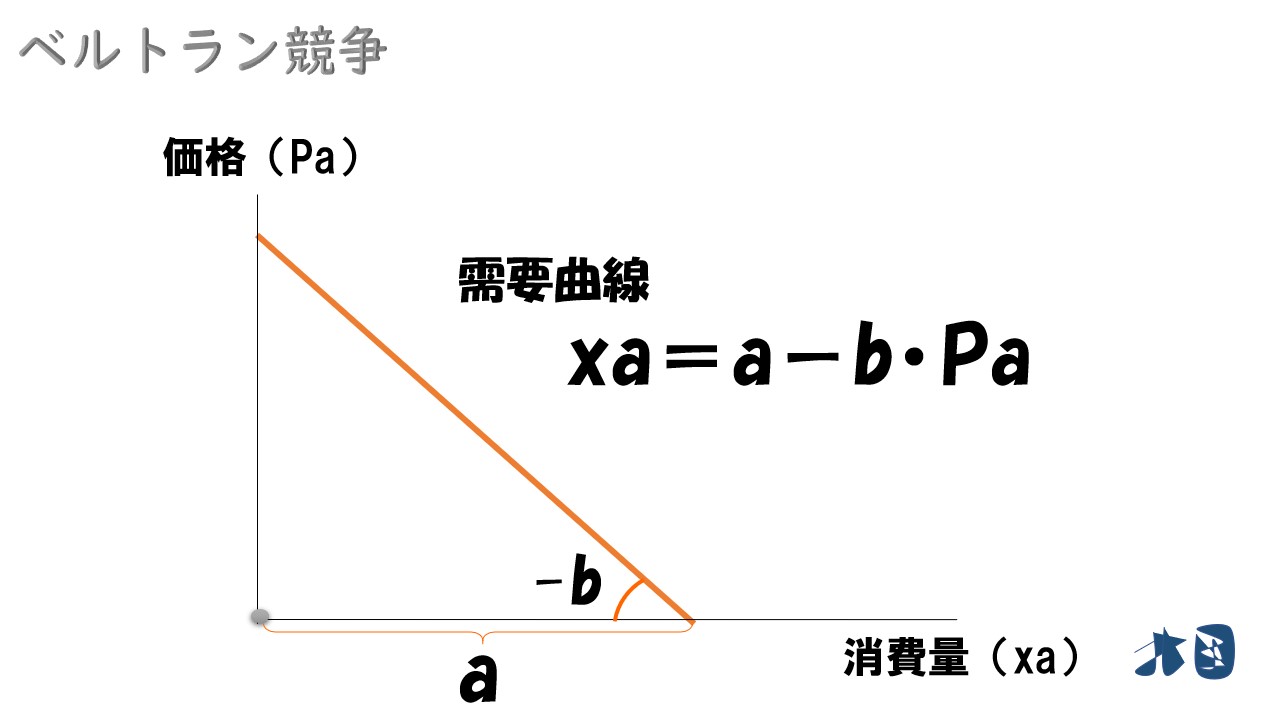
ふつうの需要曲線(xa)だと「a-b・Pa」みたいになる(グラフ参照)
- 価格が高いほど消費量が減る
- 価格が低いほど消費量が増える
クールノー競争では逆需要関数「P=a-b・x」で考えたのに、ベルトラン競争では「x=a-b・P」と考えている理由
・通常の需要関数「価格(P)→生産消費量(x)」
・逆需要関数「生産消費量(x)→価格(P)」
ベルトラン競争では、企業は価格を操作して利潤最大化を目指すと考えています。なので「価格(P)が決まることで生産消費量(x)が決まる」と考えている普通の需要関数を使う方がモデルにあっているわけです(ただし、その影響でクールノー競争とベルトラン競争を単純に比較するのが難しくなってしまうデメリットもあります)。
ここで
商品Aと商品Bは製品差別化しているけれど、似た商品なのでお互いの販売価格によって需要が影響を受けます。
例えば「ペプシ」と「コカ・コーラ」を考える。一般的にコカ・コーラの方が人気ですが「ペプシ=50円」「コカ・コーラ=200円」なら、コカ・コーラの需要はペプシに流れます。つまり、お互いの価格設定次第で需要が変化するイメージ。
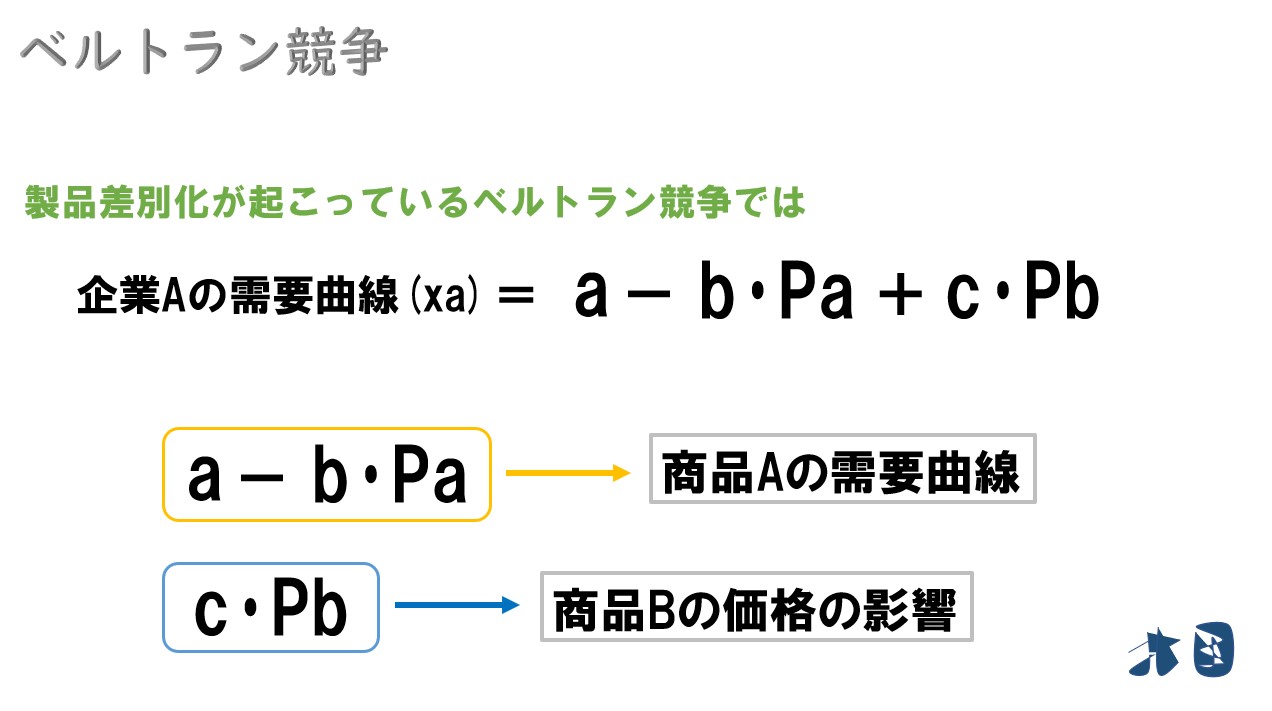
⇒それを反映した需要曲線(xa)が「a-b・Pa+c・Pb」
最後の「+c・Pb」は、ライバル商品Bが価格(Pb)を高く設定するほど、商品Aの需要(xa)が増えるという意味です。ちなみに、前の部分「a-b・Pa」はこれまでの需要曲線と同じです。
次に
- 企業Aの利潤(πa)は?
πa=(商品Aの価格)×(生産量)-(生産コスト)
πa=(Pa)・(xa)-(Ca)
ここで
「企業Aの費用関数(Ca)=C・xa」と置いていたので「πa=(Pa)・(xa)-(C・xa)」です。
式を変形します⇒「πa=(Pa-C)・xa」
「xa」に注目。「需要曲線(xa)=a-b・Pa+c・Pb」と考えていたので代入する。
- πa=(Pa-C)・(a-b・Pa+c・Pb)
企業もB同様
- πb=(Pb-C)・(a-b・Pb+c・Pa)
以上より
- 企業Aの利潤(πa)=(Pa-C)・(a-b・Pa+c・Pb)
- 企業Bの利潤(πb)=(Pb-C)・(a-b・Pb+c・Pa)
次に
- 企業Aの利潤最大化を求める
ポイント
製品差別化が行われる市場でも、もちろん企業は利益追求します。そのため、企業A・Bは利潤最大化を目指すと考えて、上記の式(利潤)を最大化させると考えます。
先ほど求めた企業Aの利潤関数を展開します。
- (πa)=(Pa-C)・(a-b・Pa+c・Pb)
- (πa)=(Pa・a-b・Pa^2+Pa・c・Pb)-(C・a-C・b・Pa+C・c・Pb)
式を展開すると「-b・Pa^2(2乗)」が登場するため「πa=(Pa-C)・(a-b・Pa+c・Pb)」は2次式です。中学校の数学を思い出してもらえればいいのですが、〇の2乗が登場する数式は放物線を描くようなグラフになります。
グラフで考えると分かりやすい。
横軸が「価格(Pa)」という少し変なグラフですが2次関数のグラフは上記のようになります。ここで利潤が最大化するのはグラフの頂点部分のときだと分かります。
そのときの価格は‥?
ポイント このグラフは、企業Aが価格(Pa)を高くしていくと利潤(π)がどのように変化するのかを表している。グラフより、企業Aはグラフが頂点を描くときの価格(Pa*)にすれば利潤最大化を実現できることが分かる。 グラフの頂点では「傾きが0」になることにも注目する。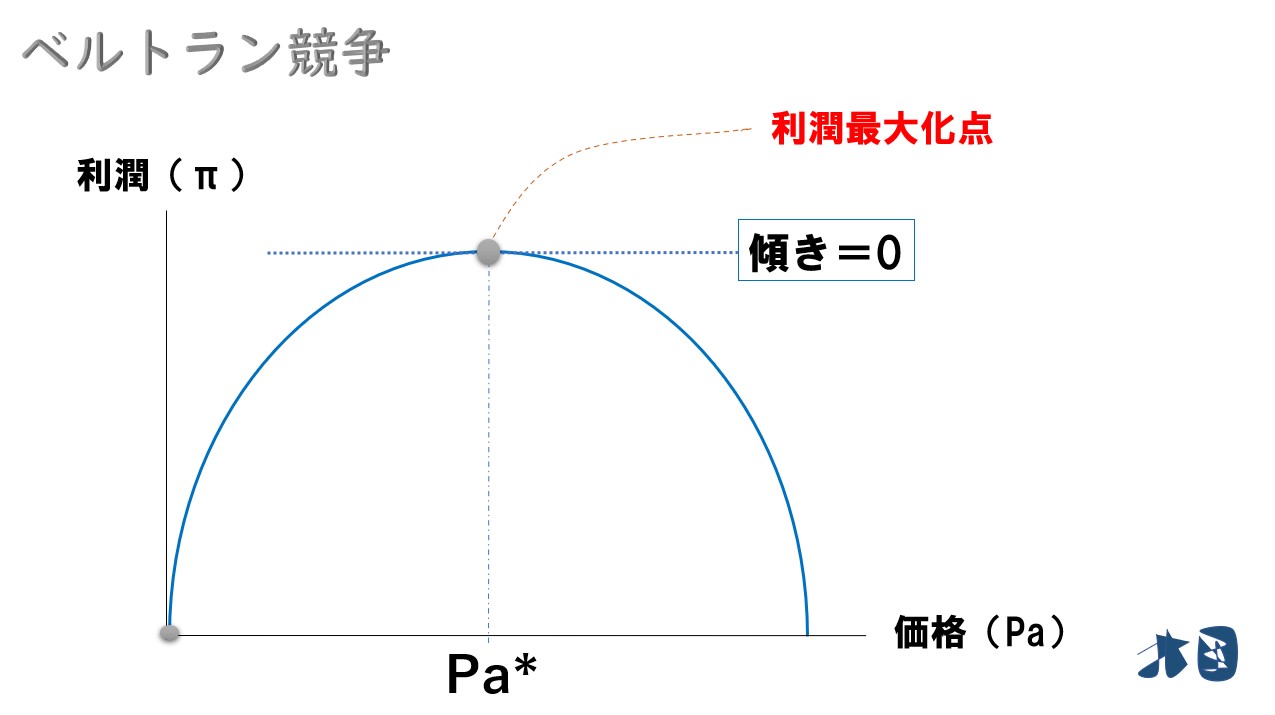
つまり
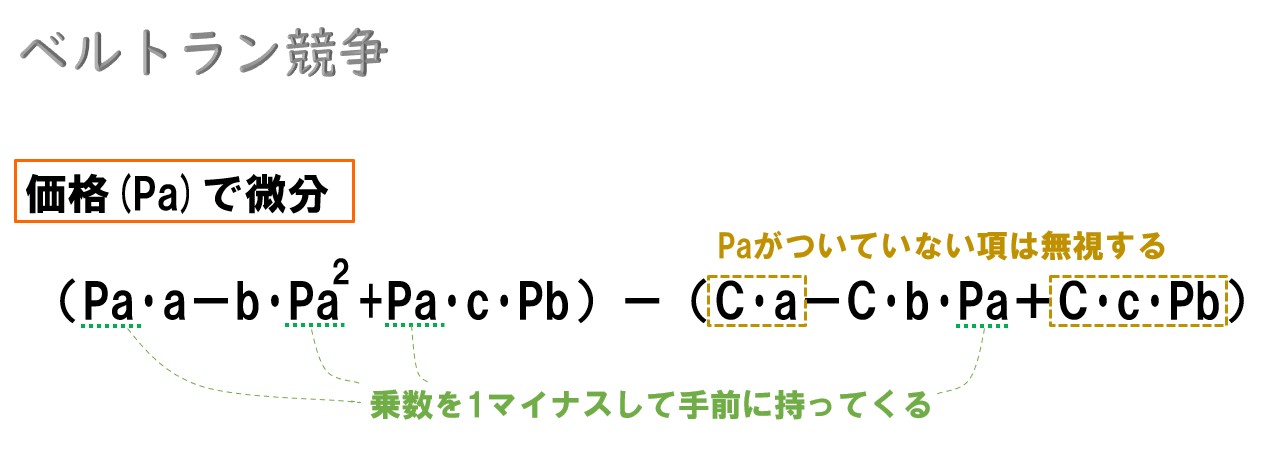
- (πa)=(Pa・a-b・Pa^2+Pa・c・Pb)-(C・a-C・b・Pa+C・c・Pb)
↑この式の傾きが0になる瞬間を求めれば利潤最大化点が分かる。
計算方法は‥?
数学的には「微分して、イコール0」にすればOKです!
微分の意味が分からない人向けに簡単に補足です。微分は、グラフを細分化して、その小さな点の傾きがどれくらいなのかを計算できます。つまり、グラフの放物線の傾きが0になる⇒「微分した結果がイコール0になるはず」というわけです。
以上より
- 企業Aの価格(Pa)で微分します。
最後に=0で結びます。


企業Bも同様
(企業Aと同様の計算方法で求まる)
ポイント
製品差別化が行われているベルトラン競争の均衡を求めるための条件が整いました。
(念のため)今は製品差別化が行われる複占市場を考えています。企業A・Bは利潤最大化を目指して活動するので、その結果、どのような状態(ベルトラン均衡)にたどり着くのか?を考えている最中でした。ここまでで「複占市場で企業A・Bが利潤最大化を目指して活動している」という前提条件までを数式で表現できたところです(1階条件)。


step
2ベルトラン均衡を求める
- 2社の条件式を連立方程式として解く
クールノー均衡を求める時と同じ考え方です。まずは「Pa」「Pb」の値を求めてみましょう。
ポイント
わざわざ計算する必要があったのか不明ですが、対照的な連立方程式になっているので「Pa=Pb」となります。
ここでは、企業Aの利潤式の「Pb」に「Pa」を代入して計算を続けます。
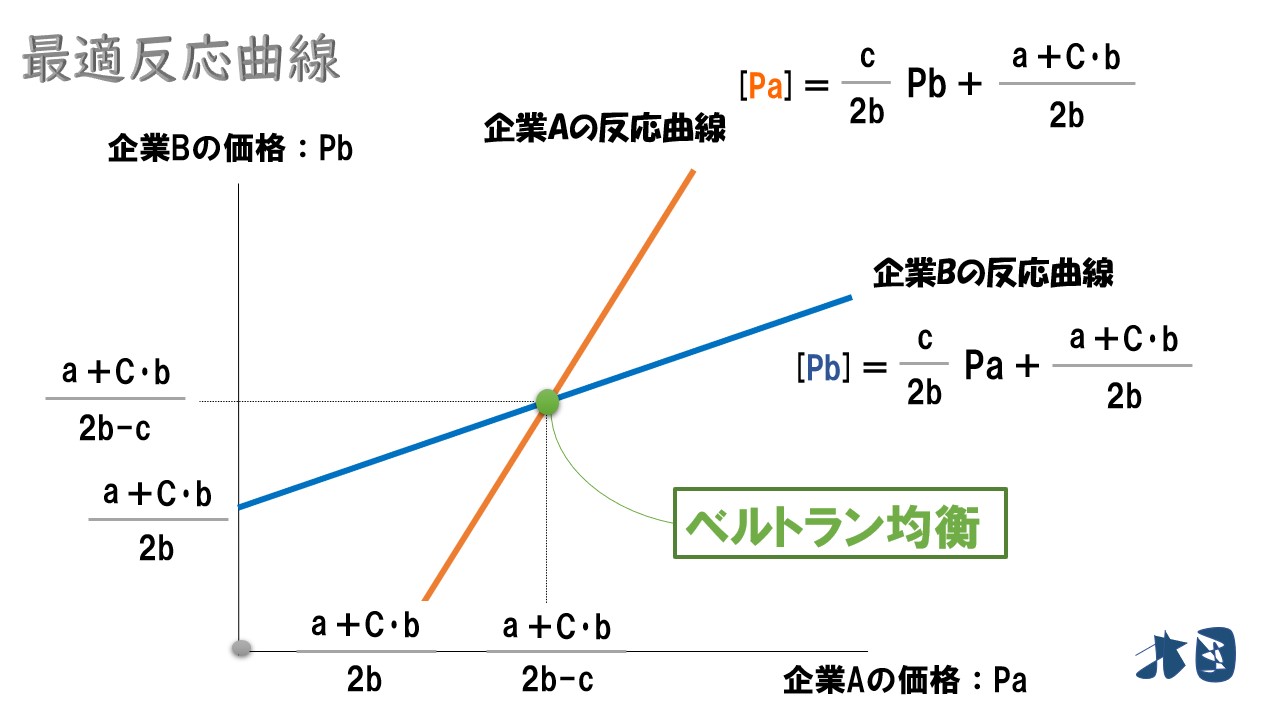
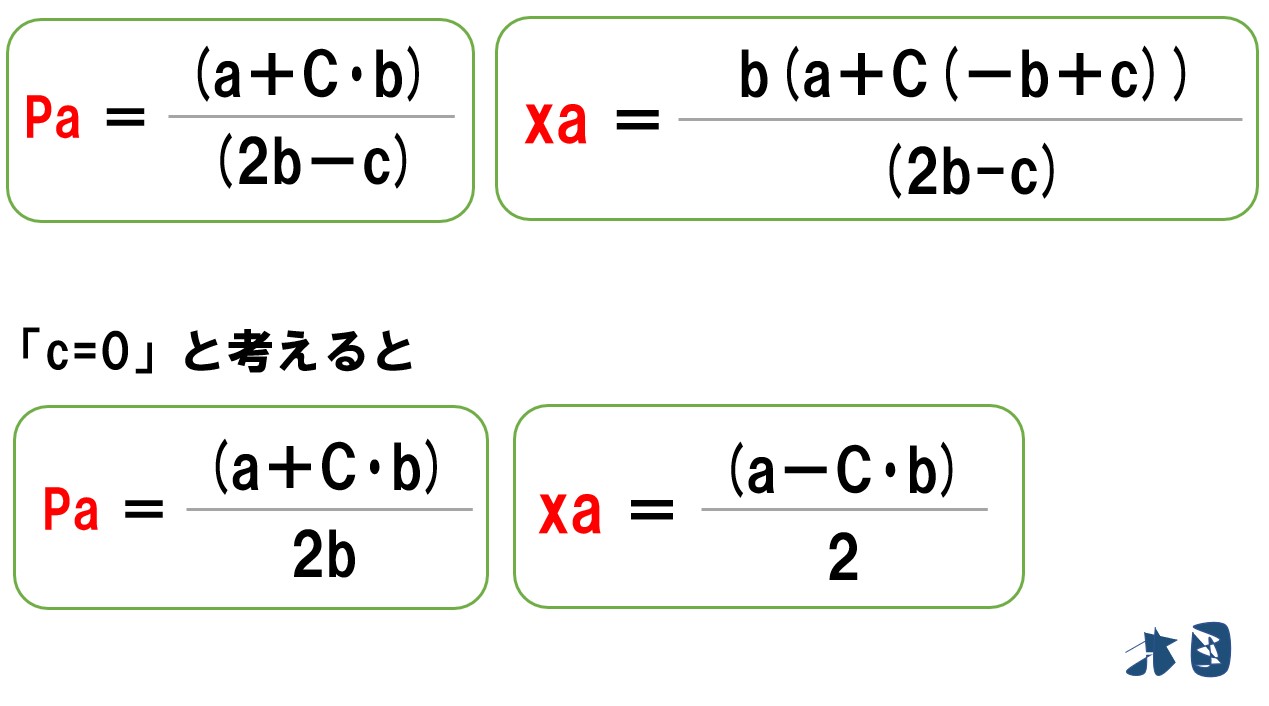
ベルトラン競争で製品差別化が行われるとき、企業Aは価格を「Pa=(a+C・b)/(2b-c)」と設定する。また、「Pa=Pb」なので ⇧製品差別化が行われているベルトラン競争の最適な価格設定が分かった。
次に、この結果を企業Aの需要曲線(xa)に代入する
ベルトラン競争で製品差別化が行われるとき、商品Aの需要(xa)は「xa=b(a+C(-b+c))/(2b-c)」と求まる。また、途中で計算していませんが、価格と同様に「xa=xb」となります。以上より ⇧製品差別化が行われているベルトラン競争の消費量が分かった。
最後に
2つの計算結果を説明します。
製品差別化が行われている複占市場の2社の行動を考えてきました。
- A社の価格設定=Pa
- A社の生産量=xa
- B社の価格設定=Pb
- B社の生産量=xb
- 市場の逆需要関数(D)「P=a-b・x」‥①
- 2社の費用関数(C)「C・x」‥②
この条件のとき、A社とB社が利潤最大化を実現させるために取る行動(価格設定)は・・「Pa=Pb=(a+C・b)/(2b-c)」と計算されました。
ポイント
製品差別化が行われている複占市場で上記の条件のとき、2社とも相手の価格設定を考えながら利潤最大化を目指して自社の価格設定を調整する。最終的に次の価格と生産量に落ち着くことが分かった。
- 企業Aの価格設定=(a+C・b)/(2b-c)
- 企業Bの価格設定=(a+C・b)/(2b-c)
- 企業Aの生産量=b(a+C(-b+c))/(2b-c)
- 企業Bの生産量=b(a+C(-b+c))/(2b-c)
ベルトラン競争で最終的にたどり着く、上記の2社の価格設定と生産量を「ベルトラン均衡(ベルトラン・ナッシュ均衡)※」と呼ぶ。複占市場で製品差別化が行われている場合、企業が利潤最大化を目指すと上記の価格設定と生産量に落ち着く。その状態を「ベルトラン均衡」と呼んでいる。
※「需要曲線と供給曲線が交わるところで均衡が決まる」という従来の考え方とは、全く異なる考え方なので注意する。複占・寡占市場の「均衡」の考え方は基本的にゲーム理論と同じです。
全体的な流れ
- 寡占市場でベルトラン競争が始まると、一番安い価格設定にした企業が需要を独占
- 価格勝負には限界があり、各企業は製品差別化へと舵を取る
- 製品差別化が行われるベルトラン競争では、上記のベルトラン均衡にたどり着く


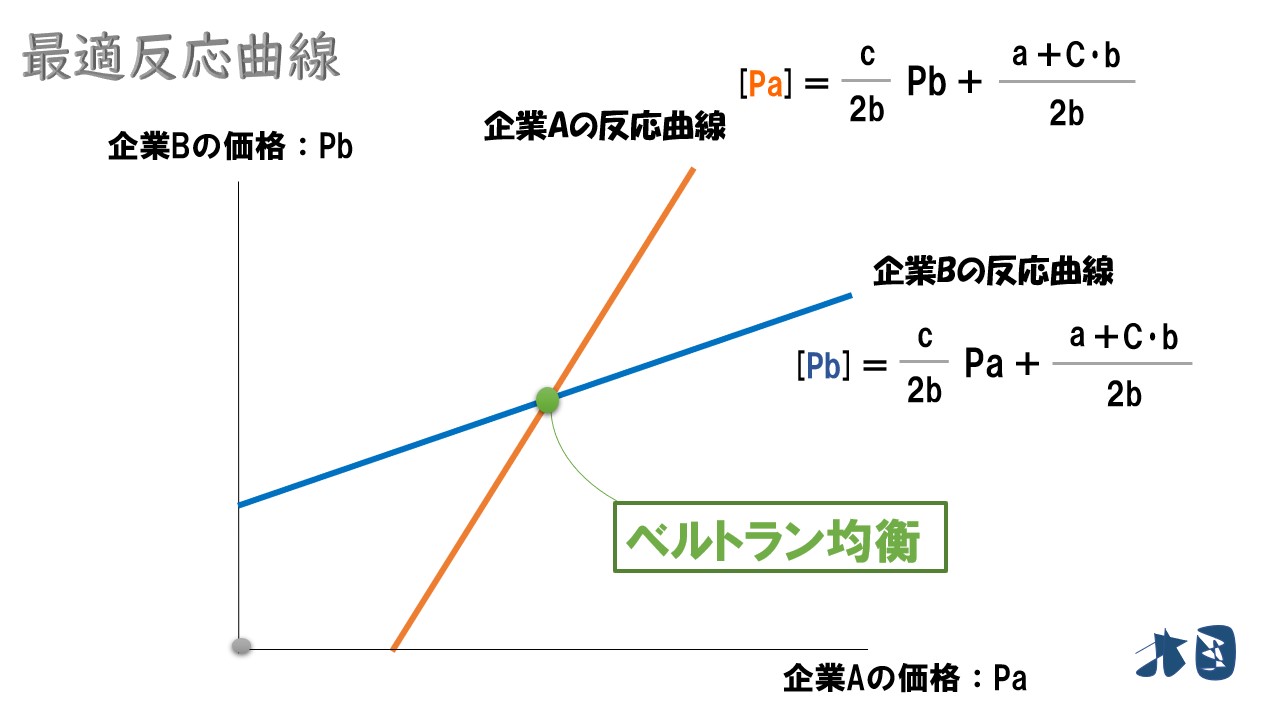
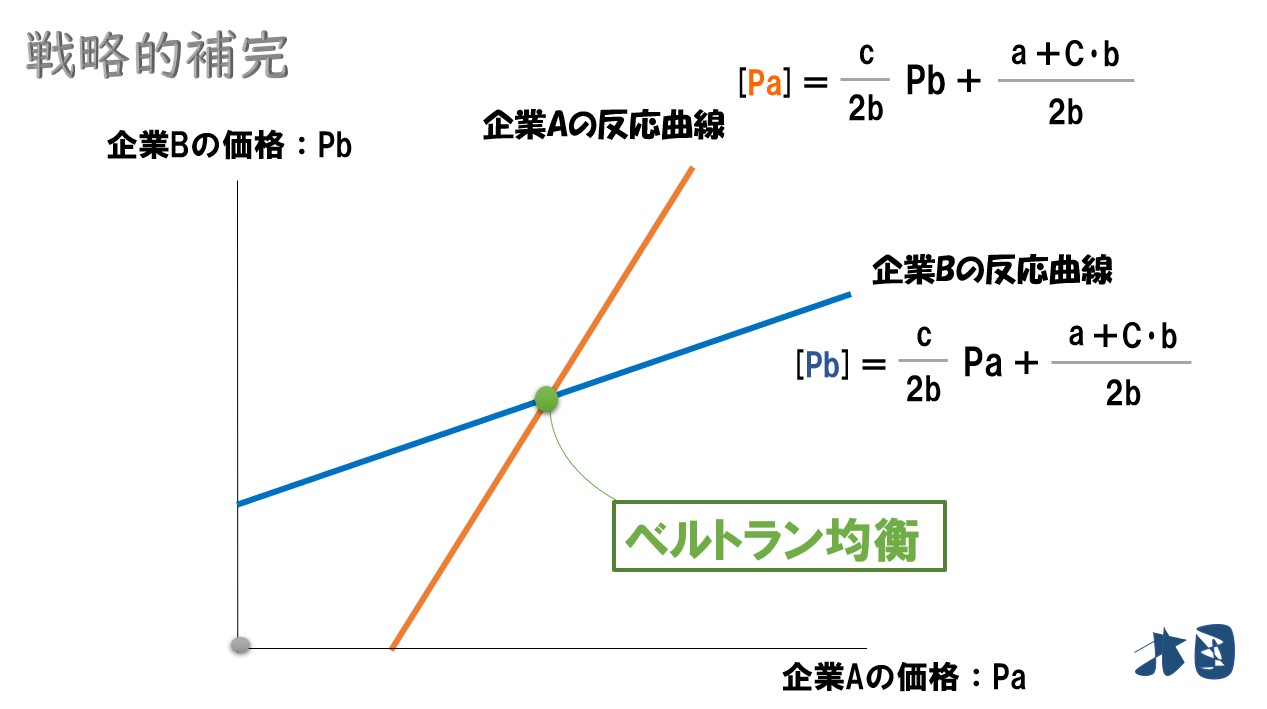
最適反応曲線
はてな
相手の価格に応じて、自社の価格をどれくらいにしたらよいのかを表した曲線(もしくは関数)。「反応曲線」「最適反応関数」とも呼ばれる。
例えば
(先ほどの例)製品差別化が行われる複占市場を考えます。企業Aは企業Bの商品の価格設定を1万と予想します。このとき、企業Aは「うちは9000円で売ろう」と考えます。
このように、相手の価格設定に対して、どのような価格設定にするのかを数式・グラフ化したのが最適反応曲線です。
はじめに
グラフを描く前に、最適反応を表す式を求めます。
ベルトラン均衡を求めるときに登場した式を使います。どのような経緯でこの式が出てきたのか理解できない人は戻って確認してください。
この2つの式は、製品差別化が行われる複占市場で企業Aと企業Bが利潤最大化を実現するための条件式です(1階条件)。
つまり、企業Aの最適な価格設定(最適反応)を求めるには、この式を「価格(Pa)=~」の形にすればOKです。
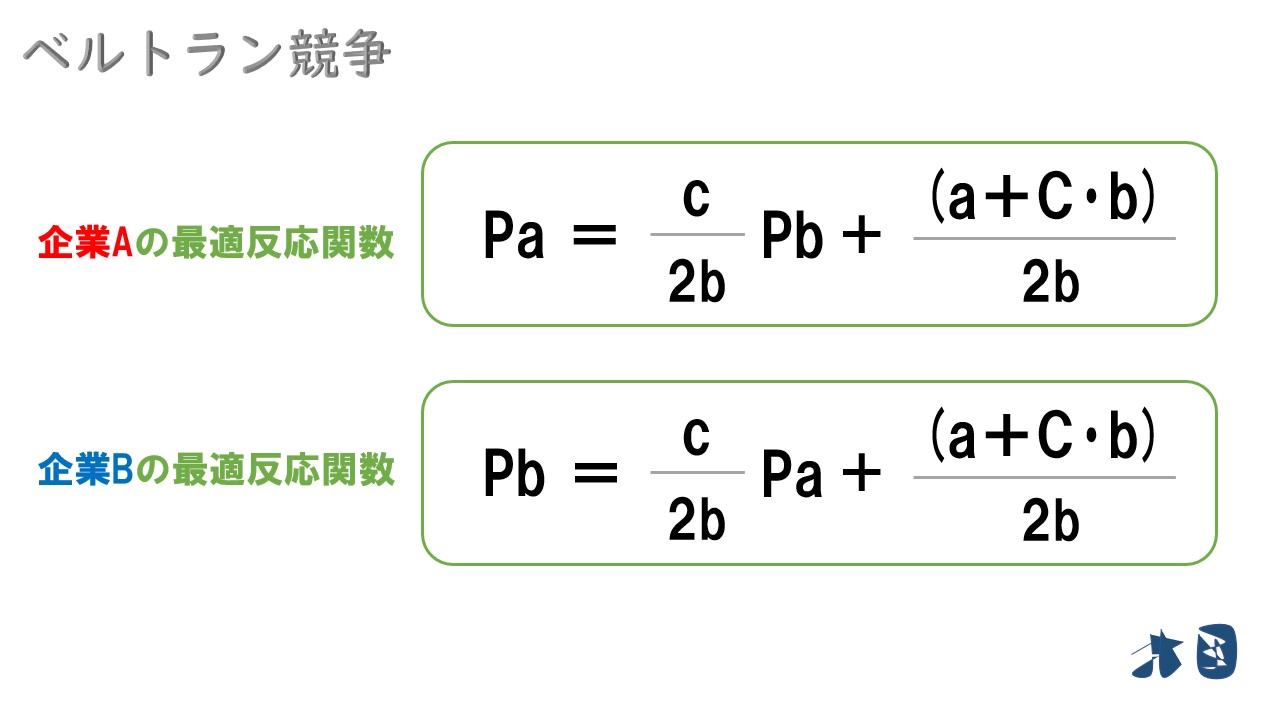
企業Aの式を変形してみる
ポイント
企業Aの最適反応関数(Pa)=(c/2b)Pb+(a+C・b)/2b
よって、A社・B社の最適反応関数は‥
上記の2つの式をグラフにします。
グラフにすると‥
2つの最適反応曲線が交わっている点はベルトラン均衡です。
この点は、2社がそれぞれ最適な価格を実現している点です(製品差別化が行われるベルトラン競争の結果、たどり着いた2社の価格設定を表しています)。ベルトラン均衡がグラフ上で確認できましたね。
少し厳密にグラフを見る
先ほどの話を理解できればOKですが、念のため厳密な値も付け加えます(飛ばしてもOK)
ベルトラン均衡の意義
ポイント
製品差別化が行われなていない場合、とにかく安い価格設定をした企業が需要を独占するため、各社の利益が0になるところまで値下げ競争が進む(ここがベルトラン均衡になる)。
しかし、企業は利益を出すために商品の製品差別化へと進むことになる。このとき、製品差別化が行われるベルトラン均衡ではどのようなことが言えるのかを考える。⇒先に答えを書くと、製品差別化が進むほど、ベルトラン均衡では独占市場と同じような結果になる。


商品の製品差別化が進むということは、その商品が唯一無二の存在になるということ。
つまり「唯一無二の商品を扱っている企業=独占企業」となる。
製品差別化が進むと独占市場と同じ結果が生まれるのかを数式で見ていきます。
はじめに
最初に登場した企業Aの需要曲線を思い出す。
- 企業の需要曲線「a-b・Pa+c・Pb」
最後の「+c・Pb」は、ライバル商品Bが価格(Pb)を高く設定するほど、商品Aの需要(xa)が増えるという意味。
製品差別化が行われている寡占市場では、自社商品の需要は、ライバル商品の価格の影響も受けると考えていました。
ここで
差別化が進んだ結果、自社商品の魅力のみで需要が決まると考えてみましょう(ライバル商品の価格の影響は受けない)。
数式で考えると「c・Pb」の「c」が0ということ。
「c・Pb」なので「c=0」ならライバル企業の商品価格「Pb」がいくらでも、企業Aの需要(xa)には何の影響も与えない。
- 「c=0」より
製品差別化が行われていたベルトラン均衡の価格と生産量は‥


企業Aの需要曲線「a-b・Pa+c・Pb」で「c=0」より
- 企業Aの需要曲線(xa)は「a-b・Pa」
ここで
「xa=a-b・Pa」を「Pa=」の形にする
独占企業の利潤最大化を計算をするために「限界収入(MR)」を求める。
「Pa=」の傾きを2倍にするればOK
- これまで2社の費用関数(C)を「C・x」と考えていたので「限界費用(MC)=C」と分かる
「C・x」を「x」で微分すればOK(説明省略)
また、独占市場の利潤最大化条件「MR=MC」より
- MR=a/b-(2/b)・xa
- MC=C
⇒「a/b-(2/b)・xa=C」
- a/b-C=(2/b)・xa
- (a/b)・(b/2)-C・(b/2)=xa
- a/2-(C・b)/2=xa
- (a-C・b)/2=xa
- xa=(a-C・b)/2
この計算結果を途中で計算した逆需要関数「Pa=a/b-(1/b)・xa」に代入する。
- Pa=a/b-(1/b)・xa
- Pa=a/b-(1/b)・(a-C・b)/2
- Pa=a/b-(a-C・b)/2b
- Pa=2a/2b-(a-C・b)/2b
- Pa=(a+C・b)/2b
グラフで見ると‥
以上より
製品差別化が進んだ場合のベルトラン均衡は、独占市場と同じ価格(Pa)・生産量(xa)が実現する。
まとめ
- 寡占市場でベルトラン競争が始まると、一番安い価格設定にした企業が需要を独占するため「P(価格)=C(限界費用)」になるまで価格競争が進む。
- 価格勝負には限界があり、各企業は製品差別化を進める
- 製品差別化を進めて、その企業にしか作れない商品を生み出せば、市場を独占できる
- 市場を独占することで、独占価格「P=(a+C・b)/2b」を設定できる。
- 企業は製品差別化を進める方が合理的であることが分かる


余剰分析(社会的厚生)
ベルトラン競争の社会的余剰(消費者余剰・生産者余剰)は、3つパターンに分けて考えることが出来ます。
- 製品差別化が行われていない場合
- 製品差別化が行われている場合(ライバル商品の価格の影響を受ける)
- 製品差別化が行われている場合(完全に差別化される)
パターン①
- 製品差別化が行われていない場合(P=MC)
ポイント
基本的に完全競争市場と同じ。
製品差別化のないベルトラン競争※では、価格競争が進み「価格(P)=限界費用(MC)」になるところで均衡となる。企業は利潤が出ないので「生産者余剰(PS)=0」「残りは全て消費者余剰(CS)」となる。
※戻って確認する(製品差別化のないベルトラン競争)
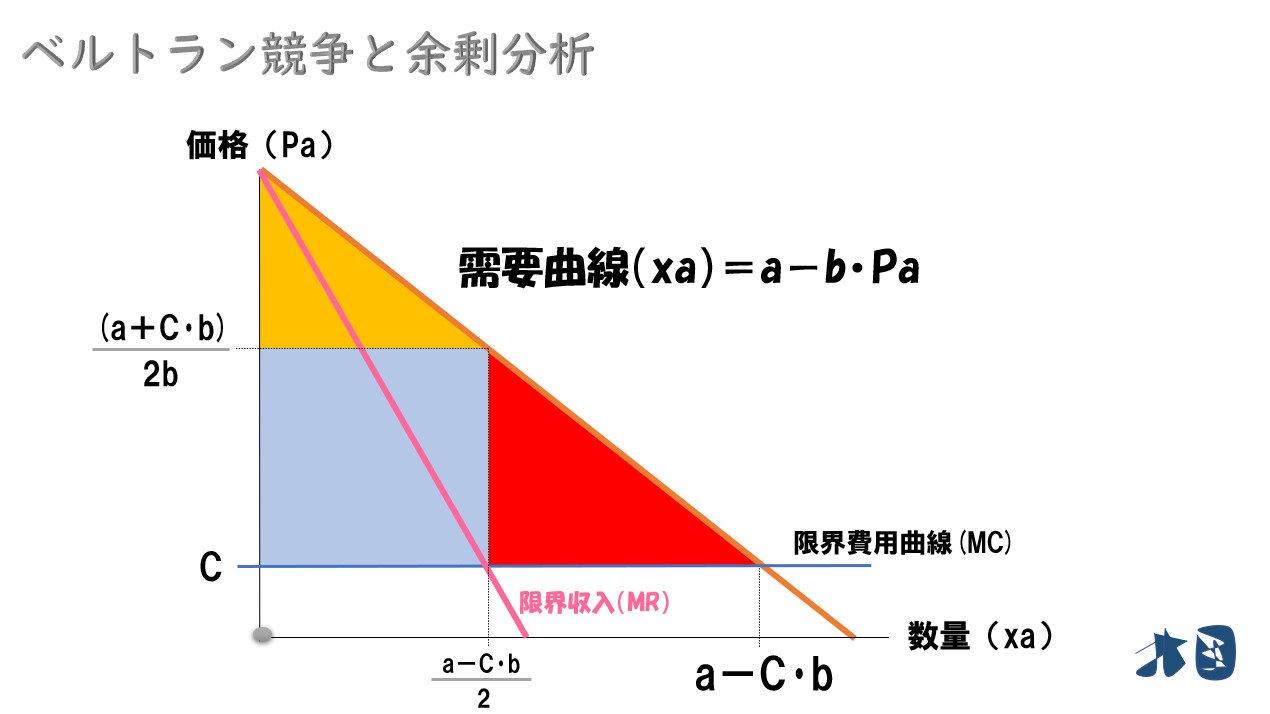
パターン②
- 製品差別化が行われている場合(ライバル商品の価格の影響を受ける)
ポイント
死荷重(赤色三角形)が生じる(総余剰は最大化しない)
製品差別化が行われているベルトラン競争では、ベルトラン均衡で得られた価格と生産量※が実現するが、完全競争とは異なり「C」よりも高いところで価格が決まるため死荷重が生まれている。
- 消費者余剰(CS)=黄色部分
- 生産者余剰(PS)=青色部分
※戻って確認する(ベルトラン均衡で得られた価格と生産量)
パターン③
- 製品差別化が行われている場合(完全に差別化される)
ポイント
独占市場と同じ結果が得られる(総余剰は最大化しない)
製品差別化が進んで完全に他社商品の価格の影響を受けなくなった場合※、需要曲線の「c・Pb」部分を無視して考える。すると独占市場と同じ価格・生産量が実現する。
- 消費者余剰(CS)=黄色部分
- 生産者余剰(PS)=青色部分
- 死荷重=赤色部分
※戻って確認する(製品差別化が進んで完全に他社商品の価格の影響を受けない)
戦略的補完
ポイント
ライバルが値上げすれば、自社も値上げするのが最適行動になる(ライバルが値下げするなら自社も値下げするのが最適行動になる)。
ベルトラン競争の最適反応曲線を見ると、企業の競争戦略が分かる。
最適反応曲線の求め方は途中の解説部分を参照してください(戻って確認する)。
例えば
企業B
最近、原材料費が高くなってきたし、うちは値上げしよう。
このとき企業Aはどうすれば良い?
この市場が企業A・企業Bの複占市場でベルトラン競争が行われていると仮定すると、企業Aの最適な対策を考えます。


最適反応曲線を確認する
ベルトラン競争で得られる最適反応曲線は右上がりになるため、ライバル企業が値上げすれば、自社も値上げするのが最適な行動となる。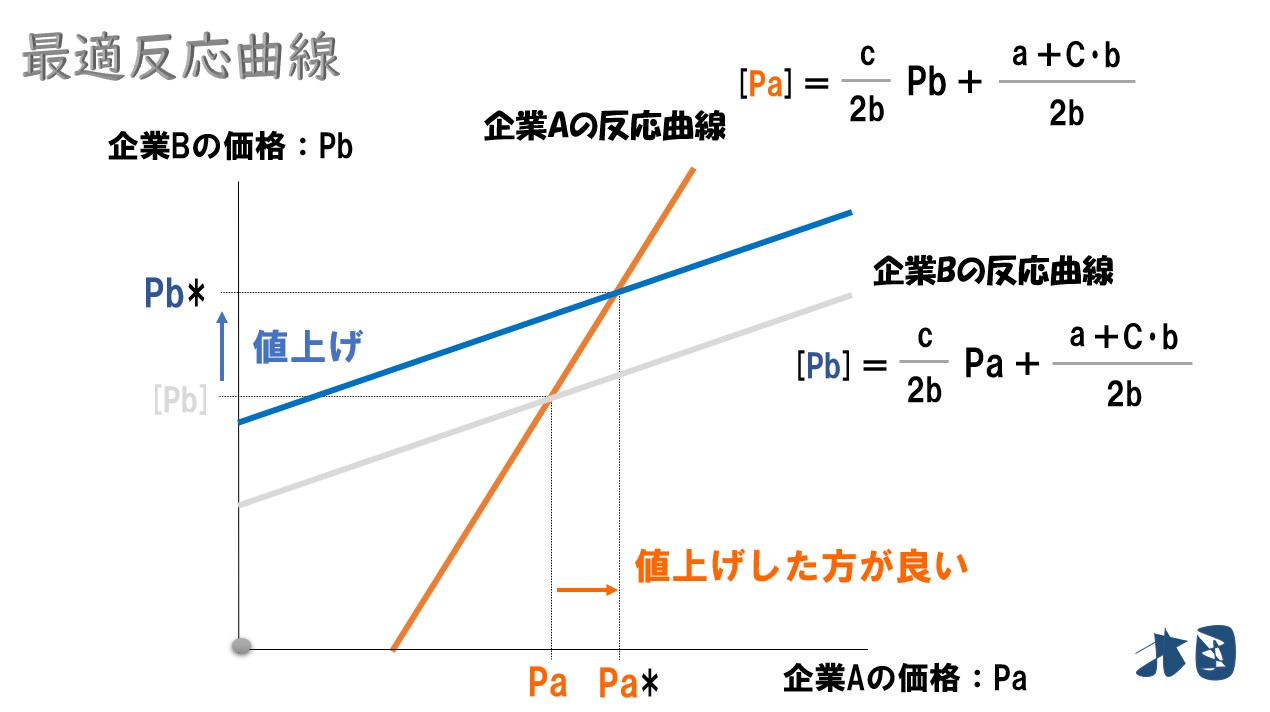
ポイント
ベルトラン競争では、相手と同じ価格戦略を取ることが最適反応になる。このような関係性を「戦略的補完(戦略的補完性)」と呼ぶ。
ちなみに
逆に相手が値下げするなら、自社も値下げしないといけない。

現実では「牛丼」の値下げ競争などが良い例です。
牛丼市場は3社(Y屋・M屋・S屋)で寡占状態です。牛丼の差別化にも限界があるため、泥沼の価格競争が始まりました(3社とも、独占価格を設定できるほどの差別化を図ることが出来なかった)。
とにかく安い価格設定にすれば需要を総取りできるような時代で、牛丼は「デフレの申し子」と呼ばれていた(特に2008年リーマンショック以降は値下げ競争に拍車がかかった)。こうした時代背景もあることから、牛丼市場は典型的なベルトラン競争に陥っていた。


計算問題

(1)企業Xと企業Yの2社が支配する複占市場を考える。2社は同質的な財を生産している。
- 需要関数:D=12-P
- X社の生産量=x
- Y社の生産量=y
- X社費用関数(Cx)=2・x
- Y社費用関数(Cy)=2・y
このとき、ベルトラン均衡における下記2つを求めよ。
- 価格
- 2社の利潤
(2)企業Aと企業Bの2社が支配する複占市場を考える。2社は同質的な財を生産している。
- 企業Aの需要関数(xa)=180-2Pa+Pb
- 企業Bの需要関数(xb)=180-2Pb+Pa
- A社費用関数(Ca)=30・xa
- B社費用関数(Cb)=30・xb
このとき、ベルトラン均衡における下記2つを求めよ。
- 価格
- 2社の利潤
(1)から回答
製品差別化が行われていないベルトラン競争では、安い価格を設定した企業が需要を総取りする。そのため、各企業は価格競争を行い「価格(P)=限界費用(MC)」になるまで値下げする。
というわけで、限界費用(MC)を求める。
「X社費用関数(Cx)=2x」を「x」で微分する
- よって「MC=2」
「x」という文字がついている部分の乗数を減らして手前に持ってくる。また0乗になった部分は「1」となることに注意する。
企業Y社も同じく「MC=2」と計算できる。
「P=MC」なので、2社の価格設定は「Px=Py=2」
以上より、ベルトラン均衡は(Px,Py)=(2,2)である。
X社の利潤式は「価格×生産量-総費用」で求められるので
- Px・x-C・x=(Px-C)・x=(Px-2)・(12-Px)
問題文の「需要関数:D=12-P」を「x」へ代入する。また、「X社費用関数(Cx)=2・x」より「C=2」
企業Yも同様に
- Py・y-C・y=(Py-C)・x=(Py-2)・(12-Py)
2社の利潤式へ「Px=Py=2」を代入する
- X社利潤=(Px-2)・(12-Px)
- Y社利潤=(Py-2)・(12-Py)
代入すると「0×(12-P)」となるため、利潤が0になることが分かる。
X社・Y社の利潤はともに「0」
(2)の回答
企業Aの利潤を考える。
- A社の利潤=「価格×生産量-費用」
- πa=「Pa・xa-C・xa」
- πa=(Pa・180-2Pa^2+Pa・Pb)-(5400-60・Pa+30・Pb)
- πa=-2Pa^2+240Pa+Pb・Pa-(30Pb+5400)
問題文の「企業Aの需要関数(xa)=180-2Pa+Pb」を「x」へ代入。また、「A社費用関数(Ca)=30・xa」より「C=30」
ここで企業Aの利潤式を微分して「=0」とする。
ポイント
製品差別化が行われているベルトラン競争では「利潤式を微分して「=0」とおく」ことで利潤最大化が求められる。
「-2Pa^2+240Pa+Pb・Pa-(30Pb+5400)」を「価格(Pa)」で微分する
Δπa/Δpa=
・-4Pa+240+Pb=0
「Pa」という文字がついている部分の乗数を減らして手前に持ってくる。また0乗になった部分は「1」となることに注意する。「Pa」がついていない項は無視する。
ここで「Pa=」の形にして企業の反応曲線を求める
・-4Pa+240+Pb=0
・4Pa=240+Pb
・Pa=60+0.25Pb(企業Aの反応曲線)
企業Bも同様に計算すると
・Pb=60+0.25Pa(企業Bの反応曲線)
ここで2つの式を使って連立方程式を解く
- Pa=60+0.25Pb(企業Aの反応曲線)
- Pb=60+0.25Pa(企業Bの反応曲線)
ここでは企業Aの反応曲線に「Pb=」を代入する
・Pa=60+0.25・(60+0.25Pa)
・Pa=60+15+0.0625Pa※分数なら(1/16・Pa)
・15/16Pa=75
・Pa=80
答えを「企業Bの反応曲線」に代入して
・Pb=60+0.25×80
・Pb=80
以上より、ベルトラン均衡は(Pa,Pb)=(80,80)である。
途中で計算した企業Aの利潤式へ「Pa=Pb=80」を代入する
- πa=-2Pa^2+240Pa+Pb・Pa-(30Pb+5400)
- πa=-2×6400+19200+6400-7800
- πa=-12800+19200-1400
- πa=5000
企業Bの利潤も同様に計算すると
- πb=5000
A社・B社の利潤はともに「5,000」