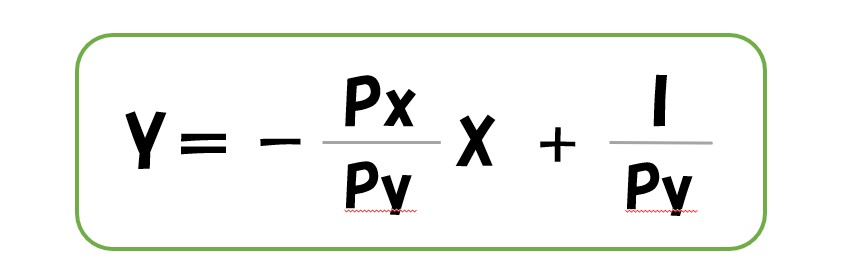「予算制約線」は、基礎的な話をおさえることが重要です。
- 予算制約線とは
- 予算制約線の傾き・相対価格
- 予算制約線のシフト
「予算制約線」は、無差別曲線とあわせて、次の「最適消費点」を求める際に重要になります。ここでは、次のステップで重要になる基礎的な話をまとめました。
予算制約線とは
予算制約線
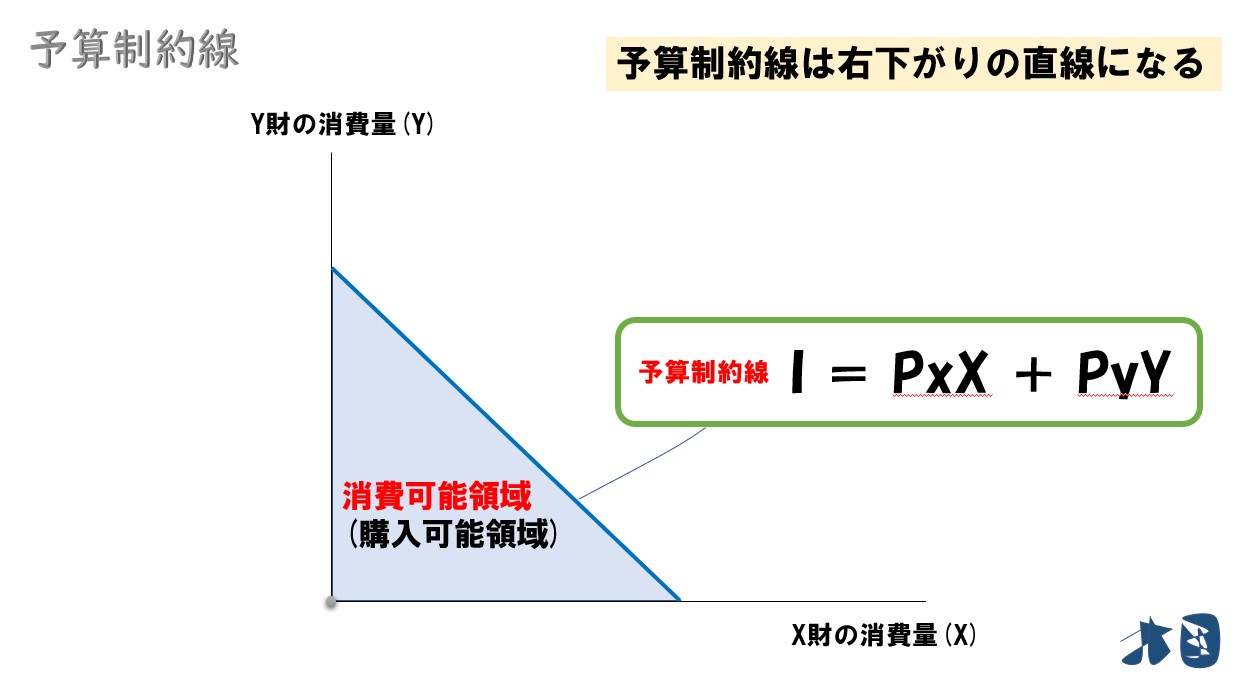
所得(予算)と財の価格から、消費者が購入可能な財の組み合わせを表した直線。


例えば
- 財布に1,000円
- X財の価格100円
- Y財の価格200円
この時の「1,000円以内で、どのような組み合わせでX財・Y財を購入できるか」を表すのが予算制約線です。
実際の数式で考えてみる
- 所得(予算)=「I」
- X財の価格=「Px」
- Y財の価格=「Py」
- X財の消費量=「X」
- Y財の消費量=「Y」
「I」は「Income」の略です。「P」は「Price」の略です。「I」では「数字の1」と紛らわしいので「所得=M(Money Income)」と置く場合もあります。
この情報から、予算制約線を求めると次の通りになります。
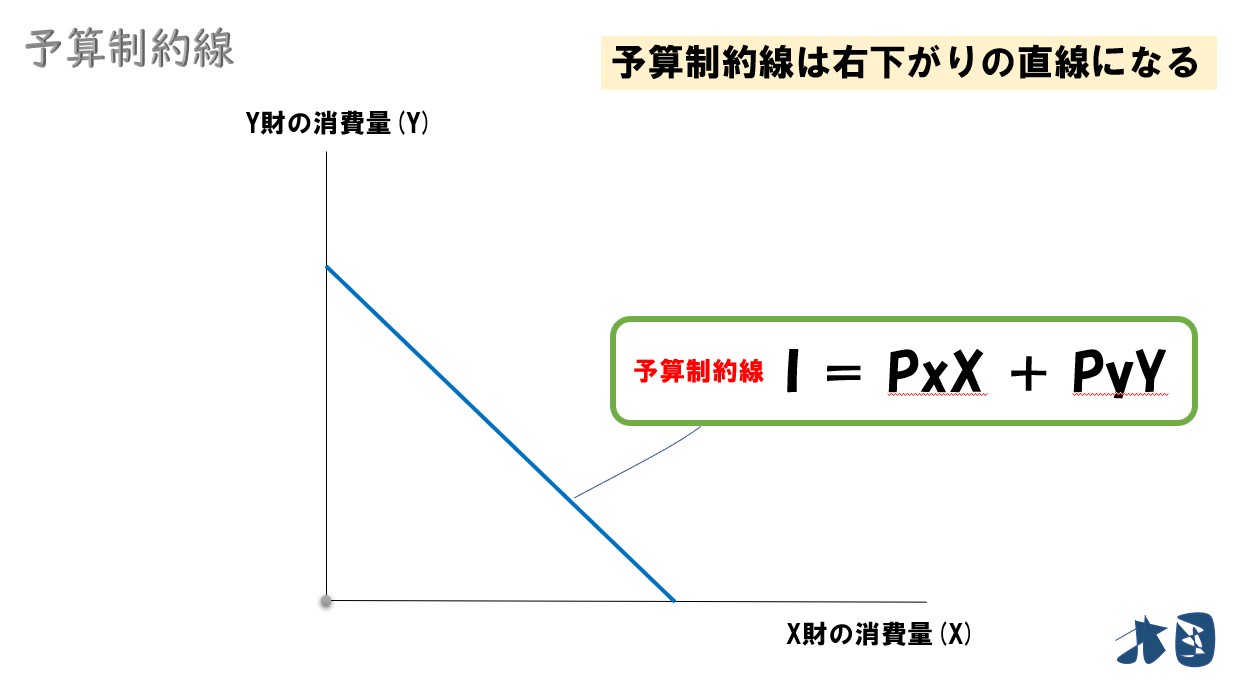
予算制約線の式
「I」=「PxX」+「PyY」
※所得 = (X財の価格)×(X財の消費量)+(Y財の価格)×(Y財の消費量)
グラフで見ると
ちなみに①
予算制約”線”を求めているため「=」で結んでいます。
単純に「予算制約(式)」ということを考えるなら「≦」です。1,000円あったら、1,000円を全部使わない消費の組み合わせも可能だからです。ただし、経済学では予算を使いきって効用を最大化させることを前提にしているので「=」で結んだ状態で考えます。
ちなみに②
予算制約線の内側を「消費可能領域(もしくは購入可能領域)」と呼びます。ここでは、あまり論点にならないので特に踏み込んだ話はありません。
予算制約線の傾きと相対価格
ポイント
予算制約線で重要になるのは「傾き(相対価格)」です。


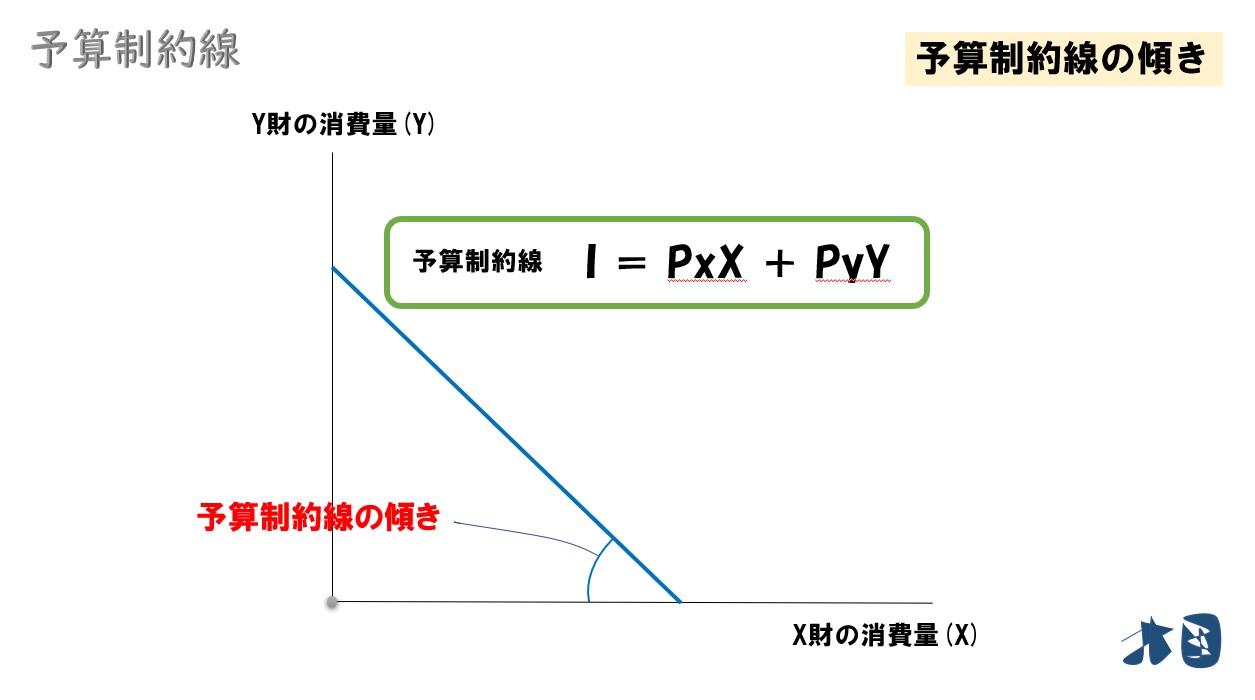
予算制約線の傾き
- 予算制約線の傾きを「相対価格」と呼ぶ
- 予算制約線の傾き(相対価格)は2財の交換比率を表す
ポイント
無差別曲線の傾きを「限界代替率(MRS)」と呼んだように、予算制約線の傾きは「相対価格」と呼びます。
相対価格は2財の交換比率を表していますが、無差別曲線と組み合わせて最適消費点を求めるさいに必要な情報になります。
まずは、予算制約線の傾きを求めます。
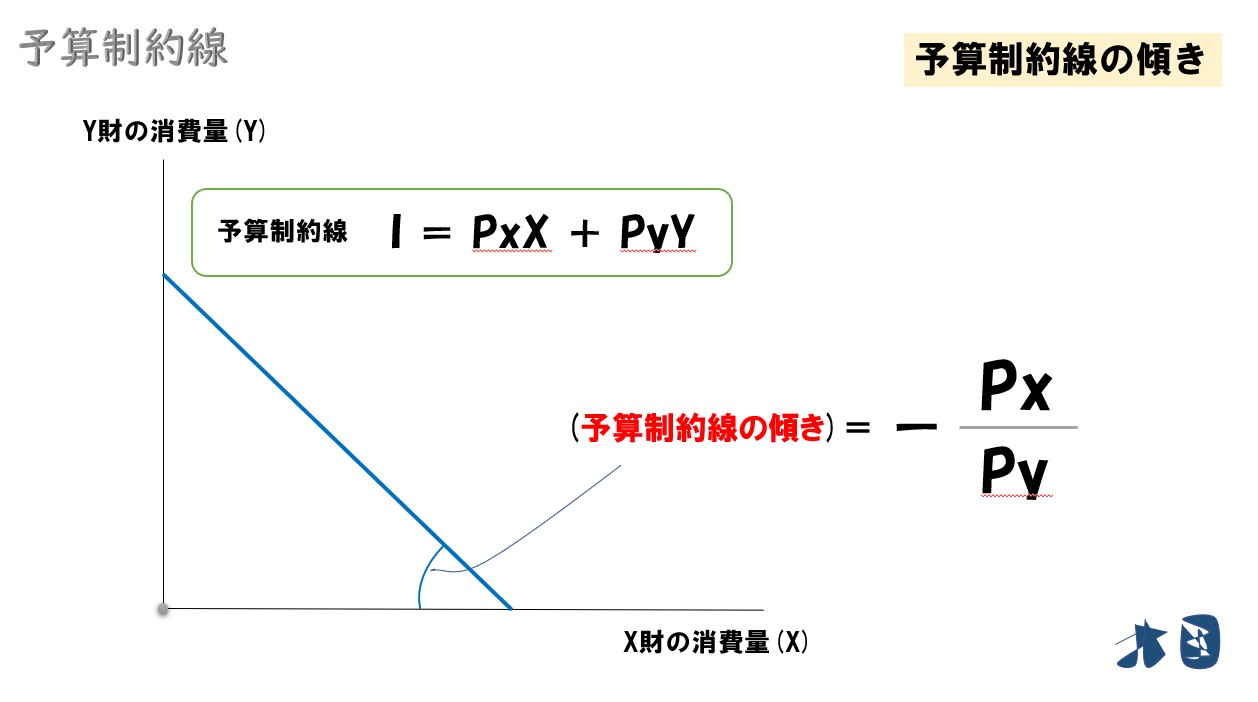
予算制約線の傾きとは、グラフで描いているところです。
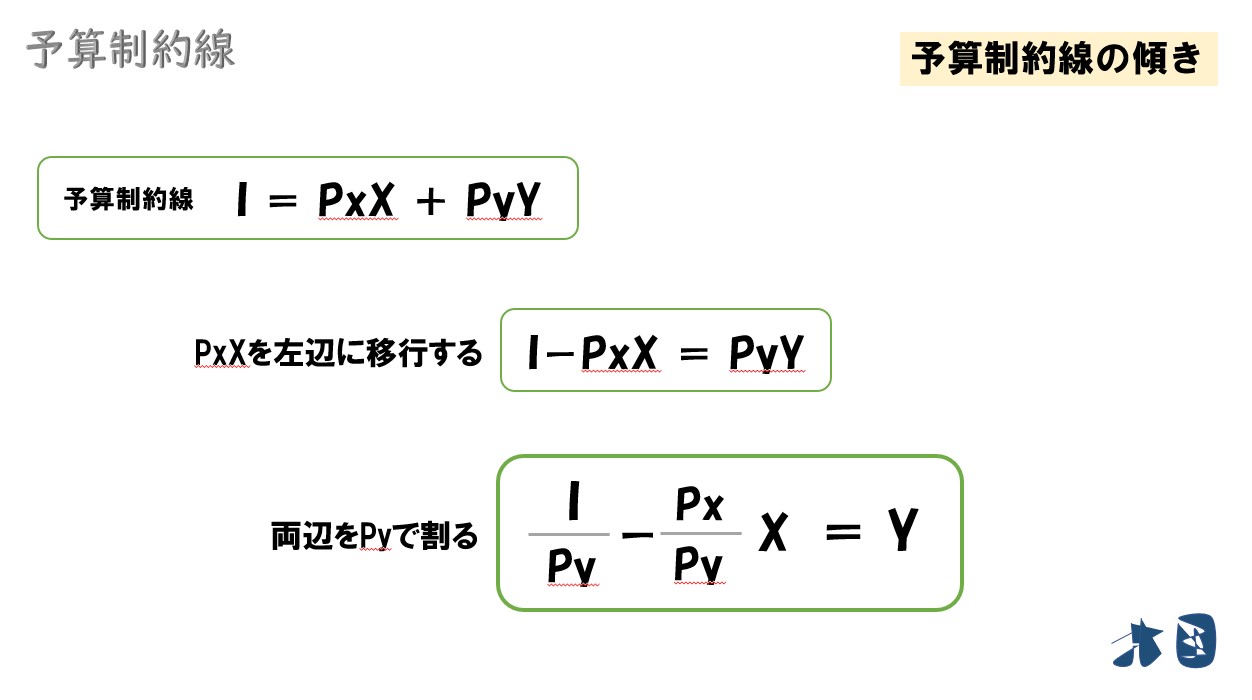
「縦軸(Y)=」の式に変形する
変形完了!


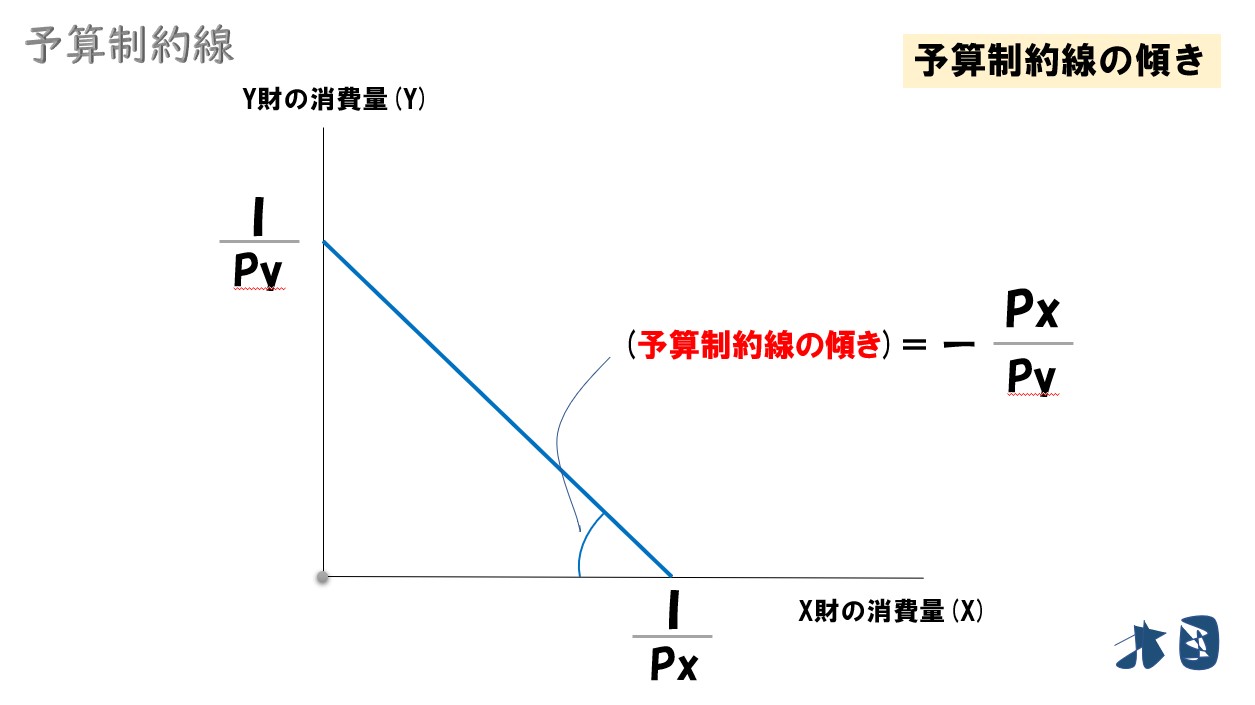
予算制約線の傾き=「-(Px/Py)」
ここで「Px」「Py」は、2財の価格を表していたことを思い出してください。
- X財の価格=「Px」
- Y財の価格=「Py」
ポイント
予算制約線の傾きは、2財の価格比になっている(予算制約線の傾きを相対価格と呼ぶのは、2財の価格比になるからです)。
※分数で表記されていますが、例えば「2:1」の比を分数で表すと「1/2」となります。
交換比率
予算制約線の傾き(相対価格)=「Px/Py」は「Py:Px」とも表記できます。
つまり、相対価格は[価格基準で考えたとき「X財1単位」と「どれくらいのY財」を交換できるか]を表した交換比率とも言えます。
ちなみに①
「傾き」に焦点を当てましたが、切片を文字で表してグラフを書くと次の通りになります。
それぞれの切片は「予算(I)」を「X財・Y財の価格」で割った数字になります。
ちなみに②
- 予算制約線の傾き(相対価格)
- 無差別曲線の傾き(限界代替率)
この2つを使って、最適消費点(効用最大化)を求めることになります。
予算制約線のシフト(変化)
ポイント
- 所得が増減した場合
- 財の価格が増減した場合
それぞれで予算制約線がどのようにシフト(変化)するかをおさえる。


step
1所得が増加(減少)した場合
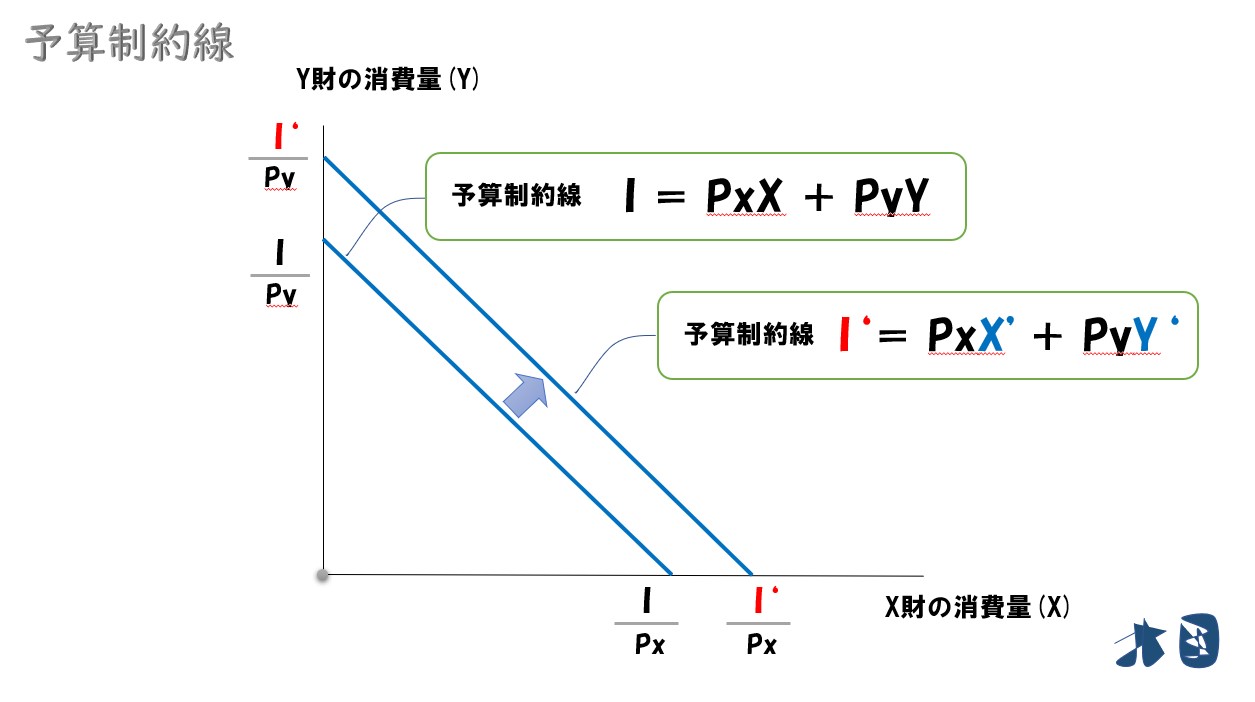
所得が増減した場合は、予算制約線が平行移動します。
- 増加する場合は、右上に平行移動
- 減少した場合は、左下に平行移動
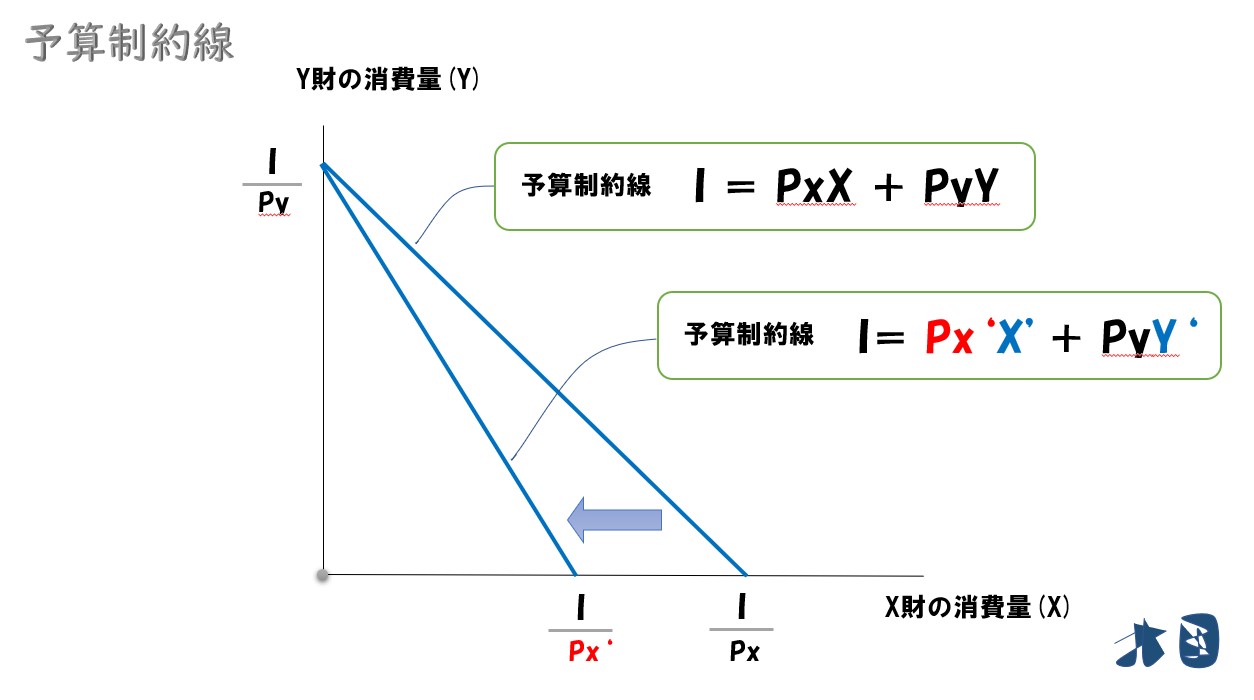
※増減後の所得(I)を「’」を付けて「I ’」などと表記します。また、X・Y財の消費量(X・Y)も変化するので「X’」「Y’」としています。
step
2財の価格が増加(減少)した場合
価格が変化した場合、予算制約線は次のように動きます。
- 価格が上昇した場合は、内側へ移動する
- 価格が減少した場合は、外側へ移動する
ちなみに、価格が上昇すると消費できる量が減るため、予算制約線は内側(原点方向)に移動します。上のグラフなら「縦軸(Y軸)を交点に、横軸(X軸)がより内側(時計回り)にシフトする」などと表現できます。
※価格変化後のX財価格(Px)を「'」を付けて「Px ’」と表記します。また、X・Y財の消費量(X・Y)も変化するので「X’」「Y’」としています。