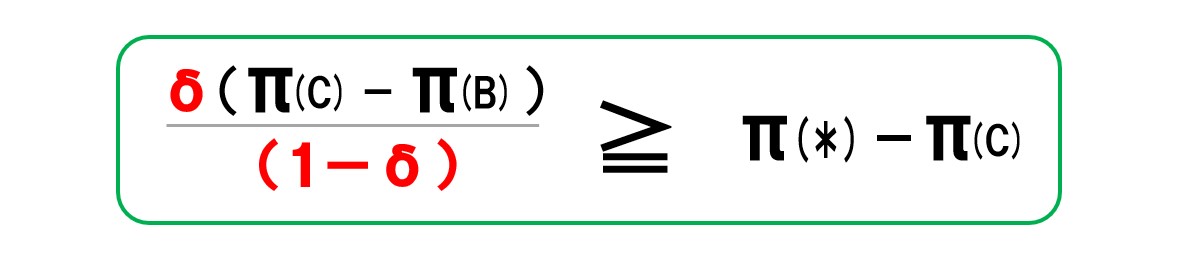現実の世界では、カルテルが維持されたり、裏切りが発生したりします。これはどうして起こるのか?経済学的に考えていきます。
- カルテルの「安定」と「裏切り」
- カルテルと繰り返しゲーム
- カルテルの条件式を求める
- カルテルの分析
カルテル価格や生産量、各市場との比較、基本的な計算問題の解き方は別記事で記載しています。
カルテルの安定性と裏切り(カルテル破り)

はてな
カルテルが結ばれて維持される(安定する)か、裏切り(カルテル破り)が発生するか、この2つの状態の優劣具合をここでは「カルテルの安定性」と呼ぶ(カルテルが維持されるなら「カルテルが安定的」と考える)。
カルテルが安定するかは「条件式」を使って考えることができる。
市場でカルテルが結ばれるとどうなるか?は、こちらの記事を参照ください。ここではカルテルが維持されるか裏切られるかに焦点を当てています。
ここでは
- どのような条件でカルテルが成立・維持されるのか?を考えます
ポイント
そもそも、各企業が協力しなければカルテルは成立しません(どこかの企業が出し抜けたり、裏切ったりしたらカルテルは崩壊する)。
現実ではカルテルが存在しているので、カルテルが成立・維持される条件があるはずです。ここからはそれを考えていきます。


カルテルを結ぶ理由
カルテルを結んで、維持する方が各企業が得をするから。


次の条件を考える
市場にはA社・B社の2社がいる。この2社は互いに競争するより、カルテルを結んで利益を確保した方が得だと考え、カルテルを結ぶことにした。
一度カルテルを結ぶと、各企業は次のことを考える。
- カルテルを維持した方がよいか
- カルテル破りをして裏切った方が良いか
裏切るのではなく「互いに合意してカルテルを解消する」という選択肢はないのか?と考える人がいるかもしれません。互いに納得してカルテルを解消する場合、ただの完全競争市場や寡占市場へ移行するため、特別取り上げません。もちろんそういう選択肢も考えられます。
企業A
カルテルを結んだけど、しばらく維持した方が良いかな・・。それとも裏切って出し抜けようか・・。
ポイント
カルテルは、各企業が得をすると考えて結ぶので、カルテルを維持しても得しないと分かれば、カルテルを破ります。
各企業は、常にカルテルを維持するかを考えることになります。
ここで
カルテルを裏切るとA社・B社の関係性は壊れるので、カルテル崩壊後は完全競争に移ります。
ビジネスは絶え間なく続いており、今後の企業間の関係性にも影響を与えます。このような戦略的な状況を「繰り返しゲーム」と呼びます。特に、商売は半永続的に続くため「無限繰り返しゲーム」に該当します。
「繰り返しゲーム」はゲーム理論に登場する言葉ですが、ここでは次のようなイメージを持てばOKです。
各企業は「カルテルを維持するか」「裏切るか」を選択する状況が、常に訪れる(例えば毎年判断する必要がある)。これを繰り返しゲームと考える。


言葉で説明すると「ああ、なるほど。そういう話ね」となるのですが、本題はこれからです。今の話を数式を使って考えることで、現実世界に起こるカルテルの特徴を説明することができます。
というわけで数式で考えます・・。
カルテルの条件式を導出する
前提
いま、寡占市場にいる企業2社を考える。この2社でカルテルを結んだが、各社はカルテルを維持するか、裏切るかの戦略的な状況に置かれている。
step
1カルテルを維持するときの利潤の合計を考える
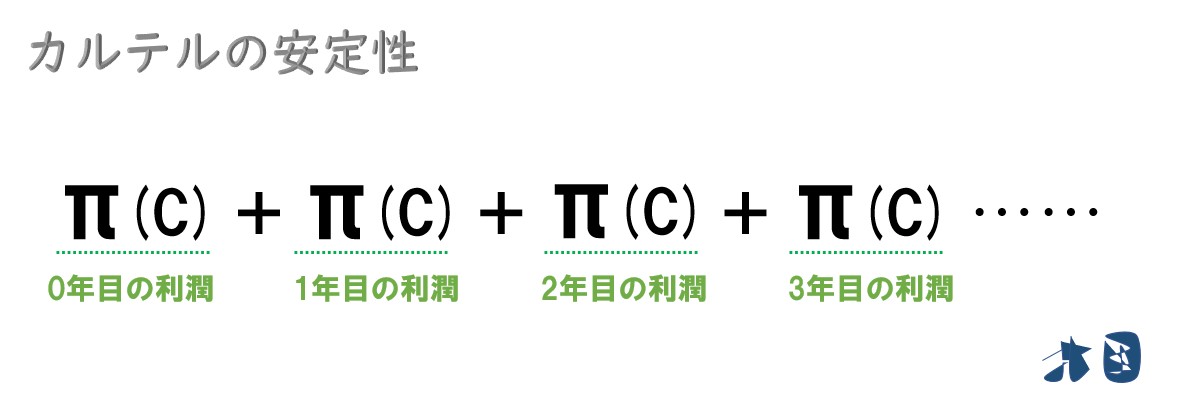
カルテルを結んだ結果、各社が得られる1年間の利潤を「π(C)」とする。
※カルテル(Cartel)のCを取っています。
ポイント①
- カルテルを維持するか裏切るかは「(無限)繰り返しゲーム」なので、今後得られる利潤の総和は次のように表すことができる。
ポイント②
- 将来得られる利潤には割引因子(δ)をかける


ポイント
「割引因子」は、将来のお金をどれくらいの価値で見積るのかを考えるときに登場する計算式のこと。
専門的に言えば、将来の貨幣価値を、現在価値に割り戻すときに使われる「1/(1+割引率)^t」のこと。
例えば
「今100万円をもらう」のと「50年後に100万円をもらう」のなら、今100万円貰いたい人が多いはずです。
一般に「今100万円をもらう」>「50年後に100万円をもらう」という価値関係になりますが、これは将来のお金の価値を低く見積もっているので引き起こる現象です。これを「割引」と呼んでいます。
このとき
同じ100万円でも「50年後の100万円」の方が価値が低いことを説明するために「割引率」という考えを使います。
「50年後の100万円」を「80万円」程度の価値しかないと考えていれば、割引率は20%です(20%割引されているから)。※厳密には違いますがイメージ出来ればOKです。
ちなみに「今」と「将来」のお金を考えるときには、すべて「今(現在価値)」に置き換えて比較するのが経済学やファイナンスなどの慣例です。
というわけで「50年後の100万円」を今の価値に換算します。
公式みたいなものがあるのでこれを使います。
- 100万円×(1/1+割引率)
割引率が20%だとすると・・
- 100万円×(1/1+0.2)
- 100万円×(1/1.2)
- 100万円÷1.2
- ⇒83.333...万円
つまり「50年後の100万円」は「今の83.333万円の価値」となる。
ポイント
本題ですが、この現在価値に換算するときに登場した(1/1+割引率)や(1/1+0.2)を割引因子(δ)と呼んでいます…!
以上より
カルテルによって今後得られる利潤の総和は、割引因子(δ)を使ってさらに次のように表す。
2乗・3乗…となっていますが、これは年数を期間(年数)を表しています。「2年後なら割引因子を2乗」「3年後なら割引因子を3乗」して、時間的な表現するのが一般的です。より遠い将来の方がお金の価値は下がります(100万円貰えるなら20年後よりも1年後に欲しい)。それを表現するために期間分を〇乗するのが経済学やファイナンスの一般的な考え方です(実際には少々違う気がしますが、簡便的にそうしていると考えて下さい)。
ここで
割引因子δですが、ふつう0%~100%に収まります。
つまり「0<δ<1」となります。
※数式では「%」ではなく数字で表現します。
数学の集合を使って表現すると「δ∈(0,1)」です。これは「δが0~1に含まれている(範囲に収まっている・属している)」という意味です。
ポイント
割引因子が0%というのは「今の100万円」と「50年後の100万円」の価値を比べたとき、50年後の100万円の価値なんて0円(100万円×0%)だ!と考えるせっかちな人を表します。
逆に「今の100万円」も「50年後の100万円」も、どっちでもいいや(100万円×100%)という人は、割引因子が100%です。
なので、ふつうは割引率(割引因子)は0%~100%に収まるよね、と考えます。
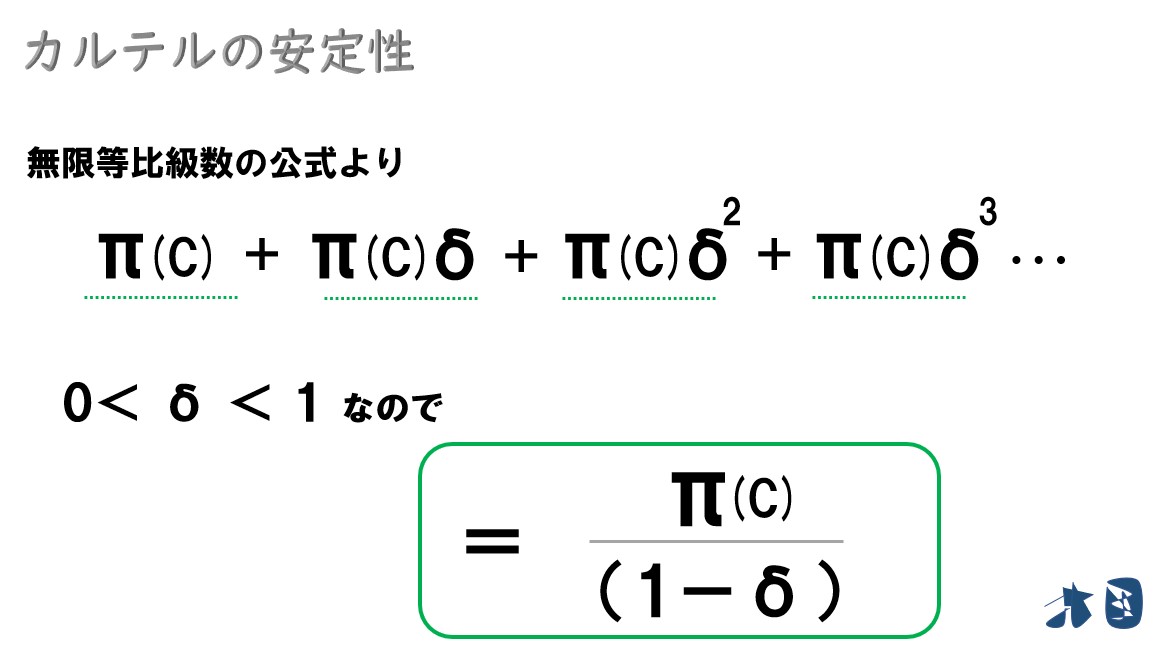
よって「0<δ<1」なので、無限等比級数の和の公式より・・


「等比数列」は数学B、「極限」は数学Ⅲで学習する?と思います。上記は無限に続く等比数列の和がどうなるかの公式です。証明すると長くなるので、ここではこういう風になると考えてください。証明は「無限等比級数の和の公式」とかで検索すると出てきます。
繰り返しゲームなので、カルテルを結んだときの1年間の利潤「π(C)」をずっと得られると考えて、無限等比級数の和の公式を使います。
以上より
ポイント
今後カルテルを維持することで得られる利潤の総和は「π(C)/(1-δ)」だと分かった。
step
2カルテルを裏切るときの利潤の合計を考える
カルテルを裏切るときに得られる利潤を「π(*)」とする。
ポイント
カルテル時は各社が高価格を維持して生産販売を行っているため、裏切って少し価格を下げることでカルテルを結んでいたライバル企業から顧客を奪うことができます。
そのため、カルテルを裏切ると一時的に利潤が増加します。
しかし
カルテルを裏切るとライバル企業との競争が始まるため、一時的に利潤が増加しても、その後の利潤は減少する。
カルテルを裏切った後に得られる利潤を「π(B)」とする
※裏切る(betray)のBを取っています。
カルテルを裏切ったときの利潤の総和は・・
- カルテルを裏切るときに得られる利潤を「π(*)」
- カルテルを裏切った後に得られる利潤を「π(B)」
「π(*)+π(B)」がカルテルを裏切ったときの利潤の合計となります。
ここで
カルテルを維持するときに考えた割引因子(δ)を使って、より厳密な表記にします。
ポイント
カルテルを裏切ってから競争が始まった後の利潤「π(B)」は、割引因子(δ)を使って利潤の総和を表現する。
裏切ったときの利潤の「π(*)」は、裏切ってすぐに得られる利潤なので「割引」する必要はありません。
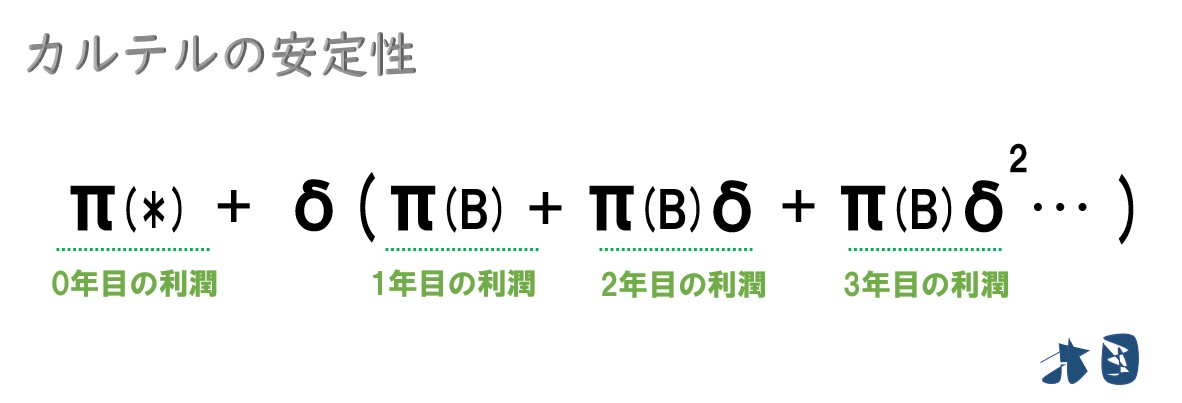
以上より
0年目は裏切った瞬間に得られる利潤「π(*)」として、1年目以降は、競争が始まって得られる利潤「π(B)」に割引因子(δ)をかけて表現する。カルテル維持の場合と同じように、2乗・3乗…は期間(年数)を表しています。将来の方がより価値が下がり割引されるため「2年後なら割引因子を2乗」「3年後なら割引因子を3乗」としています。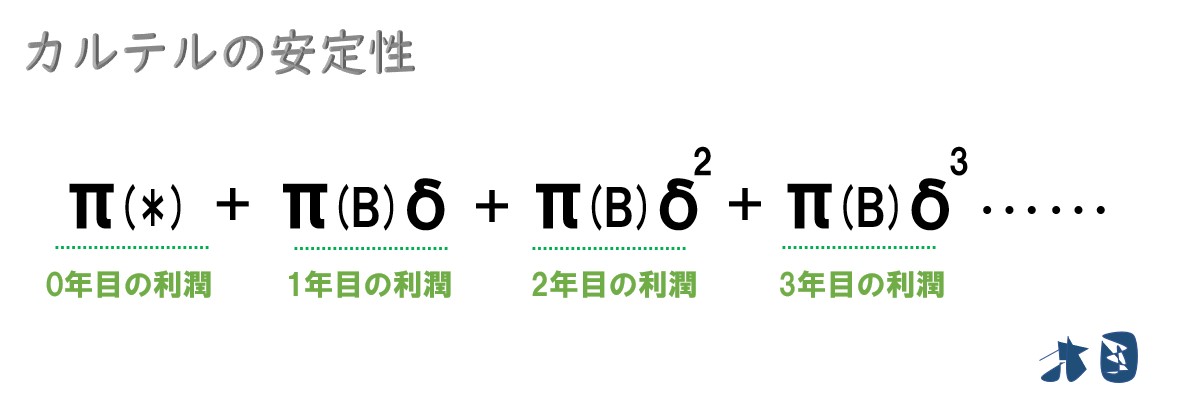


最終的に無限等比級数の和の公式を使いたいので、式を少し変えます。
というのも「π(*)」と「π(B)」で2つ違う文字式が入ってしまっているので、公式に当てはめるために変形する必要があります。
「π(B)」の部分は割引因子(δ)でくくる
無限等比級数の和の公式より
ポイント
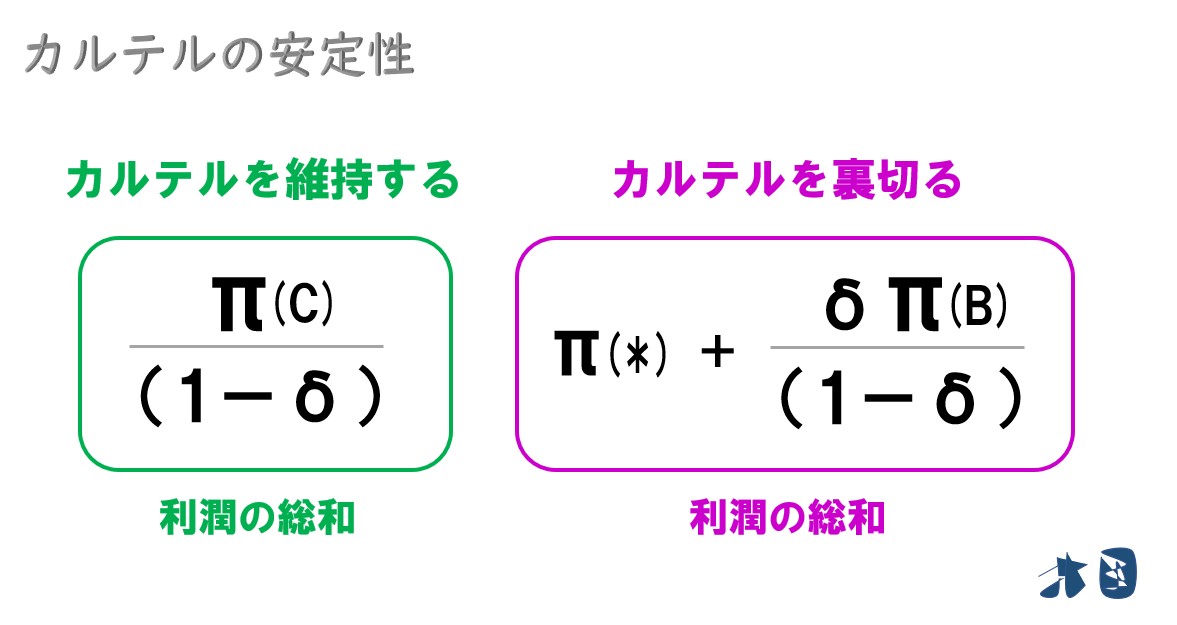
カルテルを裏切るとき得られる利潤の総和は「π(*)+δ・π(B)/(1-δ)」だと分かった。


「カルテルを維持or裏切る」の条件を分析
カルテルを維持するか裏切るかは、どちらの利潤の総和が大きくなるかで決まる。
以上より
- カルテルが安定的に機能する条件は…
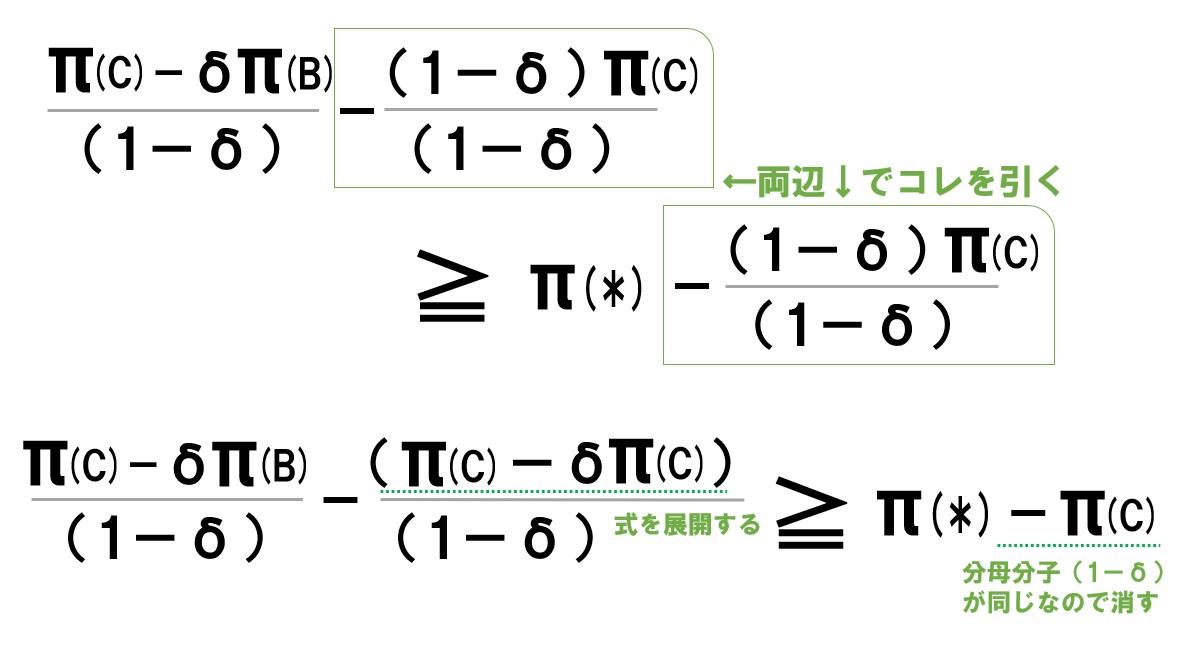
ポイント 「π(C)/(1-δ)」が「π(*)+δ・π(B)/(1-δ)」よりも大きくなるとき、カルテルは安定する。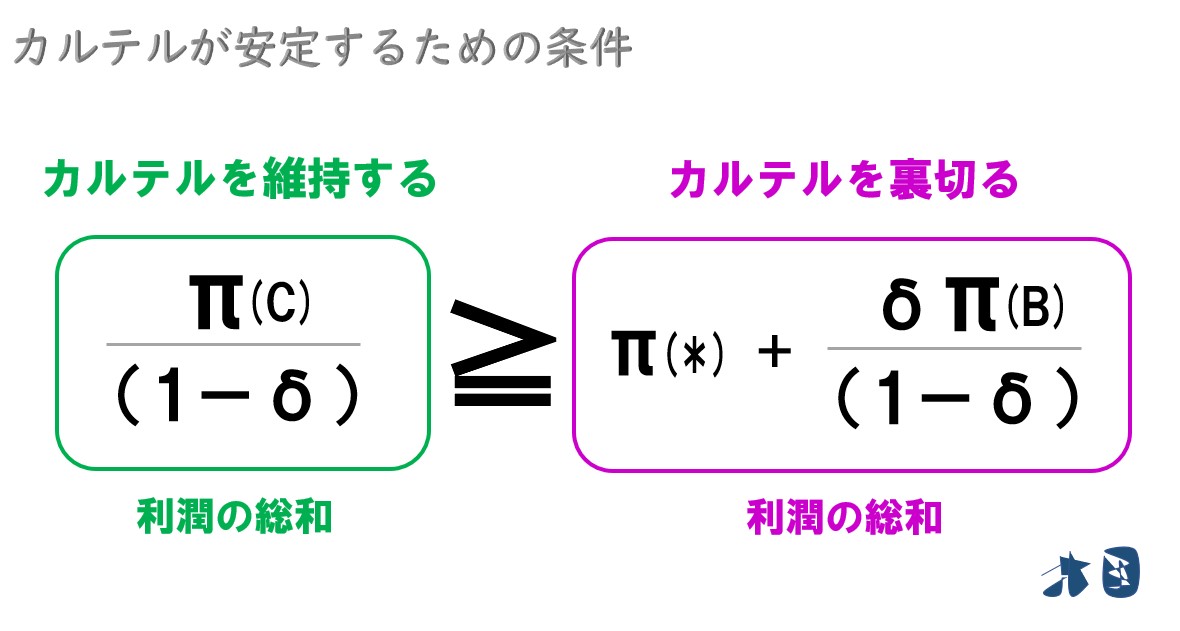


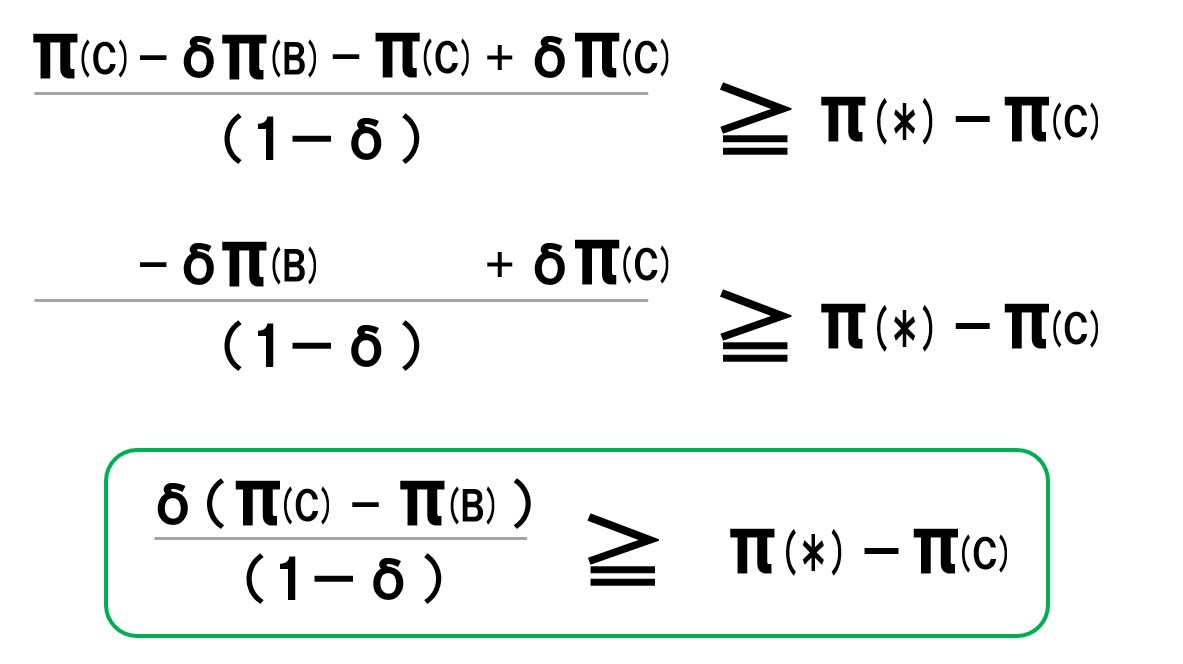
分析のために式を変形します(長いので一番下の緑枠だけ注目してOK)
step
①割引因子(δ)に注目する
はじめに注目するのは「δ/(1-δ)」です。
この条件式が成り立つためには割引因子(δ)が大きい必要があります。
割引因子(δ)が大きいというのは、将来のお金を割り引かない状態(将来のお金も大事)。
例えば、割引因子(δ)が0.9なら「100万円×0.9=90万円」と将来のお金を見積もりますが、割引因子(δ)が0.1なら「100万円×0.1=10万円」と低く将来のお金を見積もります(将来よりも今のお金が大事)。
例えば
割引因子(δ)=0.9(図上側)
割引因子(δ)=0.1(図下側)
ポイント 割引因子(δ)が高いほど左辺の数字が大きくなる。逆に割引因子(δ)が低いと左辺の数字が低くなる。 式を見ての通り、割引因子(δ)が大きいほど「≧」が成り立つ可能性が高まる。←企業が目先の利潤に価値を置いていない(δが大きい)ほど、カルテルが成り立ちやすいことを示している。 別の言い方をすれば、業績が苦しく資金繰りが厳しい企業(δが低い)は、裏切って一時的な利潤を欲しがるのでカルテルが維持されにくい。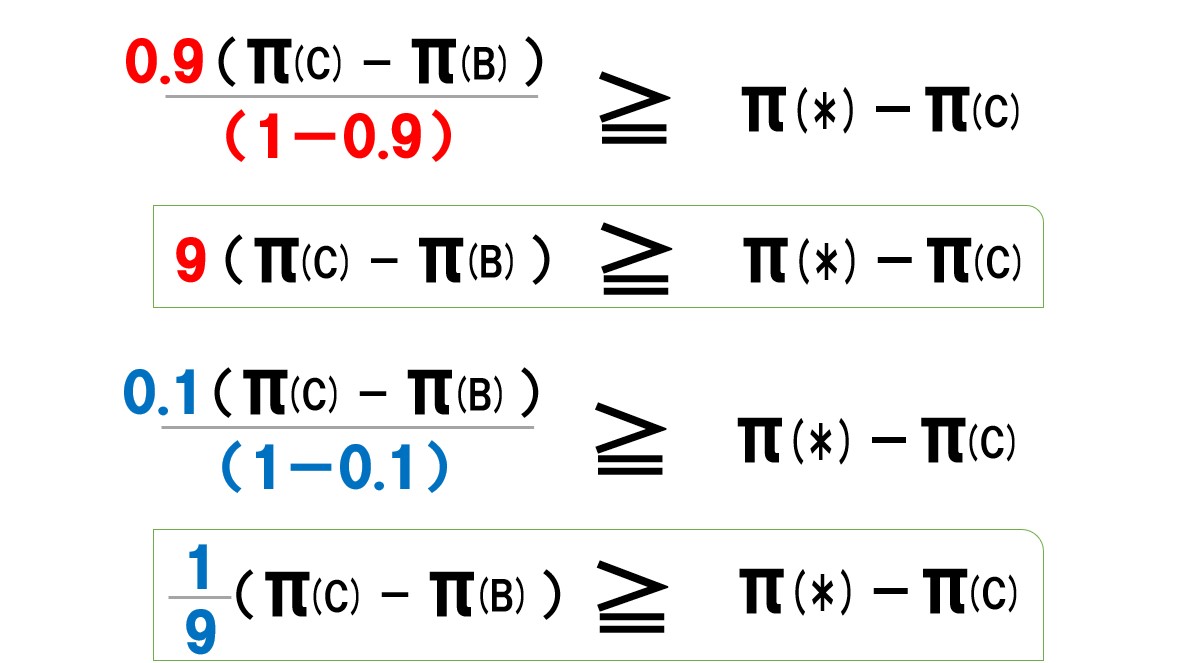
step
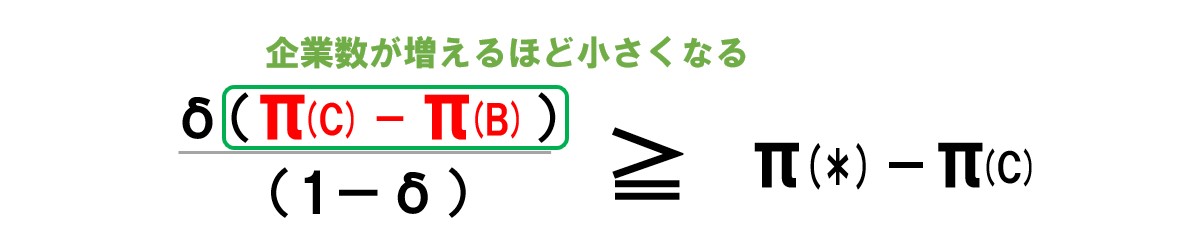
②「π(C)-π(B)」に注目する
次に注目するの左辺の分子部分です。
「π(C)」はカルテルを維持するときの利潤でしたが、企業数が増えるほど利潤が小さくなります(同じ市場で考えれば、カルテルを結ぶ企業が多いほど配分される利潤が少なくなる)。 「π(B)」は競争が始まったときの利潤です。こちらも競争相手が多いほど得られる利潤が小さくなるはずです。


ポイント 市場の企業数が増えるほど、左辺の分子の値が小さくなる。 式を見ての通り、左辺の分子の値が小さいほど「≧」が成り立つ可能性が低くなる。←企業数が増えるほどカルテルを維持するのが難しくなる。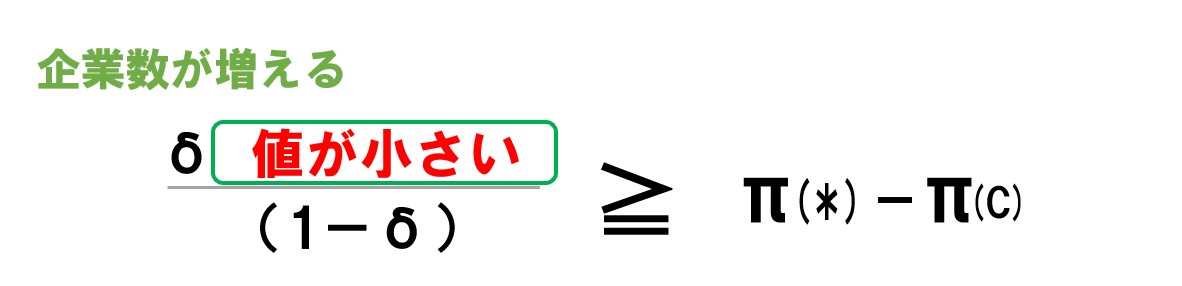


step
③「π(*)」に注目する
最後に注目するのが右辺「π(*)」です。
「π(*)」は裏切ったときに手に入る利潤でした。 見ての通り「π(*)」が小さいほど「≧」が成り立つ可能性が高くなります。裏切ったときに得られる利潤が少ないほどカルテルが維持される。
課徴金減免制度(リニエンシー制度)※を考える
※カルテルを行った企業が、規制当局から調査される前にカルテルの事実を告白すれば、課徴金等の罰金を最大で全額免除される制度のこと。最初の課徴金減免制度は1978年にアメリカの反トラスト法に導入された。日本では2005年に独占禁止法に導入が決まり、2006年から施行された。
カルテルを結んでいるときに「裏切ることで罰金がなくなる=裏切ったときの利潤が高くなる」と考えれば次のようになる。
ポイント 課徴金減免制度(リニエンシー制度)により、右辺の値を大きくすることができる。 式を見ての通り、右辺の値が大きいほど「≧」が成り立つ可能性が低くなる。←課徴金減免制度(リニエンシー制度)により、カルテルを破壊する可能性が高くなる。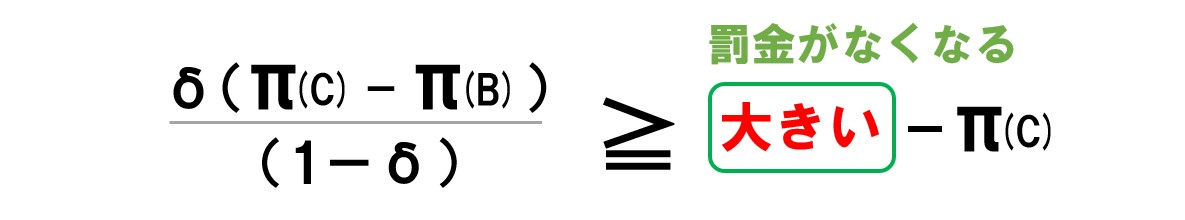


というわけで、カルテルが維持されるか、瓦解するかの条件を見てきました。
カルテルはニュースでも取り上げられることがある経済トピックスなので、興味があれば勉強を進めてみてください。
この記事は、公正取引委員会の「カルテル規制における経済分析の活用-CPRCハンドブックシリーズ No. 2-」を参考にしました。