消費者余剰に関する基本情報をまとめています。
- 消費者余剰
- 消費者余剰のグラフ
- 消費者余剰の問題点
- 消費者余剰の計算方法(求め方)
消費者余剰とは?
消費者余剰とは
財の取引によって消費者が得た便益のこと。市場価格(取引価格)から消費者が支払っても良いと考えていた価格を差し引きしたものが余剰となる。
※英語で「consumer's surplus」と書くので略して「CS」と表現することが多い。
例えば
- 300円のアイスコーヒーを買う
300円のアイスコーヒーを買うのは、消費者が300円以上の効用を得られると考えているからです。


アイスコーヒーを買った人の中には
女性
400円くらいまでなら支払っても大丈夫
男性
500円以下ならOK
という風に、もっと高い値段でも購入したいと考える人もいます。
- 400円-300円=100円
- 500円-300円=200円
それぞれ100円・200円程度、余分にお得感があります。
ポイント
市場には買い物をして”お得感”を感じている人がたくさんいて、そのお得感を消費者余剰と呼んでいます。


ちなみに・・

消費者余剰を定式化したのは経済学者アルフレッド・マーシャルです。
彼は、消費者余剰を「個人の購買から得た満足度の余剰に由来して、”その財をなしで済ませるよりも、その財を購入するために支払っても良いとする価格の合計”と”実際の支払い額”との差額」と表現しています。
グラフで確認する
右下がりの需要曲線があります
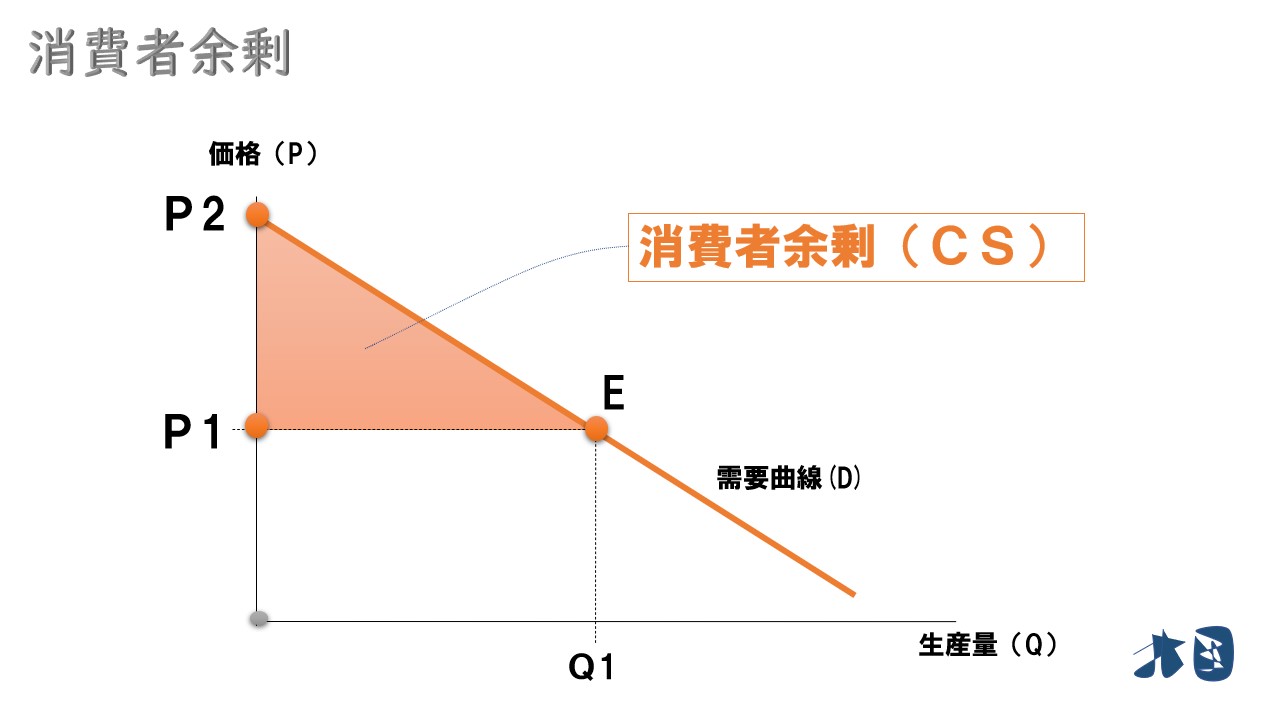
価格が「P1」で決まって生産量は「Q1」となりました。
このときの消費者余剰は?
- 市場価格「P1」
- 市場均衡点「E」
- 需要曲線の切片となる「P2」
この3つの点からなる三角形部分が消費者余剰となります
消費者余剰(CS)=「三角形P1・E・P2」


消費者余剰の問題点

ポイント
消費者余剰では、所得効果が0(ゼロ)という仮定を置いている。
一般的な余剰分析で登場する「消費者余剰」は、分析を直感的に理解できるようにするために需要曲線が直線で描かれます。
ここで、需要曲線が直線というのは特殊な状態であることを知っておく必要があります。
教科書にも載っていますが、イメージし辛いので2段階に分けて説明をしていきます。
ポイント①
- 所得効果が0の意味
「所得効果」とは、ある財の価格が変化したとき、消費者の使えるお金が変化するため、財の購入量に影響を与える現象のこと。詳しくはこちら⇒【代替効果・所得効果】グラフで視覚的に理解する
使えるお金が変われば、消費行動が変わるのは当たり前です。
- 年収が1億円の人
- 年収が300万円の人
当然、年収が1億円の人の方が豪華な買い物をするはずです。
しかし、所得効果が0というのは、言ってみれば年収が300万円から年収1億円になった人の消費行動が変わらない状態を想像しています。

300円のアイスコーヒーを買っていた人が、年収1億円になっても同じアイスコーヒーを買い続けている感じです
ポイント②
- 所得効果が0だとなぜ需要曲線が直線?
さきほどの話が理解できれば、すぐに分かります。
いま、アイスコーヒーの価格が300円から150円になったケースを考えます。

これまで300円でアイスコーヒーを買っていた人は、150円でアイスコーヒーを買えるので手元に150円余分にお金が残ります。
男性
もう1杯アイスコーヒーを飲めるな・・


所得効果が0なので「アイスコーヒーをもう1杯買おうかな~」とは思わない
ポイント①で書いた通り
- 年収が1億円の人
- 年収が300万円の人
所得効果が0というのは「どちらの年収でも消費行動が変わらない状態」です。
注意ポイント
アイスコーヒーが300円⇒150円になって、手元にお金が残ったということは、実質的に年収が150円プラスになったと言えます。
年収が実質150円プラスになって「もう一杯買おうかな~」と思ってしまうと、所得効果が0ではなくなってしまいます。


もし、アイスコーヒーが300円→150円になって「もう一杯買おうかな~」と考える人が続出すれば‥
市場には次の消費者が生まれます。
- 150円ならアイスコーヒーを買いたい
- 150円なら2杯目を買っちゃおう!
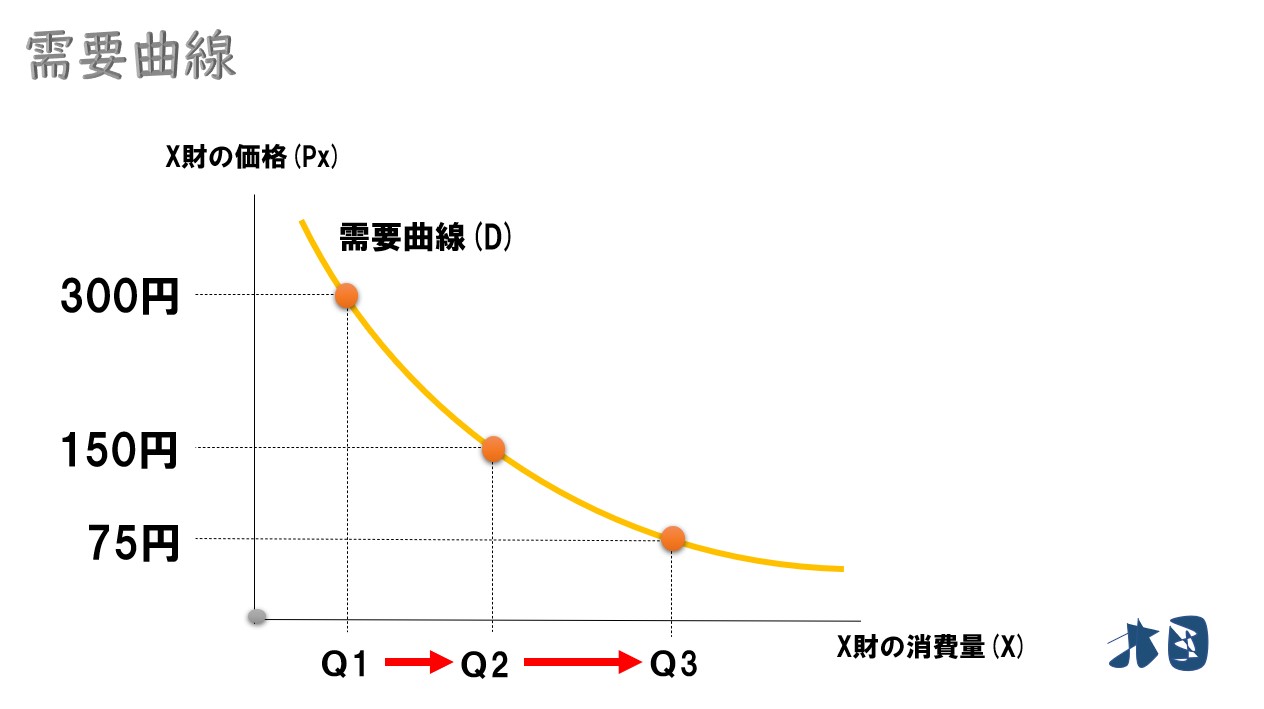
ふつう、価格が安くなるほど「2杯目を買っちゃおう!」と考える人が多くなります。そのため、価格が安くなるほど需要量が一気に増加するグラフが描けます。
金額が安くなれば、どんどん消費量は増えていきます。
- ①300円→150円のとき「Q1→Q2」
- ②150円→75円のとき「Q2→Q3」
①は150円安くなっていますが、②は75円しか安くなっていません。それにも関わらず、②の方が消費量が増加しています。
これは、金額が安くなればなるほど、手元に残るお金が増えるので、その分を再度その財の消費に充てる人が増えるためです。
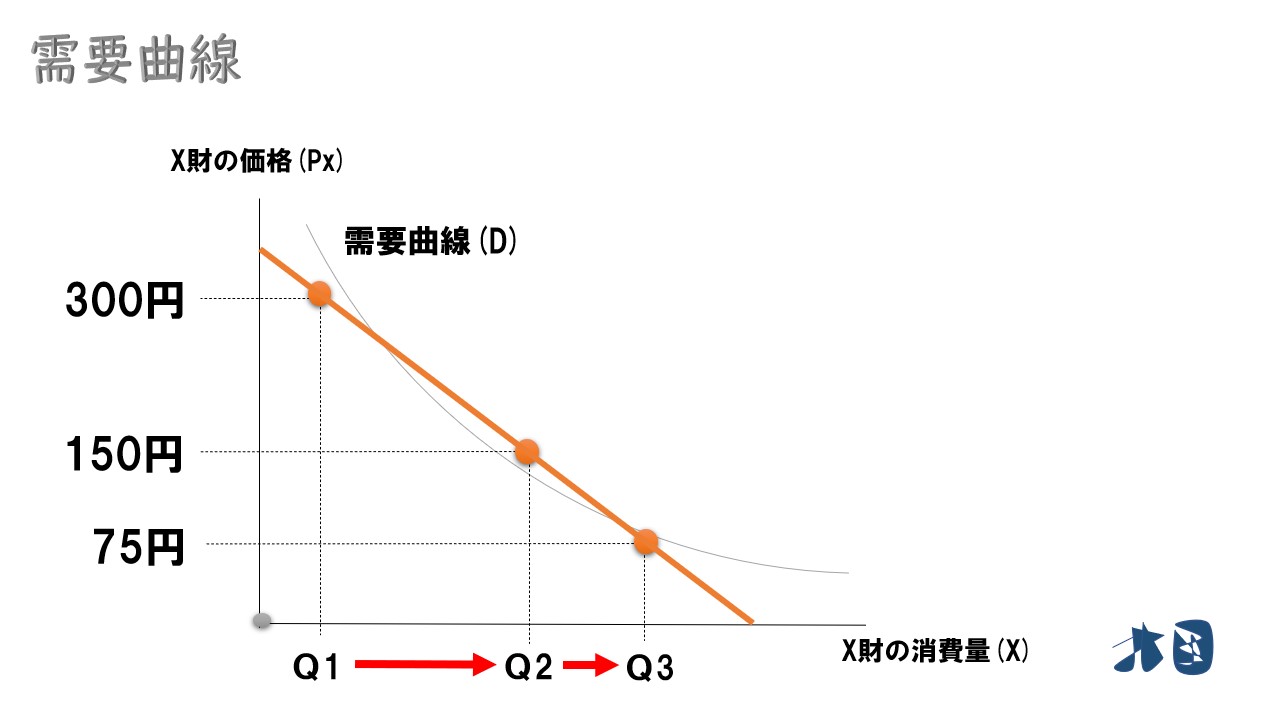
所得効果が0ならば、手元にお金が残っても「アイスコーヒーをもう一杯買う」という選択肢は取らなくなるので需要曲線は直線になります。
- ①300円→150円のとき「Q1→Q2」
- ②150円→75円のとき「Q2→Q3」
①は150円安くなっており、②は75円安くなっています。先ほどとは違い、金額に見合った消費量の増加幅になっています。
まとめ
- 消費量余剰では所得効果が0だと想定している
その結果、需要曲線が直線になって分析が簡単に行えるようになっている。
しかし、途中で書いた通り、所得効果が0だと、ふつうの消費者の行動である「安いし、もう一杯買おうかな」という当たり前の消費行動が存在しないことになるので、消費者余剰は現実から乖離しているという問題点を抱えている
厳密に分析しようと思えばおかしいのですが、あくまで余剰分析は直感的な理解をするためのツールなので、所得効果が0として考えられていると思ってください。


さらに詳しく
このように所得効果が0として考える場合、効用関数(U)が特殊な形になります。
教科書などでは「準線形効用関数(U(x,m)=V(x)+m)」と呼ばれます。
この式の意味は
- 「V(x)」は、x財を消費した時の効用
- 「m」は、現金(貨幣)のことで”1円=1効用”というイメージ※
※ちなみに「現金(貨幣)の限界効用を一定(1円=1効用)」と仮定したのは、先ほど紹介したマーシャルです。彼はこの考えを消費者余剰以外にも部分均衡分析などにも応用していきました。
ここで、xという財の消費は、限界効用逓減の法則が働く通常の効用関数(非線形・カーブを描く形)だけど、m(=現金)は”1円=1効用”で効用が直線的に増える(線形・直線になる)ので、2つ合わせて「準線形」と言われています。
ふつうの効用関数は、2財を掛け合わせて「U=xy」などのようにします。しかし「準線形効用関数」では、x財は単独で効用水準が決まるので、現金(m)がいくら増えようとx財の消費量には影響を与えません。これで所得効果が0ということになります。
先ほど書いたように、この準線形効用関数は現実的ではありませんが、数学的な処理が簡単なので、消費者余剰の話になると、たびたび登場します。
消費者余剰の計算方法・求め方

ポイント
基本的には三角形の計算を思い出す。
例えば
- 財Aの需要曲線が「D=-20P+500」
- 財Aの供給曲線が「S=30P」
このとき、市場均衡点における消費者余剰はいくらか?
均衡点は「需要曲線と供給曲線が交わる」という事を意味しているので「D=S」として計算します。
- -20P+500=30P
次に均衡点における市場価格を計算します。
- 50P=500
- P=10
「D=-20P+500」に市場価格のP=10を代入します。
- D=-200+500=300
これで、市場均衡点における価格と需要量(消費量)が分かりました。
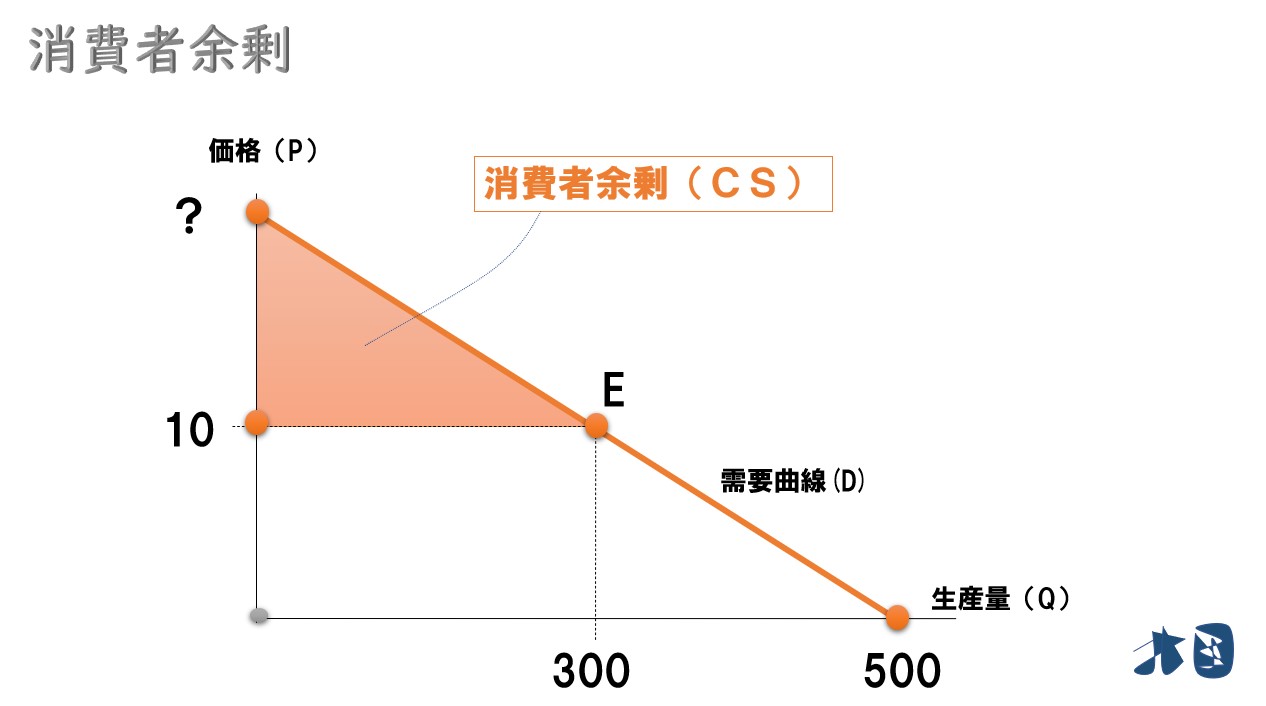
グラフで見ると
三角形の面積を求めるには、切片(?)の値が必要です。
- 需要曲線「D=-20P+500」を「P=●●の形(逆需要関数)」にする
20P=-D+500
P=(-D+500)/20
切片なので横軸の需要量(D)は0となります
グラフの横軸は”生産量Q”という表記になっていますが、需要量(D)・供給量(S)と同じ意味です。
P=(-0+500)/20
P=(500)/20
P=25
以上より
ポイント
後は「(縦×横)÷2」で三角形の面積を求めるだけです。
- 縦=(25-10)=15
- 横=300
(15×300)÷2=2250
以上より、消費者余剰(CS)=2250