エッジワース･ボックス（純粋交換経済）の項目で登場する契約曲線について基礎知識をまとめています。
- 契約曲線とは？
- 契約曲線のグラフ
- 契約曲線とコア配分
- 計算方法･求め方
契約曲線とは
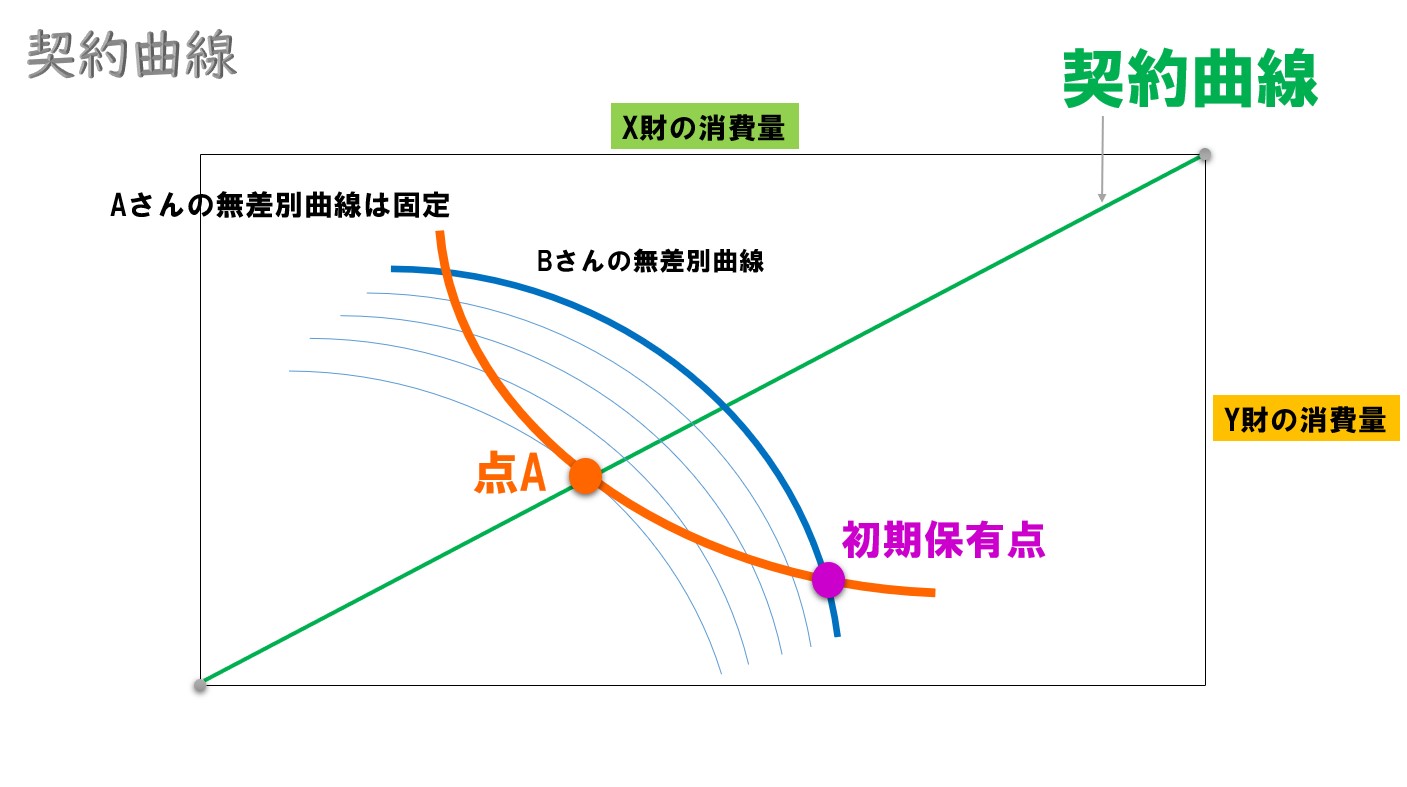
契約曲線
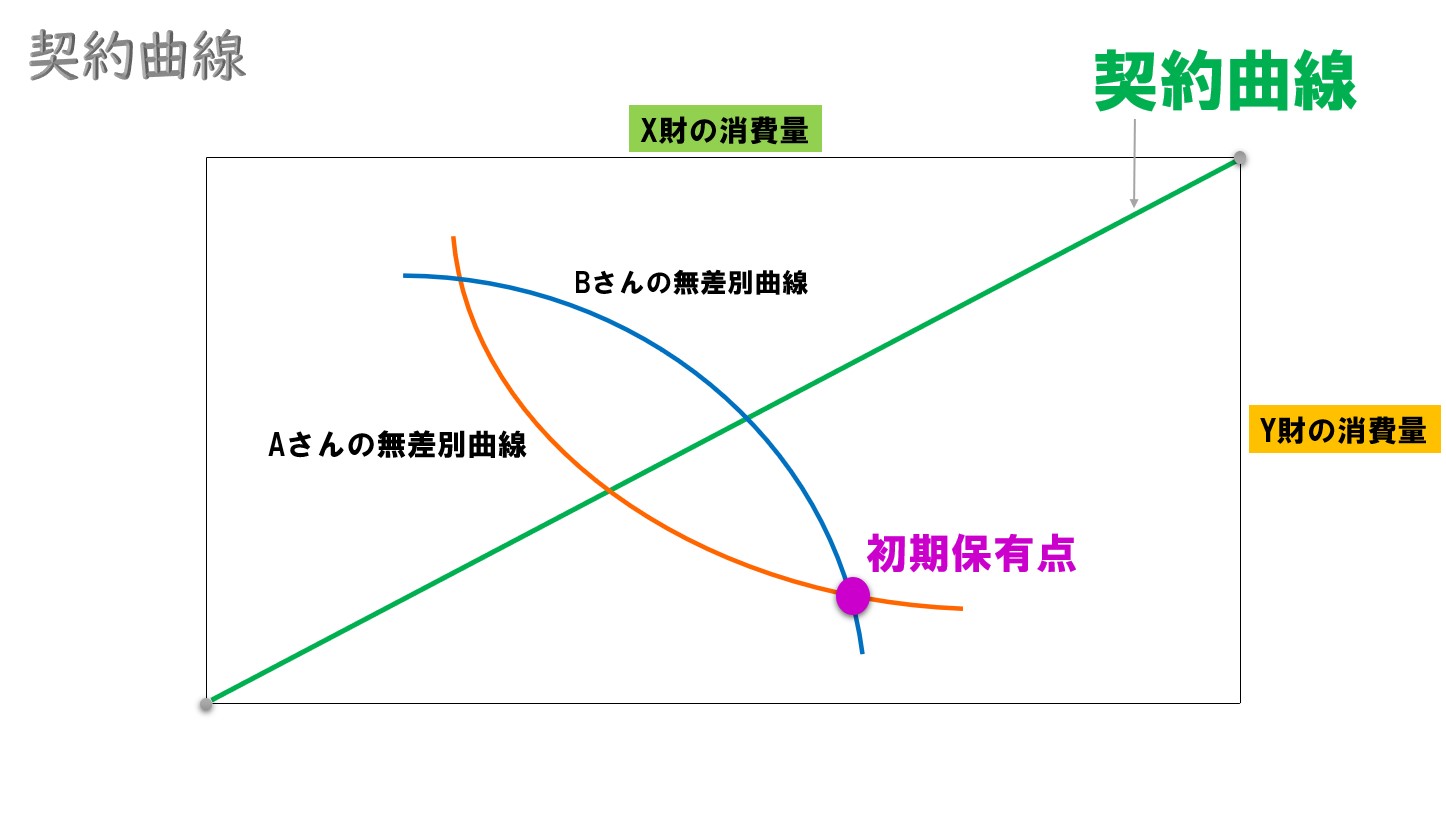
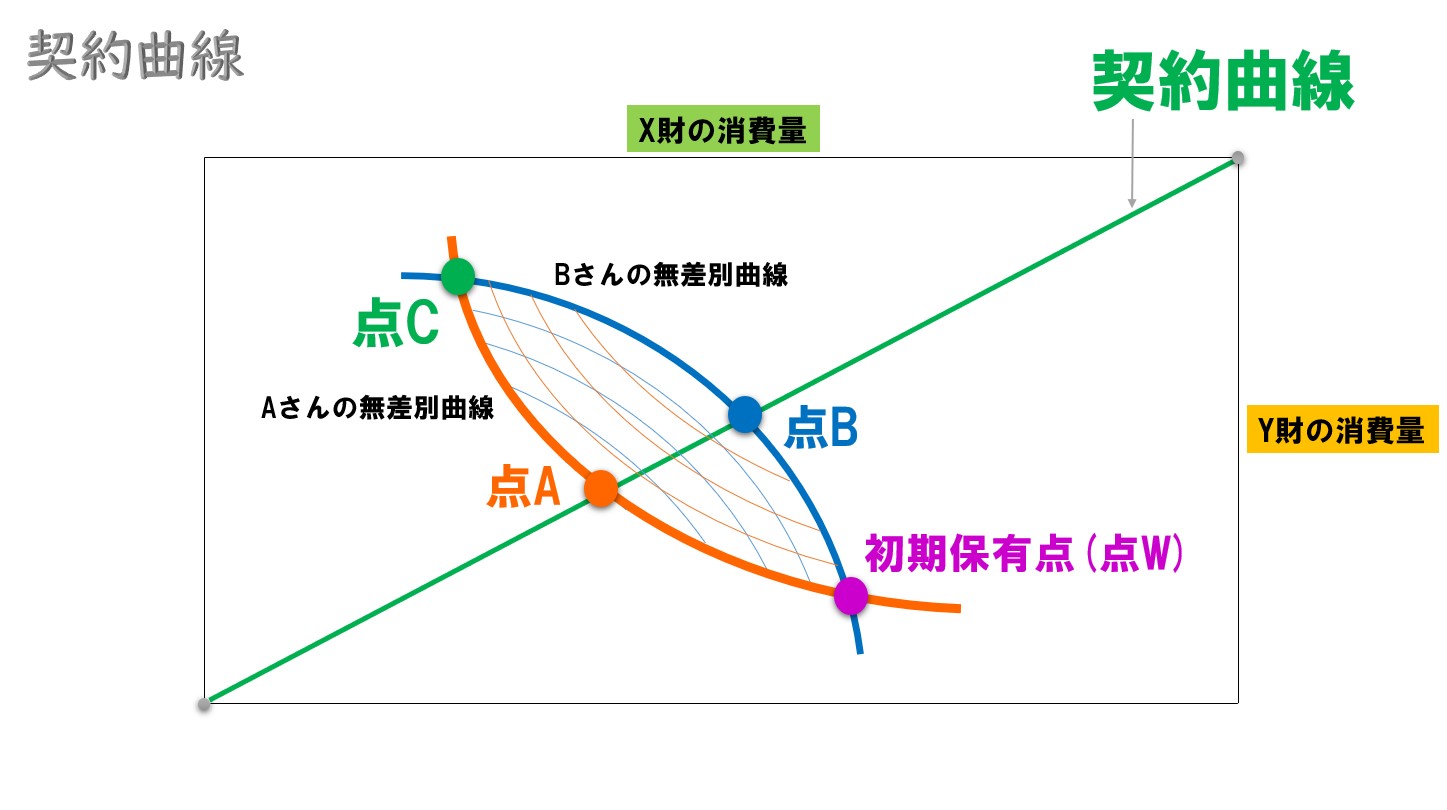
エッジワース･ボックスで、パレート効率的(パレート最適)な資源配分が実現している点を結んだ線（パレート最適が実現する点の軌跡）のこと。
グラフで見ると‥
ポイント①
ポイント①
契約曲線上では、2人の消費者の限界代替率(MRS)が常に一致している。
参考：限界代替率・エッジワース･ボックス
パレート効率的な資源配分では、2人の消費者の限界代替率が一致します。
つまり、パレート効率的な資源配分の軌跡である契約曲線上は「常に2人の消費者の限界代替率が一致している」ことになります。
これは計算問題とかで使うので、頭の片隅にでも入れておきましょう。
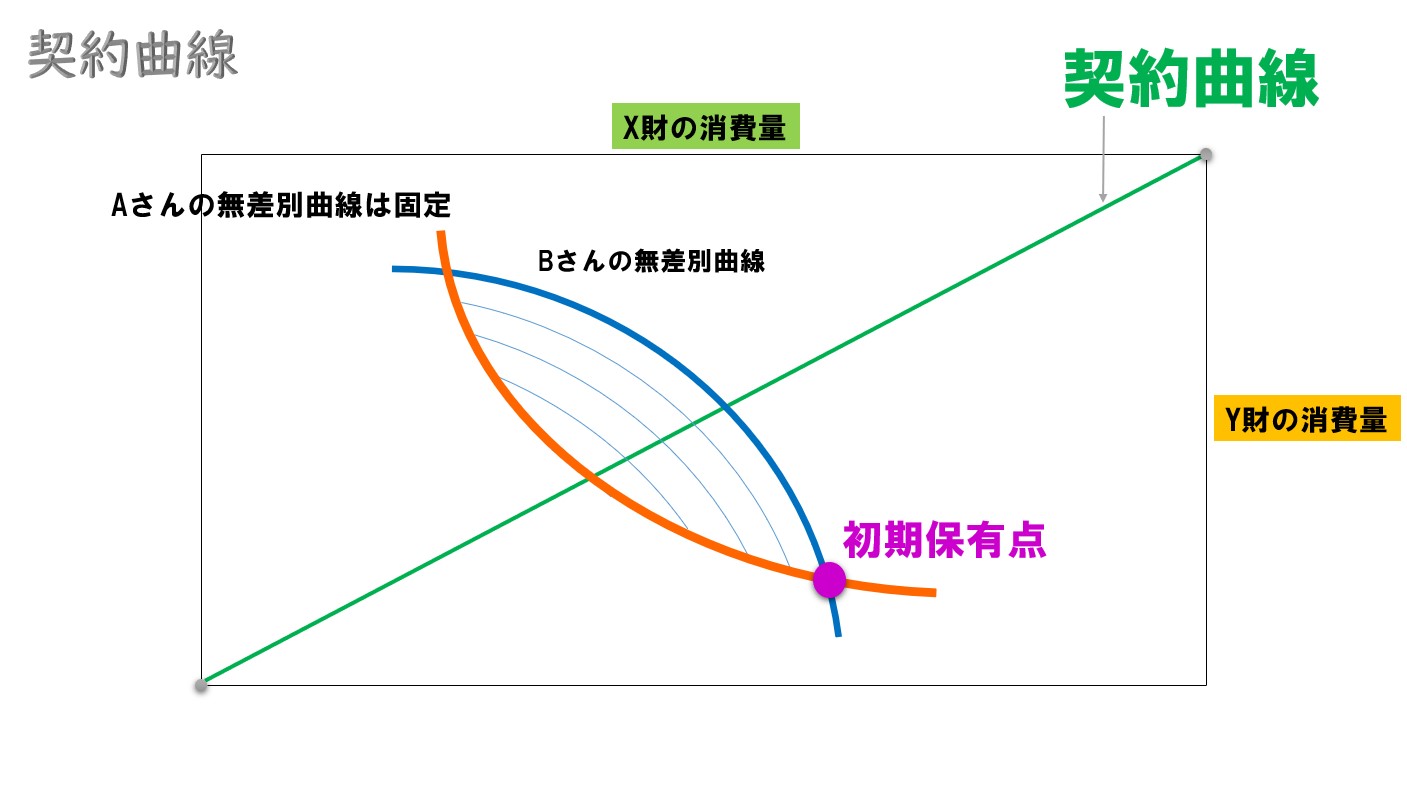
ポイント②
ポイント②
契約曲線上はすべてパレート効率的ではあるが、それぞれの資源配分が実現できるかは初期保有･財の価格比に依存する（パレート効率的ではあっても、全てが競争均衡配分というわけではない）。
契約曲線は「このエッジワース･ボックス内なら、この部分が効率的な資源配分ですよ」ということを示しています。
しかし、効率的な資源配分だからと言って、実現が出来るかどうかは分かりません。
例えば
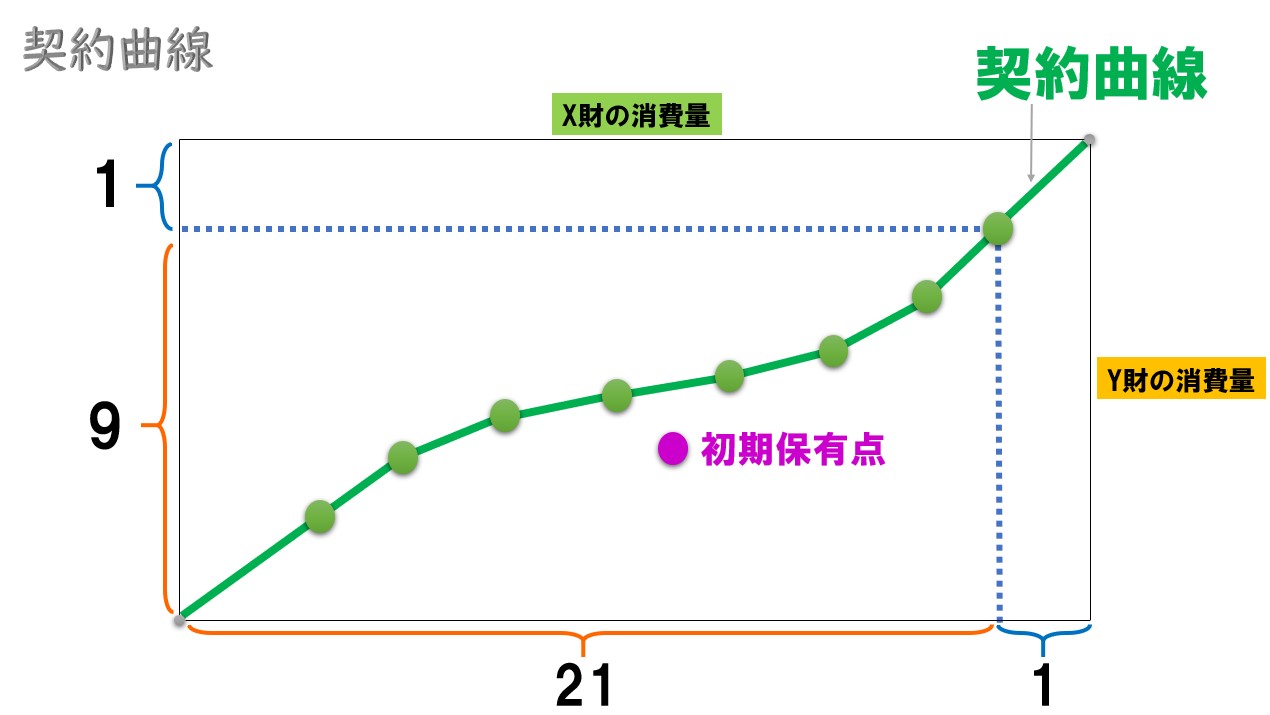
2人の初期保有は下記の通り いま2人が財の交換を行います。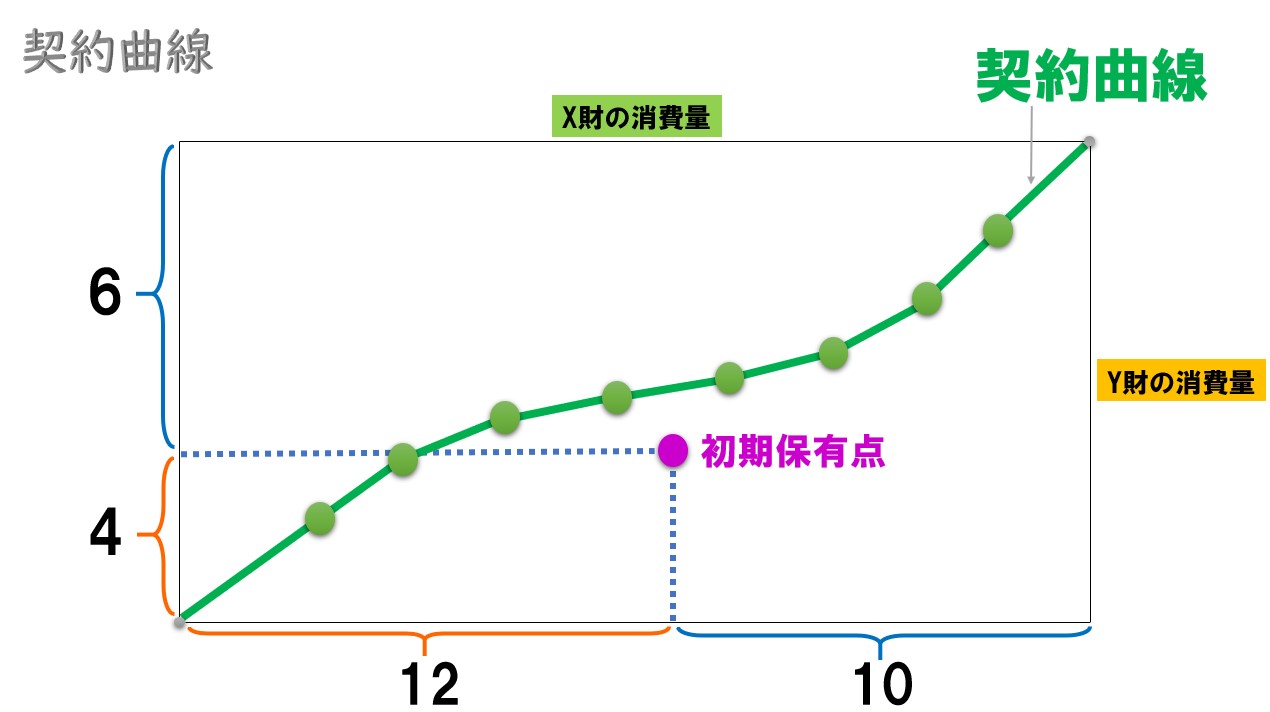
ここで
財の交換をした結果
- Aさん（X財=21･Y財=9）
- Bさん（X財=1･Y財=1）
となるでしょうか？
相手がジャイアンではない限り、普通に考えればここまで偏った資源配分にはなりません。
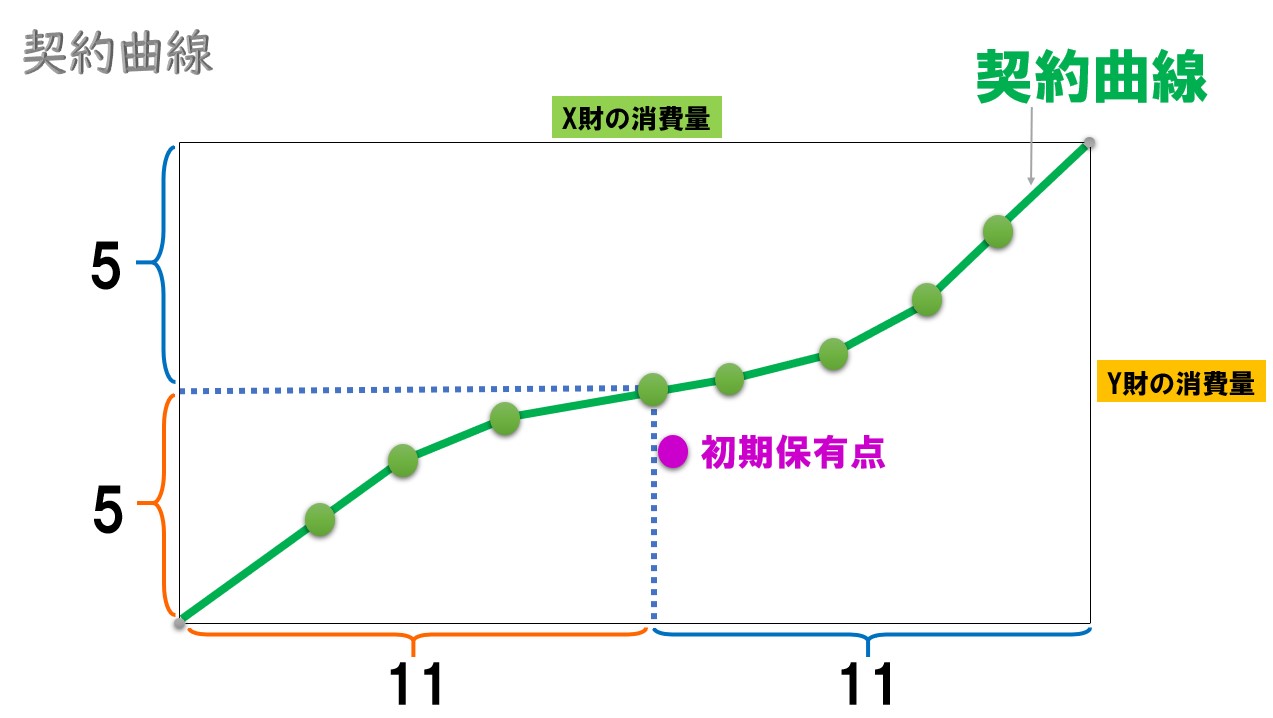
普通に考えると‥
- Aさん（X財=11･Y財=5）
- Bさん（X財=11･Y財=5）
という風になるのが自然です。
これが「契約曲線上はすべてパレート効率的な資源配分だけど、どの資源配分が実現できるかは初期保有に依存する」という意味になります。
コア配分
はてな
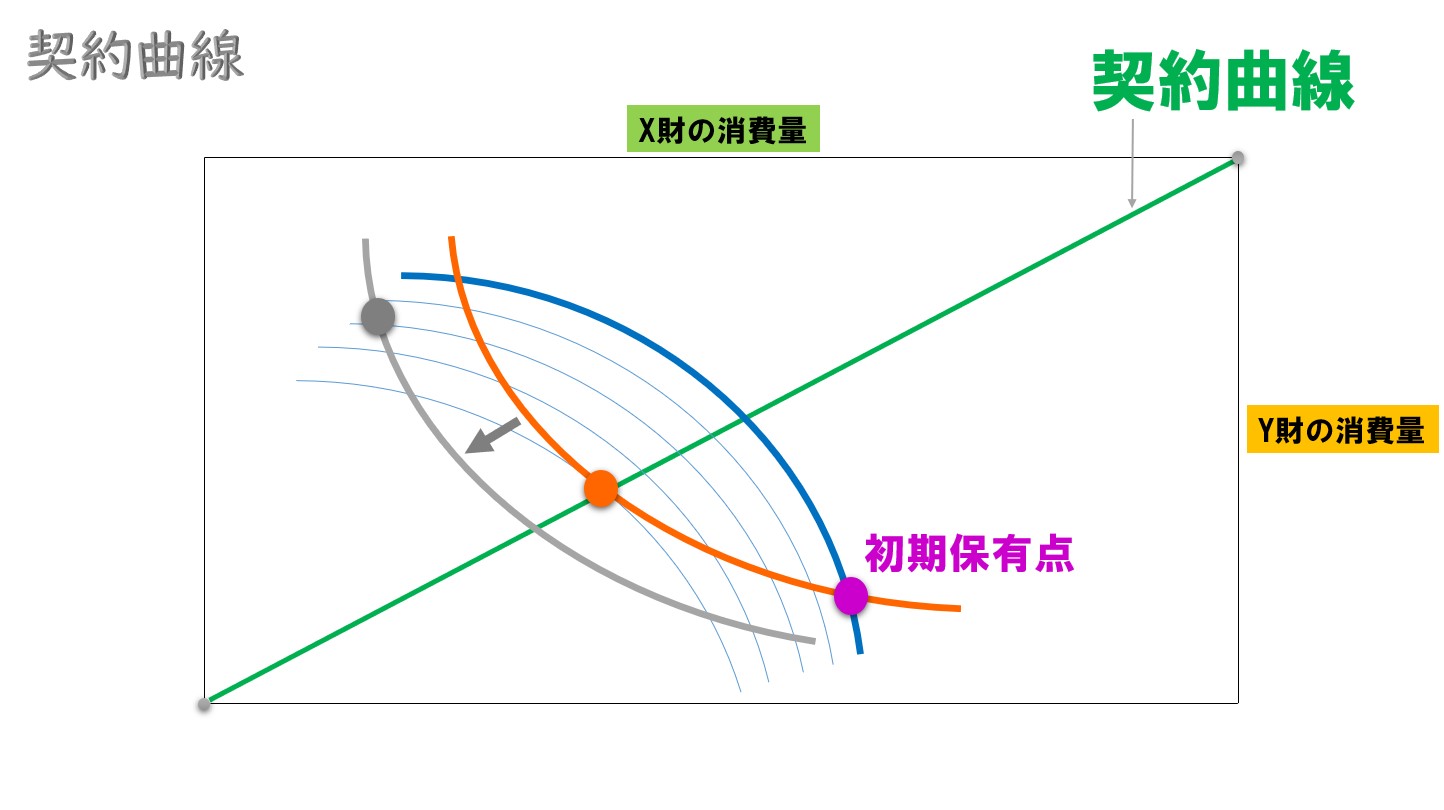
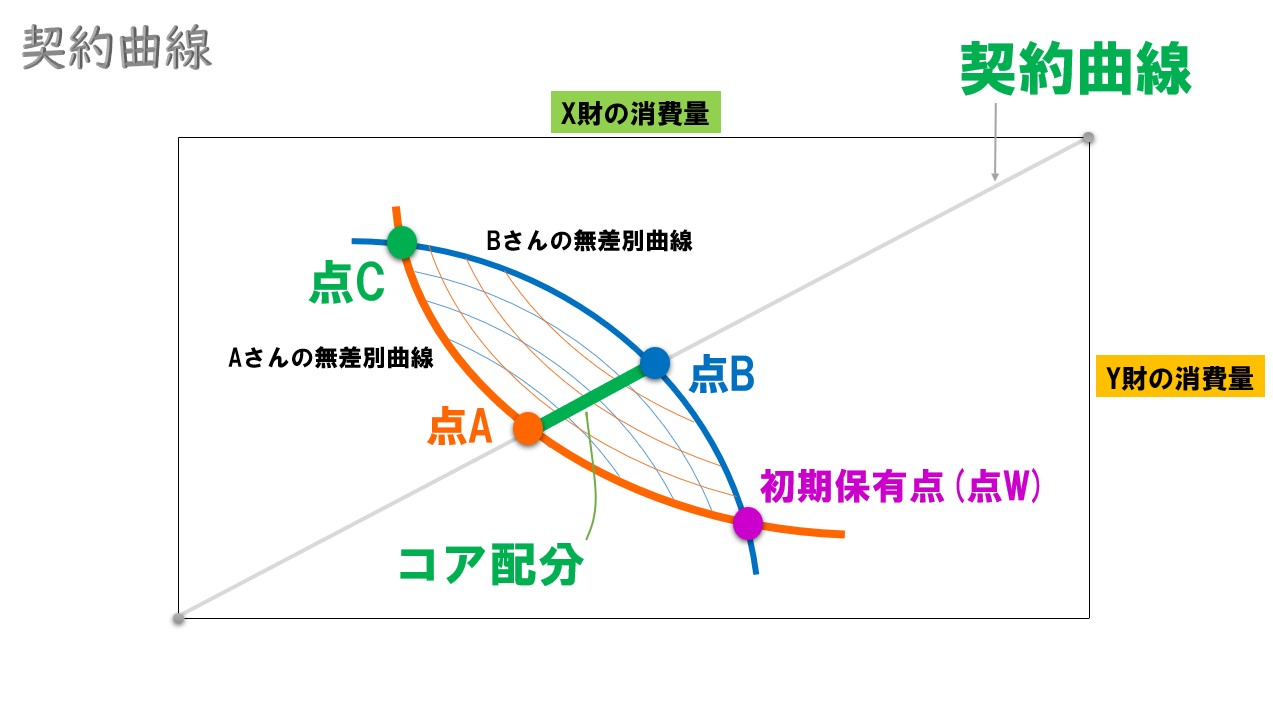
初期保有点よりもパレート改善が実現する領域で、かつ契約曲線上にある資源配分のことを「コア配分」と呼ぶ。
いま、2人の消費者の初期保有が次のようになっている。
初期保有点よりもパレート改善となる資源配分は・・？
パレート改善は「誰かの効用水準を下げることなく、誰かの効用水準を高める」という意味です。
例えば
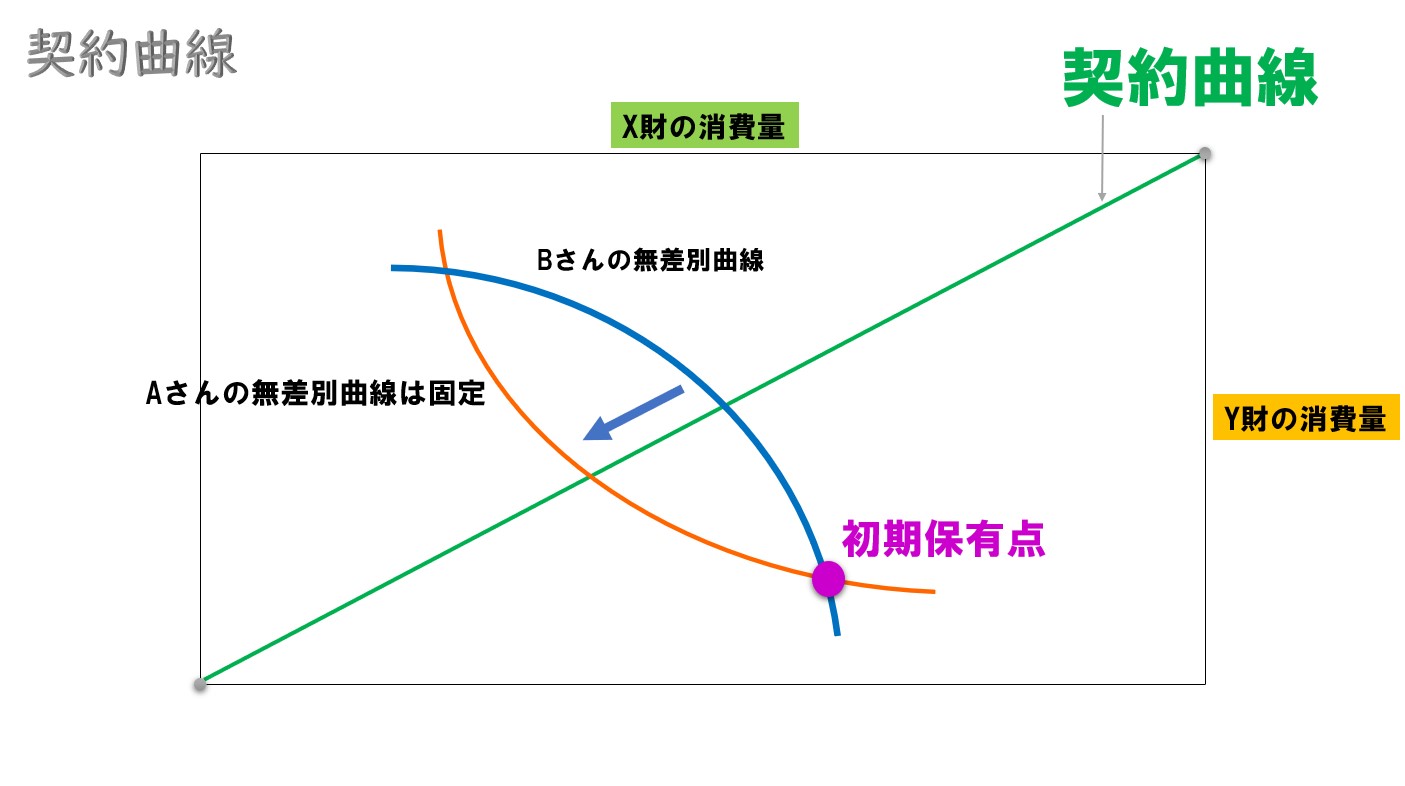
Aさんの効用水準を下げないで、Bさんの効用水準を高めます。
Bさんの効用水準を高める（無差別曲線を移動していく）
Aさんの効用水準を変えずに、Bさんの効用水準は点Aまで高めることが出来ます。
Aさんのオレンジ色の無差別曲線上なら、どの部分も同じ効用水準なので、ぎりぎり(点A)までBさんの無差別曲線を移動させることが出来ます。
Aさんの無差別曲線からはみ出た部分は除く
はみ出た部分では、Aさんの効用水準を引き下げる必要がある。
逆に、枠内ならAさんの効用水準を高めることで実現が可能です。
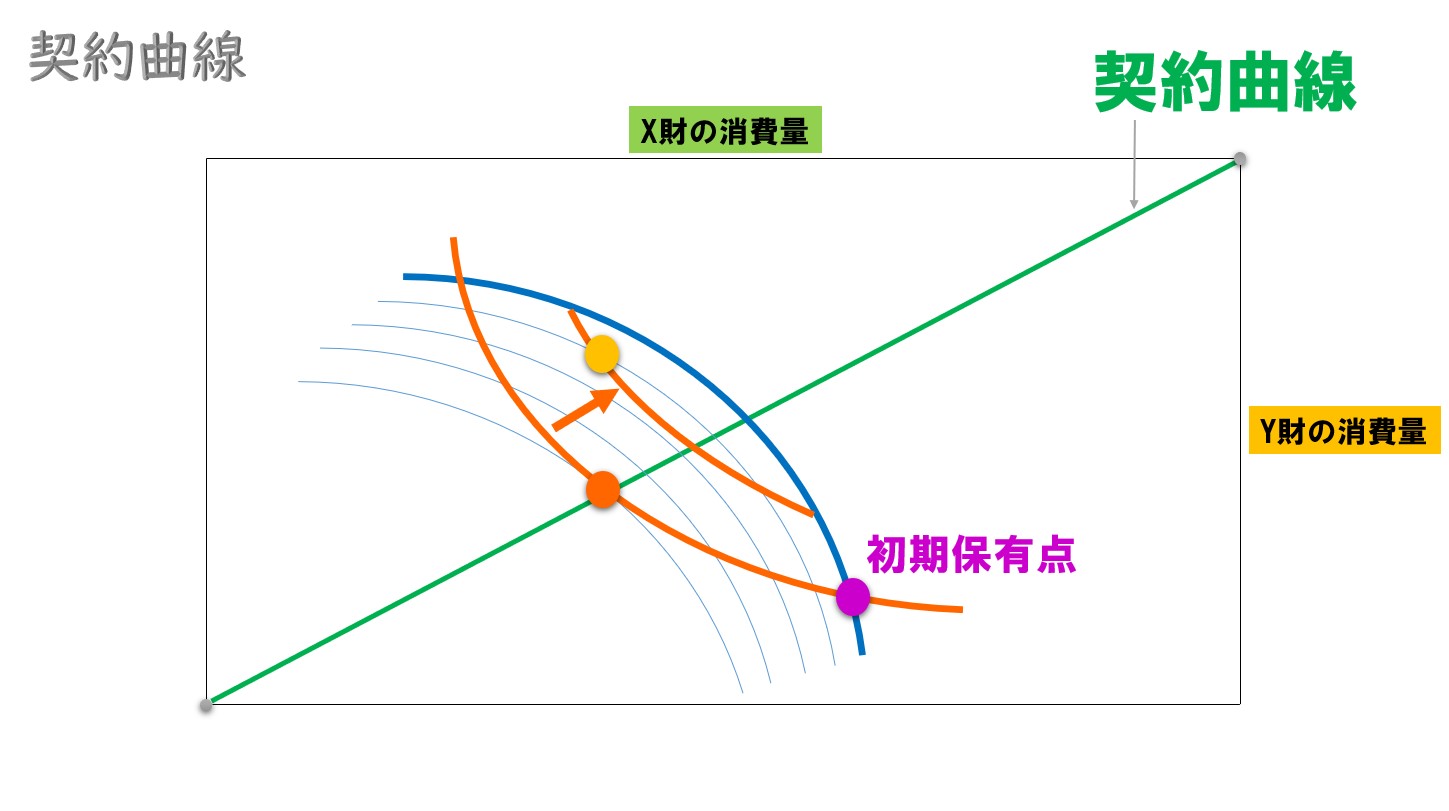
以上より
ポイント
「初期保有点W･点A･点C･点B」内の資源配分なら、初期保有点(W)よりもパレート改善が実現する。
「初期保有点W･点A･点C･点B」の領域内にある契約曲線に注目します。
この点A～点Bの契約曲線部分をコア配分と言います。
- 初期保有点よりもパレート改善が実現する領域
- かつ、パレート最適が実現する資源配分（契約曲線上）
この2つの条件を満たす部分がコア配分と呼ばれます。
問題で「コア配分」はどの部分か？などの問いがあったりするので、しっかりと覚えておきましょう。
計算方法（例題）
いま、2人の消費者(Aさん･Bさん)が2種類の財を保有している。
- AさんはX財20個･Y財80個
- BさんはX財80個･Y財20個
また2人の効用関数は以下の通りである。
- Aさん「U=3xy」
- Bさん「U=2xy」
契約曲線を求める
step
1限界代替率を求める
ポイント
効用関数(無差別曲線)を微分すれば「傾き(限界代替率)」が求められます。
参考：最適消費点の計算方法
- Aさんの効用関数「U=3xy」より
「y＝U／3x」とする
「y=U／3x」を微分すると⇒「U／－3xの2乗（＝U･－3xの－2乗)」
ちなみに分数は「(1／2)＝2の－1乗」なので注意しましょう。
ここで
「U」という文字が邪魔なので、Uを「xとy」に置き換えます。
「U＝3xy」を「U／－3xの2乗」に代入します。
「U(＝xy)／－3xの2乗」⇒「3xy／－3xの2乗」＝「－(y／x)」
Bさんの限界代替率も同様に求めると「－(y／x)」となります。
以上より
- Aさんの限界代替率＝「－(y／x)」
- Bさんの限界代替率＝「－(y／x)」
step
22人の資源配分を考慮する
問題文の情報より各財の総量は‥
AさんはX財20個･Y財80個
BさんはX財80個･Y財20個
- X財の総量＝100個
- Y財の総量＝100個
ポイント
- AさんがX財を「x個」消費するとき、Bさんは「100－x」を消費
- AさんがY財を「y個」消費するとき、Bさんは「100－y」を消費
また、Bさんの2財の消費量は「100－y」「100－x」と表現できるので、Bさんの限界代替率を「－(y／x)＝－(100－y)／(100－x)」と考えます。
以上より
- Aさんの限界代替率＝－(y／x)
- Bさんの限界代替率＝－(100－y)／(100－x)
ここで、契約曲線上では2人の限界代替率が等しいことを思い出します。
つまり「(y／x)＝(100－y)／(100－x)」となります。
計算がややこしくなるのでマイナスは消しました。
後は「(y／x)＝(100－y)／(100－x)」を計算して「y＝○○x」などの形にすればOKです。
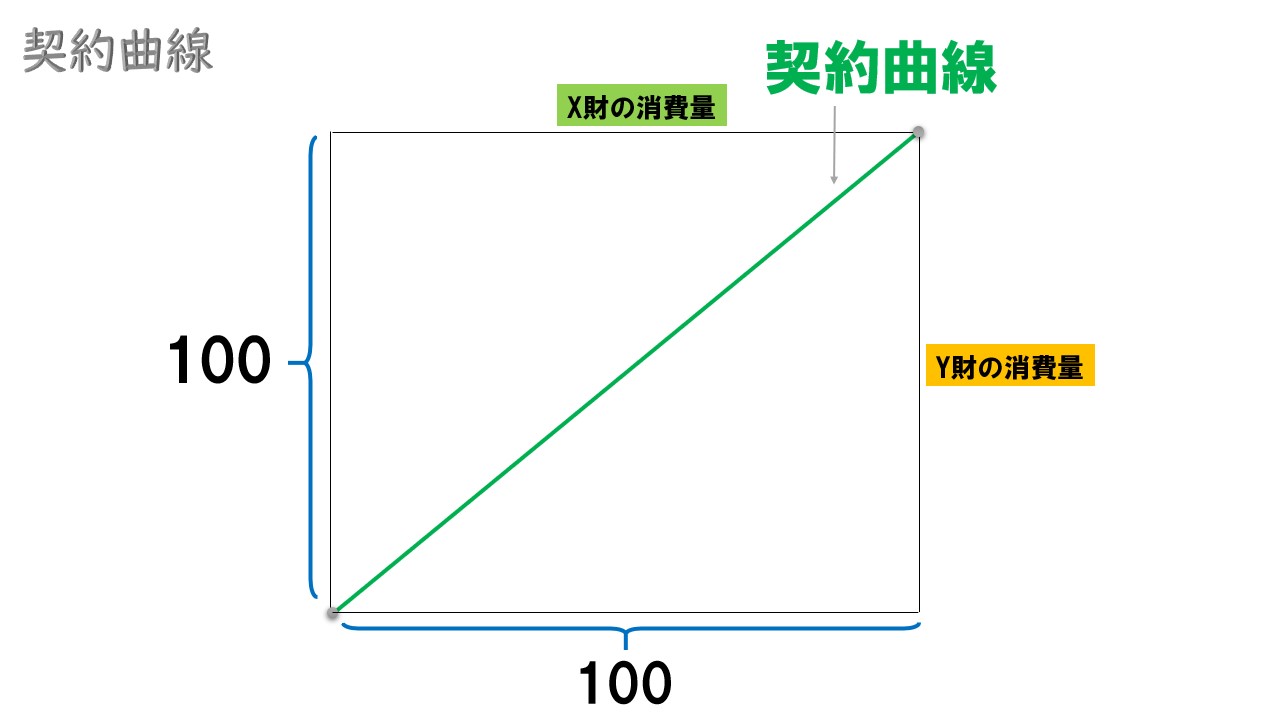
契約曲線は「(縦軸)＝(横軸)」という式になる。
(y／x)＝(100－y)／(100－x)
(y／x)(100－x)＝(100－y)
(100y－xy／x)＝(100－y)
(100y－xy)＝(100－y)x
100y－xy＝100x－xy
100y＝100x
y＝x
契約曲線は「y＝x」
ちなみに
「y＝x」ということは、契約曲線はグラフのような直線になります。
