完全代替財などで登場する「端点解(コーナー解)」
- 端点解(コーナー解)とは？
- 端点解と完全代替財
- 端点解とリニア型の効用関数
- 端点解のパターン
最適消費を求める問題を解くと、途中で計算できないケースがあります。その最適消費は「端点解(コーナー解)」かも。
端点解(コーナー解)では、加重限界効用均等の法則やラグランジュ未定乗数法が使えません。端点解(コーナー解)をしっかりと理解していれば、そんな状態は防ぐことが出来ます。
端点解(コーナー解)とは？
端点解(コーナー解)
最適消費量の答えに「0が含まれる」とき、その答えを端点解という。2財の(x, y)の最適消費量が「0=x, y＞0」もしくは「x＞0, y=0」のどちらかの場合をいう。
逆に「0が含まれない」最適消費量は内点解という。(x=1,y=2)などの普通の答え。
端点解では、計算問題を解くときにイレギュラーが発生する
- 加重限界効用均等の法則が使えない
- ラグランジュ未定乗数法が使えない
上の2つは、端点解では答えが出ないので注意してください。
端点解になるケース
効用関数(U)が「x＋y」などの足し算のケースは注意。
効用関数が「x＋y」なら、端点解になる可能性があるので注意が必要です。
「x＋y」などの効用関数を「リニア(linear=線形)」と呼びます。
足し算になる理由
一般的な効用関数(U)は「U＝x･y」などのように掛け算になっています。
2財を消費することで、相乗効果を生んで効用が高まるとイメージすれば分かりやすいです。
しかし
一方で、効用関数が「U＝x＋y」なら「x」「y」には関係性がありません。（2つ消費しても相乗効果が得られない。）
このような財を完全代替財と呼びます。「どっちでも良い」という財です。
例えば
- 5,000円札と1,000円札*5枚を考えてみます。
どちらかを消費することで効用が得られますが、買い物が出来れば「5,000円札」「1,000円札*5枚」どっちでも良いです。
ポイント
このように、X財･Y財にどっちでも良いもの（完全代替財）が並んだ時に、効用関数が「U=x＋y」などの足し算になります。
他にも「バターとマーガリン」など、人によってはどっちでも良いモノ(完全代替財)が、リニア型の効用関数になります。
ちなみに、完全代替財の無差別曲線は、次のような直線になります。
グラフで見ると
「U＝x＋y」のときの無差別曲線
「完全代替財」や「リニア型の効用関数」などの基礎知識が分かったところで、実際に端点解が出現するケースを見ていきましょう！
端点解① 縦軸上に最適消費点
ポイント
縦軸上に最適消費点が出現する場合、端点解(コーナー解)となります。
ここでは
- 縦軸：Y財の消費量＝y
- 横軸：X財の消費量＝x
- Y財の価格＝Py
- X財の価格＝Px
予算制約線「I＝xPx＋yPy」と効用関数「U＝x＋y」から導かれる無差別曲線がグラフに描かれる。
最適消費点で「y＝0」ということは、Y財を消費せずに、X財だけを消費すれば効用最大化が実現するという事になる。
ポイント
- X財･Y財は完全代替財なので、どちらを消費しても同じ
- X財の方が安いため（Py ＞Px）、全てX財を消費した方が良い
X財の方が価格が安い場合「予算制約線の傾き」と「無差別曲線の傾き」は下のような関係になっています。
傾き（勾配）に注目する
ポイント
ここでは「Px／Py ＞1」ならば、縦軸(Y軸)上に最適消費点が現れるため端点解となる。
下線の部分は、下記のように表現したりします。
- 予算制約線の方が無差別曲線よりも急勾配
- 予算制約線の方が無差別曲線よりも傾きが(絶対値で見て)大きい
端点解② 横軸上に最適消費点
ポイント
横軸上に最適消費点が出現する場合、端点解(コーナー解)となります。
先ほどと同じく
- 縦軸：Y財の消費量＝y
- 横軸：X財の消費量＝x
- Y財の価格＝Py
- X財の価格＝Px
予算制約線「I＝xPx＋yPy」と効用関数「U＝x＋y」から導かれる無差別曲線がグラフに描かれる。
最適消費点で「x＝0」ということは、X財を消費せずに、Y財だけを消費すれば効用最大化が実現するという事になる。
ポイント
- X財･Y財は完全代替財なので、どちらを消費しても同じ
- Y財の方が安いため（Py＜ Px）、全てY財を消費した方が良い
Y財の方が価格が安い場合「予算制約線の傾き」と「無差別曲線の傾き」は下のような関係になっています。
傾き（勾配）に注目する
ポイント
ここでは「Px／Py ＜ 1」ならば、横軸(X軸)上に最適消費点が現れるため端点解となる。
下線の部分は、下記のように表現したりします。
- 予算制約線の方が無差別曲線よりも勾配が緩やか
- 予算制約線の方が無差別曲線よりも傾きが(絶対値で見て)小さい
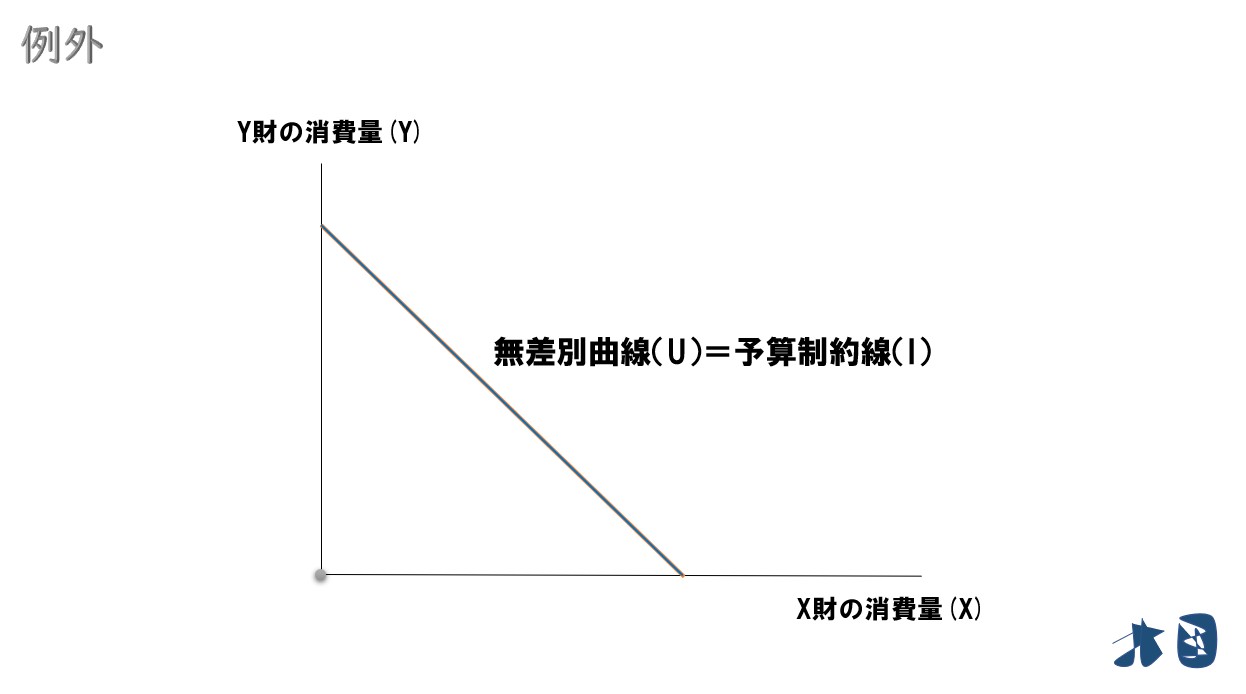
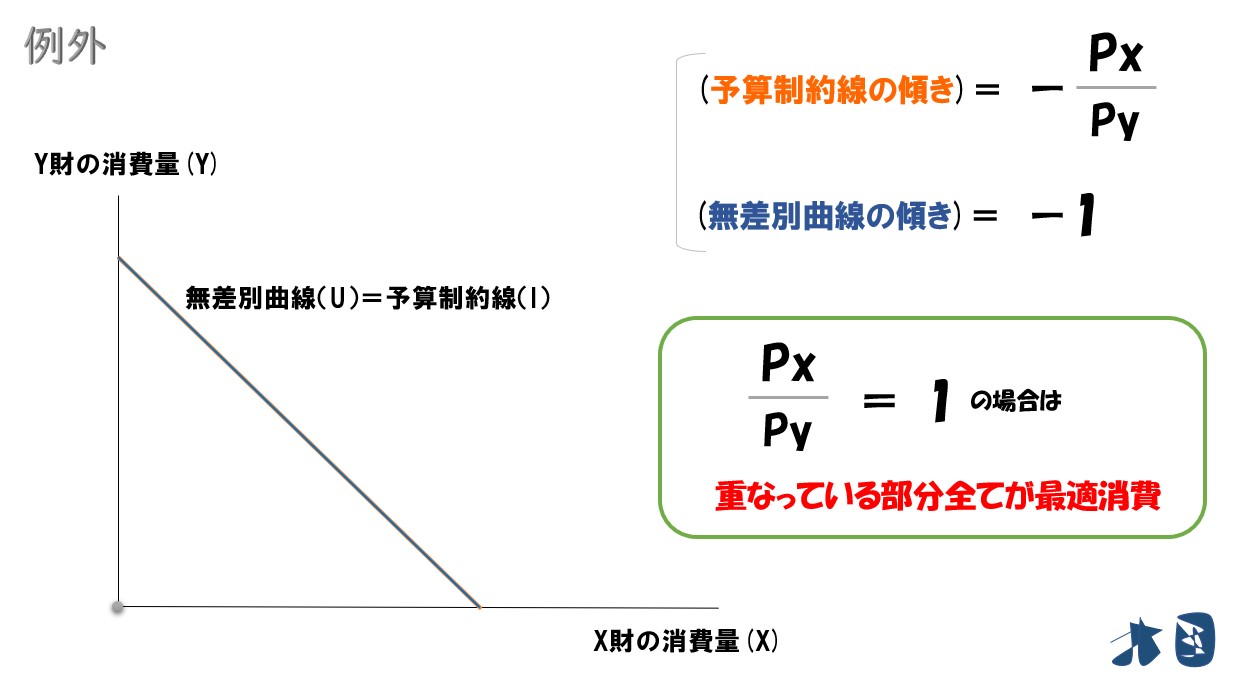
【例外】予算制約線と無差別曲線が重なる
この場合
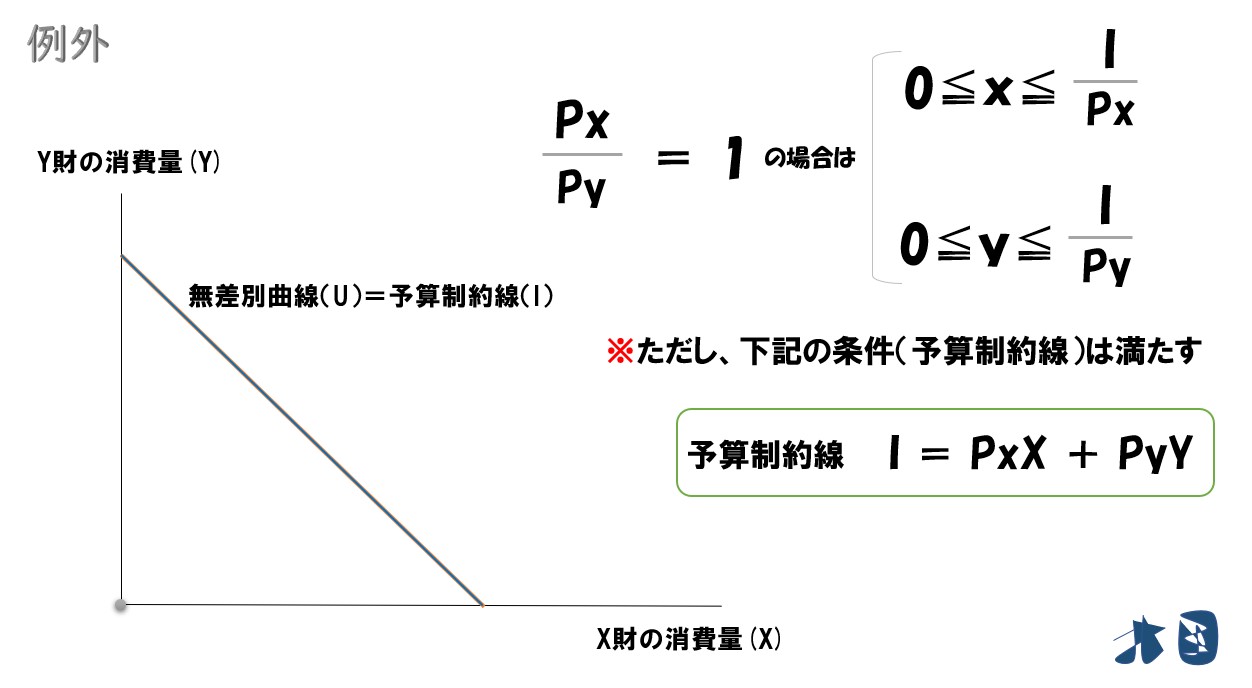
予算制約線と無差別曲線が重なっている部分は、全て最適消費が実現していると考えます。
どの点でも最適消費が実現するようなケースでは、「x」「y」の値を不等号を使って表します。
ポイント
完全代替財では、リニア型の効用関数（「U＝x＋y」などの足し算型）になる。その場合、無差別曲線が直線になるため、縦軸上 or 横軸上に最適消費点が求まる。
軸上の最適消費点は、答えに「0」が含まれるため端点解である。端点解では「加重限界効用均等の法則」「ラグランジュ未定乗数法」などが使えないため注意する。
」 端点解(コーナー解)とは？ 端点解と完全代替財 端点解とリニア型の効用 ...){kind=link}