「無差別曲線・予算制約線」や「限界効用」を使えば右下がりの需要曲線を求めることが出来ます。
- 需要曲線が右下がりの理由
- 最適消費点から求める方法
- 限界効用から求める方法
「右下がりの需要曲線」を簡単に説明した後、求め方を2つ紹介します。
「右下がりの需要曲線」の簡単な説明

右下がりの需要曲線は、大学で経済学を学んでいなくても簡単に想像できる話です。
ポイント
ある財を考えます。
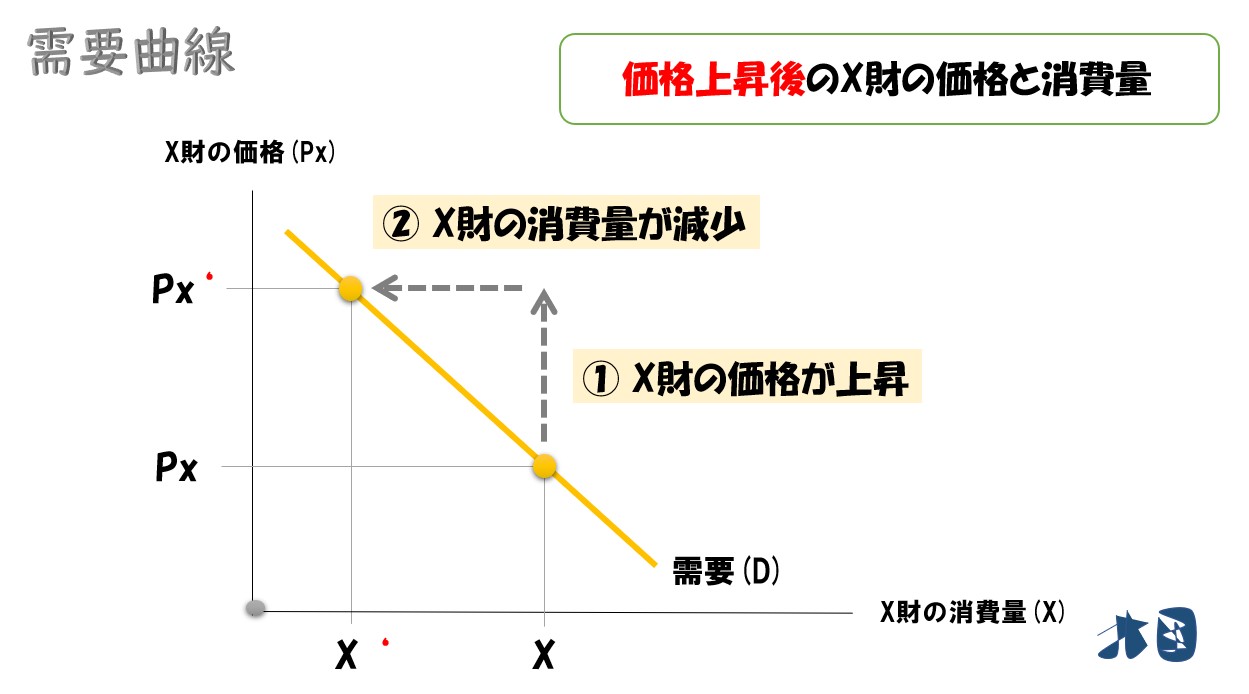
価格が高いと、その財を消費しようとする人が少ないです。しかし、価格が安くなれば、その財を消費したいと考える人が多くなります。
この関係を「縦軸に価格」「横軸に需要量」としたグラフに描けば、右下がりの曲線として描くことが出来ます。


「右下がりの需要曲線」は普通に考えれば当たり前で、高校生や初学者が需要曲線を考える分には上の説明で事足ります。
ちなみに
「最適消費点(無差別曲線・予算制約線)」や「限界効用」を使って需要曲線を求める場合もあります。これは、その項目(最適消費・限界効用)をしっかりと理解できているか?を含めて問われているため、単純に需要曲線が云々だけではありません。そもそも各項目を理解していないと需要曲線の話なんて出来ないからです。
ここからは、大学で経済学を勉強しているような人向けに、需要曲線の求め方を2パターンまとめています。
① 最適消費点を使った需要曲線の導出
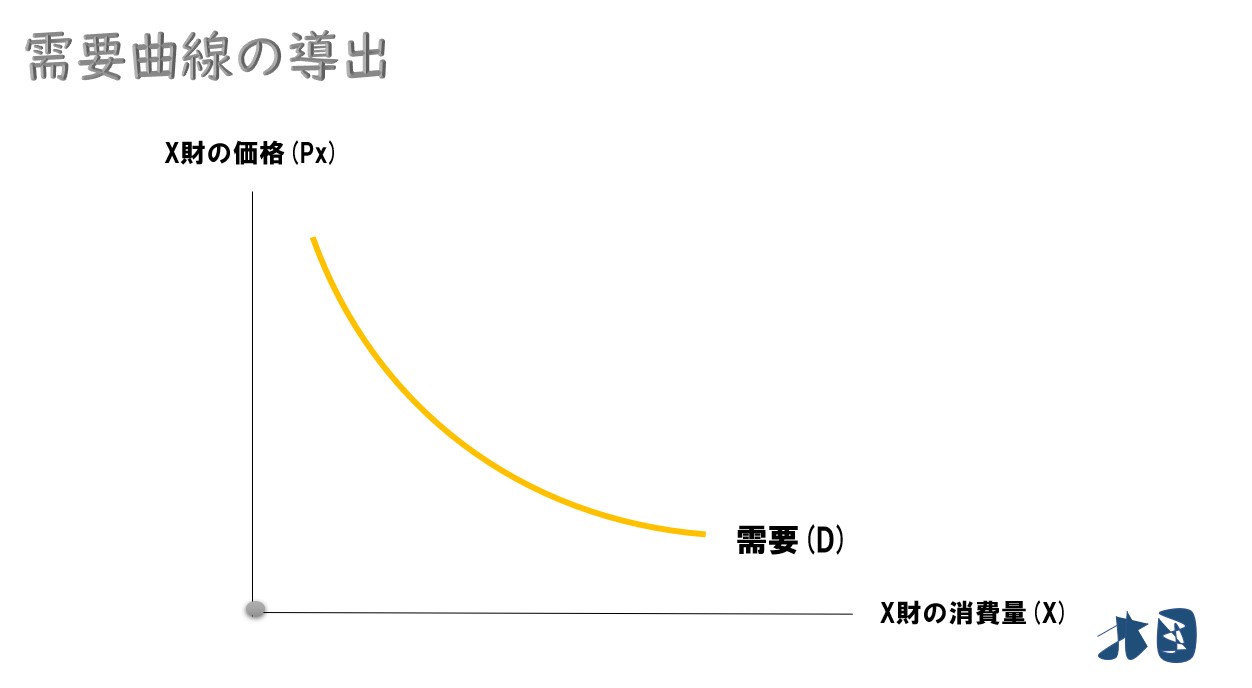
需要曲線とは
ある財の価格と消費量を対応させた曲線のこと。ミクロ経済学では「最適消費点」を使って需要曲線を求めることが出来る。


ポイント
需要曲線を言葉で説明するのは簡単ですが、最適消費点を使うことで経済学的な理由を説明できます。
なので「最適消費」までの流れを知っておくと良いです。
まずは
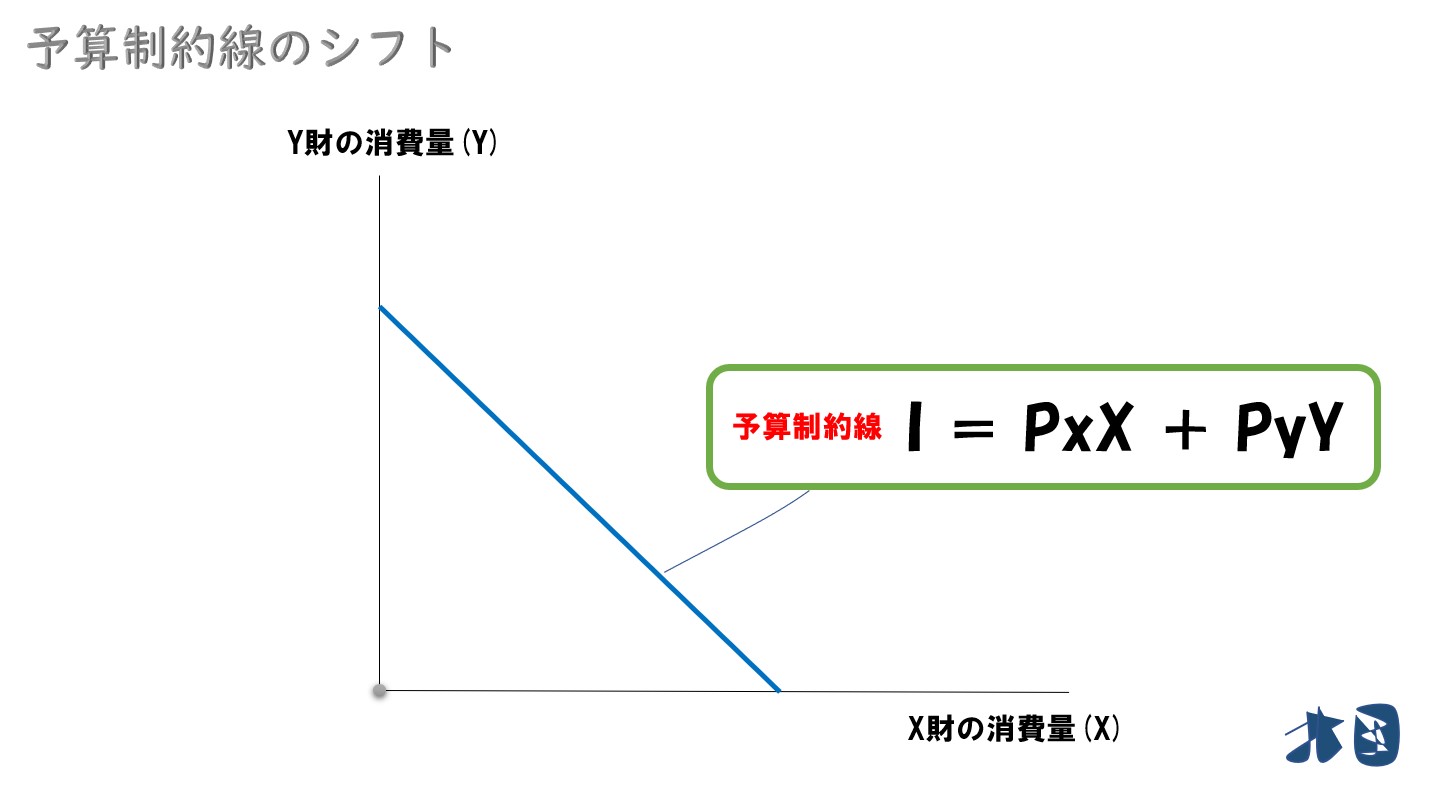
予算制約線のシフトを思い出す
- 所得=I
- X財の価格=Px
- Y財の価格=Py
- X財の消費量=X
- Y財の消費量=Y
グラフ
ポイント
X財の価格(Px)のみを変化させる。
ここでは、X財の価格が上昇した場合を考える。
価格が上昇すれば予算制約線が内側へ移動します。この話が分からなければこちらで確認⇒【予算制約線】確認する


ポイント
ポイント
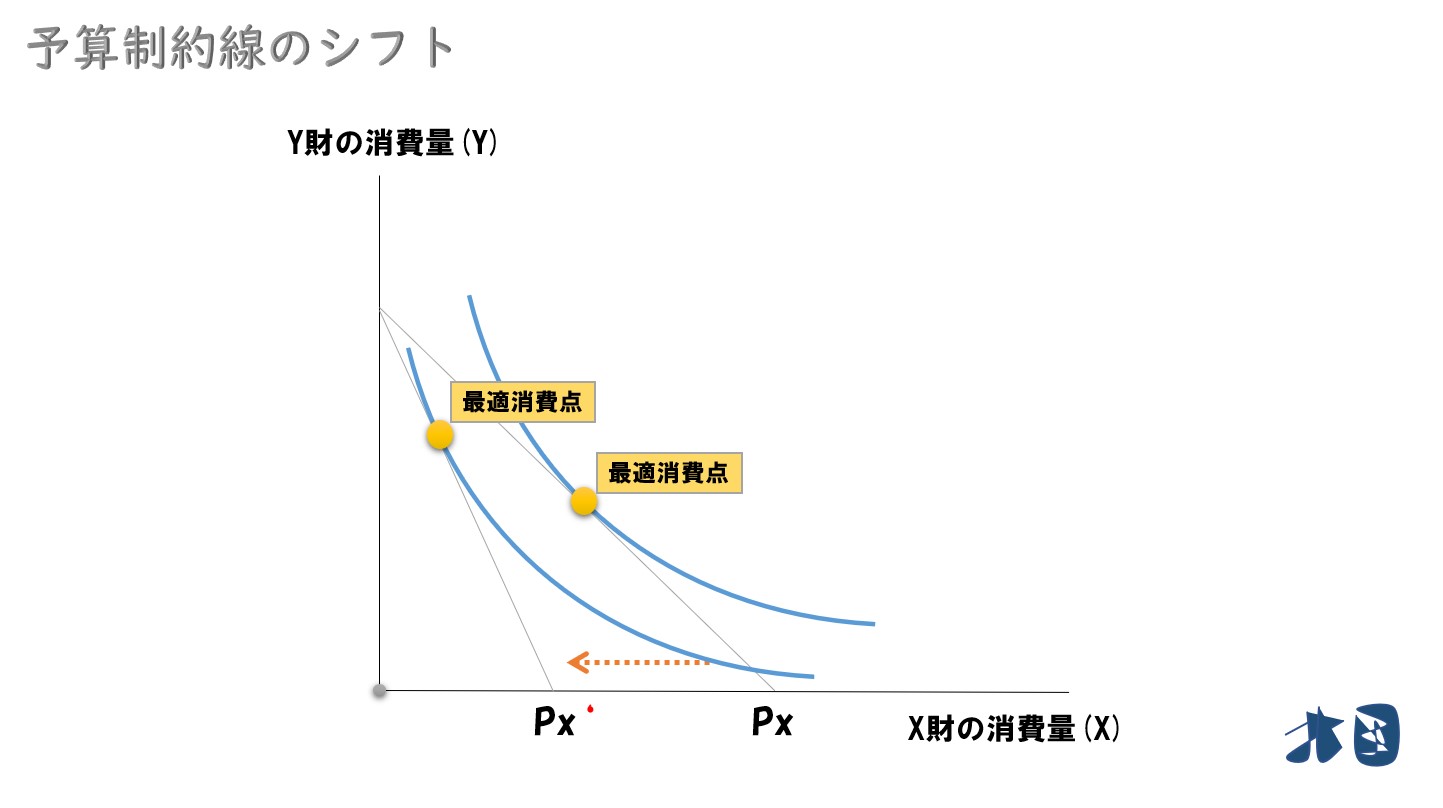
Y財価格は変わらずに、X財価格が上昇した場合、最適消費点は左側へシフトします。予算制約線が内側へ移動すれば、最適消費点は必ず左側へ移動します (グラフでは左上に移動しています)。
補足
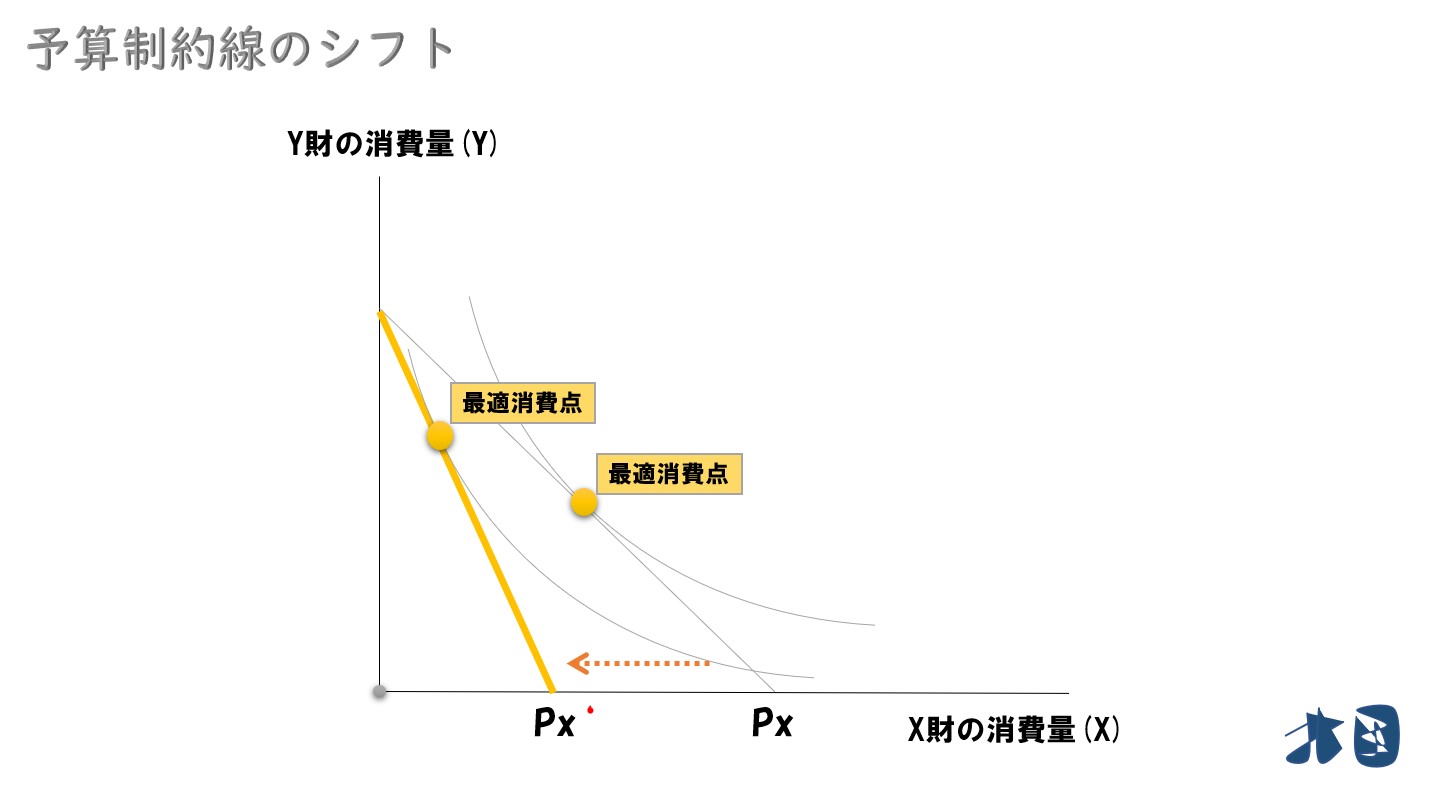
最適消費点は、予算制約線と無差別曲線の接点です。そのため、予算制約線が左側へシフトすれば、最適消費点も必ず左側へシフトします(X財の消費量が0の場合(端点解)は除きます)。
このグラフから
- 価格と消費量の関係が分かる
ポイント
X財の価格が上昇した場合(=予算制約線が内側へシフトすると)、最適消費点も内側へ移動しました。
これはX財の価格が上昇すると、X財の消費量が減ること意味しています。ちなみにX財の価格が下落すると、予算制約線は外側へシフトして、最適消費点も外側へ移動します。(X財の価格下落→X財の消費量が増加)
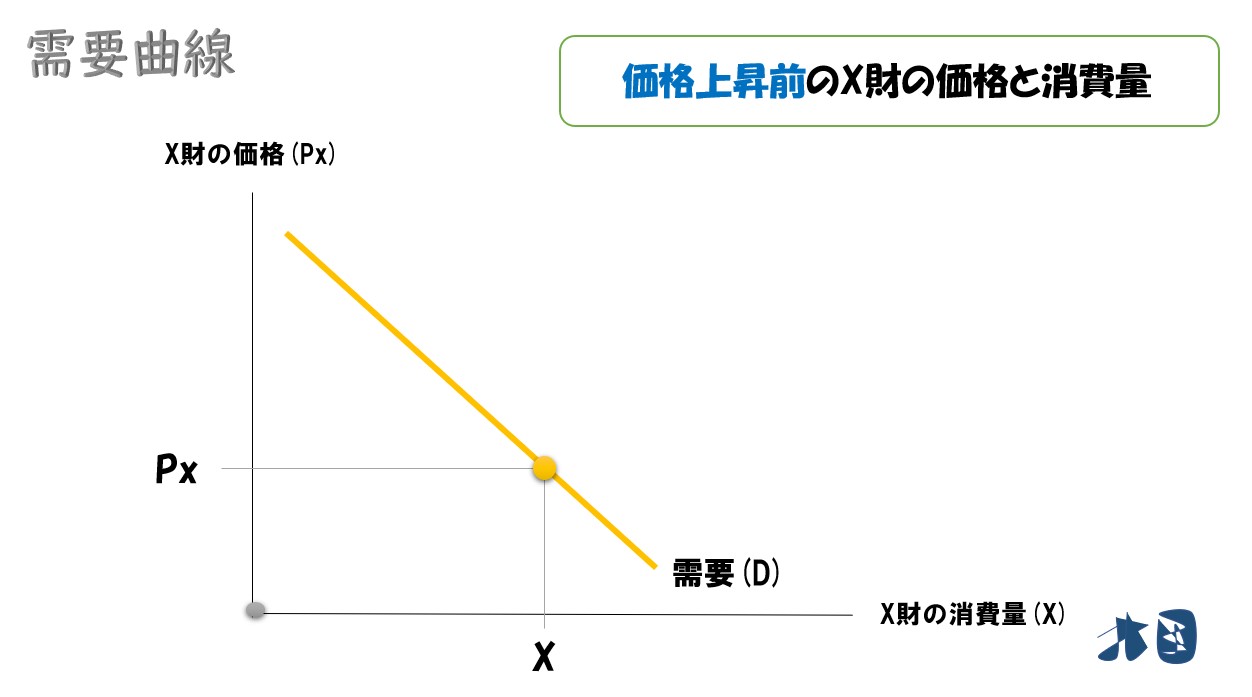
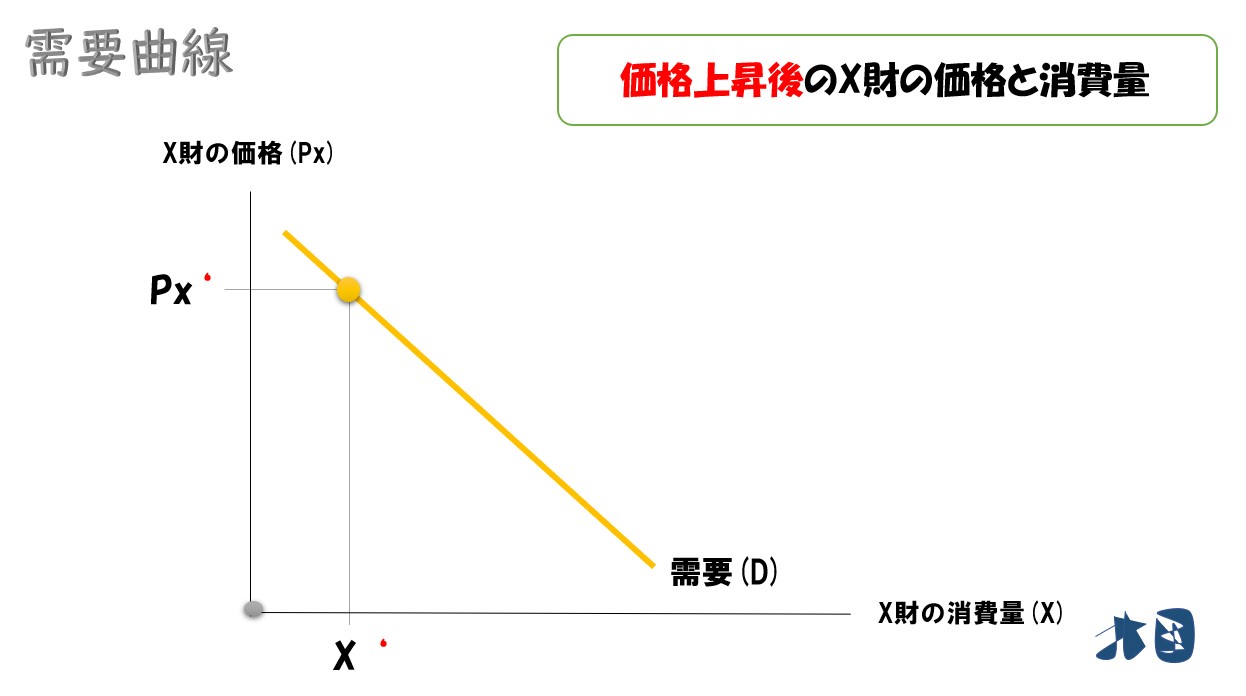
X財の価格と需要の関係を「縦軸に価格」「横軸に消費量」としてグラフを描きます


念のため
詳しく見てみます
このように、価格変化と最適消費点の移動方向を分析していくと、価格と消費量の関係を右下がりの曲線としてまとめることが出来ます。価格と消費量の関係を表した曲線なので、これを「需要曲線」と呼びます。
ここまでの流れをおさらい
① 価格が上昇(下落)
↓
② 予算制約線がシフト
↓
③ 最適消費点が移動する
↓
④ ①~③から、価格(縦軸)と消費量(横軸)の関係をまとめたグラフを作ると、右下がりの曲線が描ける(需要曲線の導出)
次に
- 個別需要曲線と市場需要曲線
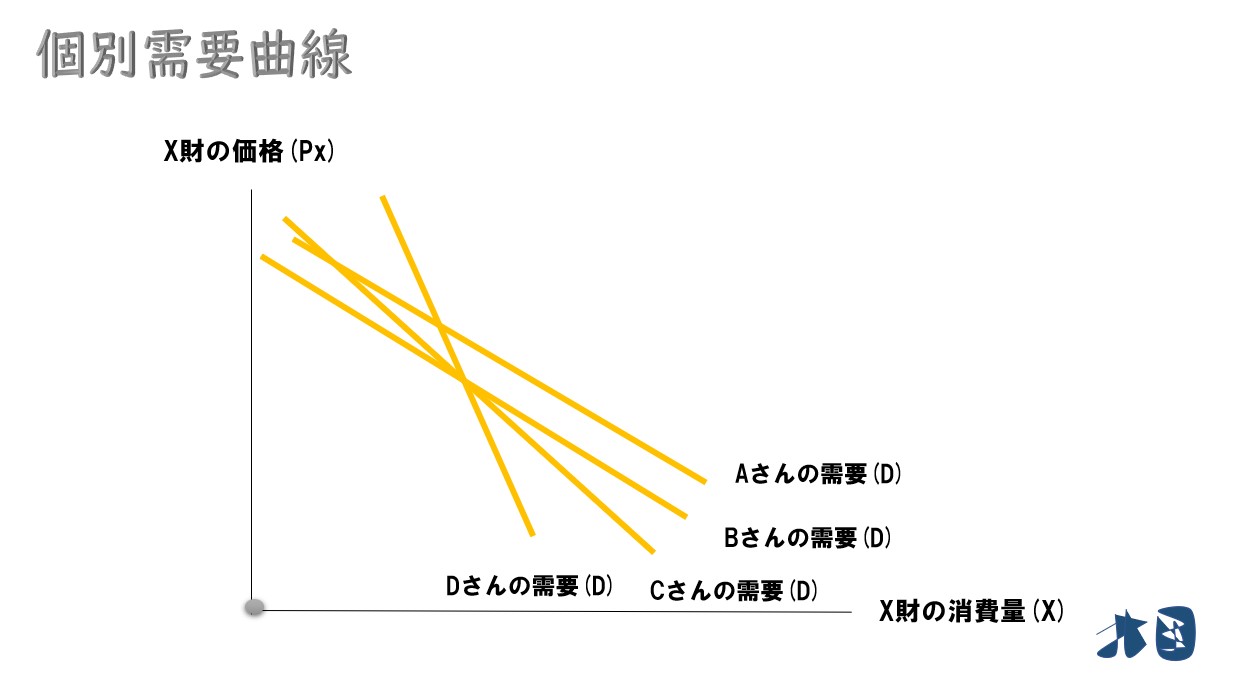
先ほどまでは、ある消費者の最適消費点をもとに需要曲線を求めました。このように、1人の消費者の需要曲線を個別需要曲線と言います。
複数の消費者の個別需要曲線を合算していきます。
よく言われる需要曲線は、個別需要曲線を無数に足し合わせた市場需要曲線のことです。
個別需要曲線→市場需要曲線という流れは飛ばされることが多いので、最終的な市場の需要曲線が、個別需要曲線の無数に足し合わせたものだ、ということだけ簡単に知っておけば十分です。


需要曲線について補足
最適消費点の関係から導き出される需要曲線は、マーシャルの需要曲線※と言います。最適消費点は、無差別曲線と予算制約線の関係から導出できますが、更に話を戻すと「限界効用・限界効用逓減の法則」が関係しています。
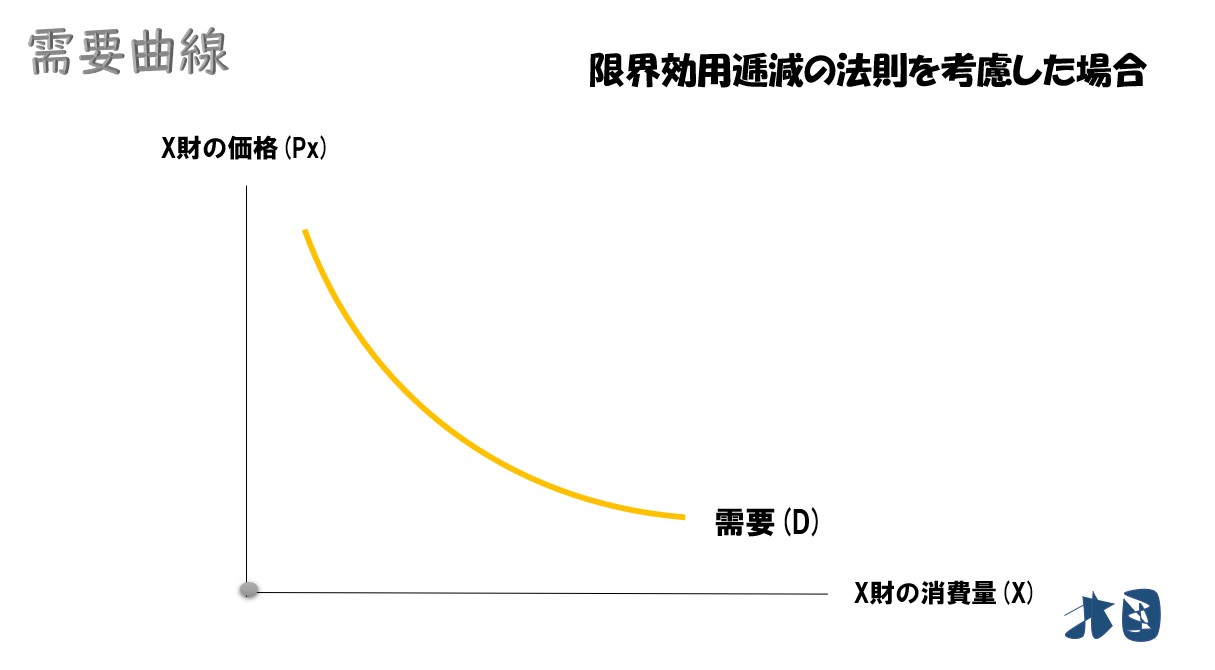
ここでは右下がりの直線の需要曲線を考えましたが「限界効用逓減の法則」を考慮すると、皆さんがイメージする需要曲線が描けます (下のグラフを参照)。
※所得を一定にして、価格変化と消費量の関係から導出した需要曲線のこと。
X財の価格が安くなって消費量が増加しても、限界効用逓減の法則により、得られる効用が減っていきます。
つまり、X財の価格が0円に近づけば、X財を消費しやすくなる一方で、得られる効用が少なくなります。その結果、効用水準を維持するために、たくさんX財を消費する必要があり、安くなればなるほど、顕著に消費量が増大していきます。
もちろん、安くなったから消費量が指数関数的に増えているとも言えますが、限界効用という側面からも説明できるので頭の片隅に入れておくと良いでしょう。
② 限界効用を使った需要曲線の導出
先ほどまでは、最適消費点を使った需要曲線の求め方を紹介しました。
ここからは
限界効用を使った需要曲線の求め方を説明していきます。
逆需要関数と限界効用
逆需要関数(逆需要曲線)
需要曲線と同じもの。
先ほどの財の価格が変化して消費量がどう変化するか?(価格(P)→需要(D))から導出した需要曲線は、通常の需要曲線です。※「D=●P+●●」という数式になる。
一方で、ある消費量(需要量)に対して価格がいくらになるか?(需要(D)→価格(P))と考えて需要曲線を導出すると逆需要関数(曲線)と呼びます。※「P=●/●D+●●」という数式になる。


まずは簡単に説明
- 自動車1台を購入するときを考える

自動車1台を購入すれば、もちろん効用が得られます。(自動車1台の購入を「財の追加的な1単位の消費」と考えれば限界効用とも言えます。)
ここで「高い効用を得られる=それだけお金を支払う価値がある」と考えます。
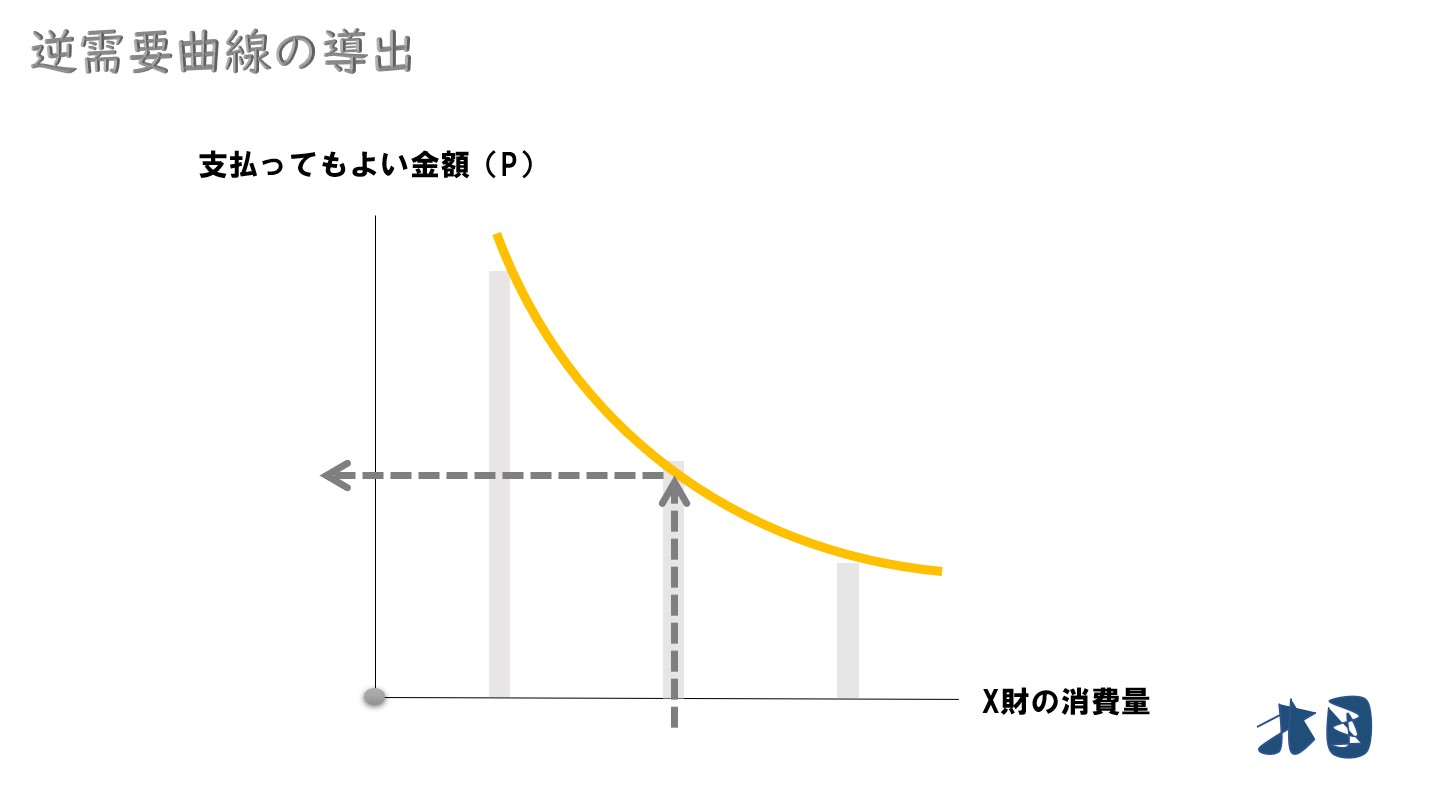
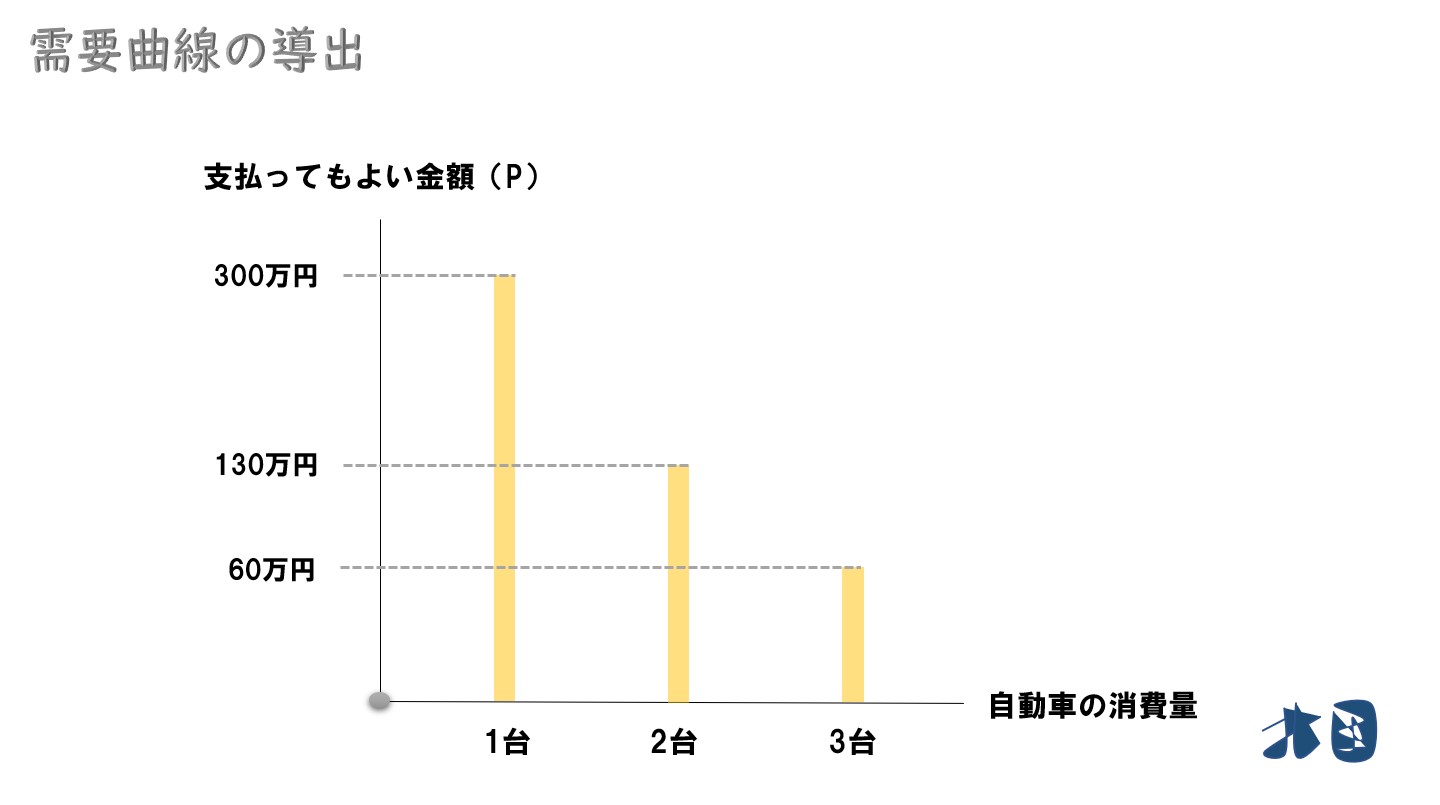
このとき、このようなグラフが描けます。
ポイント
ここで「自動車1台なら300万円支払ってもいい」と考えましたが、車を2台も3台も購入する余裕はないので、徐々に支払ってもいい金額が小さくなっていきます。
※普通に考えれば、駐車スペースにも困るので車は3台も必要ないです。なので1台当たり60万円で3台180万円くらい安くないと購入したいとは思わない、という状態を表しています。
「いくら支払っていいか?=どれくらい効用が得られるか」としていたので、限界効用逓減の法則が働いていることが分かります。


需要曲線の導出
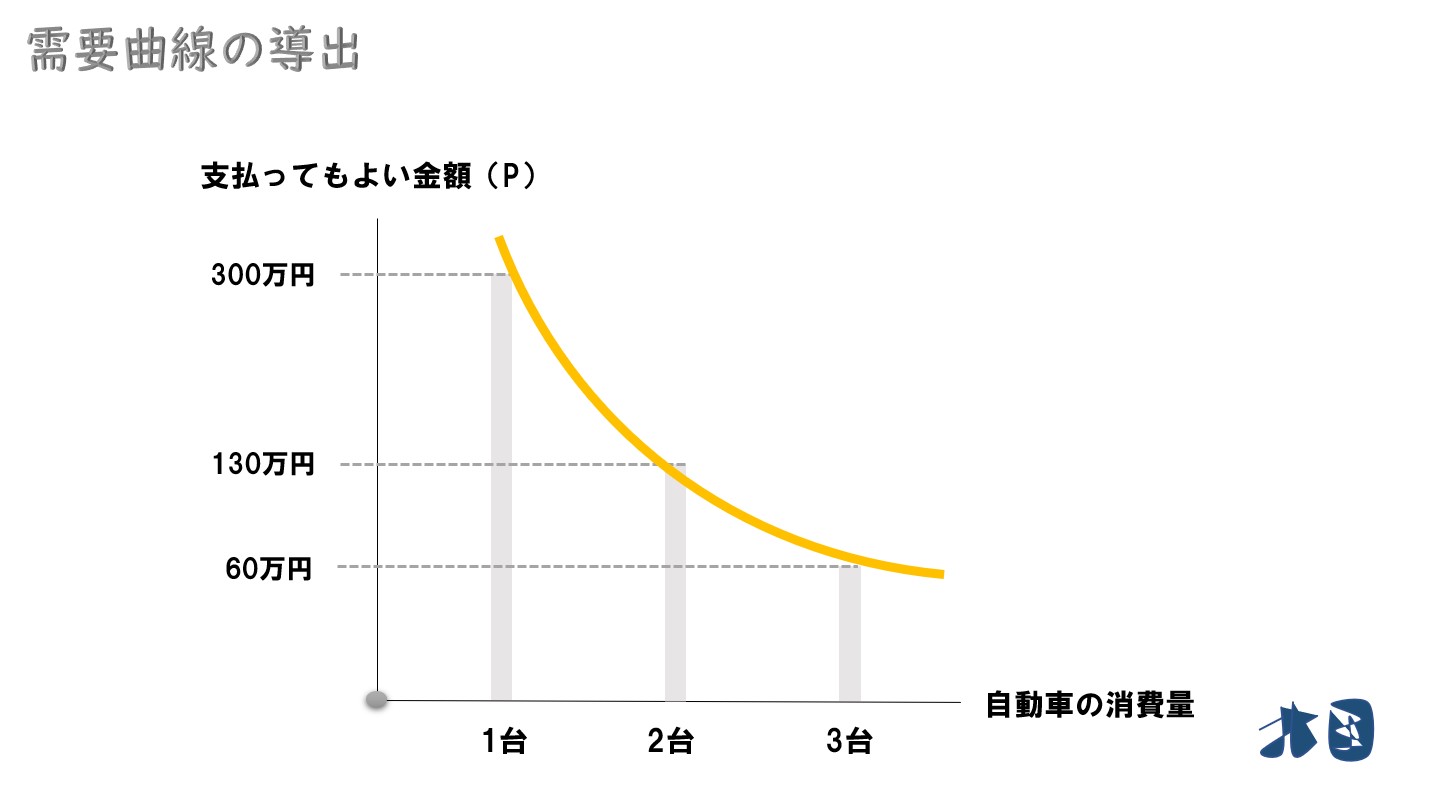
- 「車の購入台数」と「支払っても良い金額」の関係を線で結んでいく
「限界効用逓減の法則」が働くため、財の消費量が増えるにつれて、お金を支払っても良いと思う総額が減少していきます。その関係を「縦軸に価格」「横軸に需要」とすれば、右下がりの曲線が描けるのです。
この曲線は、財の価格と需要量の関係を示しているので、需要曲線と言えます。
最後に
個人の需要曲線を無数に足し合わせていけば市場全体の需要曲線が分かります。
ちなみに
「車1台なら300万円支払ってもいい(=300万円分の効用が得られる)」というのは「消費量(D)→価格(P)」という関係なので、限界効用を使って求めた需要曲線は逆需要曲線だと言えます。
「通常の需要曲線」か「逆需要曲線」なのかは、ここでは重要ではないので、あまり神経質に考えなくてもいいです。
別解
- 2財の関係を限界代替率と置くことも可能
限界代替率で考える
ここまでは「車1台なら300万円支払ってもいい」という話で進めてきました。実はこの話を「限界代替率(MRS)」と置き換えることが可能です。
ここでは、限界代替率を「2財の交換比率」としておきます。詳しくはこちら⇒【限界代替率】確認する
例えば
- X財(横軸)=自動車
- Y財(縦軸)=現金
という風に考えてみます。最適消費点上の限界代替率は「X財価格(横軸)/Y財価格(縦軸)」なので「自動車の価格/現金の価格」となります。最適消費点上で「X財・Y財の価格比=限界代替率」になる理由はこちらで確認。※本来は「マイナス」が付くが、ここでは絶対値で考える。
ここで
- 「Y財価格=現金1単位の価格」を1円とする
すると、限界代替率は「自動車の価格/1(円)」なので「限界代替率=自動車の価格」となります。
ちなみに1円じゃなくてもいいですが、ここではX財(自動車)の需要曲線を求めたいので、分かりやすく1円と置いています。


ポイント
限界代替率は2財の交換比率です。
つまり、同じ効用を得るためには、自動車と現金をどのレートで交換すれば良いか?を表しています。
先ほど「限界代替率=自動車の価格」と分かったので、2財の交換比率は、自動車の価格に依存します。
自動車の価格が300万円ならば、現金との交換比率は300万円です。


「自動車の価格が300万円ならば、現金との交換比率は300万円」の意味
凄く簡単です。
現金1単位を1円と考えた場合、限界代替率は自動車の価格になる。なので「車1台の価格が300万円」なら「現金300万円分」と交換しないと、同じ効用水準にならない。
逆に言えば、車を買う人は、車1台に300万円の価値があると思っています。なので、300万円の現金を支払って、車1台と交換します。


ここで
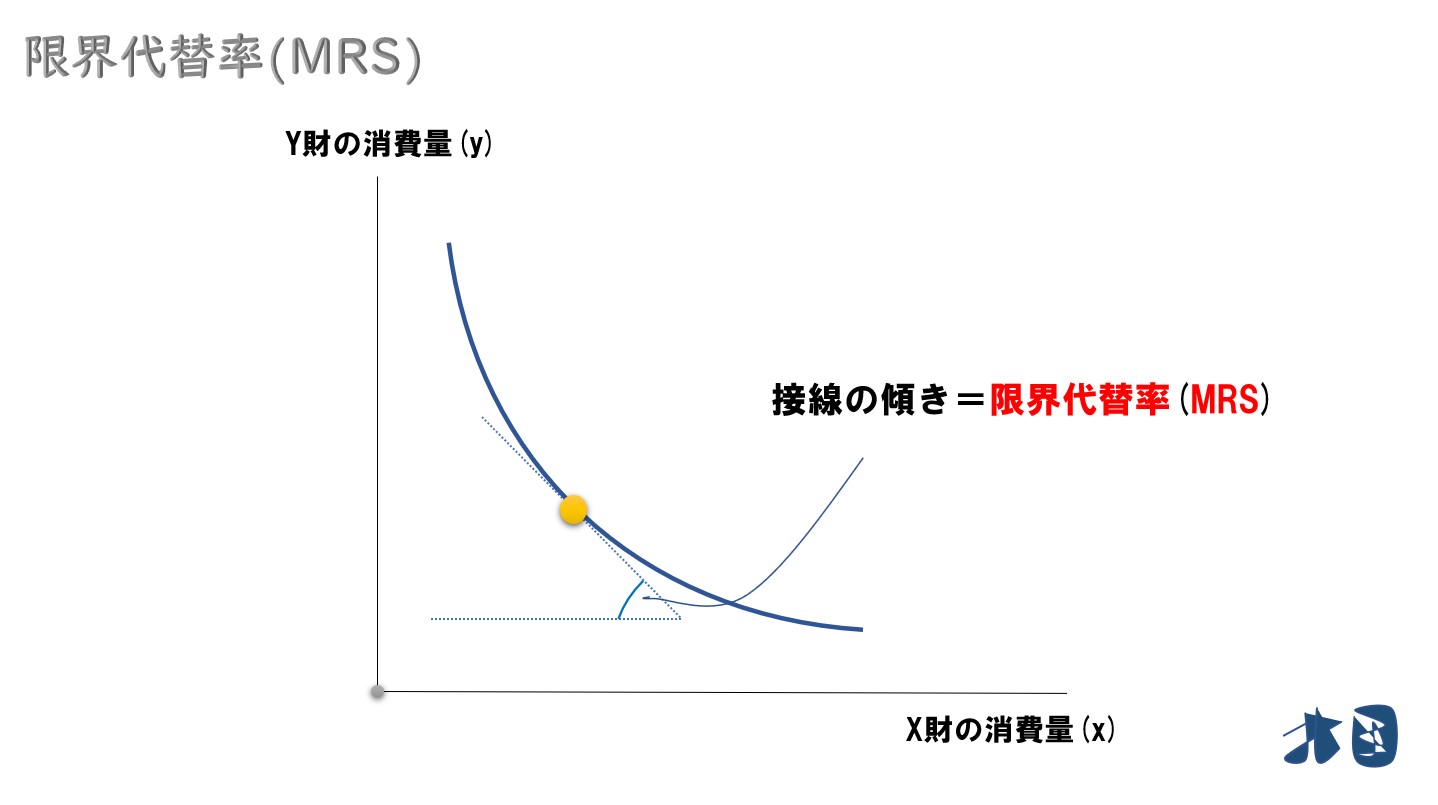
- 限界代替率のグラフを描いてみる
縦軸にY財(現金)・横軸にX財(自動車の台数)の無差別曲線から限界代替率を描きます。


ポイント
限界代替率は逓減する。(限界代替率逓減の法則)
ここまでは車1台で考えてきましたが、車3台で考えてみましょう。
限界代替率逓減の法則より、自動車の数量が増えれば限界代替率は小さくなっていきます。
最後に
そもそもX財・Y財の限界代替率を使って考えましたが、「Y財=現金」を簡単に「Y財=現金=価格(P)」と置き換えます。


さらに詳しく
限界代替率を使って需要曲線を求めることは基本的には無いと思います。教科書に「限界代替率で需要曲線を~」と出てきて混乱したら、上の話をしているんだなって思ってください。やっぱり重要なのは「最適消費点」「限界効用」から需要曲線を求められることです。そこをしっかりと押さえましょう!