利潤最大化の説明で登場する「等利潤線」
- 等利潤線とは(求め方)
- 等利潤線の式
- 等利潤線と利潤最大化
- 等利潤線と限界生産力
生産関数・利潤最大化・限界生産力との関係を含めて情報をまとめています。
等利潤線とは?求め方
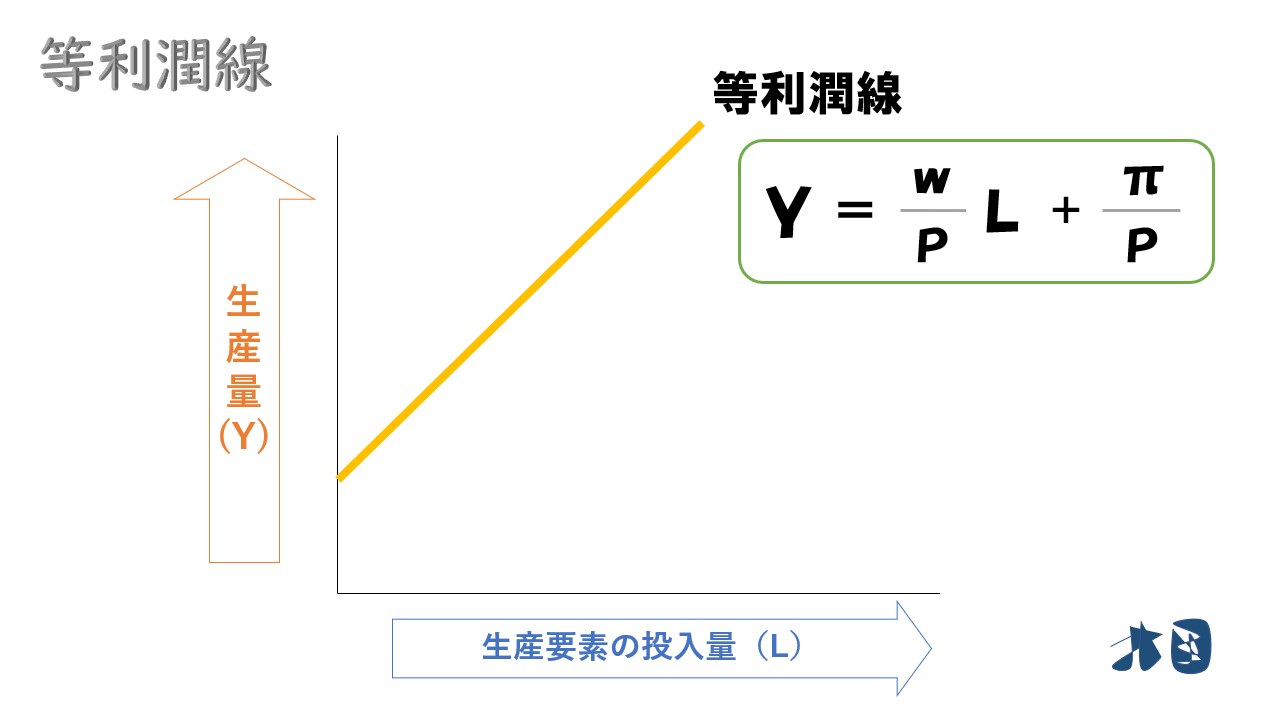
等利潤線とは
縦軸=生産量・横軸=生産要素の投入量を取るとき、利潤の関係を表した直線のこと。
ここでは、ロビンソン・クルーソー経済で登場する等利潤線とは区別してまとめている。


例えば
- 利潤=π
- 生産量=Y
- 販売価格=P
- 労働投入量=L
- 賃金=w
このとき、利潤(π)は次の式で表される。
利潤(π)=(総収入)-(総費用)
利潤(π)=P・Y-wL
この「利潤(π)=P・Y-wL」を「生産量(Y)=●●」の形にすると等利潤線となる。
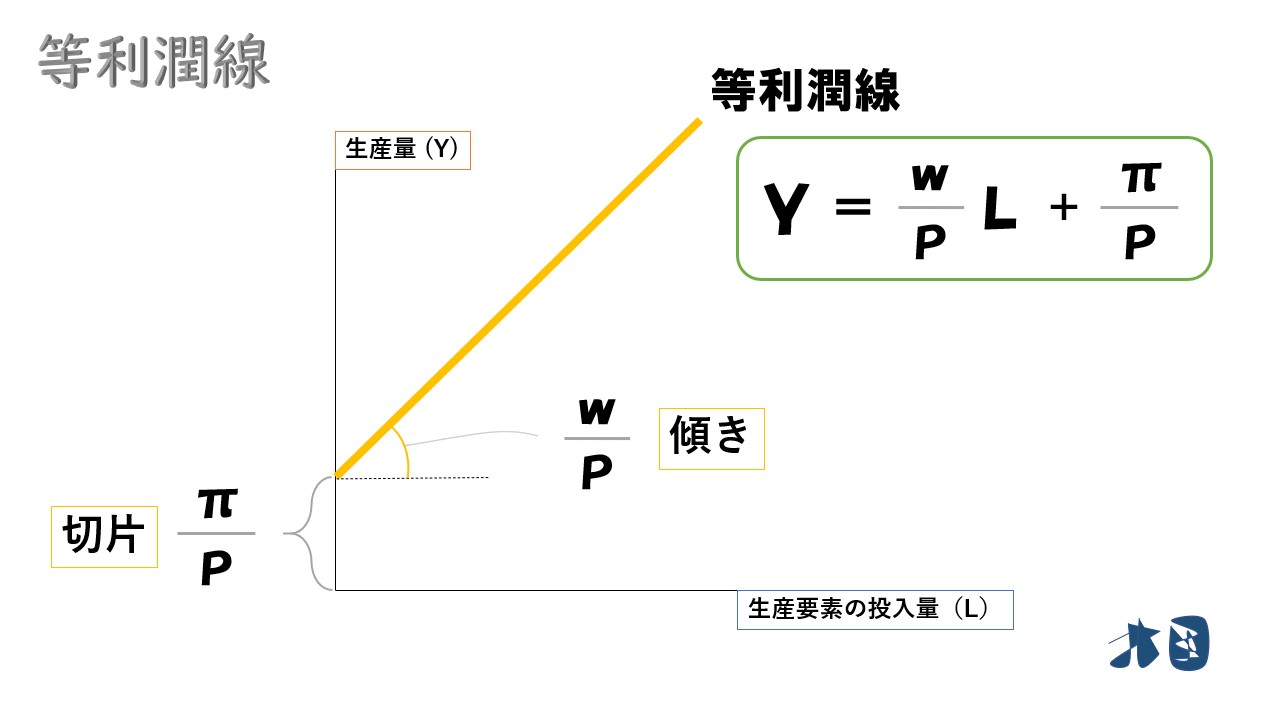
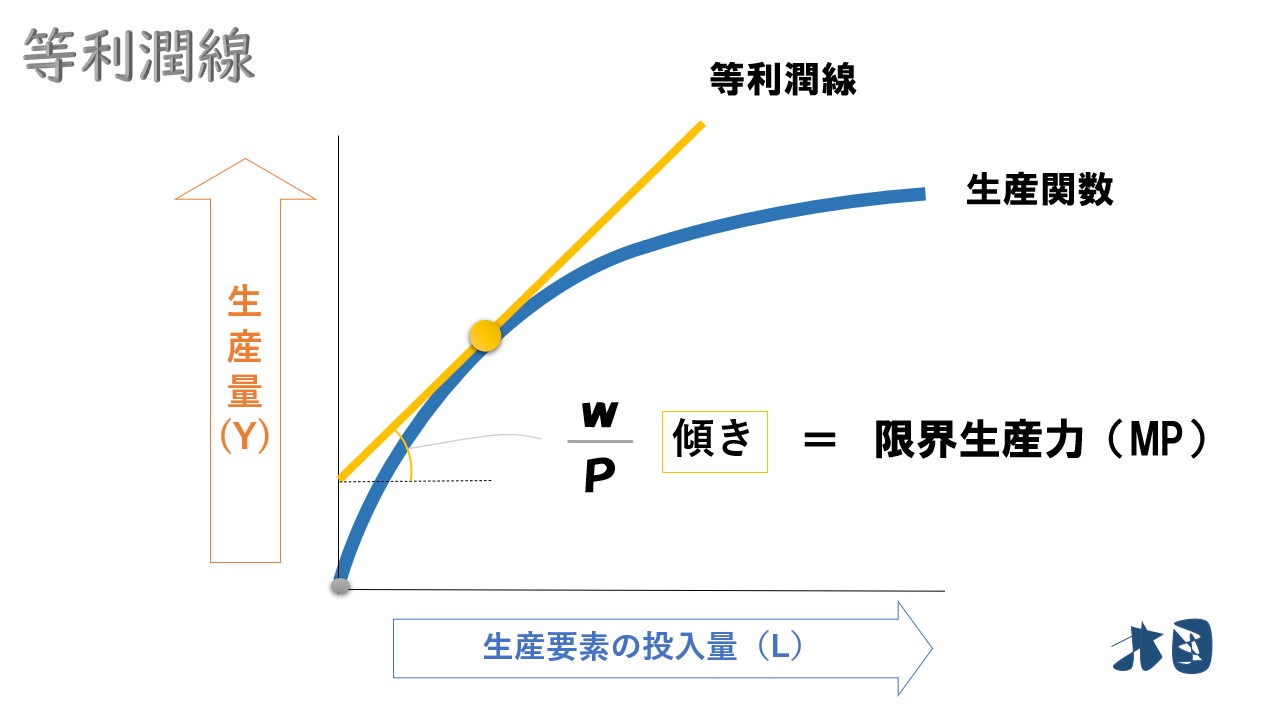
グラフで見ると‥
切片・傾きも確認


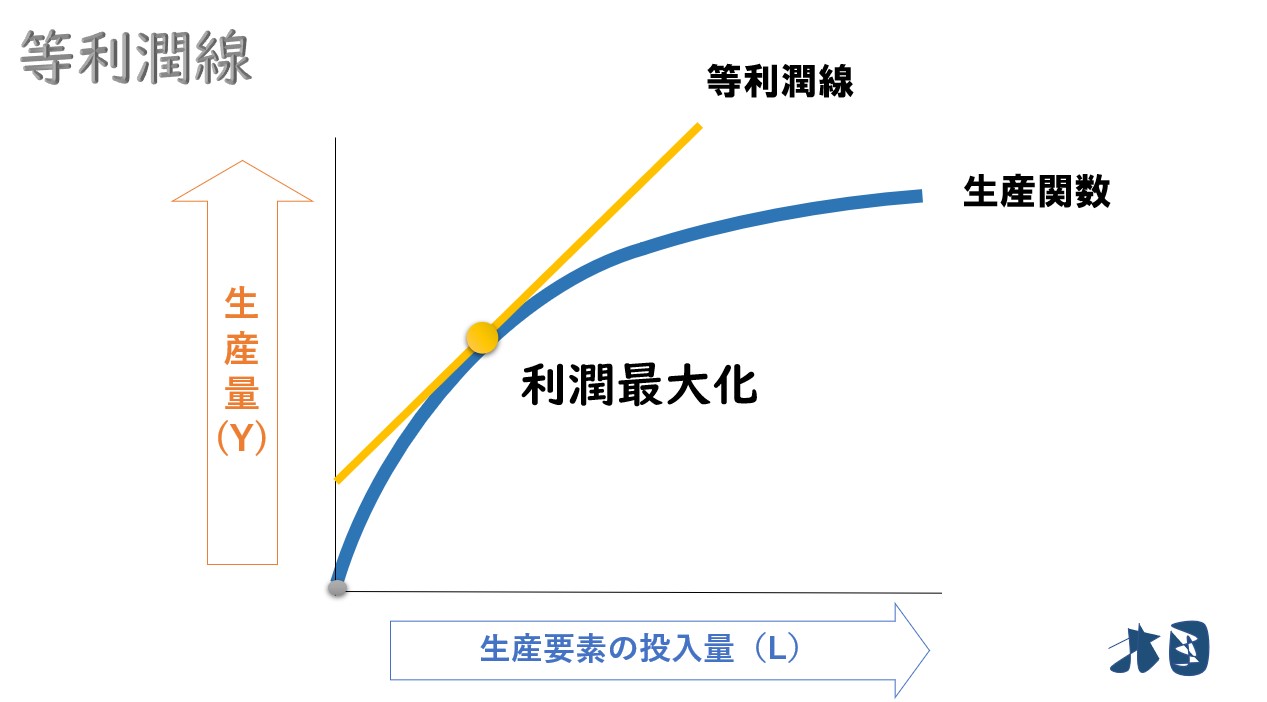
等利潤線は、生産関数との関係を使うことで利潤最大化が実現するポイントを表すことが出来ます。
等利潤線と利潤最大化
ポイント
等利潤線と生産関数の関係を使って、利潤最大化が実現する最適な投入量・生産量を表せる。
ここからは等利潤線のほかに、生産関数(Y)も重要になります。
生産関数についてはこちら⇒【生産関数】限界費用・利潤最大化・供給関数の求め方を分かりやすく
生産関数は「Y=●●」という風に表されて、生産要素(労働など)を投入すると、どれくらい生産物が作れるのかを表す関数です。


初めに
商品・サービスの生産量は生産関数(Y)を使って表せます。ここで、ある生産関数(Y)が与えられているときの利潤最大化を考えます。
この生産関数(Y)で利潤最大化ポイントを探すときに登場するのが等利潤線です
等利潤線が生産関数(Y)に触れるところが、実現可能な利潤を表しています。このとき実現する利潤=利潤最大化となります。
それ以外では利潤は最大化しないの?
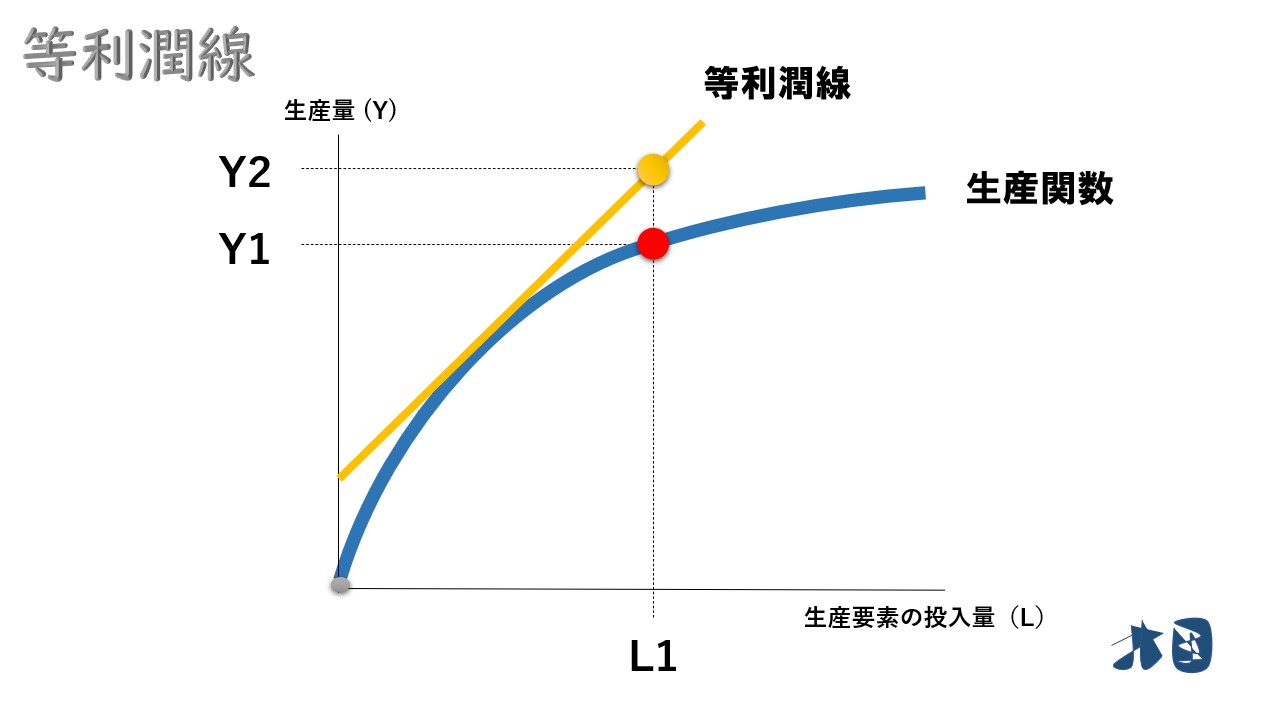
等利潤線と生産関数(Y)が触れていないケースを考えます。
いま、労働の投入量が「L1」だったとき、等利潤線には届かない部分で生産量「Y1」が決まります。
ここで、等利潤線の情報から「労働の投入量がL1だった場合、Y2の生産量がないと利潤の水準を維持出来ません」
つまり
等利潤線が求める生産量を実現できない労働の投入量・L1は非効率ということになります。
ここで
等利潤線は、同じ線上なら利潤の額は変わりません。
同じ利潤を得るなら、実現可能な労働の投入量(L)にした方が当然良いわけです。
労働の投入量(L)を減らせば…
等利潤線が求める生産量を得られる労働の投入量・L*のとき、実現可能な利潤となり、利潤最大化となります。


等利潤線と利潤最大化の関係が分かったところで、次に、利潤最大化との関係をもう少し深く見ていきます。
等利潤線と限界生産力(MP)
ポイント
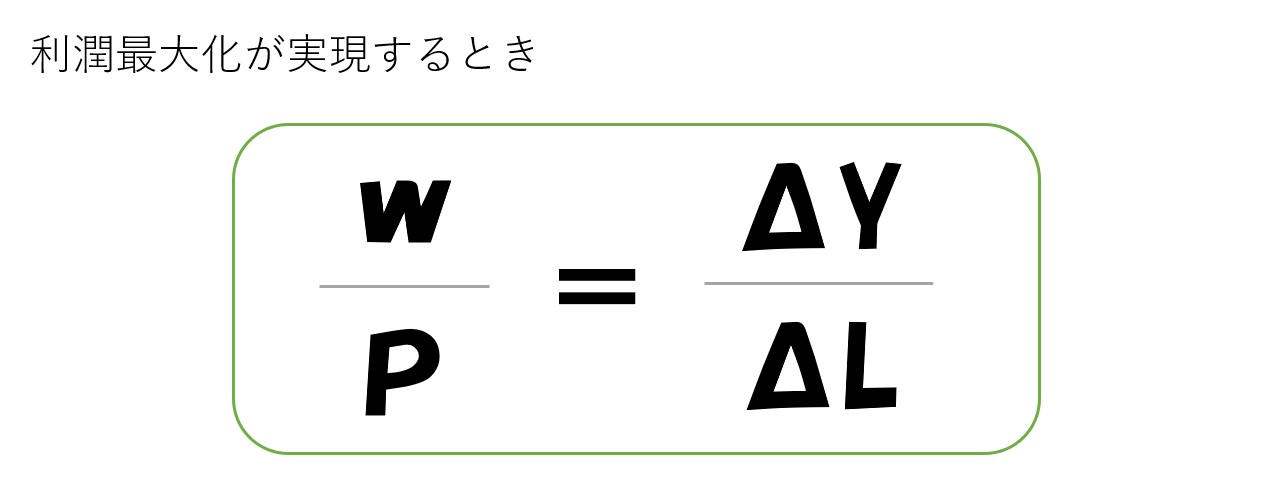
利潤最大化が実現するポイントでは、等利潤線の傾きと限界生産力(MP)が一致する。
ここからは等利潤線のほかに、限界生産力(MP)も重要になります。
限界生産力についてはこちら⇒【限界生産力・限界生産力逓減の法則】求め方・収穫逓減は当てはまらない?
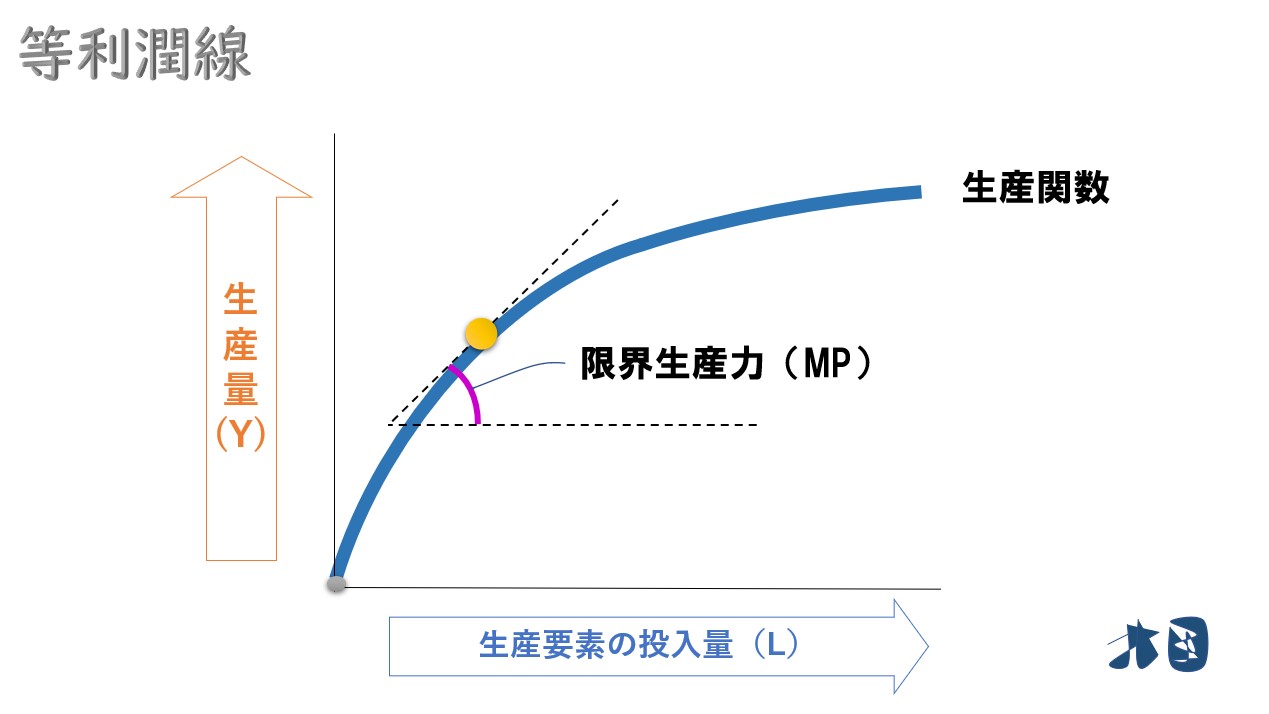
限界生産力は、生産要素を1単位追加的に投入した場合の生産量の増加分のこと。つまり、生産要素(労働など)を投入したときに、どれくらい生産量を増やすことが出来るかを意味する言葉です。
重要
限界生産力(MP)は、生産関数(Y)を微分すると求められる
生産関数と限界生産力の関係についてはこちら⇒【限界生産力・限界生産力逓減の法則】求め方・収穫逓減は当てはまらない?


限界生産力のグラフを見る
生産関数(Y)の傾きを求める(微分する)と限界生産力になります。
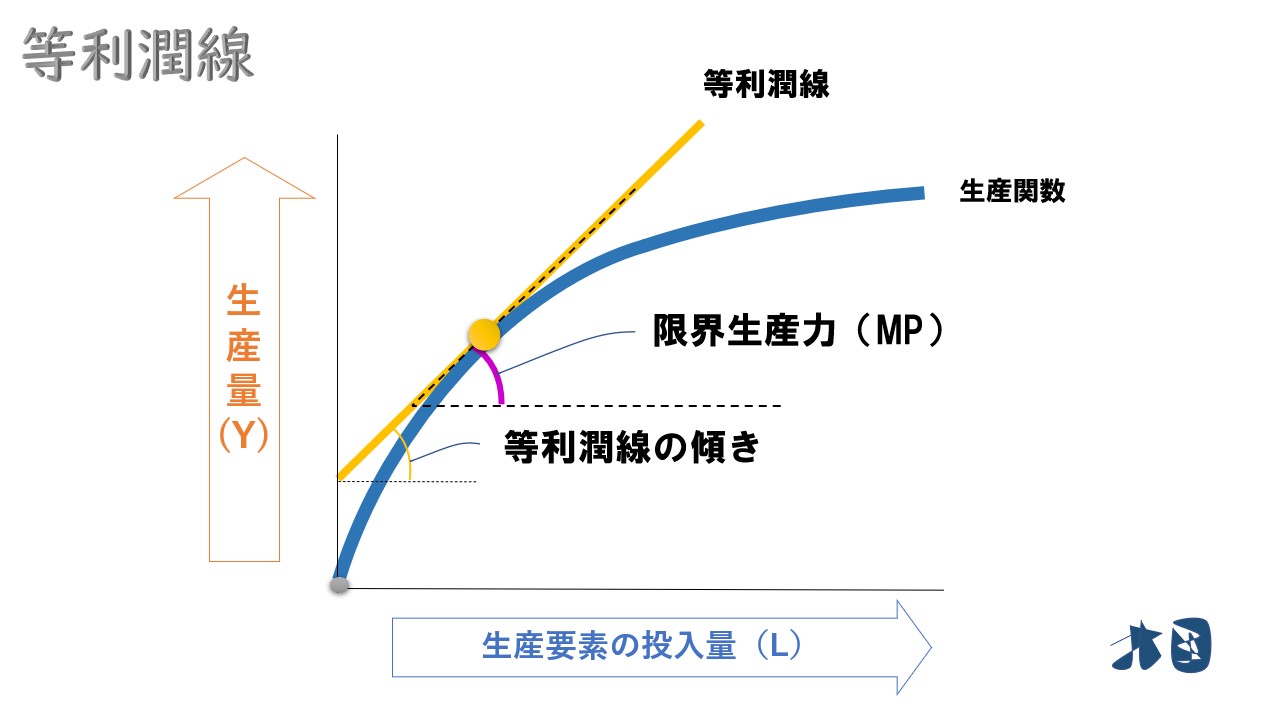
等利潤線の傾きを重ねる
等利潤線の傾き=生産関数の接線の傾き=限界生産力
つまり
利潤最大化するポイントでは「等利潤線の傾き=限界生産力」となる


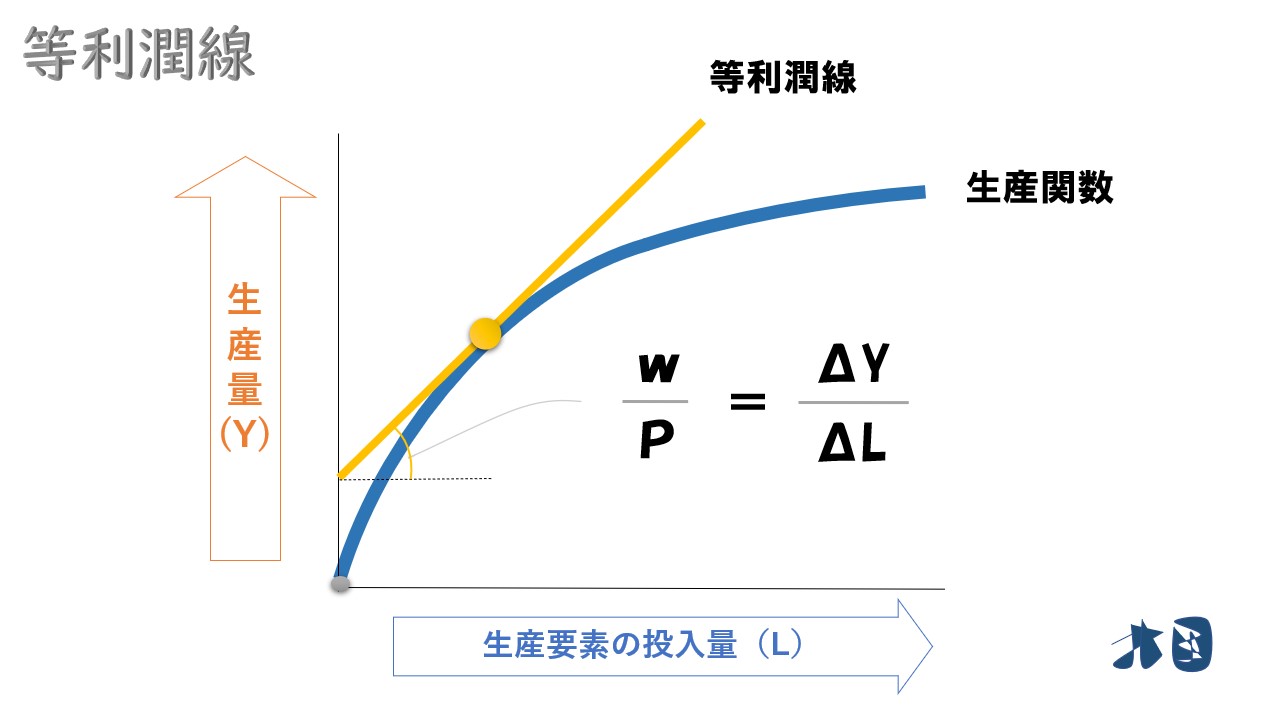
- 等利潤線の傾き=(w/P)
- 限界生産力=ΔY/ΔL
「ΔY/ΔL」は生産関数(Y)を労働の投入量(L)で微分したことを表しています。詳しくはこちら⇒【限界生産力・限界生産力逓減の法則】求め方・収穫逓減は当てはまらない?
グラフで見ると
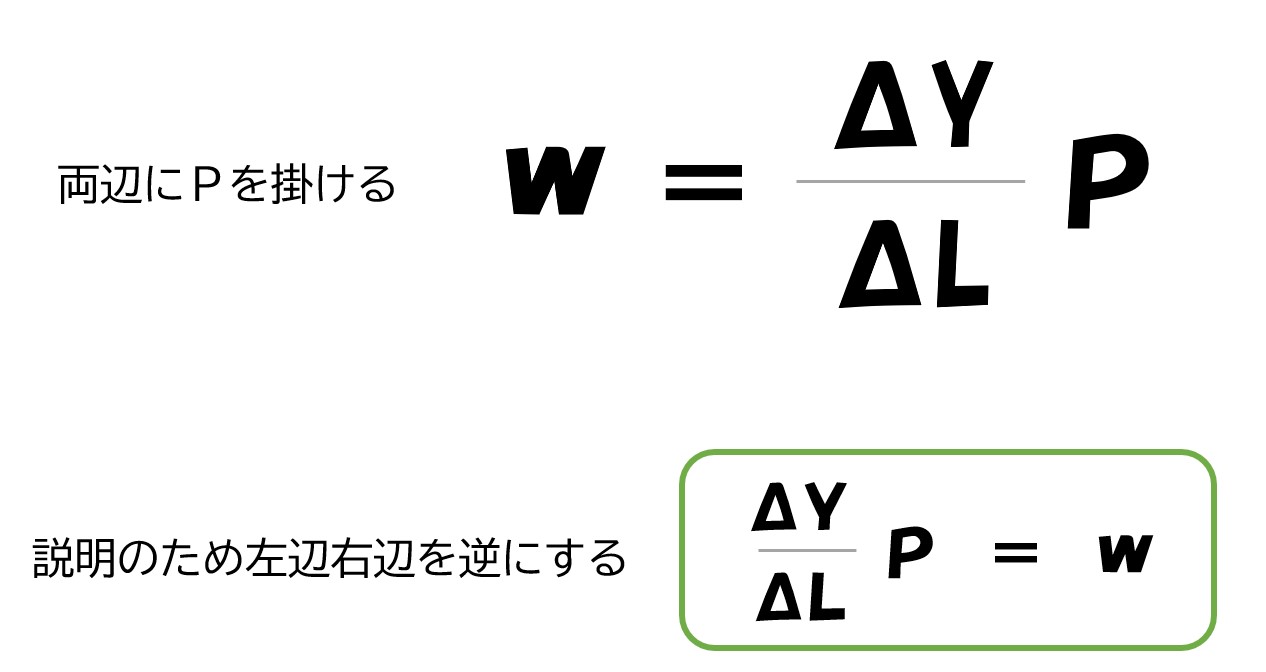
この式を変形する
ポイント
- 「(ΔY/ΔL)P=w」の意味を考える


まず
「ΔY/ΔL」が限界生産力(労働の限界生産性)を表しています
改めてですが、労働の限界生産力は「労働を投入した時に、どれくらい生産量が増えるのか」を表している。
次に
「P」は生産物(商品・サービス)の販売価格を表しています
つまり「(ΔY/ΔL)P」を言葉で説明すると‥
- 労働を投入して生産物が増加(ΔY/ΔL)
- 販売価格を掛ける(P)
ポイント
「労働の投入量によって得られた生産物」×「販売価格」なので、言い換えると「その労働の投入量には、どれくらいの金銭的な価値があるのか?」を表していると言える。
ここで
「w」は賃金を表しています
ポイント
「(ΔY/ΔL)P=w」この式の意味
全てをまとめると「その労働の投入量で得られる金銭的な価値」と「その労働の投入量で発生する賃金」が一致するとき、利潤最大化が実現する。
さらに詳しく
例えば「その労働の投入量で得られる金銭的な価値」>「その労働の投入量で発生する賃金」ならば、更に労働投入量(L)を増やして生産量(Y)を増やすほうがお得です。
逆に「その労働の投入量で得られる金銭的な価値」<「その労働の投入量で発生する賃金」ならば、労働の投入量(L)を減らさないと、費用の方が大きいため損失になります。
つまり「その労働の投入量で得られる金銭的な価値」=「その労働の投入量で発生する賃金」のとき、これ以上は労働の投入量(L)を増やしても利潤が大きくならない限界点となり、利潤が最大化することになります。
おまけ
「(ΔY/ΔL)P」を限界生産物価値と呼ぶことがあります。
限界生産物価値
限界生産力(MP)と価格(P)を掛けたものを「限界生産物価値」と言います。
「限界生産物価値」という言葉を使って次のように利潤最大化を表記することがあります。
他には‥
- 労働の限界生産物価値=w
と表記することもあります。
賃金(w)を要素価格と言います。そのため「限界生産物価値が要素価格と等しくなる時に、利潤が最大化する」と言葉で表現することもあります。
※このあたりの話は、完全競争市場での利潤最大化の説明でも登場します⇒【完全競争・利潤最大化】条件や求め方・計算方法をグラフを使って理解する