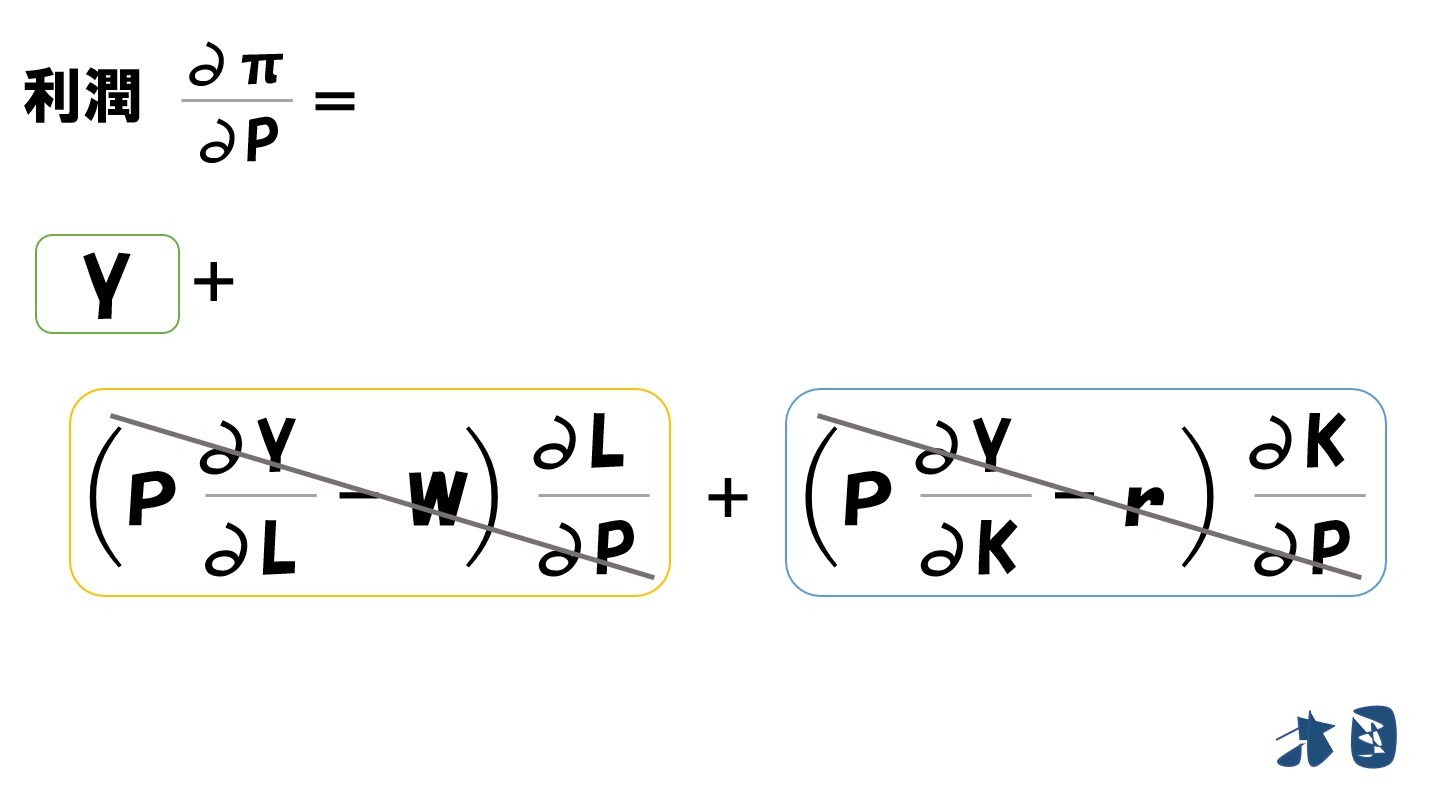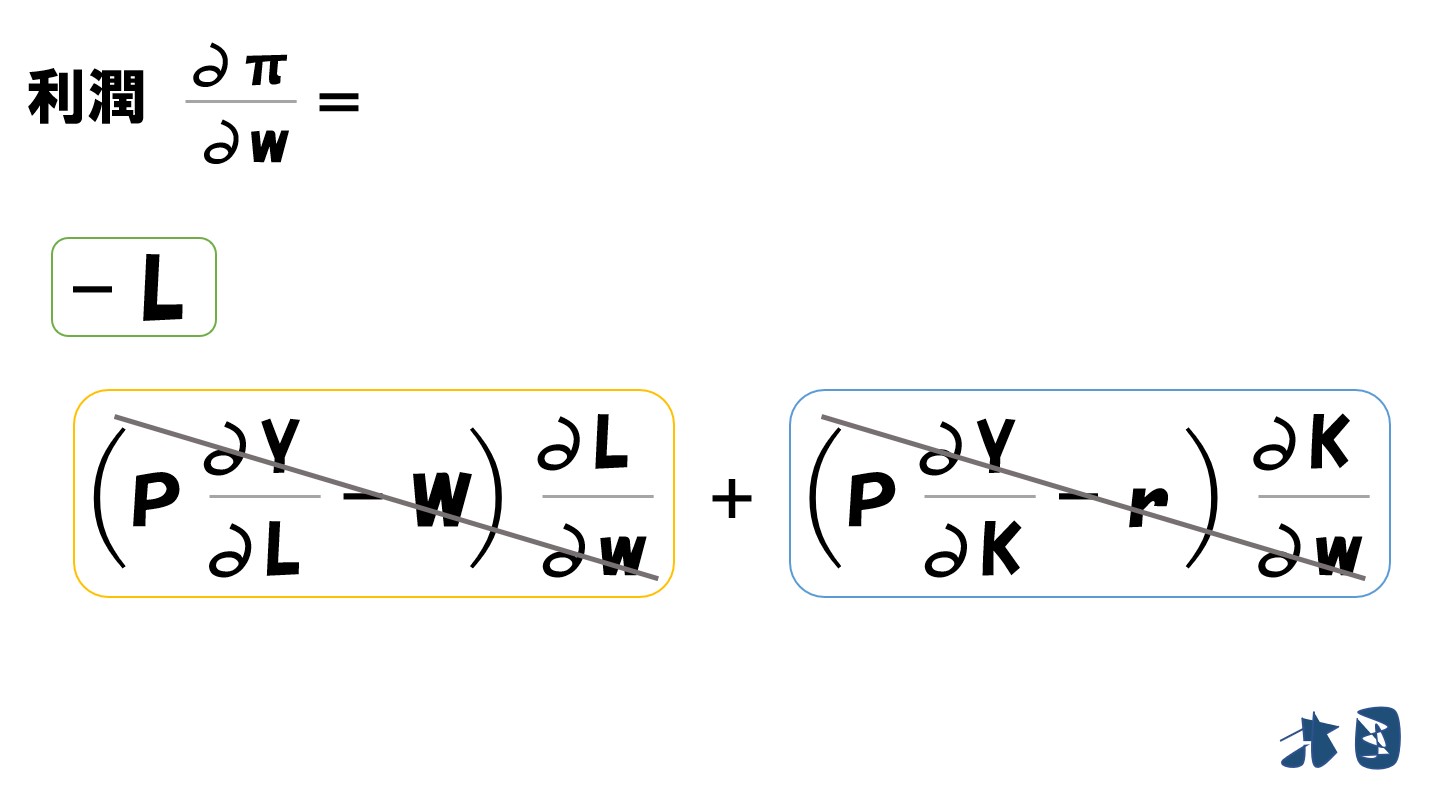【ホテリングの補題】利潤関数を微分して簡単な証明をする

2020年5月10日

中級以上のミクロ経済学で登場する「ホテリングの補題」

証明は教科書にも載っていますが、それでは理解できない人向けに詳しい説明を加えて、出来るだけ簡単な証明を行っていきます。

ホテリングの補題の簡単な証明

(Wikipediaより)

ホテリングの補題とは

利潤関数(π)を「生産物の価格(P)」で偏微分したものが「供給関数(生産量)」に等しく、「生産要素の価格(w･r)」で偏微分したものは「生産要素の投入量(L･K)のマイナス」に等しいことを証明したもの。

実際にそうなるのか確認してみます。

利潤関数(π)を「生産物の価格(P)」で偏微分

はじめに

利潤＝π
生産物価格＝P
生産量(供給量)＝Y
賃金＝ｗ
労働の投入量＝L
レンタル料＝ｒ
資本の投入量＝K

このとき、利潤を「利潤(π)＝PY－(wL＋rK)」と表せます。

確認する

まずこの2つに注目します。

労働の投入量＝L
資本の投入量＝K

利潤が最大化するときの「労働の投入量」「資本の投入量」は要素需要関数と言われています。

要素需要関数は、価格(P)･賃金(w)･レンタル料(r)の3つの文字で表記します。

すると

労働の投入量＝L(p,w,r)
資本の投入量＝K(p,w,r)

L･Kのカッコ内の（p,w,r）は、価格(P)･賃金(w)･レンタル料(r)の3つの要素で構成される(置き換えることが出来る)という意味です。

次に確認する

生産量(供給量)＝Y

利潤が最大化するときの「生産量」は供給関数と言われています。

供給関数は、生産関数に含まれるL･Kを要素需要関数に置き換えます。

すると

生産量＝Y（L(p,w,r), K(p,w,r)）

例えば「生産関数(Y)＝LK」と与えられているとき「LK」に要素需要関数を代入することで供給関数が求められます。

つまり、生産量(Y)はさきほど登場した「L(p,w,r)」「K(p,w,r)」の2つによって構成される(置き換えることが出来る)ことが分かります。

それを「Y（L(p,w,r), K(p,w,r)）」と表しています。

ちなみに

生産物価格＝P
賃金＝ｗ
レンタル料＝ｒ

この3つは、市場価格を受け入れるのでそのままです。

まとめると

利潤＝π
生産物価格＝P
生産量(供給量)＝Y（L(p,w,r), K(p,w,r)）
賃金＝ｗ
労働の投入量＝L(p,w,r)
レンタル料＝ｒ
資本の投入量＝K(p,w,r)

このとき、利潤を「利潤(π)＝P･Y(L(p,w,r), K(p,w,r))－(wL(p,w,r)＋rK(p,w,r))」と表せます。

北国宗太郎

意味は分かったけど、ごちゃごちゃしてるね‥。

ひとまず意味が分かればOKだよ。

牛さん

証明

「利潤(π)＝P･Y(L(p,w,r), K(p,w,r))－(wL(p,w,r)＋rK(p,w,r))」を価格(P)で偏微分して、供給関数になるかを確認する

注意点

微分のやり方に気を付けましょう

「利潤(π)＝PY－(wL＋rK)」なので、価格(P)で微分して「利潤(π)＝Y」とすると話が終ってしまいます。

ここで思い出すのが‥

生産量＝Y（L(p,w,r), K(p,w,r)）
労働の投入量＝L(p,w,r)
資本の投入量＝K(p,w,r)

ポイント

Y･L･Kを構成する要素にも価格(P)が含まれているため、それらも微分します。

緑丸の部分を微分します。

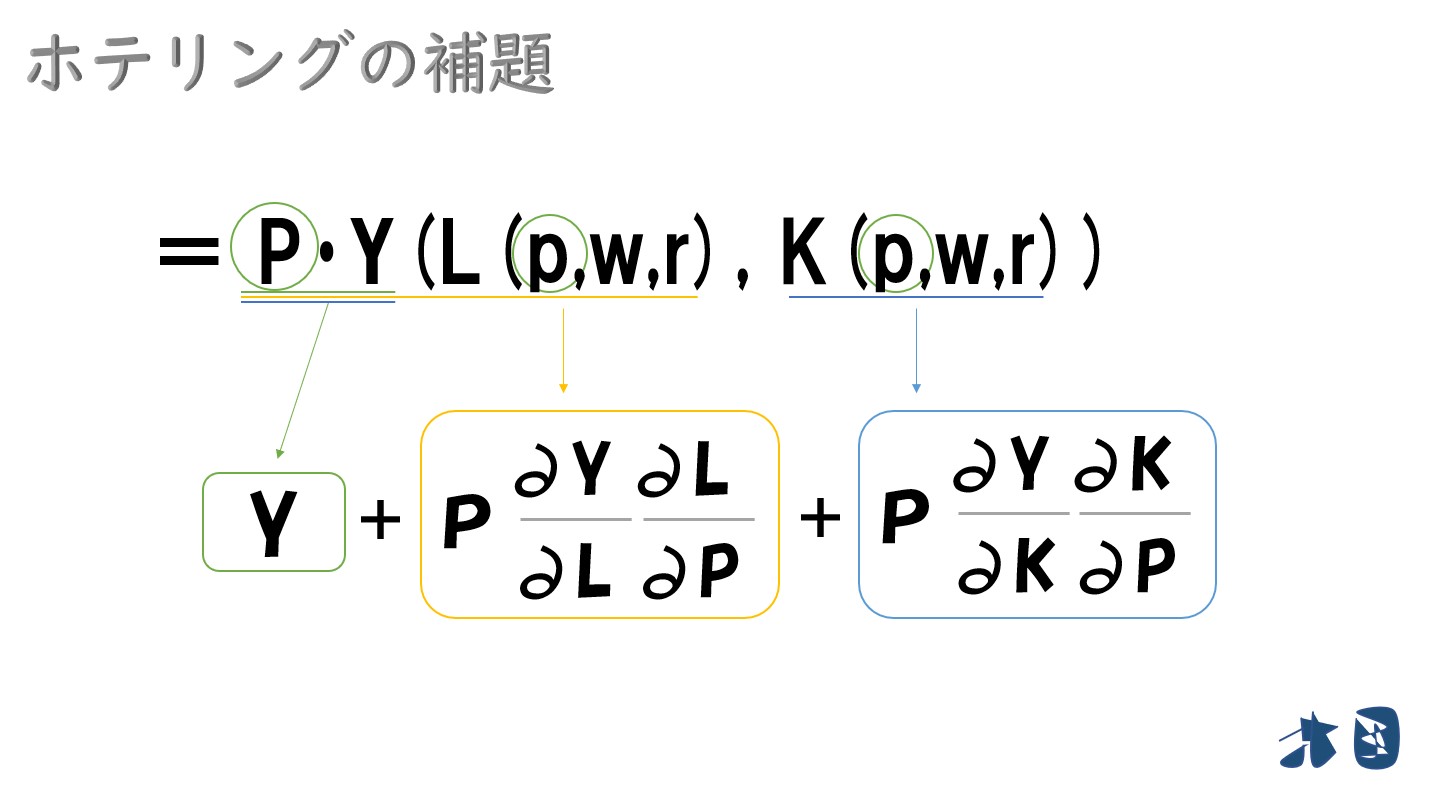
①まずは「P･Y(L(p,w,r), K(p,w,r))」の部分

「∂Y/∂L･∂L/∂P」は「∂Y/∂P」じゃないの(分母分子に∂Lがあるので消せる)？と思うかもしれませんが、この形は後で役立つのでそのまま進みます。

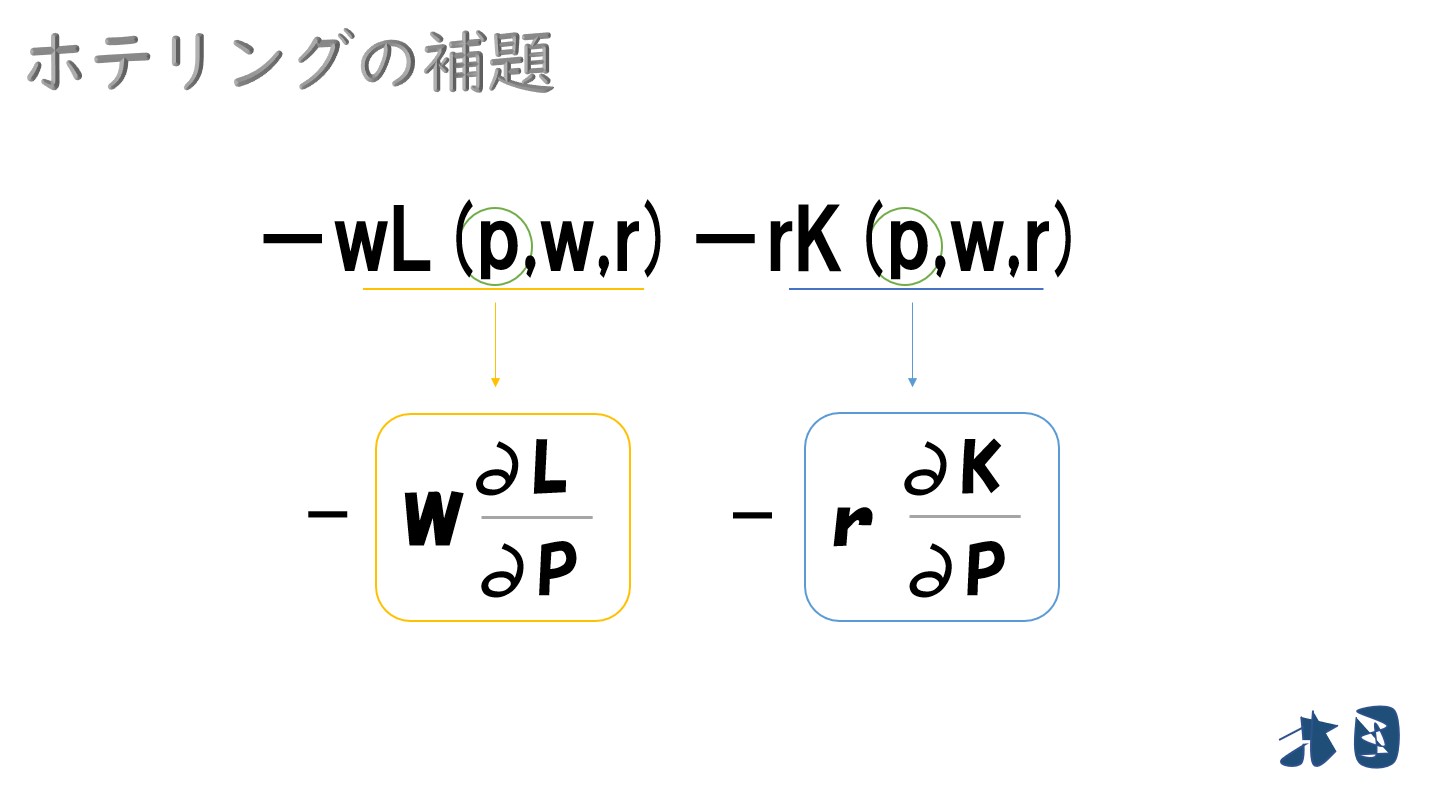
②次に「－(wL(p,w,r)＋rK(p,w,r))」の部分

まとめると

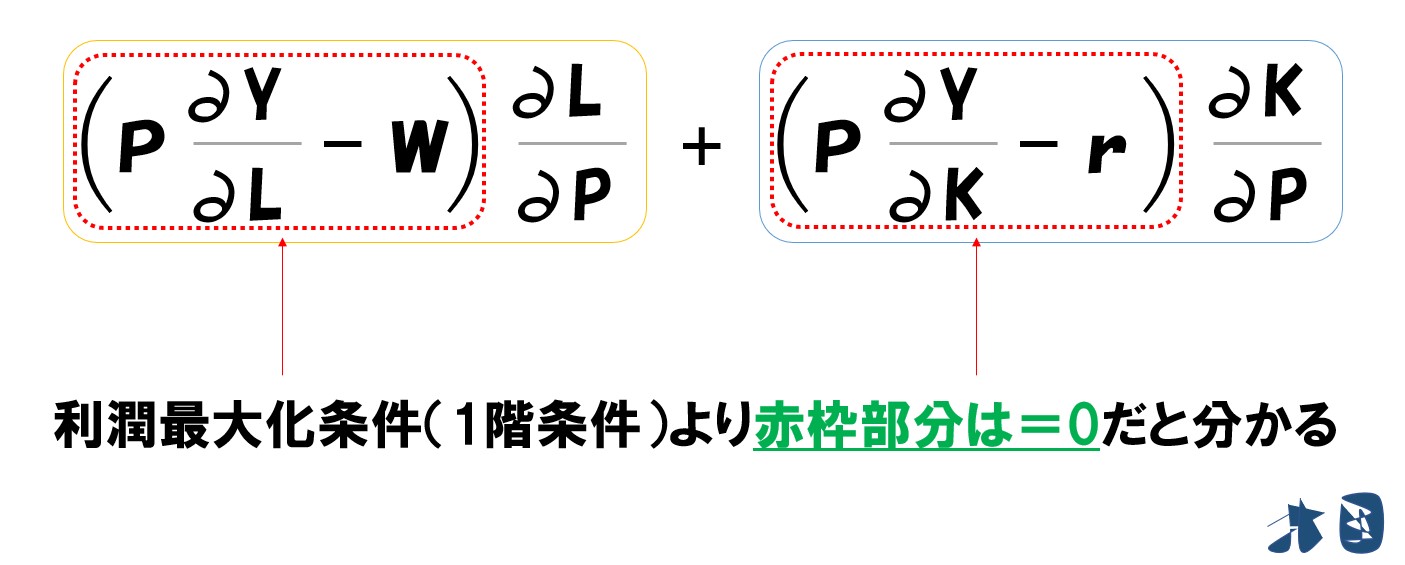
ここで黄色･青色の枠に注目します

どちらも「∂L／∂P」「∂K／∂P」が含まれているため式をまとめます。

ここに注目

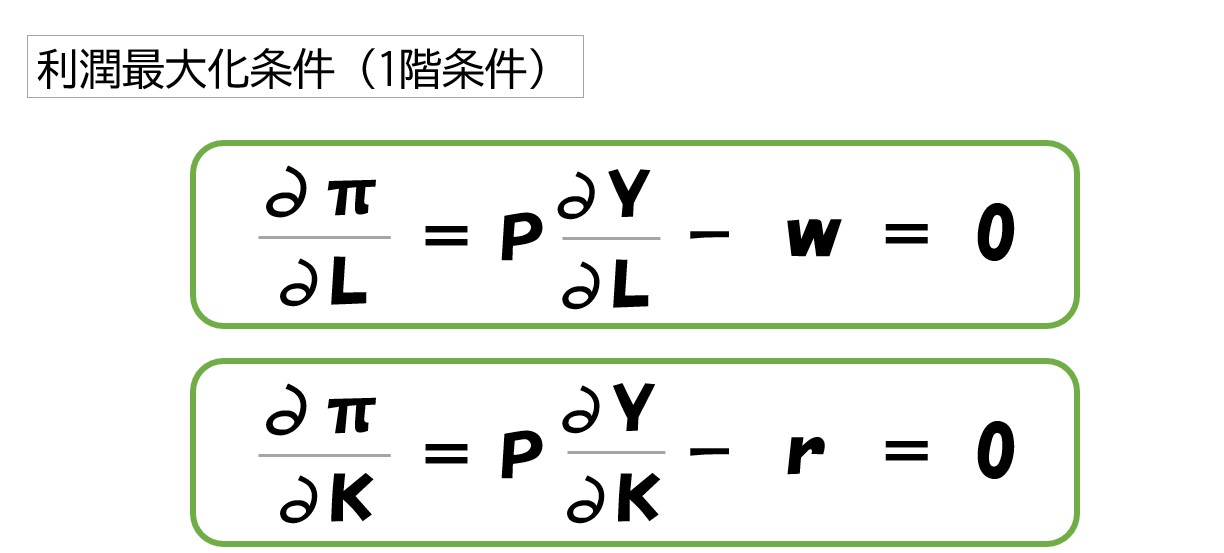
ちなみに

利潤最大化条件についてはこちらで確認してください。【完全競争･利潤最大化】条件や求め方･計算方法をグラフを使って理解する※②数式で考えるを参照

以上より

0に何を掛けても0なので、黄色枠と青色枠は消えます。

残ったのは・・

生産量(供給量)＝Yだけ！

最初に説明したとおり、この「Y(生産量･供給量)」は「Y（L(p,w,r), K(p,w,r)）」と表記できます。

今さらですが、利潤最大化が実現するときの生産量(供給量)を表しているため、これが供給関数となります。

北国宗太郎

ぶじ証明出来ました。

次は生産要素の価格で偏微分してみよう！

牛さん

利潤関数(π)を「生産要素の価格(w･r)」で偏微分

ここでは「w」で偏微分してみます

さきほどと同じ

利潤＝π
生産物価格＝P
生産量(供給量)＝Y（L(p,w,r), K(p,w,r)）
賃金＝ｗ
労働の投入量＝L(p,w,r)
レンタル料＝ｒ
資本の投入量＝K(p,w,r)

このとき、利潤を「利潤(π)＝P･Y(L(p,w,r), K(p,w,r))－(wL(p,w,r)＋rK(p,w,r))」と表せます。

緑丸部分を微分していきます

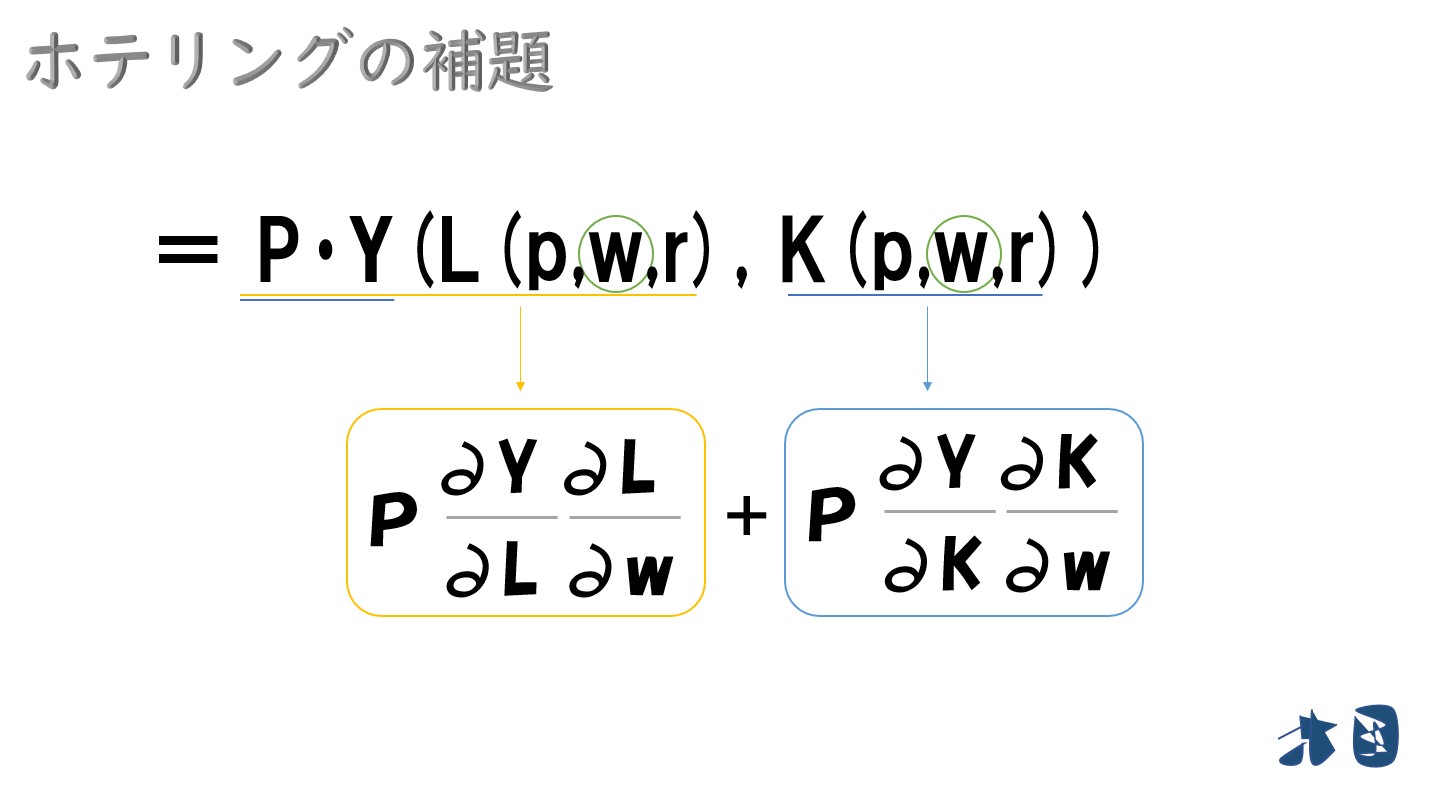
①まずは「P･Y(L(p,w,r), K(p,w,r))」の部分

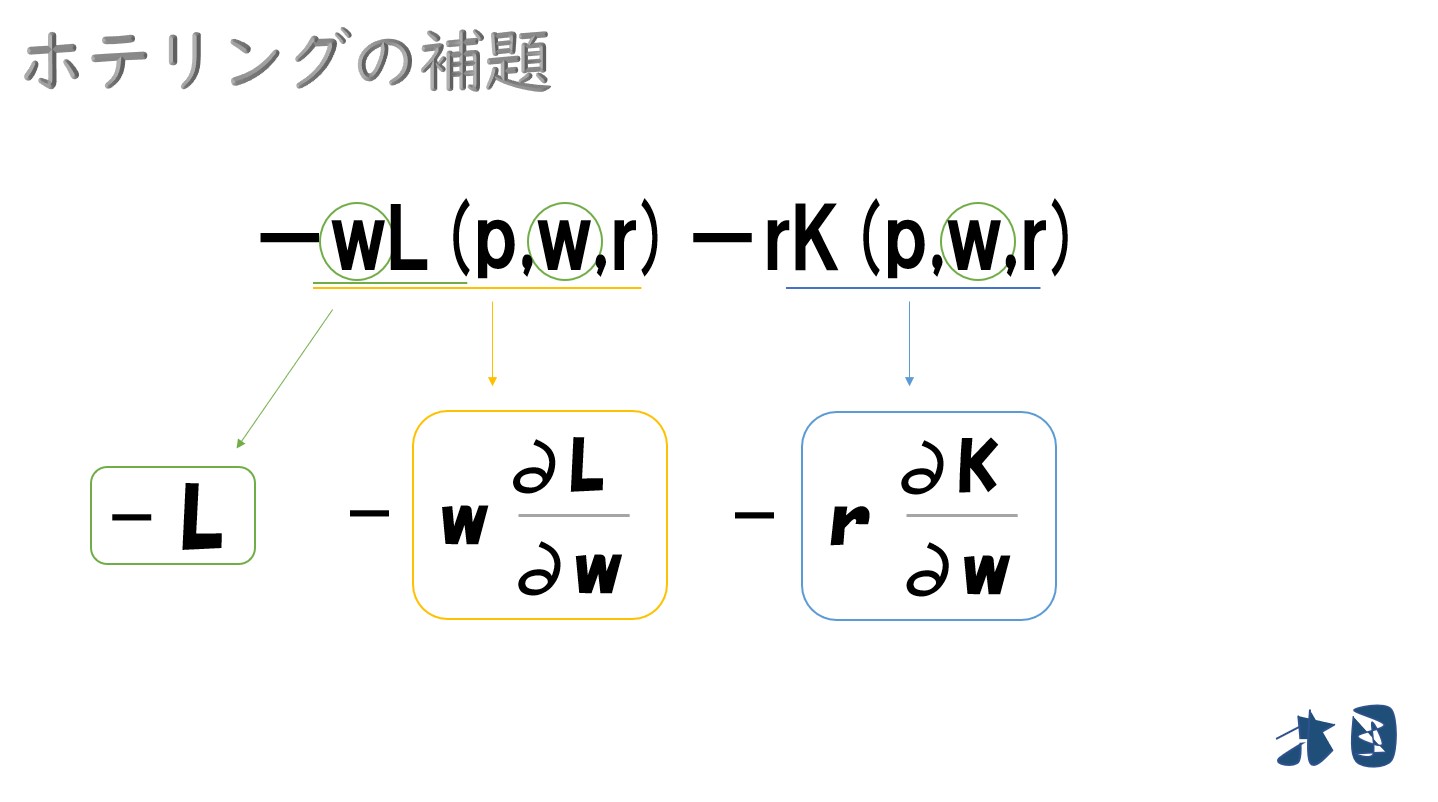
②次に「－(wL(p,w,r)＋rK(p,w,r))」の部分

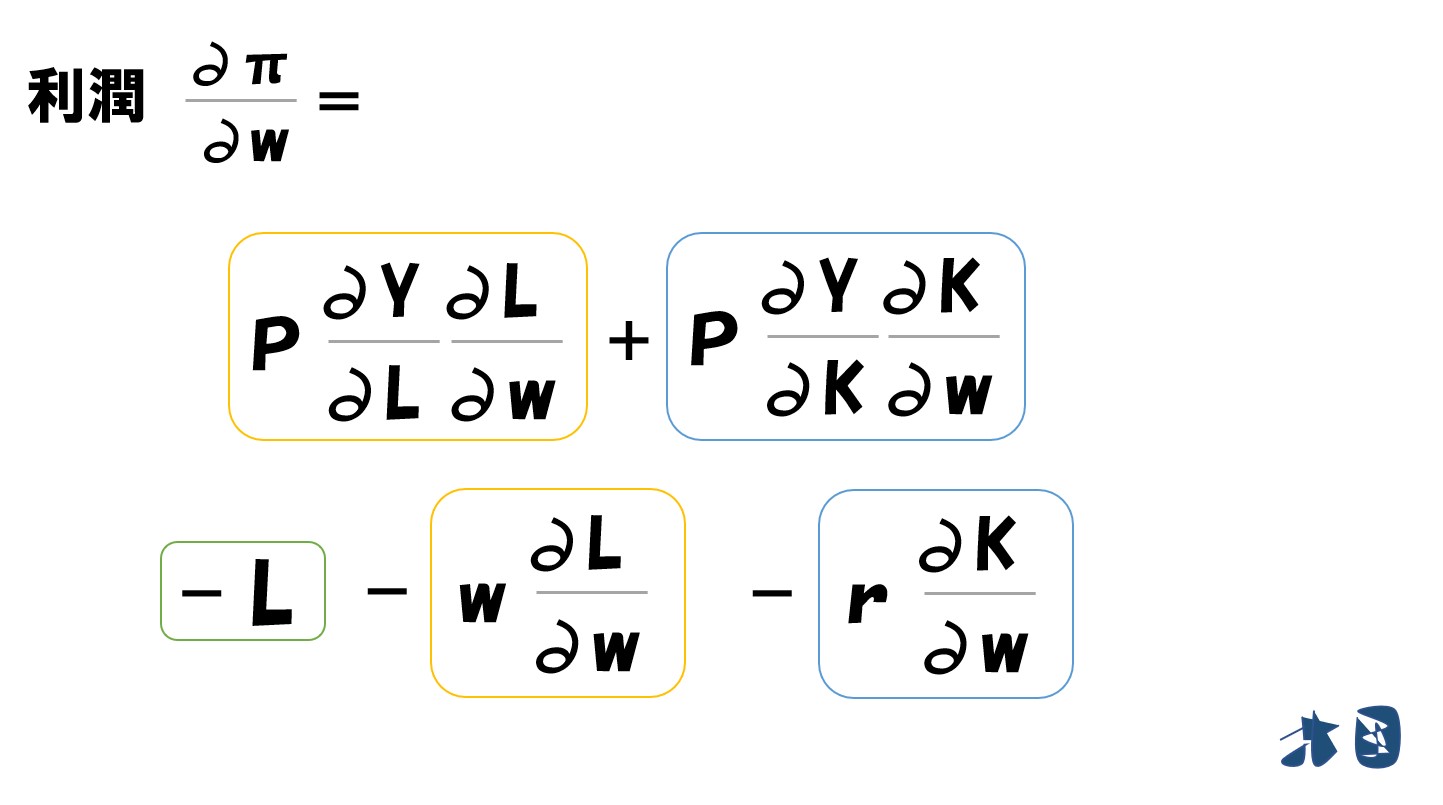
まとめると

ここで黄色･青色の枠に注目します

どちらも「∂L／∂w」「∂K／∂w」が含まれているため式をまとめます。

利潤最大化条件より

残ったのは・・

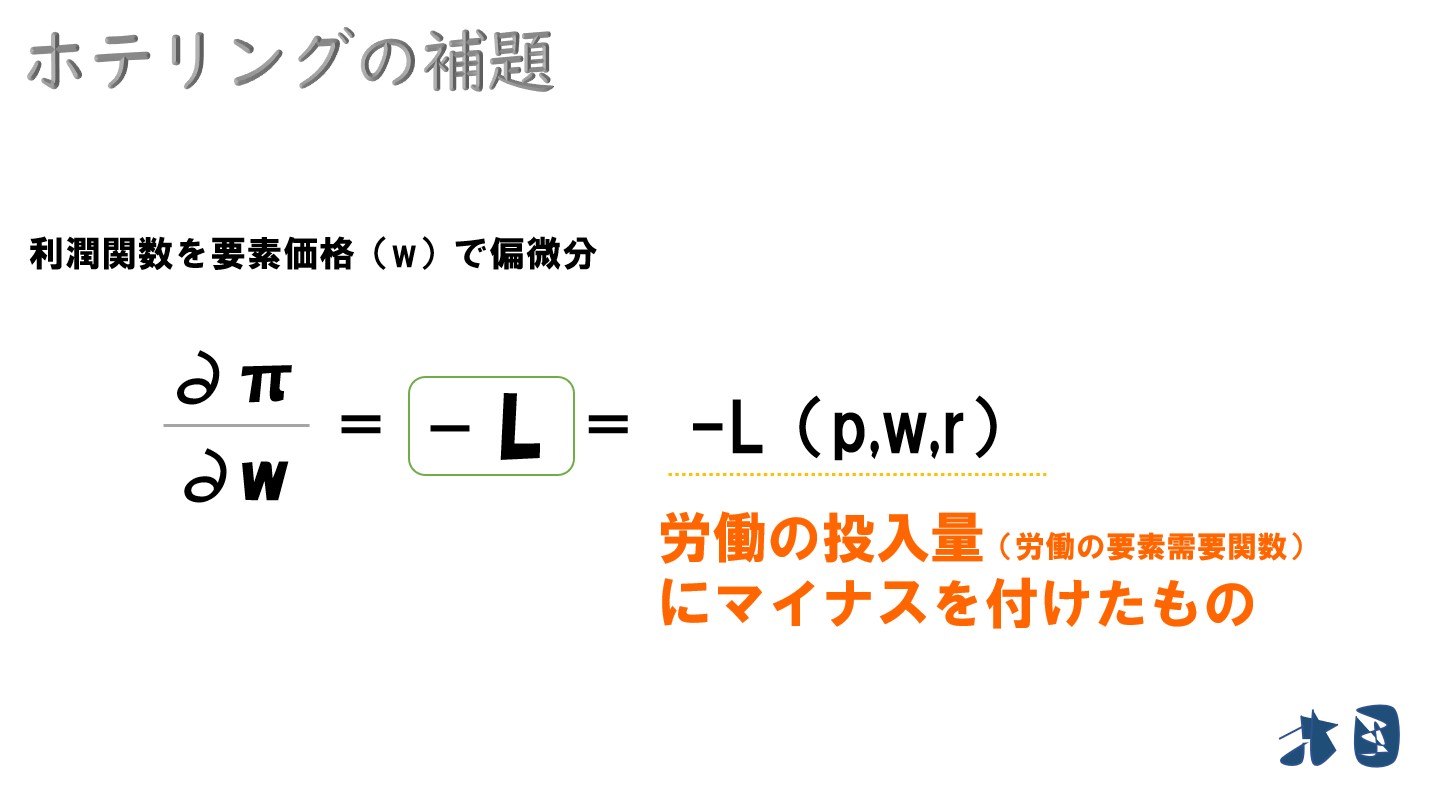
－L（労働の投入量のマイナス）だけ！

最初に説明したとおり、この「L(労働の投入量)」は「L（p,w,r）」と表記できます。

利潤関数(π)を要素価格(賃金:w)で偏微分した結果、利潤最大化が実現するときの労働の投入量(要素需要関数)にマイナスを付けたものとなりました。

ちなみに

要素価格(レンタル料:r)でやっても同様の結果が得られます

その場合は「∂π/∂r＝－K(p,w,r)」となります。

これで証明完了です。

北国宗太郎

内容よりも微分の仕方を勉強しないと難しい‥。

中級レベルだと、数学の知識が必須になってくるから勉強を頑張ろう‥！

牛さん

関連コンテンツ

消費者理論のもくじ

・効用とは何か？
・効用関数(1財･2財の場合･種類)
・限界効用･限界効用逓減の法則
・無差別曲線(性質･よくある疑問)
・無差別曲線の簡単な証明
・特殊な無差別曲線(直線･L字･円形･右上がり･凹型)
・限界代替率･限界代替率逓減の法則(無差別曲線の傾き)
・予算制約線(相対価格)
・最適消費･効用最大化問題の解き方
・限界効用均等の法則･加重限界効用均等の法則
・ラグランジュ未定乗数法
・端点解･コーナー解
・右下がりの需要曲線の導出

・所得消費曲線とエンゲル曲線
・価格消費曲線と需要曲線
・代替効果･所得効果(スルツキー分解)
・需要の所得弾力性
・需要の価格弾力性
・需要曲線シフトの要因
・ギッフェン財･右上がりの需要曲線
・顕示選好理論の弱公理･強公理
・ヒックスの補償需要曲線
・支出関数(補償所得関数)
・マッケンジー(シェパード)の補題
・間接効用関数
・ロイ(ロワ)の恒等式
・消費者理論における双対性

生産者理論のもくじ

・生産要素とは何か？
・生産関数(生産要素が1つ･2つの場合･種類)
・限界生産力･限界生産力逓減の法則
・規模に関して収穫逓減･一定･逓増
・等量曲線(性質･よくある疑問)
・技術的限界代替率･技術的限界代替率逓減の法則
・等費用線(生産要素の価格比)
・費用最小化･最適投入量の解き方
・制約付き要素需要関数
・費用関数
・短期費用曲線(総費用･固定･可変･平均可変･限界)
・長期費用曲線(長期総費用･長期平均･長期限界)

・限界費用
・総収入曲線
・限界収入
・価格(P)=限界費用(MC)=限界収入(MR)
・完全競争･利潤最大化
・プライステイカー(価格受容者)
・損益分岐点･操業停止点
・等利潤線
・供給曲線の導出
・供給曲線シフトの要因
・定額税･従量税･従価税と供給曲線のシフト
・供給の価格弾力性
・要素需要関数
・シェファードの補題
・ホテリングの補題

【一般均衡】
・一般均衡理論と部分均衡理論
・市場の調整過程（ワルラス･マーシャル･くもの巣）
・パレート効率性･パレート最適
・エッジワース･ボックスと純粋交換経済
・契約曲線とコア配分
・オファー曲線(オファー･カーブ)
・生産のパレート効率性
・生産可能性フロンティア･限界変形率
・完全競争市場(消費と生産)のパレート効率性
・ロビンソン･クルーソー経済とパレート効率性
・ワルラス均衡･ワルラス法則
・厚生経済学の基本定理の意義と証明

【不完全競争市場】
独占市場
・独占市場の利潤最大化
・ラーナーの独占度
・独占企業の価格差別戦略（第1種･第2種･第3種）

寡占市場
・クールノー･モデル（数量競争）
・ベルトラン･モデル（価格競争）
・戦略的代替と戦略的補完（ｸｰﾙﾉｰとﾍﾞﾙﾄﾗﾝの分析）
・シュタッケルベルグ競争
・カルテル（結託･共謀）
・カルテルの安定性･カルテル破り(裏切り)
・独占的競争

この記事タイトルとURLをコピー

-ミクロ経済学
-生産者理論