所得と財の消費量の関係を表した「所得-消費曲線」「エンゲル曲線」
- 所得-消費曲線とは?
- エンゲル曲線とは?
- 上級財と下級財の判別方法
- 奢侈品と必需品の判別方法
- 所得-消費曲線の式の求め方
「所得-消費曲線」「エンゲル曲線」は意外と理解しづらい項目なので、グラフをたくさん使ってまとめています。
所得-消費曲線とは?
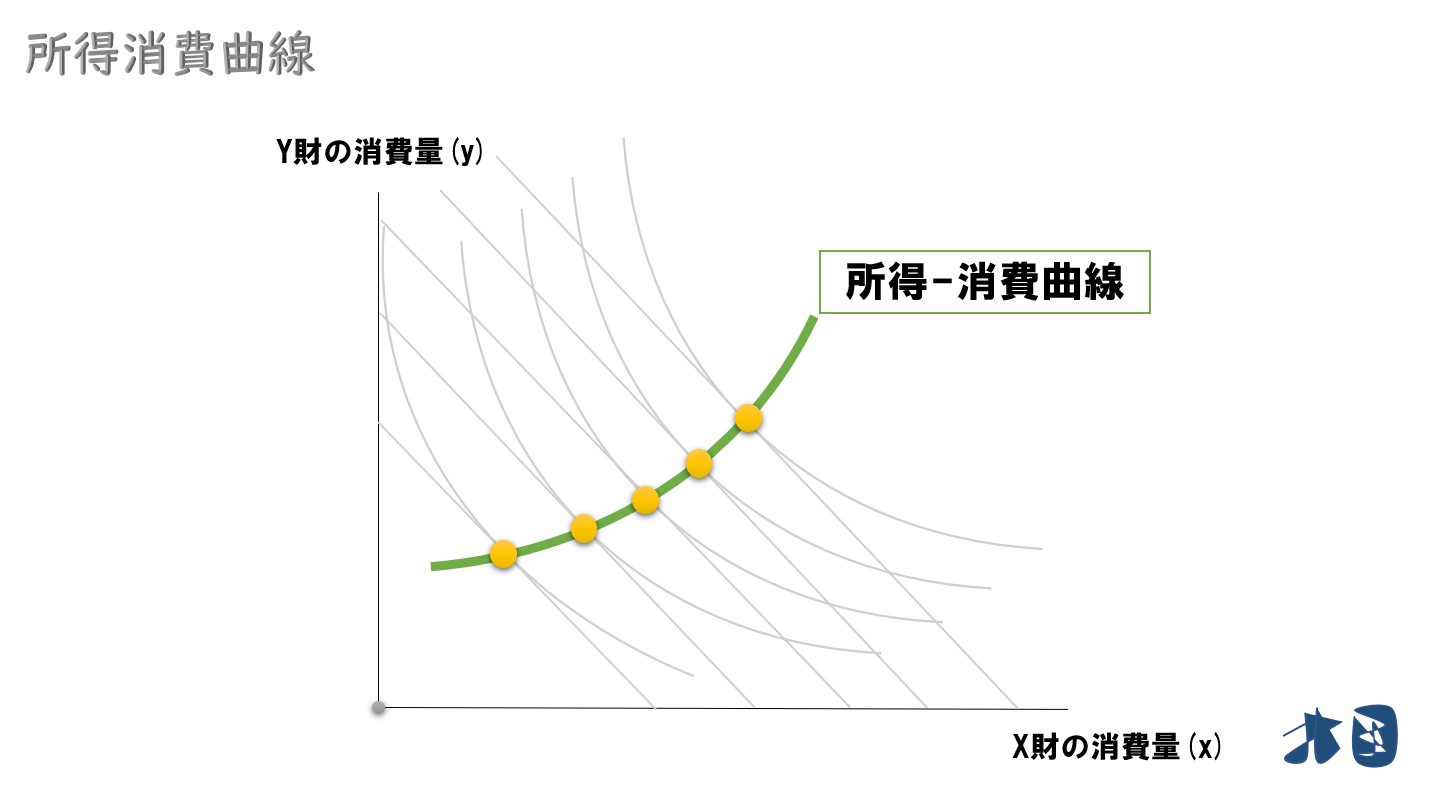
所得-消費曲線
所得の変化によって、最適消費点がどのように変化するかを示した曲線。「所得変化」と「財の消費量」の関係が分かる。※所得拡張経路と呼ぶこともある。
まずは、所得消費曲線がどのように書かれるかを見ていきます。
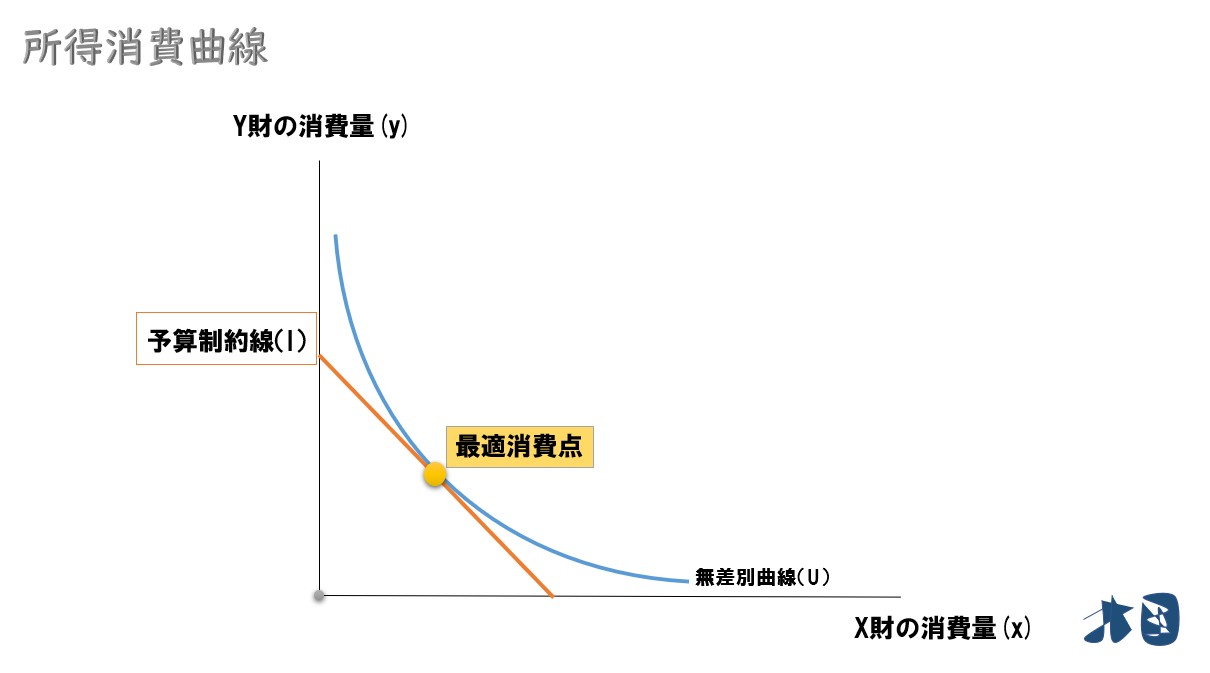
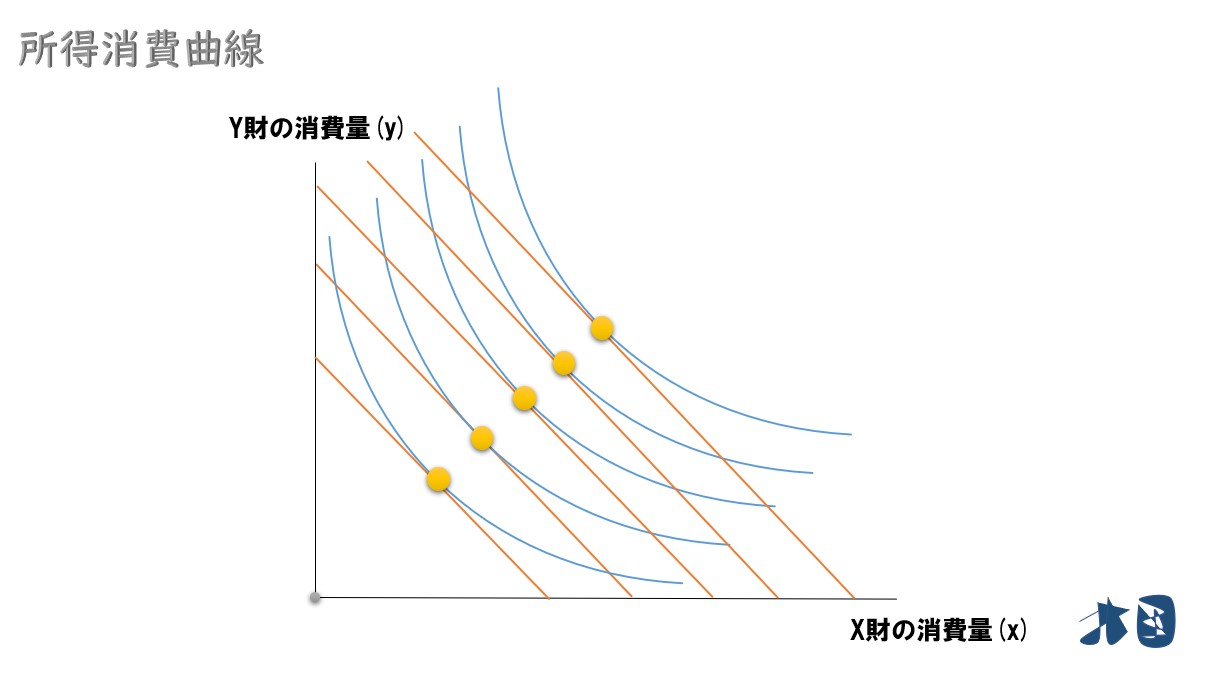
グラフ
「ある所得(予算制約線)」と「財の選好(無差別曲線)」が与えられていて、最適消費点が上のグラフのようになっていた時を考えます。
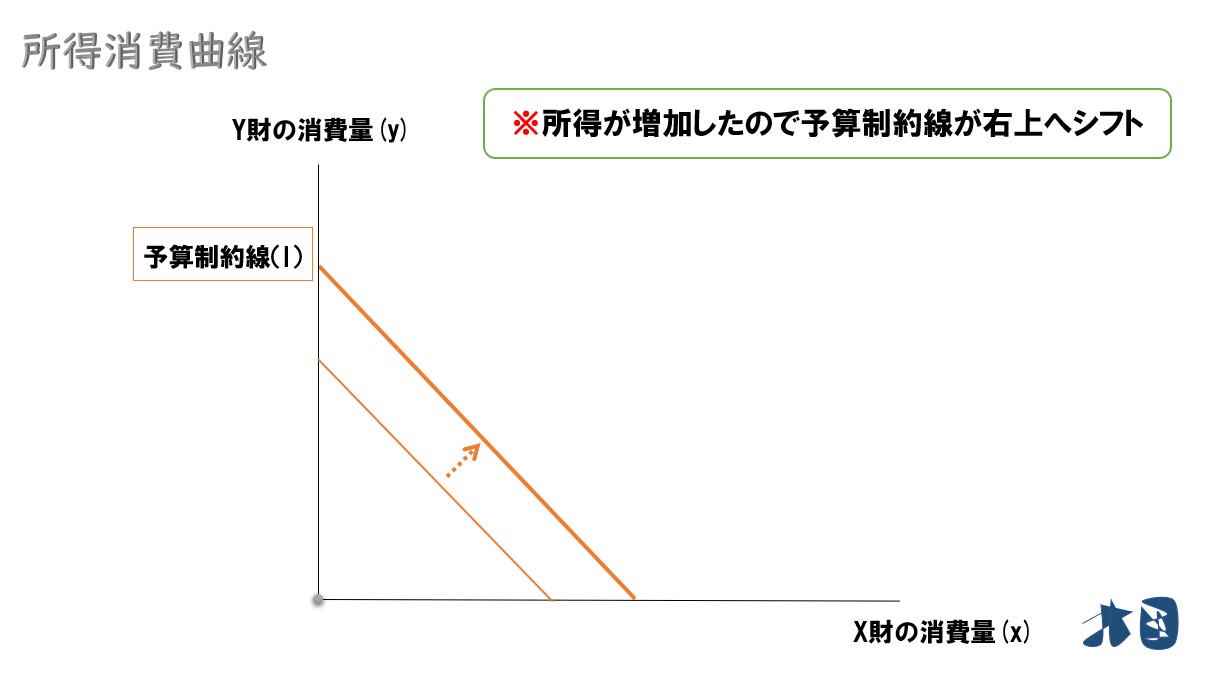
所得が増えた場合
ここでは所得が増加した場合を考えます。所得増加によって予算制約線が右上にシフトします。予算制約線の話が分からない人は確認する
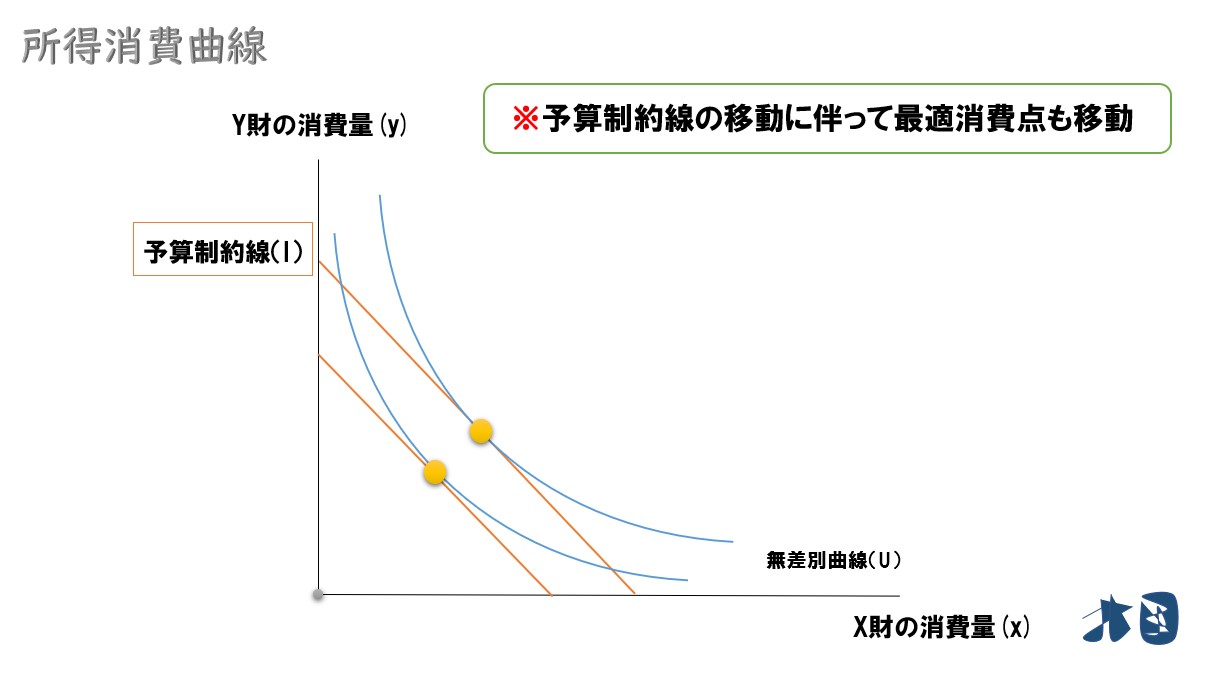
最適消費点も移動
同じことを何回も繰り返す
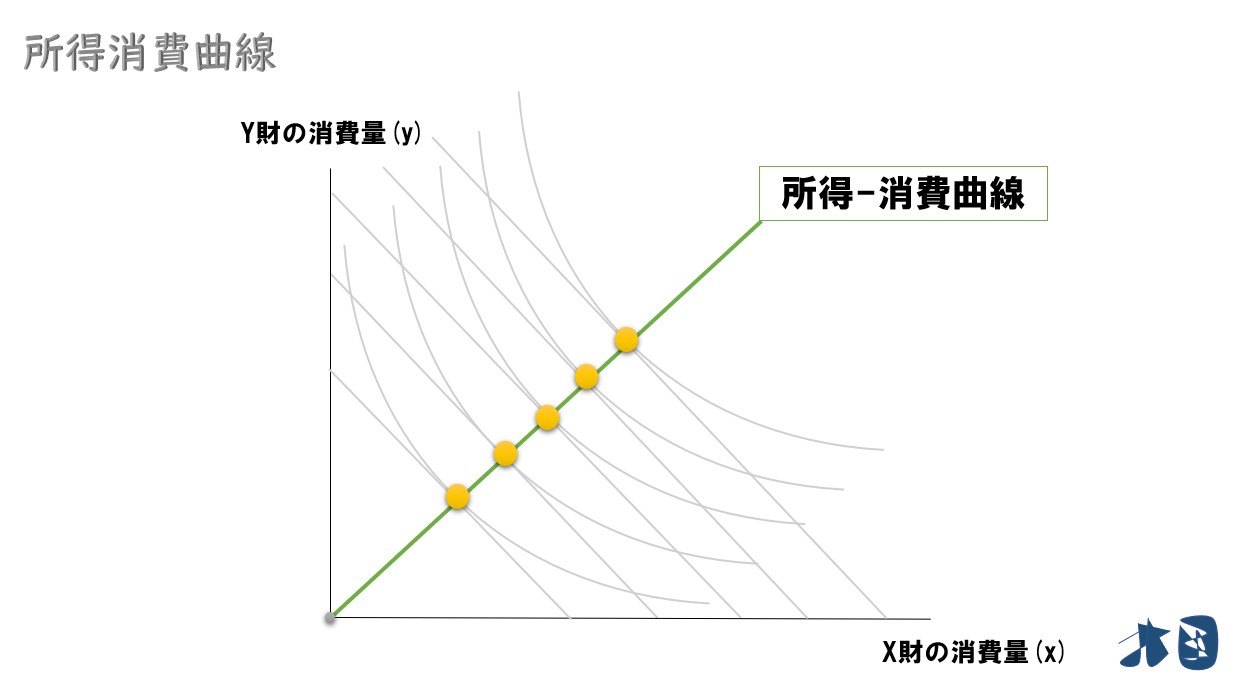
最適消費点の軌跡を結んでいくと・・
ポイント
所得(予算制約線)が変化すると、最適消費点が変化します。その軌跡を結ぶと所得消費曲線が登場します。
上のグラフでは直線となっていますが、急カーブになったり、右下がりの所得消費曲線などの形状もあります。


ポイント1
所得消費曲線は、財の性質によって形状が変わります。そのため「所得消費曲線の形状から、X財は上級財・下級財のどちらか?」みたいな問題が登場します。
ポイント2
また、所得消費曲線からエンゲル曲線というものが導けます。そのエンゲル曲線に関する問題が出されることもあります。
ここからは、上記の2つと、所得消費曲線の求め方(計算方法)について見ていきしょう!
上級財(正常財)と下級財(劣等財)の判断

大きなパターンは5つ
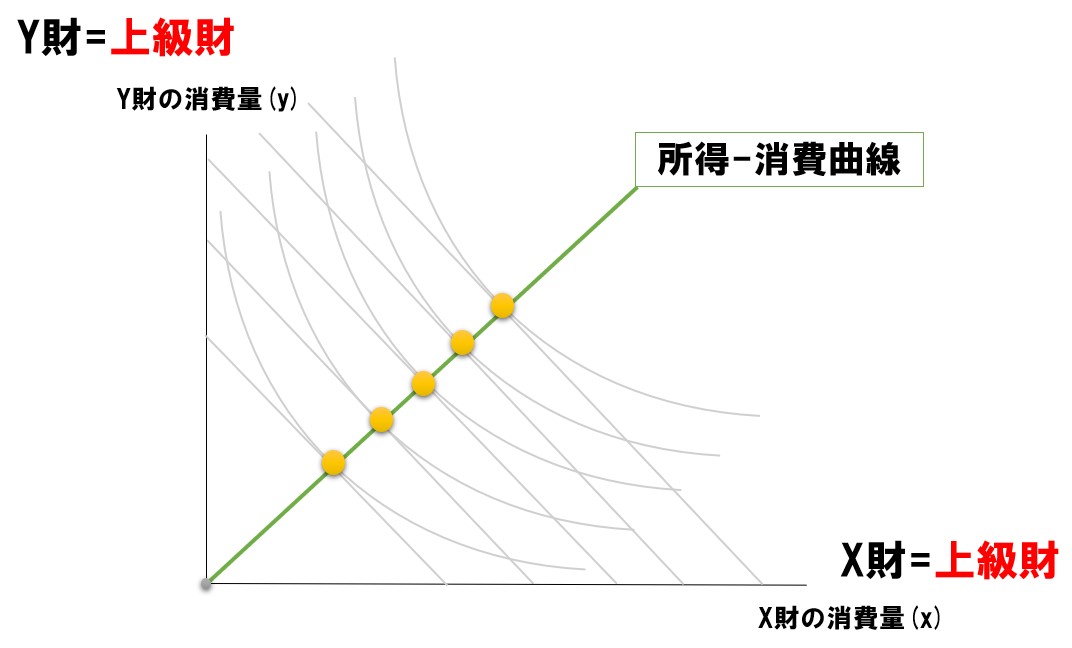
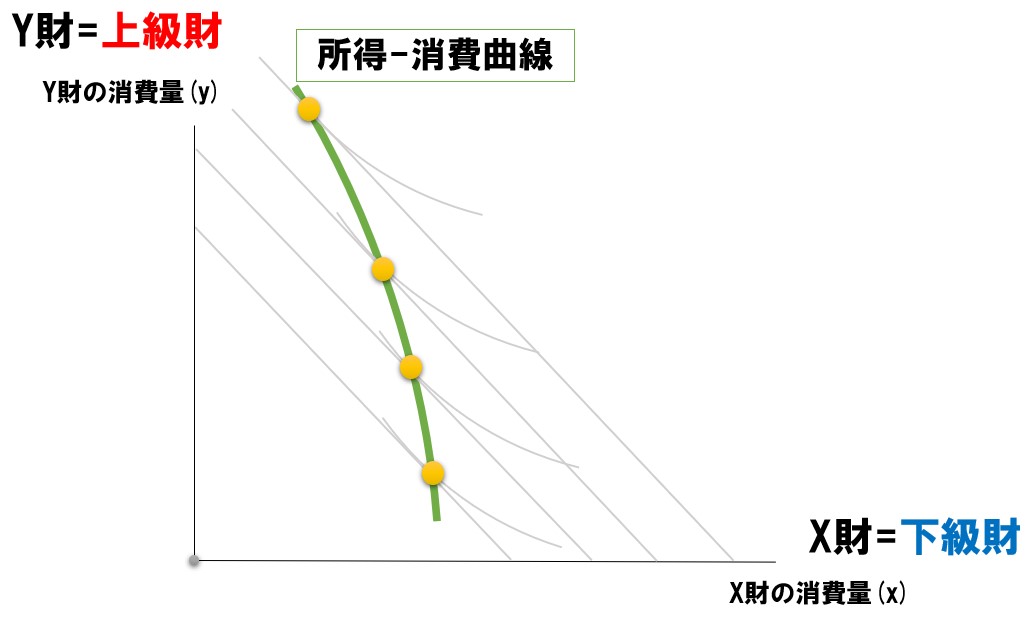
【2財とも上級財(正常財)】
オーソドックスな形状です。左側は直線・右側は急勾配な右上がりの曲線で、2財とも上級財のケースです。
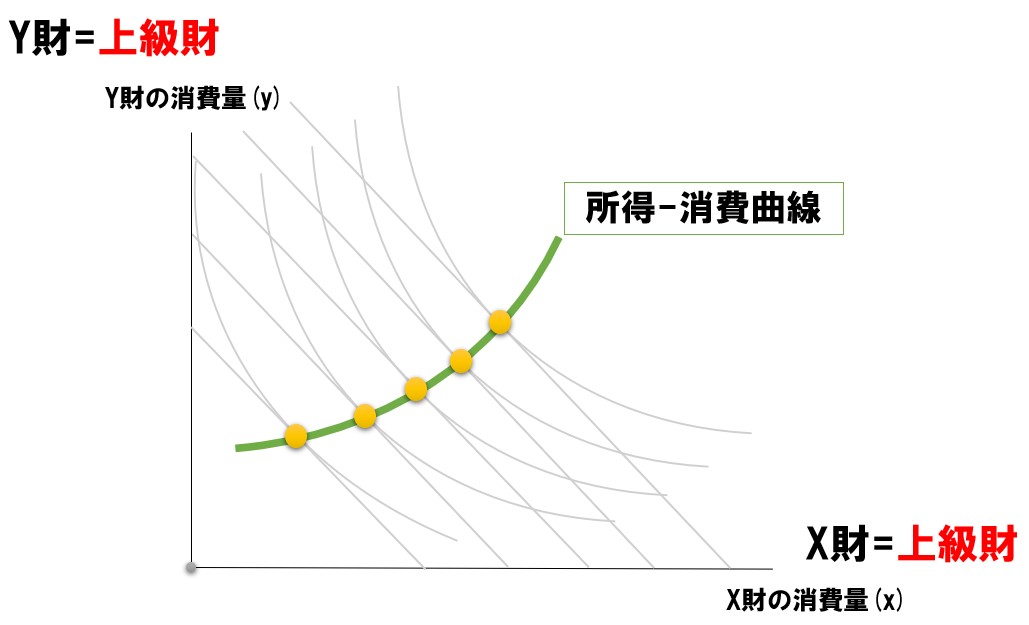
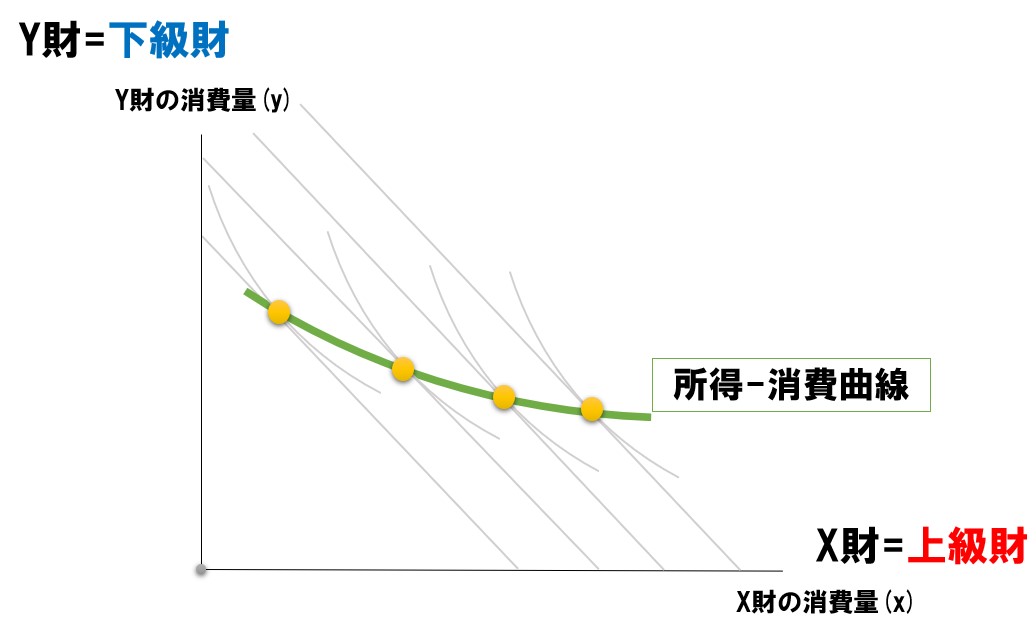
【片方が下級財(劣等財)】
片方に下級財(劣等財)が含まれる場合は、所得消費曲線は右下がりになります。縦軸と横軸のどちらが下級財(劣等財)かで、傾き具合が変わります。
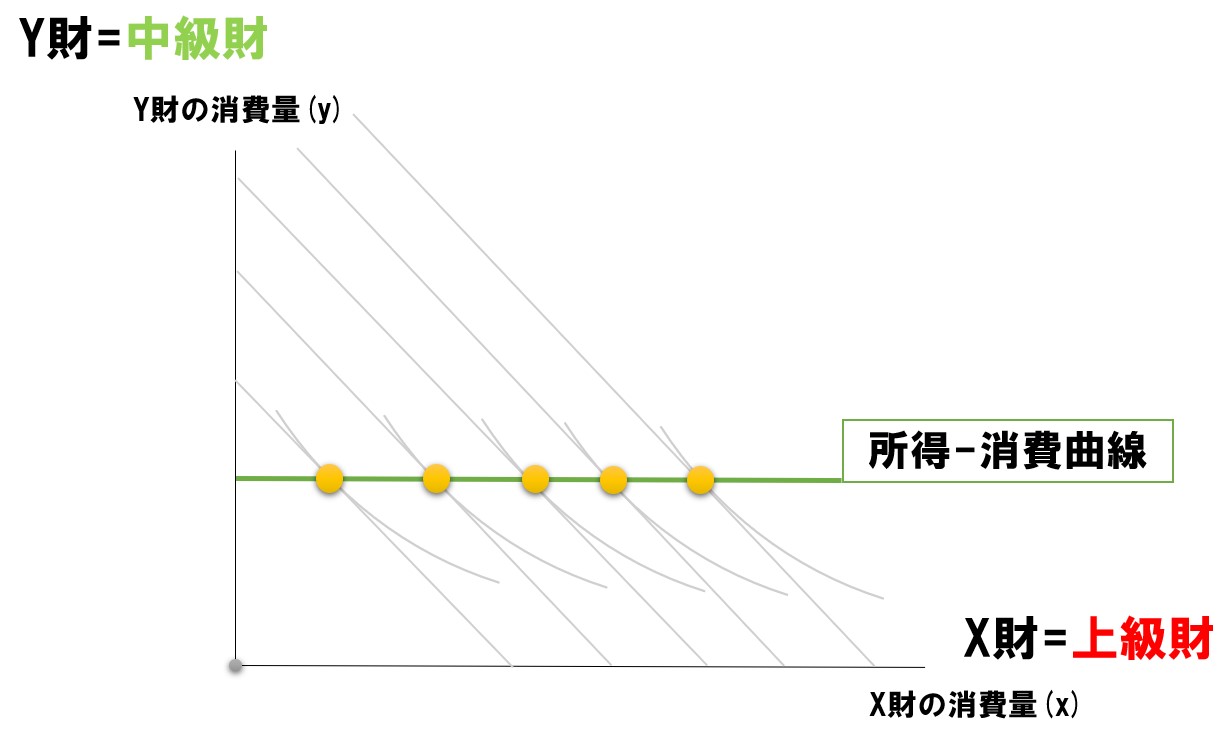
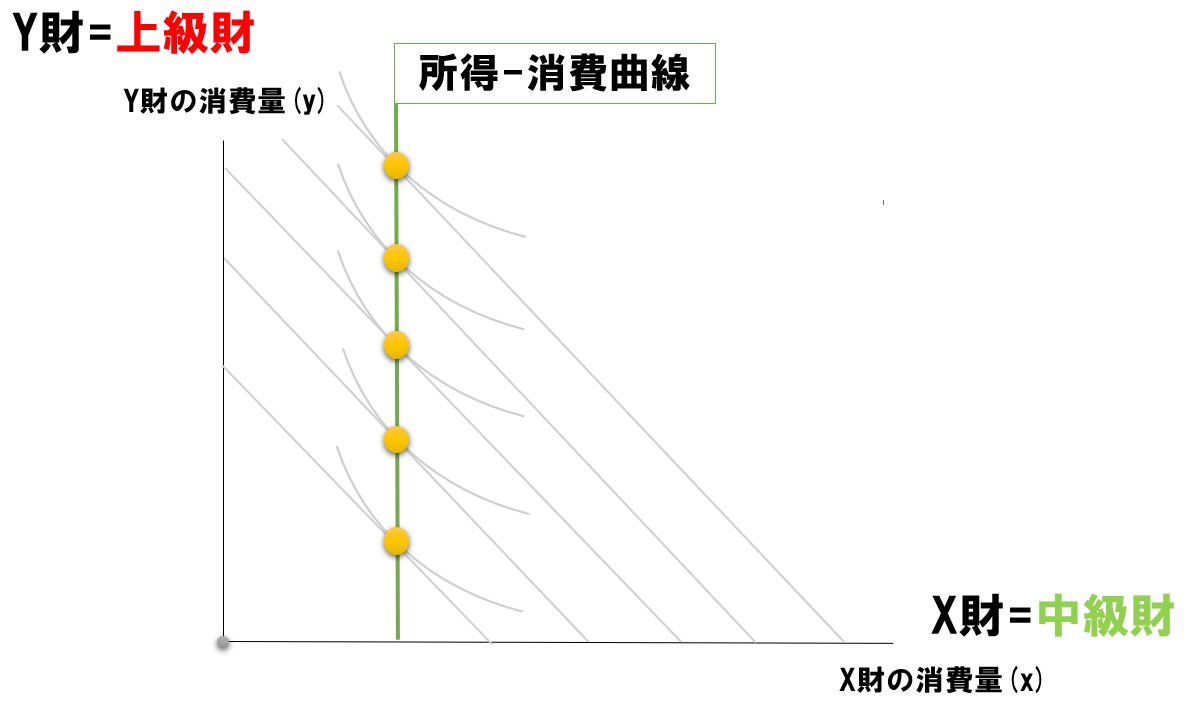
【片方が中級財(中立財)】
片方に中級財(中立財)が含まれる場合は、所得消費曲線は水平・垂直になります。縦軸が中級財なら水平、横軸が中級財なら垂直になります。
まとめ
| Y財(縦軸)の種類 | X財(横軸)の種類 | 所得-消費曲線の形状 |
|---|---|---|
| 上級財(正常財) | 上級財(正常財) | 右上がり |
| 上級財(正常財) | 下級財(劣等財) | 急勾配な右下がり |
| 下級財(劣等財) | 上級財(正常財) | 緩やかな右下がり |
| 中立財 | 上級財(正常財) | 水平 |
| 上級財(正常財) | 中立財 | 垂直 |
2財モデルでは、2財とも下級財・中立財というケースは無いので注意が必要です。


補足
最適消費点は「予算を全額使って、効用を最大化させる消費の組合わせ」のことです。
2財が下級財(劣等財)だった場合、所得が増えたのに2財とも消費量が減ってしまい、予算が余ってしまいます。
つまり、2財モデル(縦軸・横軸に財の消費量をとって分析するモデル)では、必ずどちらかに上級財(正常財)が含まれることになります。
ちなみに
「上級財」「下級財」は相対的なもの
貧乏な時にカップ麺を食べていた人が、所得が増えて牛丼を食べるようになります。
この時、所得が増えたことで消費量が増えた牛丼は上級財です。
ここから、更に給料が上がって、牛丼よりも定食屋でご飯を食べることが増えます。
この時、牛丼は下級財となって、定食が上級財となります。
ココがポイント
状況によって上級財と下級財の分類は変わります。
カップ麺やインスタント麺のように、下級財っぽいものが2つ並んでも、どちらかは、相対的に上級財の性質を持つと言えます。
このことから、2財モデルでは、2財とも下級財というケースは存在しなことになっています。


奢侈品と必需品の判断方法

上級財には2種類あります。
奢侈品と必需品の見分け方ですが、2財とも上級財ではないと、判断することが出来ないので注意が必要です。
ポイント
所得が増えたとき「どちらの財が、より多く消費されるようになっているか」で判断します。
- 奢侈品=より多く消費されている財
- 必需品=そうではない財
普通に考えれば理由が分かります。
奢侈品(ぜいたく品)は、所得が増えれば消費量が増えます。
必需品は所得が増えても減っても、消費量があまり変わりません。
具体的な判断方法
- 所得-消費曲線上の点Qにおいて、奢侈品・必需品を判断する場合
- 「原点」と「点Q」を線で結ぶ
- その線と所得消費曲線の関係を見る
所得消費曲線がその線よりも左側に曲がっている=縦軸が奢侈品
所得消費曲線がその線よりも右側に曲がっている=横軸が奢侈品
他のグラフも見てみよう
【Y財=奢侈品・X財=必需品】
最適消費点Qでは、点Qから所得が増えるにつれて、Y財(縦軸)の方が消費量が増えているので奢侈品です。X財(横軸)は、Y財(縦軸)よりも消費量が増えていないため必需品と判断できます。
【Y財=必需品・X財=奢侈品】
最適消費点Qでは、点Qから所得が増えるにつれて、X財(横軸)の方が消費量が増えているので奢侈品です。Y財(縦軸)は、X財(横軸)よりも消費量が増えていないため必需品と判断できます。


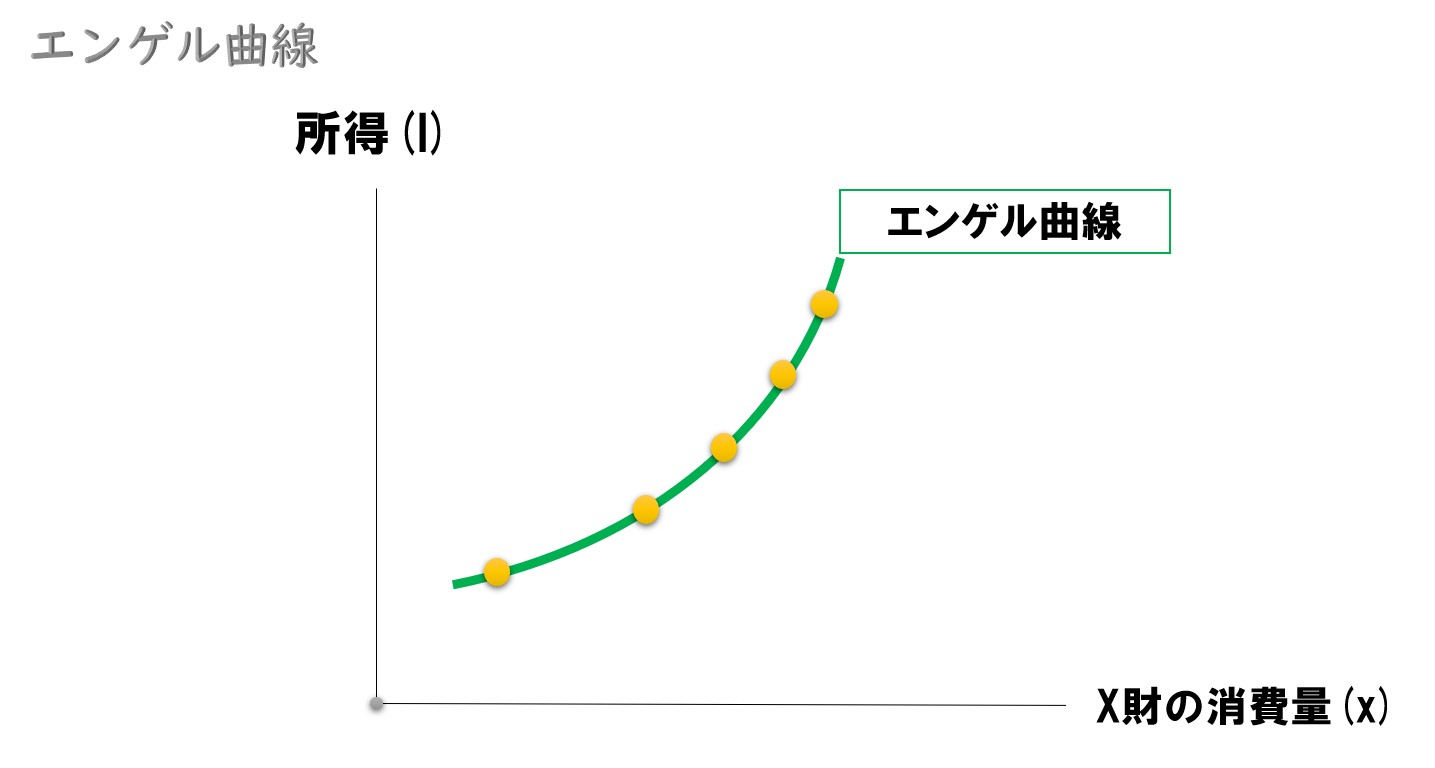
エンゲル曲線とは?
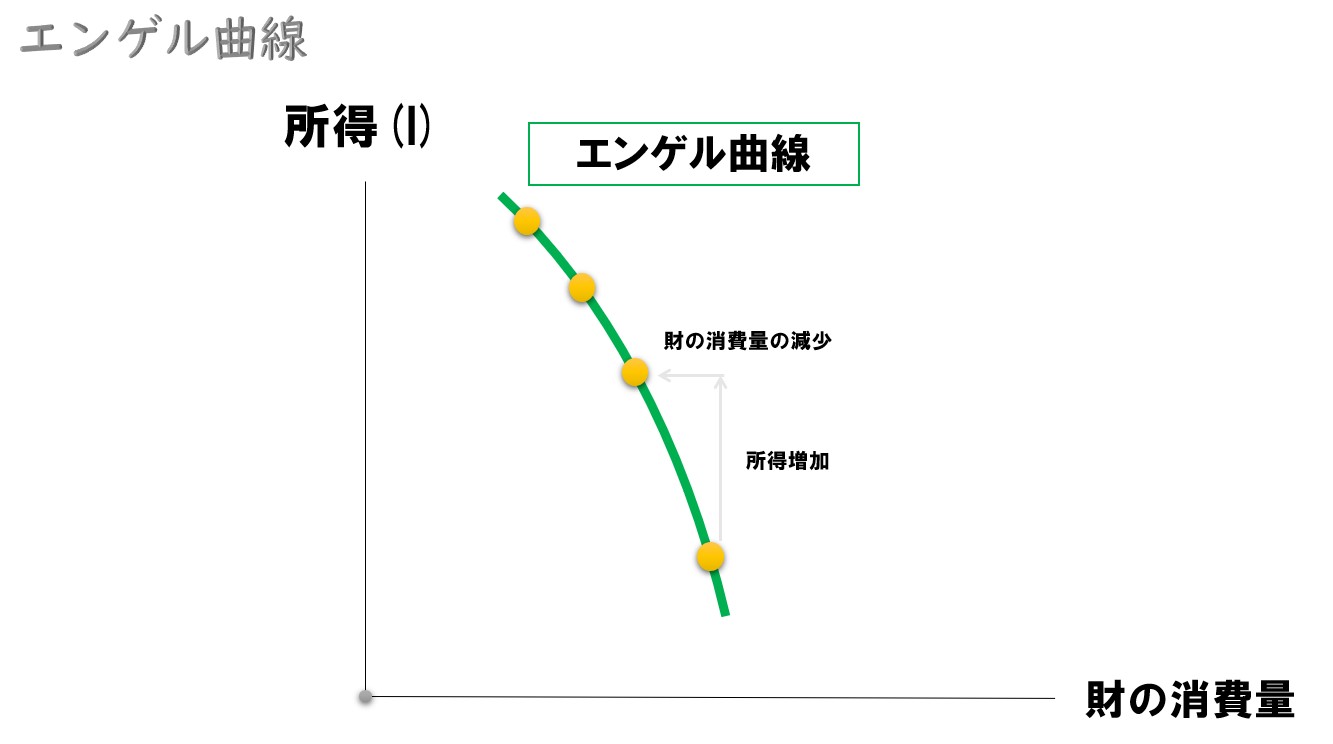
エンゲル曲線
消費者の所得変化と、特定の1つの財の消費量を対応させた曲線。
所得-消費曲線は、最適消費点の変化をX財・Y財の関係で見たものです。最適消費点の変化を片方の財だけに注目したものをエンゲル曲線と呼びます。
所得-消費曲線を「最適消費点の関係をY財-X財平面に図示したもの」エンゲル曲線を「最適消費点の関係を所得-X財平面に図示したもの」と言う場合もあります。
ここでは
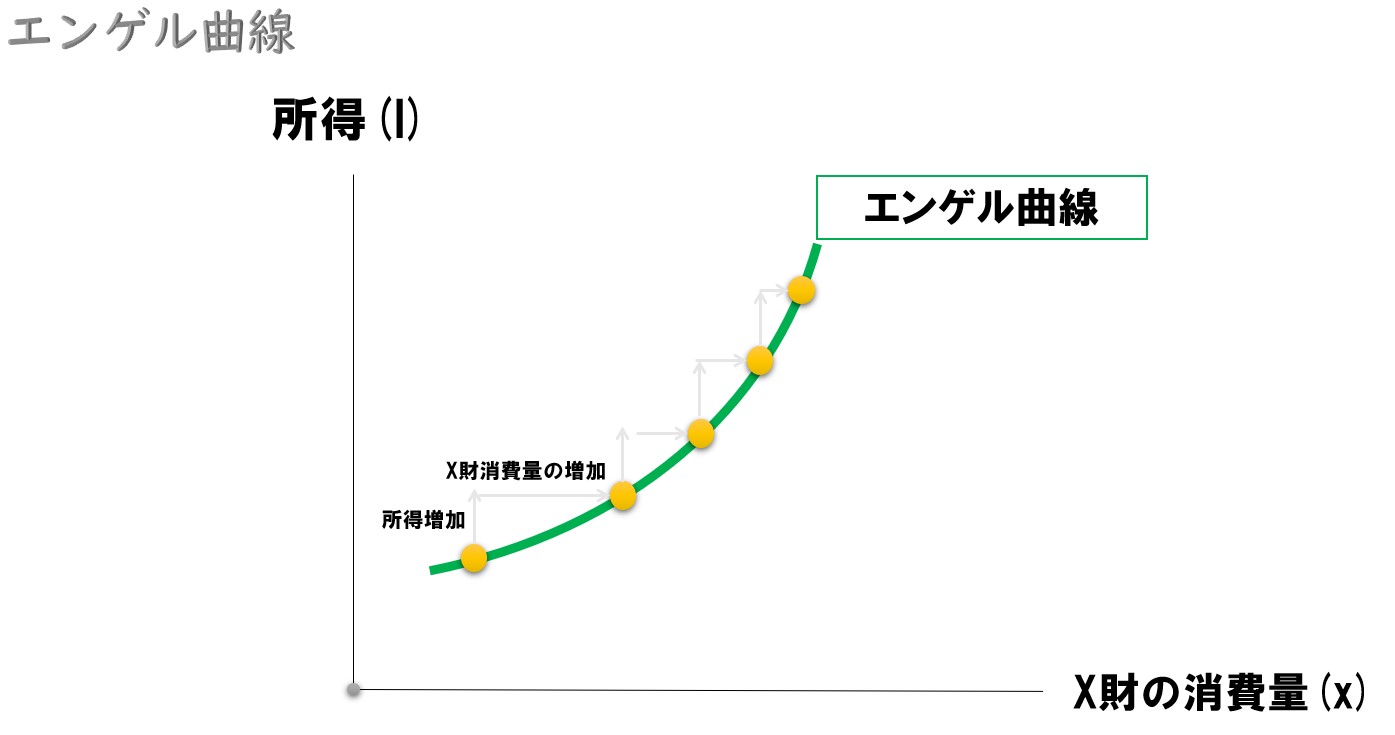
- X財に注目してエンゲル曲線の説明を進めます。
縦軸に所得、横軸にX財を取った場合を考えてみましょう。
経済学では「縦軸に所得・価格」「横軸に消費量」をとるイメージが強いですが、エンゲル曲線では「縦軸=財の消費量」「横軸=所得」と取るケースもあります。
エンゲル曲線は「所得が変化して、消費量がどう変化するのか?」を確認するのが目的です。通常の数学では「Y(縦軸)=aX(横軸)+b」という記載になるので「最終的に求めたいもの(消費量)=所得(変化する情報)+切片など」となる方が、自然な数式になるからです。ただし、ここでは数学の慣習に沿うよりも、経済学の慣習に合わせて「縦軸=所得」「横軸=消費量」とします。
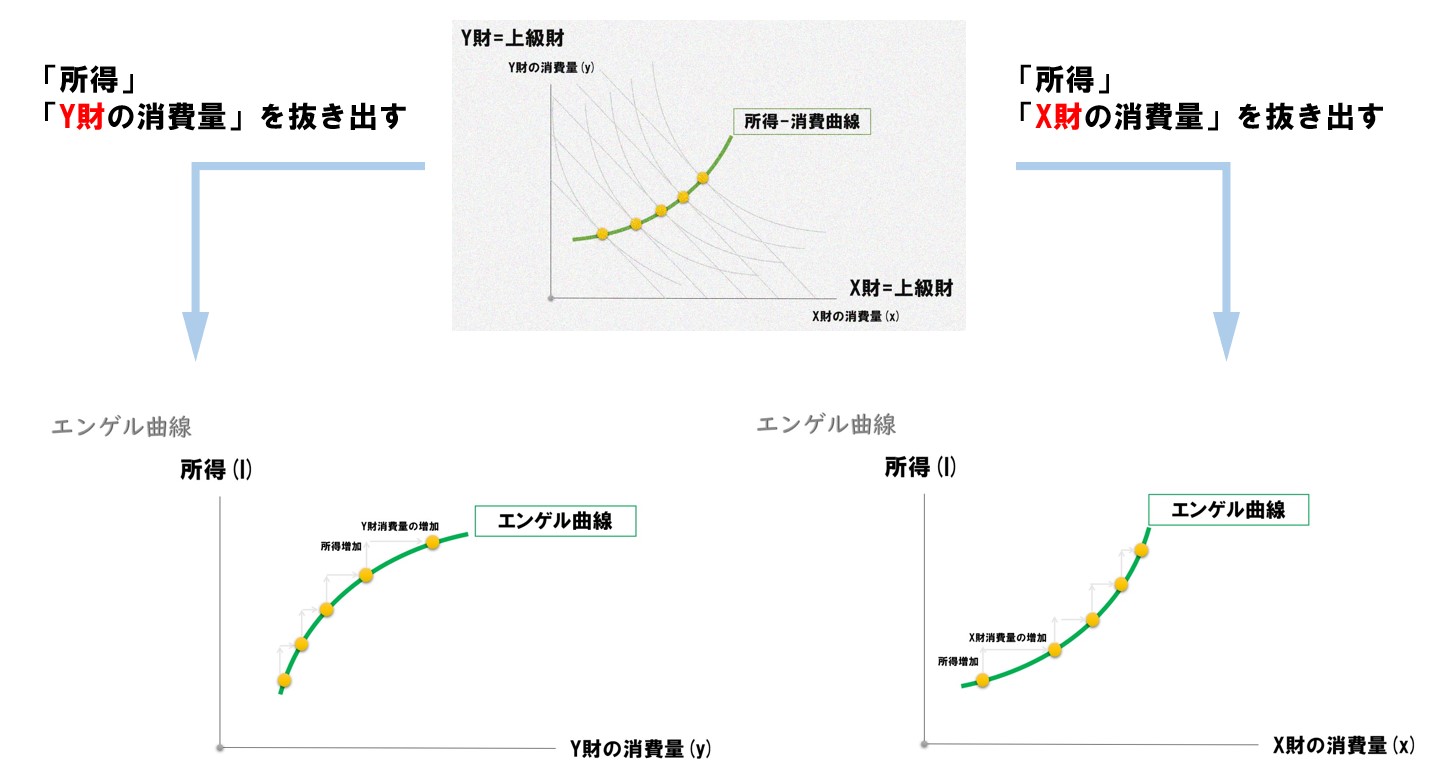
所得消費曲線
この所得消費曲線から「所得」「X財の消費量」を抜き出して、エンゲル曲線として描きます。
エンゲル曲線
所得消費曲線と似た形状になっていますが、たまたまです。「縦軸=所得」「横軸=X財の消費量」となっています。
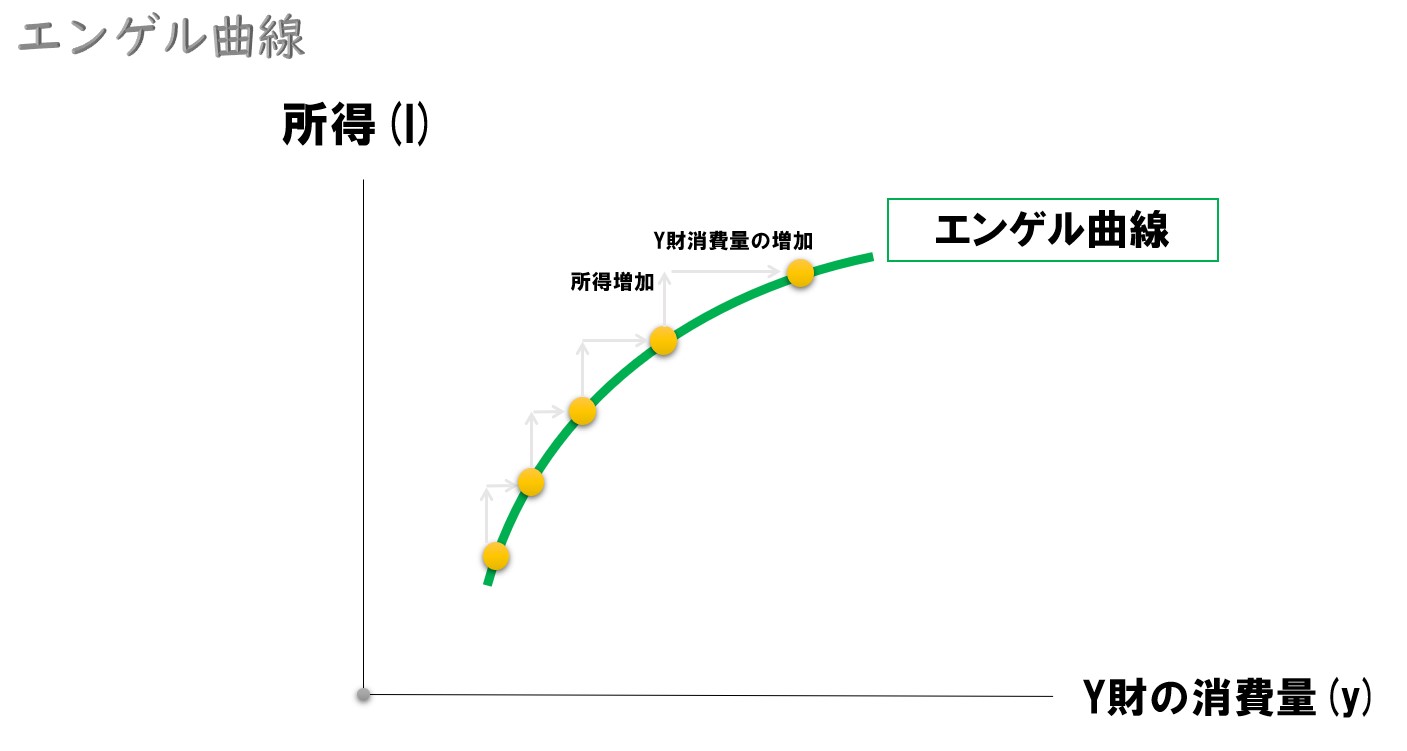
ちなみに
Y財だった場合のエンゲル曲線
まとめ


エンゲル曲線も形状によって財の種類を判断することが可能です。
上級財(正常財)と下級財(劣等財)の判断

所得消費曲線と同じように、「曲線が右上がり」「曲線が右下がり」で、財の種類が判別できます。
【上級財(正常財)】
エンゲル曲線が「右上がり=所得が増えて、財の消費量が増えている」ので、上級財(正常財)です。
【下級財(劣等財)】
エンゲル曲線が「右下がり=所得が増えて、財の消費量が減っている」ので、下級財(劣等財)です。
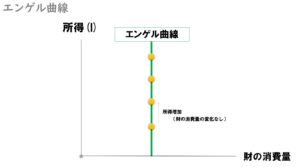
【中級財(中立財)】
エンゲル曲線が「垂直=所得が増えても、財の消費量が変わっていない」ので、中級財(中立財)です。
ココに注意
今紹介した3つは「縦軸=所得」「横軸=財の消費量」でエンゲル曲線を図示した場合の話です。「縦軸=財の消費量」「横軸=所得」ならば、全く逆になるので注意が必要です。
まとめ
| 財の種類 | エンゲル曲線の形状 |
|---|---|
| 上級財(正常財) | 右上がり |
| 下級財(劣等財) | 右下がり |
| 中級財(中立財) | 垂直 |
※上記は「縦軸=所得」「横軸=財の消費量」のケース
エンゲル曲線も上級財(正常財)を「奢侈品」「必需品」と分けて考えることが出来ます。
奢侈品と必需品の判断方法

エンゲル曲線で奢侈品と必需品を判断する方法は、所得消費曲線と似ています。
具体的な判断方法
- エンゲル曲線上の点Qにおいて、奢侈品・必需品を判断する場合
- 「点Q」の接線を書く
- 接線と原点の関係を見る
接線の伸ばした先が、原点よりも左側に行く=奢侈品
接線の伸ばした先が、原点よりも右側に行く=必需品
これも「縦軸=所得」「横軸=財の消費」とした場合です。「縦軸=財の消費」「横軸=所得」なら逆になります。
グラフを見てみよう
【必需品の場合】
【奢侈品の場合】
改めてですが「縦軸=所得」「横軸=財の消費」とした場合です。「縦軸=財の消費」「横軸=所得」なら逆になります。
補足
奢侈品(ぜいたく品)は、所得が増えれば消費量が増えます。
必需品は所得が増えても減っても、消費量があまり変わりません。
詳しい説明をしませんでしたが、グラフの判断方法は、結果的に所得の増加に比べて、財の消費量の増え方が大きい(奢侈品)か、小さいか(必需品)を見ています。
- 原点よりも接線が右側に来る=傾きが急=所得の増加割合の方が大きい(必需品)
- 原点よりも接線が左側に来る=傾きが緩やか=財の消費量の増加割合の方が大きい(奢侈品)


確認する
最後に、所得-消費曲線の式を求める方法を簡単に説明します。
所得-消費曲線の求め方(計算)

例えば
- 効用関数「U(x, y)= x・y」
- 所得がM
- X財の価格が1
- Y財の価格が3
この時、所得消費曲線を表す式を求める。
まずは最適消費点を求める
ここからは、最適消費点の求め方を知っている前提で計算していきます。もし分からない所が出てきたら、最適消費点の求め方で確認してください。
① 予算制約線の傾きを求める
「X財の消費量=x」「Y財の消費量=y」として「予算制約線:M=1x+3y」とします。
- M=1x+3y
- 3y=-1x+M
- y=-(1/3)x+(1/3)M
② 効用関数から限界代替率を求める
「U=xy」から「y=U/x」へ変形後に微分します。
- 「y=U/x」⇒「U/xの2乗(=U・xの-2乗)」
- 「U/xの2乗」に「U=xy」を代入
- 「U(=xy)/xの2乗」⇒「xy/xの2乗」=「y/x」
③ 予算制約線の傾き=限界代替率で最適消費点を求める
「-1/3」=「-y/x」
- y= (1/3)x
- x=3y
M=1x+3(1/3x)
=1x+1x
=2x
M=2x(x=1/2M)
M=1×3y+3y =6y
M=6y(y=1/6M)
補足
普通の最適消費点を求める問題なら、所得をMとおかずに、具体的な数字を設定しているはずなので、「M=2x(x=1/2M)」「M=6y(y=1/6M)」を計算することが出来ます。
ここでは、所得-消費曲線の数式だけを求める問題なので、所得=Mとしています。
ポイント
所得-消費曲線の数式は、2財の最適消費量をイコールで結ぶ
- M=2x(x=1/2M)
- M=6y(y=1/6M)
「M=2x=6y」より「x=3y」もしくは「y=1/3x」が所得-消費曲線の式です。
「X財について所得-消費曲線の式を求めよ」なら「x=3y」「Y財について所得-消費曲線の式を求めよ」なら「y=1/3x」です。