無差別曲線を単調性や推移性を使って、証明する問題があります。
- 無差別曲線が右下がりになる理由
- 無差別曲線は右上ほど効用が高い理由
- 無差別曲線は交わらない理由
- 無差別曲線が原点に対して凸の理由
無差別曲線の4つの性質について、簡単な証明をまとめています。
無差別曲線が右下がりになる
最初に
X財とY財の2財を考える。
2財の消費について単調性(非飽和性)を満たしているとする(=消費者の選好が単調性(非飽和性)を満たすとする)。
ポイント
2財とも消費をすればするほど効用が増加する。これを単調性(非飽和性)と呼ぶ。


通常は、消費を続けると飽きたり、限界を迎えたりします。しかし、証明をする際は、状況を簡単にするために、永遠に消費を続けることが出来ると考えます。
次に
同じ無差別曲線上ならば、「どのX財・Y財の消費の組み合わせ」も同じ効用となる。
先ほど記載した通り、2財の消費について、単調性(非飽和性)を満たすため、X財・Y財どちらも、消費するほど効用が高くなる。
仮に
X財の消費量を増やすとき、それに合わせてY財の消費量を減らさないと、同じ効用を保てなくなる。
ポイント
2財が単調性(非飽和性)を満たすとき、片方の財の消費量を増やした場合、もう片方の財の消費量を減らさないと、同じ効用を保てなくなる。
つまり
- 同じ無差別曲線上なら、どの点(2財の消費の組合わせ)でも、同じ効用を示す。
- 2財が単調性(非飽和性)を満たすとき、X財の消費量を増やした場合、Y財の消費量を減らさないと、同じ効用を保てなくなる。
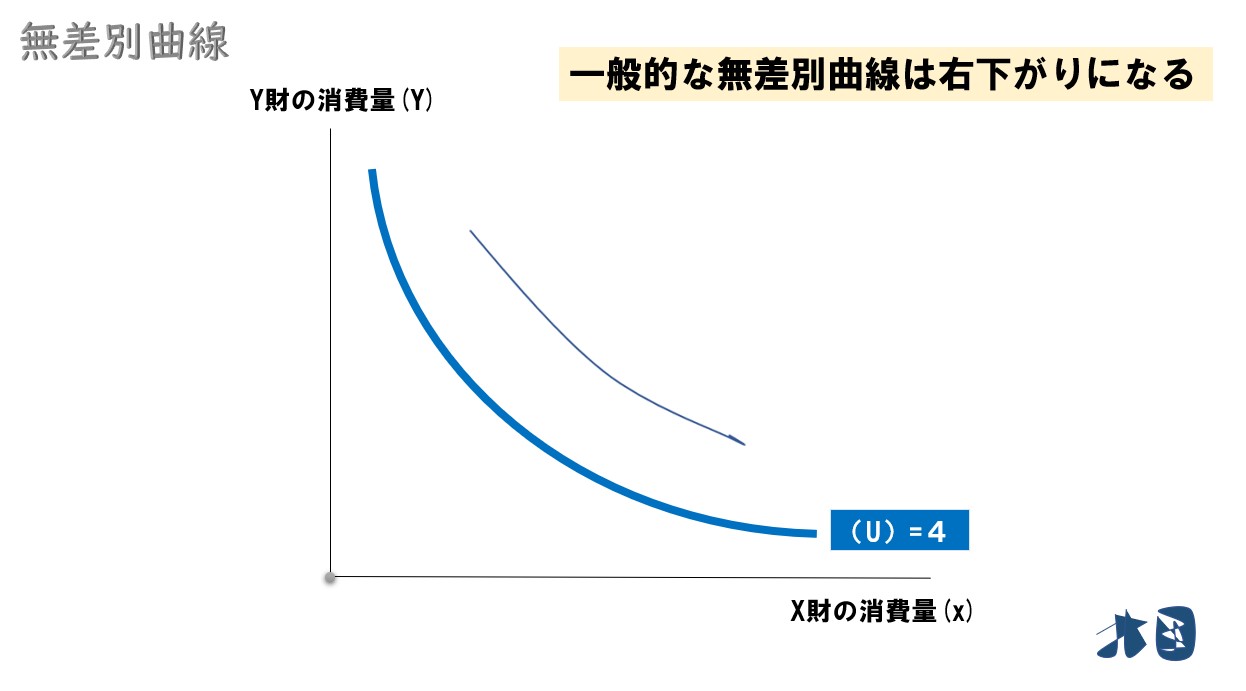
この2つから、無差別曲線は右下がりの曲線となる。


例えば
- 効用(U)=10とする
「効用(U)=(X財の消費量)×(Y財の消費量)」で表されるときを考える。
効用(U)=10なので、X財とY財の消費量の組み合わせは次の通りになる。
- (X=10, Y=1)
- (X=5, Y=2)
- (X=2, Y=5)
- (X=1, Y=10)
「横軸にX財の消費量」「縦軸にY財の消費量」をとってグラフを作ると、右下がりの曲線になります。
無差別曲線は右上ほど効用が高い
最初に
X財とY財の2財を考える。
2財の消費について単調性(非飽和性)を満たしているとする(=消費者の選好が単調性(非飽和性)を満たすとする)。
ポイント
2財とも消費をすればするほど効用が増加する。これを単調性(非飽和性)と呼ぶ。


ここで
2財とも単調性(非飽和性)を満たすとき、財の消費量を増やせば効用が高くなる。
ポイント
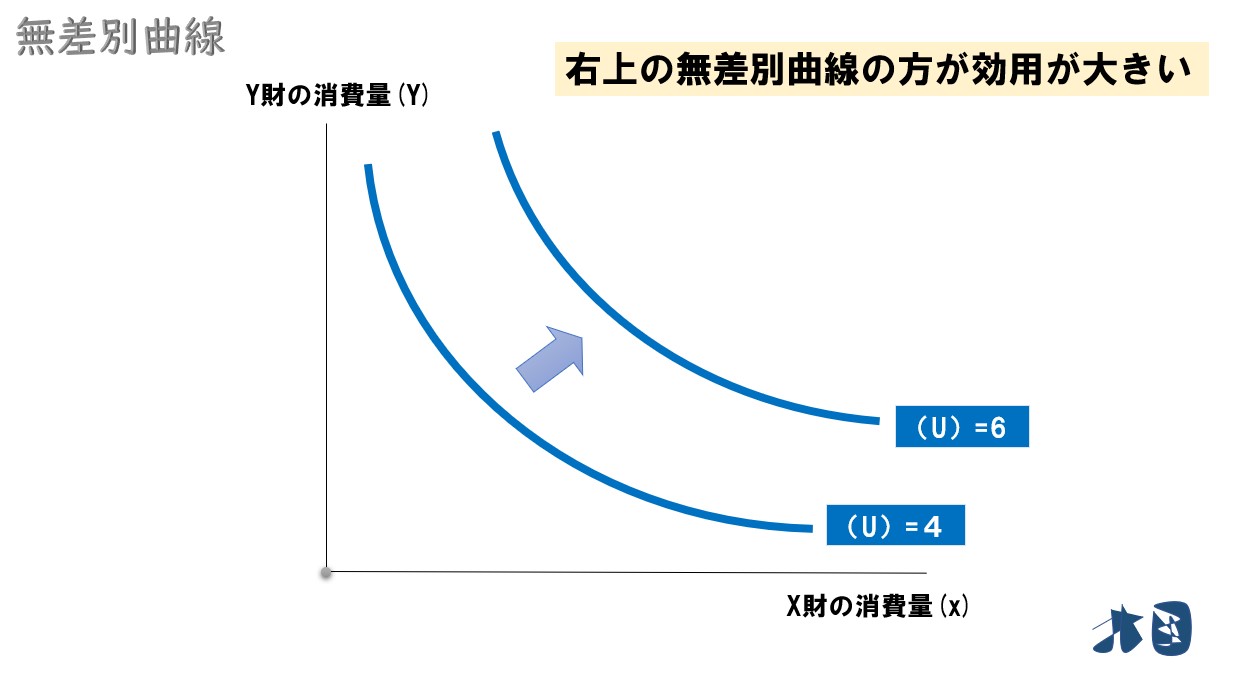
X財・Y財の消費量のどちらかの消費量を増やした場合、グラフ上では、より上方向か右方向に無差別曲線を書くことが出来る。
つまり
2財が単調性(非飽和性)を満たしていれば
- 財の消費量の増加=効用の増加
- 財の消費量の増加=グラフ上では、上方か右方向で無差別曲線が書ける
この2つから、右上の無差別曲線ほど効用が高くなる。
無差別曲線は交わらない
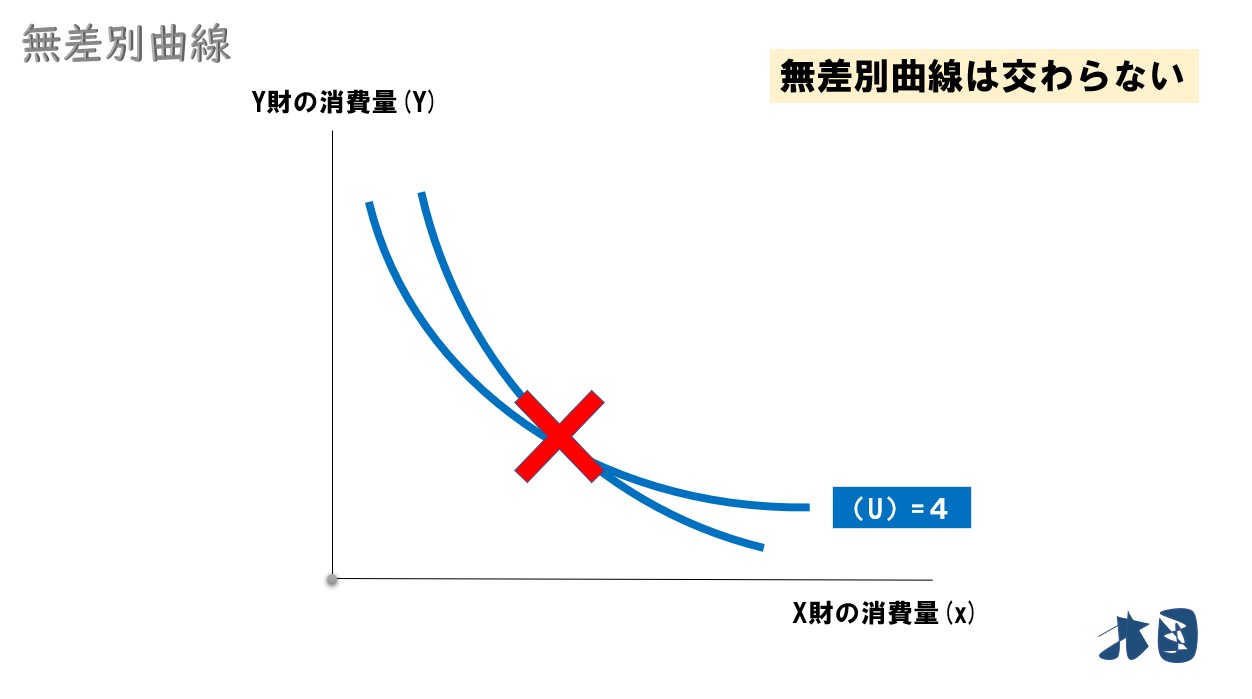
最初に
X財とY財の2財を考える。
- 2財の消費について単調性(非飽和性)を満たしているとする(=消費者の選好が単調性(非飽和性)を満たすとする)。
- 消費の組み合わせについて推移性を満たしているとする。
ポイント
2財とも消費をすればするほど効用が増加する。これを単調性(非飽和性)と呼ぶ。
X財とY財の消費の組合わせ「A・B・C」があった場合、「A ≧ B」「B ≧ C」という選好なら「A ≧ C」を満たすことを推移性と呼ぶ。


ここで
無差別曲線(U=1)と無差別曲線(U=2)が交わっているとします。
- 無差別曲線(U=1)上に点Aと点B
- 無差別曲線(U=2)上に点Aと点C

次に
同じ無差別曲線上ならば、「どのX財・Y財の消費の組み合わせ」も同じ効用となる。
- 無差別曲線(U=1)上にある点Aと点Bは同じ効用の大きさ
- 無差別曲線(U=2)上にある点Aと点Cは同じ効用の大きさ
ここで
推移性を満たしているため、「点Aと点Bの効用の大きさが同じ」「点Aと点Cの効用の大きさが同じ」という情報から「点Bと点Cも効用の大きさが同じ」となる。
しかし
グラフから、点Cは
- 点Bよりも右上に存在している
- X財の消費量・Y財の消費量ともに点Bより多い
単調性(非飽和性)を満たしていることから、点Cは、点Bよりも効用が大きくなるはずである。
単調性(非飽和性)は、消費をすればするほど効用が増加することを言いました。ここでは、点Cの方がX財の消費量・Y財の消費量がともに点Bより多いため、消費量が多い=より効用が高いと判断できます。


そのため
2財の消費について推移性・単調性を満たすことから、2つの無差別曲線が交わることで矛盾が生じるため、2つの異なる無差別曲線が交わることはない。
無差別曲線が原点に対して凸
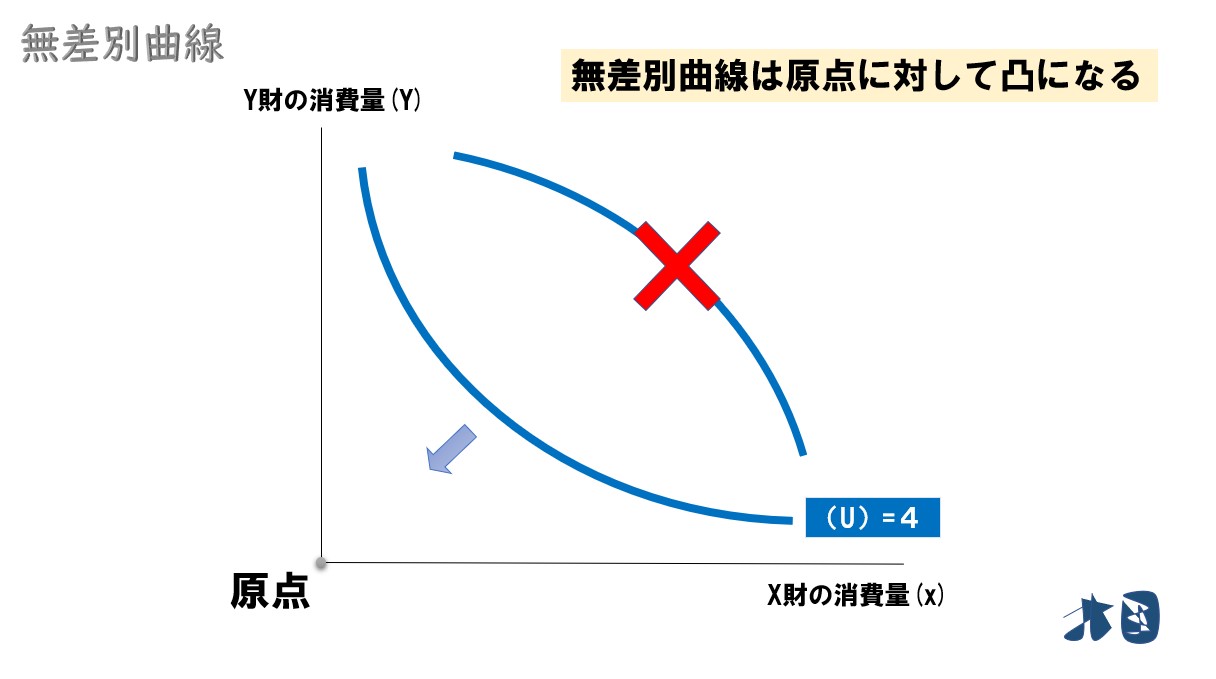
ポイント
限界代替率逓減の法則を知る。


最初に
X財とY財の2財を考える。
ポイント
普通は、同じものをずーっと消費するよりは、どちらもバランスよく消費したいです。
例えば
紅茶とケーキで考える。
普通なら、ケーキを食べ続けるよりも、紅茶も飲みながらケーキを食べたい。


「限界代替率逓減の法則」は、同じものを消費し続けるよりも、2財をバランスよく消費したいという人の性質を表した考え方です。
さらに詳しく
限界代替率は「X財の消費量を1つ増やしたとき、同じ効用を維持するために、どれくらいY財の消費量を減らす必要があるか」を表している。通常、この限界代替率は「X財の消費量を1つ増やすほど、減らすY財の消費量は小さくなる」。これを「限界代替率逓減の法則」という。
ポイント
限界代替率逓減の法則が成り立つとき、無差別曲線は原点に対して凸となる。
例えば
パンにソーセージを挟んで食べます。
- パン1つ・ソーセージ1つ
- パン2つ・ソーセージ2つ
1つ食べるより、2つ食べる方が効用は増えます。
ここで
- パン4つ
という風に食べるときを考えてみましょう。


ポイント
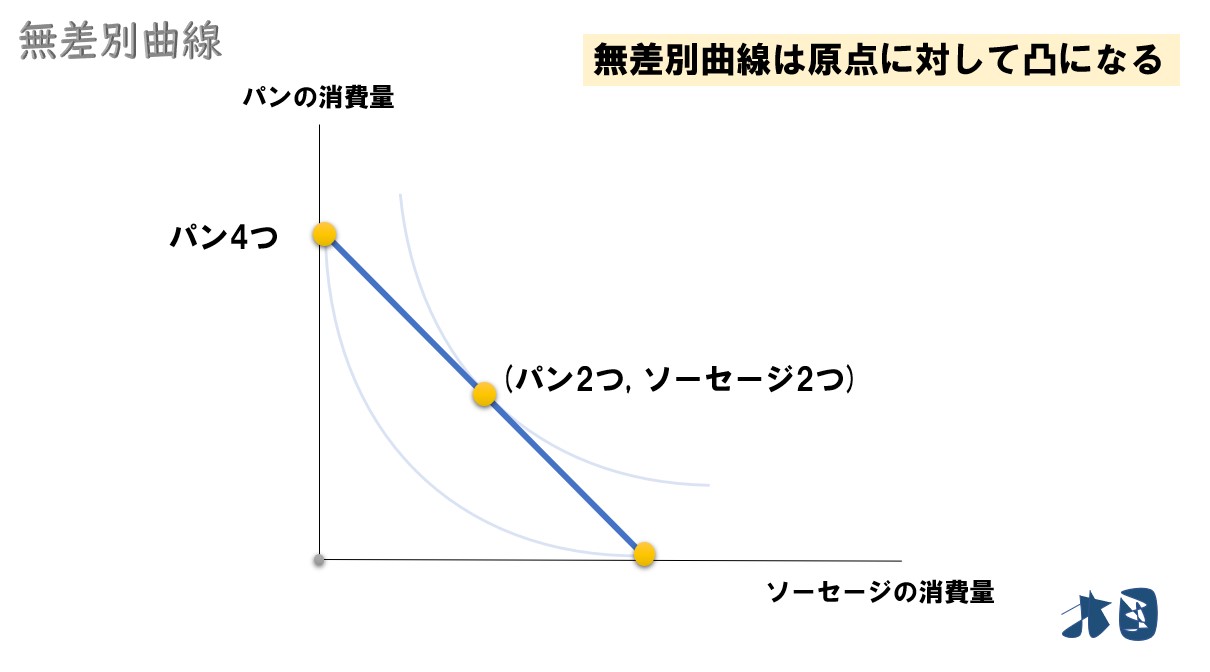
「パン4つ」を食べるよりも「パン2つ・ソーセージ2つ」とバランスよく消費する方が、得られる効用が大きくなります。
グラフで見ると
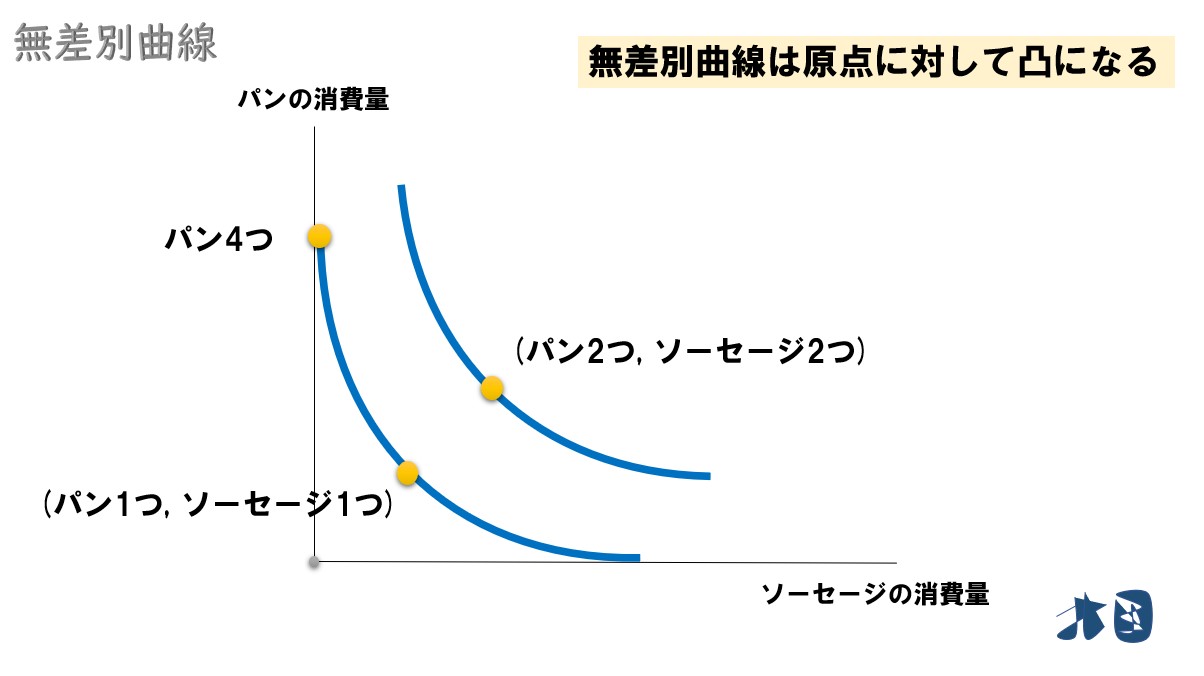
ここで「パン4つ」と「パン2つ・ソーセージ2つ」は、どちらも財を4つ消費しています。
しかし、先ほど書いたように、パンだけを4つ食べるより、ソーセージもバランスよく食べたいです。そのため、同じ4つ消費するでも「パン2つ・ソーセージ2つ」という組み合わせの方が効用が高くなります。
仮に
「パン4つ」と「パン2つ・ソーセージ2つ」が同じ効用ならば、無差別曲線は直線になる。


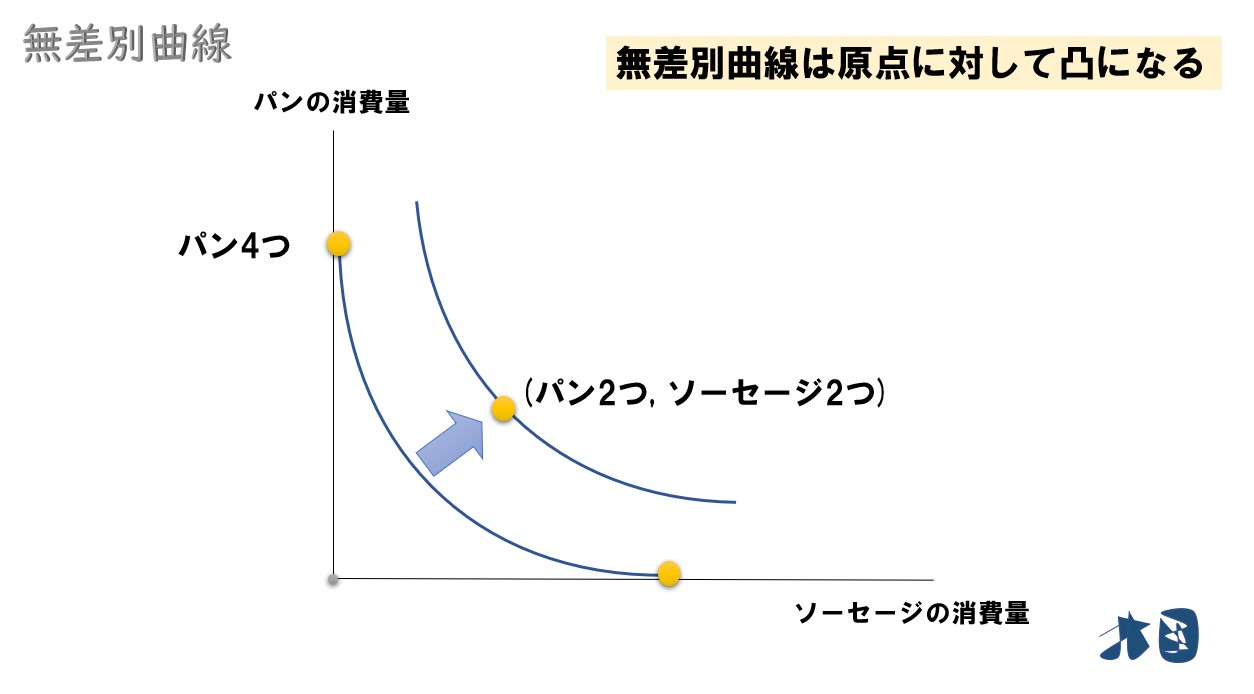
「パン4つ」よりも「パン2つ・ソーセージ2つ」の方が効用が高くなるため、「パン2つ・ソーセージ2つ」は右上の無差別曲線上に存在することになります。
つまり
- 「パン4つ」と「パン1つ・ソーセージ1つ」が同じ効用
- 「パン4つ」よりも「パン2つ・ソーセージ2つ」の方が効用が高くなる
この条件を満たす無差別曲線を書こうとすると、原点に対して凸の曲線を書くことになります。したがって、無差別曲線は原点に対して凸となります。


なので
通常は、限界代替率逓減の法則が成り立つため「パン4つ」よりも「パン2つ・ソーセージ2つ」の方が効用が高くなる。そのため、無差別曲線は原点に対して凸になるような曲線となる。
などのように、簡単に書かれることが多いです。
無差別曲線の形状には例外もあります。
例外についてはこちらから⇒特殊な無差別曲線【直線・L字・円形・右上がり・原点に対して凹】