どのくらい市場では独占が進んでいるかを判断するための指標として有名な「ラーナーの独占度(マークアップ率)」
- ラーナーの独占度の意味
- 式の導出
- 需要の価格弾力性との関係
- 計算問題や求め方
ラーナーの独占度の基本的な情報をまとめています。
ラーナーの独占度とは

(Wikipediaより・アバ・ラーナー)
はてな
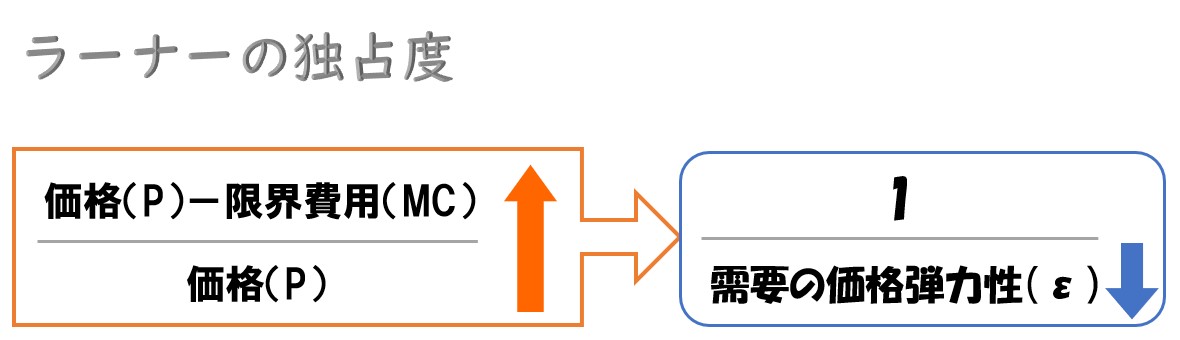
市場の独占がどれくらい進んでいるかを判断するための指標。完全競争市場なら0となり、独占市場ならば1となる。
※マークアップ率と表現されることもある。


ポイント
ラーナーの独占度は、価格が限界費用からどれくらい離れているかで値が決まる。
完全競争市場ならば「価格(P)=限界費用(MC)」という数式が成立します。一方で、不完全競争市場だと「価格(P)>限界費用(MC)」となります。
つまり
完全競争市場なら「価格(P)=限界費用(MC)」となるので、「価格(P)」と「限界費用(MC)」の差が大きくなるほど、完全競争から離れていく(=市場で独占が進んでいる)と考えています。
簡単な考え方を理解したところで、「ラーナーの独占度」の式の導出をしてみます。
ラーナーの独占度は、需要の価格弾力性とセットで語られることが多いですが、実際にどうして需要の価格弾力性(の逆数)が登場するのかを見ていきましょう。
式の導出
まずは、左辺から簡単に説明します。
最初に記載した通り、完全競争市場なら「価格(P)=限界費用(MC)」となるので、「価格(P)」と「限界費用(MC)」の差が大きくなるほど、完全競争から離れていく(=市場で独占が進んでいる)と考えているのがラーナーの独占度です。
左辺の「(P-MC)/P」がそれを表しています。
「価格(P)」と「限界費用(MC)」の差を求めるために「P-MC」として、割合で示すために「P」で割っています。
ここから本題
右辺に「需要の価格弾力性(ε)の逆数」が登場するのは何故か


はじめに「需要の価格弾力性(ε)の計算式」を思い出す
ポイント
需要の価格弾力性(ε)=-(需要の変化率(%)/価格の変化率(%))
=-「需要の変化量(ΔD)/元の需要量(D)」/「価格の変化量(ΔP)/元の価格(P)」
=-「ΔD/D」/「ΔP/P」


式を変形する
需要の価格弾力性(ε)=-「ΔD/D」/「ΔP/P」
- 分母分子を逆にする(逆数にする)
「1/ε」=-「ΔP/P」/「ΔD/D」
- 右辺を掛け算にして整える
「1/ε」=-「ΔP/P」×「D/ΔD」
「1/ε」=-「ΔP/ΔD」×「D/P」
- 両辺に-Pを掛ける
「-P/ε」=「ΔP/ΔD」×「D」‥‥①
ここで
限界収入(MR)を計算します。限界収入(MR)を求めるには総収入(TR)を生産量(x)で微分する必要があります。
「総収入(TR)=価格(P)×生産量(x)」です。
市場では需要(D)と供給=生産量(S)が一致して取引されるため、生産したものは全て販売すると考えて、価格(P)と生産量(x)を掛けた金額が総収入(TR)です。
「総収入(TR)=価格(P)×生産量(x)」の「価格(P)」に注目します。
価格(P)を需要関数を使って表す。需要関数と言われてもピンと来ないかもしれませんが、グラフで需要と供給を描いた時の需要曲線のことです。
価格(P)を需要関数を使って表すと「P=-○x+○○」と表記できます。
グラフの縦軸に価格(P)を取ったとき、価格(P)は、横軸の生産量(x)によって値が決まるため「P(x)」と表記します。
教科書的には「P=-○x+○○」の形にした式を逆需要関数と呼びます。
以上より
「総収入(TR)=需要関数P(x)・生産量(x)」と表すことが出来る。つまり、この式を微分すれば限界収入(MR)になる。
ポイント
ここで「需要関数P(x)」「生産量(x)」のどちらにも「x」が関わっています。このとき「P(x)」「x」のどちらも「x」で微分可能と考え、積の微分公式を使います。
限界収入の計算に当てはめる
- f(x)=P(x)
- g(x)=x
と考えて「P(x)・x」をxで微分するなら、下記の2つを足し合わせればよいので
- P(x)をxで微分したもの=「ΔP(x)/Δx・x」
- xをxで微分したもの=「P(x)・Δx/Δx」
「(ΔP(x)/Δx)・x+P(x)・Δx/Δx」が微分した結果になる。
最後の「Δx/Δx」は「1」になるので「(ΔP(x)/Δx)・x+P(x)」が答え。


「限界収入(MR)=(ΔP(x)/Δx)・x+P(x)」と求まったが、この後の計算のために末尾の「+P(x)」を左辺へ移行する。
- 「MR-P(x)=(ΔP(x)/Δx)・x」
最後のステップ
ここまで「需要(D)」「生産量(x)」として話してきましたが、市場では需要(D)と供給(S)が一致するところで生産と消費が行われます。つまり「需要量(D)=供給量・生産量(x)」です。
なので、さきほどの下記式の「x」をDへ置き換えます。
「MR-P(x)=(ΔP(x)/Δx)・x」
⇒「MR-P(x)=(ΔP(x)/ΔD)・D」
さらに「P(x)」は、もともと価格(P)を需要関数として表記したものだったので、ややこしくなるため「P」という表記へ統一します。
「MR-P=(ΔP/ΔD)・D」‥‥②
①②より「-P/ε=MR-P」
①「-P/ε」=「ΔP/ΔD」×「D」
- 両辺を-Pで割る
1/ε=(MR-P)/-P
1/ε=(-MR+P)/P
1/ε=(P-MR)/P
最後に、独占市場の利潤最大化条件より「MC=MR」が成り立つため
1/ε=(P-MC)/P
⇩両辺を入れ替えると
(P-MC)/P=1/ε


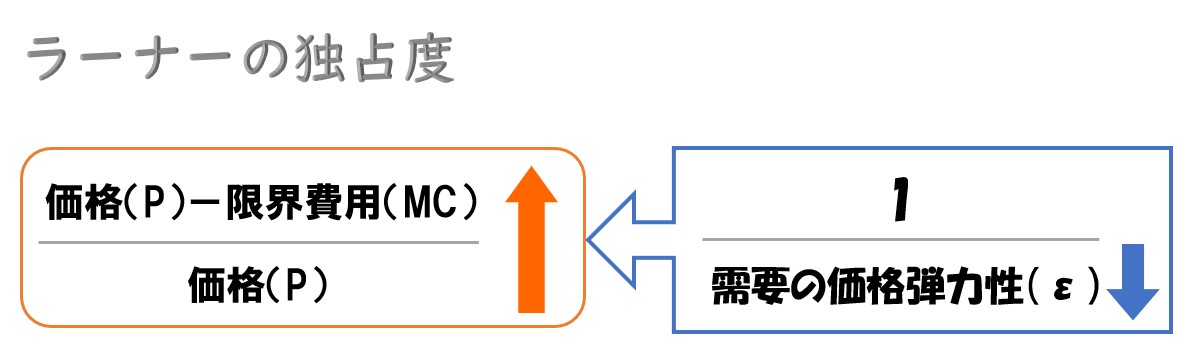
独占度と「需要の価格弾力性」の関係性
ポイント
ラーナーの独占度は需要の価格弾力性の逆数と等しい。このことから、需要の価格弾力性が小さいほど、独占度が高くなることが分かる。
※式の導出は「前の段落」で確認してください。
はじめに
ラーナーの独占度を大きくするには、需要の価格弾力性を小さくする必要があります。
逆に言えば
需要の価格弾力性が小さいほど独占度が大きくなる。
なぜ需要の価格弾力性が小さいほど、独占度が大きくなるのか
数式上は「需要の価格弾力性が小さいほど、独占度が大きくなる」ことが分かっても、現実で考えると、これはどういう意味合いがあるのでしょうか。
思い出す
- 「需要の価格弾力性が大きい」ほど「価格変化に対して敏感に反応する」
- 「需要の価格弾力性が小さい」ほど「価格変化に対してあまり反応しない」
ちなみに、ラーナーの独占度では、需要の価格弾力性が「弾力的(ε>1)」である場合を前提にしており、「非弾力的(ε<1)」な状態を想定していません。独占度を計算する式の右辺が「1/ε」となっているため、εが1よりも小さいと独占度が「1」を超えるためです。※ラーナーの独占度は「0~1」の範囲で考えます。
例えば
日常品や代替品がないような商品・サービスは「需要の価格弾力性が小さい」

(例)仮にすべてのトイレットペーパーの価格が100円から150円(1.5倍)になっても、トイレの回数は減らないのでトイレットペーパーの購入量はあまり変化しません。
このような状態を「需要の価格弾力性が小さい」と言います。需要の価格弾力性についてはこちら。
ここで、需要の価格弾力性が小さい市場での企業側の行動も見ておきます。
企業
価格を上げても消費量はそんなに変わらないし、値上げして利益を出そう。
以上より
ポイント
「需要の価格弾力性が小さい」市場では価格が高くなっても消費量が減りづらい。価格を上げても消費量が減りづらいため、企業は価格を吊り上げて利益を出そうとする。
企業は価格を自由に設定できるプライスメイカー(価格決定者)になるため、市場では独占の色合いが強くなる。
現実世界では、日常品や代替品がないような商品・サービスでは「需要の価格弾力性が小さい」傾向があるため、独占度が高くなる傾向にある。


例えば
- 通信費

①今の時代、スマホが無いと生活ができないため、通信費は需要の価格弾力性が小さい(価格が高止まりしても契約しないわけにはいかない)と考えられる。
②日本のキャリア3社(K社・S社・N社)は、高い価格設定で殿様商売をしている。
⇒ラーナーの独占度で考えれば独占度は高くなるはず。
- 映画館の飲み物とポップコーン

日本の映画館で飲み物とポップコーンを購入すると700円~800円程度は普通にかかる時代です。
①映画を見に行っているのに、飲み物もポップコーンも買わないという選択肢は意外と取りづらい(需要の価格弾力性が小さいと考えられる)。
②映画館を運営している業者だけが飲食物の販売を行っているため価格が高いまま。
⇒ラーナーの独占度で考えれば独占度は高くなるはず。
- 航空機の繁忙期の価格

学校や会社のスケジュールに合わせると、年末年始・ゴールデンウィーク・お盆などに、旅行や帰省が集中するのはごく自然です。
①休みを取れる期間は決まっており、他の日付で代替することが難しい(需要の価格弾力性が小さいと考えられる)。
②航空機は普通、繁忙期の方が値段が高く設定されます。
⇒ラーナーの独占度で考えれば独占度は高くなるはず。


欠点

ラーナーの独占度は比較的有名な指標ですが、もちろん欠点もあります。
ポイント
企業の限界費用(MC)や、市場の需要の価格弾力性がどれくらいなのかを計算するのが難しい。
計算問題などでは、すんなりと計算出来て難しさをあまり感じない項目ですが、現実問題として、限界費用(MC)や価格弾力性を計算するのは難しいです。
そのため、独占度を測る指標としては生産集中度などの別の指標が用いられることもある。
生産集中度
ある商品・サービスにおいて、それを生産している企業を数社挙げたとき、その数社でどれだけ全体のシェアを占めているかを示す割合のこと(Wikipediaより)


計算問題

ある独占企業が支配する市場において、次の条件のとき、均衡におけるラーナーの独占度と需要の価格弾力性(ε)を求める。
- 価格=P
- 財の需要量=D
- 財の生産量=x
- 市場の需要関数:D=-P+40
- 独占企業の費用関数:C=xの2乗+10
はじめに
独占企業の費用関数(C)から限界費用(MC)を求める。
ポイント
限界費用(MC)を求めるには、(総)費用関数(C)を生産量(x)で微分すればOKです。
「限界費用曲線」の項目で総費用との関係性を知りましょう⇒【費用曲線の要点を分かりやすく】総費用・固定・可変・平均可変・限界 ※特に「接線の傾き」がポイント
費用関数(C)を生産量(x)で微分する
- C=xの2乗+10
- C’=2x
以上より「限界費用(MC)=2x」
微分は、乗数を「-1」して手前に持ってくる。なお、微分する文字がついていない部分は無視する。ここでは+10にはxがついていないので0として考える。
次に
需要関数(D)から限界収入(MR)を計算する。
ポイント
独占市場で限界収入(MR)を求めるには、需要関数(D)を逆需要関数(P)にして傾きを2倍すればOKです。
- D=-P+40
- P=-D+40 ←傾きを2倍する
- P=-2D+40
以上より「限界収入(MR)=-2D+40」
ここで
限界費用(MC)=2x
限界収入(MR)=-2D+40
独占市場の利潤最大化条件「MC=MR」より
- 2x=-2D+40
また、異なる文字で考えていた下記の2つは同じものを表している
- 財の需要量=D
- 財の生産量=x
独占市場においても、市場で生産された財の数だけ消費者は財を消費するため「生産量=需要量」と考える。
以上より
- 2x=-2D+40
- 2x=-2x+40
- 4x=40
- x=10
また、市場の需要関数「D=-P+40」だったため
- 10=-P+40
- P=30
次に「限界費用(MC)=2x」より
- MC=2×10
- MC=20
最後に
ラーナーの独占度の計算するために必要な「価格(P)」「限界費用(MC)」がわかったので、後は式に当てはめて計算するだけ。
ラーナーの独占度「(P-MC)/P」より
(30-20)/30=10/30=1/3
ラーナーの独占度は需要の価格弾力性(ε)の逆数に等しいので
「(P-MC)/P=1/ε」よりε=3
- ラーナーの独占度=1/3
- 需要の価格弾力性(ε)=3