「限界生産力」「限界生産力逓減の法則(収穫逓減の法則)」について
- 限界生産力とは?
- 限界生産力(収穫)逓減の法則とは?
- 限界生産力の求め方・計算
- 限界効用を求める時に微分する理由
限界生産力の意味・求め方・計算方法が分からない人に向けて、限界生産力について簡単にまとめています。
限界生産力・限界生産力逓減の法則とは?
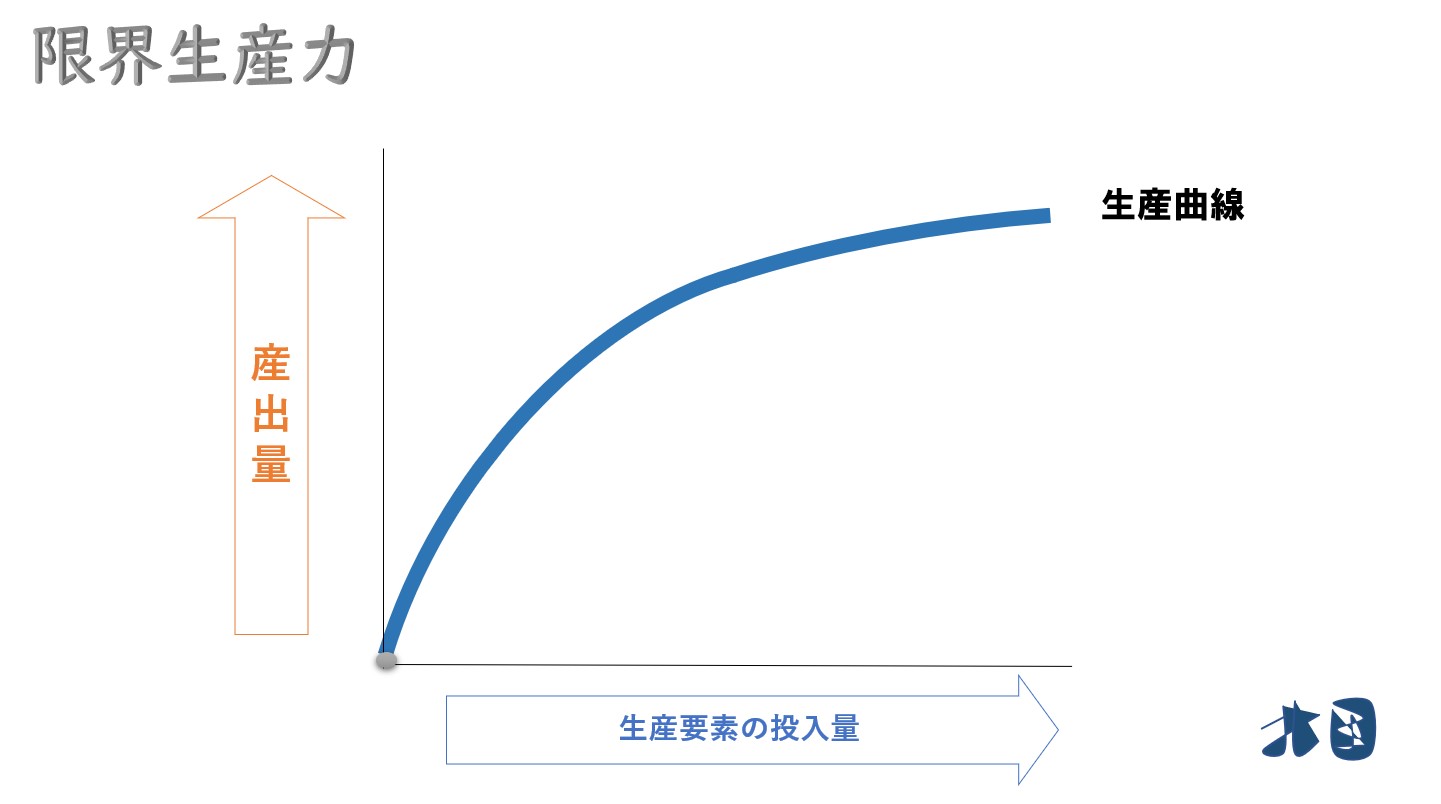
限界生産力(MP)とは
生産要素(労働力など)を1単位追加的に投入した場合の生産量の増加分のこと。
経済学で登場する「限界 (Marginal)」には「追加で発生する・追加的な」という意味がある。
英語で「Marginal Productivity」と書くのでMPと略すことがある。
例えば
- お米の収穫をする

1人で収穫すると、40kgのお米を収穫できます
ここで
もう1人に手伝ってもらいお米を収穫したところ、合計で100kg収穫できました。
つまり、労働力を1人分追加して60kgも多くお米を収穫できたと言えます。
ポイント
このときの限界生産力は”60kg”です。
「労働力1人」という生産要素を追加したことで60kgの生産物が得られた。


機械を1台追加して、商品をプラス100個生産したなら「限界生産力は100個」です。このように、生産要素(労働・資本・土地)なら、全て限界生産力という考え方が登場します。
- 労働の限界生産力
- 資本の限界生産力
- 土地の限界生産力
「限界生産力」と単純に表現することの方が多いです。
注意点
限界生産力は、1つの生産要素だけで考えています。
土地と労働力があった場合に、土地は一定として労働力を追加したときに、産出量がどれくらい増えるか?を表したのが限界生産力です。
この前提がないと限界生産力の特徴を理解できなくなるので気を付けましょう。
特徴
- 限界生産力には「限界生産力逓減の法則」という特徴があります
ポイント
生産要素を追加するにつれて、1単位追加で生産要素を投入したときに得られる生産物は減少していく。これを「限界生産力逓減の法則」もしくは「収穫逓減の法則」という。
お米の収穫で考えてみましょう。
- お米の収穫をする

1人で収穫すると、40kgのお米を収穫できます
もう1人に手伝ってもらいお米を収穫したところ、合計で100kg収穫できました。この時の限界生産力は”60kg”です。
ここで
更に人を増やすとどうなるでしょうか・・?
実っているお米は全部で150kgとします。
3人目を雇ったことで、残りの50kgを収穫できたので限界生産力は”50kg”です。


注意ポイント
ここで先ほどの注意点が重要になります。
限界生産力は1つの生産要素だけに注目して、他の生産要素は一定と考えます。
「実っているお米は全部で150kgとします」という前提があったので、3人目の限界生産力が”50kg”でしたが、土地も増やして作っているお米を1万kgとかにすれば、限界生産力は逓減しません。


全ての生産要素を増やせば「限界生産力逓減の法則が当てはまらないのでは・・?」と思ってしまいますが、そういう話では無いので注意しましょう。
また「最初は生産要素を追加すれば効率的になるのでは?」と感じる人もいるかと思います。それは正しいですが、あくまで「生産要素を追加し続ければ最終的に限界生産力は逓減していく」と考えてください。
本当に当てはまらない?
1990年代以降のネットビジネスが主流の世界では、本当に「限界生産力逓減の法則」が当てはまらないのでは?という意見もあります。
例えばグーグルは、世界中に検索サービスを提供しているので、関連サービスを開発すれば無限に利益が出るように思えます。
しかし、それにはエンジニアを雇ったり、物理サーバを設置したり、セキュリティ機器も必要です。
つまり、開発エンジニアだけを雇い続けたり、機材を買い続けるだけではダメです。労働も資本もバランスよく追加しないと機能しなくなります。
もともと「限界生産力逓減の法則」は1つの生産要素だけを追加し続けると、限界生産力が逓減するという話だったので、その意味で考えればIT企業も例外ではないと考えられますが、現実世界でそうなっているかは議論が続いています。
限界生産力の求め方

限界生産力を求める場面で「微分」するという言葉が出てきます。
- なぜ微分するのか?
- どのように微分すればいいのか?
この2つが分かるように限界生産力の求め方と計算方法をまとめました。
生産要素が1つの場合
ポイント
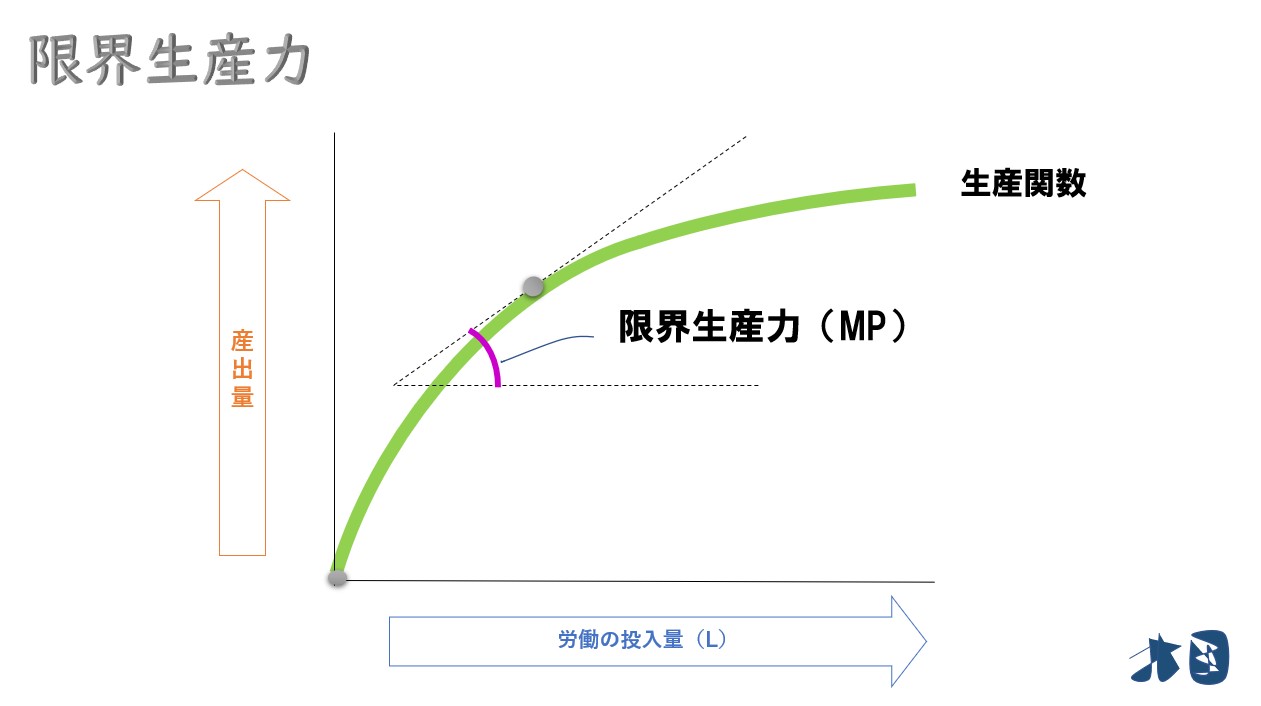
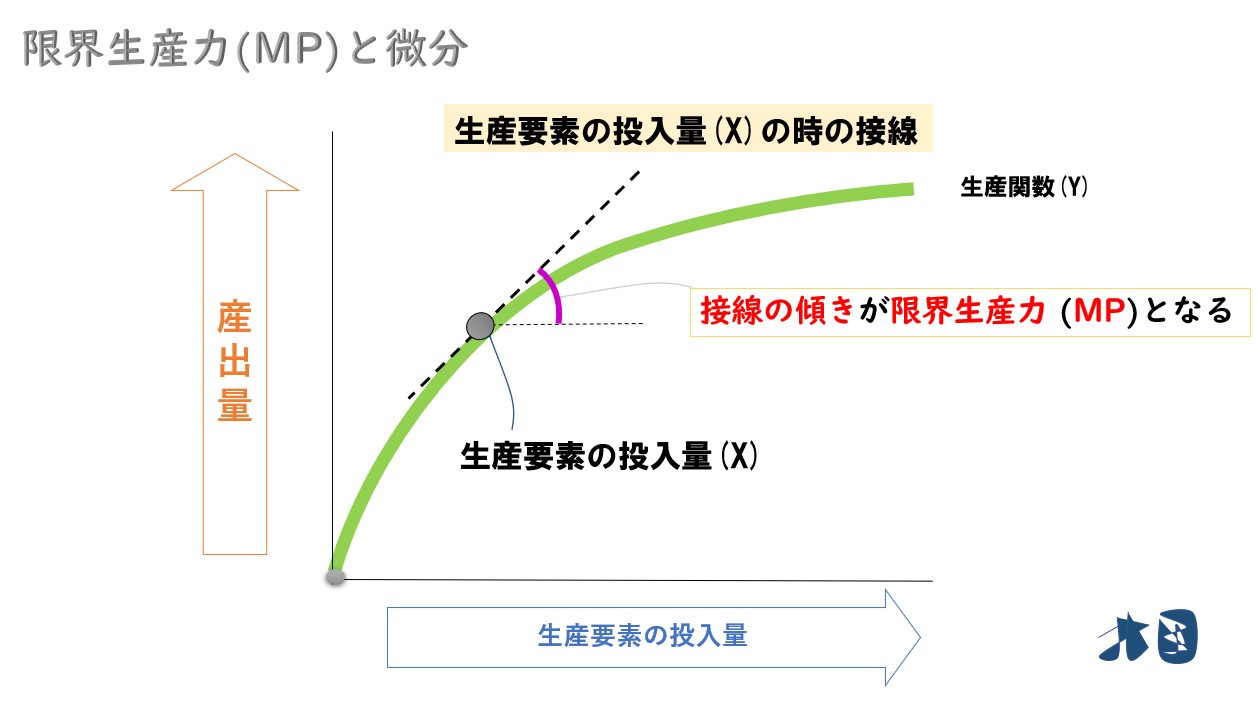
生産関数(Y)を生産要素の投入量(労働量や資本量)で微分すると限界生産力(MP)になる。


限界生産力は、生産要素を1単位追加的に投入した場合の産出量の増加分のこと。
なので
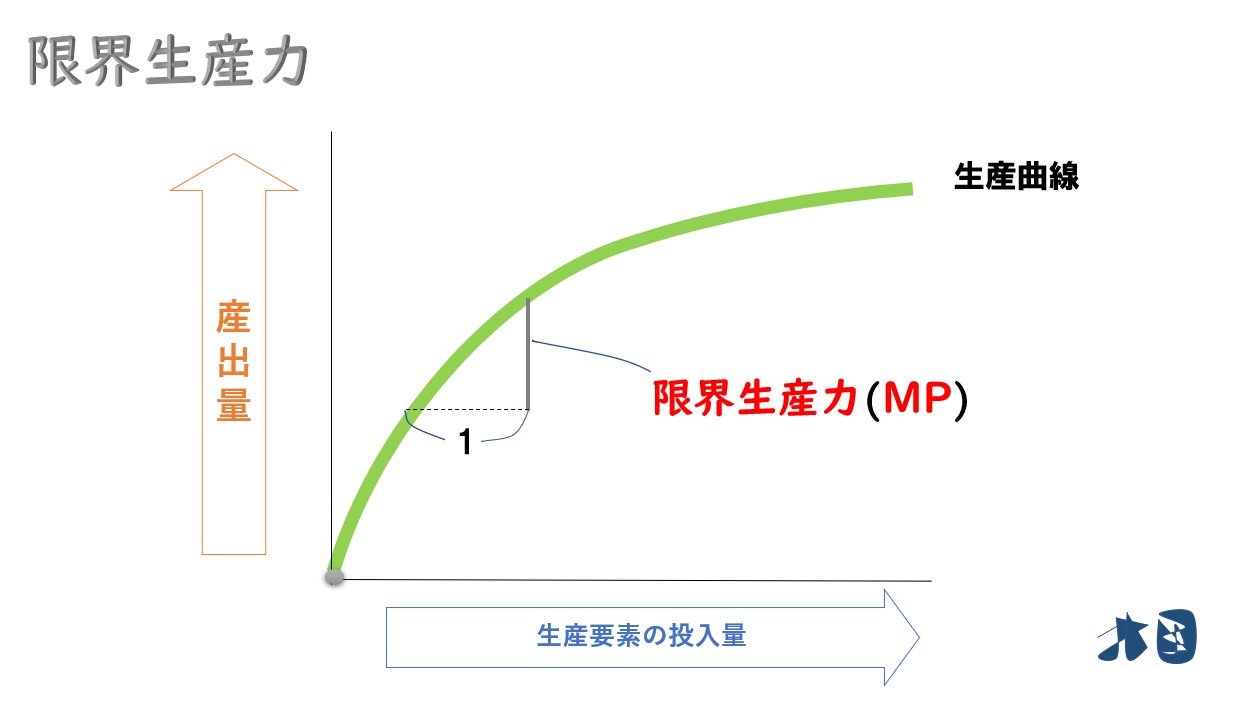
グラフを見ると分かりやすいですが、横軸へ1つずらした時に、縦へ動いた分が限界生産力になります。


1つ1つ横軸を動かして、縦にどれくらい動くかを考えるのは非常に面倒です。
そこで、数学の知識を使って解くことになります。
そもそも
なぜ生産要素の投入量(ここでは労働力=L)で微分するのか?
ポイント
限界生産力を求めるのに微分をする理由は、傾きを求めるため。
重要!
「横軸へ1つずらした時に、縦へ動いた分が限界生産力」ならば「傾き」を求めれば良い。
限界生産力と傾きの関係
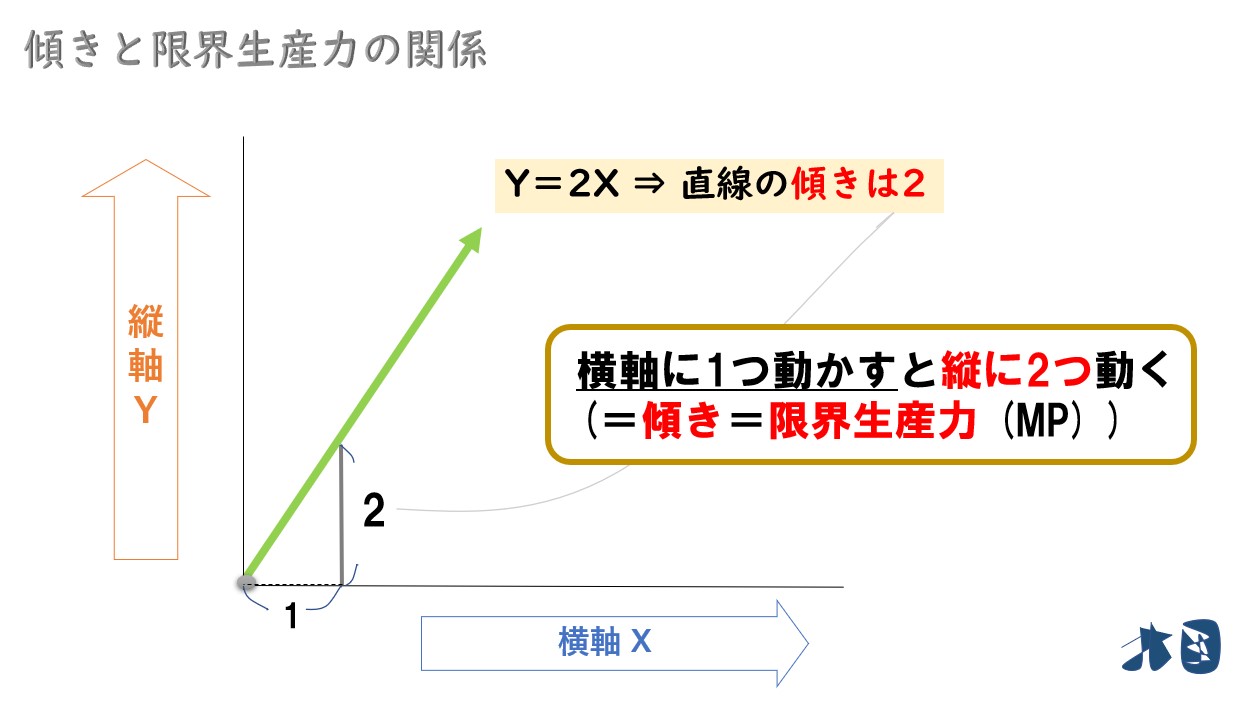
「Y=2X」という関数で考えてみます。
「2X」なので、この関数の傾きは2です。※仮に3Xなら傾きは3です。
傾きは、横軸へ1つ移動した時に、縦にいくら移動するかを表しています。
つまり「傾き」と「限界生産力(MP)」は同じことを言っています。なので限界生産力(MP)を求めるために傾きを求めています。ここでは「傾き=限界生産力(MP)=2」です。
ここで
傾きを求めるために微分をする理由
「Y=2X」の例ではグラフが直線でした。なので、すぐに傾きを求めることが出来ます。
しかし
限界生産力(MP)は「限界生産力逓減の法則」があるため、グラフが次第に緩やなカーブになります。


ポイント
微分は文字通り、グラフを細かく分けて1つの点として処理します。「その点を通る接線の傾き」がどれ位あるかを計算すれば良いのです。
グラフで見ると・・
まとめ
傾きと限界生産力(MP)は同じになるので、傾きを求めれば限界生産力(MP)も分かる。
また、限界生産力(MP)は、限界生産力逓減の法則により、グラフが直線ではないため、微分しないと傾きが定まらない。


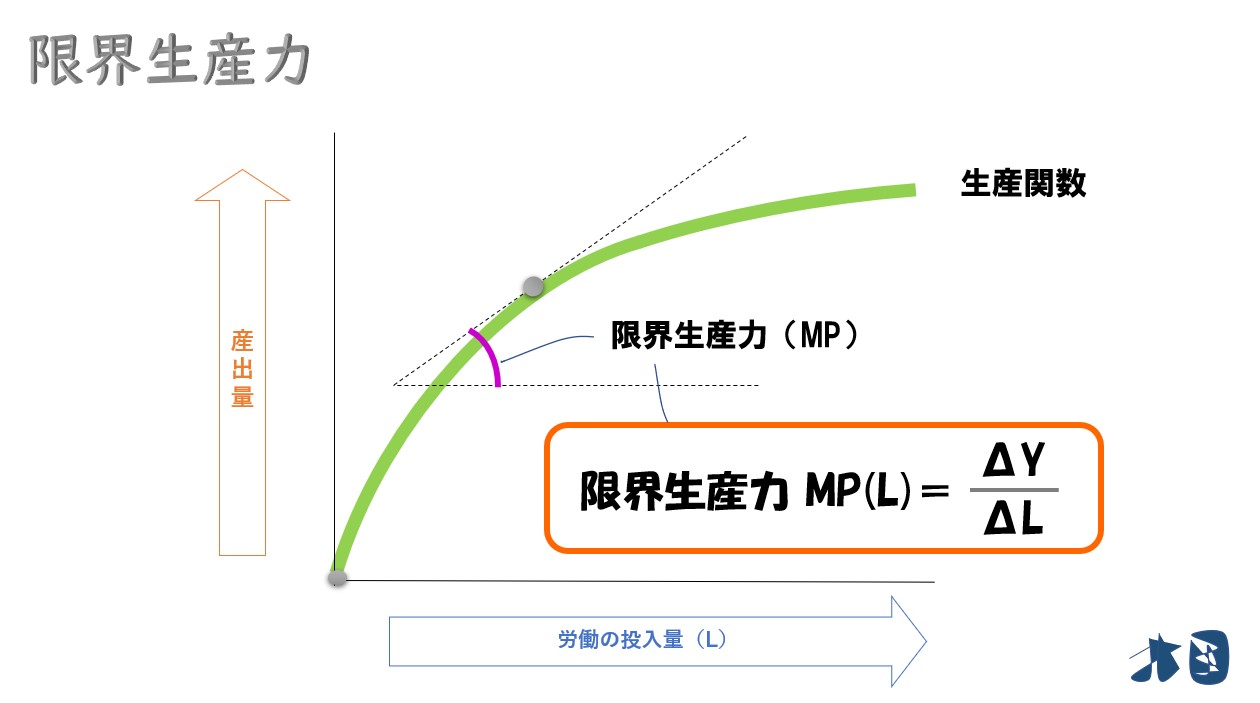
生産関数(Y)を労働(L)で微分する
- 生産関数 Y=F(L)
- 労働(生産要素)の投入量(L)
- 変化量を「Δ(デルタ)」
生産要素が労働力(L)だった場合で考えていきます。
微分すると・・
例えば「Y=2L」という数式があったとき「2L」なので「傾きは2」です。
変化量を「Δ (デルタ)」とします。
- 労働(生産要素)の投入量(L)が1増えたとき、変化量は「ΔL=1」と書けます。
- 「Y=2L」なので、Lが1増えれば「Yは2増えます (ΔY=2)」
まとめると「傾き2」=「2/1 = ΔY/ΔL」となります。
ポイント
「ΔL」は横軸に移動したことを表します。
つまり「ΔY(縦軸への移動距離)/ΔL(横軸への移動距離)」という意味合いです。
生産関数(Y)を労働の投入量(L)で微分したときの限界生産力(MP)は「ΔY/ΔL」となる。
ちなみに
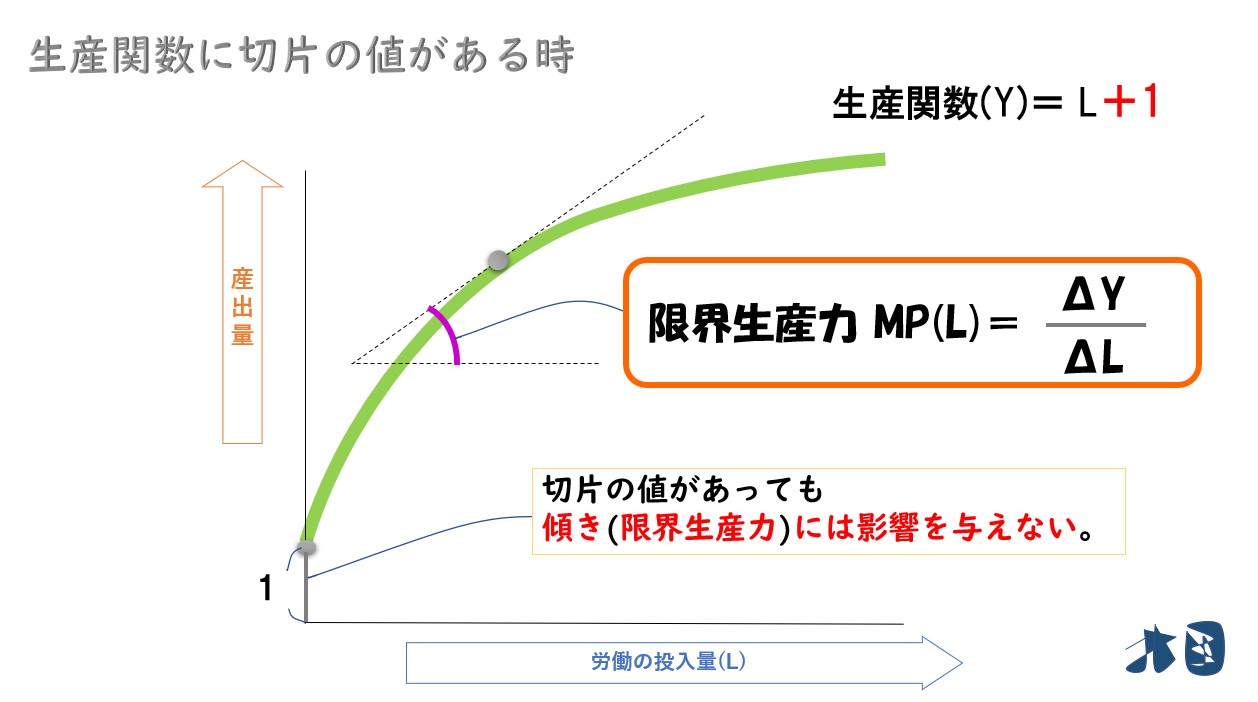
- 生産関数が「Y=L+1」のように、切片の数字が0ではない時
+1などと出てきても、微分する時には+1は無視されます。
「Y=L+1」を労働の投入量(L)で微分しても、限界生産力は「ΔY/ΔL」になる。
微分はあくまで傾きを求めるための計算なので、+1が出てきても傾きには影響しないため無視できます。
生産要素が2つの場合
ポイント
生産要素が2つ以上ある場合は、生産関数を偏微分して限界生産力を求める。


先ほどまでは生産要素が1つ(労働力のみ)として扱ってきました。
どうして?
生産要素が2つ以上で偏微分をする理由
ポイント
生産要素が2つ以上ある場合は、偏微分をすれば片方の生産要素の限界生産力が求められる。
生産要素が2つ以上ある場合は、それぞれの限界生産力を求めていきます。
「労働の限界生産力」「資本の限界生産力」をそれぞれ計算していくイメージ。
この時
片方の生産要素の限界生産力が知りたいので、不要な方を一定として考えます。
労働の限界生産力を知りたいので、資本は変化させずに(一定と)考える。
また
限界生産力は、生産関数(Y)を生産要素の投入量で微分することで求められました。
詳しくは「生産要素が1つの場合」を参照
つまり
片方の変数を一定として、片方の変数を微分することで、限界生産力が求められます。
変数は、数式に登場する「L」「K」などのこと。
ポイント
偏微分は、片方の変数を一定として、片方の変数だけを微分することを言います。なので、生産要素が2つ以上ある場合は、偏微分をすれば片方の生産要素の限界生産力が求められるのです。


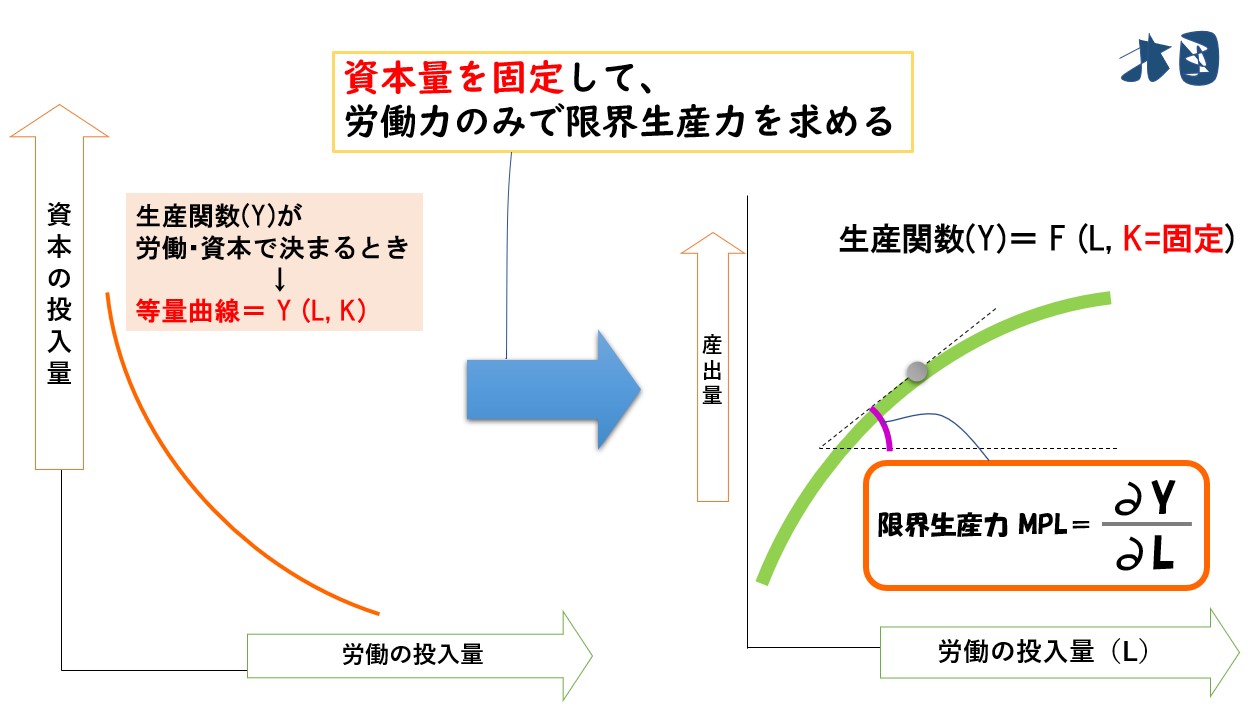
生産関数(Y)を労働力(L)と資本量(K)で偏微分する
- 生産関数 Y=F(L, K)
- 労働量(L)
- 資本量(K)
- 変化量を「∂ ※」
※読み方がたくさんあります。「ラウンド」「ラウンドディー」「デル」「ディー」など。ここでは「ラウンド」と読みます。微分の時は変化量をΔ(デルタ)と書きましたが、偏微分のときは ∂(ラウンド)と表記します。
まずは労働量(L)で偏微分すると・・
MPL (労働の限界生産力)=「∂Y/∂L」
グラフを見ると複雑に見えますが、生産要素が1つの場合と同じです。
※Δ(デルタ)が ∂(ラウンド)という表記に代わった以外は同じ。
分数の理由
労働の限界生産力(MPL)は分数で表記されますが「生産要素が1つの場合」で説明した理由と同じです。
次に資本量(L)で偏微分すると・・
MPK (資本の限界生産力)=「∂Y/∂K」
労働(L)で偏微分した時と同じです。
ポイント
- MPL (労働の限界生産力)は、Y(L, K) をLで偏微分する⇒「∂Y/∂L」
- MPK (資本の限界生産力)は、Y(L, K) をKで偏微分する⇒「∂Y/∂K」


計算問題を解く

最後に簡単な例題を解いてみます。
例題
- 生産関数(Y)=2√L・2√K
この時の「労働の限界生産力」「資本の限界生産力」を求める。
step
1労働の限界生産力(MPL)を求める
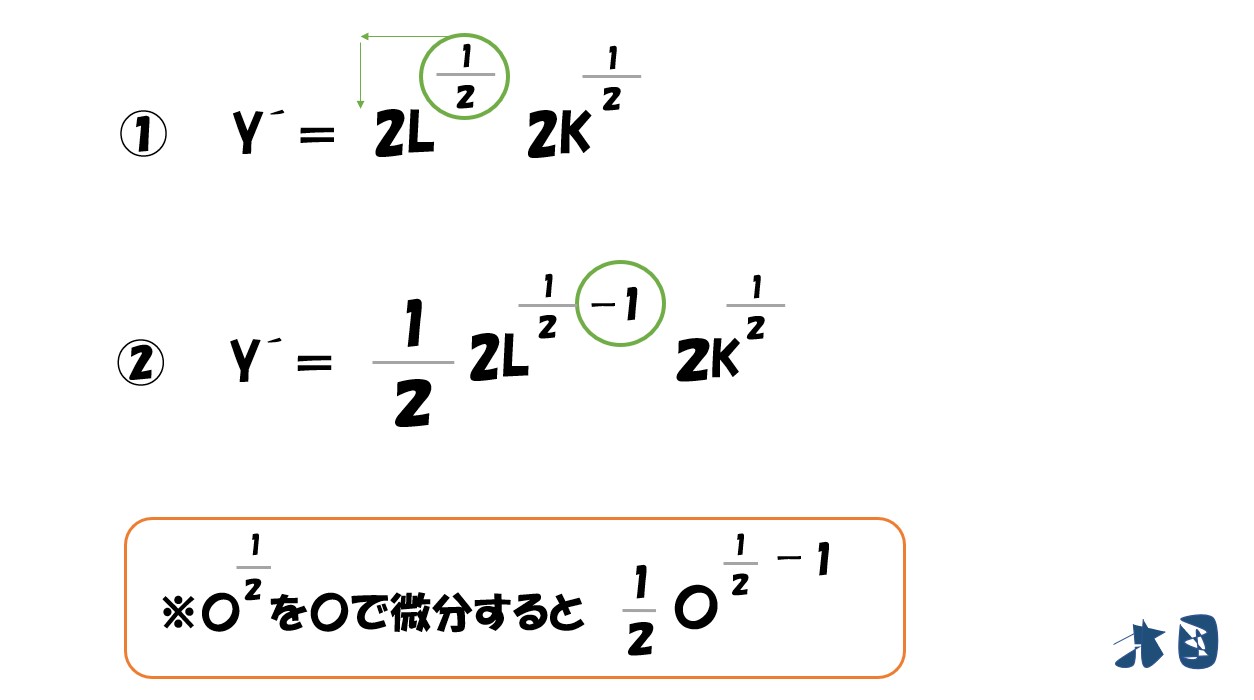
「生産関数(Y)=2√L・2√K」を「L」で偏微分します。
まず「Y=2√L・2√K」を微分できるように変形します。
変形すると・・
知っておく
「√L」は「Lの2分の1乗」とイコールです。


変形後の式を「L」で偏微分します。
微分をするときは
- 乗数を手前に持ってくる
- 乗数を「1」マイナスする
後はこれを計算するだけ
知っておく
マイナス2乗は分数を意味する
「-2分の1乗」だと・・
となります。
最終的な計算


step
2資本の限界生産力(MPK)を求める
「生産関数(Y)=2√L・2√K」を「K」で偏微分します。
計算過程は「労働の限界生産力」を求めた時と同じです。