「限界効用」「限界効用逓減の法則」は経済学では基本的な考え方になります。
- 限界効用とは?
- 限界効用逓減の法則とは?
- 限界効用の誕生(限界革命)
- 限界効用の求め方(経済学)
- 限界効用を求める時に微分する理由
「限界効用の意味が分からない」
「限界効用の求め方・計算方法が分からない」
そんな人向けに、限界効用についてまとめました。
限界効用・限界効用逓減の法則とは?

限界効用
財・サービスを1単位追加的に消費した場合の効用の増加分のこと。
経済学で登場する「限界 (Marginal)」には「追加で発生する・追加的な」という意味がある。効用は満足度のこと。
似た言葉に「限界便益(Marginal Benefits)」がありますが、これは限界効用を金銭評価したもので、市場分析を行うときに用いられる概念です。なので、ここでは限界便益という言葉は使いません。
例えば
- 自動販売機で飲み物を買う

飲み物を1口飲むと、100の効用(満足度)を得られます。
ポイント
このときの限界効用は”100”です。
「1口飲む」という追加的な消費に100の効用(満足度)が得られる。


限界効用には次の特徴があります。
特徴
- 財の消費が増えるにつれて、1単位追加で消費したときに得られる満足度(効用)は減少していく
この特徴を「限界効用逓減の法則 (ゴッセンの第1法則)」と言います。
先ほどの飲み物の例で考えてみましょう。
飲み物を1口飲むと、100の効用(満足度)を得られます。

この飲み物を2口、3口と飲んでいくとどうでしょうか?
段々と、得られる喜び・満足度が減っていきます。
注意ポイント
ジュースでもお酒でも、最初の1口目というのは、抜群に美味しいものです。しかし、ずーっと同じものを飲んでいくと、1口飲んで得られる満足度は小さくなっていきます。
グラフにしてみると・・
ココがポイント
1870年以降の近代経済学では、限界効用という考え方に基づいて理論が作られている (特に消費者理論)。また、限界効用の特徴の1つとして「限界効用逓減の法則(ゴッセンの第1法則)」が成り立つ。
ちなみに
なぜ1870年代以降なのかと言われると、この年代に経済学では限界革命と呼ばれる考え方の変革がありました。詳しくはこちら⇒ 効用とは何か?経済学的な意味と関連する話を紹介!


限界効用の求め方

経済学を勉強していると限界効用を求める(計算する)場面がたくさんあります。
どのように求めるのか最初は混乱する人も多いかと思います。ここでは簡単に限界効用の求め方・計算方法をまとめました。
財が1つの場合
ポイント
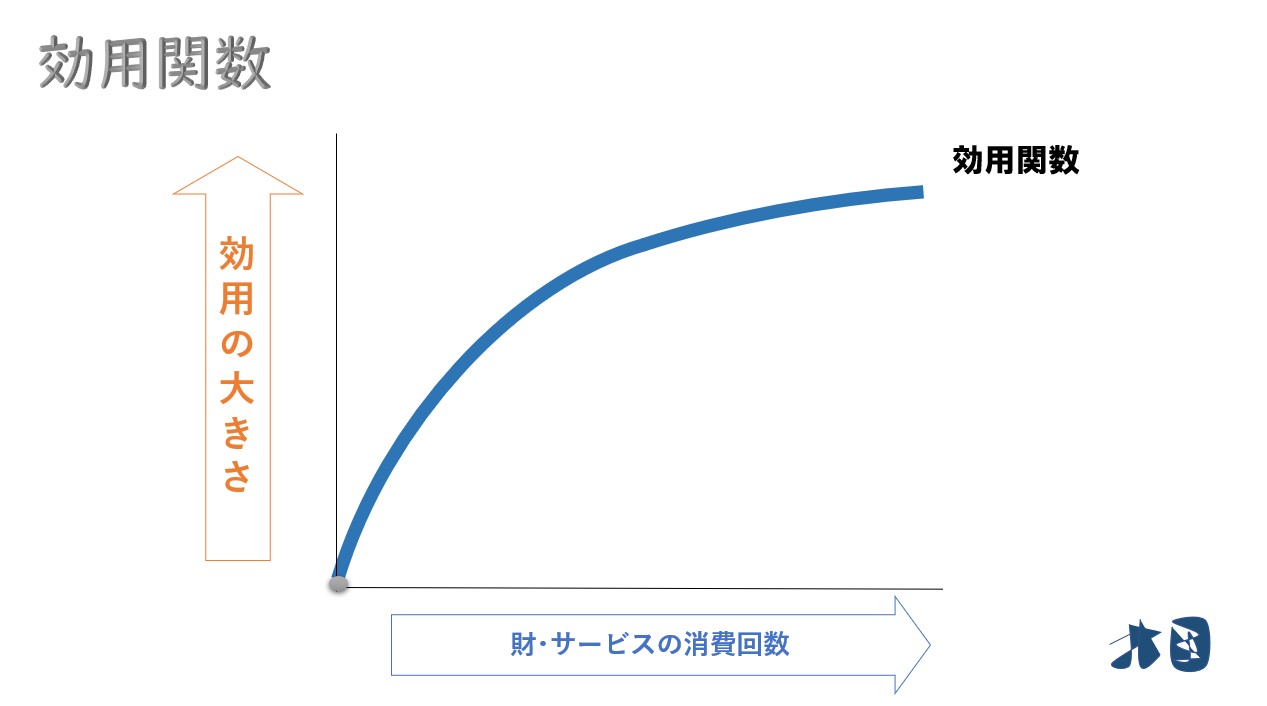
効用関数(U)を消費量(X)で微分すると限界効用(MU)になる。


限界効用は、財・サービスを1単位追加的に消費した場合の効用の増加分のこと。
なので
グラフを見ると分かりやすいですが、横軸へ1つずらした時に、縦へ動いた分が限界効用になります。


1つ1つ横軸を動かして、縦にどれくらい動くかを考えるのは非常に面倒です。
そこで、数学の知識を使って解くことになります。
そもそも
どうして消費量(X)で微分するのか?
ポイント
限界効用を求めるのに微分をする理由は、傾きを求めるため。
重要!
「横軸へ1つずらした時に、縦へ動いた分が限界効用」ならば、「傾き」を求めれば良い。
限界効用と傾きの関係
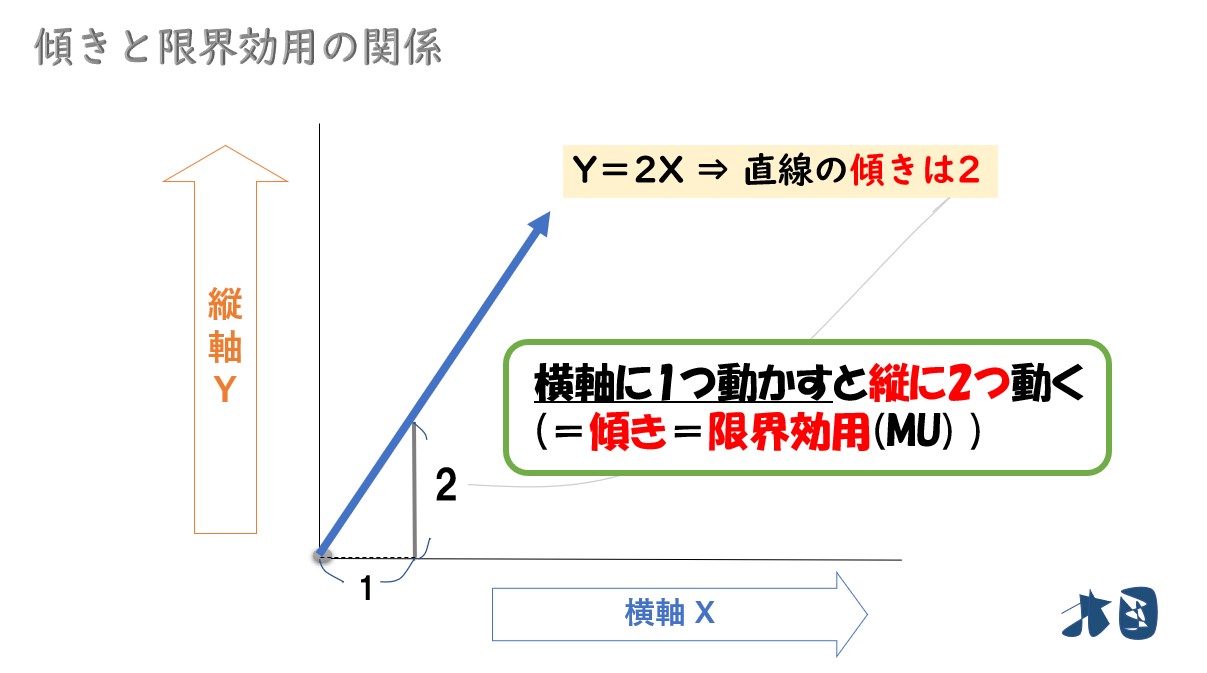
「Y=2X」という関数で考えてみます。
「2X」なので、この関数の傾きは2です。※仮に3Xなら傾きは3です。
傾きは、横軸へ1つ移動した時に、縦にいくら移動するかを表しています。
つまり「傾き」と「限界効用(MU)」は同じことを言っています。なので限界効用(MU)を求めるために傾きを求めています。ここでは「傾き=限界効用(MU)=2」となります。
ここで
傾きを求めるために微分をする理由
「Y=2X」の例ではグラフが直線でした。なので、すぐに傾きを求めることが出来ます。
しかし
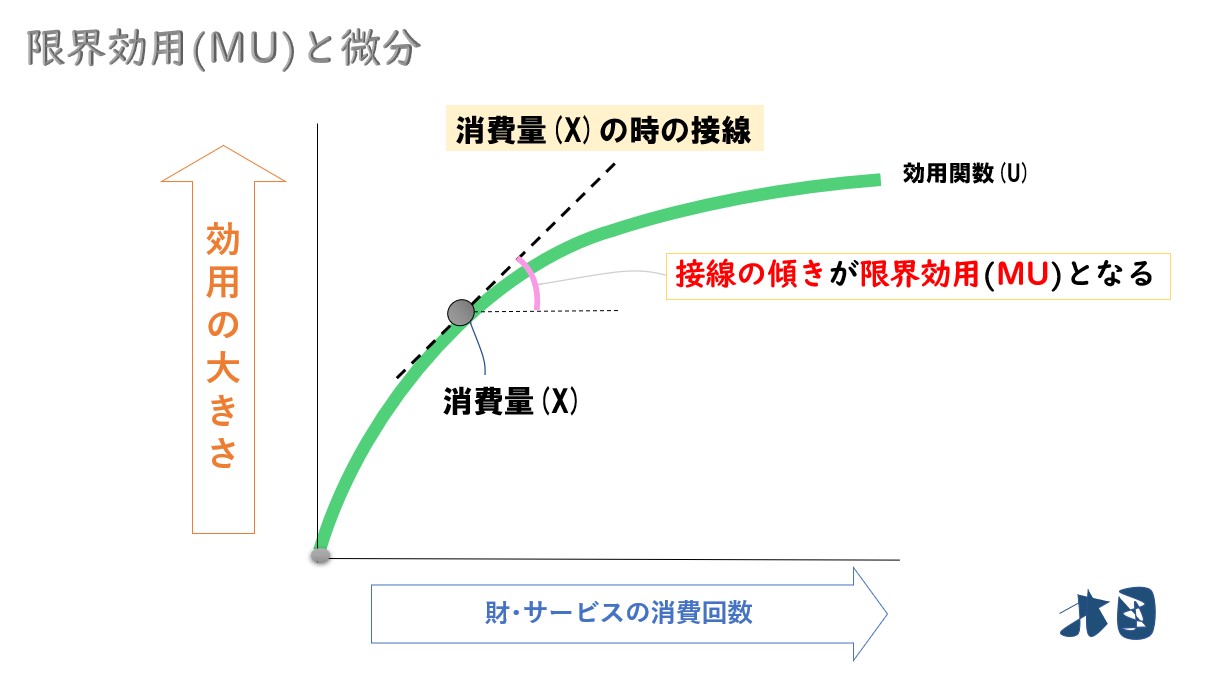
限界効用(MU)は「限界効用逓減の法則」があるため、グラフが次第に緩やなカーブになります。


ポイント
微分は文字通り、グラフを細かく分けて1つの点として処理します。「その点を通る接線の傾き」がどれ位あるかを計算すれば良いのです。
グラフで見ると・・
まとめ
傾きと限界効用(MU)は同じになる。なので、傾きを求めれば限界効用(MU)も分かる。
また、限界効用(MU)は、限界効用逓減の法則により、グラフが直線ではないため、微分しないと傾きが定まらない。


効用関数(U)を消費量(X)で微分する
- 効用関数 U=U(X)
- 消費量(X)
- 変化量を「Δ(デルタ)」
微分すると・・
例えば「Y=2x」という数式があったとき「2x」なので「傾きは2」です。
変化量を「Δ (デルタ)」とします。
- 消費量(x)が1増えたとき、変化量は「Δx=1」と書けます。
- 「Y=2x」なので、xが1増えれば「Yは2増えます (ΔY=2)」
まとめると「傾き2」=「2/1 = ΔY/Δx」となります。
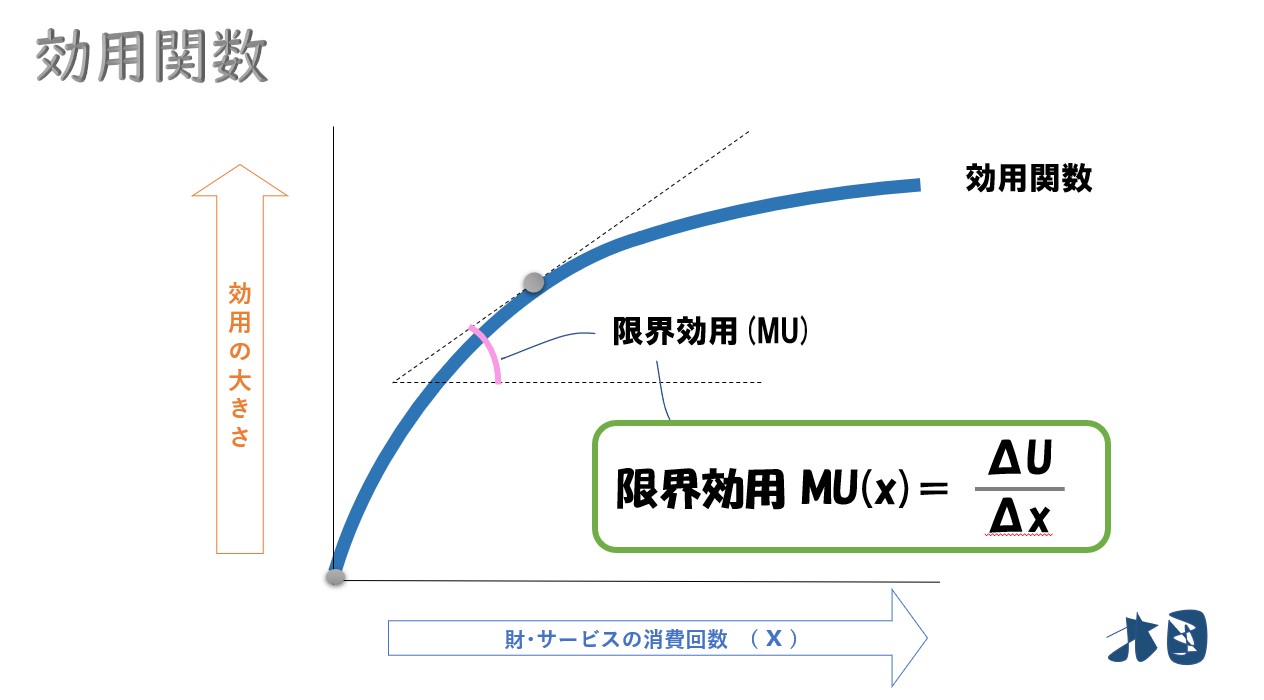
効用関数で考えれば U=U(x) ⇒「ΔU/Δx」となります。
ポイント
「Δx」は横軸に移動したことを表します。
つまり「ΔU(縦軸への移動距離)/Δx(横軸への移動距離)」という意味合いです。
効用関数(U)を消費量(X)で微分したときの限界効用(MU)は「ΔU/Δx」となる。
ちなみに
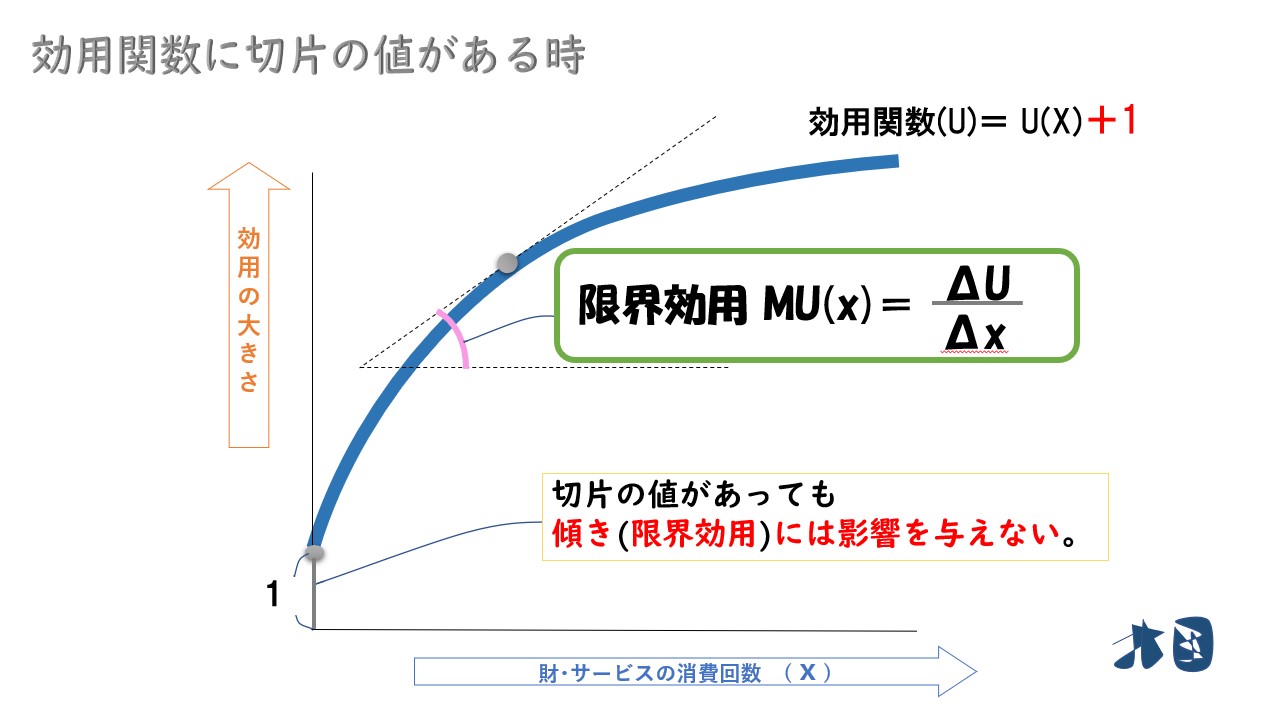
- 効用関数が「U=U(X)+1」のように、切片の数字が0ではない時
+1などと出てきても、微分する時には+1は無視されます。
「U=U(X)+1」を消費量(X)で微分しても、限界効用は「ΔU/Δx」になる。
微分はあくまで傾きを求めるための計算なので、+1が出てきても傾きには影響しないため無視できます。
財が2つの場合
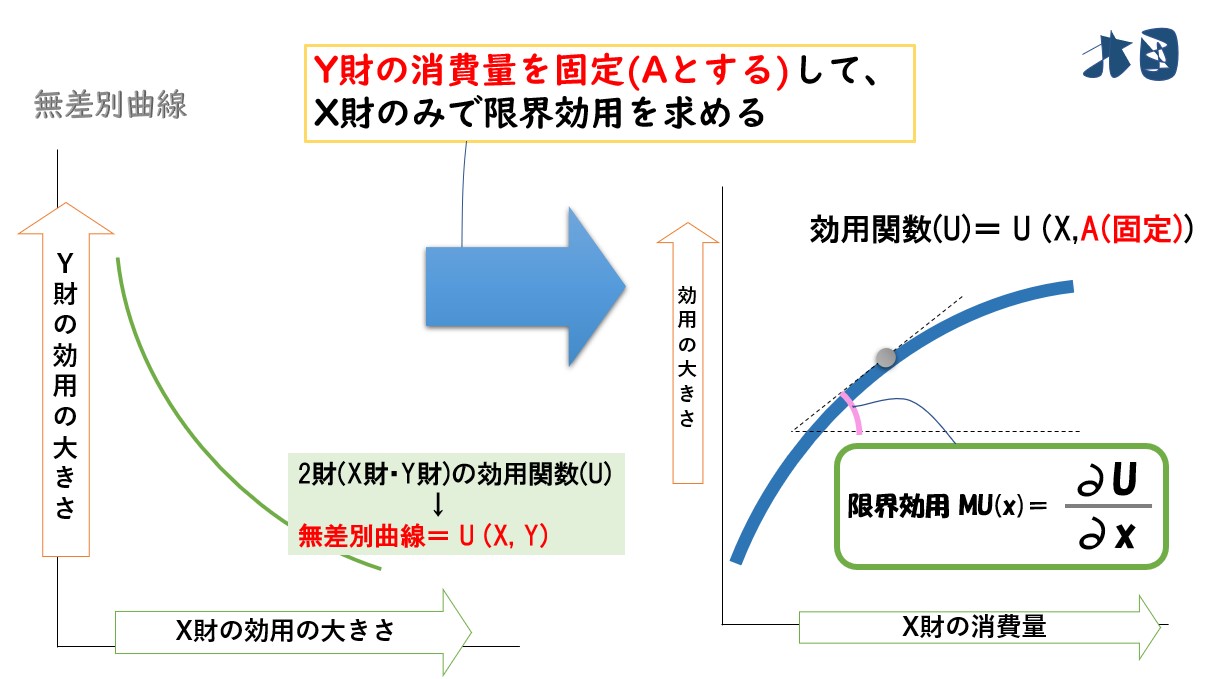
財が2つ以上ある場合は、無差別曲線から限界代替率を求めることが多いですが、各財についての限界効用を求める場合もあります。
無差別曲線と限界代替率はこちら!
ポイント
財・サービスが2つ以上ある場合は、効用関数を偏微分して限界効用を求める。


先ほどまでは財・サービスが1つとして扱ってきました。
しかし
私たちの満足度は色々なものを消費して決まります。
例えば
- ビール・枝豆


ビールを飲みながら枝豆を食べれば、それぞれから効用を得られます。
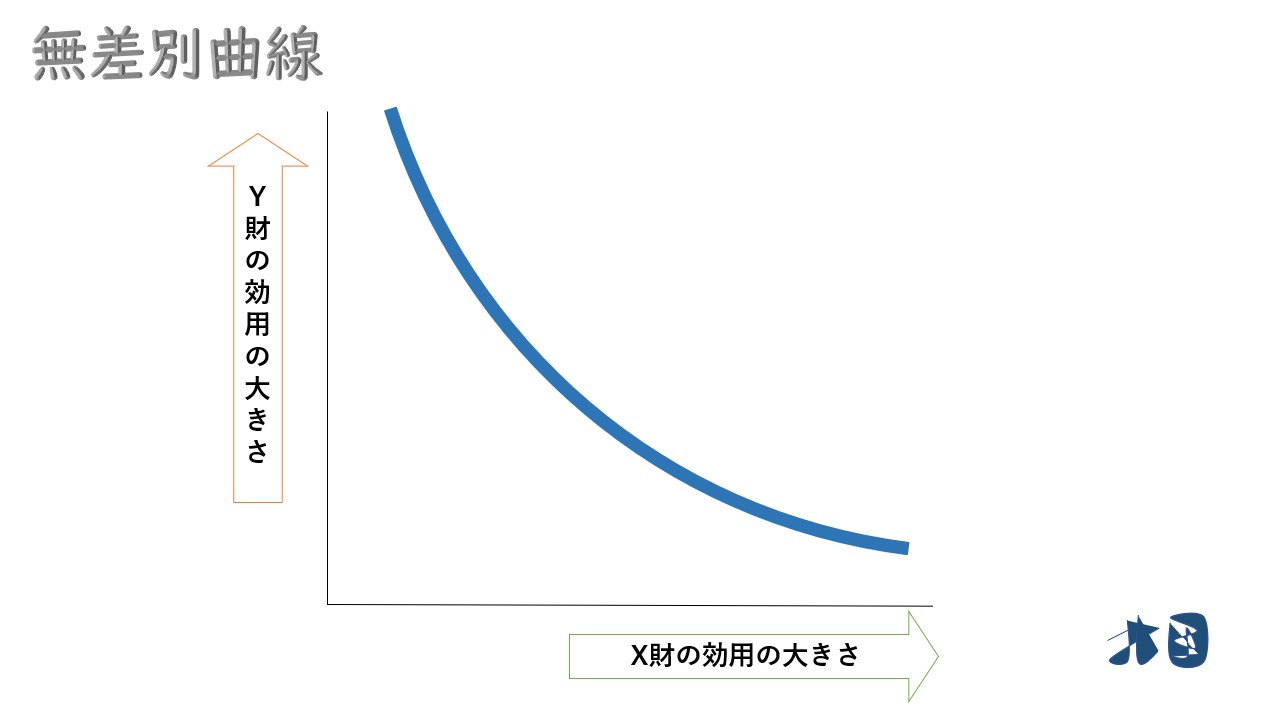
財・サービスが「X・Y」と2つある状態です。
今度は、この状況の時に「X・Y」の限界効用を計算してみようという問題になります。


どうして?
財が2つ以上で偏微分をする理由
ポイント
財が2つ以上ある場合は、偏微分をすれば片方の財の限界効用が求められる。
財が2つ以上ある場合は、それぞれの限界効用を求めていきます。
「ビールの限界効用」「枝豆の限界効用」をそれぞれ計算していくイメージ。
この時
片方の財・サービスの限界効用が知りたいので、不要な方を一定として考えます。
ビール1杯の限界効用を知りたいので、枝豆については変化させずに(一定と)考える。
また
限界効用は、効用関数(U)を消費量(X)で微分することで求められました。
詳しくは「財が1つの場合」を参照
つまり
片方の変数を一定として、片方の変数を微分することで、限界効用が求められます。
変数は、数式に登場する「X」「Y」などのこと。
ポイント
偏微分は、片方の変数を一定として、片方の変数だけを微分することを言います。なので、財が2つ以上ある場合は、偏微分をすれば片方の財の限界効用が求められるのです。


効用関数(U)を消費量(x)と(y)で偏微分する
- 効用関数 U=U(x, y)
- 消費量(x)
- 消費量(y)
- 変化量を「∂ ※」
※読み方がたくさんあります。「ラウンド」「ラウンドディー」「デル」「ディー」など。ここでは「ラウンド」と読みます。微分の時は変化量をΔ(デルタ)と書きましたが、偏微分のときは ∂(ラウンド)と表記します。
まずは(x)で偏微分すると・・
MUx (x財の限界効用)=「∂U/∂x」
グラフを見ると複雑に見えますが、財が1つの場合と同じです。
※Δ(デルタ)が ∂(ラウンド)という表記に代わった以外は同じ。
分数の理由
限界効用(MUx)は分数で表記されますが「財が1つの場合」で説明した理由と同じです。
次に(y)で偏微分すると・・
MUy (y財の限界効用)=「∂U/∂y」
xで偏微分した時と同じです。
ポイント
- MUx (x財の限界効用)は、U(X, Y) をXで偏微分した関数⇒「∂U/∂x」
- MUy (y財の限界効用)は、U(X, Y) をyで偏微分した関数⇒「∂U/∂y」


「限界効用」は経済学では基本的な話です。
需要関数(D)を求める話にもつながるのでしっかりと理解しましょう!