等量曲線の傾きを求める「技術的限界代替率」
等量曲線が分かっても、技術的限界代替率の意味や計算で苦労する人も多いです。
- 技術的限界代替率とは?
- 技術的限界代替率逓減の法則とは?
- 等量曲線の接線の傾き
- 計算の方法・求め方
技術的限界代替率について、イマイチ理解できない人向けに簡単にまとめています。
技術的限界代替率とは?
技術的限界代替率とは
同じ生産量を維持するための生産要素の交換比率。
ある生産要素(資本量・労働量)を増やすとき、もう片方の生産要素(資本量・労働量)をどれくらい減らせば、同じ生産量を維持できるかを表す。等量曲線の接線の傾きになる。
※技術的限界代替率(MRTS)=Marginal-Rate-of-Technical-Substitution


例えば
- お米10kgの収穫を行います

お米10kgの収穫を行うには、つぎの2つの方法があります。
- 人を雇う
- 無人稲刈り機(機械)を使う
「1人を雇う」なら「機械1台」を使わずにお米10kgを収穫が出来ます。逆に「機械1台」があれば「1人を雇わず」にお米10kgが収穫できます。
ここで
人を雇ってお米10kgの収穫をしていたとき、人の代わりに「機械1台を使う」ことにします。機械1台でもお米10kgの収穫を維持できます。
このとき「1人を雇う」「機械1台」の交換比率を技術的限界代替率と言います。
※「1人を雇う」「無人稲刈り機1台」では、限界代替率は「1」となります。


重要
技術的限界代替率逓減の法則について
技術的限界代替率には「ある生産要素(資本・労働)の投入量を増やすほど、もう片方の生産要素(資本・労働)は減らす量が少なくなる」という特徴がある。


例えば
- お米1000kgの収穫を行います


はじめは人を雇わずに、無人稲刈り機を100台使うとします。
農家
う~ん、機械が多すぎて作業効率が悪いな・・


ポイント
もし、人を雇わずに機械を100台投入すると「人を雇う価値」は凄く高くなります。「機械101台目< 従業員1人」と感じる。
このように「2つの生産要素があったとき、片方の生産要素を投入し続けると、次第にもう片方の生産要素の価値が高まること」を技術的限界代替率逓減の法則と言います。
もっと具体的な話
次は、お米1000kgのうち500kgの生産を機械1台で実現したケースを考えます。
人を雇うことにすると・・
機械1台を投入して収穫量が500kgになりました。機械のメンテナンスとかも含めて、細かな作業をしてもらうために人を1人雇うことを考えます。
人を雇って機械をメンテすれば、もう500kgの収穫が実現できます。
しかし
結局人を雇うことは出来ずに高性能な機械をもう1台投入したとします。
- 機械を追加投入して+300kgの収穫
- 機械をもう1台投入して+200kgの収穫
合計1000kgの収穫になります。
ポイント
生産要素の追加的な1単位の投入から得られる収穫量
- 2台目の機械=300kgの収穫
- 3台目の機械=200kgの収穫
機械を追加で1台投入するにつれて、人を雇うことの相対的な価値が高まっています。これを、人を雇うときの収穫量を基準に考えてみます。
2台目の機械
- 2台目の機械=300kgの収穫
- 1人を雇う=500kgの収穫
300÷500=0.6
つまり、2台目の機械は「人を雇うときと比べて0.6倍の生産量」に相当します。
3台目の機械
- 3台目の機械=200kgの収穫
- 1人を雇う=500kgの収穫
200÷500=0.4
つまり、3台目の機械は「人を雇うときと比べて0.4倍の生産量」に相当します。
ココがポイント
このように「無人稲刈り機」を1台増やすにつれて、人を雇う価値が高まります。
補足
- 2台目の機械と同じ生産量(300kg)を得るには、0.6人を雇う必要があります。
- 3台目の機械と同じ生産量(200kg)を得るには、0.4人を雇う必要があります。
「片方の生産要素(機械)の投入量」を1単位増やすほど、同じ生産量を得るために必要な「もう片方の生産要素(人)の投入量」が減っていることが分かります(0.6人→0.4人)。
まとめ
技術的限界代替率は「ある生産要素(資本・労働)の投入量を1つ増やしたとき、同じ生産量を維持するために、もう片方の生産要素(資本・労働)の投入量をどれくらい減らす必要があるか」を表している。技術的限界代替率には「ある生産要素(資本・労働)の投入量を増やすほど、もう片方の生産要素(資本・労働)は減らす量が少なくなる」という特徴がある。これを「技術的限界代替率逓減の法則」という。
技術的限界代替率の求め方・計算方法

ポイント
基本的には、等量曲線の傾きを求めることで「技術的限界代替率」が分かります。
等量曲線についてはこちら⇒【等量曲線】意味や性質・よくある疑問を分かりやすく理解する
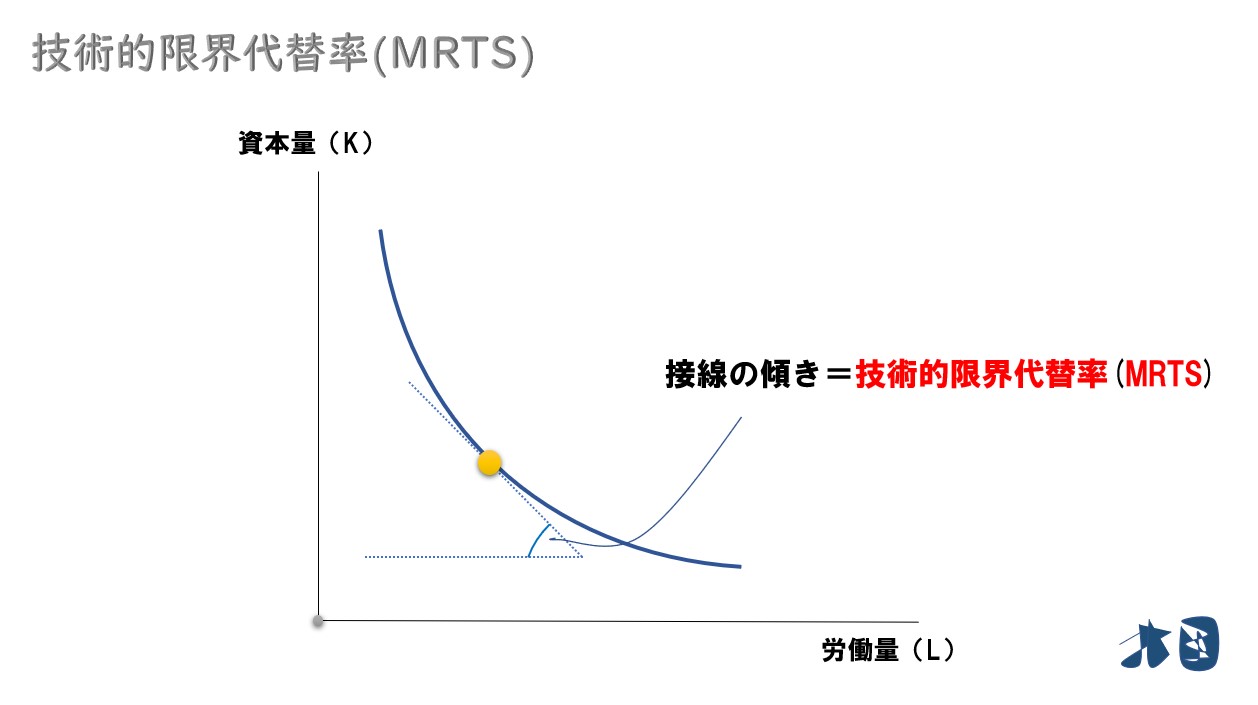
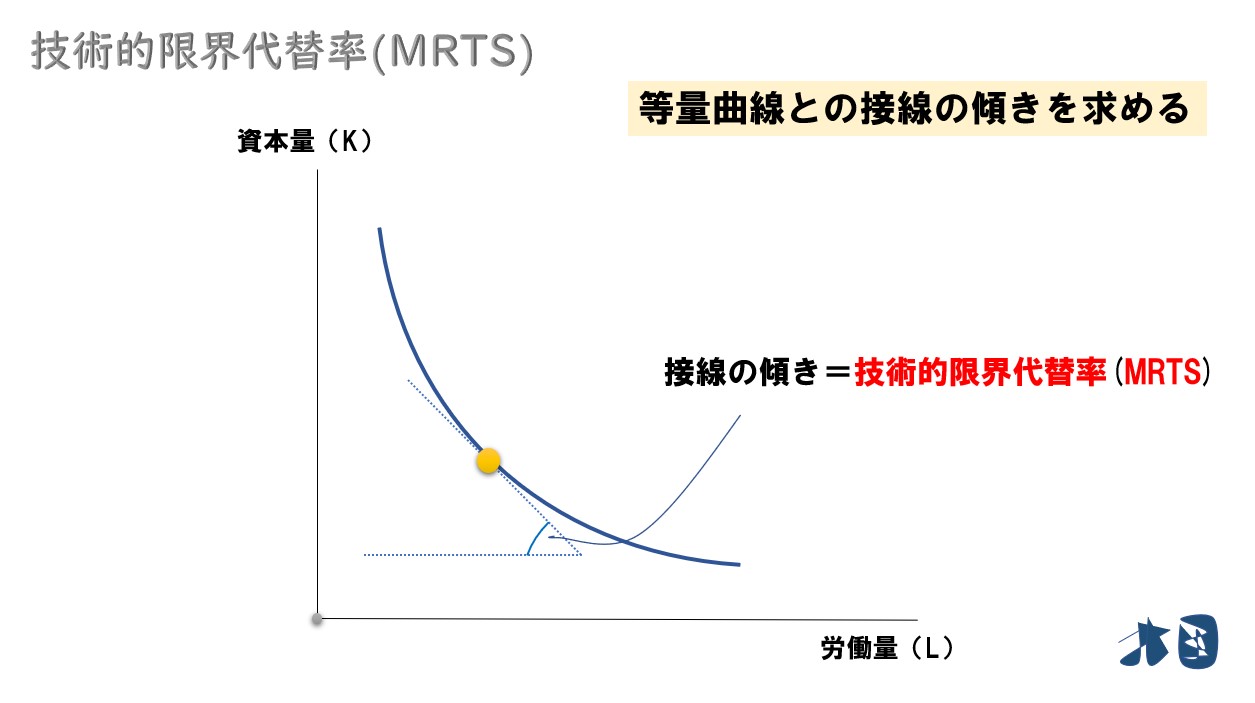
グラフで見ると


等量曲線の傾き=技術的限界代替率
まずは
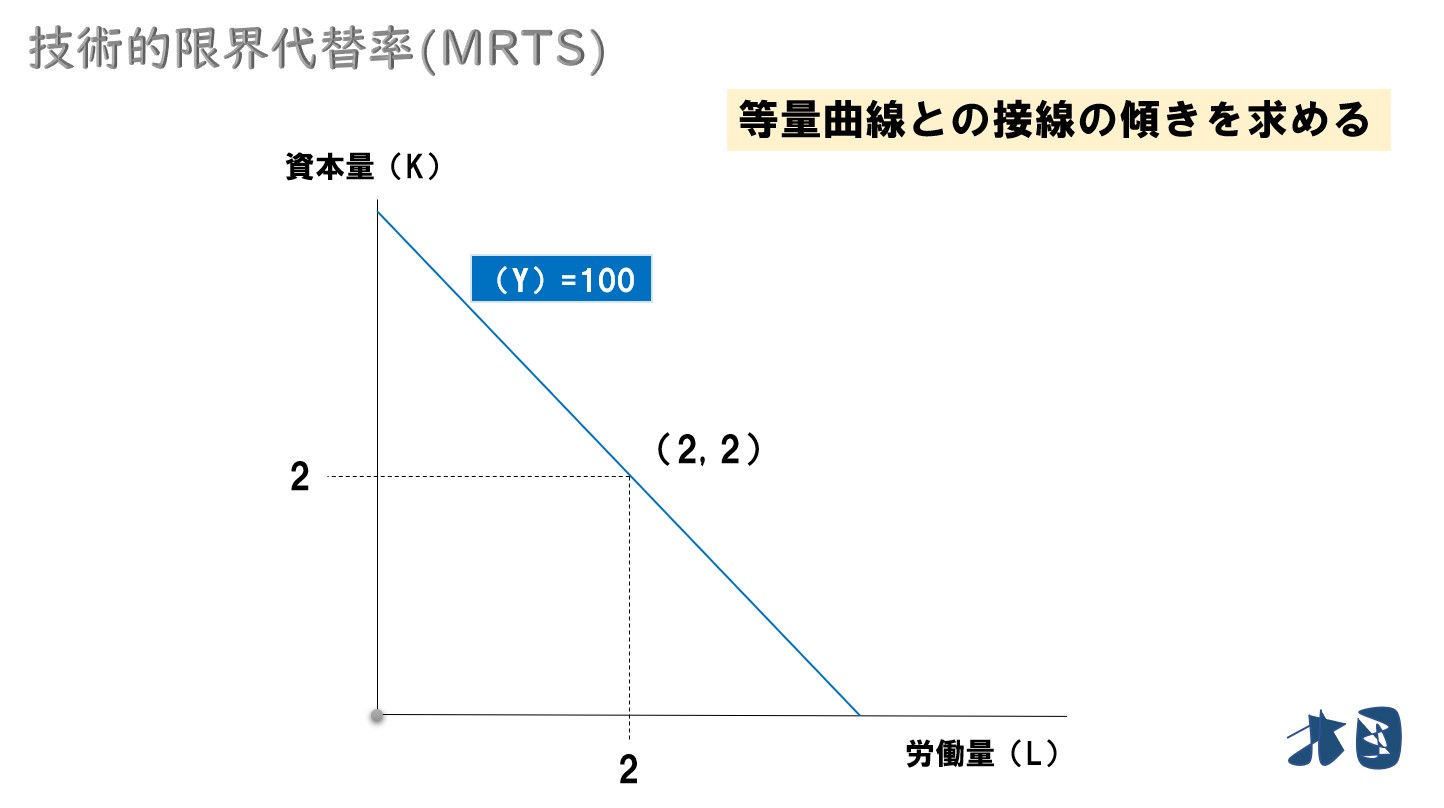
- 等量曲線が直線だった場合を考える
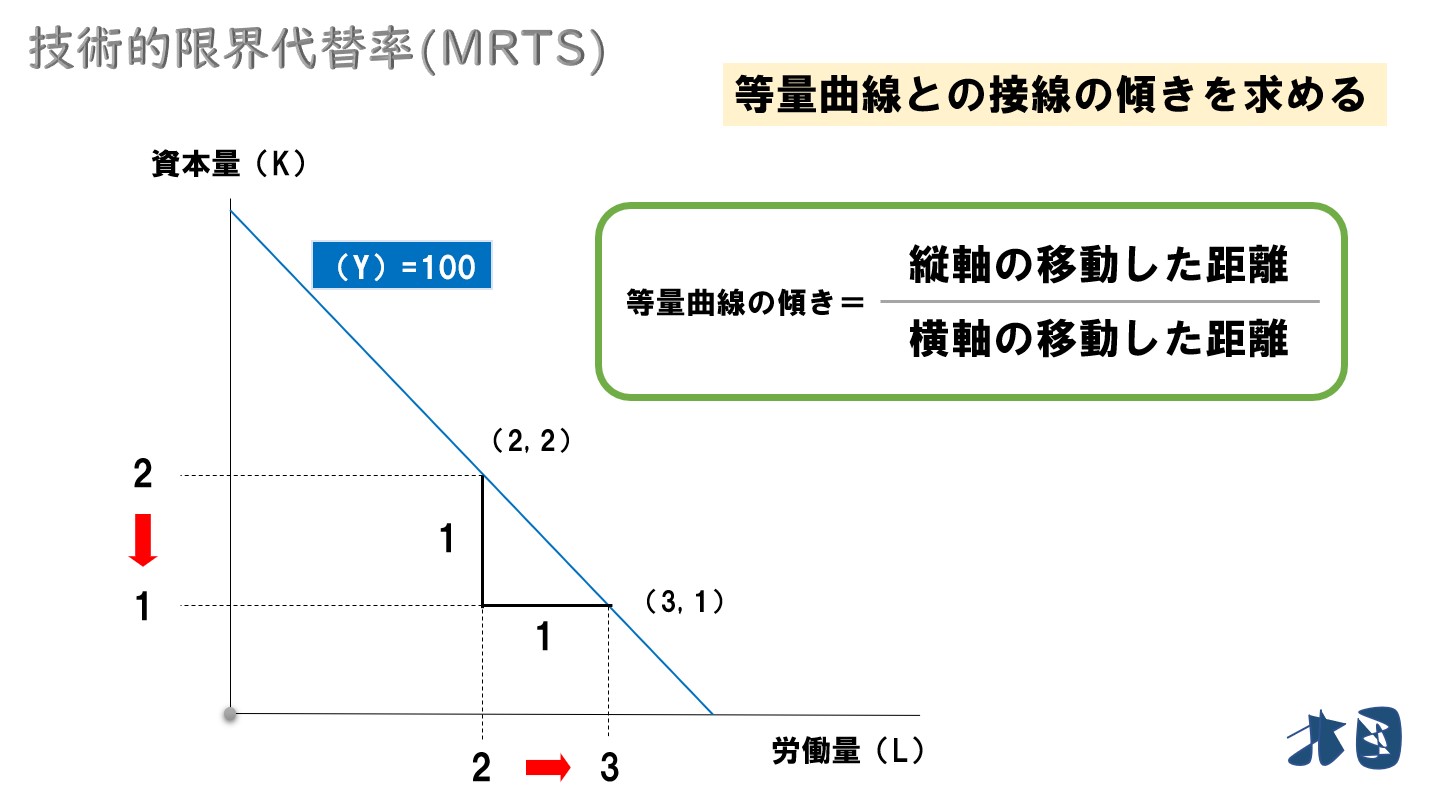
この直線(等量曲線)は、100の生産量を得られる生産要素の組合わせを結んでいます。
- 資本量=2
- 労働量=2 という状態になっています。
次に
技術的限界代替率の定義を思い出す
ある生産要素を増やすとき、同じ生産量を維持するために、もう片方の生産要素をどれくらい減らす必要があるのか(交換比率)を表したもの。
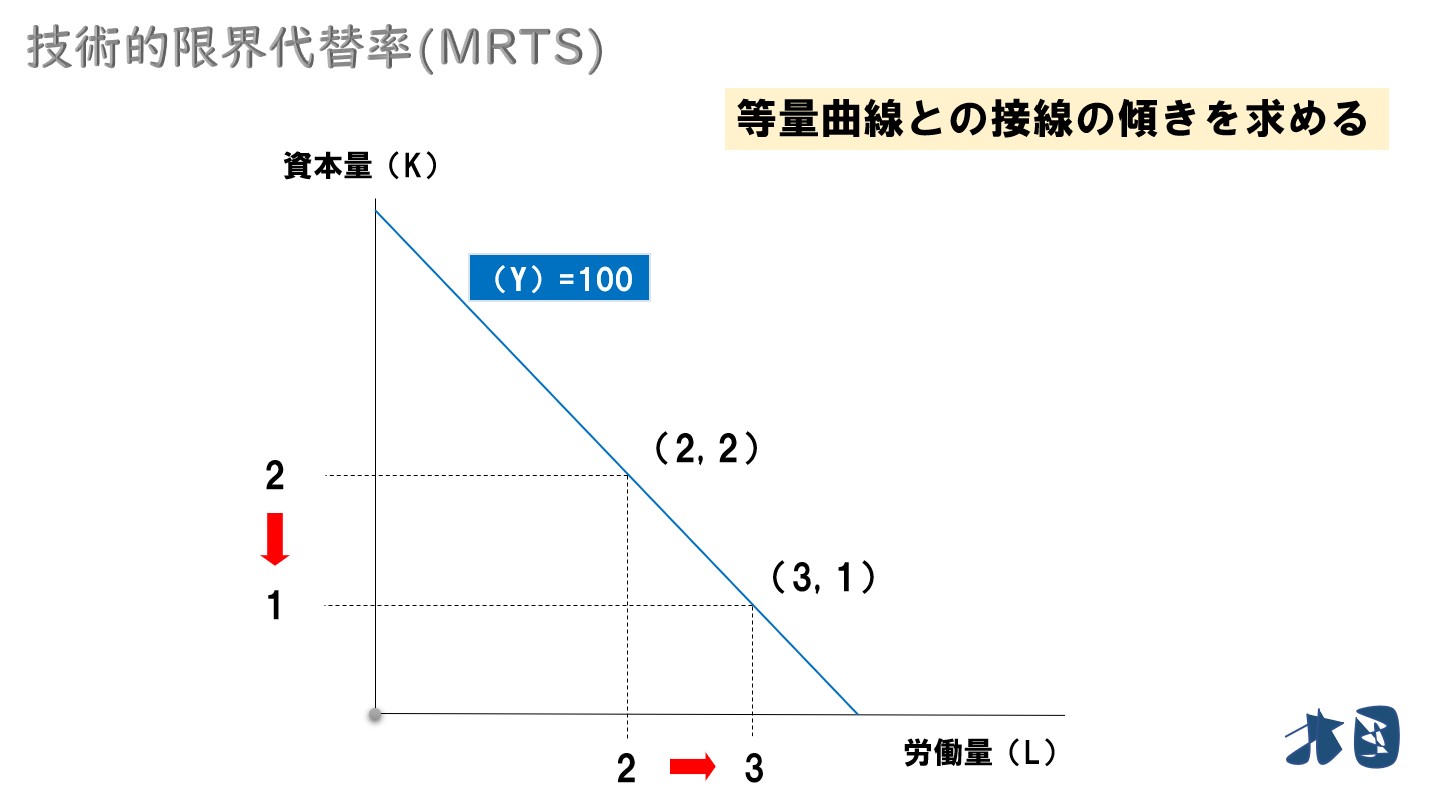
労働量を1単位増やしてみる
この時、同じ生産量(Y=100)を維持するために 資本量を1減らす必要があるとします。
同じ生産量(Y=100)を維持するためには
- 労働量を1増やす
- 資本量を1減らす
つまり、技術的限界代替率(MRTS)=1となります。労働量を1単位多く投入したら、資本量を1単位少なくすることで同じ生産量(Y=100)を保てる⇒ 交換比率=1:1(1分の1)となっている状態。
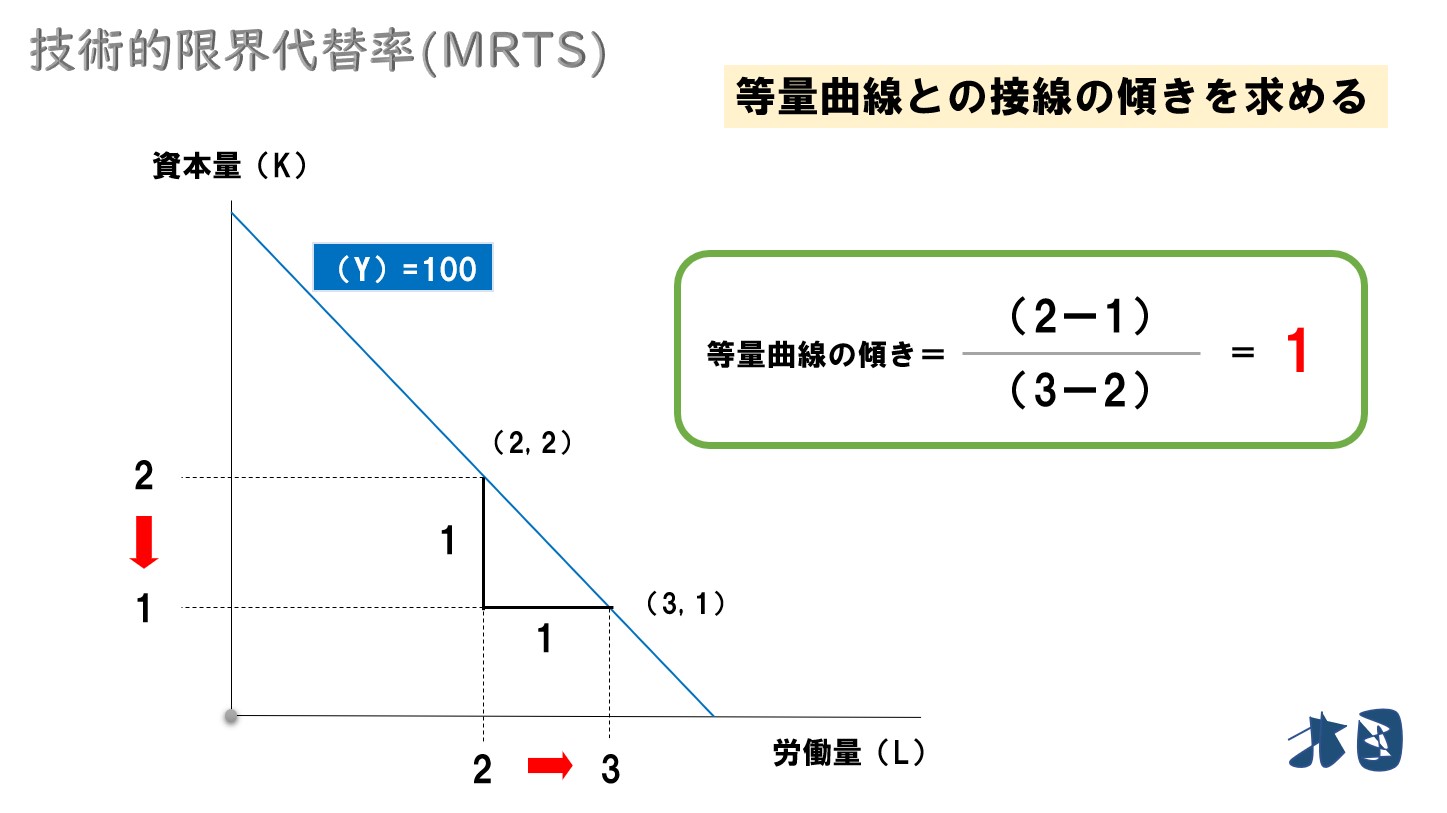
この等量曲線の傾きを考えてみる
つまり
この等量曲線(直線)の傾きは、1となります。


ポイント
技術的限界代替率(MRTS)は「労働量を1単位多く投入したとき、同じ産出量を維持するために資本量をどれくらい減少させるか」を計算することになる。
グラフ的に見れば
- 労働量を1単位多く投入したとき=横軸の移動距離
- 資本量をどれくらい減少させるか=縦軸の移動距離
となるため、数学的には、等量曲線の傾きを求めるのと同じになる。
技術的限界代替率の計算式
先ほどの「等量曲線の傾き=技術的限界代替率の理由」を理解していれば簡単です。
確認する⇒等量曲線の傾き=技術的限界代替率の理由
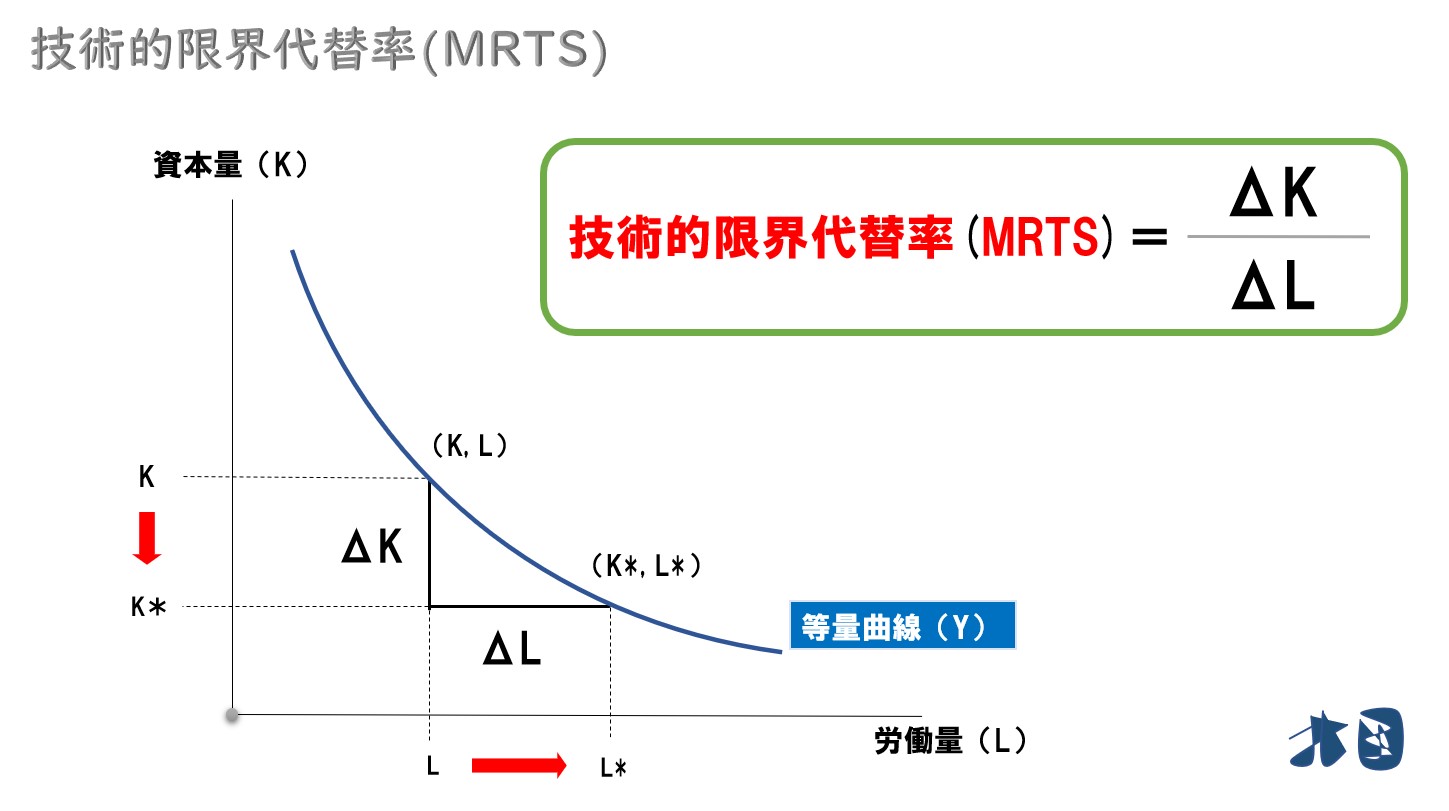
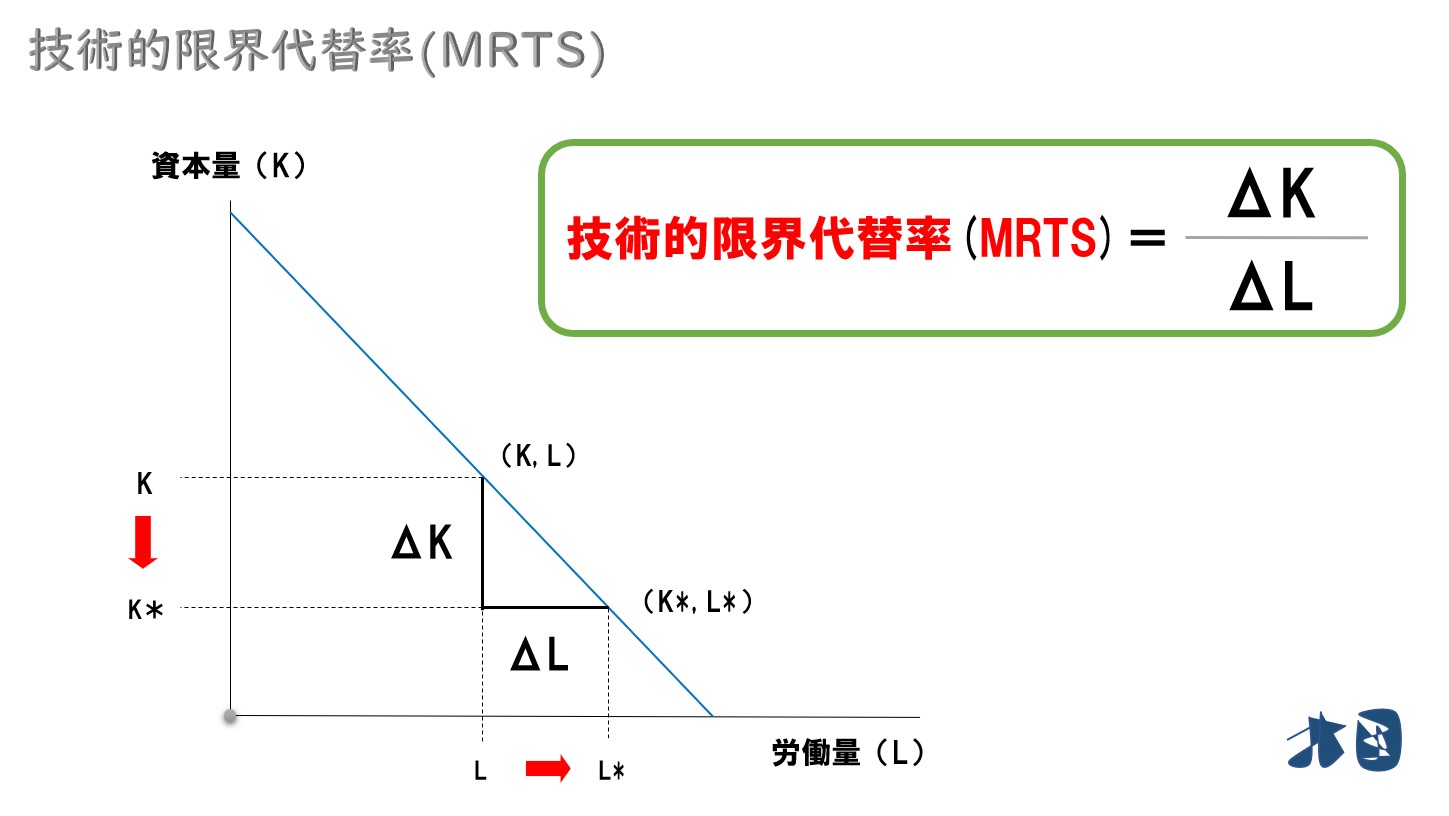
変化量をΔとする
- 労働量の増加分=ΔL
- 資本量の減少分=ΔK
普通の等量曲線でも同じ


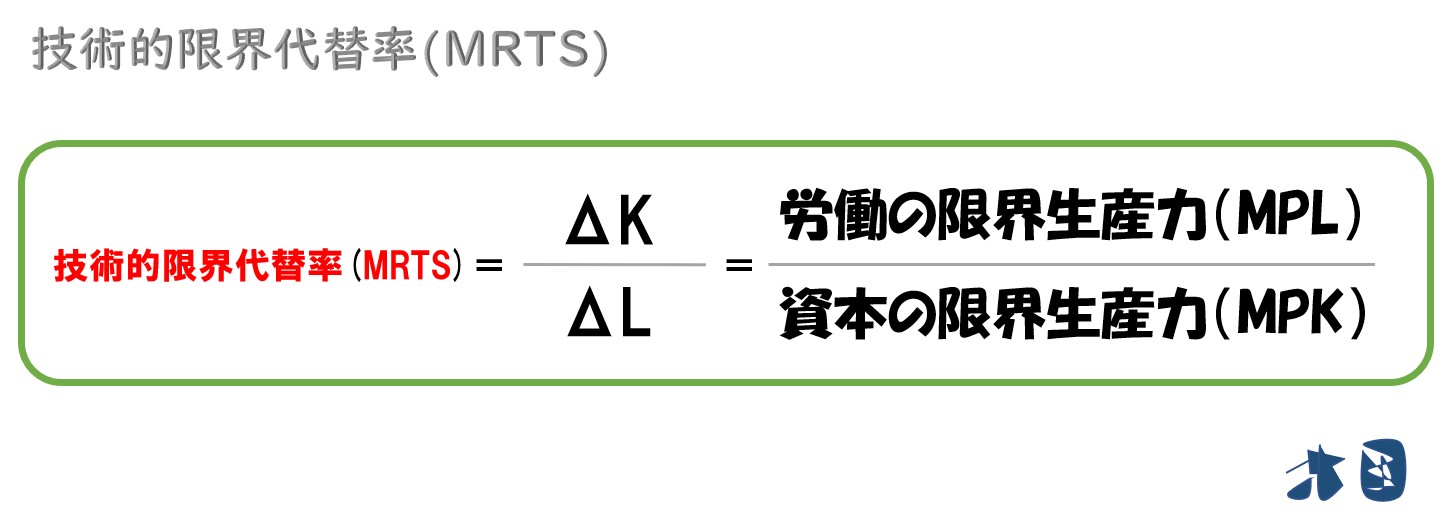
資本の限界生産力・労働の限界生産力の比

ポイント
技術的限界代替率(MRTS)は「資本の限界生産力」と「労働の限界生産力」の比率で求められる。


まずは
限界生産力(MP)が登場する理由
先ほどまでは「横軸に移動した距離」「縦軸に移動した距離」という表現を使って、技術的限界代替率(等量曲線の傾き)を求めました。実は、この移動距離が限界生産力(MP)に当たります。
先ほどのグラフを再チェック
ここで
限界生産力(MP)は「生産要素を追加的に1単位投入した時の産出量の増加分」です。
限界生産力(MP)の「生産要素を追加的に1単位投入」の部分が、グラフ上の横軸・縦軸の移動距離にあたります。


ポイント
そもそも同じ等量曲線上では、生産量は一定です。つまり、同じ等量曲線上の移動なので「労働の追加投入で増加した産出量」と「資本の投入量が減ったことで減少した産出量」は、足し引き=0になります。
つまり
- 労働の限界生産力 ⇒「横軸に移動した距離・それに伴って変化した産出量」
- 資本の限界生産力 ⇒「縦軸に移動した距離・それに伴って変化した産出量」
「それに伴って変化した産出量」は、どちらも同じになります。
- 労働の限界生産力 ⇒「横軸に移動した距離
・それに伴って変化した産出量」 - 資本の限界生産力 ⇒「縦軸に移動した距離
・それに伴って変化した産出量」
このようになるので「技術的限界代替率(MRTS)(等量曲線の傾き)」を求めるときに”資本の限界生産力”と”労働の限界生産力”の比率を使うことが出来きます。


考えると分けわからなくなります。ひとまず「資本の限界生産力(MPK)と労働の限界生産力(MPL)の比率で技術的限界代替率(MRTS)が求められる」という点を覚えておきましょう。
上の説明は、生産関数(Y)を全微分を行う過程で「dY=0となる」という過程を言葉で説明したつもりです。説明を考えながら書いてみて分かりましたが、数学的に処理する方が簡単です(汗)
実際に計算して求める

例題
- 生産関数(Y)=2√L・2√K
この時の技術的限界代替率(MRTS)を求める。
step
1資本・労働の限界生産力(MP)を求める
限界生産力(MP)を求める時は微分をしますが、微分する理由が分からない人は「限界生産力・限界生産力逓減の法則」で確認してください。
「Y=2√L・2√K」を微分できるように変形します。
変形すると・・
知っておく①
次に「L」「K」で偏微分する
知っておく②
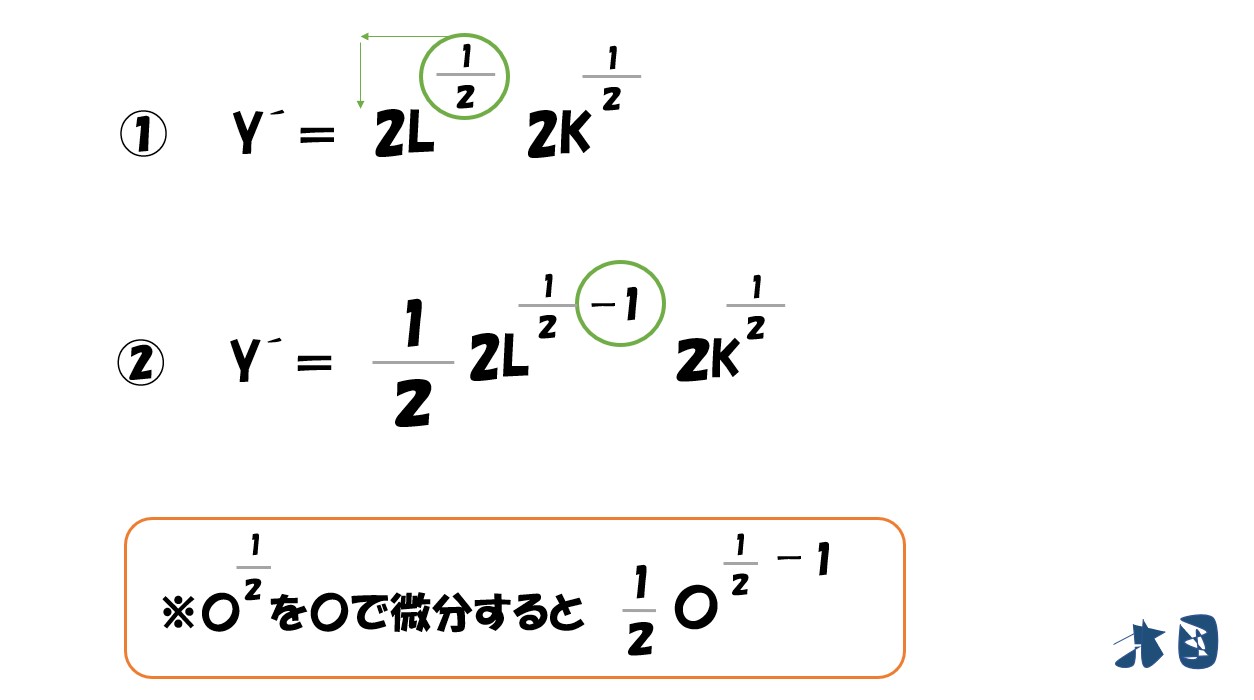
微分をするときは
- 乗数を手前に持ってくる
- 乗数を「1」マイナスする
後はこれを計算するだけ
(労働の限界生産力)
(資本の限界生産力)
知っておく③
マイナス2乗は分数を意味する
「-2分の1乗」だと・・
計算結果
step
2資本・労働の限界生産力(MP)の比率を計算する
分母に「資本の限界生産力(MPK)」が出てきて混乱する人がいますが、全微分という計算過程を経ると上の式になります。
消費者理論の限界代替率・限界代替率逓減の法則 の「2財の限界効用の比になる数学的な説明(全微分)」で確認できます。ここでは説明を省略します。


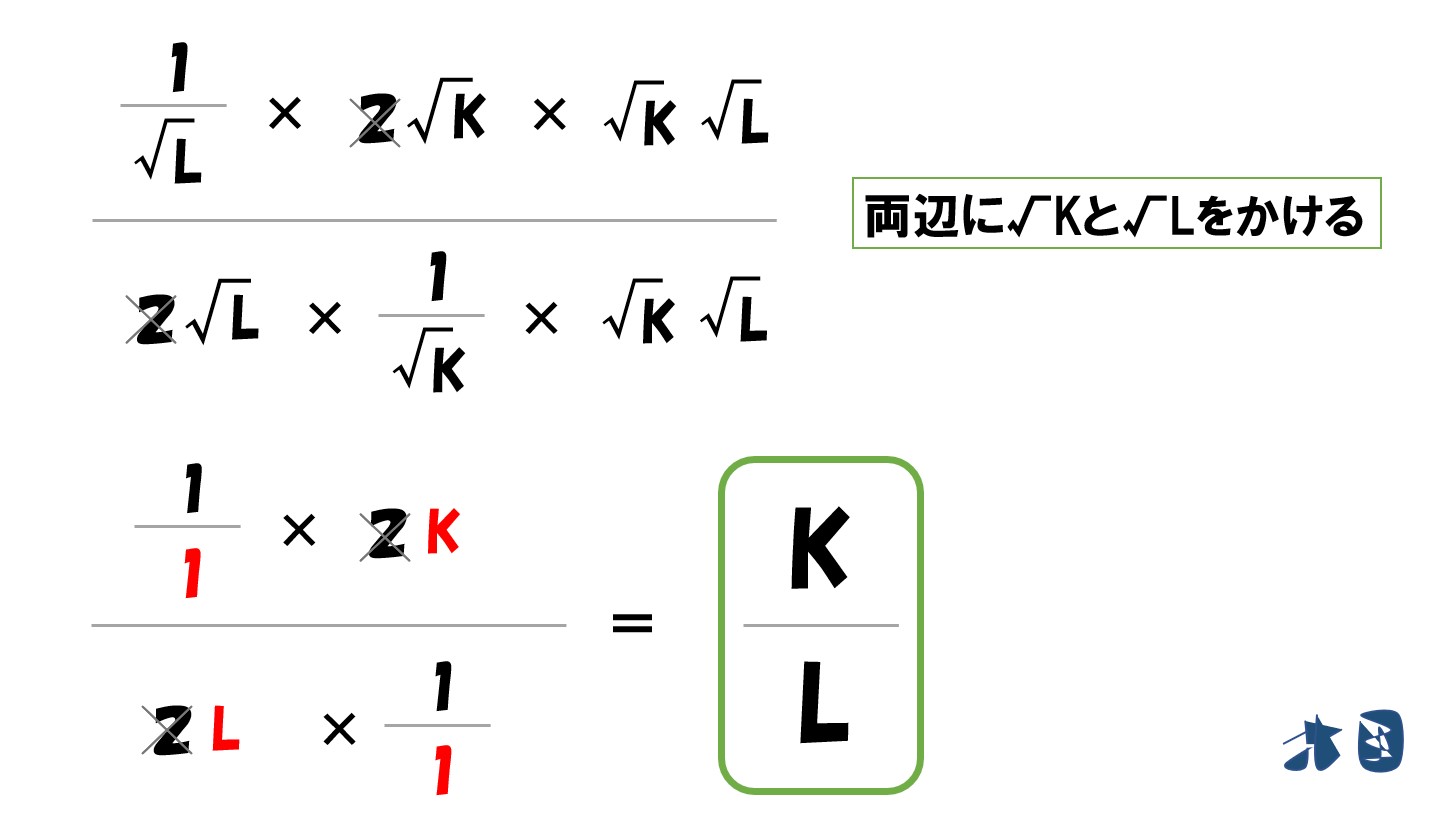
計算する


- 生産関数(Y)=2√L・2√K
このときの技術的限界代替率(MRTS)は「K/L」です。
技術的限界代替率の求め方は沢山ありますが、オーソドックスな方法で計算してみました。
もっと早く簡単に計算する方法はありますが、この分野の理解を深める意味で、オーソドックスな計算方法も知っておきましょう。