効用最大化問題を解くときに登場する「ラグランジュ未定乗数法」
そもそも数学的な解法なので「数学が分からない!」という人に向けて、簡単な説明をまとめています。
- ラグランジュ未定乗数法とは?
- 途中式の意味
- 使うときの注意点
- 簡単な例題を解く
分かりやすくイメージ出来るように、最適消費点(効用最大化)を求める時に登場する「限界効用」「予算制約線」などの言葉と関連付けて説明しています。
ラグランジュ未定乗数法とは?

(Wikipediaより ジョゼフ=ルイ・ラグランジュ)
ラグランジュ未定乗数法
「制約条件がある関数」の極値を求めることが出来る計算方法のこと。
- 制約条件=予算制約線
- 関数=効用関数
- 極値=効用最大化(最適消費点)
と置き換えることが出来るため、ミクロ経済学の最適消費点(効用最大化)を求めるときに「ラグランジュ未定乗数法」が使われる。
ちなみに「未定乗数法」は上のラグランジュさんが作ったもの。他にも「関数(F)」を微分した後の式を「導関数(F')」と書き始めたのはラグランジュです。


具体的な話
ラグランジュ未定乗数法は、次の条件のときに使える計算方法です。
関数「F(x, y)」の制約条件が「g(x, y)= 0」のとき、
関数「F(x, y)」を最大化(最小化)させる(x, y)を求める。
ポイント
変数「λ (ラグランジュ乗数)」を使って式を作ります。
ラグランジュ関数 L(x, y, λ) = F(x, y)- λg(x, y)
※λ=ラムダ
※L=ラグランジュの頭文字


ここでは次のように置き換えます
- 関数(F) ⇒効用関数=U(x, y)
- 制約条件(g) ⇒予算制約線=I=xPx・yPy
文字で書けば「ラグランジュ関数(L)=効用関数-λ(予算制約線)」となります。
ここで①
- 効用最大化問題なので予算を全部使い切る
制約条件が「g(x, y)= 0」とある通り、
予算制約線「I=xPx・yPy」は「I-(xPx・yPy)=0」となります。
予算=100なら、100使い切るようにX財・Y財が消費されます。差引き=0です。
なので
「効用関数-λ(予算制約線=0)」という状態になる(x, y)を求める
ここで②
- 効用最大化ということは、限界効用が0になっている
ある財を好きなだけ消費できると考えた場合、効用が得られる限り、消費者はその財を消費し続けます。そして、いずれ財を消費しても効用が得られない状態(限界効用=0)に到達します。
また、限界効用が「1」得られるなら、財をもう1つ消費する方が合計の効用が高くなります。つまり「限界効用=0になるまで消費を続ければ、自然と消費者の満足度が最大」になります。
なので、効用最大化が実現するなら効用関数=U(x, y) の限界効用は0になるはずです。
なので
効用関数=U(x, y)を偏微分して、X財・Y財の限界効用を求める
効用関数=U(x, y)を偏微分すると限界効用が求まる理由が分からない人は、こちらで確認してください⇒【限界効用】求め方も含めて簡単にわかりやすく※財が2つの場合を参照。
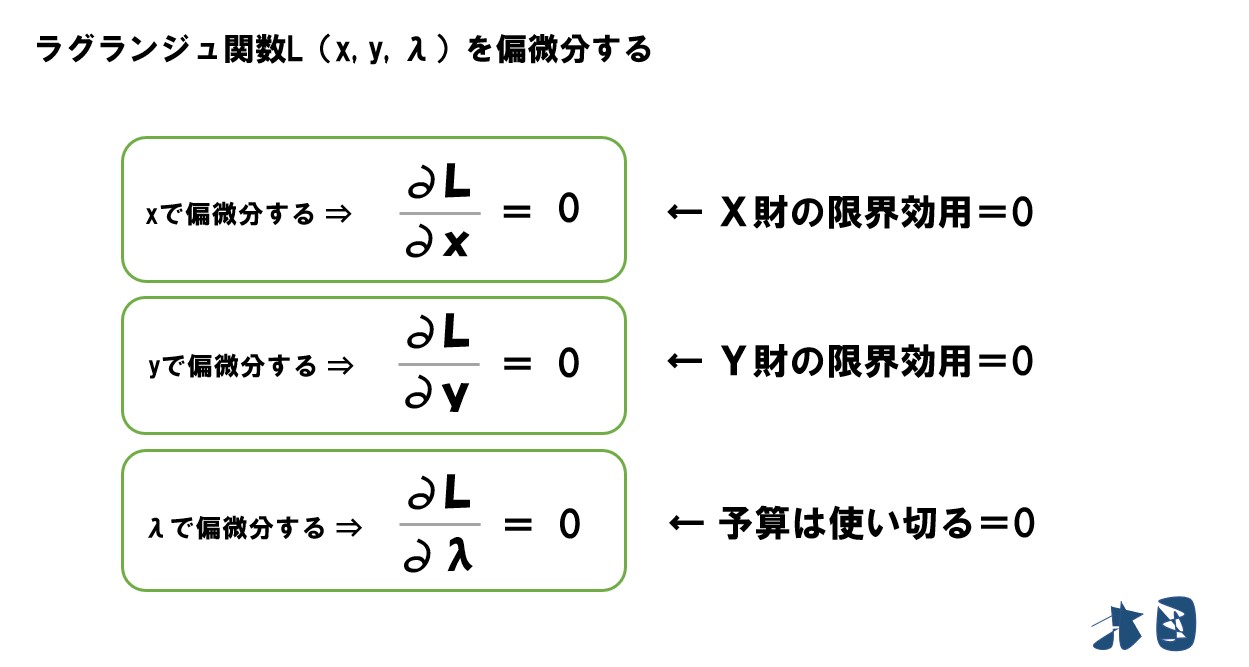
「効用関数-λ(予算制約線)」を偏微分
ポイント
ラグランジュ関数 L(x, y, λ) = F(x, y)- λg(x, y)を、3つの文字「x, y, λ」でそれぞれ偏微分すると、上の式になり、途中で説明した通り=0と出来ます。
※「∂L/∂x」「∂L/∂y」は、x財・y財の限界効用を表しています。
この理由は、こちらの【限界効用】求め方も含めて簡単にわかりやすくで確認してください。※財が2つの場合を参照


まとめ
ラグランジュ未定乗数法を使って問題を解くときの流れ
問題文から次の4つをおさえます
- 「効用関数」
- 「制約条件・予算」
- 「X財の価格」
- 「Y財の価格」
「効用関数=U(x, y)」「X財の消費量=x」「Y財の消費量=y」とします。求めるのは、制約条件は「g=(x, y)=0」の下で、効用が最大化する「x」「y」の消費量の組み合わせです。
ここで、変数「λ (ラグランジュ乗数)」を使ってラグランジュ関数を作ります。
ラグランジュ関数 L(x, y, λ) = U(x, y)- λg(x, y)
ラグランジュ関数を「x」「y」「λ」で偏微分して「=0」と置きます。
これら3つを合わせて「1階条件」と呼びます。
この3つの式を連立方程式で解くことで「x」「y」の答えが出ます。
ポイント
実際の計算では、上2つ「X財の限界効用」「Y財の限界効用」を表している式で連立方程式を組みます。この時、上2つで連立方程式を作れば「λ」を消して「x」「y」だけの式になります。
その後に、1番下の式に、求めた結果を代入して計算するという流れになります。
イメージが湧かないかもしれないので、後半でラグランジュ未定乗数法使って問題を解いてみます。


ラグランジュ未定乗数法の注意点

経済学の問題を解くときに「ラグランジュ未定乗数法」を使う場合、注意点が5つあります。
注意ポイント①
ラグランジュ未定乗数法は、制約条件が「g=○○」という風に「=(等号)」で結ばれている必要があります。「≦ (不等号)」がついている場合は使えません。
ただし、大学の学部制レベルの問題なら「≦」でも「=」的に扱ってラグランジュ未定乗数法を使って解く場合があります。
その辺は、講義を担当している教授の意向に合わせて判断しましょう。
※一応ですが、制約条件が「≦」などの不等号ならば「KKT条件(カルーシュ・クーン・タッカー条件)」という数学の知識を使って解くのが正しいです。
注意ポイント②
途中で「1階条件」と出てきましたが、本当ならば「2階条件」までを計算しないといけません。
ラグランジュ未定乗数法は、「1階条件」を満たすことで、答えが「極値」を取っている事しか分かりません。(=極大・極小は分からない状態・さらに厳密に言えば極値の候補が求まっているに過ぎない)
「2階条件」で、その極値が「極大・極小」のどちらかを判断します。
経済学の問題では「効用最大化が実現する」というケースを扱うため、普通は「第2条件」は暗黙の了解で無視されていますが、これも教授の意向に従ってください。
※一応ですが「2階条件」では「ヘッセ行列式」というのを計算します。
注意ポイント③
最適消費点が「端点解(コーナー解)」だと、ラグランジュ未定乗数法は使えません。
ちなみに「端点解(コーナー解)」になるのは、完全代替財などです。「X財・Y財の関係」が完全代替財ではないことを確認してからラグランジュ法を使ってください。
※ラグランジュの未定乗数法では「内点解」の答えしか求まりません。最適消費点が「端点解(コーナー解)」の場合は、この条件を満たさないため、計算しても正しい答えが出ないです。
ちなみに「内点解」というのは「答えに0が含まれていない」状態です。必ず(x=1, y=2)などのように、0以外の数字になります。
逆に「端点解(コーナー解)」では「答えに0が含まれる」状態です。(x=0, y=2)など。このような端点解(コーナー解)は、先ほど登場した「KKT条件(カルーシュ・クーン・タッカー条件)」を使えば解けます。
注意ポイント④
効用関数が「レオンチェフ型」だと、ラグランジュ未定乗数法は使えません。
ちなみに、レオンチェフ型の効用関数は、2財が完全補完財のケースです。「X財・Y財の関係」が完全補完財ではないことを確認してからラグランジュ法を使ってください。
※レオンチェフ型の効用関数では、無差別曲線の傾きが90度(直角L字型)になります。
この直角のポイントが最適消費になりますが、急激に尖ったようなポイントは微分できません。そのため、ラグランジュの未定乗数法で計算しても正しい答えが出ないです。
注意ポイント⑤
ここでは、ミクロ経済学の効用最大化問題をもとにラグランジュ未定乗数法の説明をしました。
数学的にラグランジュ未定乗数法を説明すると、全然話が変わってくるので注意してください。あくまで、効用最大化問題が解けるように、経済学っぽく説明してきたつもりです。


ラグランジュ未定乗数法は、本来であれば数学的なテクニックです。 厳密には色々な条件や前提があります。ミクロ経済学の問題を解くためには、暗黙の了解的なことがたくさんあるので、頭の片隅にでも入れておいてください。
ラグランジュ法を使って最適消費点を求める

ラグランジュ未定乗数法を使って簡単な問題を解いてみましょう!
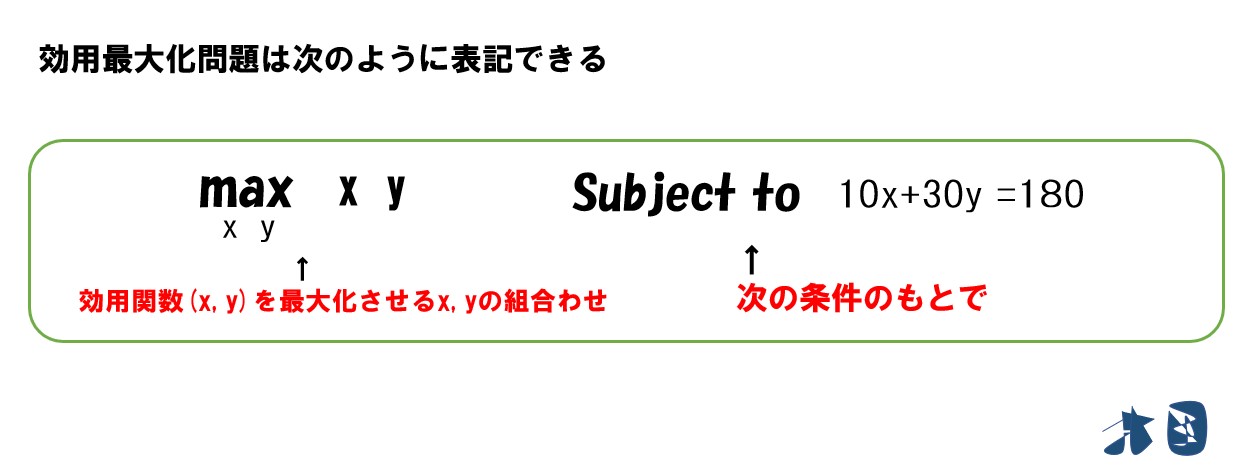
例題
- 効用関数 U(x, y)=xy
- X財の価格=10
- Y財の価格=30
- 所得=180
「max」「Subject to (S.T.)」などは「次の条件の下で効用最大化を実現する「x, y」を求めよ」という意味合いです。
変数「λ」を使ってラグランジュ関数を作ります
L (x, y ,λ)= xy-λ(10x+30y-180)
先に
「xy -λ(10x+30y-180)」の部分を計算します。
⇒「xy +(-λ10x-λ30y+λ180)」
「x, y ,λ」それぞれで偏微分して=0とします
xで偏微分:「xy +(-λ10x-λ30y+λ180)」
⇒① y-λ10=0
yで偏微分:「xy +(-λ10x-λ30y+λ180)」
⇒② x-λ30=0
λで偏微分:「xy +(-λ10x-λ30y+λ180)」
⇒③ -10x-30y+180=0
ポイント
「x」で偏微分するなら「x」という文字がついていない部分は無視されます。※あくまで微分は変化量(xという数量が変化したら式の答えがどう変化するか?)を見るため。
微分は乗数を1減らして、手前に持ってくる作業です。「x」=「xの1乗」なので「1xの0乗」となります。※「●●の0乗=1」となります。
①と②で連立方程式を組む
① y-λ10=0
② x-λ30=0
- ①を3倍します
① 3y-λ30=0
② x-λ30=0
「3y-λ30」=「x-λ30」⇒「3y=x」④
③と④で連立方程式を組む
③ -10x-30y+180=0
④ 3y=x
- ③の式に④を代入します
③ -10(3y)-30y+180=0
-30y-30y+180=0
180=60y
「y=3」
最後に「y=3」を④の式に代入
④ 3・3=x
「x=9」
したがって最適消費点は「x=9」「y=3」※(x, y)=(9, 3)とも表記できる。


ラグランジュ未定乗数法は、最適消費点(効用最大化問題)を求める時の計算テクニックとして有名です。ただし、なんでもラグランジュ未定乗数法を使えばいいわけではありません。
まずはオーソドックスな解き方を理解してから、使うようにしましょう!
効用最大化問題の解き方をまとめてます
-

-
【最適消費・効用最大化】求め方をグラフを使って分かりやすく
消費者理論で頻出の「最適消費・効用最大化」 最適消費・効用最大化とは 最適消費の求め方 効用最大化条件・計算方法 効用最 ...
続きを見る