エッジワース・ボックスで頻出するオファー曲線について情報をまとめています。
- オファー曲線とは?
- オファー曲線のグラフ
- オファー曲線と競争均衡配分
- オファー曲線の計算方法・求め方
オファー曲線とは?
オファー曲線とは
エッジワース・ボックス内の価格消費曲線(2財の価格比が変化したときの最適消費点(効用最大化)の軌跡)のこと。オファー・カーブとも言う。
貿易の輸出入に関する分析でもオファー曲線が登場するが、ここではエッジワース・ボックス(純粋交換経済)に関して話を進める。


はじめに
- 「価格比が変化したとき」の意味
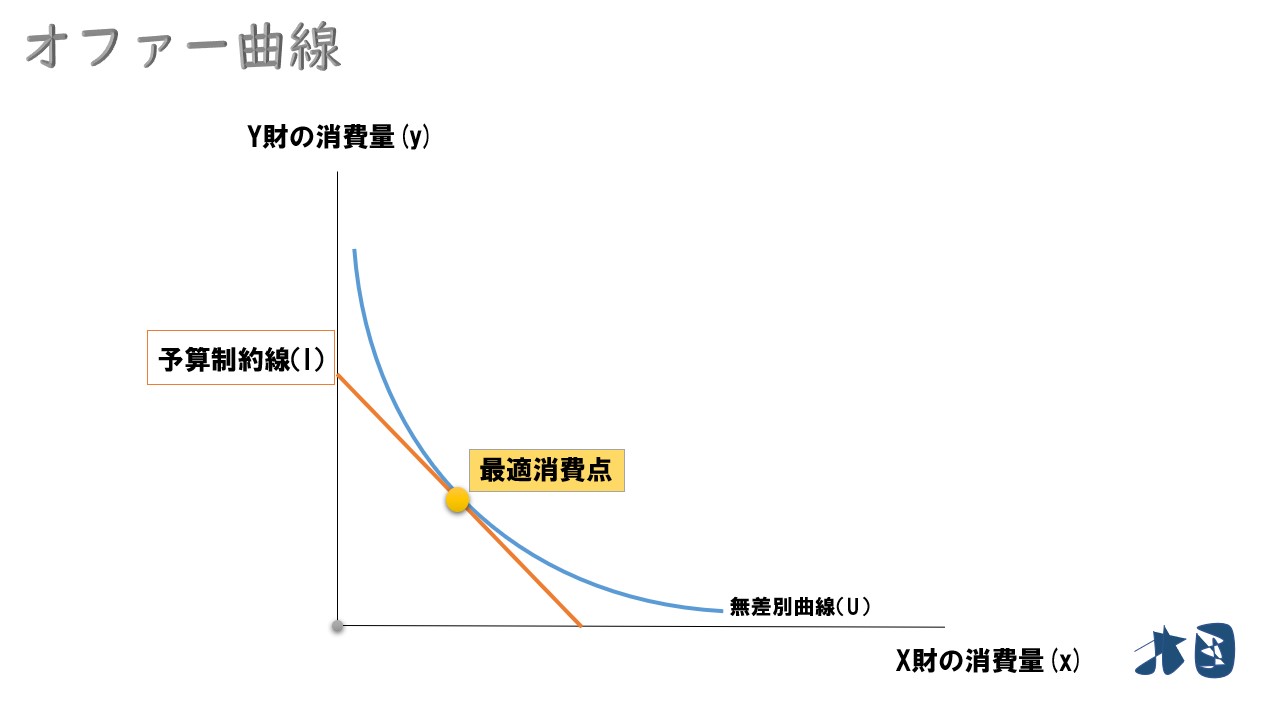
いま、グラフのように最適消費点が決まっている。
- X財の価格=50
- Y財の価格=50
と考えて2財の価格比は「50:50」とします。
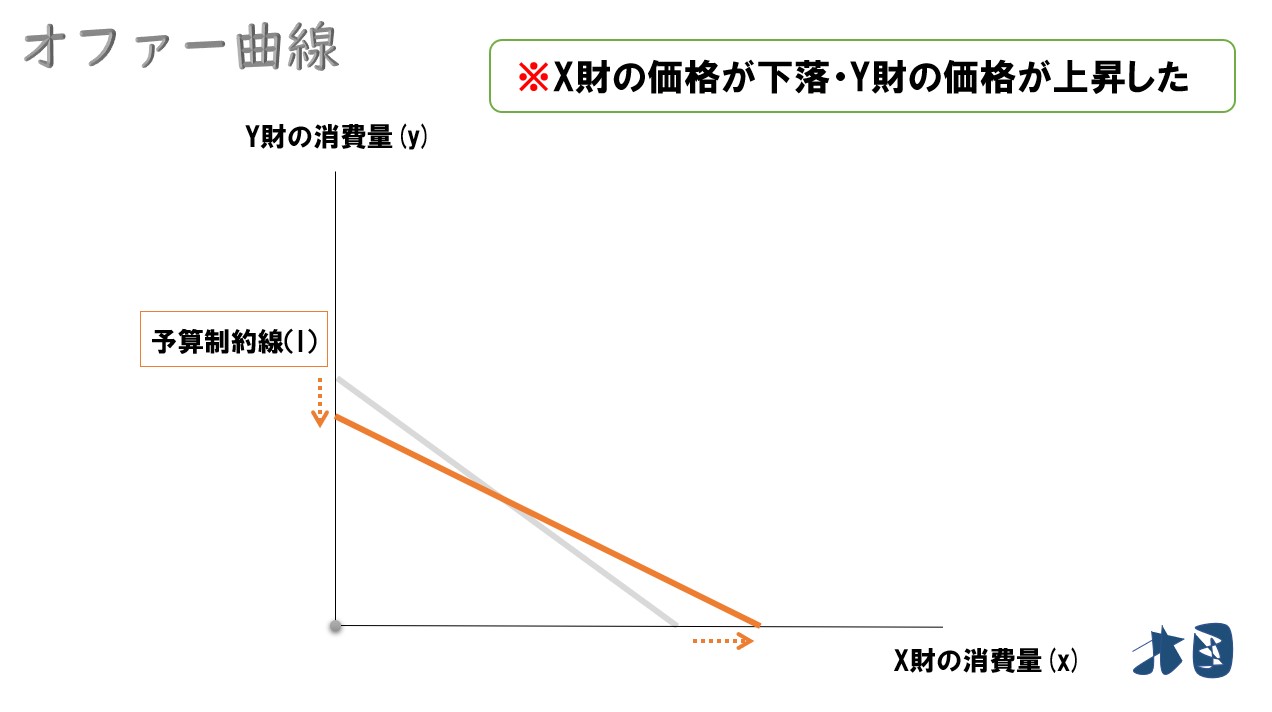
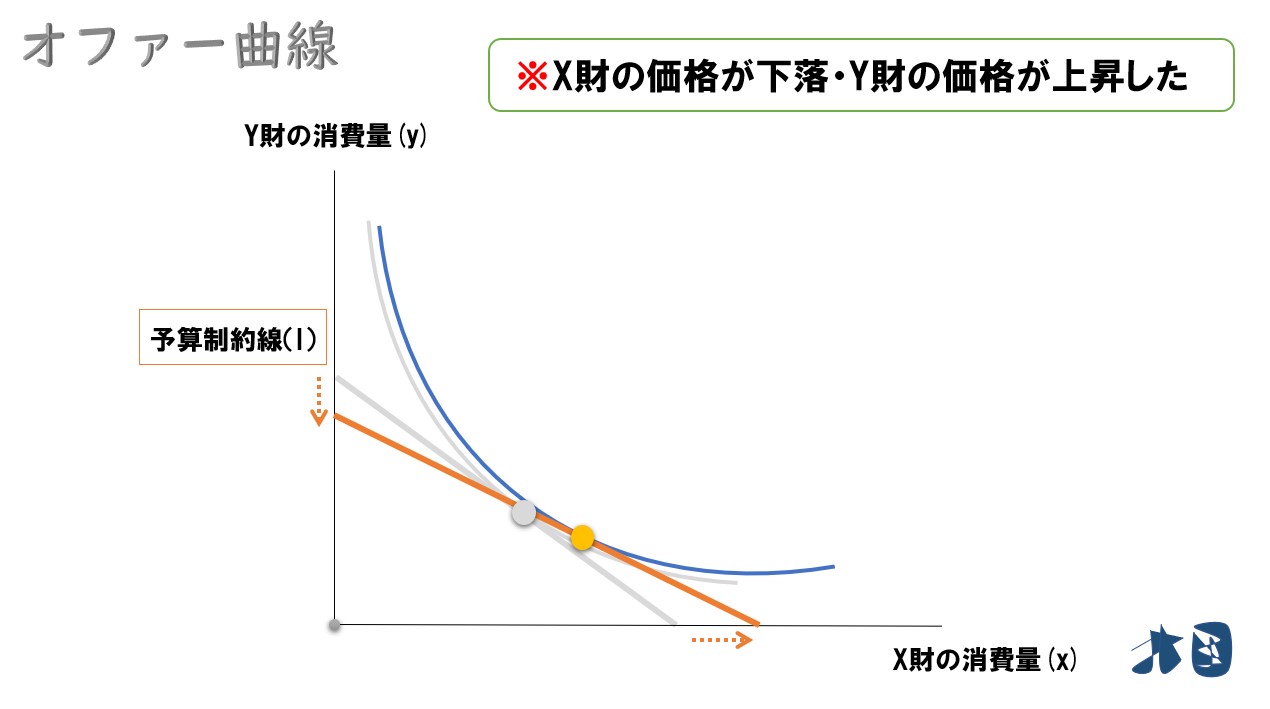
- 価格比が変化する(その1)
最適消費点は‥
下記のように最適消費点が変化しました。
- X財の価格が下落したので、X財は消費量を増やす
- Y財の価格が上昇したので、Y財は消費量を減らす
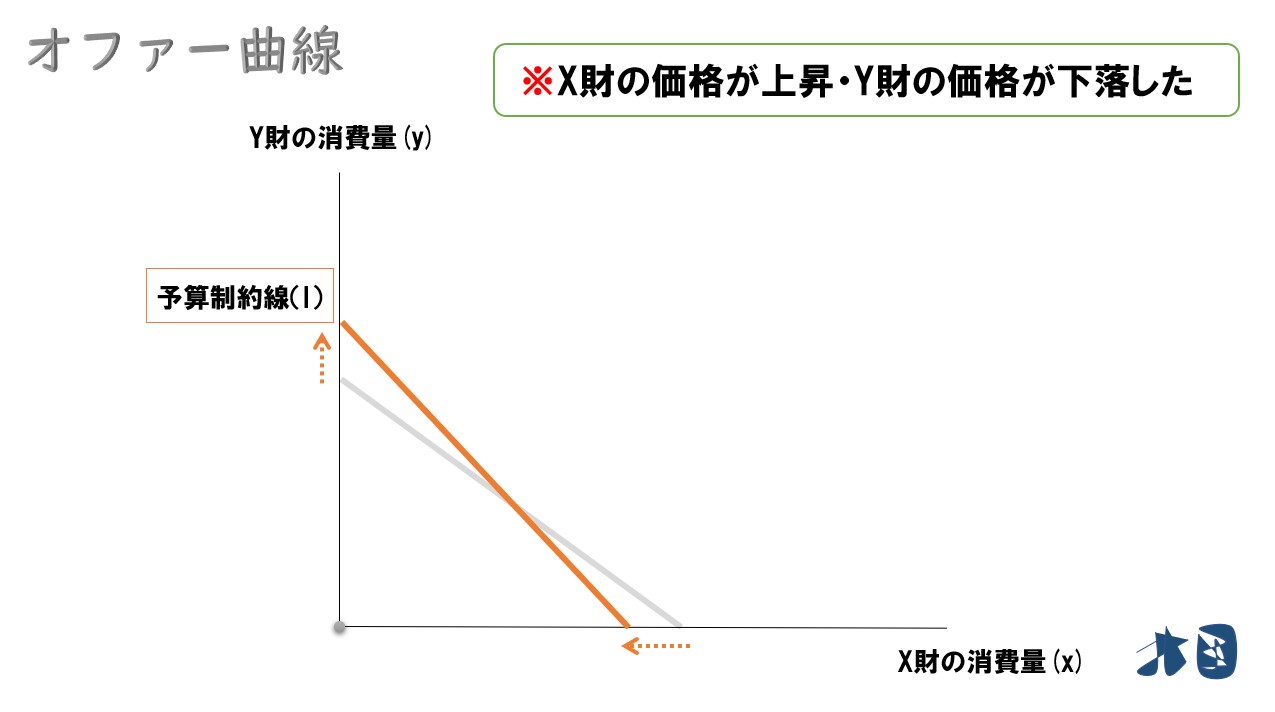
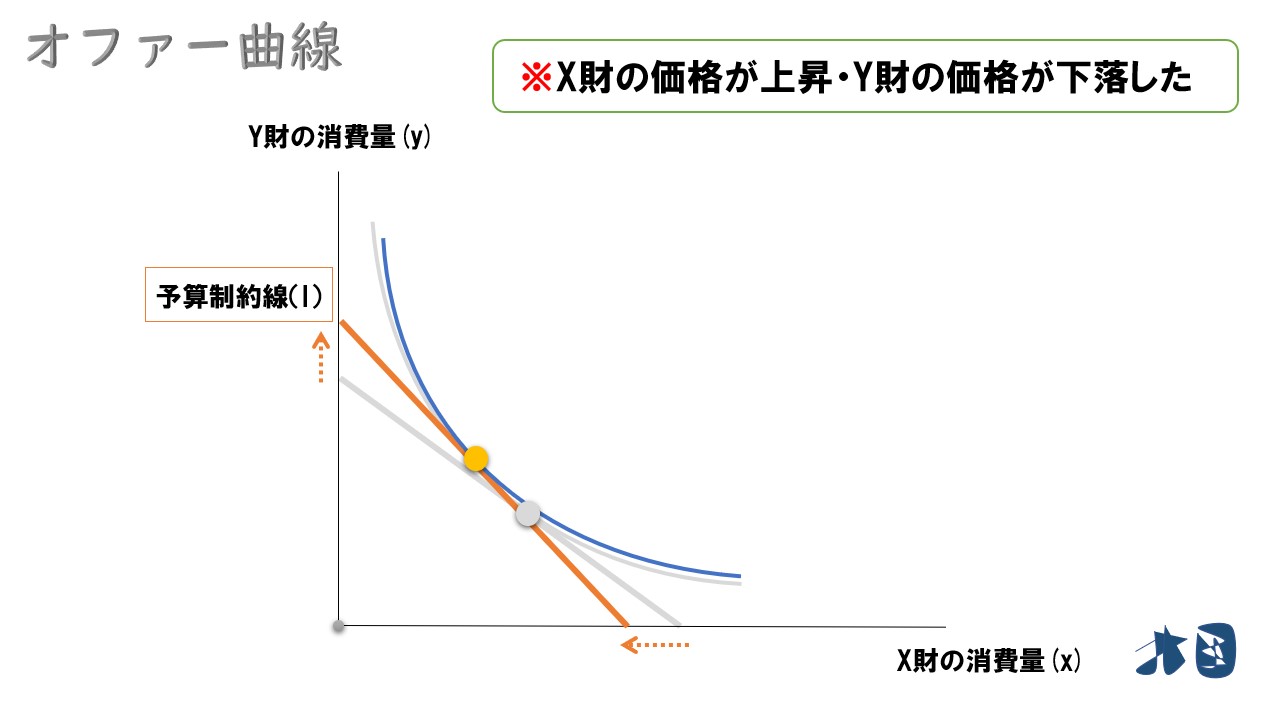
- 価格比が変化する(その2)
最適消費点は‥
下記のように最適消費点が変化しました。
- X財の価格が上昇したので、X財は消費量を減らす
- Y財の価格が下落したので、Y財は消費量を増やす
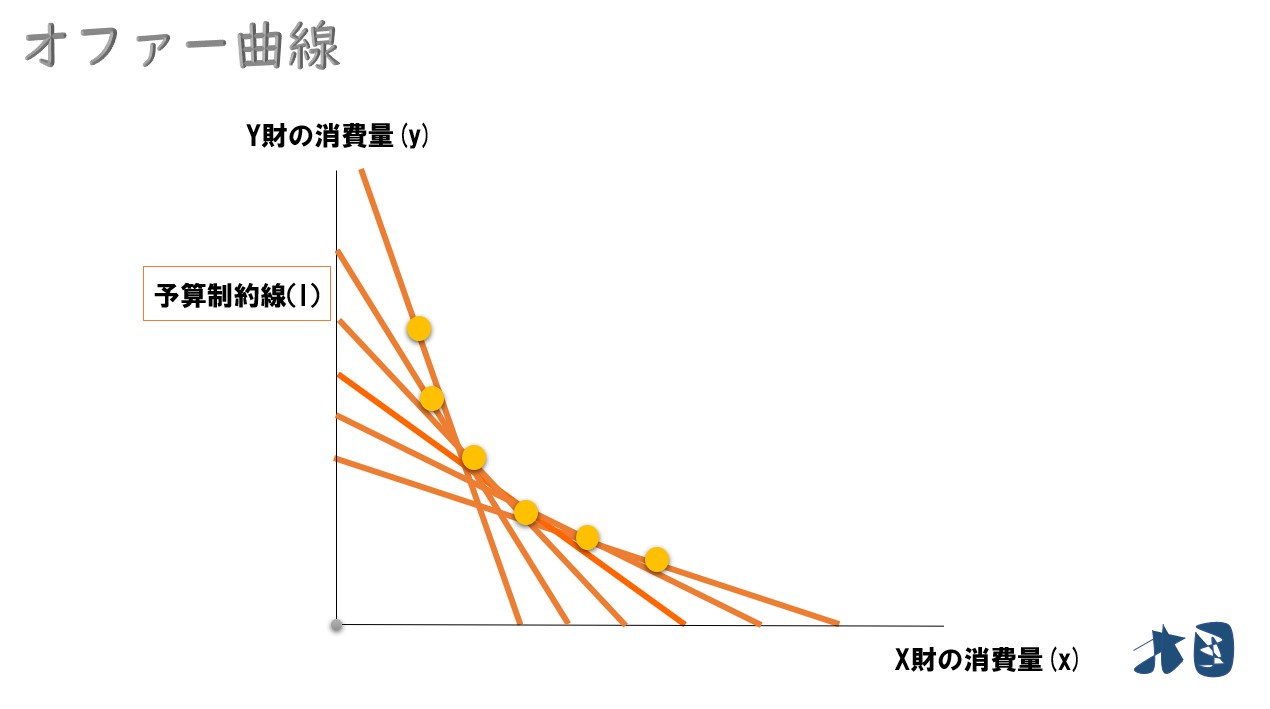
最適消費点を結んでいく
価格比が変化したときの最適消費点を描いていきます。
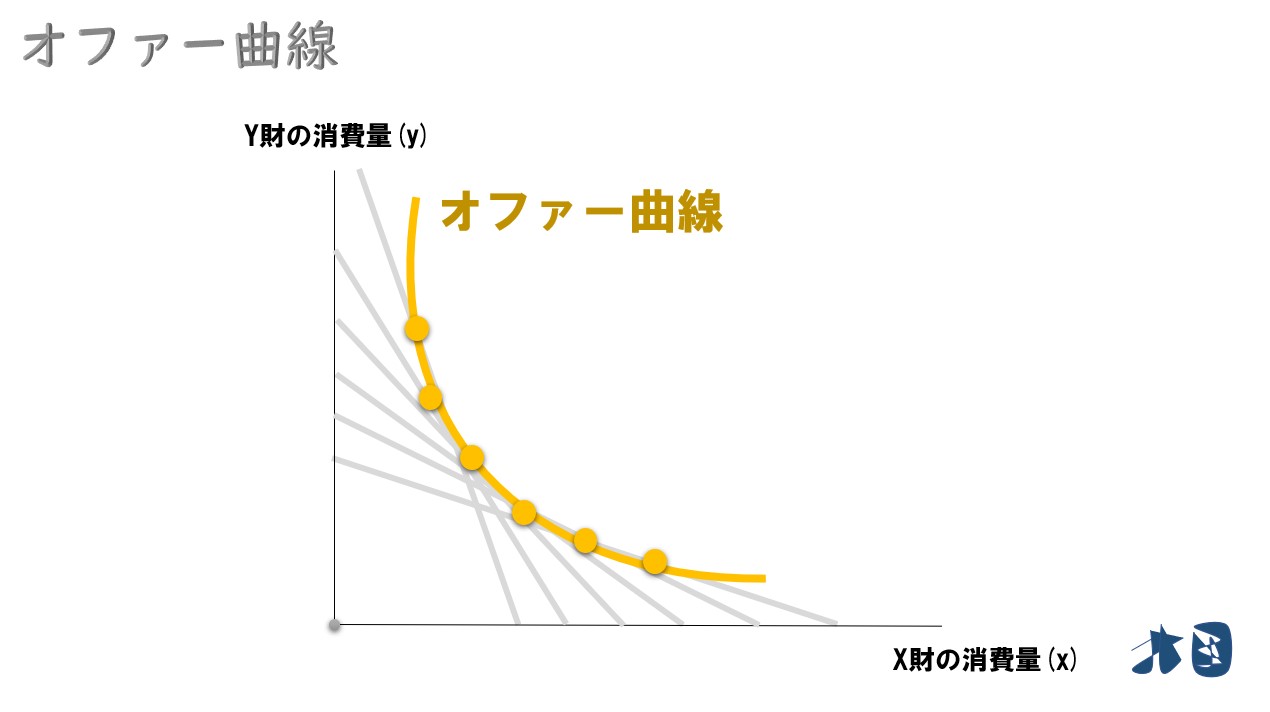
最適消費点を線で結ぶと‥
これを「オファー曲線(オファー・カーブ)」と呼びます。


オファー曲線と競争均衡配分
はてな
ここでは、初期保有から2人の消費者が財の交換を通して得られるパレート効率的な資源配分のことを「競争均衡配分」と呼ぶ。
厳密に言えば、2人の消費者が与えられた財の価格・予算制約・初期保有を条件に自身の効用最大化を目指して財の交換を行うとき、2人の消費者の効用最大化が実現して、かつ、財の需要と供給が一致するような資源配分のことを競争均衡配分(=ワルラス均衡)と呼ぶ。このとき、競争均衡配分はパレート効率的な資源配分となる(厚生経済学の第一基本定理)。
注意が必要ですが「パレート効率的な資源配分だから競争均衡配分」ではなく「財の交換という市場に任せて実現する競争均衡配分が、結果としてパレート効率的になっている(←これを厚生経済学の第一基本定理と言います)」ので、パレート効率的だから競争均衡配分という理屈ではありません。


ポイント
競争均衡配分が実現するとき、お互いのオファー・カーブが交わる。
改めてですが
2つ確認です
①競争均衡配分は「初期保有から2人の消費者が財の交換を通して得られるパレート効率的な資源配分」です。
②オファー曲線は「2財の価格比が変化したときの最適消費点(効用最大化)の軌跡)」です。
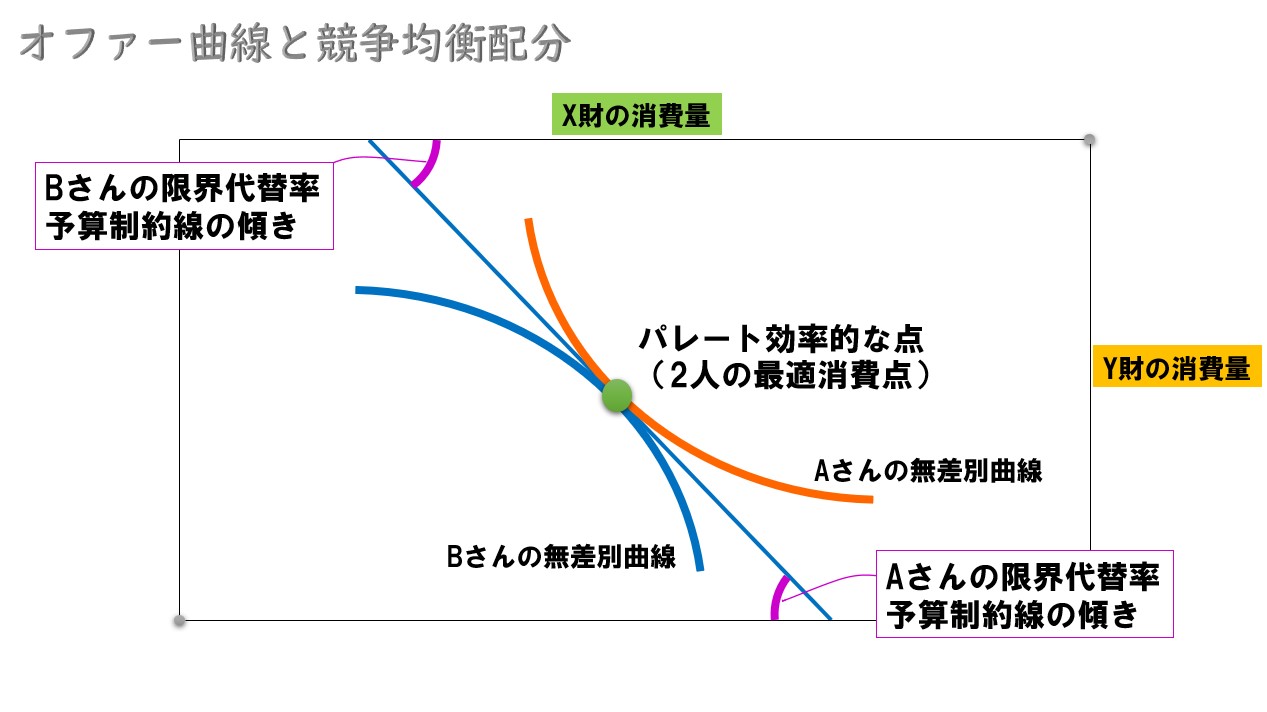
ここで、エッジワース・ボックスでパレート効率的となるポイントでは、2人の消費者の最適消費点(効用最大化点)が一致しています(←その結果、2人の限界代替率(MRS)が一致して、2財の価格比が一致しています。グラフを思い出そう↓)
以上より
- 競争均衡配分はパレート効率的となる
- エッジワース・ボックスでパレート効率的な場合は、2人の最適消費点が一致する
- オファー曲線は最適消費点の軌跡
競争均衡配分
⇒パレート効率的
⇒2人の最適消費点が一致
⇒オファー曲線は最適消費点の軌跡
⇒競争均衡配分では2人のオファー曲線が交わる
競争均衡配分ではパレート効率的となり2人の最適消費点が一致するので、その軌跡である2人のオファー曲線が交わる。
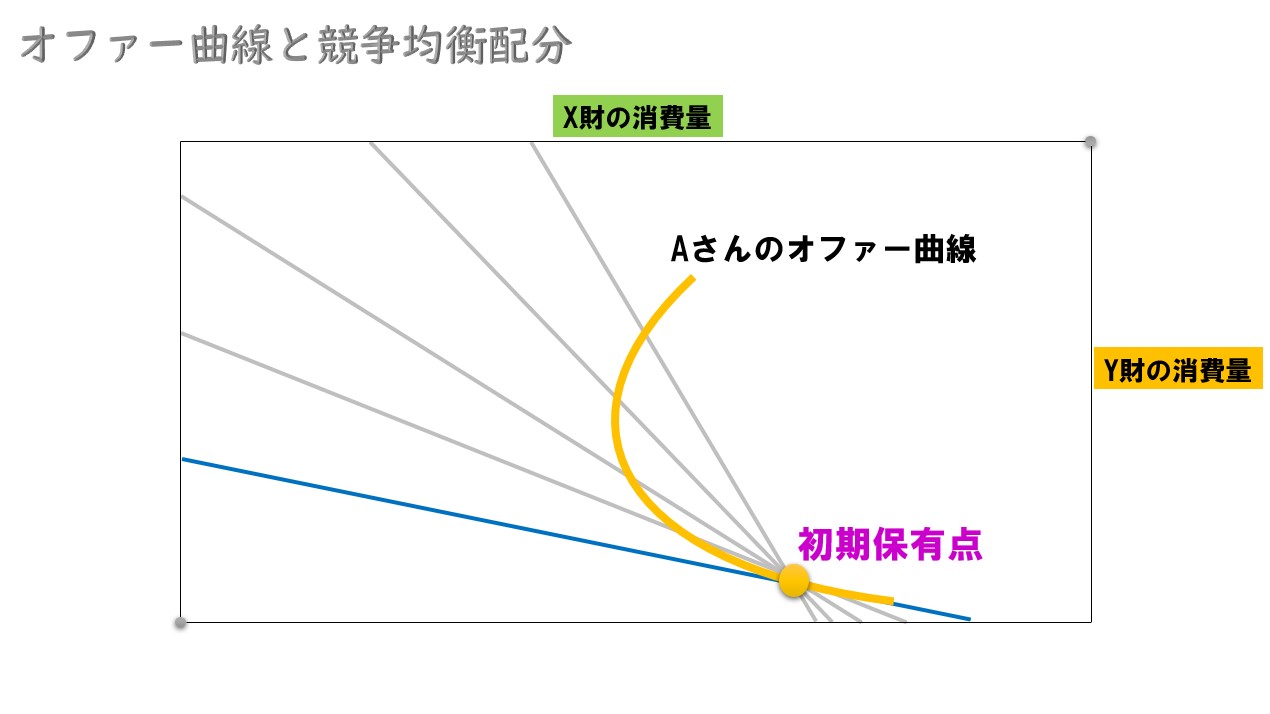
グラフで見ると‥
初期保有点との関係も見ると‥
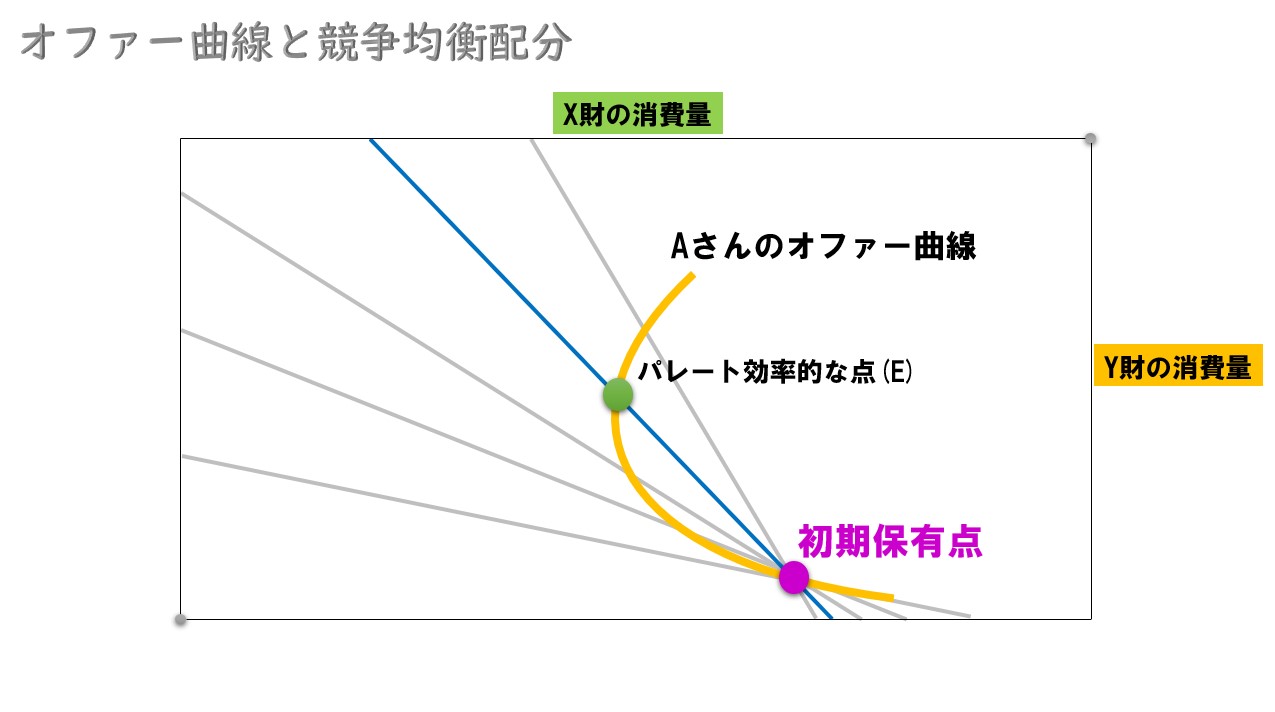
このオファー曲線は、初期保有点(W)を軸に描いたものです。
初期保有点(W)を軸に、2財の価格比を変化させています。
つまり
初期保有点(W)を軸に予算制約線の傾き(2財の価格比)を変化させているので、パレート効率的な点Eが実現する予算制約線(2財の価格比)は、必ず初期保有点(W)を通過します。
予算線が初期保有点を通過するというのはエッジワース・ボックスの説明のときにも登場しました。←エッジワース・ボックスと初期保有の関係を参照
また、初期保有点(W)=最適消費(効用最大化)となる2財の価格比も存在します
以上より、オファー曲線は初期保有点(W)を通過して、パレート効率的な点(E)を通過するような曲線となっています。
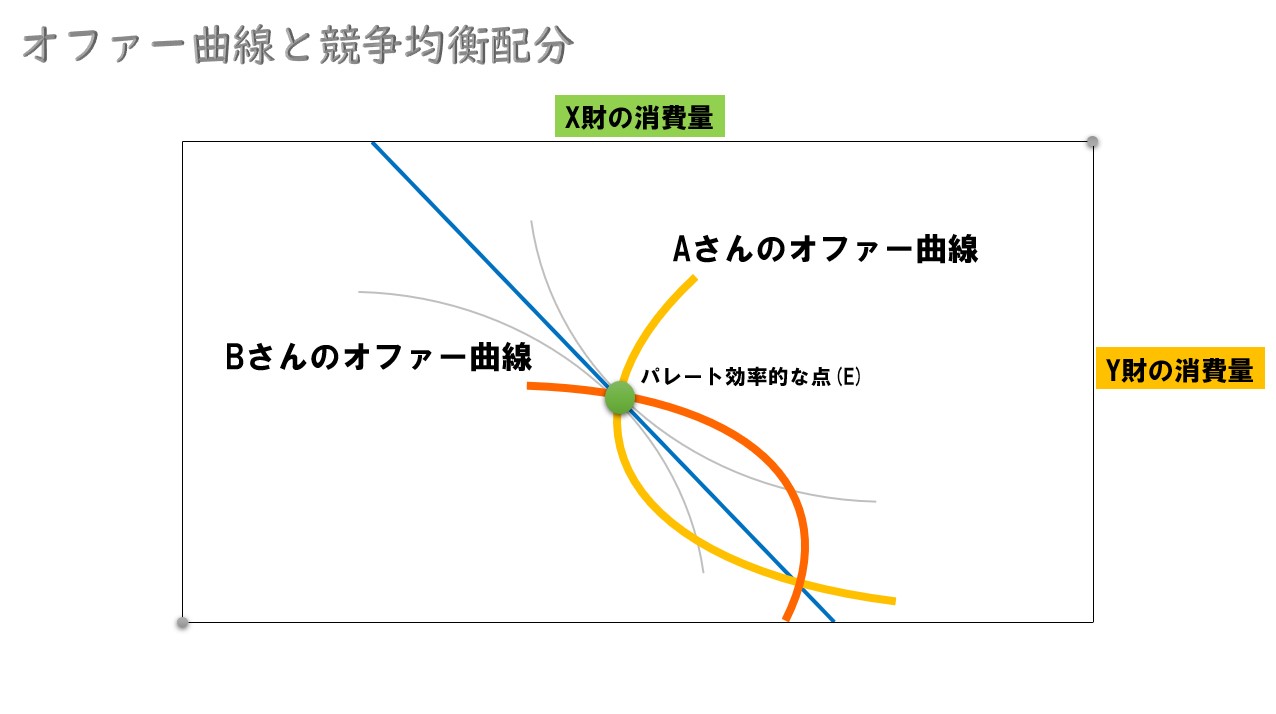
Bさんも同様のことが言えるので、2人のオファー曲線を図示すると
初期保有点で交わって、競争均衡配分⇒パレート効率的な点(E)で再び交わり合うカーブとなっています。


計算方法(例題)

いま、2人の消費者(Aさん・Bさん)が2種類の財を保有している。
- AさんはX財20個・Y財80個
- BさんはX財80個・Y財20個
また2人の効用関数は以下の通りである。
- Aさん「U=3xy」
- Bさん「U=2xy」
- Aさん・Bさんのオファー曲線を求めよ
- 競争均衡配分を求めよ
step
1限界代替率を求める
はじめに2人の限界代替率が知りたいので、問題文で与えられている効用関数(U)から求めます。
ポイント
効用関数(無差別曲線)を微分すれば「傾き(限界代替率)」が求められます。
参考:最適消費点の計算方法
- Aさんの効用関数「U=3xy」より
「y=U/3x」とする
「y=U/3x」を微分すると⇒「U/-3xの2乗(=U・-3xの-2乗)」
ちなみに分数は「(1/2)=2の-1乗」なので注意しましょう。
ここで
「U」という文字が邪魔なので、Uを「xとy」に置き換えます。
「U=3xy」を「U/-3xの2乗」に代入します。
「U(=xy)/-3xの2乗」⇒「3xy/-3xの2乗」=「-(y/x)」
Bさんの限界代替率も同様に求めると「-(y/x)」となります。
以上より
- Aさんの限界代替率=「-(y/x)」
- Bさんの限界代替率=「-(y/x)」
次に最適消費が実現する=パレート効率的な状態(競争均衡)なとき「予算制約線の傾き=限界代替率」が等しいということを思い出します。
- X財の価格=Px
- Y財の価格=Py
とするとき、予算制約線の傾きは「Px/Py」となる。
以上より、Aさん・Bさん共に(Px/Py)=(y/x)
限界代替率は厳密にはマイナスが付きますが、計算上は不要になるので外します。
これを需要関数(需要量を価格の関数で表したもの)の形にします。
- x=(Py/Px)y
- y=(Px/Py)x
step
2最適消費量(需要関数)を求める
予算制約線は「I=xPx+yPy」と表すことが出来ます。
ここで、通常の最適消費(効用最大化)を求めるのと同じように、Aさんは予算上限まで消費を行っていると想定します。
- Aさんの初期保有「X財20個・Y財80個」より
予算制約線を使って「xPx+yPy=20Px+80Py」と表すことが出来ます。
最初の説明でまとめた通り、初期保有点は予算制約線上にあるため上記の式を作ることが出来ます。
それぞれ「x=」「y=」の形に変形します。
- xPx+yPy=20Px+80Py
- xPx=20Px+80Py-yPy
- xPx=20Px+(80-y)Py
- x=20+((80-y)Py)/Px
- xPx+yPy=20Px+80Py
- yPy=20Px+80Py-xPx
- yPy=(20-x)Px+80Py
- y=((20-x)Px)/Py+80
ここから
はじめに下記のように求めたのでイコールで結びます。
- x=(Py/Px)y
- y=(Px/Py)x
「x=(Py/Px)y」
「x=20+((80-y)Py)/Px」より
- (Py/Px)y=20+((80-y)Py)/Px
(両辺にPx/Pyをかける)
- y=20(Px/Py)+80-y
- 2y=20(Px/Py)+80
- y=10(Px/Py)+40
「y=(Px/Py)x」
「y=((20-x)Px)/Py+80」より
- (Px/Py)x=((20-x)Px)/Py+80
(両辺にPy/Pxをかける)
- x=20-x+80(Py/Px)
- 2x=20+80(Py/Px)
- x=10+40(Py/Px)
Bさんも同様に
- Bさんの初期保有「X財80個・Y財20個」より
予算制約線を使って「xPx+yPy=80Px+20Py」と表すことが出来ます。
それぞれ「x=」「y=」の形に変形します。
- xPx+yPy=80Px+20Py
- xPx=80Px+20Py-yPy
- xPx=80Px+(20-y)Py
- x=80+((20-y)Py)/Px
- xPx+yPy=80Px+20Py
- yPy=80Px+20Py-xPx
- yPy=(80-x)Px+20Py
- y=((80-x)Px)/Py+20
「x=(Py/Px)y」
「x=80+((20-y)Py)/Px」より
- (Py/Px)y=80+((20-y)Py)/Px
(両辺にPx/Pyをかける)
- y=80(Px/Py)+20-y
- 2y=80(Px/Py)+20
- y=40(Px/Py)+10
「y=(Px/Py)x」
「y=((80-x)Px)/Py+20」より
- (Px/Py)x=((80-x)Px)/Py+20
(両辺にPy/Pxをかける)
- x=80-x+20(Py/Px)
- 2x=80+20(Py/Px)
- x=40+10(Py/Px)
以上より
Aさんの最適消費量(需要関数)
- x=10+40(Py/Px)
- y=10(Px/Py)+40
Bさんの最適消費量(需要関数)
- x=40+10(Py/Px)
- y=40(Px/Py)+10
step
3オファー曲線を求める
オファー曲線は「(縦軸)=(横軸)」という式になる
オファー曲線はエッジワース・ボックスの縦軸と横軸の関係を使って表現します。そのため、縦軸の消費量(y)と横軸の消費量(x)を使った式になります。
「Px・Py」は不要なので、消えるように工夫します。
Aさんの最適消費量(需要関数)より
x=10+40(Py/Px)
x-10=40(Py/Px)
(x-10)/40=Py/Px
40/(x-10)=Px/Py
「y=10(Px/Py)+40」へ代入
y=10(40/(x-10))+40
y=400/(x-10)+40
Bさんの最適消費量(需要関数)より
x=40+10(Py/Px)
x-40=10(Py/Px)
(x-40)/10=Py/Px
10/(x-40)=Px/Py
「y=40(Px/Py)+10」へ代入
y=40(10/(x-40))+10
y=400/(x-40)+10
以上より
Aさんのオファー曲線
- y=400/(x-10)+40
Bさんのオファー曲線
- y=400/(x-40)+10
step
4競争均衡配分を求める
ここまでAさんのX財の消費量・BさんのX財の消費量を同じ「x」という文字で表してきました。
ふつうは「x1・x2」とか「xA・xB」などと記載しますが、パッと見た時に混乱すると考えて同じ文字で表現してきました(Y財の消費量も同様)
ここで
AさんとBさんのX財・Y財の消費量を正確に表現します。
- Aさんの初期保有「X財20個・Y財80個」
- Bさんの初期保有「X財80個・Y財20個」
より「X財の総量=100個」「Y財の総量=100個」と分かる。
以上より
- AさんがX財を「x個」消費するとき、Bさんは「100-x」を消費
- AさんがY財を「y個」消費するとき、Bさんは「100-y」を消費
Bさんのオファー曲線を書き換えます
y=400/(x-40)+10
100-y=400/(100-x-40)+10
100-y=400/(60-x)+10
-y=400/(60-x)+10-100
-y=400/(60-x)-90
y=-400/(60-x)+90
競争均衡配分では、2人のオファー曲線が交わるのでイコールで結びます
Aさんのオファー曲線は
「y=400/(x-10)+40」なので
400/(x-10)+40=-400/(60-x)+90
400/(x-10)=-400/(60-x)+50
400(60-x)/(x-10)=-400+50(60-x)
400(60-x)/(x-10)=-400+3000-50x
400(60-x)/(x-10)=2600-50x
400(60-x)=2600(x-10)-50x(x-10)
24000-400x=2600x-26000-50x^2+500x
24000-400x-2600x+26000+50x^2-500x=0
50x^2-3500x+50000=0
x^2-70x+1000=0
AさんのX財の初期保有量は「20個」だったので
因数分解すれば0=(x-20)(●●●)となるはず
0=(x-20)(x-50)となるので「x=20,50」と分かる
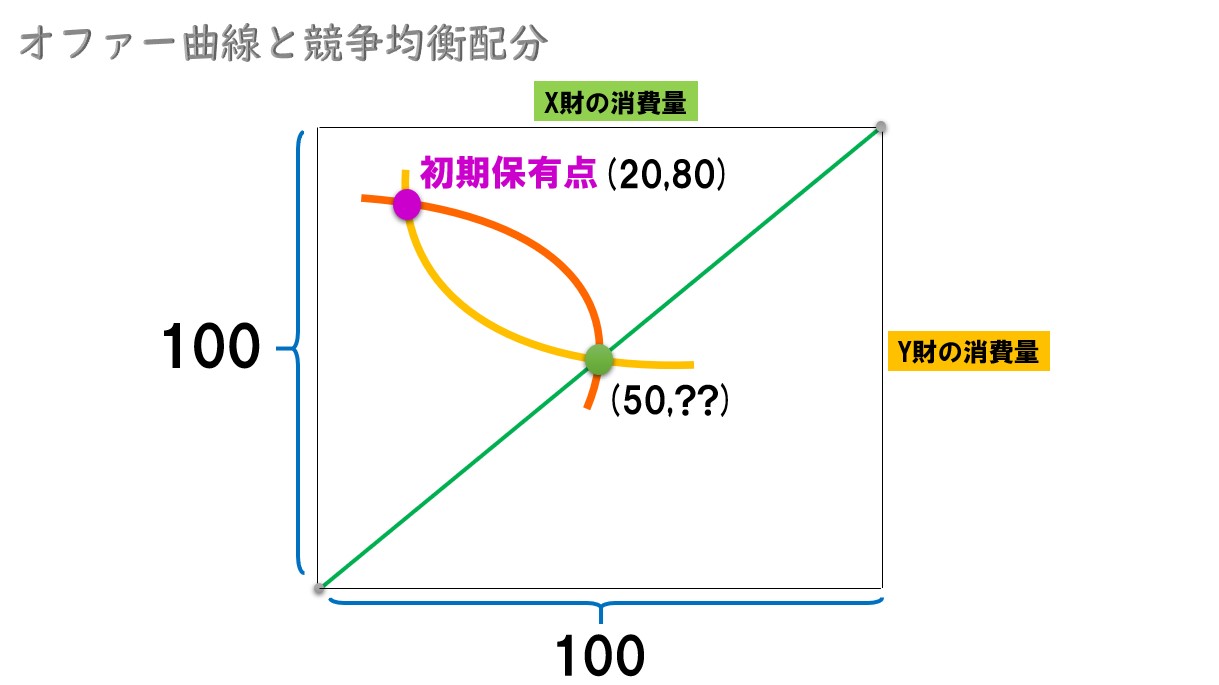
解のx=20は初期保有量なので「x=50」が競争均衡となる。
X財の総量は100なので、X財の配分は「Aさん50個:Bさん50個」
グラフで見ると‥
また
Aさんのオファー曲線
「y=400/(x-10)+40」より
y=400/(50-10)+40
y=400/40+40
y=10+40
y=50
Y財の総量も100なので、Y財の配分は「Aさん50個:Bさん50個」
以上より
Aさん(50,50)
Bさん(50,50)が競争均衡配分