価格と財の消費量の関係を表した「価格-消費曲線」「需要曲線」
- 価格-消費曲線とは?
- 粗代替財・粗補完財
- 需要曲線と通常財・ギッフェン財
- 価格-消費曲線の式の求め方
「価格-消費曲線」「需要曲線」の要点を、グラフを使って分かりやすくまとめています。
価格-消費曲線とは?
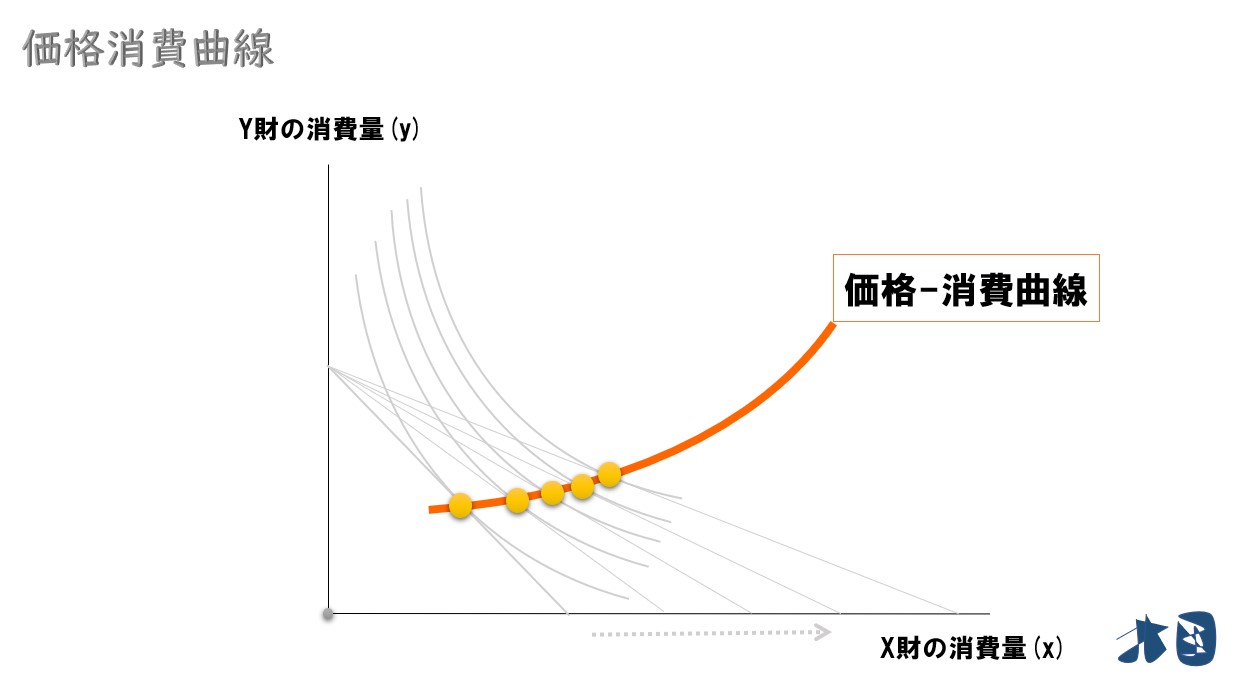
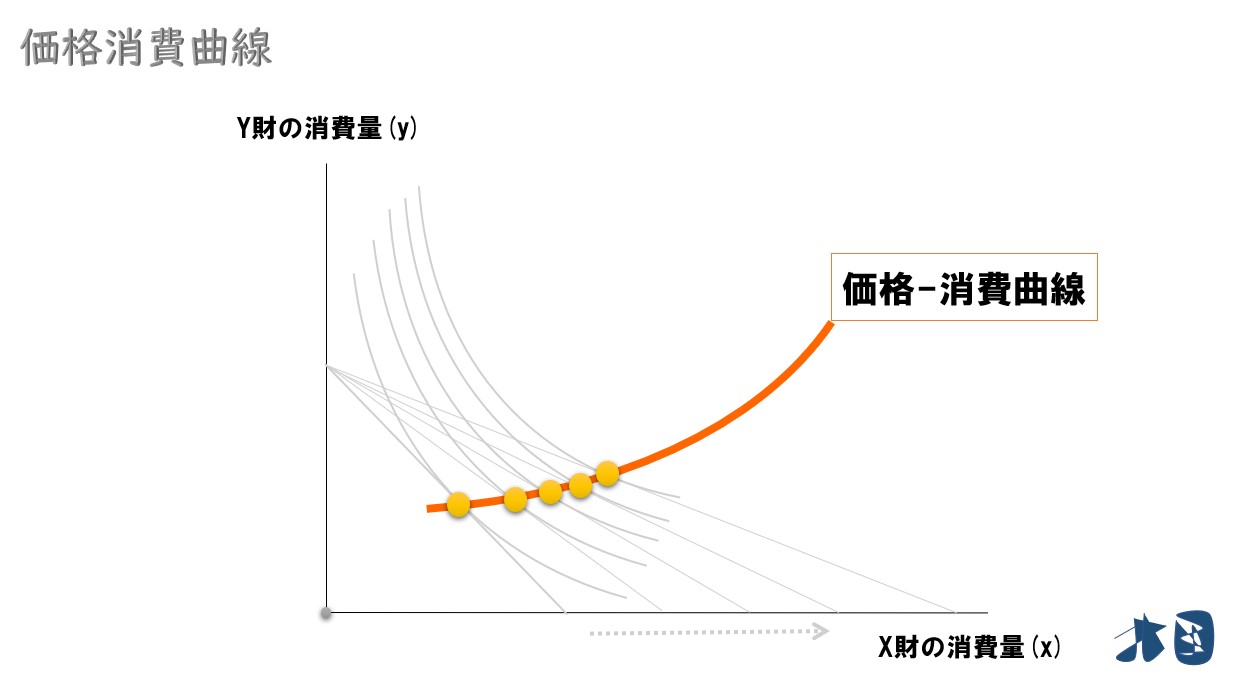
価格-消費曲線
価格が変化すると、最適消費点がどのように変化するかを示した曲線。「価格変化」と「財の消費量」の関係が分かる。
まずは、価格消費曲線がどのように書かれるかを見ていきます。
グラフ
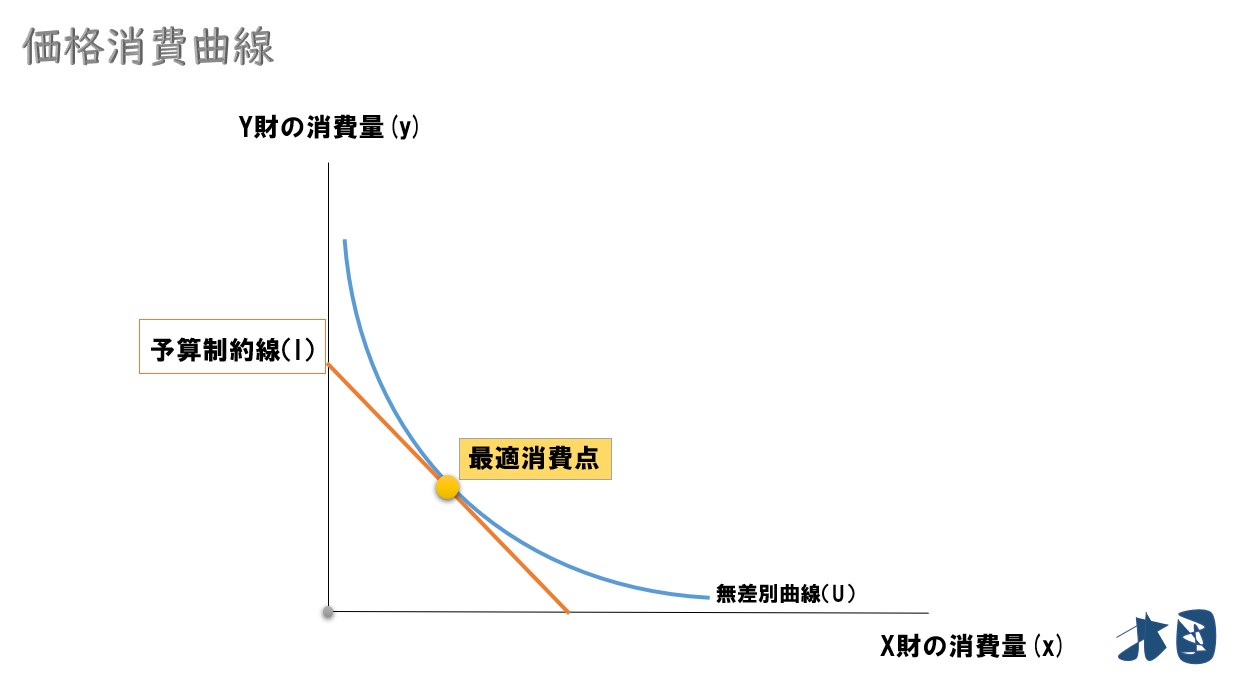
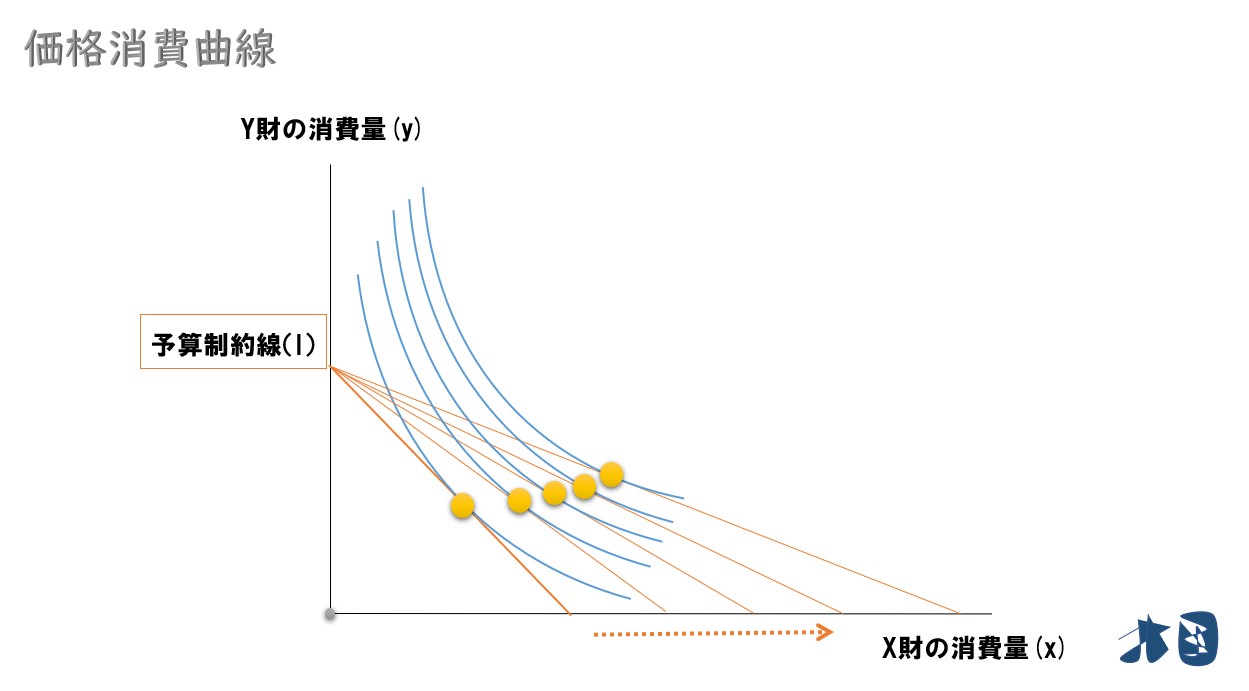
「ある所得(予算制約線)」と「財の選好(無差別曲線)」が与えられていて、最適消費点が上のグラフのようになっていた時を考えます。
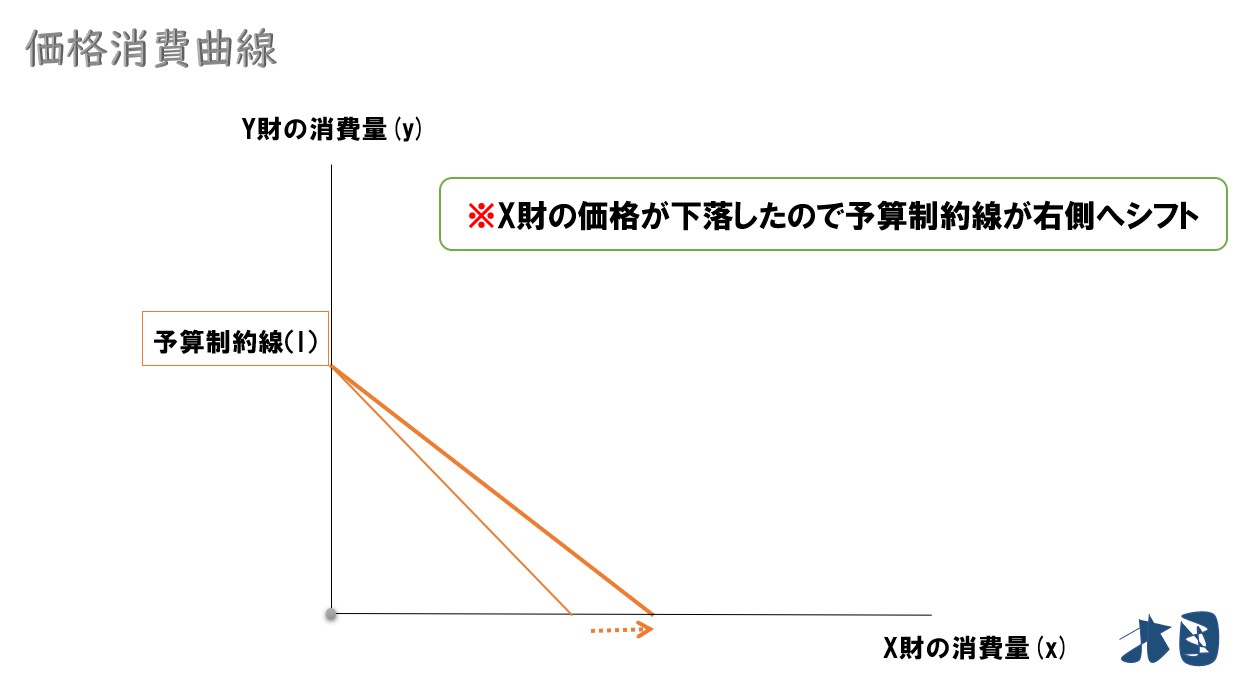
X財価格が下落
Y財の価格を固定して、X財の価格が下落したときを考えます。X財(横軸)の価格下落なので予算線が右側にシフトします。予算制約線の話が分からない人は確認する
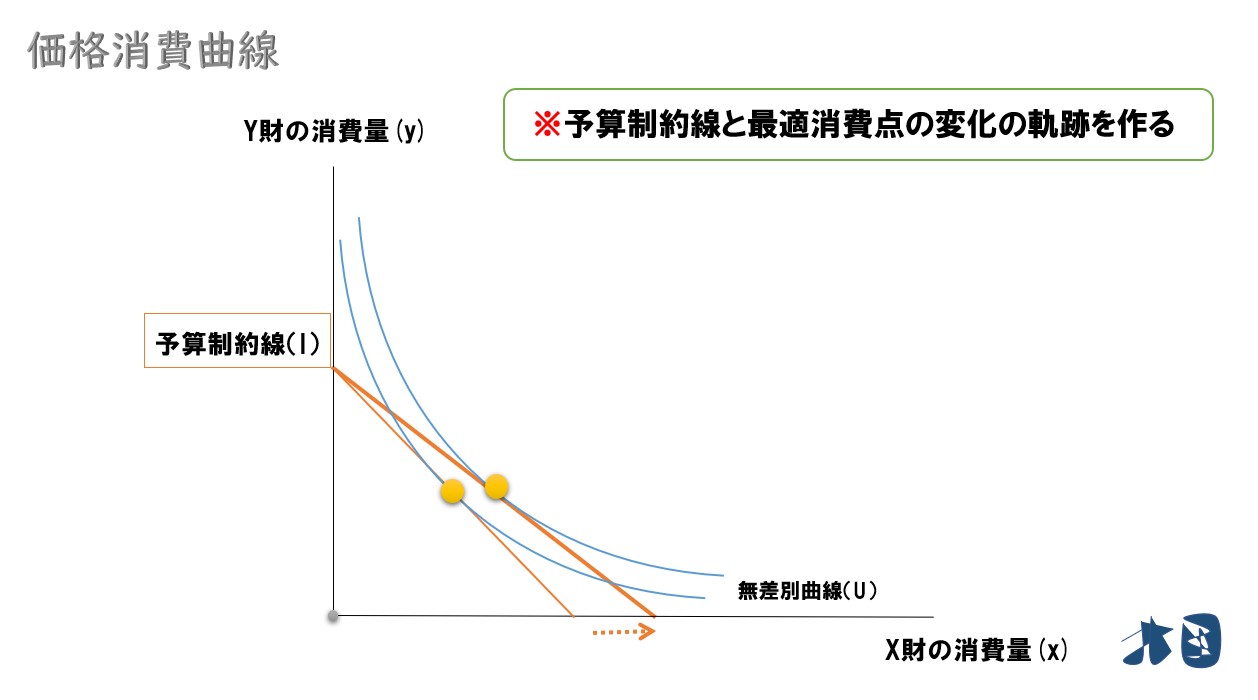
最適消費点も移動
何度も繰り返す
最適消費点の軌跡を結んでいくと・・
ポイント
所得を固定して、財の価格を変化させると、予算制約線がシフトして最適消費点が変化します。その軌跡を結ぶと価格消費曲線が登場します。


ポイント1
価格消費曲線から、価格が変動していない方の財の性質を知ることが出来ます。
ポイント2
また、価格消費曲線から需要曲線が導けます。特に、ギッフェン財の話が定番です。
粗代替財・粗補完財の判断

大きなパターンは2つ
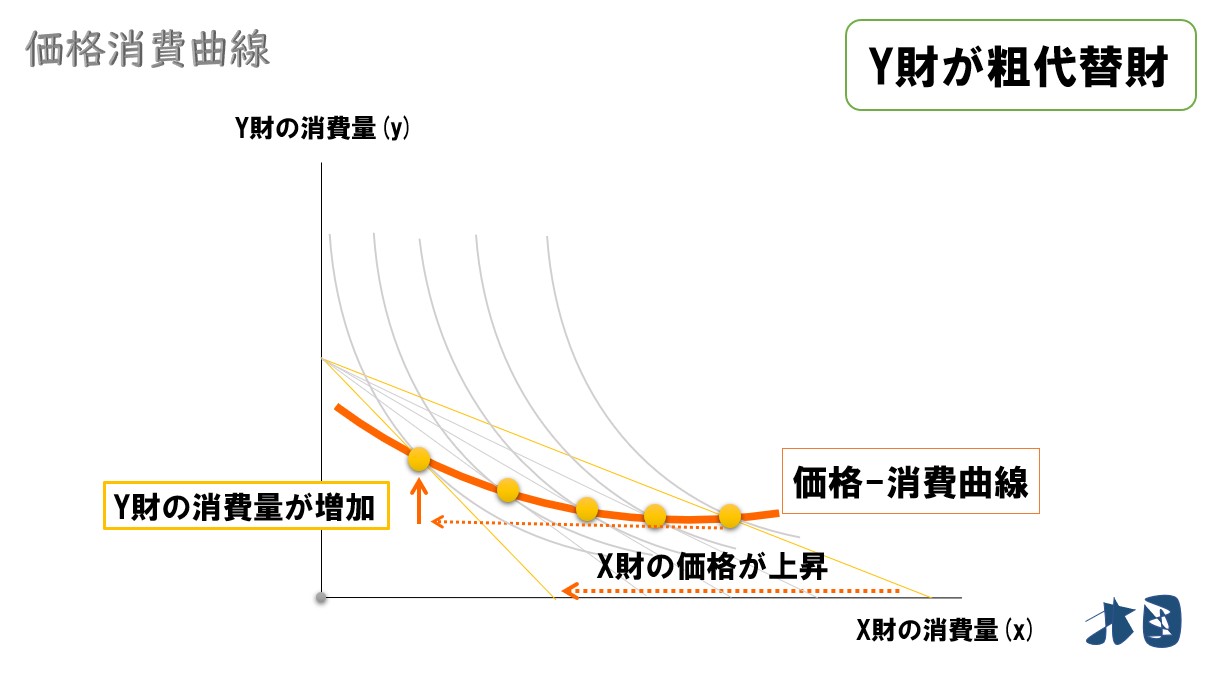
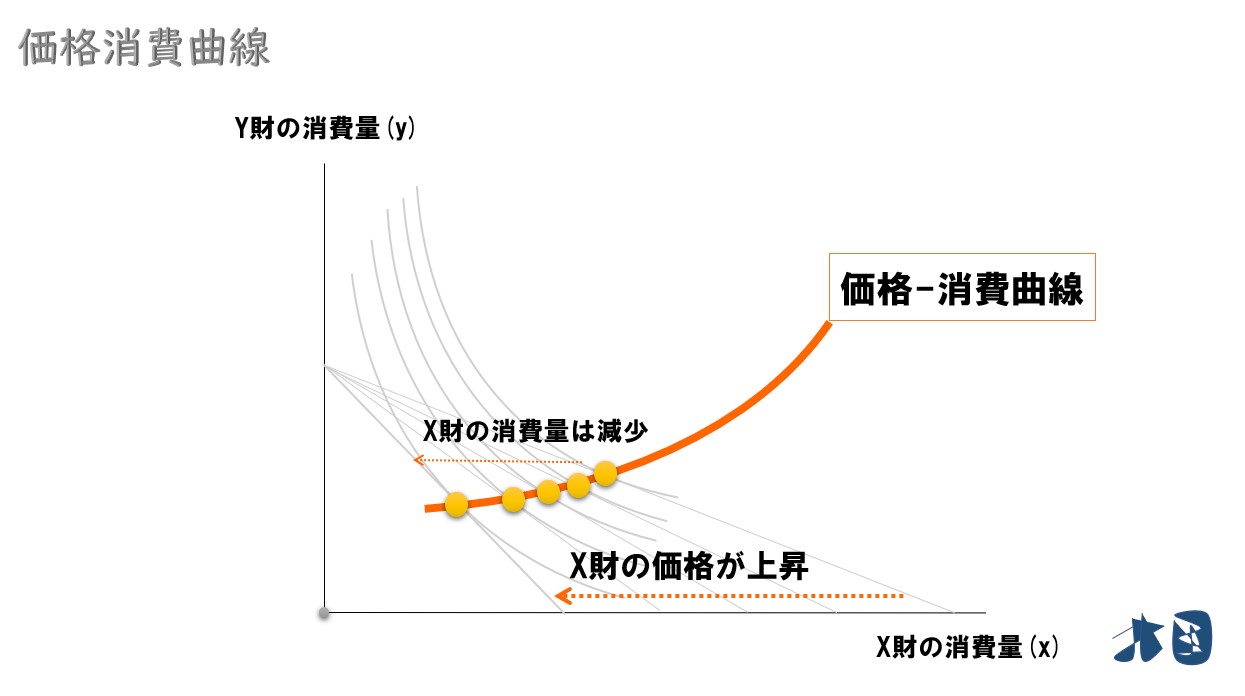
【価格変化していない財が粗代替財】
他の財の価格が上昇したときに、財の消費量(需要量)が増加しているため、Y財・X財は粗代替財と言える。
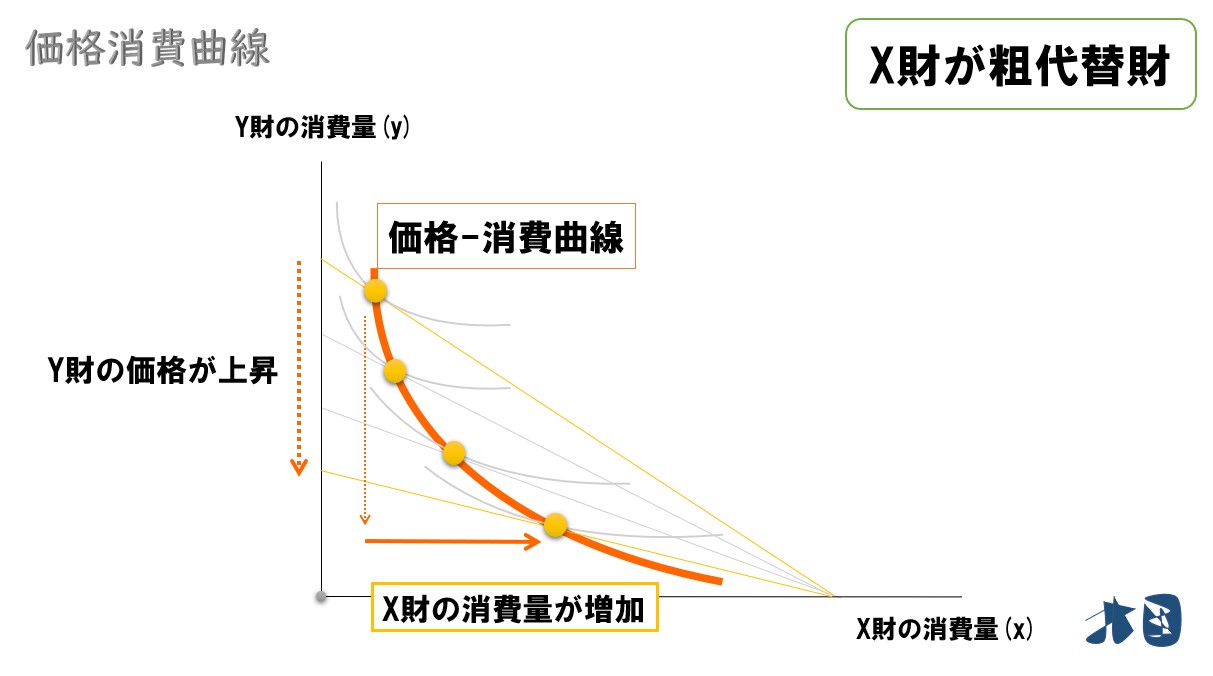
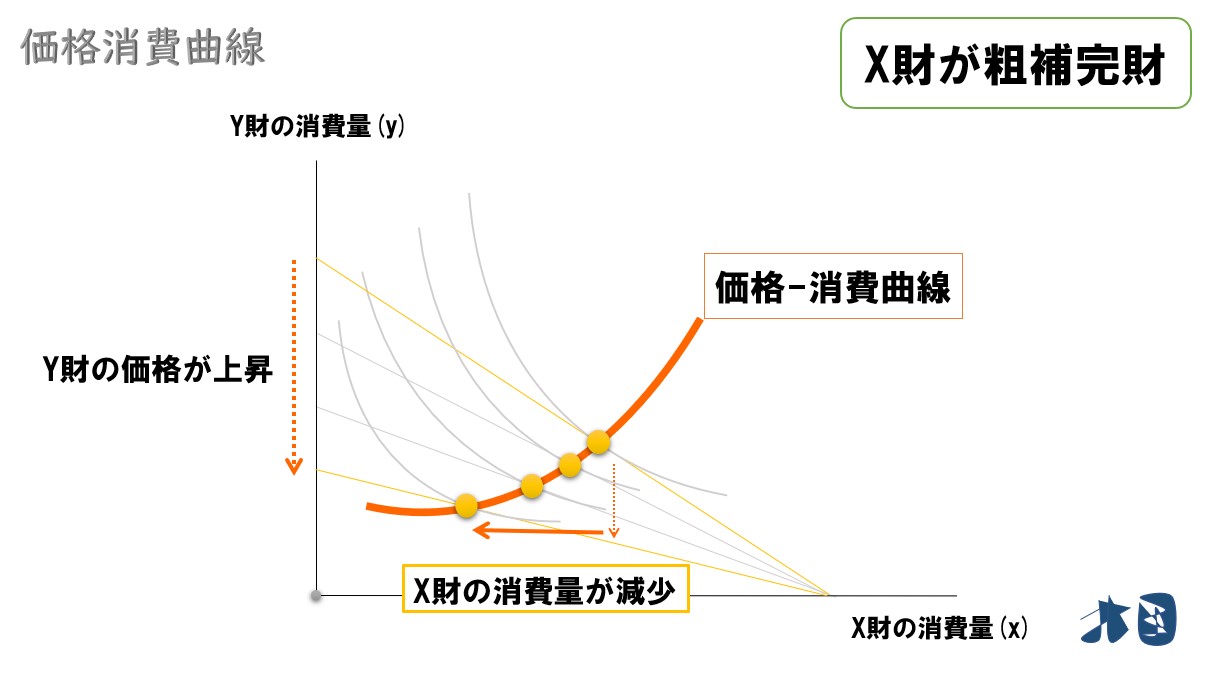
【価格変化していない財が粗補完財】
他の財の価格が上昇したときに、財の消費量(需要量)が減少しているため、Y財・X財は粗補完財と言える。
まとめ
| 価格-消費曲線の形状 | 価格が変化していない財 |
|---|---|
| 右下がり | 粗代替財 |
| 右上がり | 粗補完財 |


需要曲線と通常財・ギッフェン財の判断
需要曲線
特定の1つの財の価格と消費量を対応させた曲線のこと。価格-消費曲線より求められる。
価格-消費曲線は、最適消費点の変化をX財・Y財の関係で見たものです。最適消費点の変化を片方の財の価格と消費量だけに注目したものを需要曲線と呼びます。
価格-消費曲線を「最適消費点の関係をY財-X財平面に図示したもの」需要曲線を「最適消費点の関係を価格-X財平面に図示したもの」と言う場合もあります。
需要曲線の求め方
- 縦軸に価格(P)・横軸に財の消費量を取ればOK
ここでは、価格消費曲線からX財の需要曲線を求めてみましょう。
価格消費曲線
この価格消費曲線から「X財の価格」「X財の消費量」を抜き出して需要曲線として描きます。
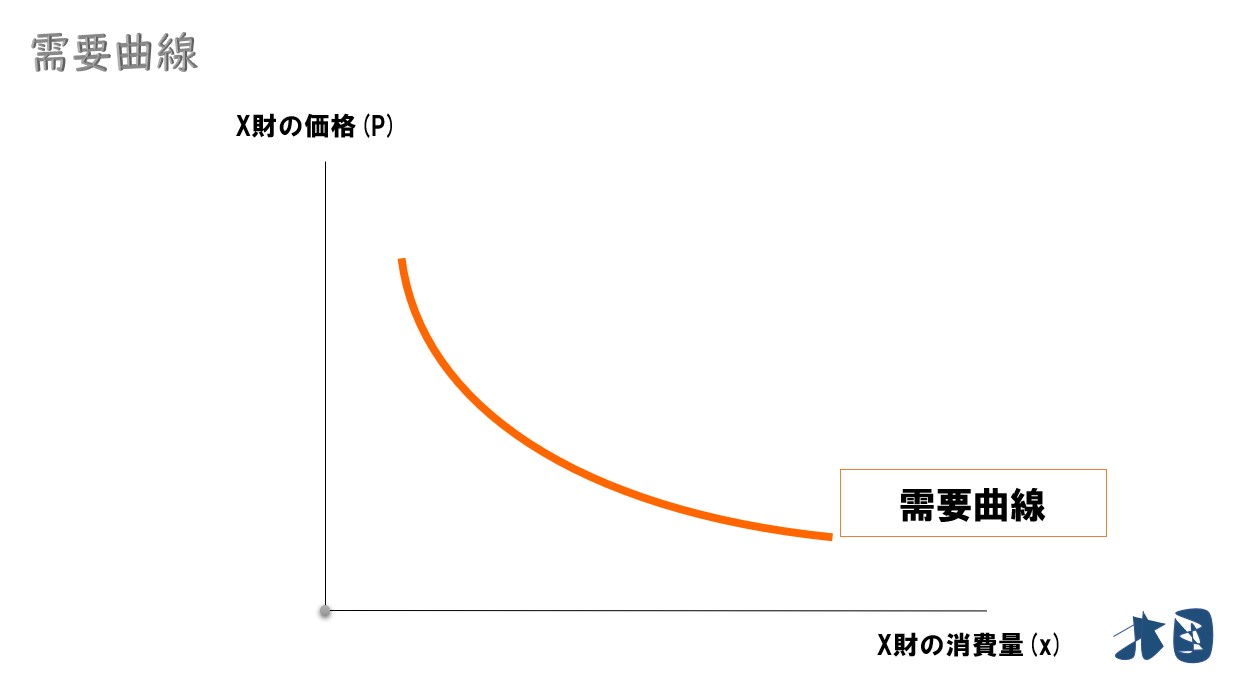
需要曲線
価格消費曲線の情報から「X財価格の上昇」⇒「X財の消費量の減少」と分かるので、それに対応したグラフを書き出せば需要曲線になります。


ポイント
財の種別に関わらず、需要曲線は基本的には右下がりになる。
ギッフェン財では、右上がりの需要曲線になるため注意が必要。
価格消費曲線の情報をもとに需要曲線が描けます。そして、基本的に需要曲線は右下がりになるので、例外を覚えれば簡単です。
例外
- ギッフェン財
普通に考えれば、価格が上がれば財の消費量は落ち込みます。しかし、価格が上がることで、逆に財の消費量が増加するギッフェン財と言うものがあります。
例外的な存在なので、たびたび問題などに登場する。
ギッフェン財(超劣等財)
価格が上昇すると、消費量が増加する財のこと。詳しくはこちら⇒【ギッフェン財】需要曲線が右上がりになる例は現実に存在するか?
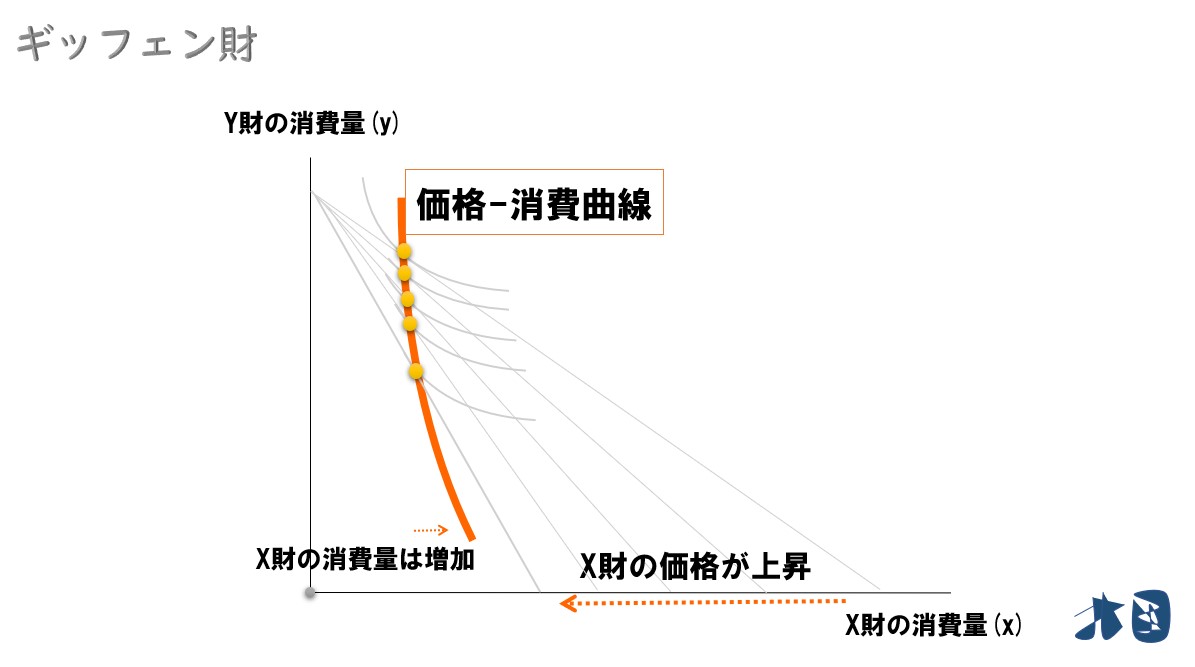
ギッフェン財の価格消費曲線
垂直に近い右下がりになります。
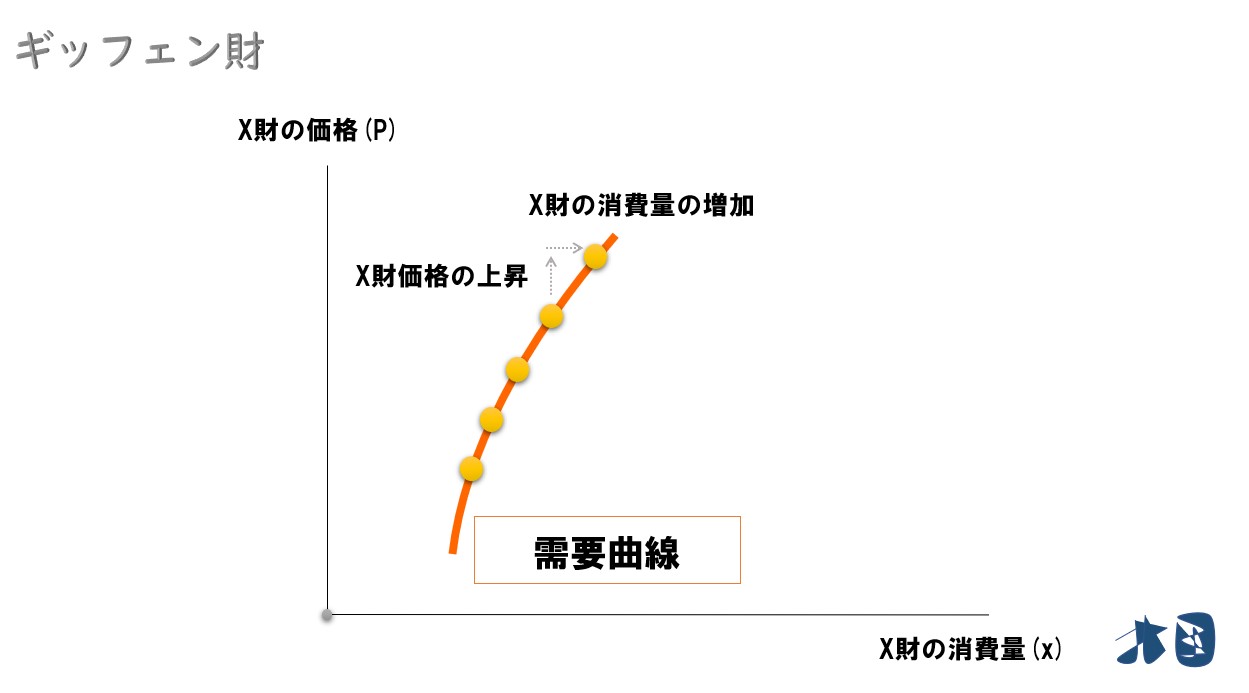
ギッフェン財の需要曲線
価格消費曲線の情報から「X財価格の上昇」⇒「X財の消費量の増加」と分かるので、それに対応したグラフを書き出せば右上がりの需要曲線になります。
詳しくはこちら⇒【ギッフェン財】需要曲線が右上がりになる例は現実に存在するか?


まとめ
| 財の種類 | 需要曲線の形状 |
|---|---|
| 通常財(上級財) | 緩やかな右下がり |
| 通常財(下級財) | 急こう配な右下がり |
| ギッフェン財(超劣等財) | 右上がり |
価格-消費曲線の求め方(計算)

例えば
- 効用関数「U(x, y)= x・y」
- 所得がM
- X財の価格がPx
- Y財の価格がPy
この時、価格消費曲線を表す式を求める。
まずは最適消費点を求める
ここからは、最適消費点の求め方を知っている前提で計算していきます。もし分からない所が出てきたら、最適消費点の求め方で確認してください。
① 予算制約線の傾きを求める
「X財の消費量=x」「Y財の消費量=y」として「予算制約線:M=xPx+yPy」とします。
- M=xPx+yPy
- y=-(xPx/Py)+M
- y=-(Px/Py)x+M/Py
② 効用関数から限界代替率を求める
「U=xy」から「y=U/x」へ変形後に微分します。
- 「y=U/x」⇒「U/xの2乗(=U・xの-2乗)」
- 「U/xの2乗」に「U=xy」を代入
- 「U(=xy)/xの2乗」⇒「xy/xの2乗」=「y/x」
③ 予算制約線の傾き=限界代替率で最適消費点を求める
「-(Px/Py)」=「-y/x」
- y=(Px/Py) x
- x=(Py/Px) y
- 予算制約線「M=xPx+yPy」に代入
M=Px(Py/Px)y+yPy
M=yPy+yPy
M=2(yPy)(y=M/2Py)
M=xPx+Py(Px/Py) x
M=xPx+xPx
M=2(xPx)(x=M/2Px)
補足
普通の最適消費点を求める問題なら、所得をMとおかずに、具体的な数字を設定しているはずなので、「M=2(yPy)(y=M/2Py)」「M=2(xPx)(x=M/2Px)」を計算することが出来ます。
ポイント
価格-消費曲線の数式は、2財の最適消費量をイコールで結ぶ
- M=2(yPy)(y=M/2Py)
- M=2(xPx)(x=M/2Px)
「M=2(yPy)=2(xPx)」より「x=yPy/Px(=M/2Px)」もしくは「y=xPx/Py(=M/2Py)」が価格-消費曲線の式です。