「需要の価格弾力性」は、問題でも頻出の分野です。
- 需要の価格弾力性とは？
- 弾力的･非弾力的な状態
- 1のとき
- 水平･垂直のとき
- 交差価格弾力性
- 価格弾力性の計算方法
需要の価格弾力性に関わる話を、このページに簡単にまとめました。
需要の価格弾力性とは
需要の価格弾力性
価格が変化するとき、どれくらい需要が変化するかを数値化したもの。
需要の価格弾力性は次の式で表されます。
需要の価格弾力性(ε)の式
需要の価格弾力性(ε)＝－(需要の変化率(％)／価格の変化率(％))
※ε＝イプシロン
η＝イータ(エータ)とする場合もあります。
価格弾力性の大きさ次第で、価格が変化したときの消費者の行動が変わるため、価格弾力性による分析が行われます。
実際に
価格弾力性の大きさで何が変わってくるのかを見ていきます。
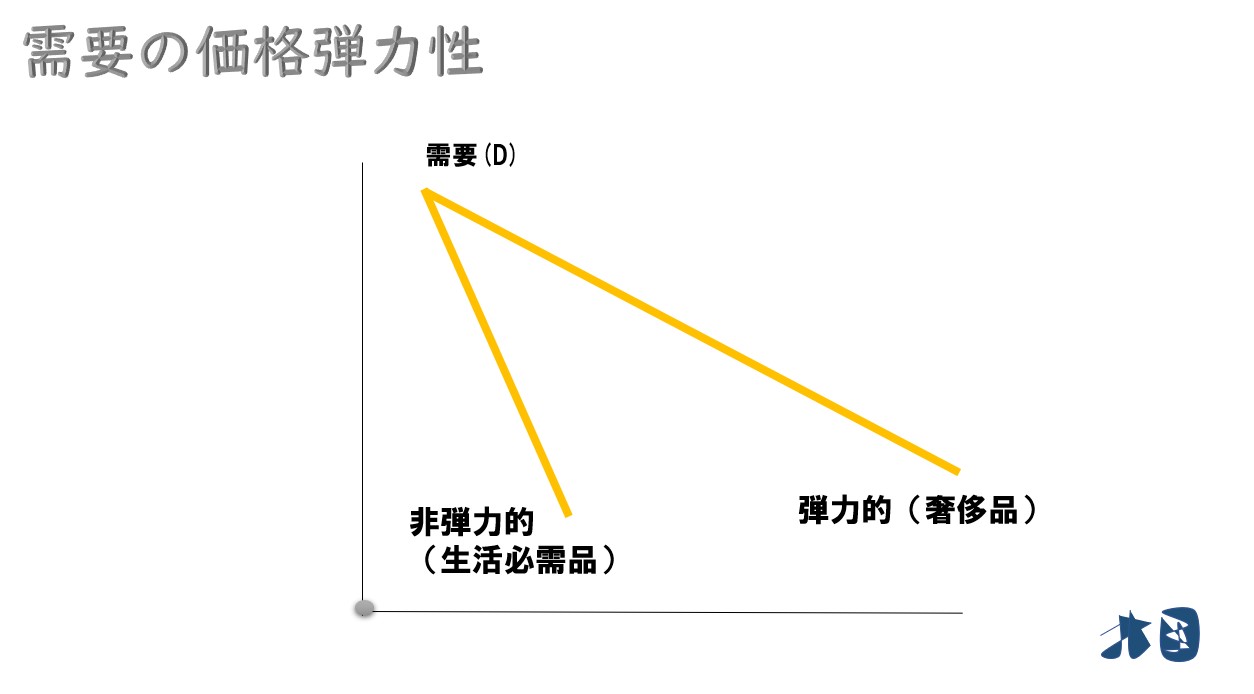
需要の価格弾力性は、1より大きいか、1より小さいかで分類される
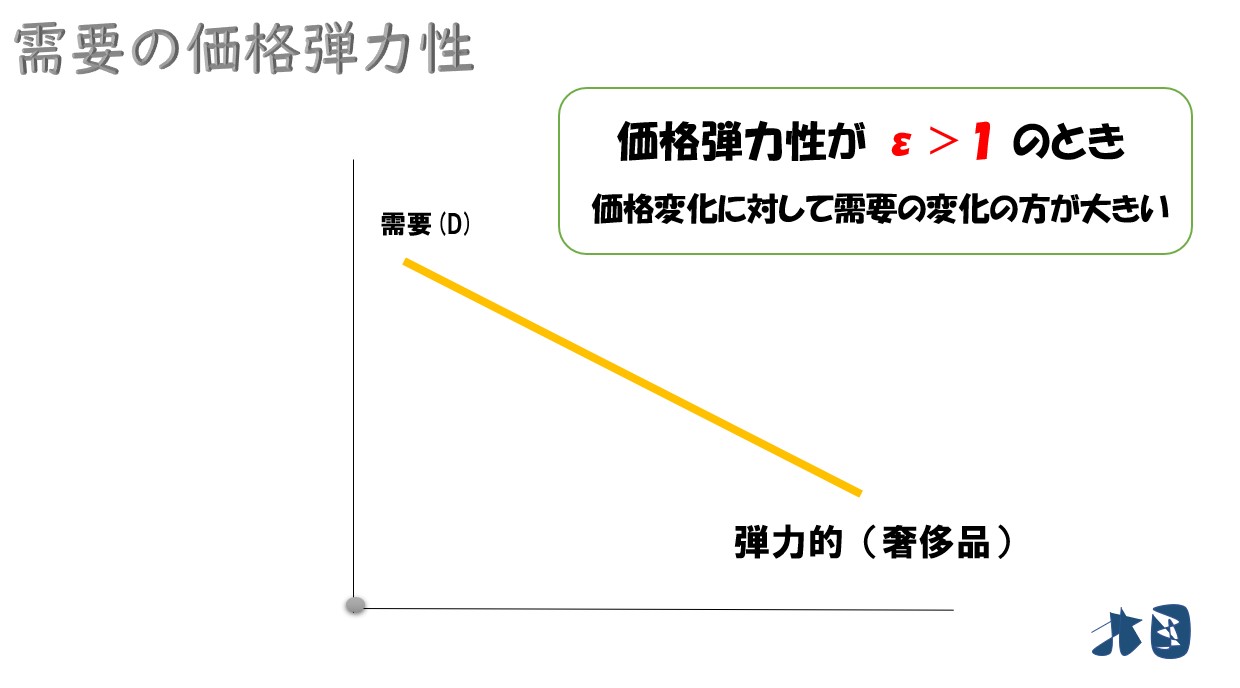
弾力的な状態（ε＞1）
価格弾力性(ε)が1よりも大きい(ε>1)
このとき、需要は弾力的という。
※ε＝イプシロン
需要の価格弾力性が「弾力的」だと次のことが言えます。
- 価格変化に対して、需要が大きく変化する
- 少しの値上がりで、一気に需要が減る
- 少しの値下がりで、一気に需要が増える
一般に、弾力的な財は「奢侈品(ぜいたく品)」が多いと言えます。
例えば
① タクシー
タクシーの初乗りが値上げしたら「少し歩こうかな」と思う人が増えて、タクシー需要が減ります。
タクシーは「需要の価格弾力性が弾力的」で奢侈品(ぜいたく品)だと言えます。
② 海外旅行
円高/外国通貨安になると海外旅行の需要が一気に増えます。これは実質的に海外旅行が安くなり、需要が一気に増したためです。
海外旅行は「需要の価格弾力性が弾力的」で奢侈品(ぜいたく品)だと言えます。
さらに詳しく
もう少し細かく話すと、需要の価格弾力性が弾力的かは、他に代替できるもの(代替財)があるか？が重要になります。
- タクシーが高いなら、電車や歩くことを選びます。
- 為替の影響で海外旅行がだめなら、他の娯楽を探します。
一方で、お昼休みに「松〇」が近くにあるのに「松〇は値上げしたから、吉野〇を探そう」と考える人は、意外といません。
お昼時間は限られていますし、代替できるお店が無ければ、そのまま松〇で食事をします。
つまり「代替できるものがある+時間がある」と需要の価格弾力性は、弾力的な傾向を持ちます。
先ほどのタクシーの話なら「時間がなくて急いでいる」＆「他に早く移動する手段がない」なら、初乗りの金額なんて気にせずに乗車しますよね。そういう場合は、弾力的にならないわけです。
※ただし、これも市場全体で見ればそういう傾向がある？程度の話です。
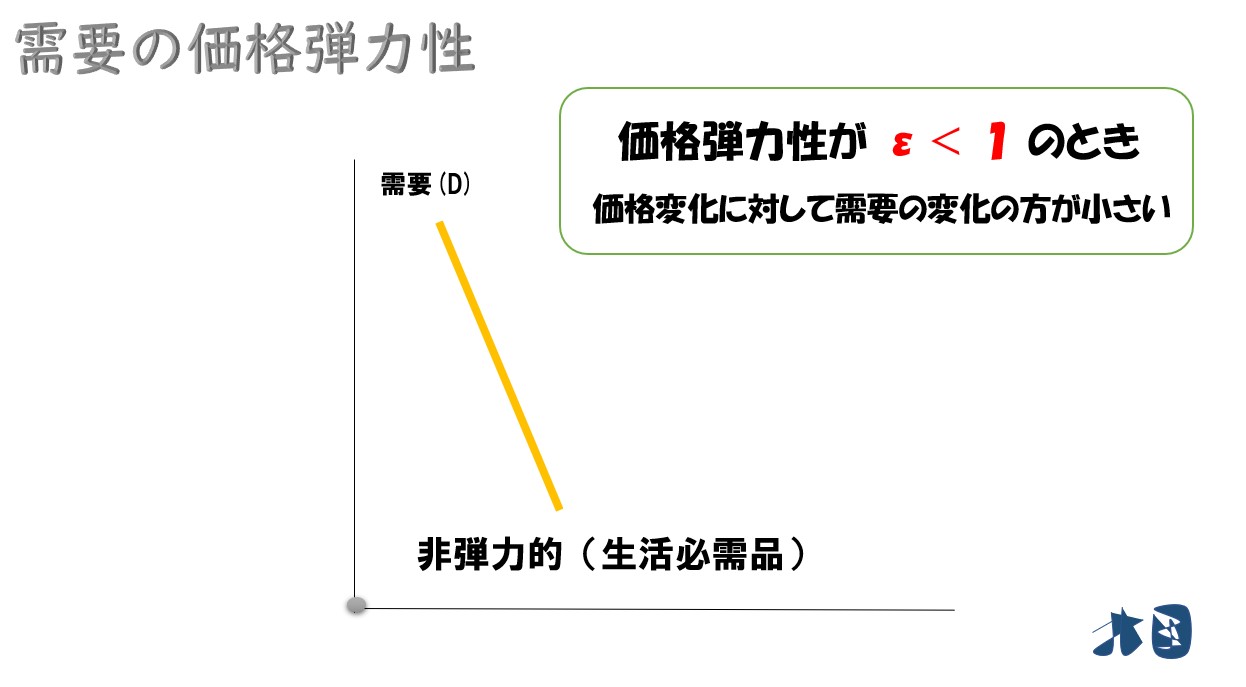
非弾力的な状態（ε＜1）
価格弾力性(ε)が1よりも小さい(ε<1)
このとき、需要は非弾力的という。
※ε＝イプシロン
需要の価格弾力性が「非弾力的」だと次のことが言えます。
- 価格変化に対して、需要があまり変化しない
- 値上げ(値下げ)しても、需要がさほど変わらない
一般に、非弾力的な財は「必需品」が多いと言えます。
例えば
① 電気代(水道光熱費)
電気代が値上げしても、電気の消費量を減らすのは一般的に難しいです。なので、電気代が値上げしたところで、電気の消費量はあまり変わりません。
電気代(水道光熱費)は「需要の価格弾力性が非弾力的」で必需品だと言えます。
② 食料品
食料品が値上げしても「何も食べない」という選択肢は取りづらいです。そのため、食料品の価格が上がっても、需要は減りづらい傾向にあります。
食料品は「需要の価格弾力性が非弾力的」で必需品だと言えます。
さらに詳しく
教科書的には、食料品は非弾力的な傾向を持ちますが、それは種類によります。
お米が主食の人なら、お米が値上げしても消費量はさほど減りません。しかし、お米･パン･カップ麺どれでもいい人は、値上げしていない食べ物を買います。
個別の食品で見れば、非弾力的かは人の食生活に依存します。
そのような個別の案件を扱うと話が難しくなるので、食料品という大きなカテゴリーで見れば、食べなきゃ死ぬので、値上がりしても需要が減らない(非弾力的)と考えている程度に思ってください。
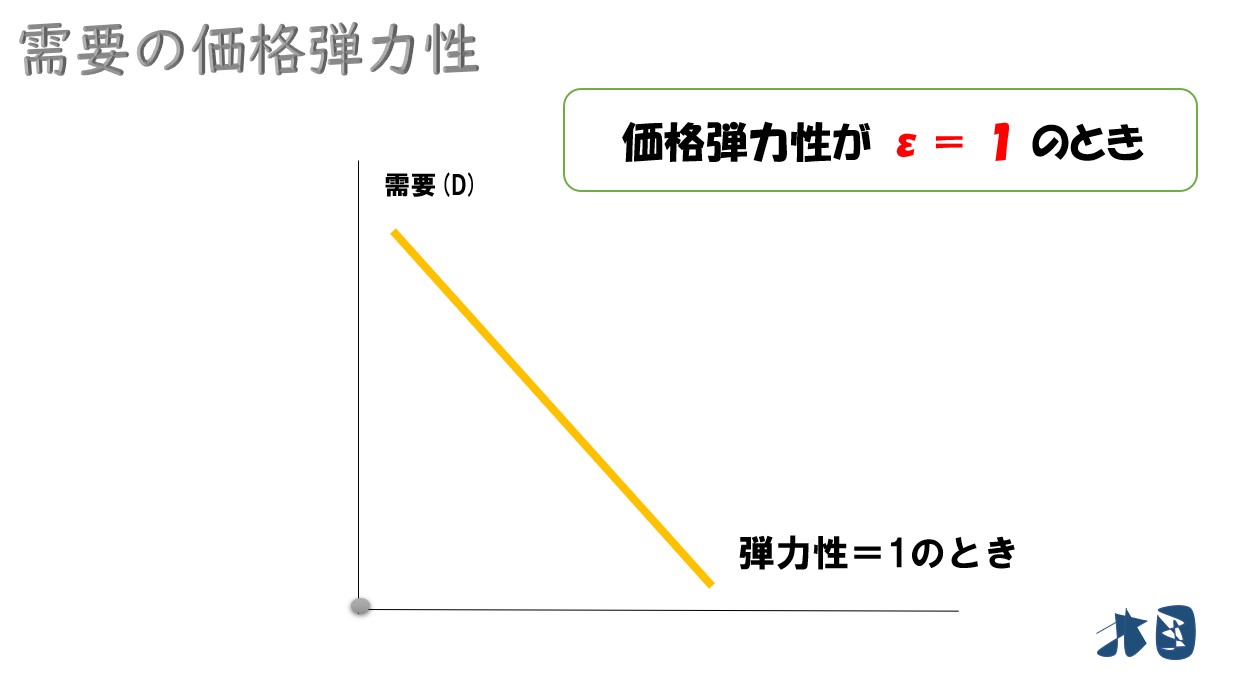
1のとき
価格弾力性(ε)が1のとき（ε＝1）
弾力性が「1の弾力性を持つ(単位弾力的)」という場合があります。
※ε＝イプシロン
需要の価格弾力性が「1」の場合は、弾力的でも、非弾力的でもない特別な状態です。
弾力性が1のとき、次の特徴があります。
ポイント
財の価格が変化しても、消費者の支出金額は変化しない。
例えば
ある財に100円を支払うつもりなら、その財の価格が何円でも100円を支出するつもりがある、という状態です。
ココに注意
ときどき混乱する人がいるので注意していください。あくまで、支出金額が変わらないのであって、消費量は変化します。
ある財が50円なら100円を支出して2個購入します。これが100円に値上げした場合、100円を支出して1個購入します。
価格が変化しても「支出金額＝100円」ですが「購入量は2個→1個」と変化しています。
更に注意
弾力性が1の場合、もう1点だけ間違えやすいところがあります。それが需要曲線の形状に関わる話です。
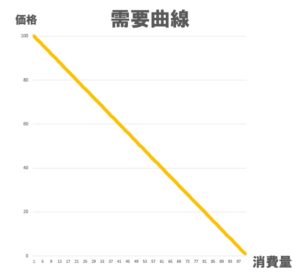
需要曲線が右下がりの直線なら、価格変化と比例して財の消費量が変化します。
| 価格 | 支出額 | 消費量 |
|---|---|---|
| 10円 | 100円 | 10個 |
| 25円 | 100円 | 4個 |
| 50円 | 100円 | 2個 |
| 100円 | 100円 | 1個 |
しかし
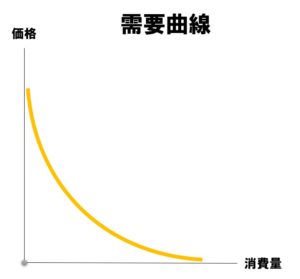
需要曲線が右下がりにカーブしていると・・
| 価格 | 支出額 | 消費量 |
|---|---|---|
| 10円 | 50円 | 5個 |
| 25円 | 75円 | 3個 |
| 50円 | 100円 | 2個 |
| 75円 | 75円 | 1個 |
| 100円 | 50円 | 0.5個 |
実は
もともと価格弾力性は、価格が少しだけ変化した時(微小量の変化)に、需要量がどう変化するかを判断する指標です。
なので、需要曲線全体で見てしまうと「財の価格が変化しても、消費者の支出金額が変化しない」という話が当てはまらなくなってしまいます。
例えば
- 価格＝100円
- 消費量＝100個
この時の支出額は「100円×100個＝10,000円(1万円)」です。
ここで、需要の価格弾力性が1だとします。
価格が1％上昇すれば、消費量は1％減少します。※価格弾力性＝1＝－(－1％／1％)
需要の価格弾力性(ε)＝－(需要の変化率(％)／価格の変化率(％))
すると・・
支出額は「101円×99個＝9,999円(約1万円)」となります。
既に支出額が1円ずれてきましたが、ほぼ同じになります。
次に価格が5％上昇、消費量は5％減少で考えてみます。※価格弾力性＝1＝－(－5％／5％)
支出額は「105円×95個＝9,975円」となります。
ポイント
「財の価格が変化しても、消費者の支出金額は変化しない」という需要の価格弾力性(ε)が1のときの特徴は、価格変化が大きくなると当てはまらなくなる。
もともと価格弾力性(ε)は、価格が少し動いたとき(微小の変化)に、需要がどれくらい変化するかの指標です。
そのため、価格が少しだけ動いた状況なら、上の特徴は当てはまりますが、そうではないと当てはまりません。
需要曲線が右下がりの直線だと影響はないのですが、普通のカーブを描いた需要曲線だと、上の計算結果のように、支出額が変化していきます。
理由
価格変化が大きいと支出額が変わってしまう理由は、経済学の用語で説明できます。
同じ財を消費し続けると飽きてきます。これを限界効用逓減の法則と言います。
価格が5％安くなって、消費量が5％増えても、同じ財を消費していると飽きてきます。つまり、それだけ価値が減っているので、支払っても良いと思う金額は小さくなっているのです。
逆に、金額が高すぎると「他の財を買ったほうがいいや」と思うので、これも支払っても良いと思う金額が小さくなる原因になります。つまり、ほどほどの値段で、ほどほどの量を消費できる時が1番支出額が大きくなる。
そして
需要曲線がカーブを描いているのは「限界効用逓減の法則」を反映しているためです。
価格変化が小さければ、限界効用逓減が働く余地が少ないので、価格弾力性＝1のときの特徴「財の価格が変化しても、支出額が一定になる」が当てはまります。
しかし、価格変化が大きいと、需要曲線がカーブを描くため誤差が大きくなります。
一方で、需要曲線が右下がりの直線の場合は、限界効用逓減が考慮されていません。そのため、需要曲線が右下がりの直線のみ、価格変化が大きくても常に支出額が一定になります。
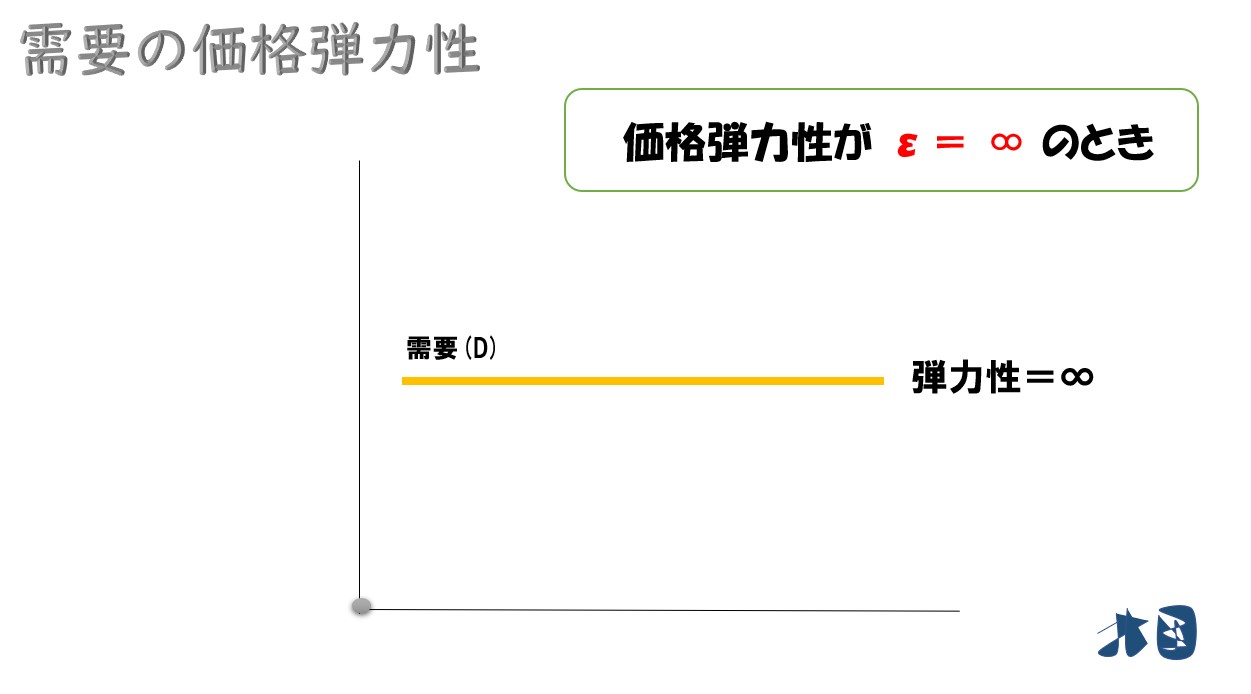
完全に弾力的（無限大･水平）
価格弾力性(ε)が無限のとき（ε＝∞）
このとき、需要は完全に弾力的という。
※ε＝イプシロン
価格が変化すると需要量が物凄く大きく変化する。
現実世界にそのような財があるのかと言うと、基本的に存在しないと考えてOKです。限りなく水平に近いような状態の財はあるかもしれませんが、完全に弾力的とはなりません。
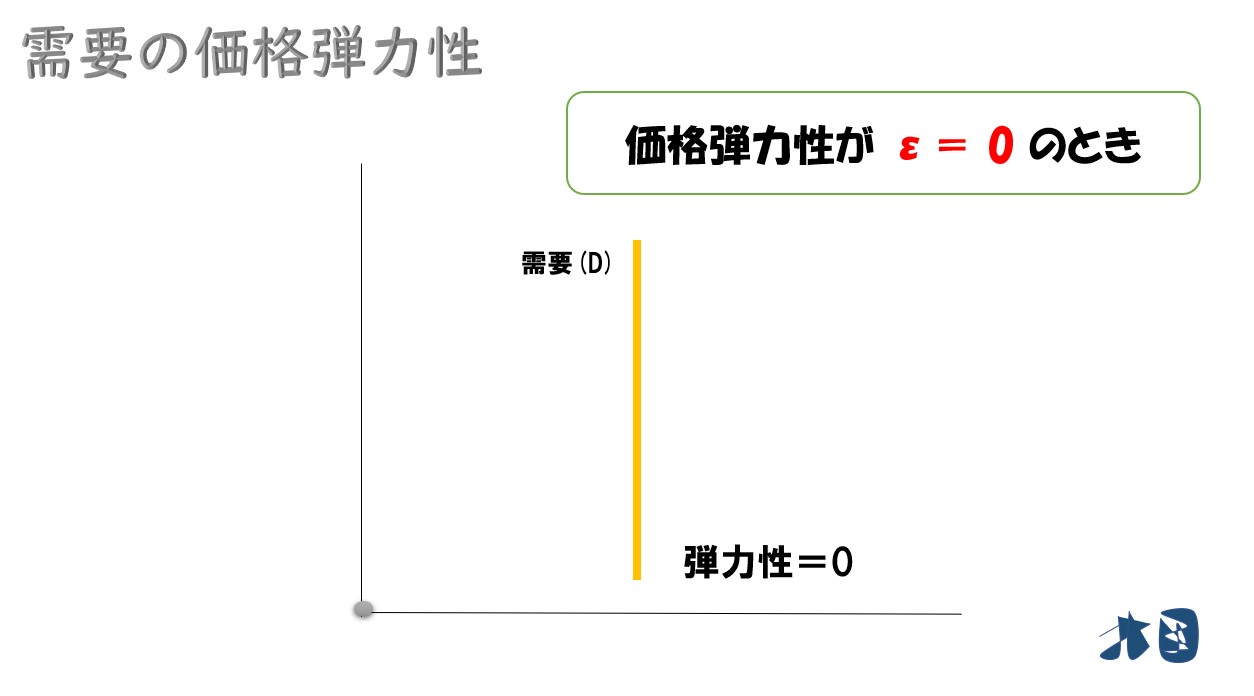
完全に非弾力的（0のとき･垂直）
価格弾力性(ε)が0のとき（ε＝0）
このとき、需要は完全に非弾力的という。
※ε＝イプシロン
価格が変化しても需要量が変わらない状態です。
例えば「不死の薬」とか「ゴッホのひまわり」は、価格がいくらでも需要がありそうです。しかし、それにも限度があります。「ゴッホのひまわり」が1000兆円と言われたら、まあ、別に要らないと考える人がたくさん出てきます。なので、完全に非弾力的な需要というのも、現実世界にはないと考えられます。
需要の交差価格弾力性
需要の交差価格弾力性
2財のケースで、一方の財の価格が変化するとき、他方の財の需要がどれくらい変化するかを表したもの。
通常の価格弾力性は、財が1つの場合を想定しています。
「交差価格弾力性」は、財が2つある時の話です。
交差価格弾力性の式
ある財の価格の変化率／他方の財の需要量の変化率
交差価格弾力性から「(粗)代替財」「(粗)補完財」を判断できます。
ある財が価格上昇した時に、他方の財の需要量が
- 増える⇒ 交差価格弾力性が＋
- 減る⇒ 交差価格弾力性が－
増える(交差価格弾力性が＋)なら、他方の財は「粗代替財」
減る(交差価格弾力性が－)なら、他方の財は「粗補完財」
交差価格弾力性は、もう一方の財が「代替財」か「補完財」かを判断するような状況で登場します。
ここでは、これ以上の深堀はしません。
「需要の価格弾力性」の求め方(計算)
計算問題では需要の価格弾力性の式を使います。
需要の価格弾力性(ε)の式
需要の価格弾力性(ε)＝－(需要の変化率(％)／価格の変化率(％))
＝－「ΔD／D」／「ΔP／P」
※Δ＝ (変化後の数字)－(変化前の数字)で求められます。ただし、微分が必要なときは微分して求めます。
「変化率」の求め方が大きく2パターンあり、どのような場面で使い分ければ良いかも簡単に説明していきます。
通常の計算で求める
微分を使わずに、普通に計算するパターンです。
普通に計算できるのは、変化前と変化後の数値が分かる場合です。
例えば
- 価格が1,000円で、消費量(需要量)が250の財がある
- その財は、価格が1,100円になり、消費量が200となった。
需要の価格弾力性を求めて、この財が奢侈品か必需品かを判断する。
計算方法
変化前と変化後の数値が分かるため、微分をせずに普通に計算します。
- 価格変化：(1,100－1,000)／1,000＝0.1
- 需要変化：(200－250／250)＝－0.2
－(需要の変化率－0.2)／(価格の変化率0.1)＝2
需要の価格弾力性が1よりも大きいため、この財は奢侈品である。
微分で求める
微分を使うのは、変化前と変化後の数値が分からない場合です。
微分を使うときは、さきほどの式を変形します。
需要の価格弾力性(ε)の式
需要の価格弾力性(ε)＝－(需要の変化率(％)／価格の変化率(％))
＝－「ΔD／D」／「ΔP／P」
＝－「ΔD／ΔP」×「P／D」
＝－「需要の変化量(ΔD)／価格の変化量(ΔP)」×「元の価格(P)／元の需要量(D)」
問題文に「変化前の数字」「変化後の数字」の情報が無ければ、微分をして、変化量を求めることになります。
例えば
- 財Aの需要曲線が「D＝－10P＋1,000」
- 財Aの供給曲線が「S＝40P」
このとき、市場均衡点における需要の価格弾力性はいくらか？
均衡点は「需要曲線と供給曲線が交わる」という事を意味しているので「D＝S」として計算します。
- －10P＋1,000＝40P
次に均衡点における市場価格を計算します。
- 50P＝1,000
- P=20
「D＝－10P＋1,000」に市場価格のP＝20を代入します。
- D＝－200＋1,000＝800
これで、市場均衡点における価格と需要量(消費量)が分かりました。
- P=20
- D=800
次に
変化後の数字を微分で求めます。
「D＝－10P＋1,000」をPで微分します。
すると「(ΔD／ΔP)＝－10」となります。
微分は乗数を1つ減らして手前に持ってくる計算です。－10Pは「－10×Pの1乗」です。「Pの1乗」の1を手前に持ってきて「－10×1＝－10」とします。また、Pの0乗になりますが「0乗＝1」なのでP=1でPが消えます。文字がついていない「＋1,000」も無視されます。
以上より
- P=20
- D=800
- (ΔD／ΔP)＝－10
パーツがそろったので、先ほどの式に当てはめます。
－「ΔD／ΔP」×「P／D」
－「需要の変化量(ΔD)／価格の変化量(ΔP)」×「元の価格(P)／元の需要量(D)」
- 価格弾力性(ε)＝－(－10)×(20／800)
- ＝10×(1／40)
- ⇒ 1／4（＝0.25）
