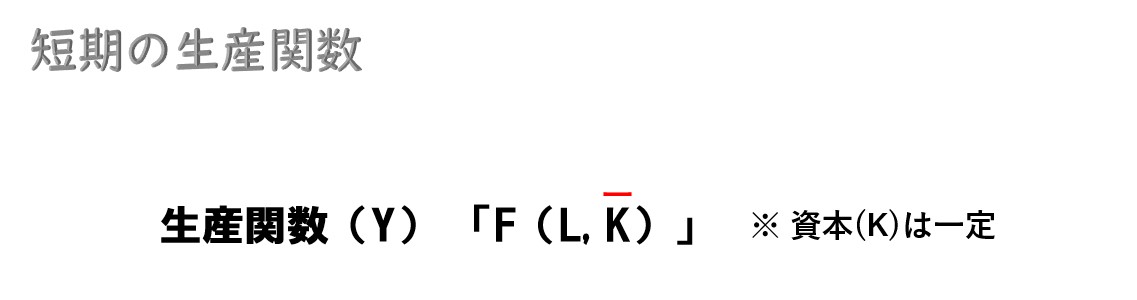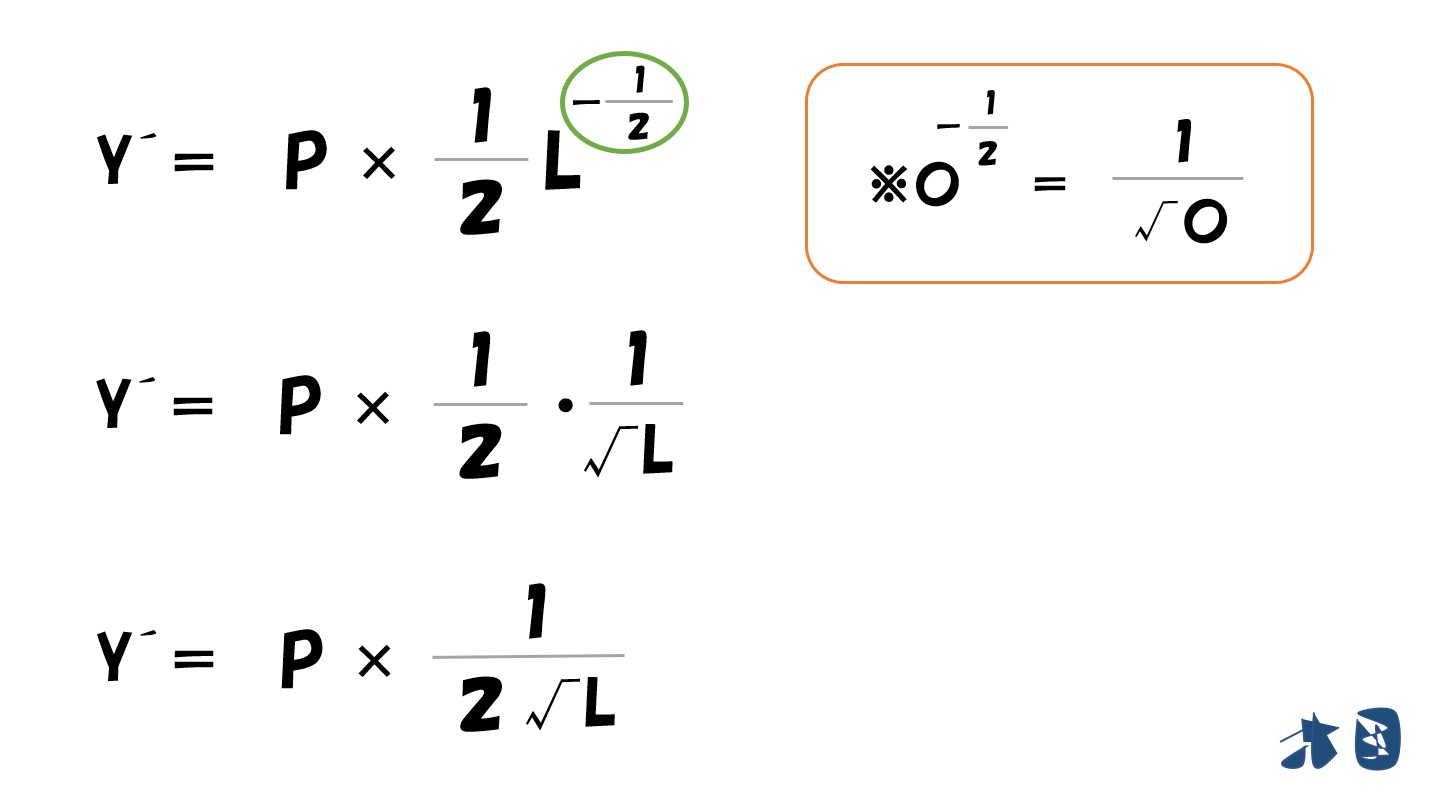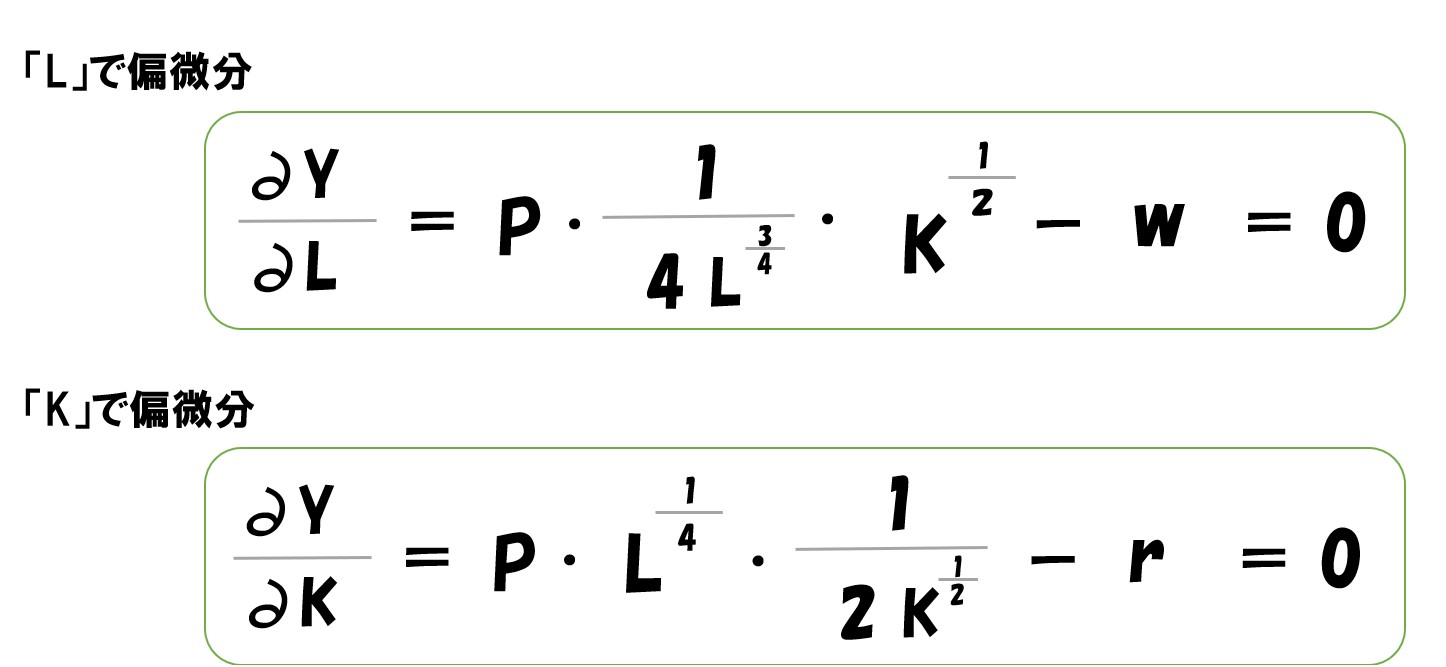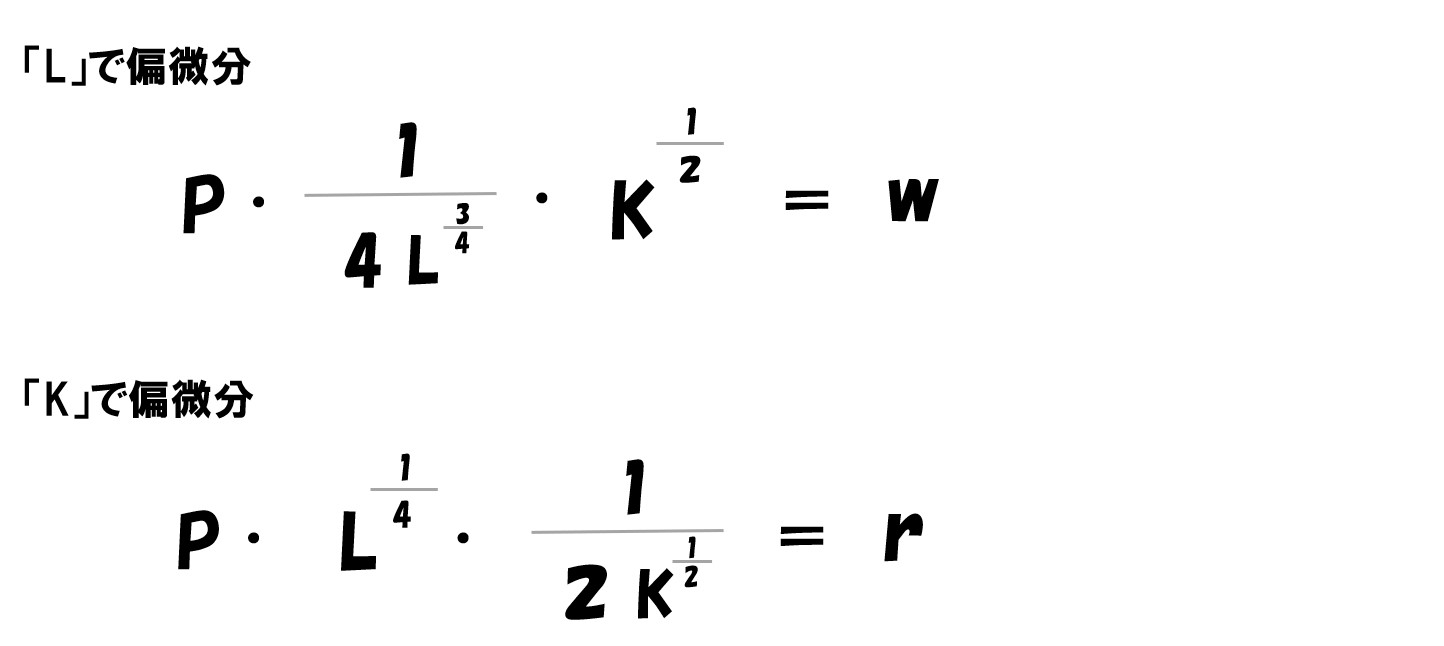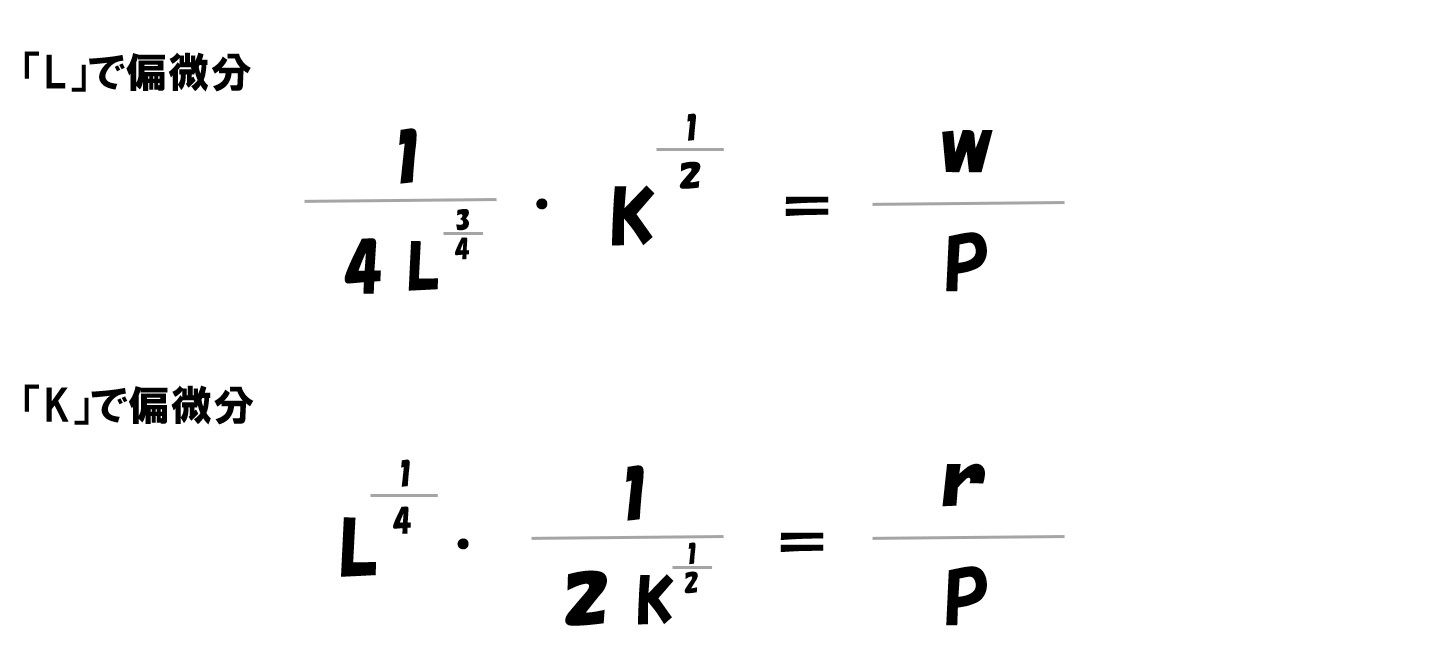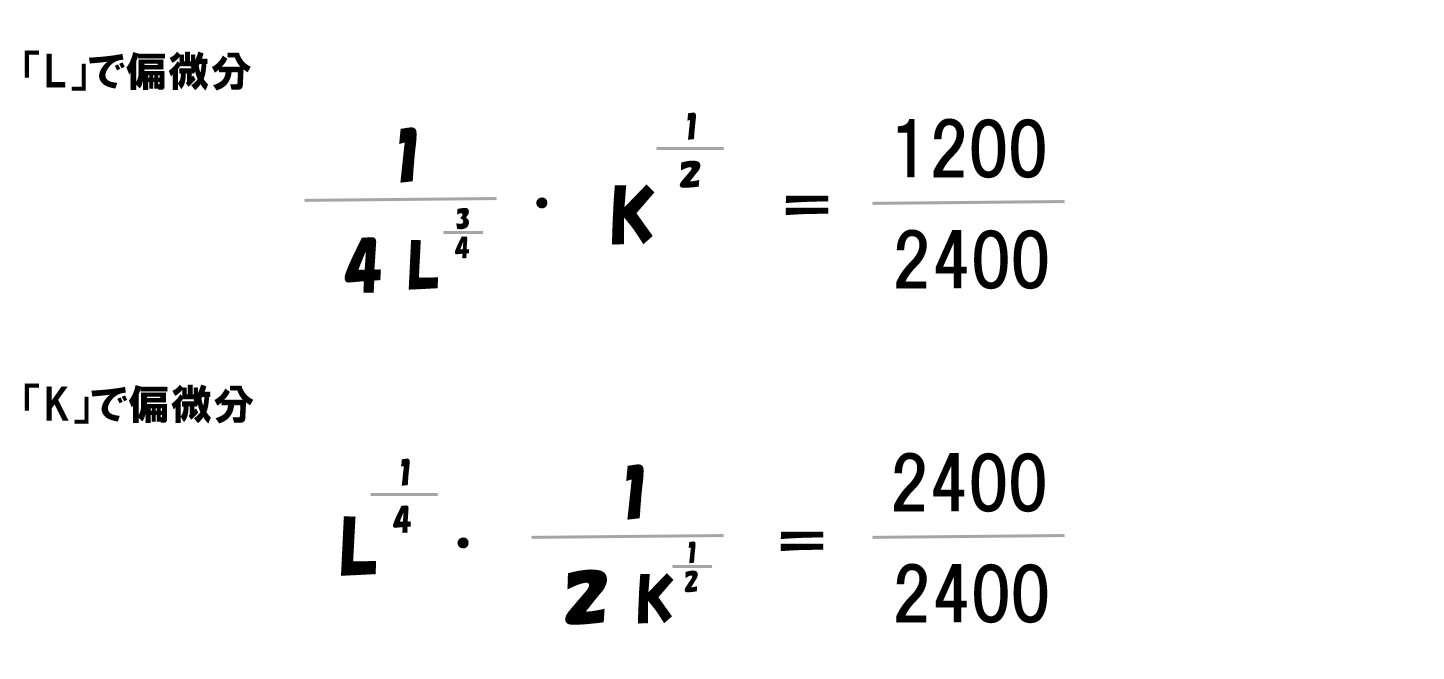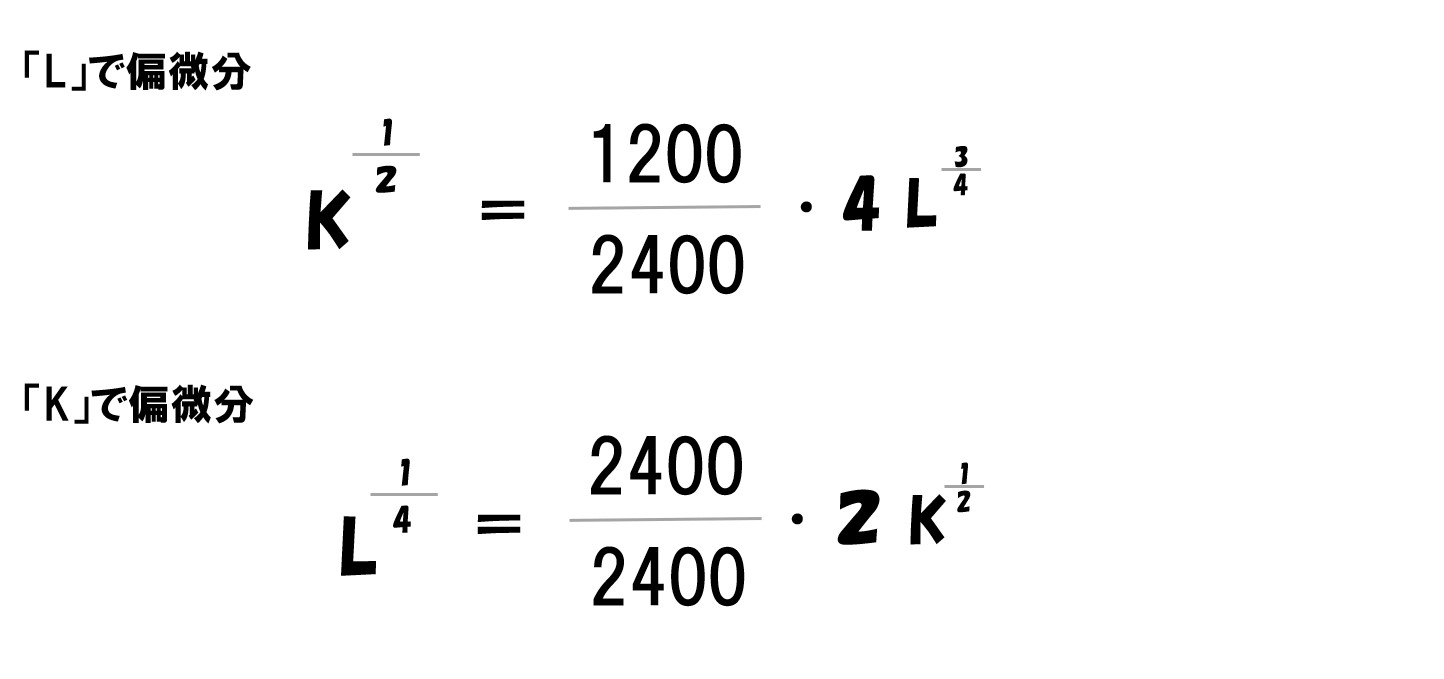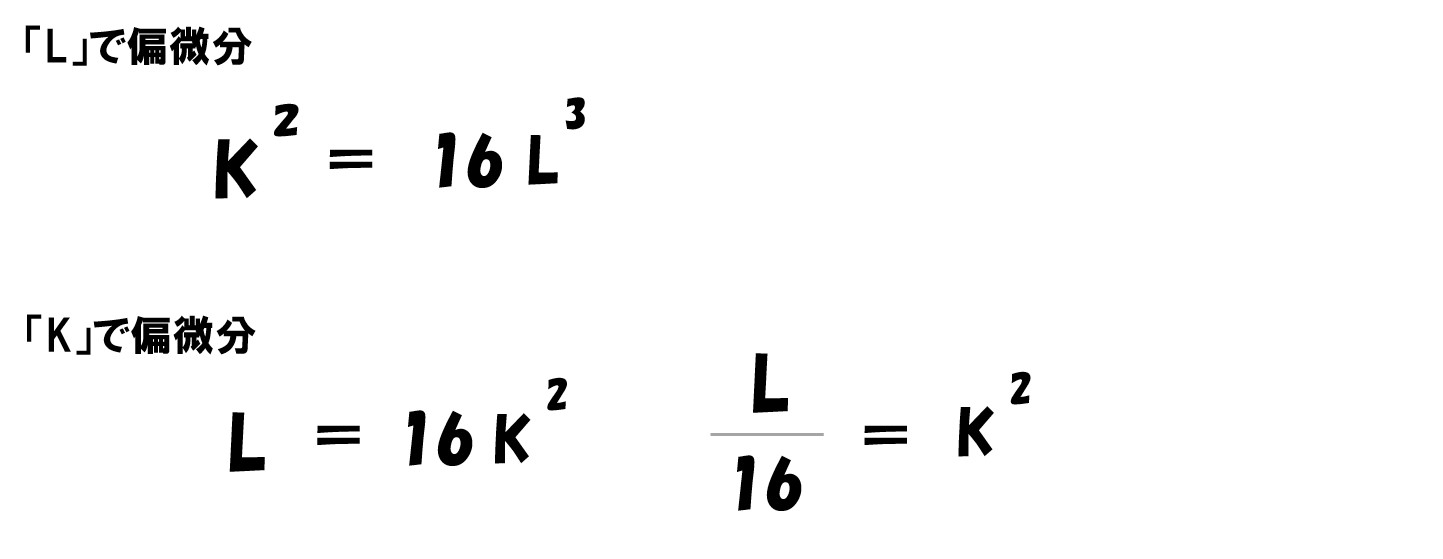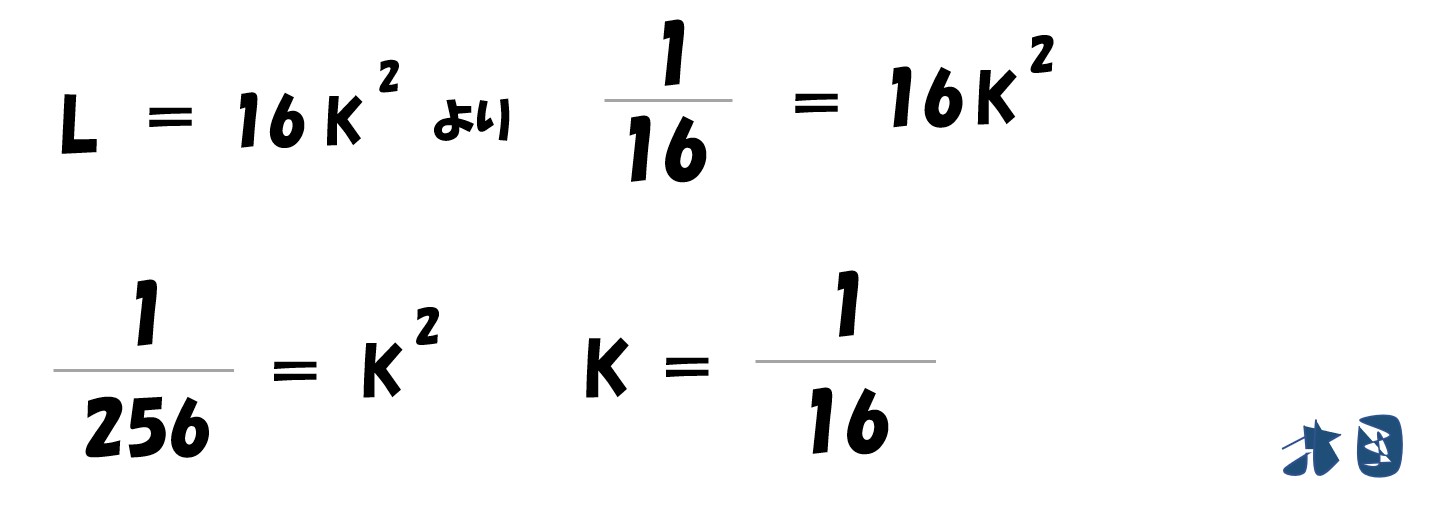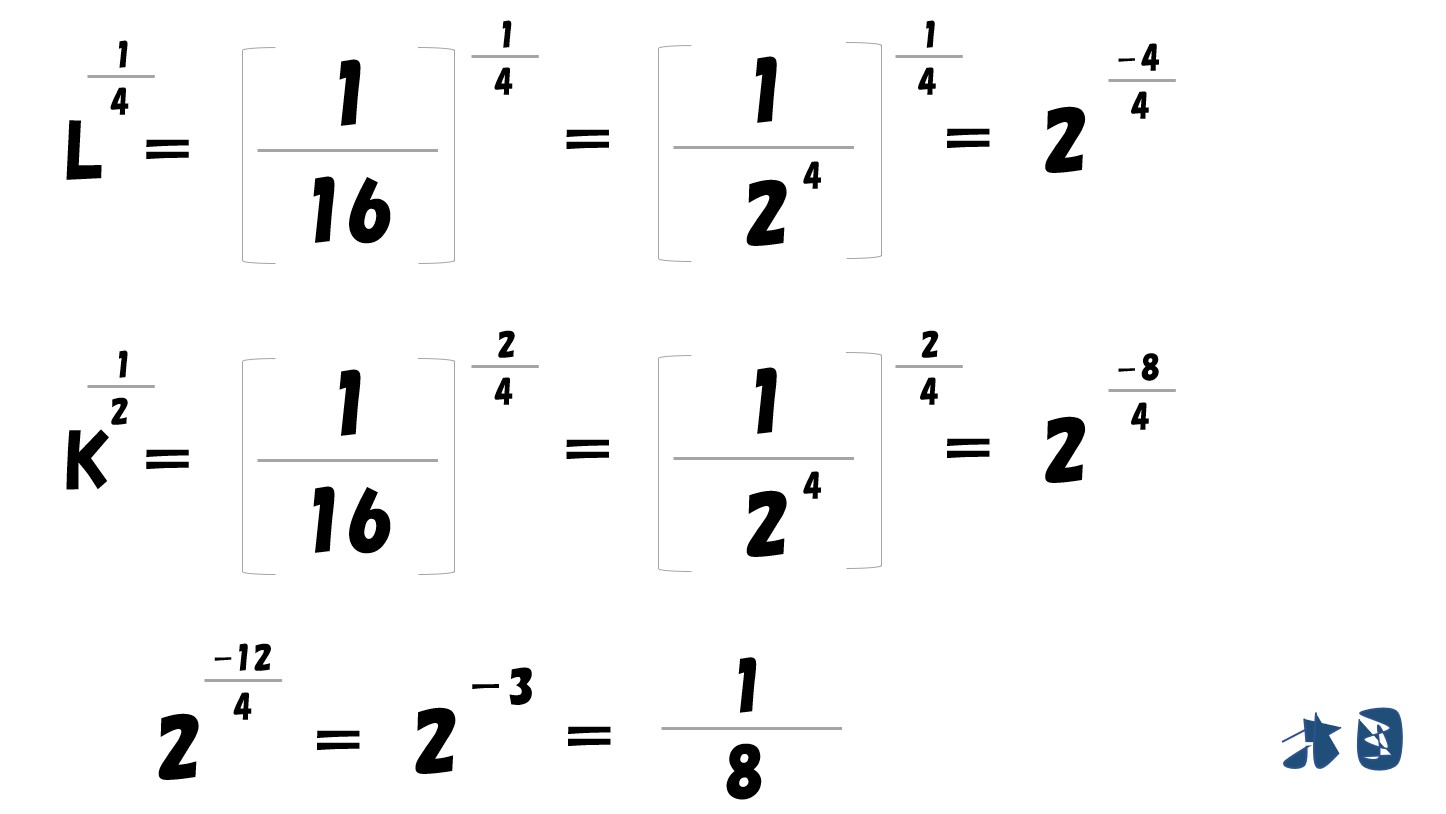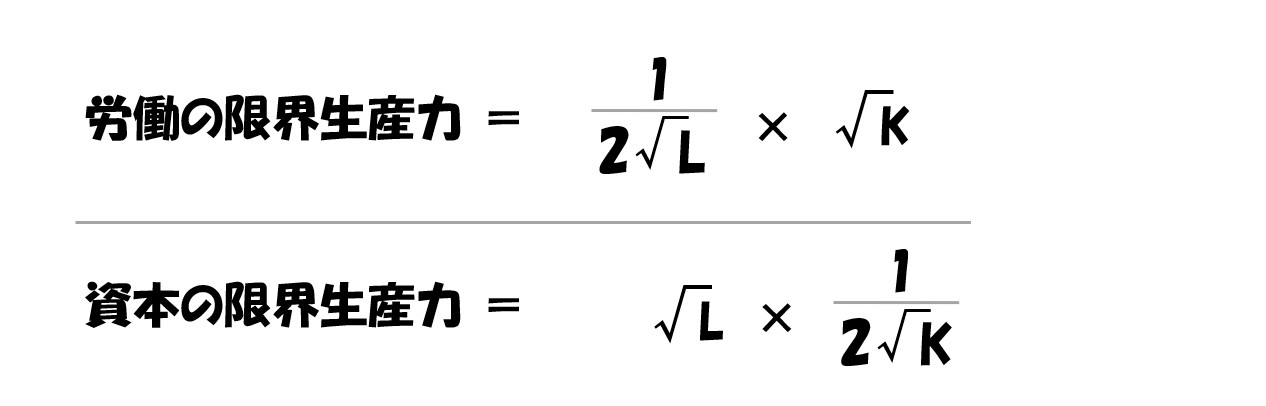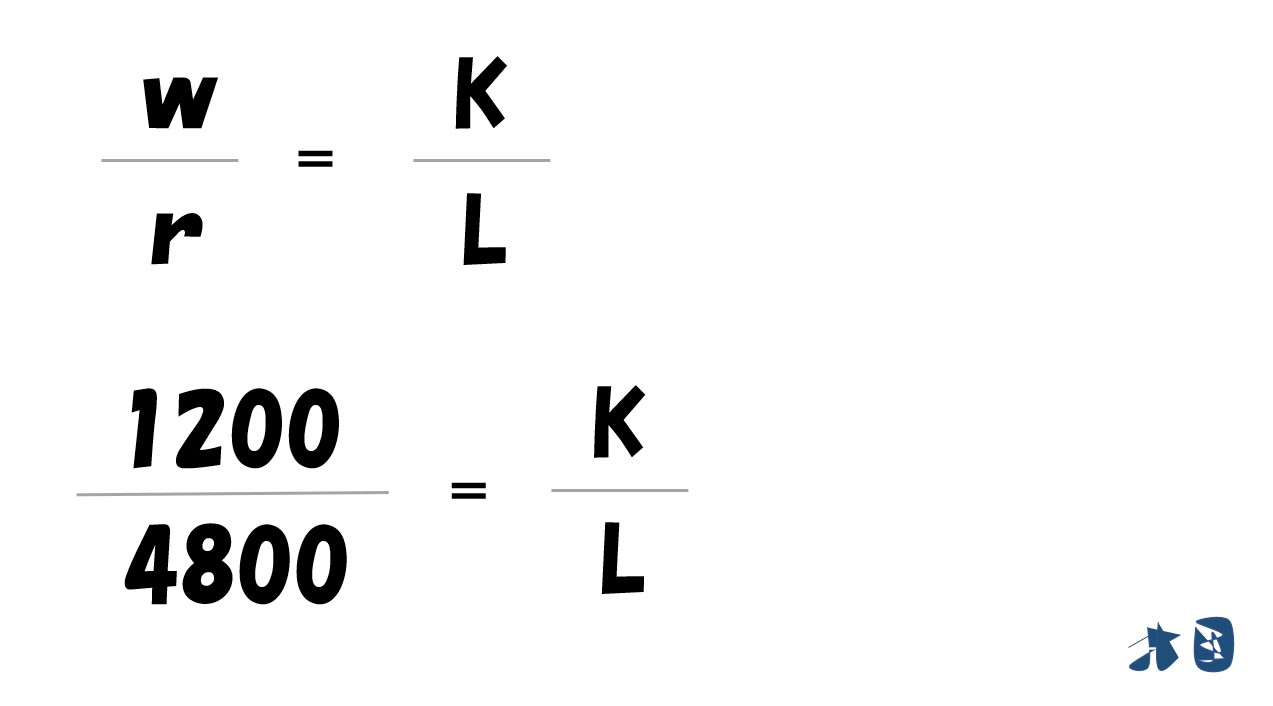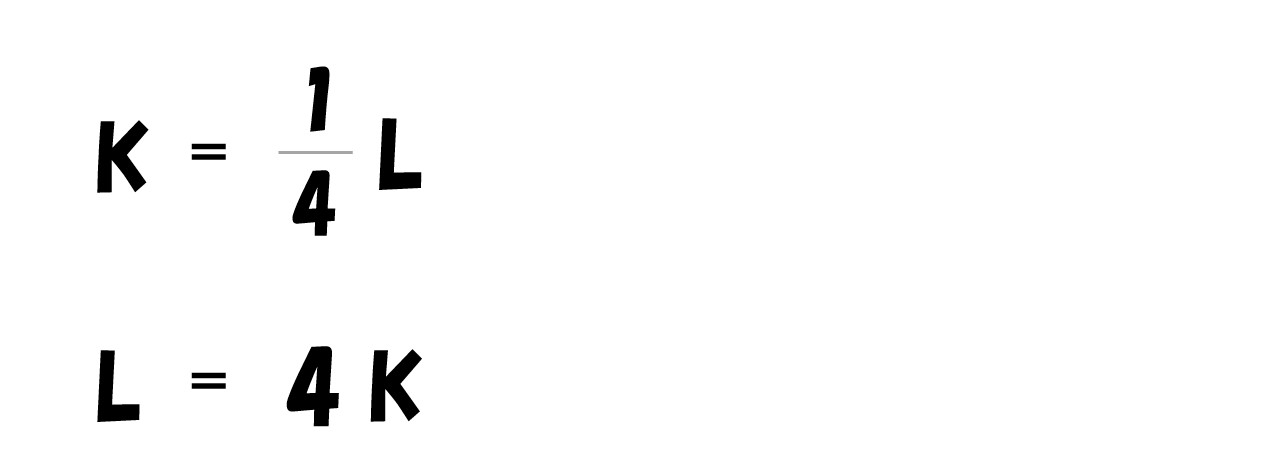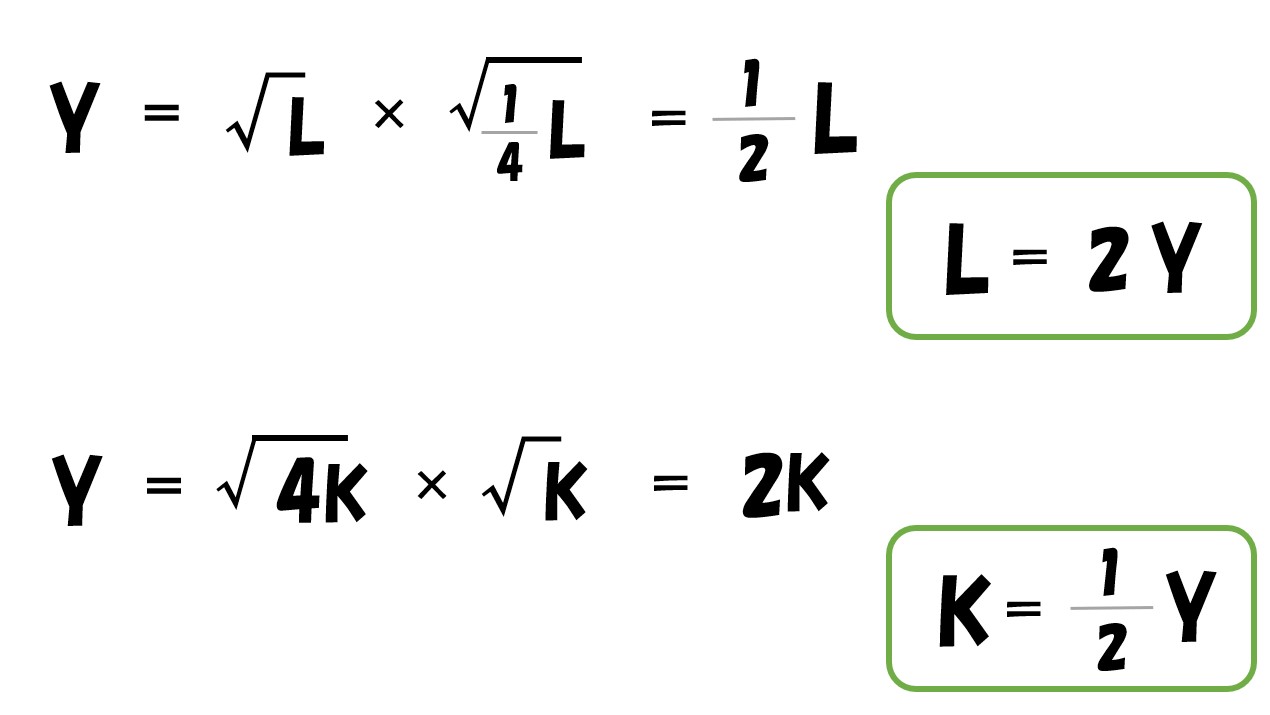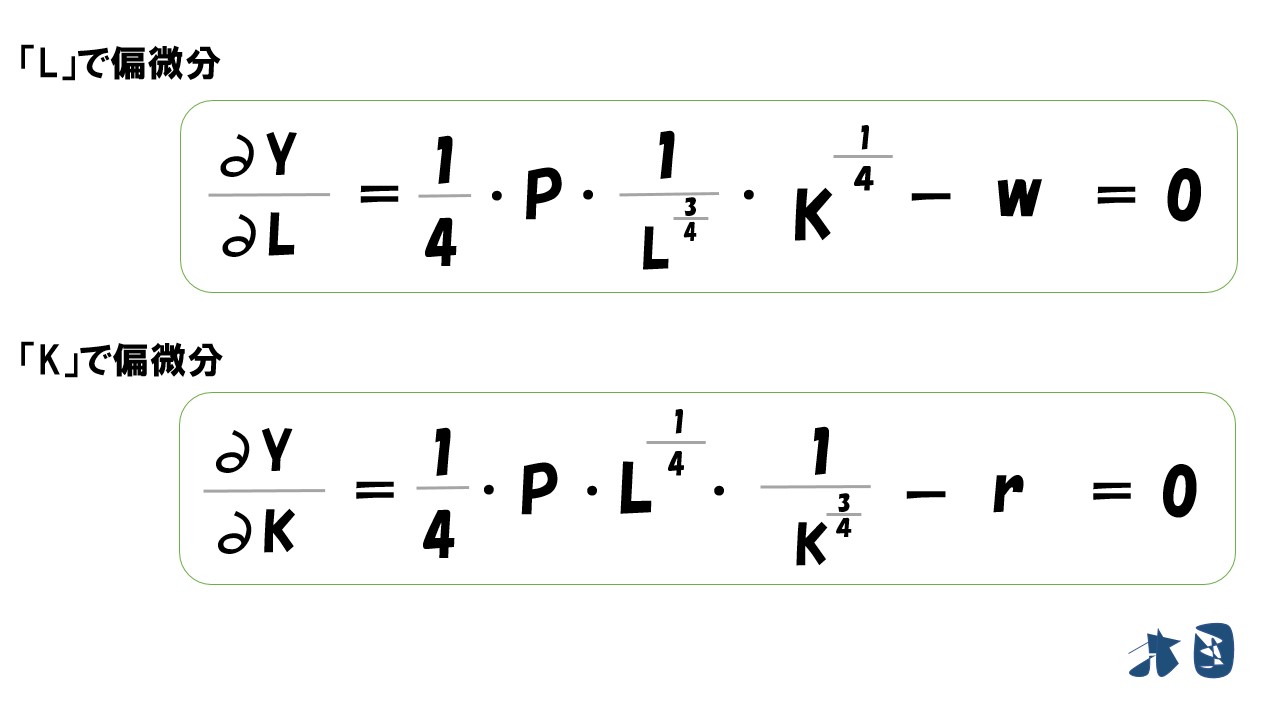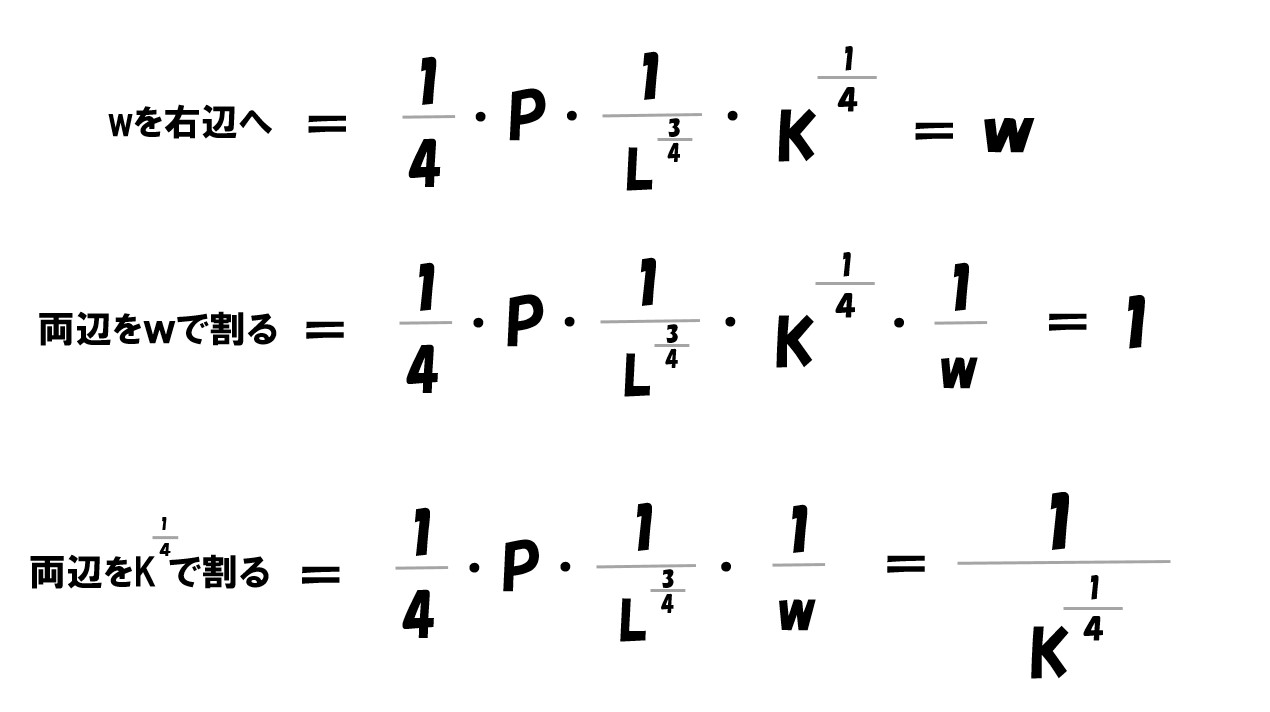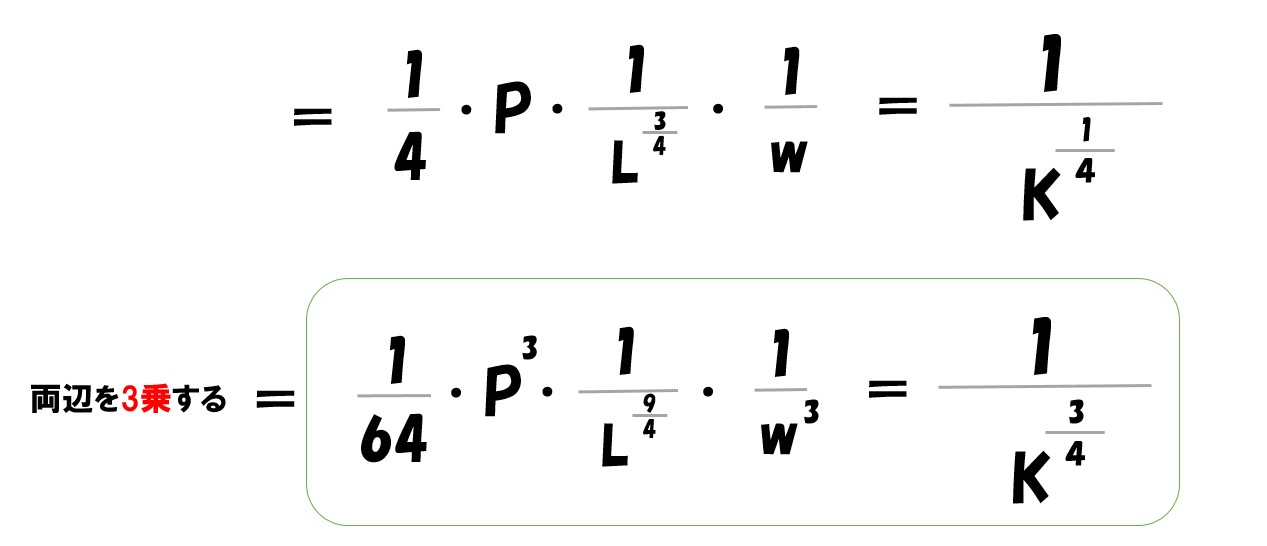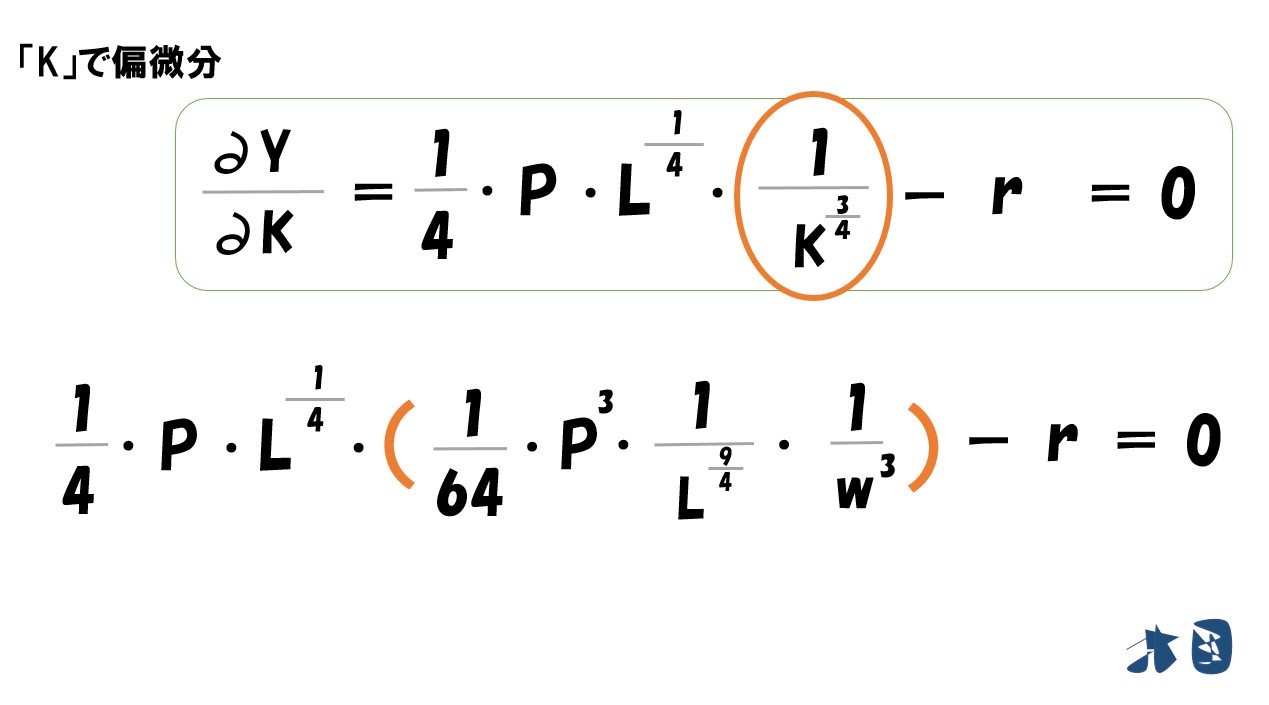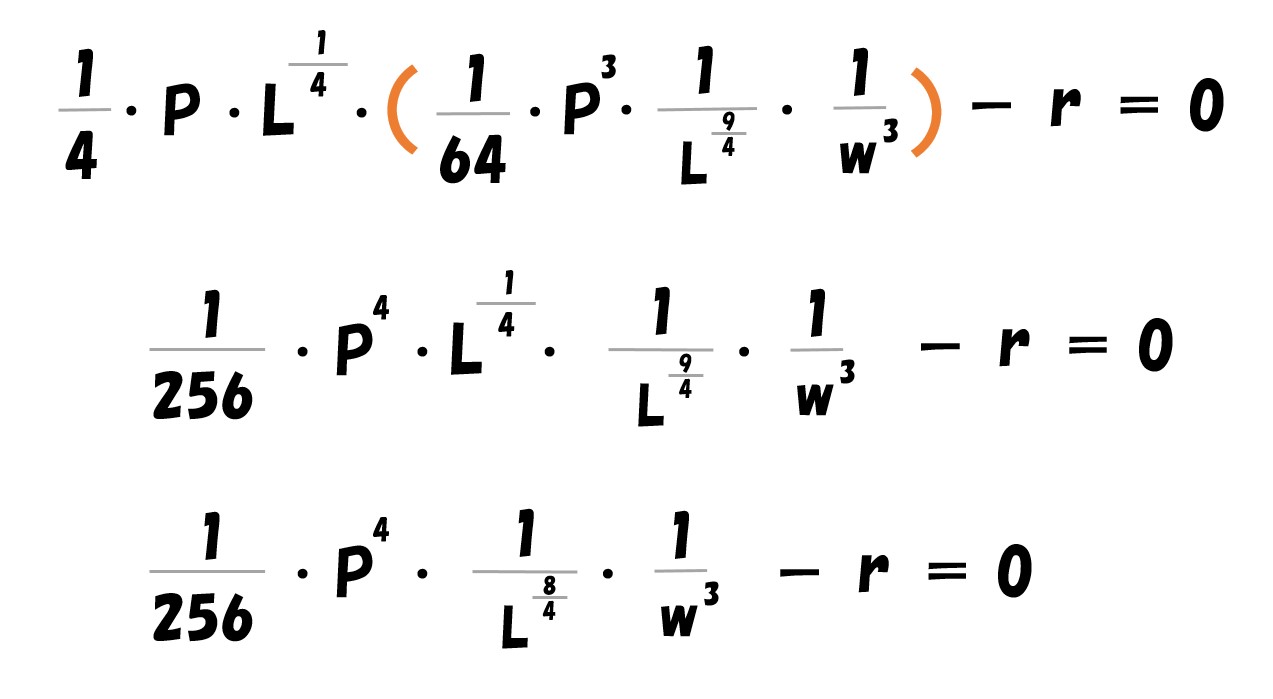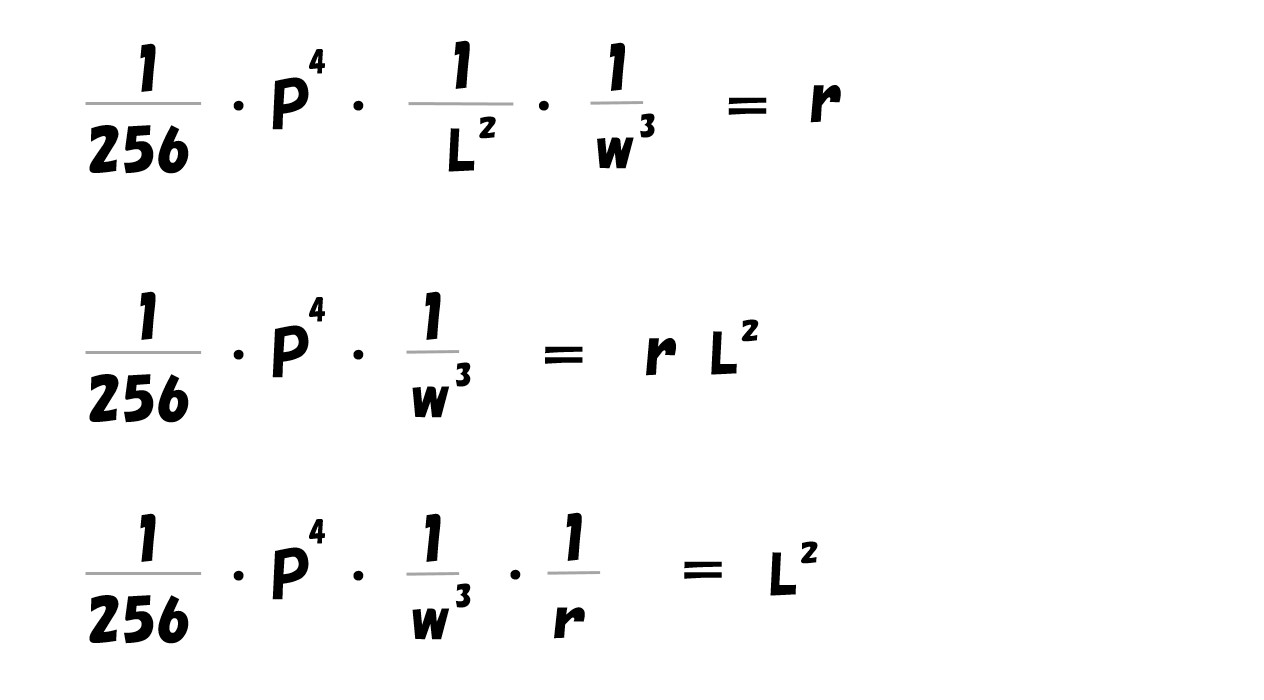「生産関数」は企業の経済活動を分析するための第1ステップです
- 生産関数とは?(式・種類)
- 生産関数の短期・長期
- 生産関数のグラフ
- 生産関数と費用関数
- 生産関数と利潤最大化
- 生産関数と供給関数
生産関数で登場する基本的な情報をまとめています。
生産関数とは?

生産関数とは
「生産要素の投入量」と「生産量」の関係を表した関数のこと。生産関数では、労働量(Labor)と資本量(Kapital)の2つが生産要素として登場することが多い。


主な相違点
- 資本の扱い方で「短期の生産関数(F)」と「長期の生産関数(F)」に分かれる
費用関数も短期と長期に分けられます。短期・長期の違いは後程紹介します。
ここからは「労働(L)」「資本(K)」で表される生産関数(F)を考えていきます。この2つの生産要素で考えた生産関数(F)は、ミクロ経済学では1番オーソドックスです。
生産関数の種類・数式

- 生産関数は「Y=F(L, K)」と表される
L(労働)と資本(K)は変数ということを意味しており「Y=○L+○K」や「Y=○L×○K」という形の数式を表しています。
具体的には
- Y=2L+5K
- Y=3L×4K
労働(L)と資本(K)を足し合わせる生産関数を「リニア型(線形)」と言います。
労働(L)と資本(K)を掛ける生産関数を「コブ・ダグラス型」と言います。
通常「Y=○L×○K」「Y=○L+○K」の○の部分は、問題文などに示されています。もちろん乗数が登場することもあります。「Y=(Lの2乗)×(Kの2分の1乗)」など。


ちなみに
経済学の問題でよく登場するのは、労働(L)と資本(K)を掛けあわせる「コブ・ダグラス型の生産関数」です。
「従業員の労働力」や「設備投資」は相乗効果が生まれると考えているため。
短期生産関数(生産要素が1つ)
「- (バー)」は数値が一定であることを表します。
企業が設備投資をしたり、土地を買ったりするのは通常は時間がかかります。
そのため、短期的な企業の生産活動を分析する時は、資本(K)の動きを考慮しません(=資本は一定)。この資本を一定(固定的生産要素)とした生産関数(F)を短期生産関数と呼びます。
ポイント
労働力(L)と資本(K)で考えた生産関数(F)なら、資本が一定になるので「実質的に労働力が商品やサービスの生産に影響を与える」と言えます。
短期の生産関数の基礎知識が分かったところで、次にグラフを見ていきましょう。
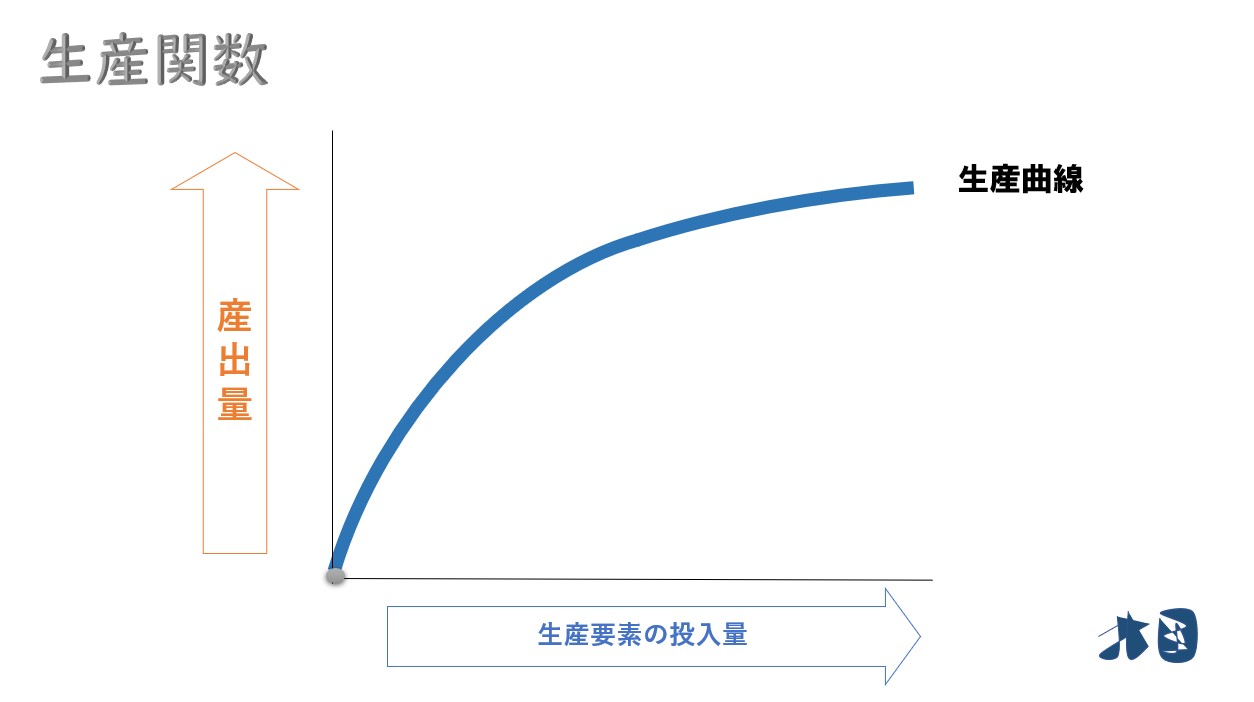
生産関数のグラフ
- 生産関数によって描かれる曲線を「生産力曲線(生産曲線)」と呼びます。
生産力曲線が緩やかになっているのは、次第に生産力が小さくなる様子を表現しています(限界生産力逓減の法則・収穫逓減の法則)。
例えば
- 農家が作物をたくさん作ります。

短期的には土地(資本)を増やすことが難しいので、労働力を増やします。
このとき
土地は限られているので人が増えても育てられる作物には限りがあります。そのため、人を増やし続けても費用対効果はどんどん悪くなっていきます。
これを限界生産力逓減と言います。追加した労働力から生産される作物がどんどん少なくなっていく現象です。


現実的な話
- 広い土地なら1人よりも2人の方が良い
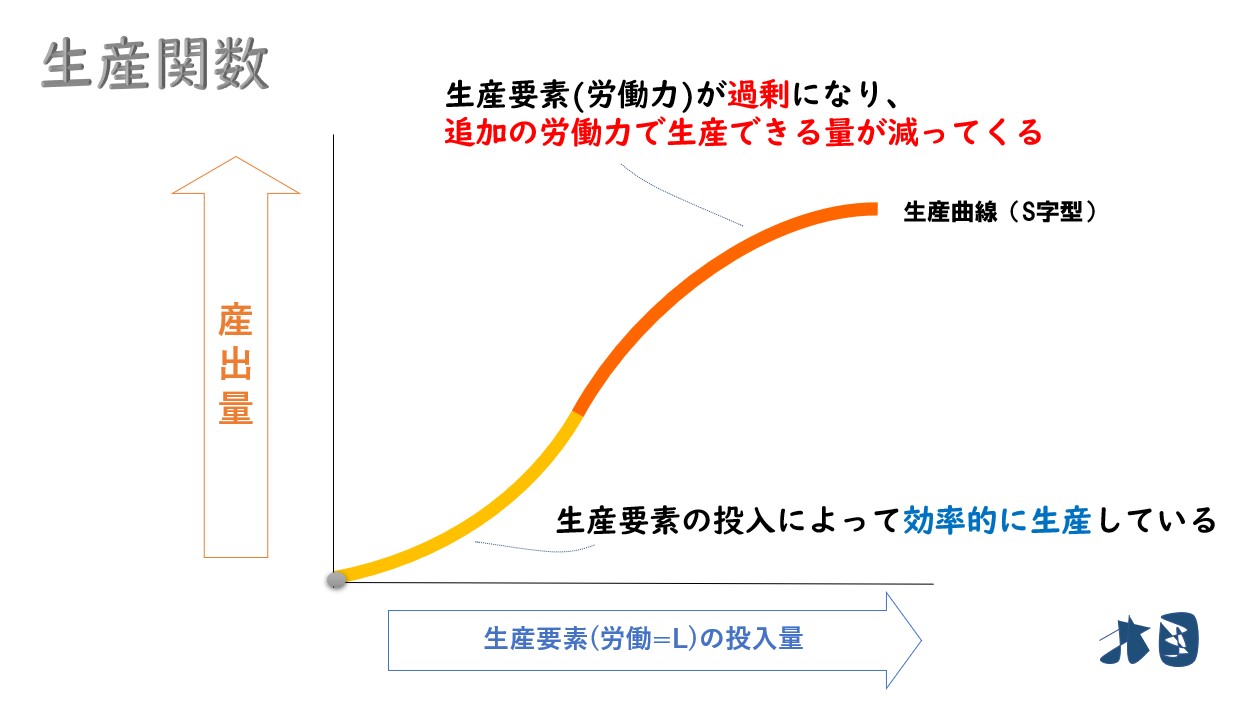
先ほどまでは「土地が一定なので、人を増やし続けると効率が悪くなっていく」という話でしたが、逆に、明らかに人手不足のときに労働力が増えれば効率的になります。
ポイント
労働力が足りないと、労働力が増えると効率的に生産が出来るようになります。一方で、人が増え続けると効率が悪くなります。
この2つの関係をグラフで表すと「S字型の生産関数」になります。
グラフ
長期生産関数(生産要素が2つ)
先ほどまでは「資本は一定」だと考えてきました。
しかし
- 長いスパンでみれば、設備投資によって効率的な生産活動が実現します
そのため、長期間で企業の生産活動を分析する時は、資本(K)を一定とせずに労働力(L)と同じく調整が可能(可変的生産要素)と考えます。
資本(K)を一定としない場合の生産関数(F)を長期生産関数と言います。
グラフ
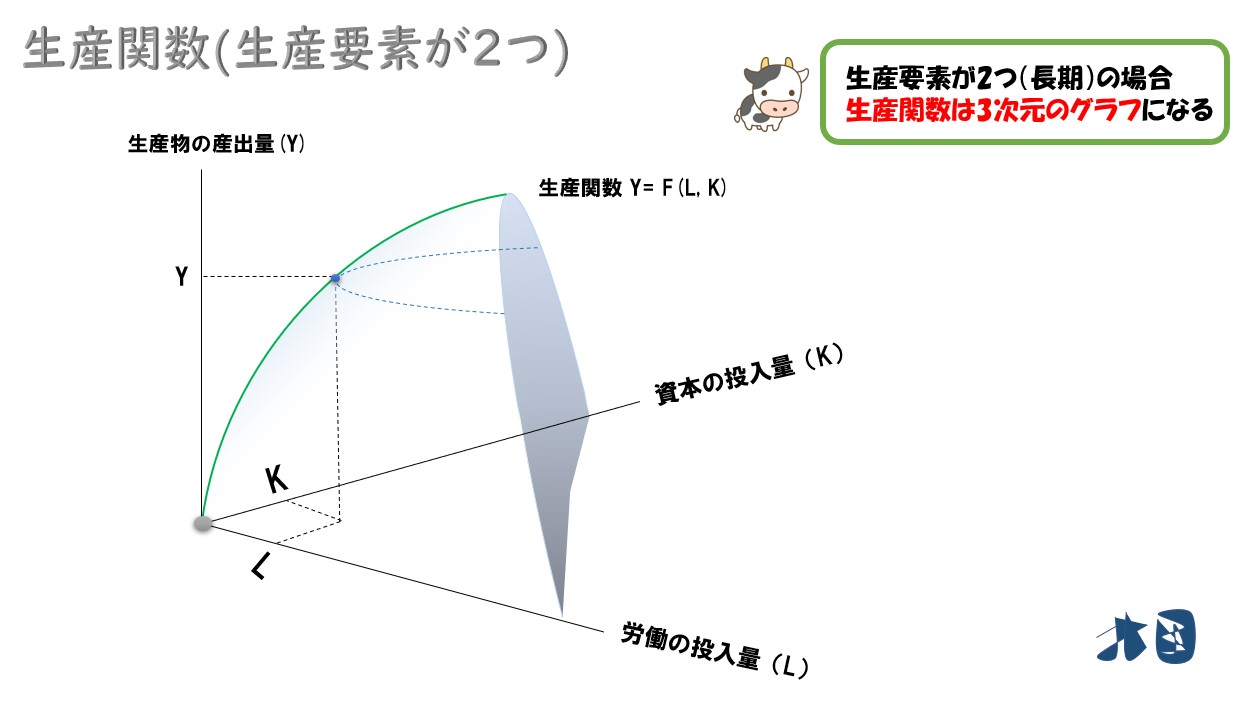
短期生産関数の場合は、資本が一定なので「縦軸=産出量」「横軸=労働力(L)」をグラフに取ればOKでした。
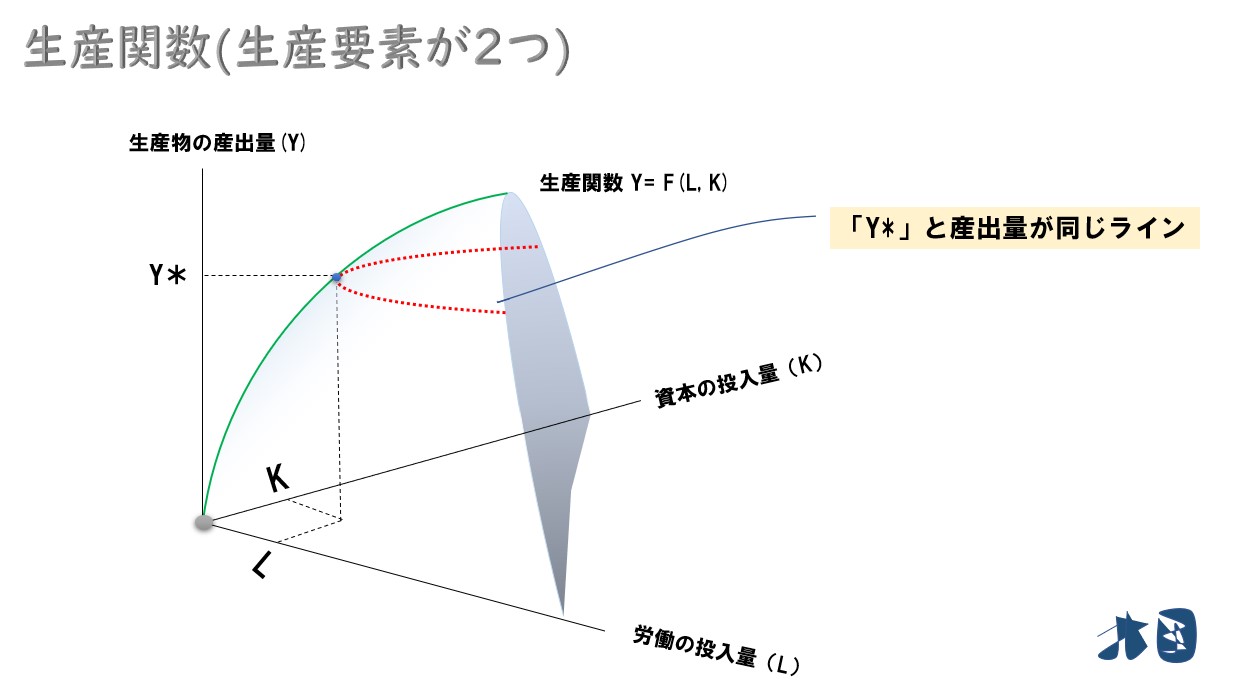
長期生産関数の場合は「労働力(L)」「資本(K)」の両方が産出量に影響を与えるので、3次元のグラフになります。
- 縦軸=資本量(K)
- 横軸=労働力(L)
- 空中(高さ)=産出量(Y)
短期生産関数のグラフと同じく、空中にS字型の生産曲線を描くことも出来ます。


空中にS字型を描くグラフを扱うことも出来ますが、3次元では処理しにくいので、ふつうは2次元に落とし込みます。
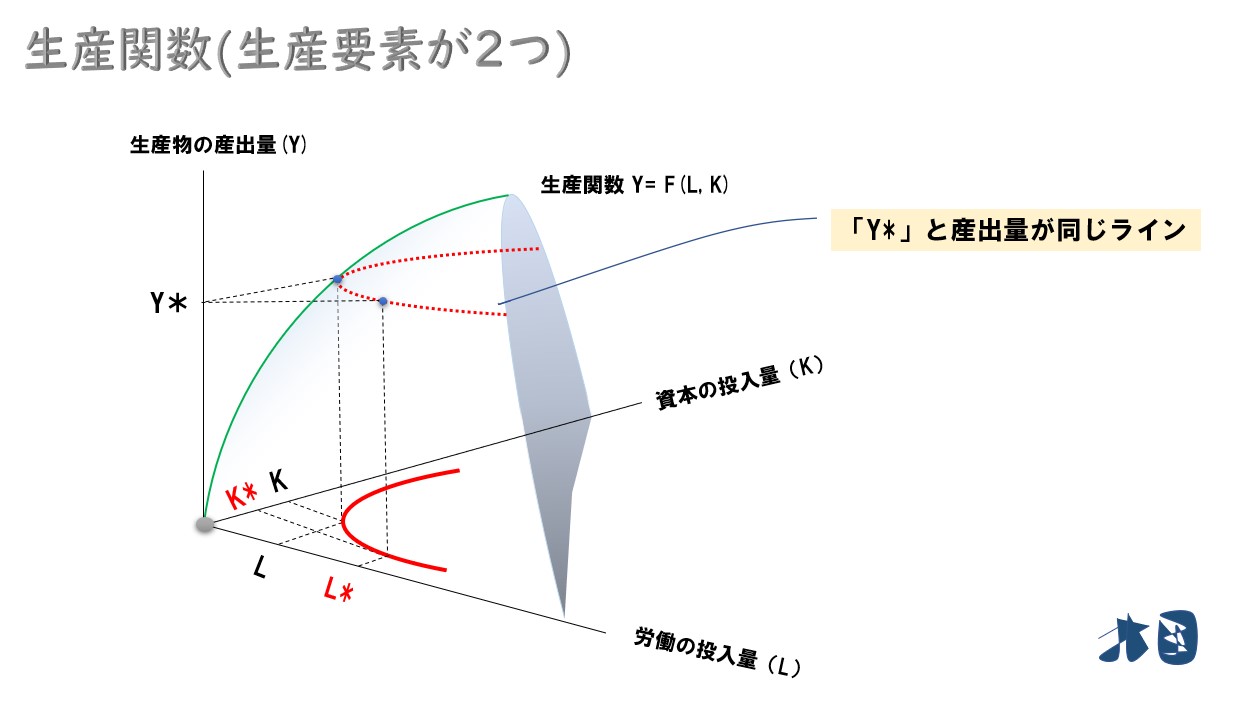
「産出量=Y*」に注目してください。
労働と資本の組み合わせが「L, K」でも「L*, K*」でも、生産物の産出量は「Y*」になります。
ポイント
例えば、100個の製品を作るのに(労働10, 資本30)という組み合わせでも(労働50, 資本10)という組み合わせでもOKという状態です。
どちらの組み合わせでも100個の製品を作れることを赤い線が表してます。
そして
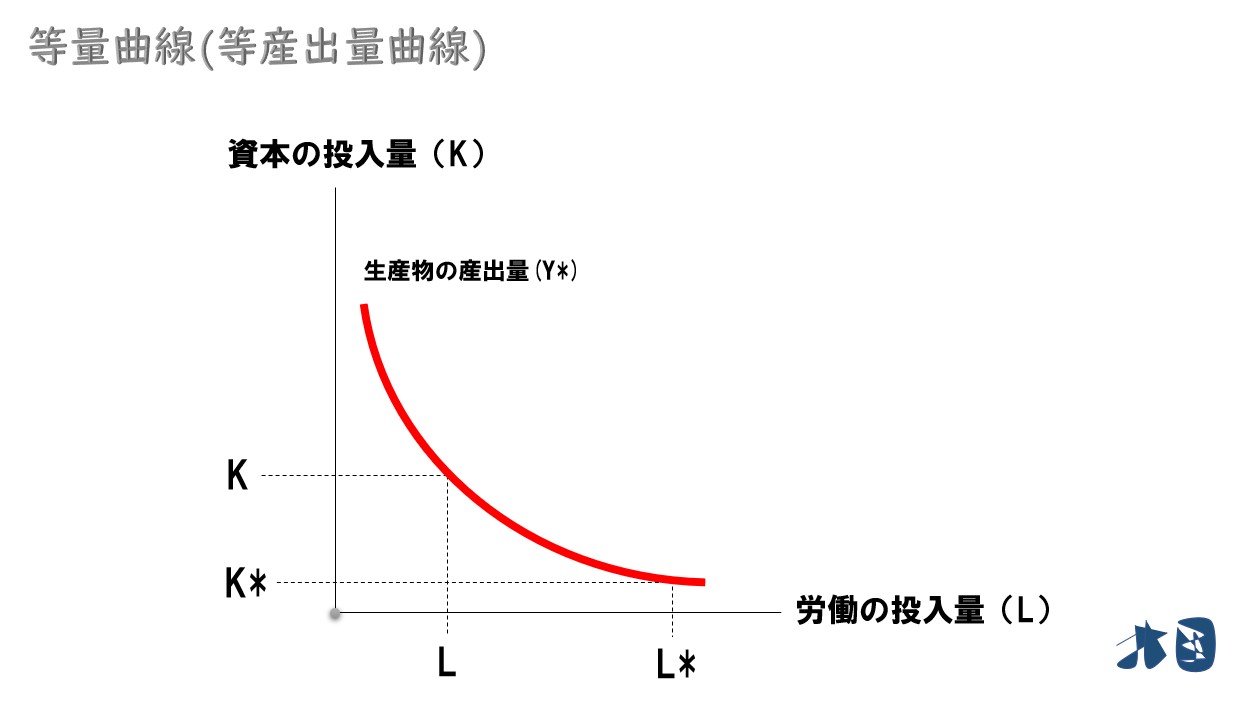
産出量が同じになる労働(L)と資本(K)の組み合わせを結び、2次元に落とし込みます。
長期生産関数を2次元に落とし込んだ曲線を「等量曲線(等産出量曲線)」と言います。
産出量が同じになる生産要素(労働・資本)の組み合わせです。似た名前の等費用線というものがありますが別物です。
長期の生産関数を扱うときは、この等量曲線を使うことが多いので、知っておきましょう。
生産関数と費用関数の求め方
-

-
【費用関数】意味・生産関数からの求め方
「費用関数」は、ある生産量を実現させるときに必要となる最小費用を示した関数のこと。 費用関数(C)とは? 費用関数(C) ...
続きを見る
2つの関係
- 生産関数は「生産要素の投入量」⇒「生産物の産出量」
- 費用関数は「生産物の産出量」⇒「総費用」
ポイント
企業がある生産量を実現させるとき、最小費用で生産が行われる(費用最小化が実現する)。
この前提のときに「生産関数(Y)=KL」を「C=●●」に組み込むというイメージです。
例題
- 生産関数(Y)=√K・√L
- 労働=L
- 賃金=w
- 資本=K
- レンタル料=r
費用関数(C)=wL+rK
※労働(L)と資本(K)の値は生産関数から求めることが出来る。
計算の続きはこちら
生産関数と利潤最大化の求め方
-
-
【完全競争・利潤最大化】条件や求め方・計算方法をグラフを使って理解する
「完全競争市場の利潤最大化」 利潤最大化の意味 利潤最大化の考え方 利潤最大化で微分が登場する理由 利潤最大化条件の計算 ...
続きを見る
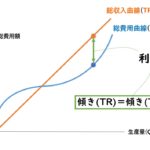
「企業の利潤(π)=総収入ー総費用」なので
- 総収入=価格(P)×生産量(Y)
- 総費用=賃金(w)×労働量(L)+レンタル料(r)×資本量(K)
したがって「利潤(π)=(PY)-(wL+rK)」と考える。
利潤を最大化させる場合は、上記の式を微分して「=0」として計算します
詳細が知りたい人はこちらで確認する⇒【完全競争・利潤最大化】条件や求め方・計算方法をグラフを使って理解する
生産要素が1つ
次の条件のとき、完全競争市場において企業が利潤最大化する生産量(Y)・労働の投入量(労働需要量・L)を求める。なお固定費用は考えないものとする。
- 生産関数(Y)=√L
- 価格(P)=4800
- 賃金(w)=1200
ここからは、完全競争市場の利潤最大化について理解している前提で計算を進めます。分からない人はこちらで確認してください⇒【完全競争・利潤最大化】条件や求め方・計算方法をグラフを使って理解する
ポイント
「利潤(π)=総収入ー総費用」なので
- 総収入=価格(P)×生産量(Y)
- 総費用=賃金(w)×労働量(L)
したがって「利潤(π)=(PY)-(wL)」と考える。
- 「利潤(π)=(PY)-(wL)」のY(もしくはL)を消す
ここではYを消す場合を考える
「Y=√L」より
- 利潤(π)=(PY)-(wL)
- 利潤(π)=(P√L)-(wL)
⇒「利潤(π)=(P√L)-(wL)」とする。
「利潤(π)=(P√L)-(wL)」を生産量で微分する
ここで、当初の「生産量=Y」は「L」の文字を使って置き換えたので、「生産量(L)」として考えます。したがって「L」で微分して「=0」と置きます。
微分する前に・・
知っておく①
「√(ルート)」は「2分の1乗」
そのため「√L=Lの2分の1乗」となります。
知っておく②
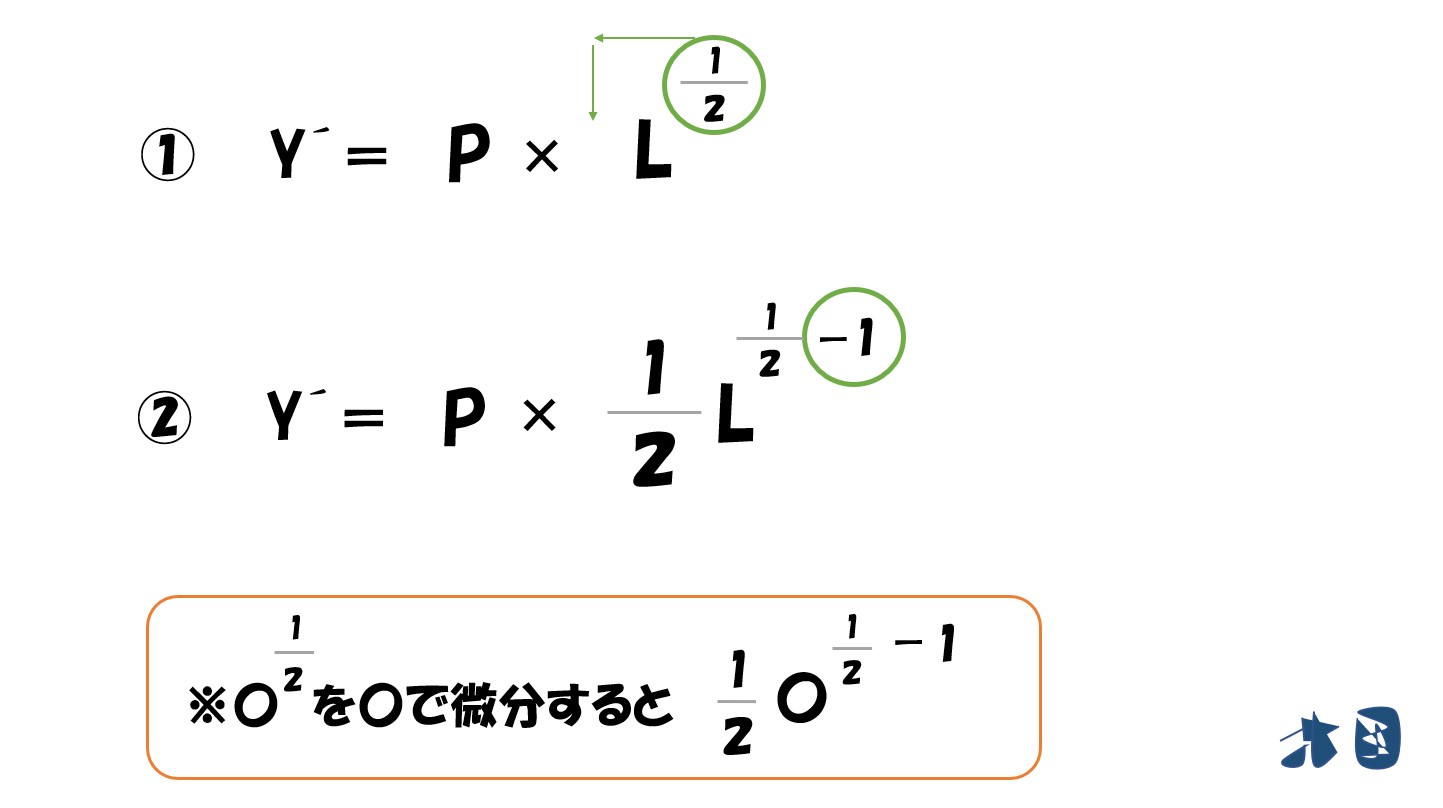
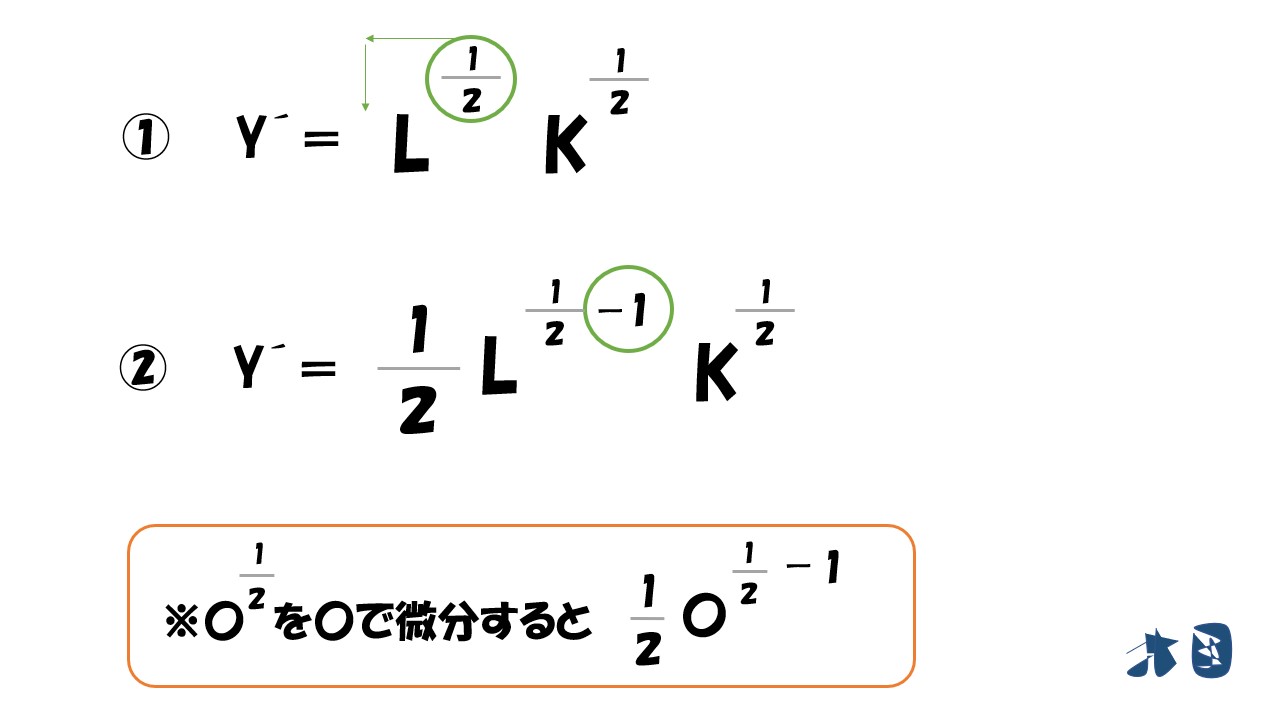
微分をするときは
- 乗数を手前に持ってくる
- 乗数を「1」マイナスする
知っておく③
「乗数がマイナス」のときは「分数になる」
というわけで
「利潤(π)=(P√L)-(wL)」を「L」で微分すると‥
- (P√L)は上で説明した通りで微分できます。
- (wL)は(Lの1乗)なので微分すると(1×Lの0乗)=1になります。よって「w×1=w」
最終的にコレ
生産量で微分して「=0」としているので、上記の式が利潤最大化が実現している状態となっている。
あとは問題で与えられた「P=4800」「w=1200」を代入して「L」の値を求めればOK!
このままでは計算しづらいので、値を代入する前に変形します。
- 「-w」を右辺へ移行する
- 両辺を「P」で割ります
ここで「P=4800・w=1200」を代入します。
- 両辺を2乗する
答え
利潤が最大化する生産量と労働投入量は‥
- 生産量(Y)=2
- 労働の投入量(L)=4
生産関数が「Y=√L」と与えられていたため「√L=2」を代入すれば生産量(Y)が得られる。
生産要素が2つ
いま、ある企業の生産関数(長期生産関数)が
と与えられているとき、完全競争市場において、この企業が利潤最大化する生産量(Y)・各生産要素の最適な投入量(L・K)を求める。
- 価格(P)=2400
- 賃金(w)=1200
- 資本のレンタル料(r)=2400
ここで、与えられた生産関数の乗数が足して1にならないことを確認してください。「Lの0.5乗」「Kの0.5乗」などのように「0.5+0.5=1」となっていると規模に関する収穫が一定となり計算過程が異なります。最後の章を確認してください。
ポイント
「利潤(π)=総収入ー総費用」なので
- 総収入=価格(P)×生産量(Y)
- 総費用=賃金(w)×労働量(L)+レンタル料(r)×資本量(K)
したがって「利潤(π)=(PY)-(wL+rK)」と考える。
初めに
- 字数を減らしたいので「利潤(π)=(PY)-(wL+rK)」のY(もしくはL・K)を消す
ここではYを消す場合を考える
より
- 利潤(π)=(PY)-(wL+rK)
- 利潤(π)=(P・L^0.25・√K)-(wL+rK)
⇒「利潤(π)=(P・L^0.25・√K)-(wL+rK)」とする。
「利潤(π)=(P・L^0.25・√K)-(wL+rK)」を生産量で微分
ここで、当初の「生産量=Y」は「L・K」の文字を使って置き換えたので、「生産量(L・K)」として考えます。したがって「L」「K」で偏微分して「=0」と置きます。
完全競争市場の利潤最大化について理解している前提で計算を進めます。分からない人はこちらで確認してください⇒【完全競争・利潤最大化】条件や求め方・計算方法をグラフを使って理解する
知っておく①
「√(ルート)」は「2分の1乗」
そのため「√K=Kの2分の1乗」となります。以下「√K=Kの2分の1乗(0.5乗)」と表記します。
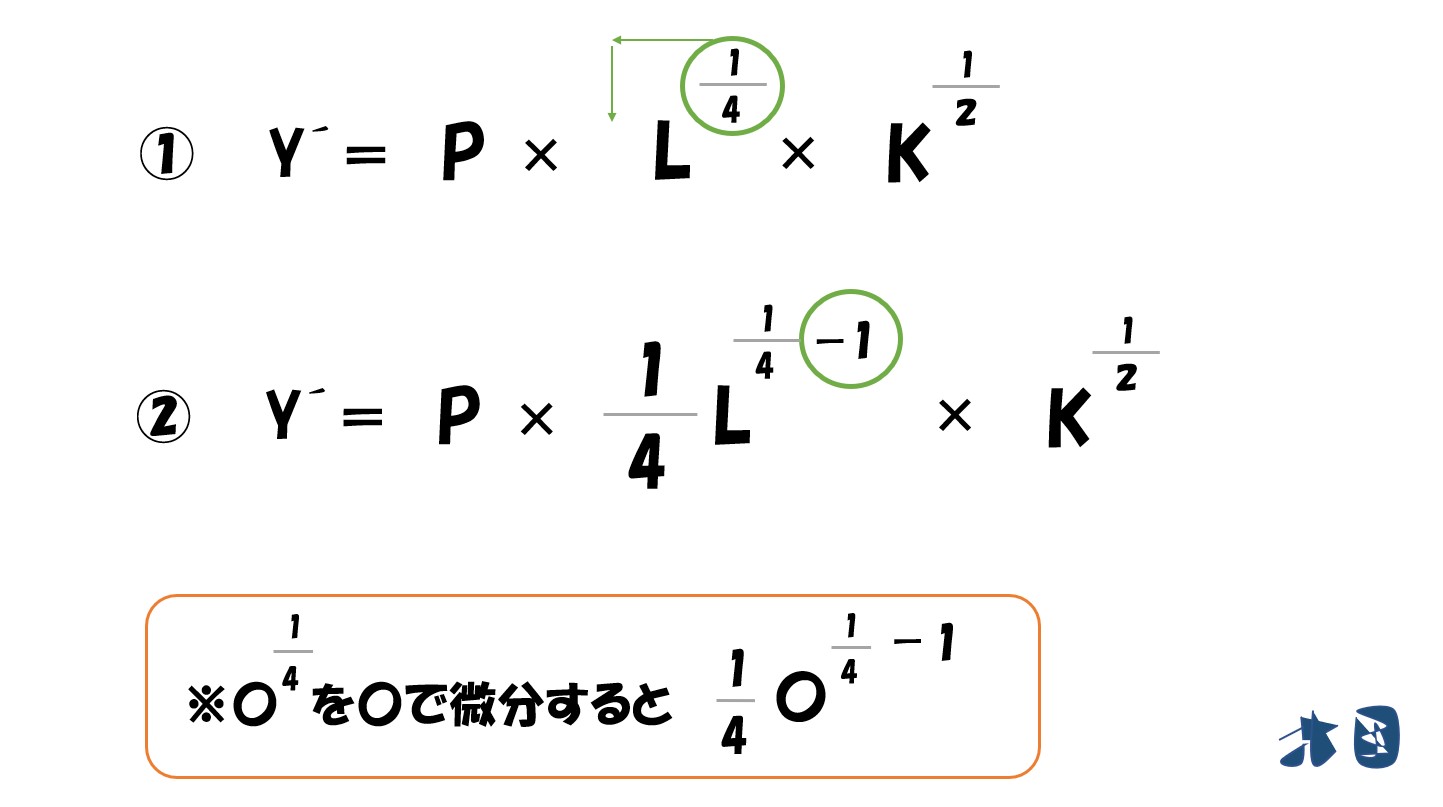
知っておく②
偏微分をするときは
- 乗数を手前に持ってくる
- 乗数を「1」マイナスする
※0.25=1/4
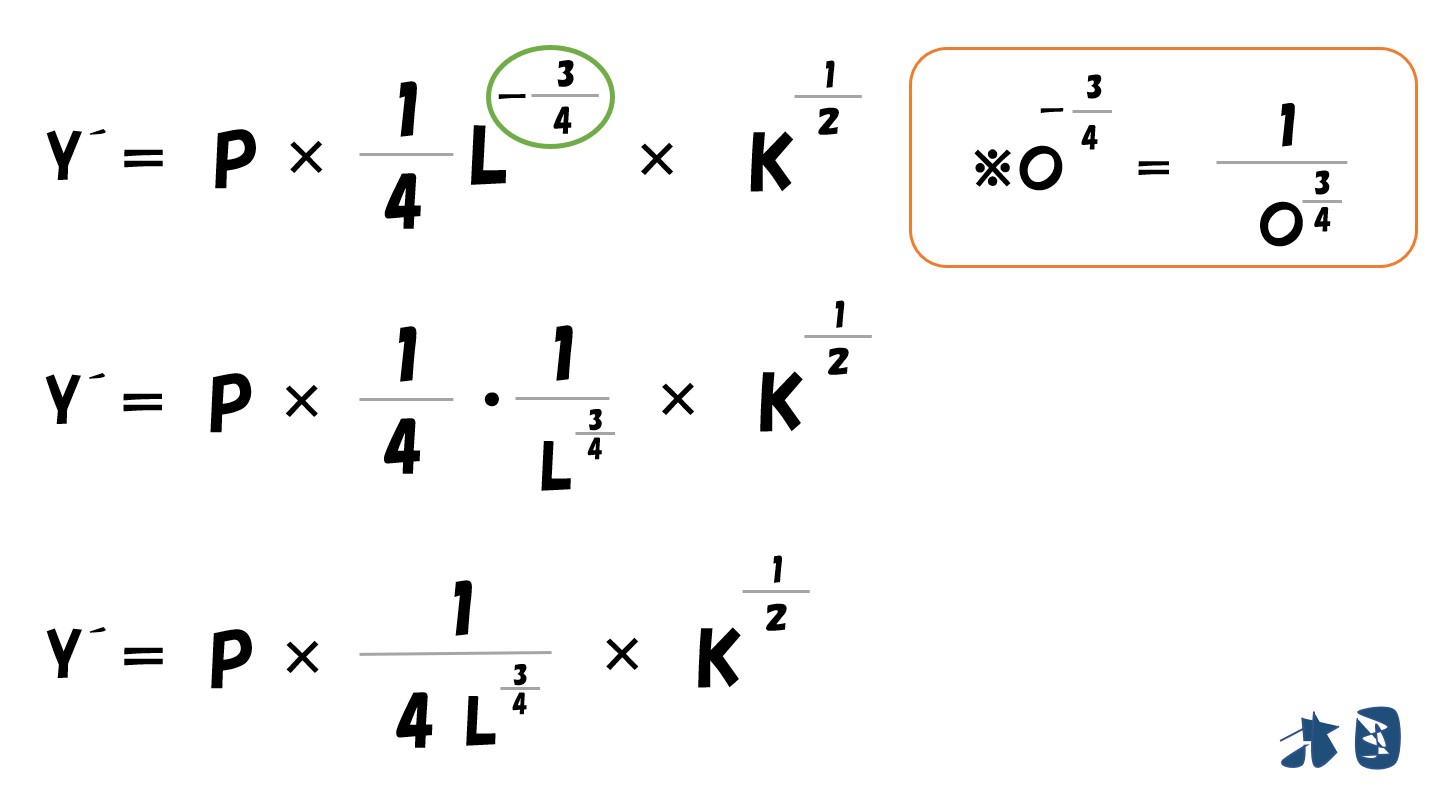
知っておく②
「乗数がマイナス」のときは「分数になる」
というわけで
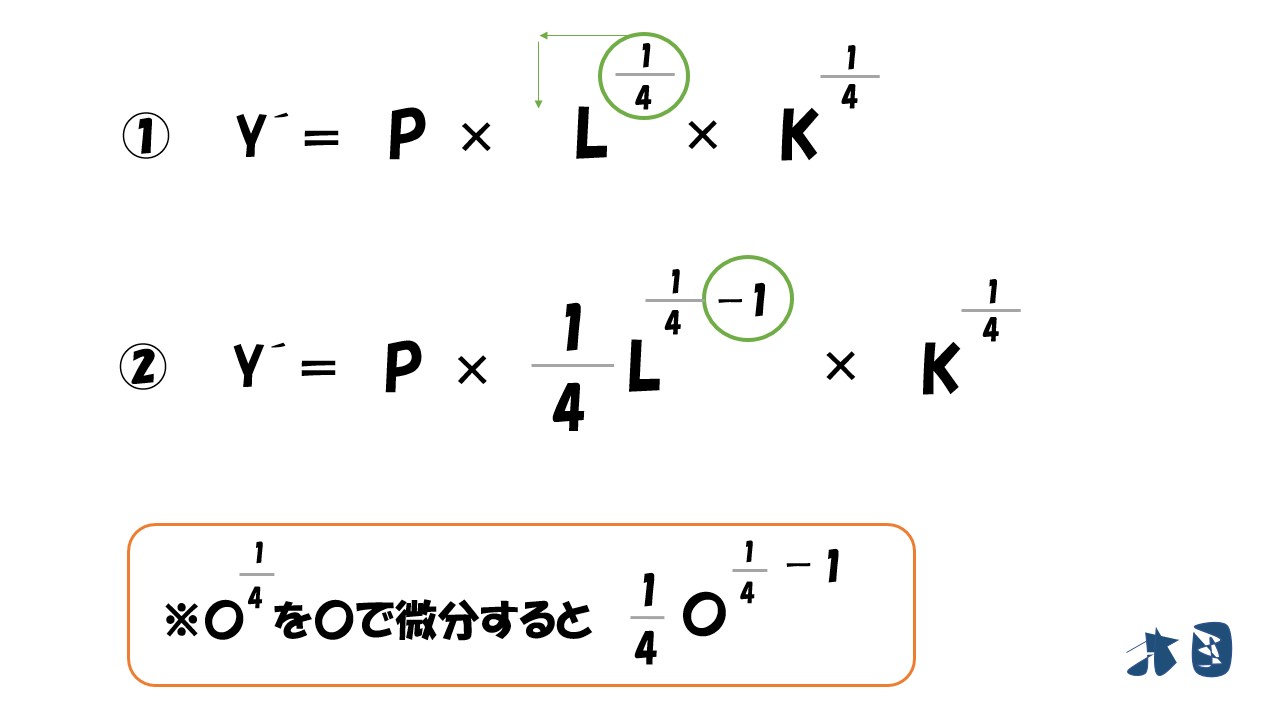
「利潤(π)=(P・L^0.25・K^0.5)-(wL+rK)」を「L」で偏微分すると‥
- (P・L^0.25・K^0.5)は上で説明した通りで微分できます。
- (wL+rK)は(Lの1乗)なので微分すると(1×Lの0乗)=1になります。よって「w×1=w」
「L」で偏微分するなら「L」という文字がついていない部分は無視されます。※あくまで微分は変化量(Lという数量が変化したら式の答えがどう変化するか?)を見るため。
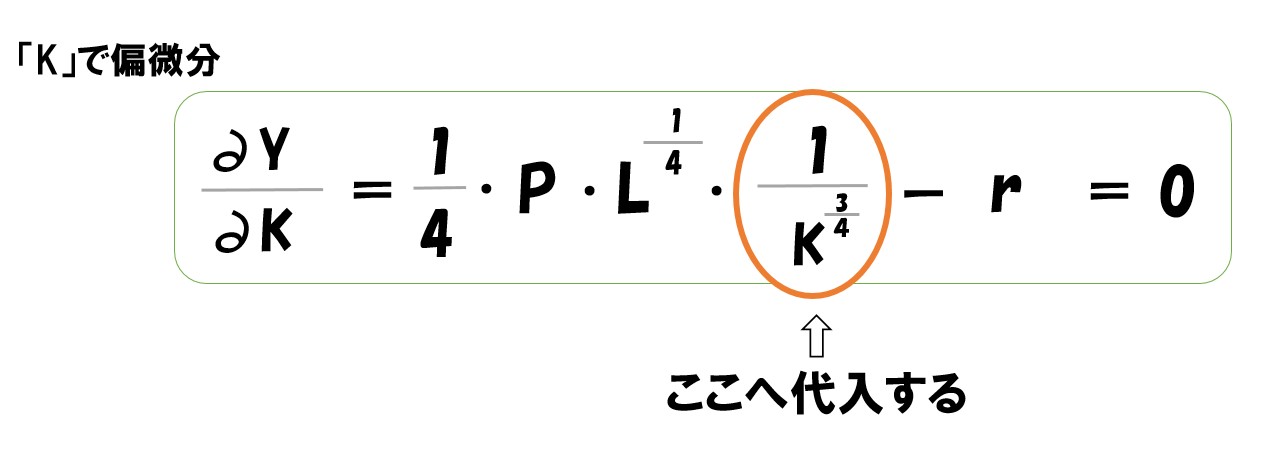
最終的にL・Kで偏微分すると
生産量で微分して「=0」としているので、上記の2つの式が利潤最大化が実現している状態となっている。
あとは問題で与えられた「P=2400・w=1200・K=2400」を代入して「L・K」の値を求めればOK!
このままでは計算しづらいので、値を代入する前に変形します。
- 「-w」「-r」を右辺へ移行する
- 両辺を「P」で割ります
ここで「P=2400・w=1200・r=2400」を代入します。
計算していく
両辺を4乗する
「16Lの3乗」と「L/16」がイコール
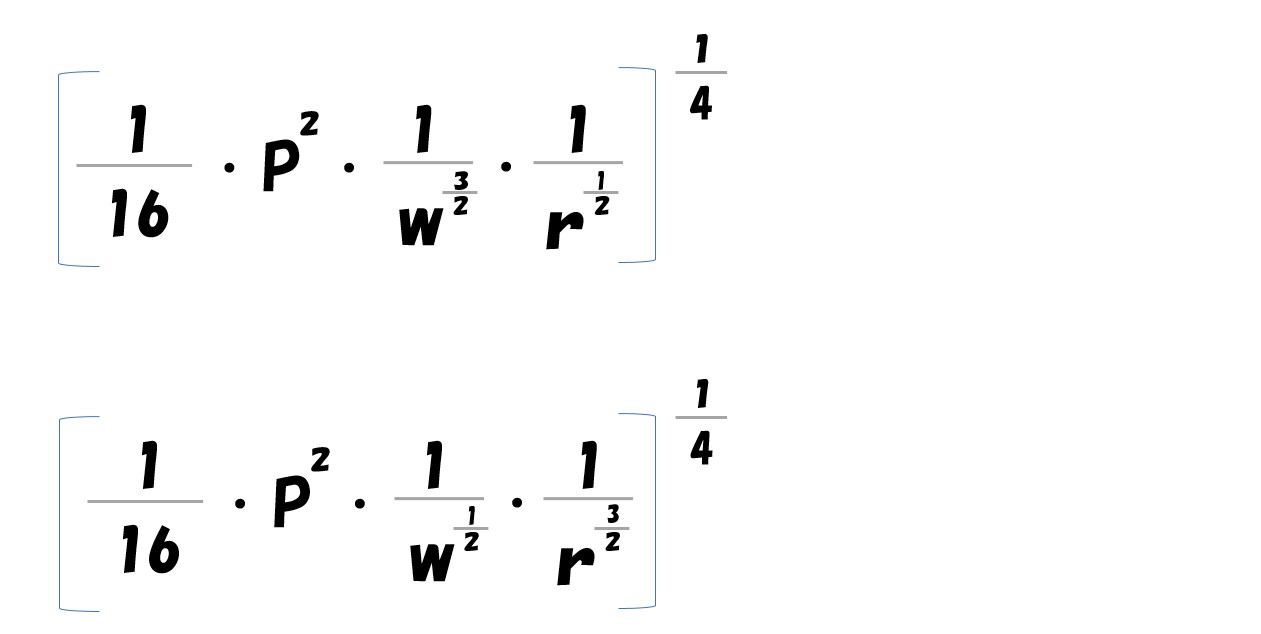
L=1/16
計算途中で登場した「L=16Kの2乗」へ代入
K=1/16
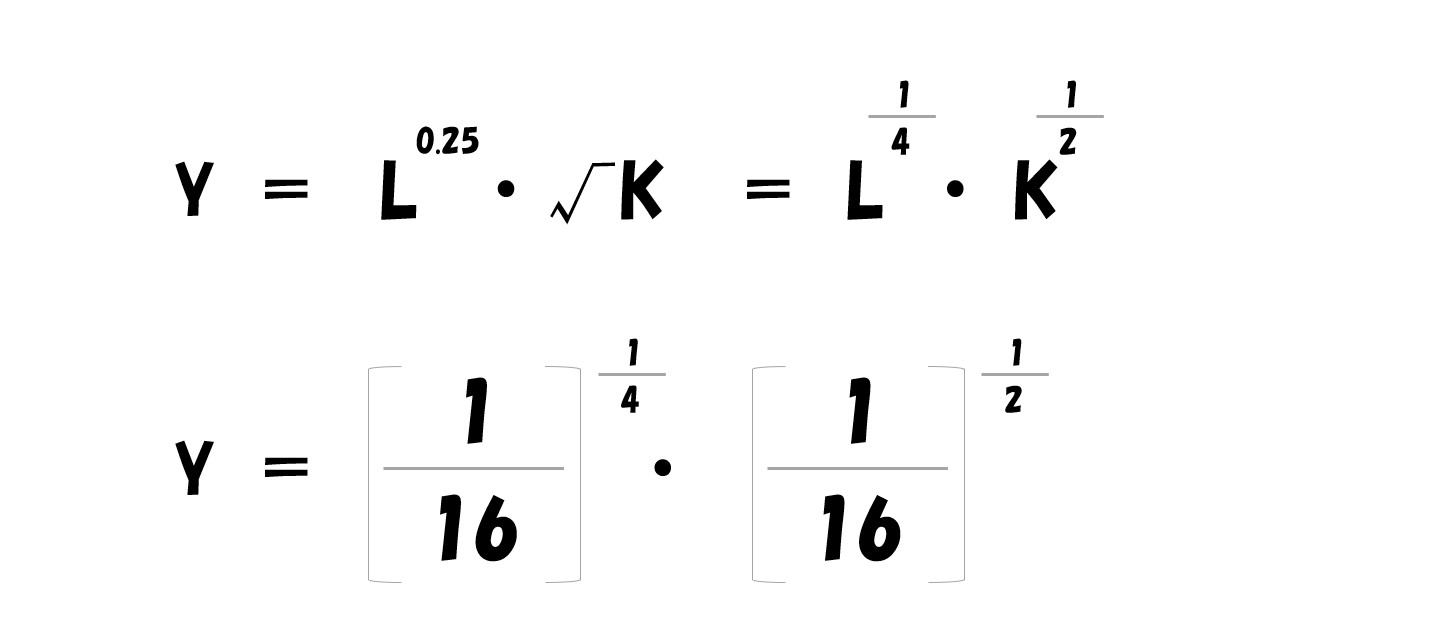
生産関数「Y=L^0.25・√K」へ答えを代入
計算していく
答え
- 利潤が最大化する生産量(Y)は「1/8」
- 最適な労働の投入量(L)は「1/16」
- 最適な資本の投入量(K)は「1/16」
生産要素が2つ(収穫一定)
いま、ある企業の生産関数(長期生産関数)が
- Y=√L・√K
と与えられているとき、完全競争市場において、この企業が利潤最大化する生産量(Y)・各生産要素の最適な投入量(L・K)を求める。
- 価格(P)=2400
- 賃金(w)=1200
- 資本のレンタル料(r)=4800
ここで、与えられた生産関数の乗数が足して1になるため収穫が一定となります。※「√L=Lの0.5乗」「√K=Kの0.5乗」⇒「0.5+0.5=1」となっている
ポイント
収穫が一定の場合は、費用最小化を求める。利潤最大化するときは、最も効率的な生産が実現しているはずなので、費用が最小化していると考える。
※収穫が一定の場合は特殊な答えになるため利潤最大化条件を使って計算することが出来ません。
費用最小化
- 「(w/r)」=「MPL/MPK」が成立
「生産要素の価格比(要素価格比)=2つの限界生産力の比」
費用最小化についてはこちら⇒【費用最小化】考え方・条件式・求め方について分かりやすく解説
というわけで、まず「労働の限界生産力(MPL)」「資本の限界生産力(MPK)」を求めます
限界生産力(MP)を求める時は微分をしますが、微分する理由が分からない人は「限界生産力・限界生産力逓減の法則」で確認してください。
計算する
- 「Y=√L・√K」を「L・K」で微分します
※「√L=Lの0.5乗(1/2乗)」「√K=Kの0.5乗(1/2乗)」
労働(L)で微分する
資本(K)で微分する
ここで、費用最小化が実現するとき、下記の式が成り立つ
- 「(w/r)」=「MPL/MPK」が成立
「生産要素の価格比(要素価格比)=2つの限界生産力の比」
費用最小化についてはこちら⇒【費用最小化】考え方・条件式・求め方について分かりやすく解説
先に
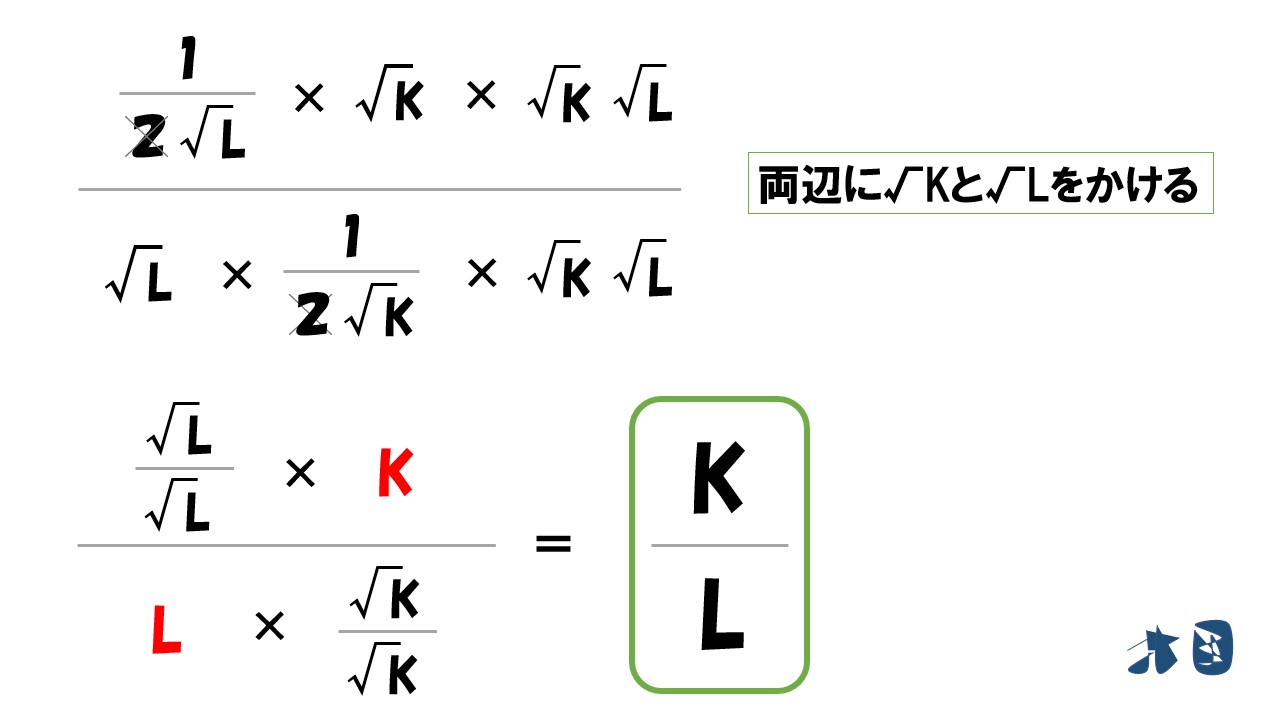
- 「MPL/MPK」を求める
- 「(w/r)」=「MPL/MPK」より
生産関数(Y)に代入
- Y=√L・√K へ代入
ここで
- 費用(C)=wL+rK
「L=2Y」「K=(1/2)Y」を費用関数(C)へ代入する
C=w2Y+r(1/2)Y
C=1200・2Y+4800・(1/2)Y
C=2400Y+2400Y
C=4800Y
この「4800Y」に注目します。
この部分は生産量(Y)を1増やすと、費用が4800かかることを表しています。つまり、費用が4800で一定のため、販売価格(P)の大きさ次第で利潤が出るかが変わります。
- 販売価格(P)が4800より大きい場合(P>4800)
収穫が一定のため、無限に利潤を生み出すことが出来ます。つまり、利潤が最大化する生産量は定まらない(=無限)になります。
- 販売価格(P)が4800より小さい場合(P<4800)
商品を売るたびに赤字になります。そのため、利潤が最大化する生産量は0(=生産しない)になります。
答え
問題文で「価格(P)=2400」とあったので、利潤が最大化する生産量は0となります。
生産関数と供給関数の求め方
ポイント
生産関数から供給関数を求める時は
- 利潤最大化を求める
- このとき最適な生産量(Y)が供給曲線となる
生産関数→供給関数と求めるまでの流れ
基本的に次の情報が与えられている。与えられていなければ自分で文字で置く。
- 生産関数(Y)
- 販売価格(P)
- 生産要素の投入量(L・K)
- 生産要素の価格(r・w)
以上の情報から利潤最大化条件を使って数式を組む
↓
最適な生産要素の投入量(要素需要関数)を求める
↓
最適な生産量を求める←供給関数
例題
あるプライステイカーの企業の生産関数が次のように与えられているとき
![]()
- 生産物の販売価格=P
- 生産量=Y
- 賃金=w
- 労働の投入量=L
- レンタル料=r
- 資本の投入量=K
このとき企業の供給関数を求める。
利潤最大化を求める
利潤最大化問題の解き方を知っている前提で計算を進めるので、分からない人はこちらで確認⇒【完全競争・利潤最大化】条件や求め方・計算方法をグラフを使って理解する
ポイント
「利潤(π)=総収入ー総費用」なので
- 総収入=価格(P)×生産量(Y)
- 総費用=賃金(w)×労働量(L)+レンタル料(r)×資本量(K)
したがって「利潤(π)=(PY)-(wL+rK)」と考える。
はじめに
利潤最大化条件「∂π/∂L=0,∂π/∂K=0」に当てはめるために「利潤(π)=(PY)-(wL+rK)」を変形する
![]()
より
- 利潤(π)=(PY)-(wL+rK)
- 利潤(π)=(P・L^0.25・K^0.25)-(wL+rK)
⇒「利潤(π)=(P・L^0.25・K^0.25)-(wL+rK)」とする。
1/4=0.25。念のためですが「L^0.25」は「Lの0.25乗」を表しています。「Lの4分の1乗」と同じです。
この「利潤(π)=(P・L^0.25・K^0.25)-(wL+rK)」を「L」「K」で偏微分して「=0」と置きます。
微分する理由が分からない人はこちらで確認してください⇒【完全競争・利潤最大化】条件や求め方・計算方法をグラフを使って理解する
知っておく
偏微分をするときは
- 乗数を手前に持ってくる
- 乗数を「1」マイナスする
知っておく②
「乗数がマイナス」のときは「分数になる」
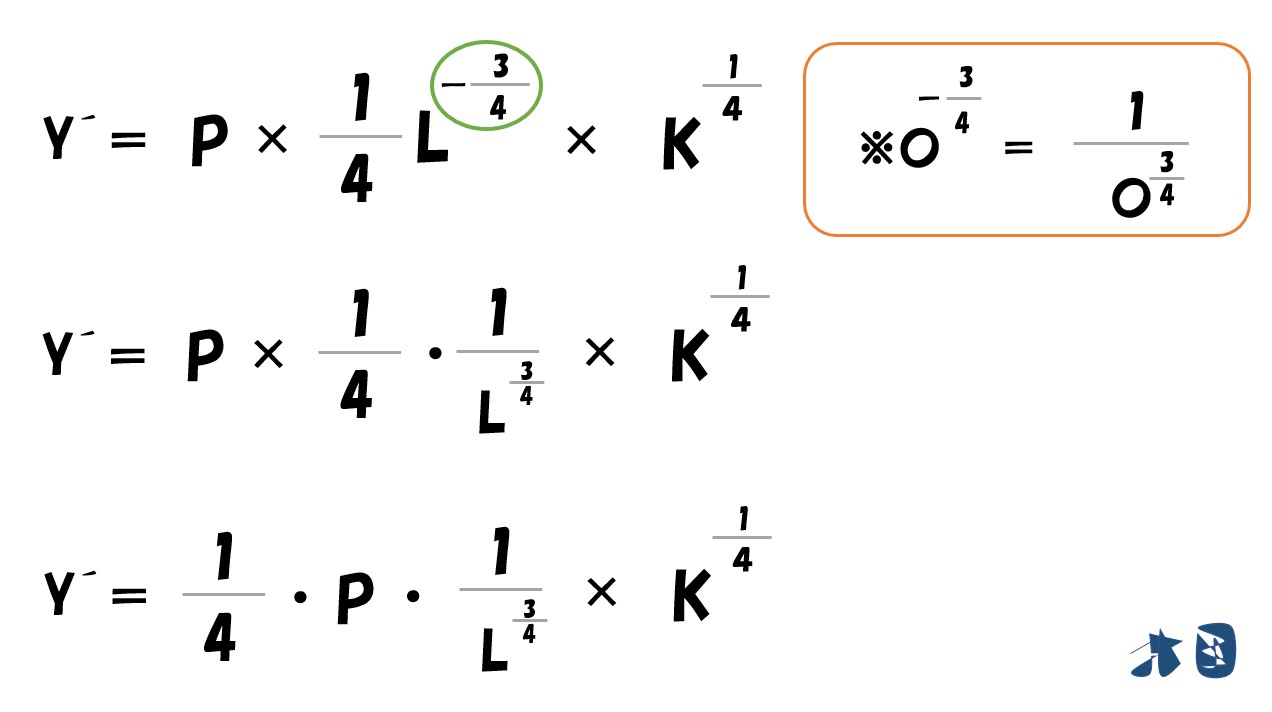
というわけで
「利潤(π)=(P・L^0.25・K^0.25)-(wL+rK)」を「L」で偏微分すると‥
- (P・L^0.25・K^0.25)は上で説明した通りで微分できます。
- (wL+rK)は(Lの1乗)なので微分すると(1×Lの0乗)=1になります。よって「w×1=w」
「L」で偏微分するなら「L」という文字がついていない部分は無視されます。※あくまで微分は変化量(Lという数量が変化したら式の答えがどう変化するか?)を見るため。
最終的にL・Kで偏微分すると
次に
- 上の条件を満たす最適な生産要素の投入量(要素需要)を求める
まず
Lで偏微分した式を「K=●●」の形にする
(計算のポイント)
「K=●●」とした上記の式は、次のステップで「Kで偏微分した方の式」に代入します。
そこで、先ほどの式を代入しやすいように変形します
ここで、上記の式を「Kで偏微分した式」に代入します。
後はこれを計算して「L=●●」の形にすれば、労働の最適な投入量(要素需要関数)となります。
計算過程をざっと
今さらですが、わざわざ分数に直さなくても乗数でマイナス●乗として計算したほうが楽です。数学が苦手な人向けに分数に直して計算しています。
資本の最適な投入量(要素需要関数)も同様の手順で計算できます(省略)
計算結果
最後に
- 労働の最適な投入量(要素需要関数)
- 資本の最適な投入量(要素需要関数)
2つを生産関数(Y)へ代入して「Y=●●」の形にすれば供給関数になります。
![]() より
より