「規模に関して収穫」がどのように変化するかを判断するために、基本となる知識を抑えましょう。
- 規模に関する収穫とは?
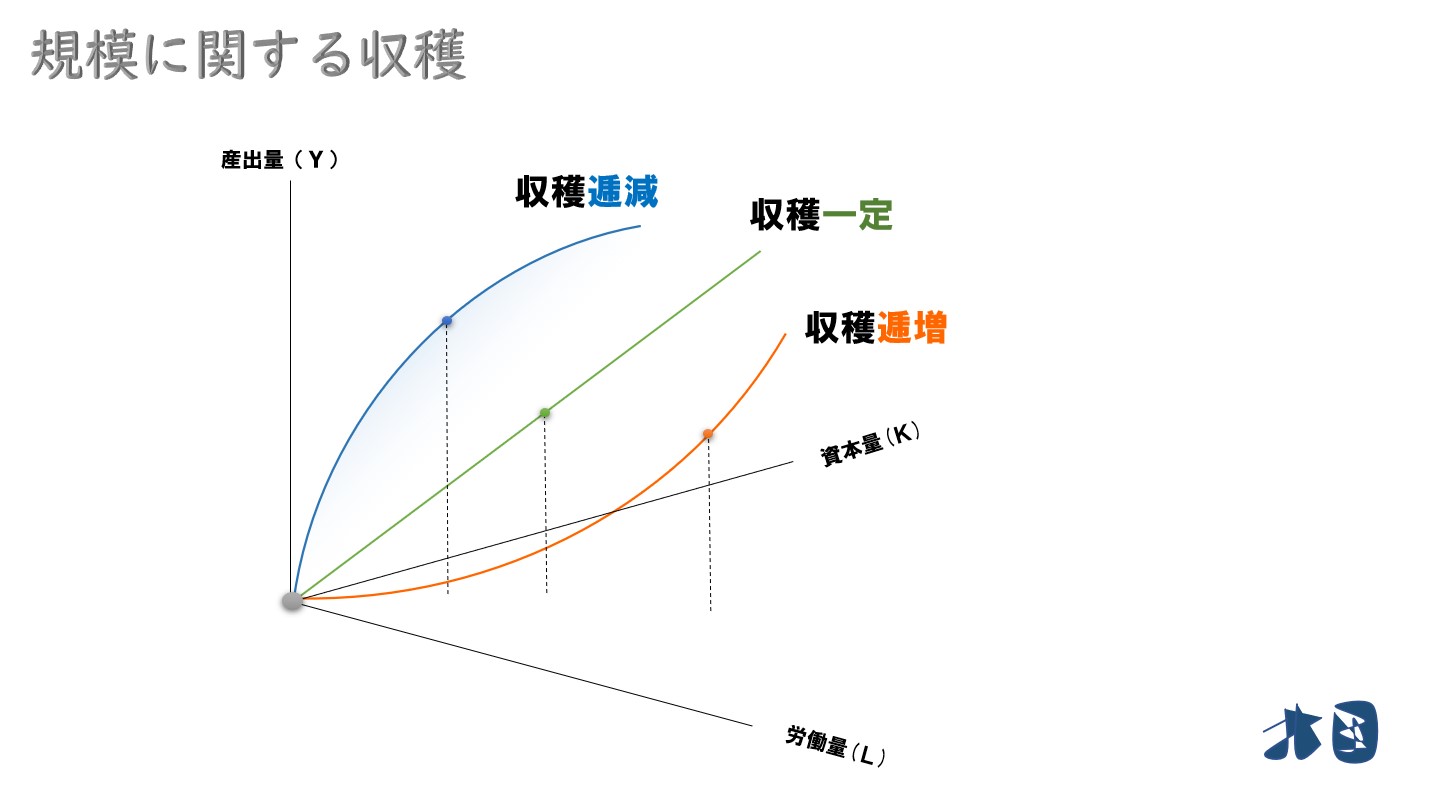
- 収穫逓減・一定・逓増
- 同次関数とは?
- 同次関数で規模に関する収穫を判断する
「限界生産力逓減の法則」と混同しやすい「規模に関する収穫」について、必要な情報をまとめています。
規模に関する収穫
規模に関する収穫とは?
全ての生産要素を増加させた場合、産出量がどのような増加具合を示すかを表した言葉。
(例) 全ての生産要素の投入量を2倍にしたとき、製品・サービスの産出量が‥
- 2倍より少ない=「収穫逓減」
- 2倍になる=「収穫一定(不変)」
- 2倍よりも増える=「収穫逓増」


確認する
限界生産力逓減の法則(収穫逓減の法則)との違い
限界生産力逓減の法則は「1つの生産要素だけを投入しつ続けると、産出量が減少する」という仮定を置いています。このとき、他の生産要素は一定(固定的生産要素)と考えます。
一方で
規模に関する収穫は「全ての生産要素の投入量を増やすと、産出量がどのようになるか?」という視点で考えます。全ての生産要素が可変的生産要素だと想定。
違いが分からないと講義などで混乱するので気を付けましょう!定義が分かったところで、簡単な例も見ていきます。
例えば
- 自動車を増産する

自動車を増産するためには、工場(K)や労働力(L)を増やす必要があります。
工場の規模(K)を2倍にして、雇用(L)もこれまでの2倍にしました。この時、車の生産量がどのように増えるのかを確認します。
これまで生産していた車は100台として考えてみます。
工場・雇用を2倍にした結果
- 車の生産量が0台~199台になった場合「規模に関して収穫逓減」
- 車の生産量が200台になった場合「規模に関して収穫一定」
- 車の生産量が201台以上になった場合「規模に関して収穫逓増」


「規模に関して収穫逓減・一定・逓増」を判断する時に「同次関数」という考え方を使います。意味は簡単ですが、数式で見ると拒絶反応を示す人もいますので、簡単に見ていきましょう。
同次関数の意味



生産関数で考える
- 資本量(K)
- 労働量(L)
- 製品・サービスの産出量(Y)
生産関数を「産出量(Y)=資本量(K)×労働量(L)」とします。
一般に、この生産関数は「Y=F(K,L)」と表現されます。
例えば、資本量(K)・労働量(L)を2倍します。
すると「2K×2L」となります。


このとき
産出量(Y)が「2のN乗×Y」となれば、N次同次関数となります。
- 産出量(Y)=資本量(K)×労働量(L)
⇩ 例えば「KとLを2倍する」
- 2K×2L
⇩ Yがどのように増加するか確認する
- 「2のN乗・Y=2K×2L」となると「N次同次関数」
仮に「4Y=2K×2L」となれば「2の2乗×Y=2K×2L」となっているので、2次同次関数となります。
2次同次関数は「資本量(K)や労働量(L)を2倍にしたときに、生産量が4倍(4Y)になる」ことを意味しています。


ちなみに
上の例で「2Y=2K×2L」となれば1次同次関数です。
「資本量(K)や労働量(L)を2倍にしたときに、生産量が2倍(2Y)になる」
ここから本題ですが「規模に関して収穫逓減・一定・逓増」なのかは、このN次同次関数から判断できます。
ポイント
生産関数がN次同次関数で
- N<1なら「収穫逓減」
- N=1なら「収穫一定」
- N>1なら「収穫逓増」
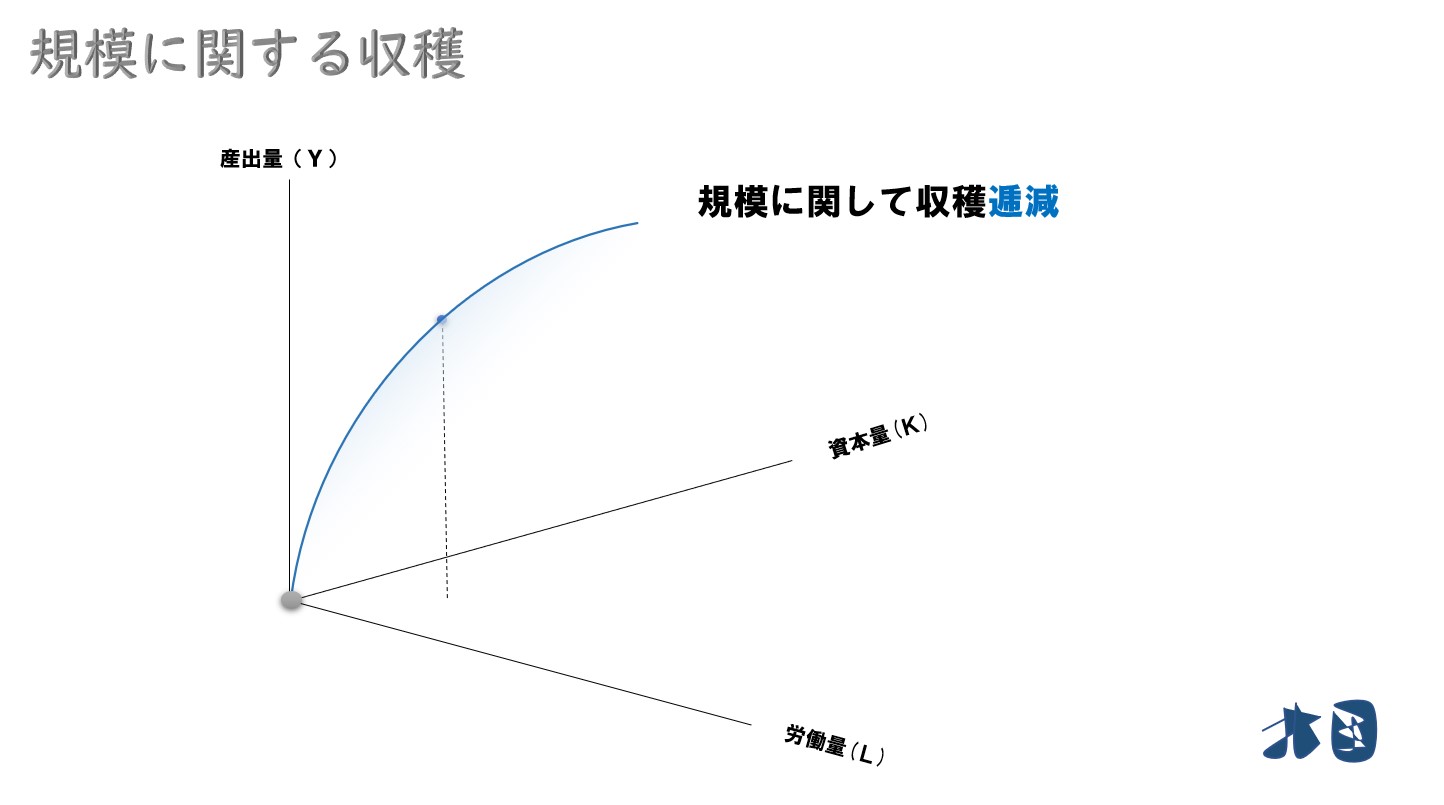
「規模に関して収穫逓減」の場合
規模に関して収穫逓減
「Y=F(K,L)」に"n"を掛ける
- nY(=nF(K,L))
- F(nK,nL)
この時「nY>F(nK,nL)」となれば収穫逓減
詳しく
「F(nK,nL)」は、全ての生産要素「資本(K)」と「労働(L)」をn倍したことを表す
「nY (=nF(K,L) )」は、産出量がn倍になったことを表す
同次関数で確認すると‥?
「nY>F(nK,nL)」が収穫逓減になることを同次関数で見ていきます。
ポイント
「nY>F(nK,nL)」を同次関数にしてみる。
同次関数にするためには「nY>F(nK,nL)」をイコールで結べばOKです。
そのとき「nY」を小さくする必要があるので、必然的に「nの0.7乗」とか「nの0.4乗」になります。
例えば
- 「nの0.5乗×Y=F(nK,nL)」でイコールになった場合
全ての生産要素をn倍したときの産出量が「nの0.5乗(=√n)×Y」なので、0.5次同次関数となります。
生産関数がN次同次関数でN<1なら「収穫逓減」なので、この場合は収穫逓減と判断できます。
さらに詳しく
生産関数「Y=K×L」で簡単に考える
全ての生産要素を2倍したら「2K×2L」となり、産出量が「2の0.5乗×Y」でイコールになった場合
「2の0.5乗=√2=約1.4...」なので「1.4Y=2K×2L」
生産要素を2倍にしたのに、産出量が2倍を下回って効率が悪い状態(収穫逓減)
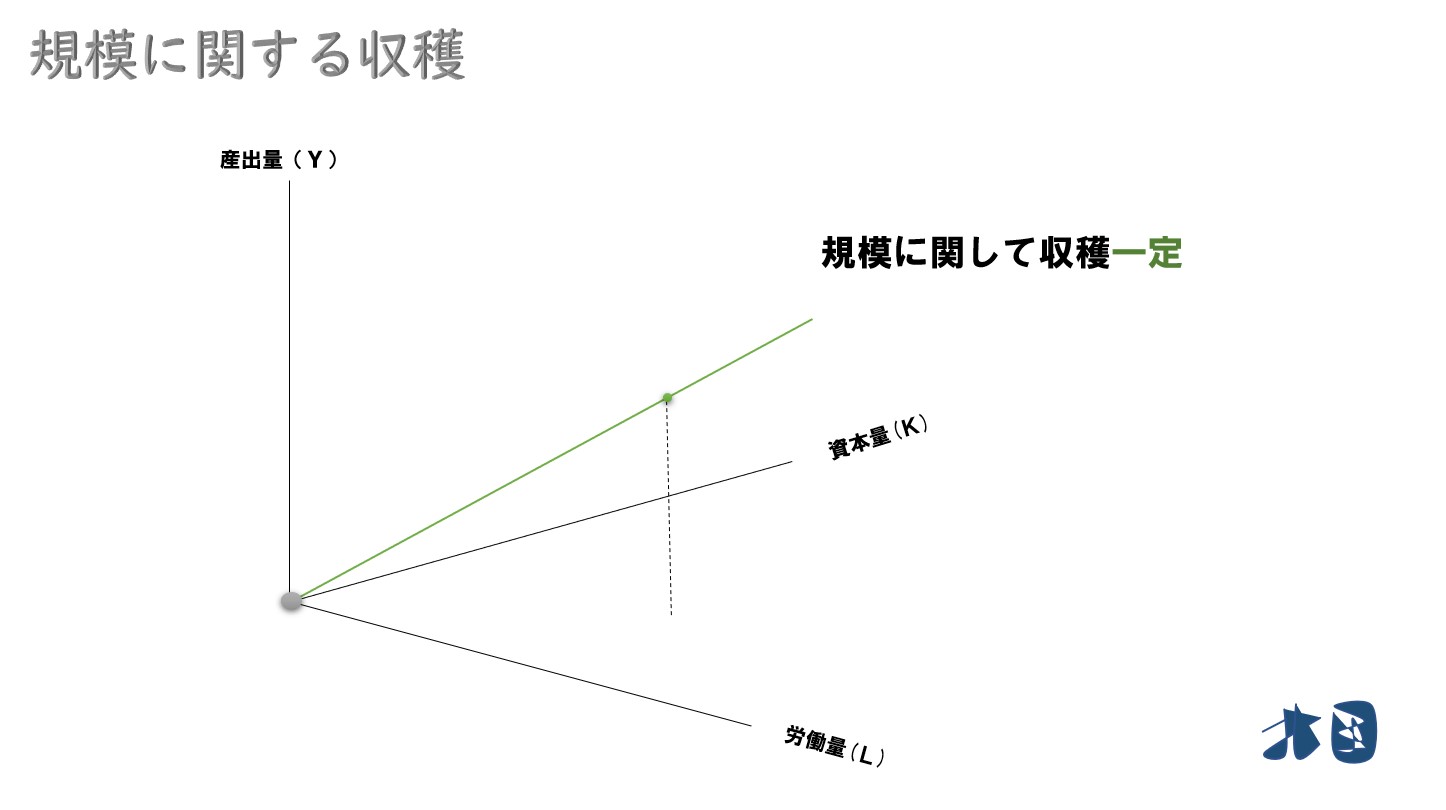
「規模に関して収穫一定」の場合
規模に関して収穫一定(不変)
「Y=F(K,L)」に"n"を掛ける
- nY(=nF(K,L))
- F(nK,nL)
この時「nY=F(nK,nL)」となれば収穫一定
詳しく
「F(nK,nL)」は、全ての生産要素「資本(K)」と「労働(L)」をn倍したことを表す
「nY (=nF(K,L) )」は、産出量がn倍になったことを表す


全ての生産要素をn倍したときの産出量が「n(=nの1乗)×Y」と表現できるので、1次同次関数となります。
生産関数がN次同次関数でN=1なら「収穫一定」なので、この場合は収穫一定と判断できます。
現実の例
- 海岸でゴミ拾いのボランティア活動

ゴミ拾いは、手で地道にゴミを拾っていくので、人数が増えようが効率が良くなったり悪くなったりしません。
1人から2人になれば、おおよそ拾えるゴミの量は2倍になります(収穫一定)。
つまり、分業できない、かつ、1人1人の労働力だけが必要な活動は、収穫が一定になると言えます。
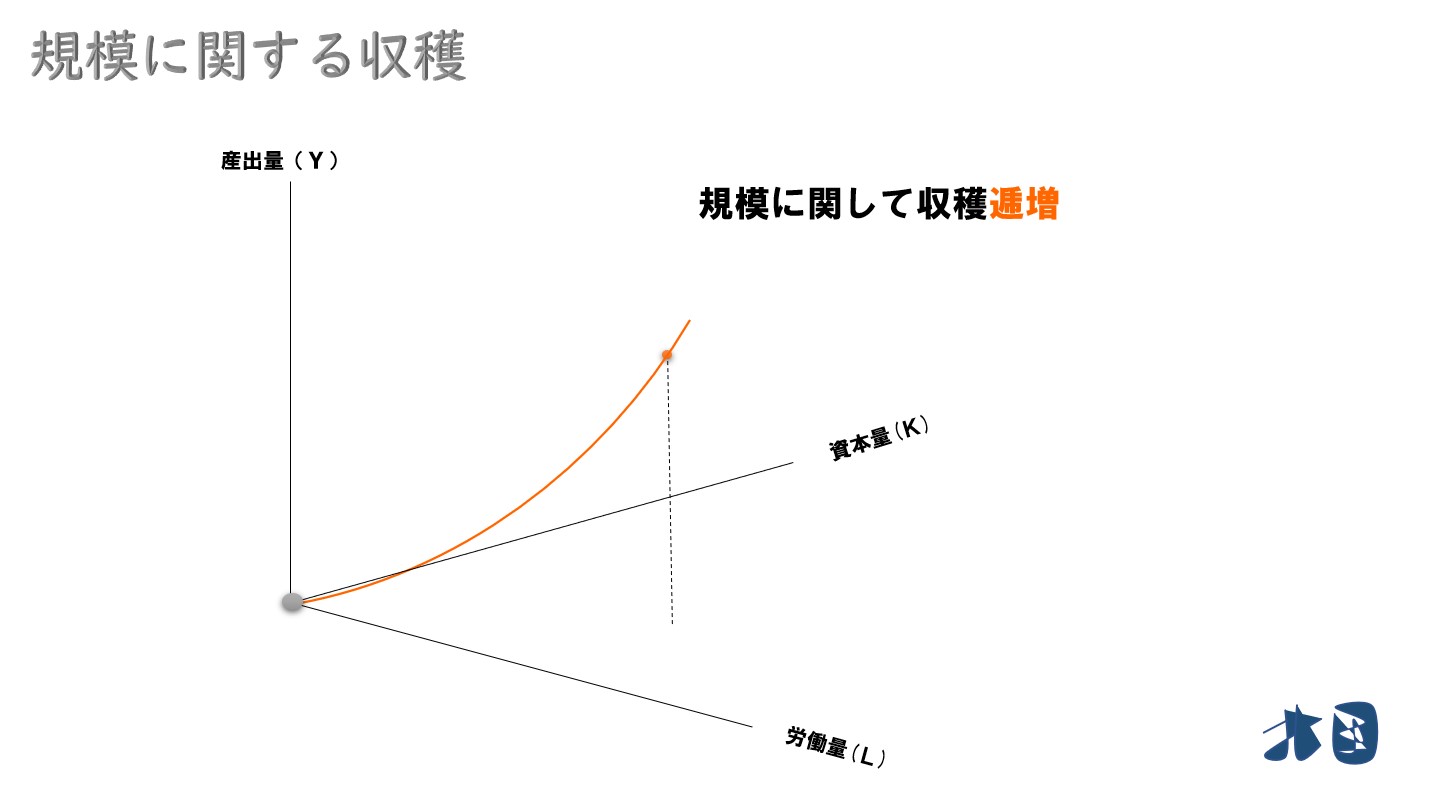
「規模に関して収穫逓増」の場合
規模に関して収穫逓増
「Y=F(K,L)」に"n"を掛ける
- nY(=nF(K,L))
- F(nK,nL)
この時「nY<F(nK,nL)」となれば収穫逓増
詳しく
「F(nK,nL)」は、全ての生産要素「資本(K)」と「労働(L)」をn倍したことを表す
「nY (=nF(K,L) )」は、産出量がn倍になったことを表す
同次関数で確認すると‥?
「nY<F(nK,nL)」が収穫逓増になることを同次関数で見ていきます。
ポイント
「nY<F(nK,nL)」を同次関数にしてみる。
同次関数にするためには「nY<F(nK,nL)」をイコールで結べばOKです。
そのとき「nY」を大きくする必要があるので、必然的に「nの2乗」とか「nの3乗」になります。
例えば
- 「nの2乗×Y=F(nK,nL)」でイコールになった場合
全ての生産要素をn倍したときの産出量が「nの2乗×Y」なので、2次同次関数となります。
生産関数がN次同次関数でN>1なら「収穫逓増」なので、この場合は収穫逓増と判断できます。
さらに詳しく
生産関数「Y=K×L」で簡単に考える
全ての生産要素を2倍したら「2K×2L」となり、産出量が「2の2乗×Y」でイコールになった場合
「2の2乗=4」なので「4Y=2K×2L」
生産要素を2倍にすると、産出量が2倍を上回って効率が良い状態(収穫逓増)