価格や消費量のデータから個人の効用関数を求めようとする「顕示選好理論」
- 顕示選好(理論)とは?
- 顕示選好の弱公理(弱公準)
- 弱公理(弱公準)と矛盾しているグラフ
- 顕示選好の強公理(強公準)
初心者には意味がよくわからない顕示選好の原理を簡単にまとめました。
顕示選好理論とは?

(Wikipediaより・ポール・サミュエルソン)
顕示選好理論(顕示選好原理)とは
ある人の消費行動を観察すれば、その人の選好順序(好き嫌いの順番)が求められると考えた理論。経済学者ポール・サミュエルソンによって創始された。
「顕示選好」は、その人の消費行動から明らかになる好みの順序(効用の大小関係)のこと。
顕示は、はっきり示す・明らかにする、という意味。
これまで
ミクロ経済学の範囲では、効用関数→無差別曲線→最適消費点(効用最大化)という順番で求めてきました。
ポイント
これを、最適消費点(効用最大化)から逆に求めることは出来るのではないか?(最適消費→無差別曲線→効用関数)と考えたのが始まりです。
というのも、個人の好き嫌い(効用関数)は、その人にしか分かりません。そこで、市場のデータを集めて分析することで、遡って個人の効用関数を求めようと考えました。
こうして経済学者サミュエルソンにより始まったのが、顕示選好理論です。
サミュエルソンは、その人の消費行動(価格・消費量のデータ)を見れば、そこから個人の効用関数(好き嫌い)を求めることが出来るはずだ、と考えました。
例えば
X財・Y財の2つがある場面を考えてみましょう。
Aさんには2つの選択肢があります。
- 選択肢①:(X財3個, Y財5個)
- 選択肢②:(X財2個, Y財6個)
Aさんの所持金(予算)は十分にあり、どちらの選択肢も選ぶことが出来ます。
この時
- Aさんは、選択肢①を選んだとします
すると「Aさんはどちらも選べる状況だったけど、選択肢②ではなく選択肢①を選んだ」という事実が残ります。


注意ポイント
「選択肢②ではなく選択肢①を選んだ」という事実が残りましたが、これは「Aさんが選択肢②よりも選択肢①を好んでいる」という事を意味していません。
つまり
「選択肢②ではなく選択肢①を選んだ」は、「選択肢②よりも選択肢①を好んでいる」とイコールではない
「選択肢①を選んだ」以上の意味はなく、本来なら好き嫌いまでは分からないのです。
しかし
これを選好順序(好き嫌いの順番)で考えると、話が変わります。
- 「選択肢②ではなく選択肢①を選んだ」は「選択肢①>選択肢②」です。
- 「選択肢②よりも選択肢①を好んでいる」は「選択肢①>選択肢②」です。
「選択肢①>選択肢②」は、「どちらも選べる状況なら、選択肢②ではなく、選択肢①を選ぶ」という意味です。普通は好きな方を選ぶので「選択肢①>選択肢②」という選好順序になります。
さきほど「”選択肢①を選んだ”以上の意味はなく、本来なら好き嫌いまでは分からない」と書きました。しかし、どちらにせよ、選好順序は同じになります。
まとめると
- 「選択肢②ではなく選択肢①を選んだ」は、「選択肢②よりも選択肢①を好んでいる」とイコールではない
- しかし、どちらの選好順序も「選択肢①>選択肢②」となる
つまり「選択肢②ではなく選択肢①を選んだ」を「選択肢②よりも選択肢①を好んでいる」と同義と考えて差し支えない。
もっと詳しく
以上より、「選択肢②ではなく選択肢①を選んだ」は、好き嫌い(効用)の大小関係を示している(顕示している)ことになる。
このとき、消費者の行動(選択肢①を選んだ)から、明らかになった好き嫌い(効用の大小関係)を「顕示選好」と呼ぶ。


こうした考えのもとで、市場(価格・消費量)のデータから、個人の選好(好き嫌い)を求めるのが顕示選好理論です。
顕示選好理論の背景が分かったところで、次に重要な2つの仮定を見ていきます。
顕示選好理論の2つの仮定
- 顕示選好の弱公理(弱公準)
- 顕示選好の強公理(強公準)
顕示選好理論は、需要曲線(需要関数)が上の2つの仮定を満たしていると考えています。特に弱公理(弱公準)が話題になることが多いです。
顕示選好の弱公理(弱公準)・WARP

例えば
- アイスコーヒーとガムシロップの組み合わせ
Aさんは甘党です。ブラックコーヒーには、いつでもガムシロップを2つ使っていました。
このとき、顕示選好は「アイスコーヒー1つ・ガムシロップ2つ」です。
なので
Aさんにアイスコーヒーとガムシロップを提供すれば「アイスコーヒー1つ・ガムシロップ2つ」という行動をします。
何の理由もなく「アイスコーヒー1つ・ガムシロップ1つ」というのはあり得ない、というのが弱公準(弱公理)です。
この弱公理(弱公準)を仮定することで、次のことが言えます。
2財について
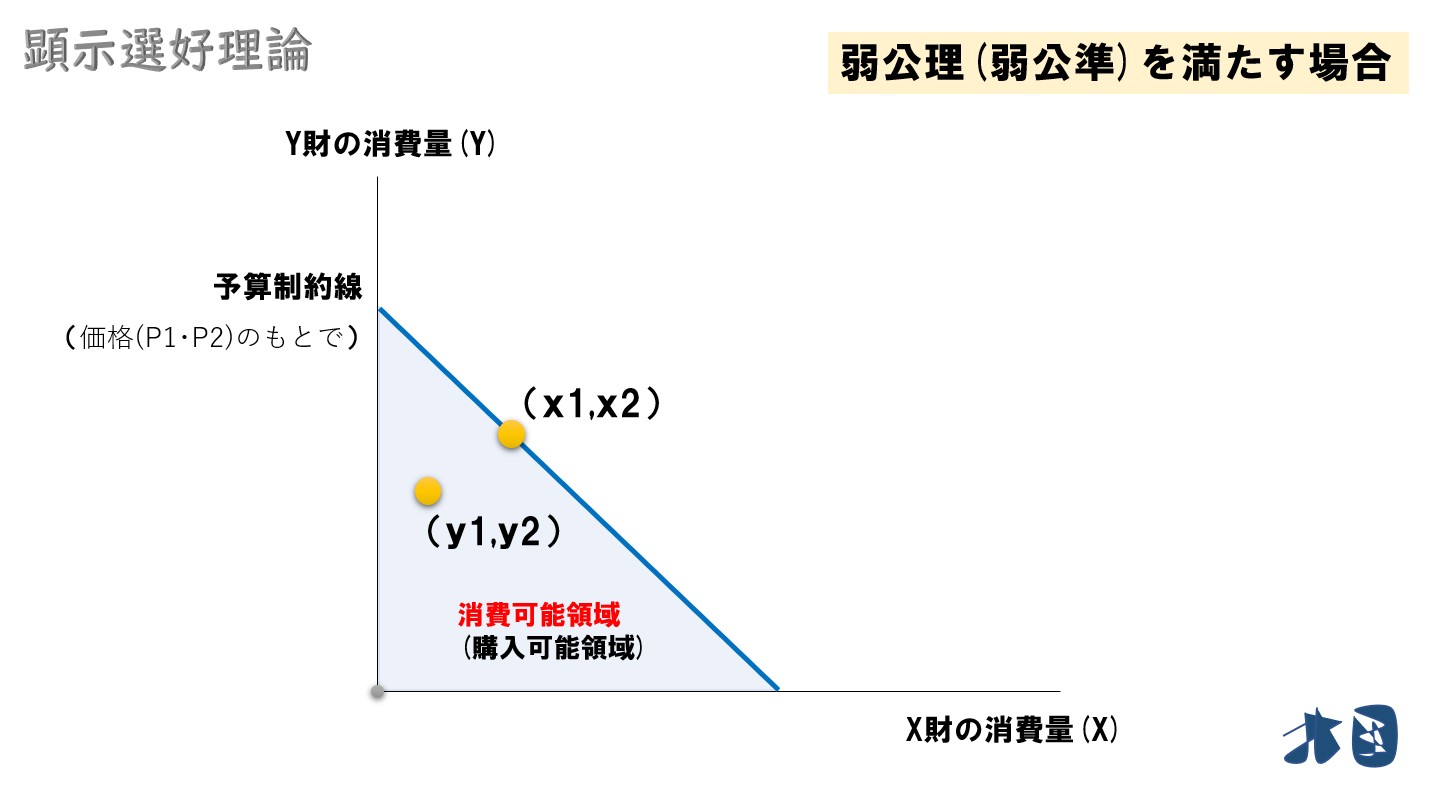
- 価格(P1・P2)では、消費の組み合わせは(x1,x2)
- 価格(P3・P4)では、消費の組み合わせは(y1,y2)
このとき、顕示選好が「P1x1+P2x2」≧「P1y1+P2y2」となるなら、「P3y1+P4y2」≧「P3x1+P4x2」は成立しない。
この話は、グラフで見る方が分かりやすいので、グラフを見てみましょう。
グラフで確認する
価格(P1・P2)では(x1,x2)が最適消費点となり、効用最大化が実現します。(y1,y2)は、予算内なので選択可能ではありますが、選ばれませんでした。
次に
価格(P3・P4)の場合を見ます。
右上にある(x1,x2)の方が効用が高いと判断できるため、価格(P3・P4)のもとで新しく引かれた予算制約線で考えても(x1,x2)が選ばれます。
つまり(y1,y2)>(x1,x2)となっている「P3y1+P4y2」≧「P3x1+P4x2」は成立しません。
仮に(y1,y2)を選ぶなら
- 予算の都合で、顕示選好の大きい方が購入できないことを意味する
グラフで見ると
価格(P3・P4)のもとで新しく引かれた予算制約線では(x1,x2)が購入できません。したがって(y1,y2)が選ばれます。
これなら「P3y1+P4y2」≧「P3x1+P4x2」は成立させず※に(y1,y2)を選ぶことが出来ます。
※そもそも(x1,x2)が選択できないため「P3y1+P4y2」≧「P3x1+P4x2」は成立しえない。


「顕示選好の弱公理(弱公準)」を定義すると、代替効果は負であること、需要関数は0次同次関数になること、などを導くことが出来ます。難しい数学の証明になるので省略します。
おまけ
顕示選好の問題で良くあるのが「グラフを見せて、顕示選好の弱公準(弱公理)と矛盾しているものは?」というパターンです。
念のため、矛盾しているケースも紹介しておきます。
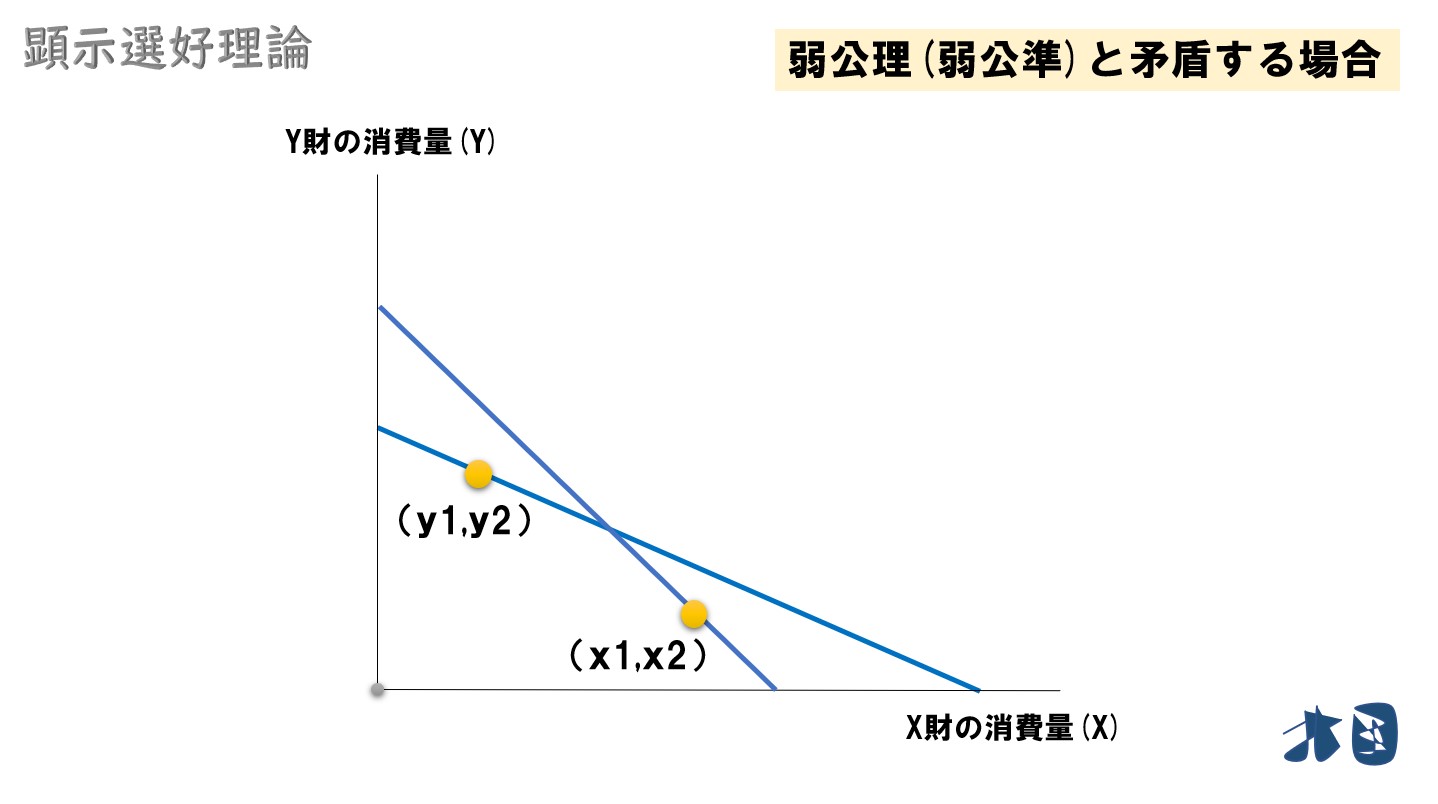
こちらは典型的な矛盾例です。
先ほど同じく、順番に見ていけば簡単です。
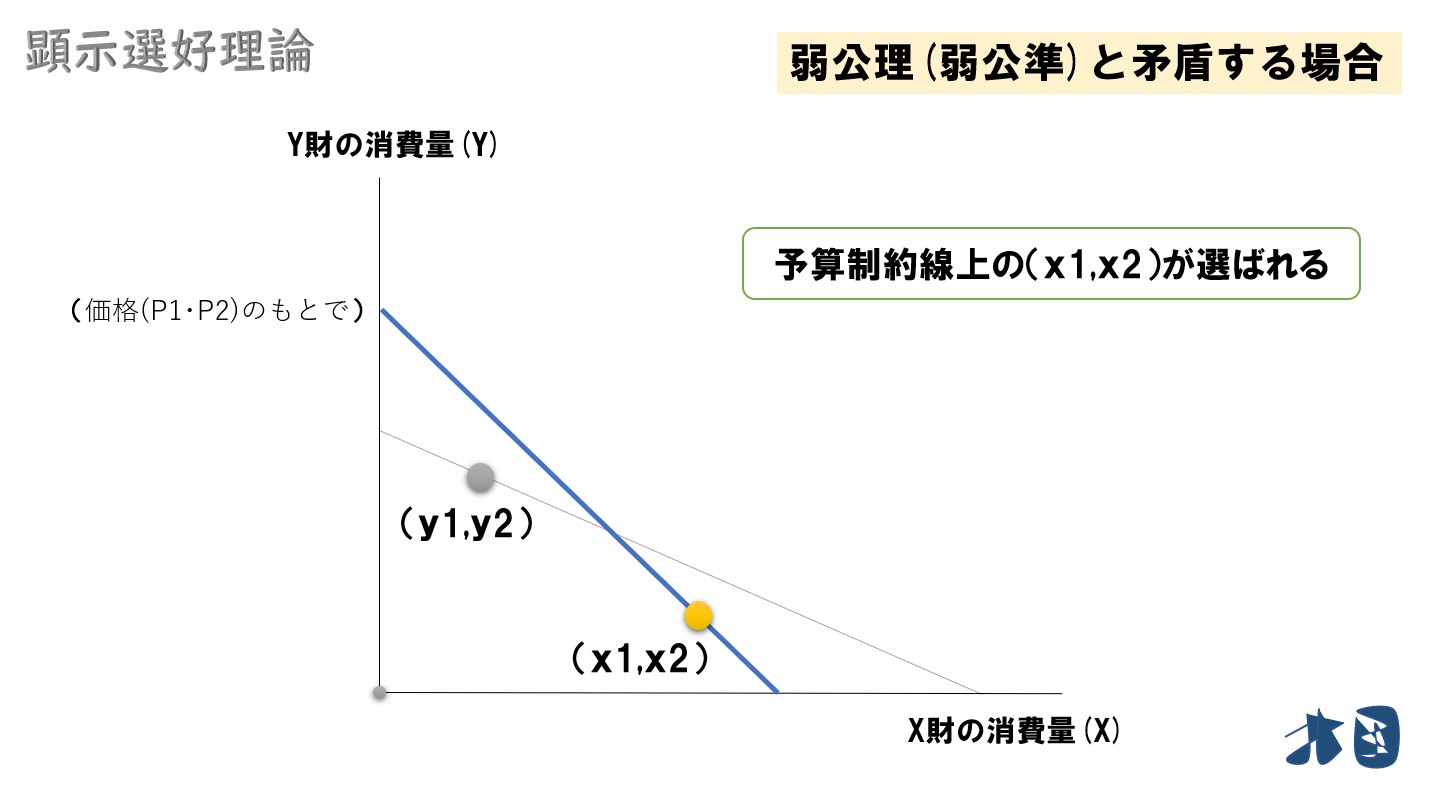
まずは
予算制約線上の(x1,x2)が最適消費点となります。
次に
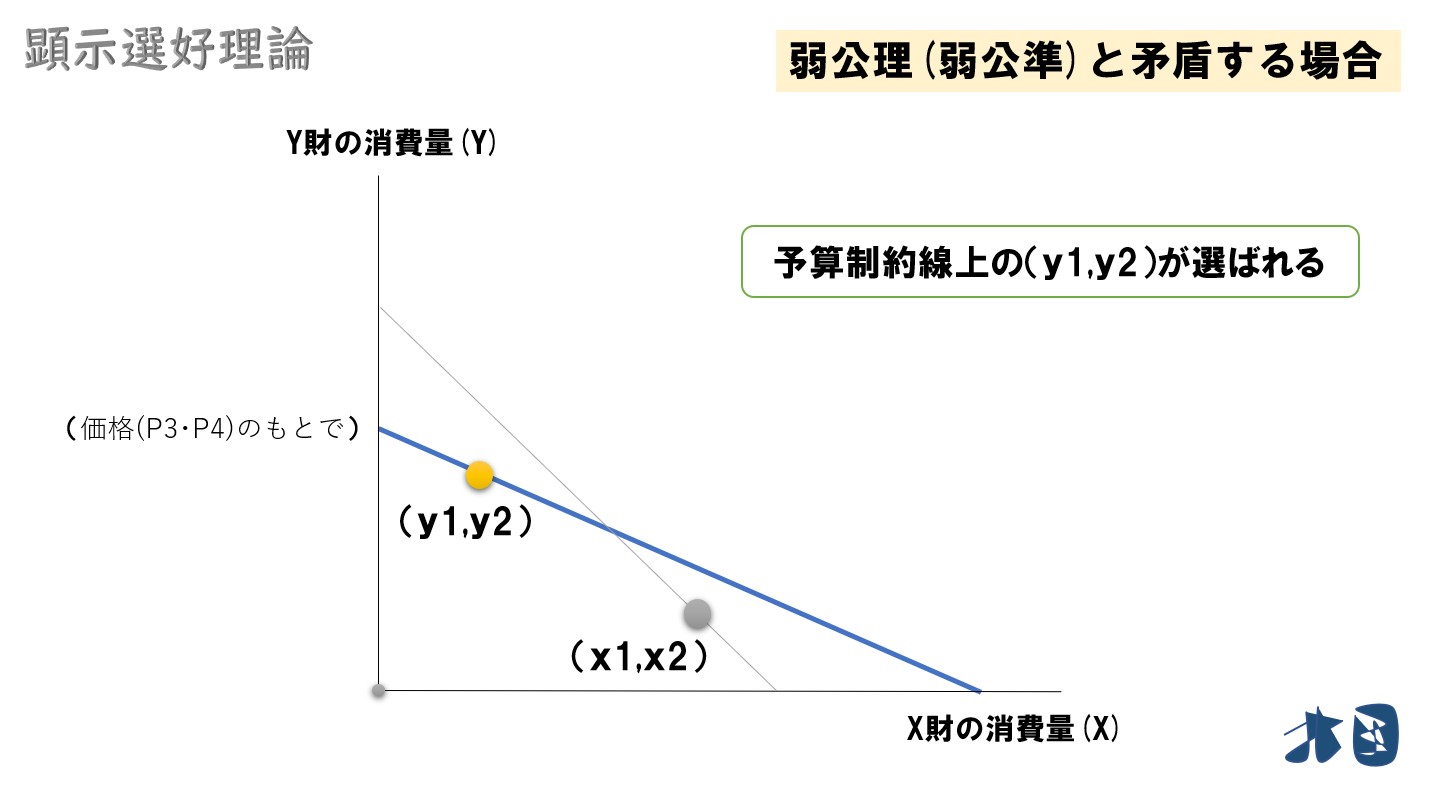
予算制約線上の(y1,y2)が最適消費点となります。
矛盾点
最初に、顕示選好が(x1,x2)>(y1,y2)と分かったのに、次の場面で(y1,y2)>(x1,x2)となっているのは矛盾。
もっと詳しく書けば、「P1x1+P2x2」≧「P1y1+P2y2」となっているのに、次で「P3y1+P4y2」≧「P3x1+P4x2」が成立してしまっているため矛盾。


顕示選好の強公理(強公準)・SARP

例えば
- アイスコーヒーとガムシロップの組み合わせ
Aさんは甘党です。ブラックコーヒーには、いつでもガムシロップを2つ使っていました。
このとき、顕示選好は「アイスコーヒー1つ・ガムシロップ2つ」です。
次に
ガムシロップが1つしかなかった時に、Aさんは「アイスコーヒー1つ・ガムシロップ1つ」を選択していました。
このとき、顕示選好が「アイスコーヒー1つ・ガムシロップ1つ」>「アイスコーヒー1つ・ガムシロップ0個」と示されました。
まとめると
Aさんの顕示選好は「①>②」「②>③」と示されました。
- ①「アイスコーヒー1つ・ガムシロップ2つ」
- ②「アイスコーヒー1つ・ガムシロップ1つ」
- ③「アイスコーヒー1つ・ガムシロップ0個」
以上より、間接的に顕示選好が「①>③」と示されました。
なので
Aさんにアイスコーヒーとガムシロップを提供すれば「アイスコーヒー1つ・ガムシロップ2つ」という行動をします。
何の理由もなく「アイスコーヒー1つ・ガムシロップ0個」という選択はあり得ない、というのが強公準(強公理)です。もちろん「アイスコーヒー1つ・ガムシロップ1つ」という選択もあり得ません。
この強公理(強公準)を仮定することで、次のことが言えます。
消費者の消費行動から
- 無差別曲線を導くことが出来る
- 最適消費(効用最大化)となる消費の組合わせを見つけることが出来る
この証明はKen Urai May 19, 2004の55Pから確認できます。
おまけ
強公理(強公準)の話をすると、専門的すぎて私の手には負えないレベルになるのでコレくらいで説明を終わりにします。研究者以外の人は上に書いたようなことが分かっていれば十分です。
不可能性定理で有名なアローが、一定の条件の下では、弱公理と強公理が同値だと証明※していますが、弱公理と強公理の数学的な関係などは、現在も結論が出ているわけではありません。
※「Kenneth J. Arrow; "Rational Choice Functions and Orderings,"Economica, Vol.26, May 1959」ネットで検索しても有料論文しか出てきません。