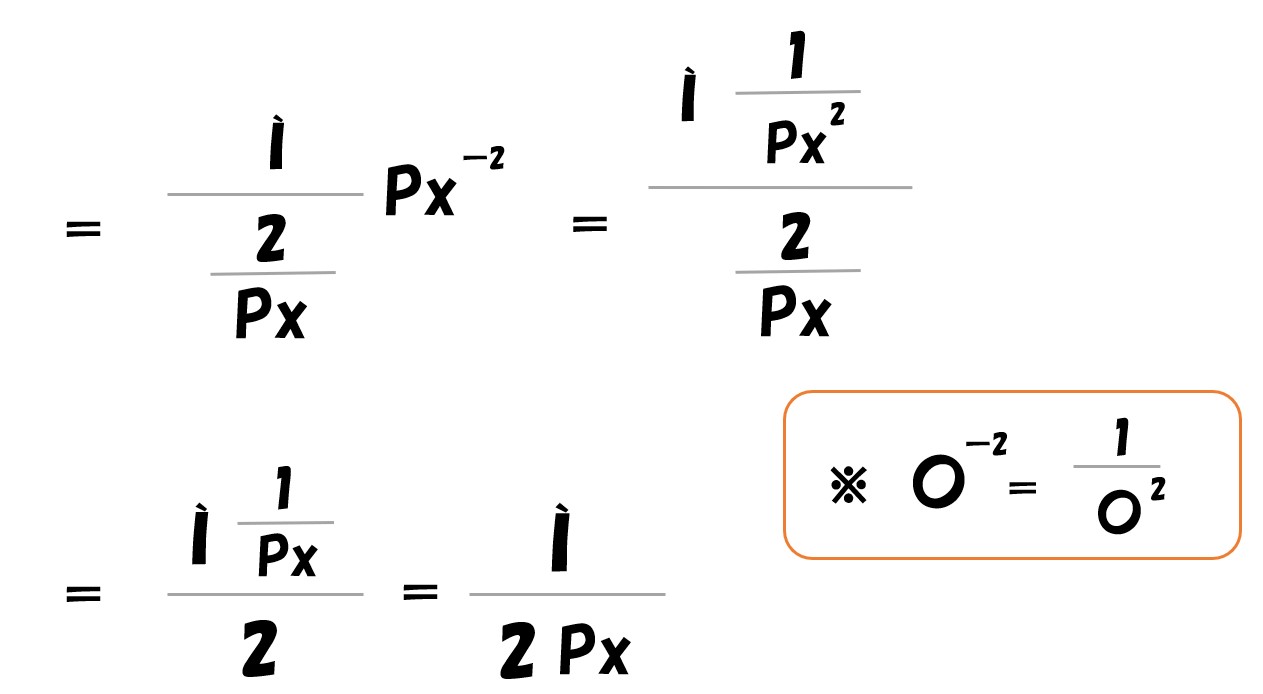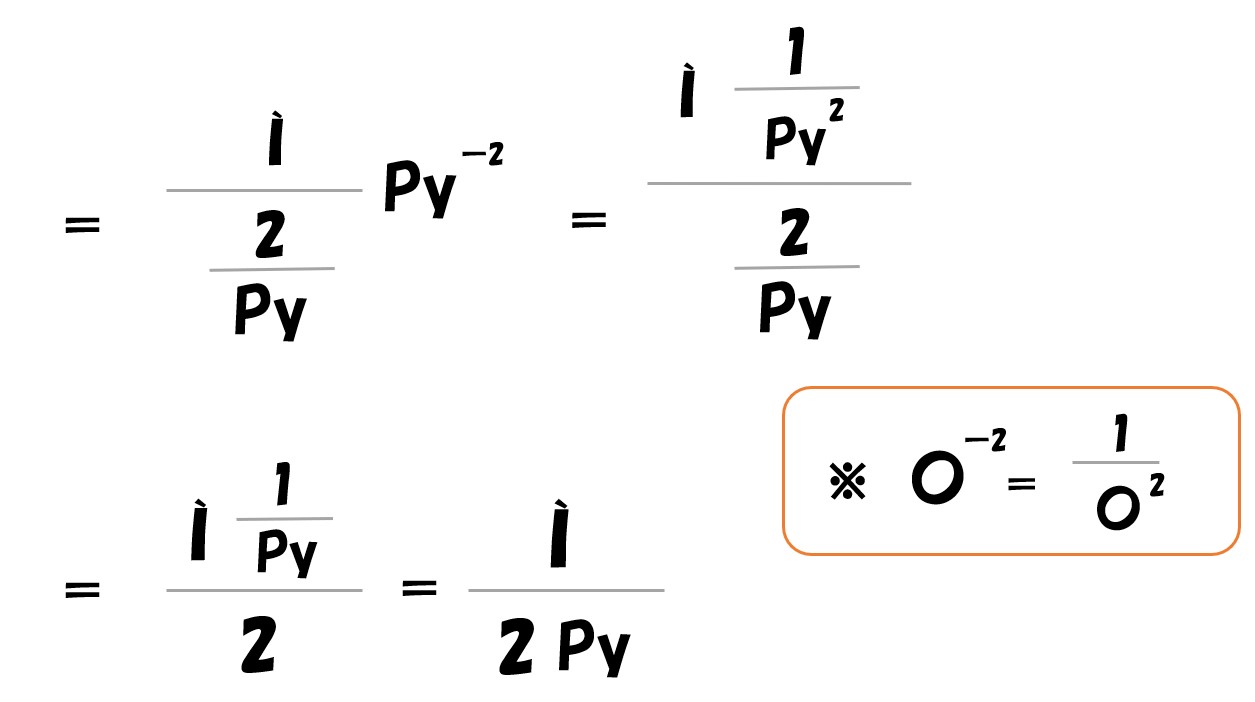間接効用関数(V)と需要関数(D)の関係を示した「ロイ(ロワ)の恒等式」
- ロイ(ロワ)の恒等式の意味は？
- ロイ(ロワ)の恒等式の証明
現実のデータ分析でも応用される「ロイ(ロワ)の恒等式」を分かりやすく簡単に解説していきます。
ロイ(ロワ)の恒等式とは？
(Wikipediaより･ルネ･ロイ)
ロイ(ロワ)の恒等式とは
間接効用関数(V)を価格･所得で偏微分して、それぞれ分子分母にすれば需要関数(D)になることを示したもの。
恒等式は変数(X)がどんな値でも式が成り立つもの。方程式は「X＝1」などのように答えが限定的なもの。
文章で見てもピンと来ないので、公式で見てみましょう。
ロイ(ロワ)の恒等式
需要関数(D)＝「間接効用関数(V)を価格で偏微分」／「間接効用関数(V)を所得で偏微分」
通常の間接効用関数の求め方
- 「需要関数(D)」
↓ - 「間接効用関数(V)」
ロイ(ロワ)の恒等式により「間接効用関数(V)」→「需要関数(D)」と遡って求めることも可能だと示されました。
ミクロ経済学の知識を使えば、効用関数(U)→需要関数と求めることが可能です。
しかし
個別の効用関数(U)から分析していくのは手間が多く、現実的ではありません。
一方で、財の価格(P)や所得(I)のデータは手に入れやすく、そこから間接効用関数(V)を推定して需要関数を求めた方が簡単に処理が出来る場面があります。
ロイ(ロワ)の恒等式は、その橋渡しをしているという点で非常に重要な役割を果たしているわけです。
ロイ(ロワ)の恒等式の証明
X財･Y財の2財を考えます。
- X財の価格=Px
- Y財の価格=Py
- X財の消費量=x
- Y財の消費量=y
- 予算制約線(Ì)＝xPx + yPy
効用関数(U)＝xyのとき、需要関数(D)＝「間接効用関数(V)を価格で偏微分」／「間接効用関数(V)を所得で偏微分」が成り立つことを証明する。
まず
効用関数(U)＝xyから、需要関数(D)を計算します。
- X財の需要関数「x＝(Py／Px)y」
- Y財の需要関数「y＝(Px／Py)x」
計算方法はこちらで確認する⇒【効用関数】限界効用･種類･需要関数の求め方を簡単に解説！
この後の流れ
この需要関数(D)を効用関数(U)に代入すると間接効用関数(V)が求められます。ただし、ロイ(ロア)の恒等式では価格(P)と所得(Ì)が必要になるため、需要関数(D)に所得(Ì)が含まれるように計算します。
step
1「予算制約線(Ì)＝xPx + yPy」に需要関数(D)を代入する
①「x＝(Py／Px)y」を代入する
②「y＝(Px／Py)x」を代入する
需要関数(D)は、所得(Ì)を含めると「x＝Ì／2Px」「y＝Ì／2Py」を表せる。
step
2間接効用関数(V)を求める
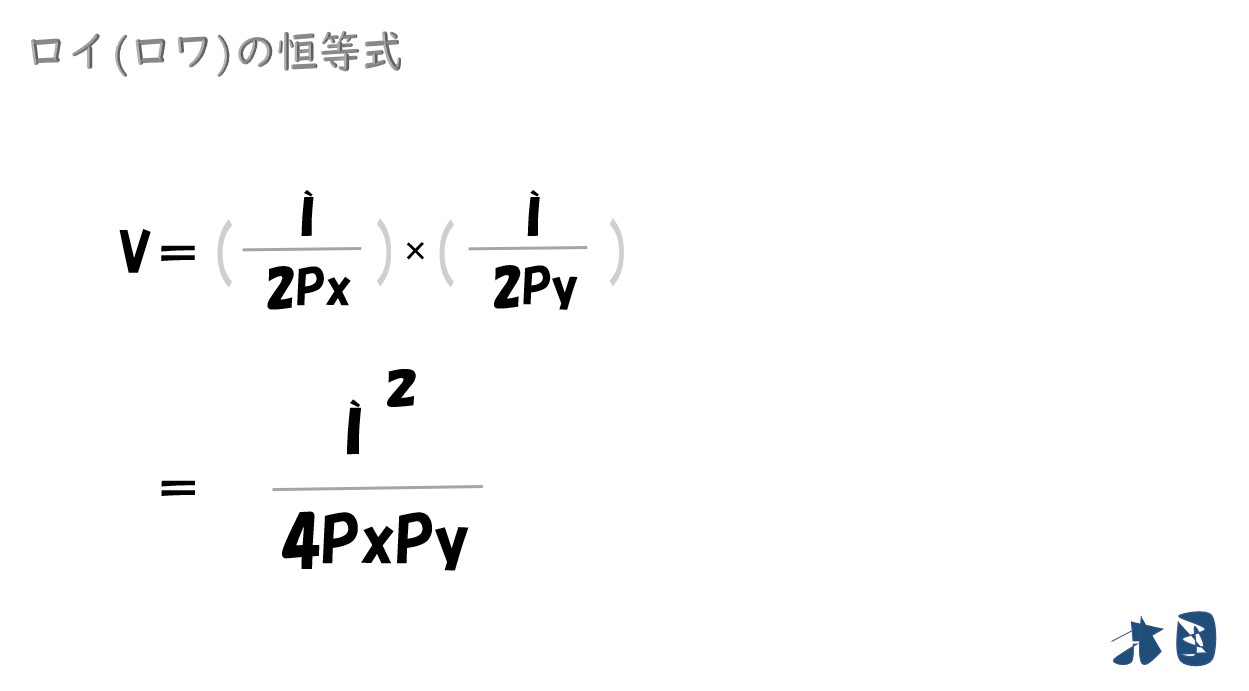
「効用関数(U)=xy」に 所得(I)を含んだ需要関数(D)を代入する
ポイント
以上より「効用関数(U)＝xy」のときの、間接効用関数(V)は「Ìの2乗／4PxPy」と表すことが出来る。
step
3間接効用関数(V)を価格と所得で微分する
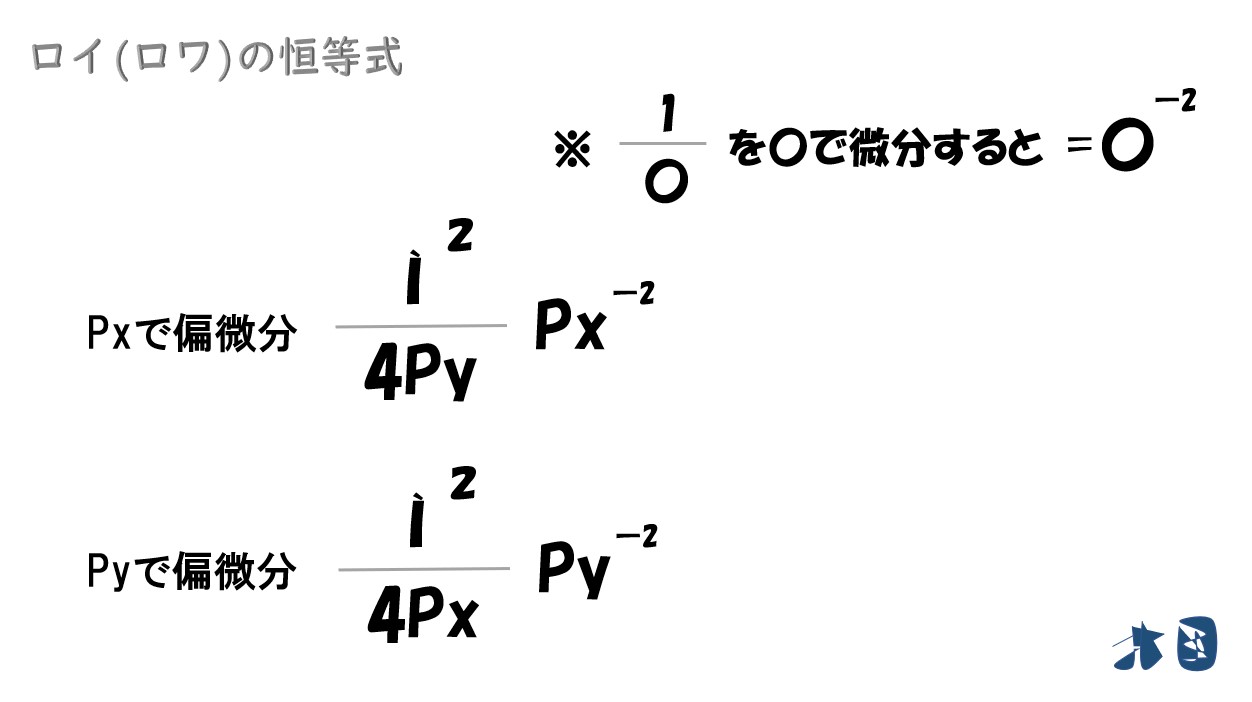
① 価格(Px･Py)で微分する
「1／x」は「xの－1乗」です。これをxで微分すると「xの－2乗」となります。分数の微分の計算結果は普通の数字の微分とは異なるので注意。
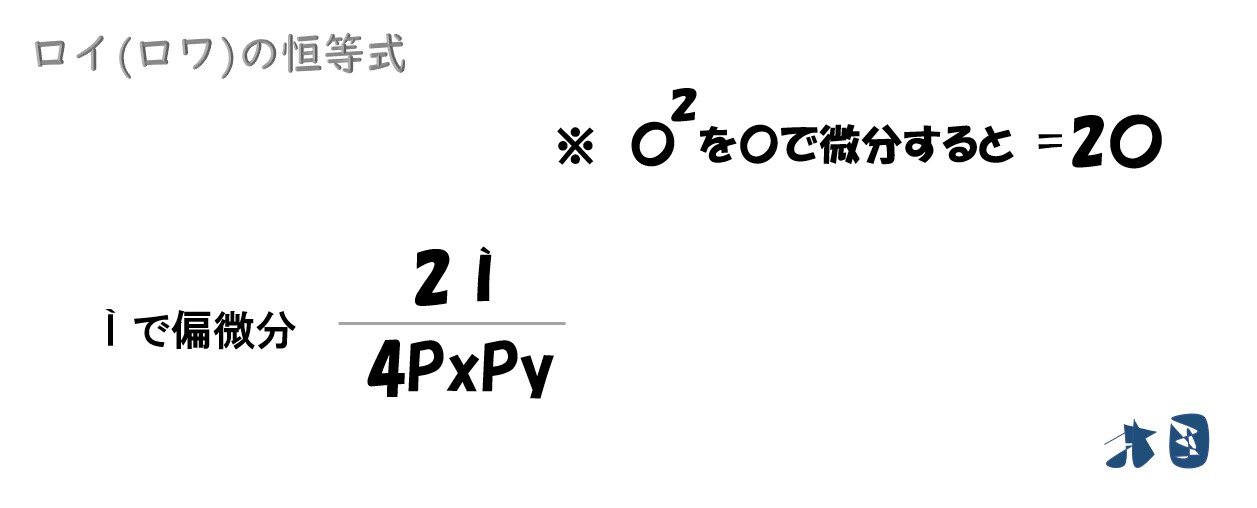
② 所得(Ì)で微分する
step
4分子分母で確認する
① Pxで微分した時の間接効用関数
「間接効用関数(V)を価格(Px)で偏微分／所得(Ì)で偏微分」＝「Ì／2Px」
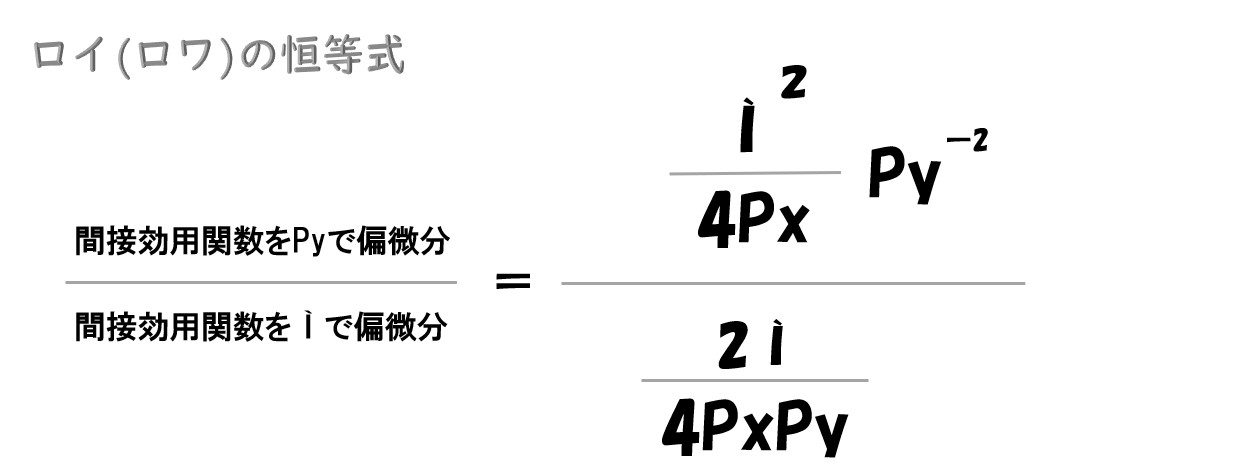
② Pyで微分した時の間接効用関数
「間接効用関数(V)を価格(Py)で偏微分／所得(Ì)で偏微分」＝「Ì／2Py」
ポイント
以上より「間接効用関数(V)を価格で偏微分」／「間接効用関数(V)を所得で偏微分」の値は
- 「Ì／2Px」
- 「Ì／2Py」
［Step1］で計算した、所得(Ì)を含んだ需要関数(D)と比べてみます。
所得(Ì)を含めた需要関数(D)は「x＝Ì／2Px」「y＝Ì／2Py」
ポイント
見ての通り「間接効用関数(V)を価格･所得で偏微分して分子分母にしたもの」と「需要関数(D)」が同じになるため、題意は証明された。
と需要関数(D)の関係を示した「ロイ(ロワ)の恒等式」 ロイ(ロワ)の恒等式の意味は？ ロイ(ロワ)の ...){kind=link}