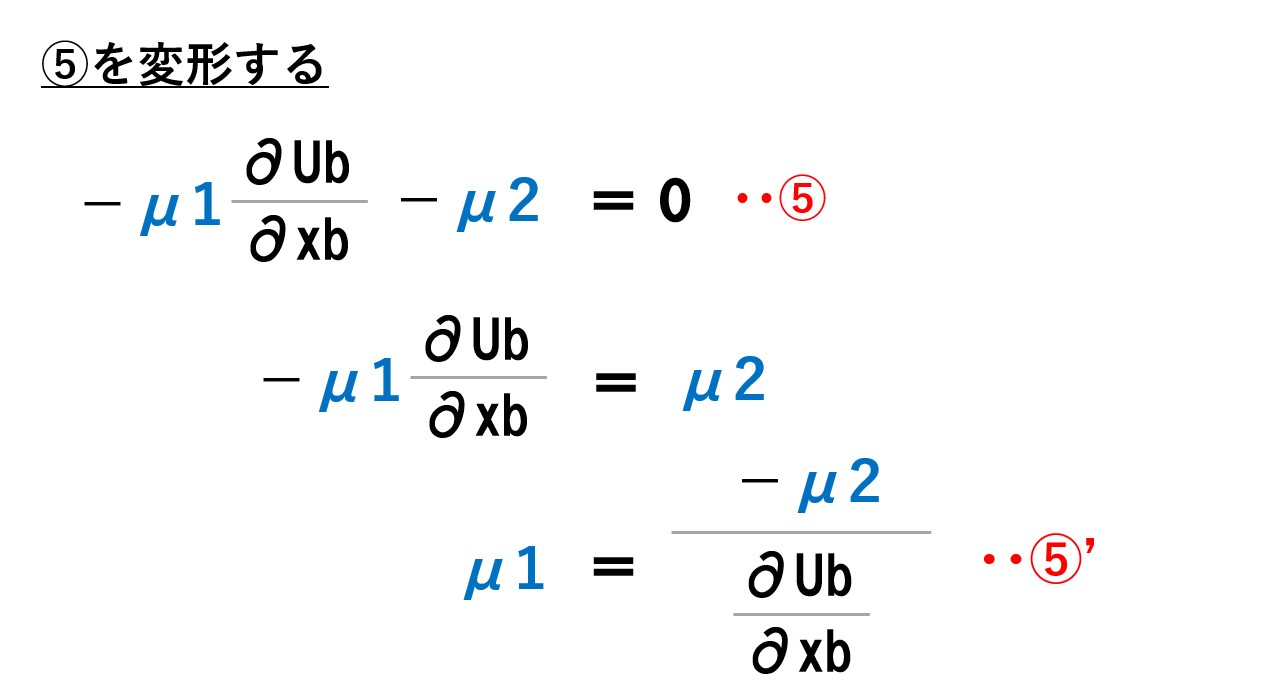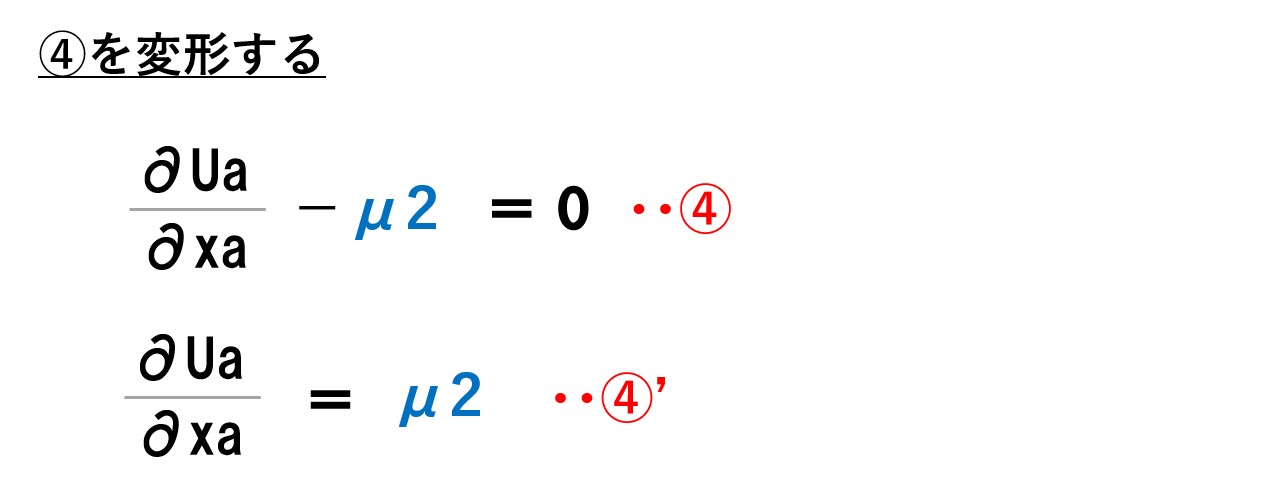公共財の最適供給とサミュエルソン条件について、教科書よりは若干細かくまとめています。
- 公共財の最適供給
- 限界評価(限界便益)
- 生産可能性フロンティア(PPF)
- サミュエルソン条件
- サミュエルソン条件の数学的な導出
- 計算問題(最適供給量を求める)
最後に簡単な例題(計算問題)も解きます。
公共財の最適供給
はてな
公共財の供給について、経済学では次の2つのポイントに注目する。
- どれくらいの量を供給するか
- 費用をどのように負担してもらうか
この記事内では「公共財はどれくらいの量を供給すればよいか」を考える。

公共財って、あるのが当たり前だと思っていたけど、どれくらいの量を供給するのが良いのかな?
分析のやり方が2つあるよ。順番に見ていこう!

「公共財をどれくらい供給すればよいか」を分析するために、次の2つの分析方法があります。
- 限界評価(限界便益)を使ったやり方(部分均衡分析)
- 生産可能性フロンティアを使ったやり方(一般均衡分析)
限界評価を使った分析の方がイメージしやすいので、はじめに紹介します。次にフロンティアを使ったやり方を説明します(中級のミクロ経済学の教科書では、どちらも紹介されているので順番に理解していきましょう!)
限界評価を使った分析(部分均衡分析)
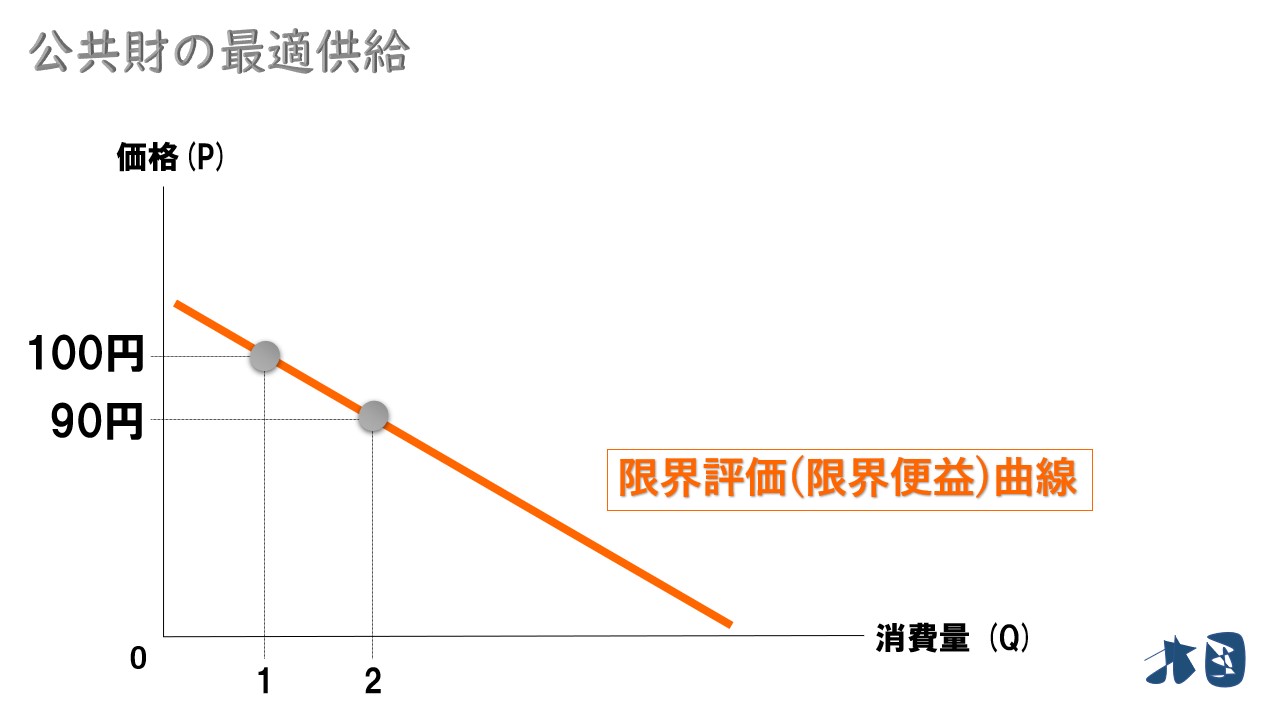
限界評価(限界便益)とは
財を消費したときに得られる効用を、金額的に評価したもの(厳密には「財を1単位消費したときに得られる効用の増加分を、金額的に評価したもの」)。

牛さん「限界効用」と「限界評価」って同じじゃないの?
同じものと考えて問題ないけど、厳密には違うんだ。

もともと「限界効用」には、金額的な意味合いはありません。「財を消費して満足度が増えた=限界効用」ですが、「限界評価・限界便益」といった場合には「財を消費して満足度が増えた←これを金額換算したもの=限界評価・限界便益」という意味になります。分からなければ無視して問題ありません。
ここで、もう1つポイントがあります。
ポイント
「限界評価・限界便益」はそのまま「公共財の需要」を意味する。
例えば
公共財を1つ消費するときに、100円分効用が得られるとする。このとき、消費者は最大で100円支払ってもいいと考えるはずです。
ここで、ふつうは同じものを消費し続けると飽きるので満足度が減っていきます。同じ公共財の2個目を消費すると90円分の効用しか得られません。これをグラフにすると・・。

イメージ出来ました。
これをイメージ出来れば、つぎに社会全体の限界評価を考えよう。

ポイント
社会にいる人の「限界評価・限界便益」を合計すれば、社会全体の「公共財の需要曲線」が作れる。
例えば
Aさん・Bさんの2人がいる社会を考える。
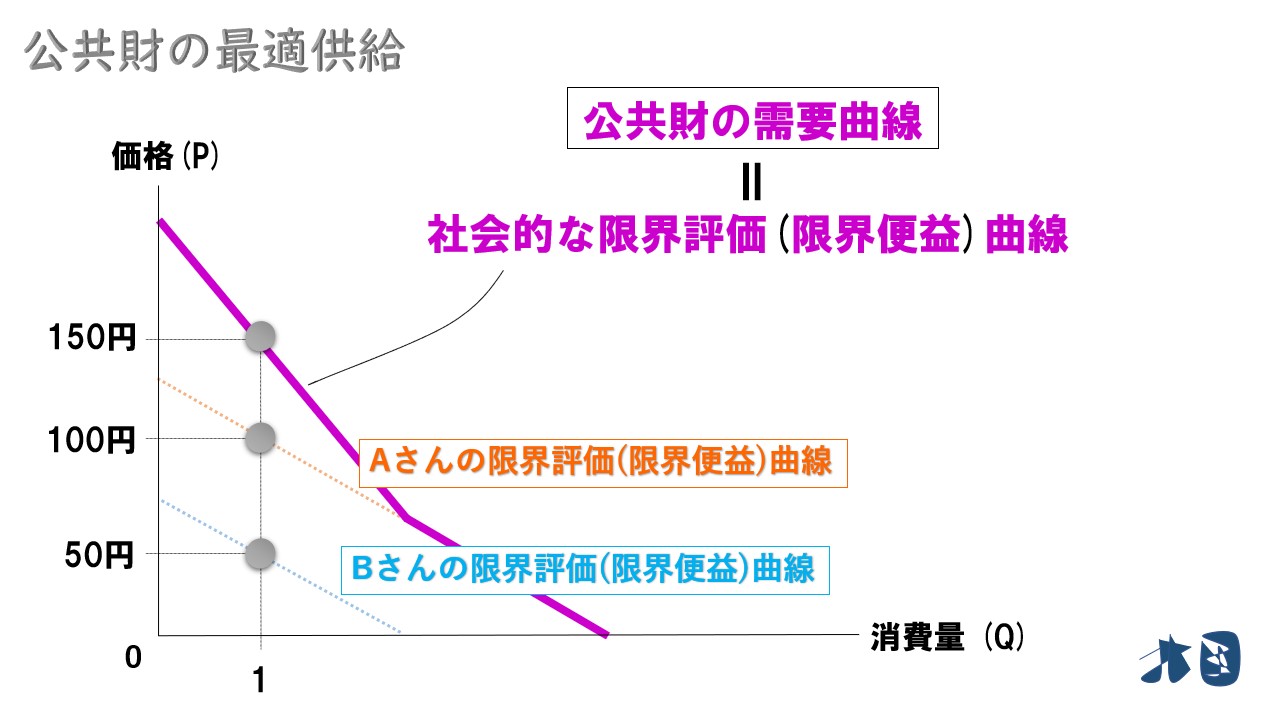
- (Aさん)公共財を1つ消費すると100円の効用が得られる
- (Bさん)公共財を1つ消費すると50円の効用が得られる
ここで、公共財には「同時にたくさんの人が消費できる」という性質(排除不可能性)があることを思い出す(公園とかをイメージしよう)。Aさん・Bさんは公共財1つを同時に消費できます。同時に消費できるので、公共財1つの限界評価(=社会的な限界評価)は「Aさんの限界評価」と「Bさんの限界評価」を単純に足せばOKです。
※仮に、1人しか消費できなければ「AさんとBさんの評価どちらを使えばいいか、平均値をとるか?」などの話になりますが、公共財では、そのようなことを考える必要がありません。
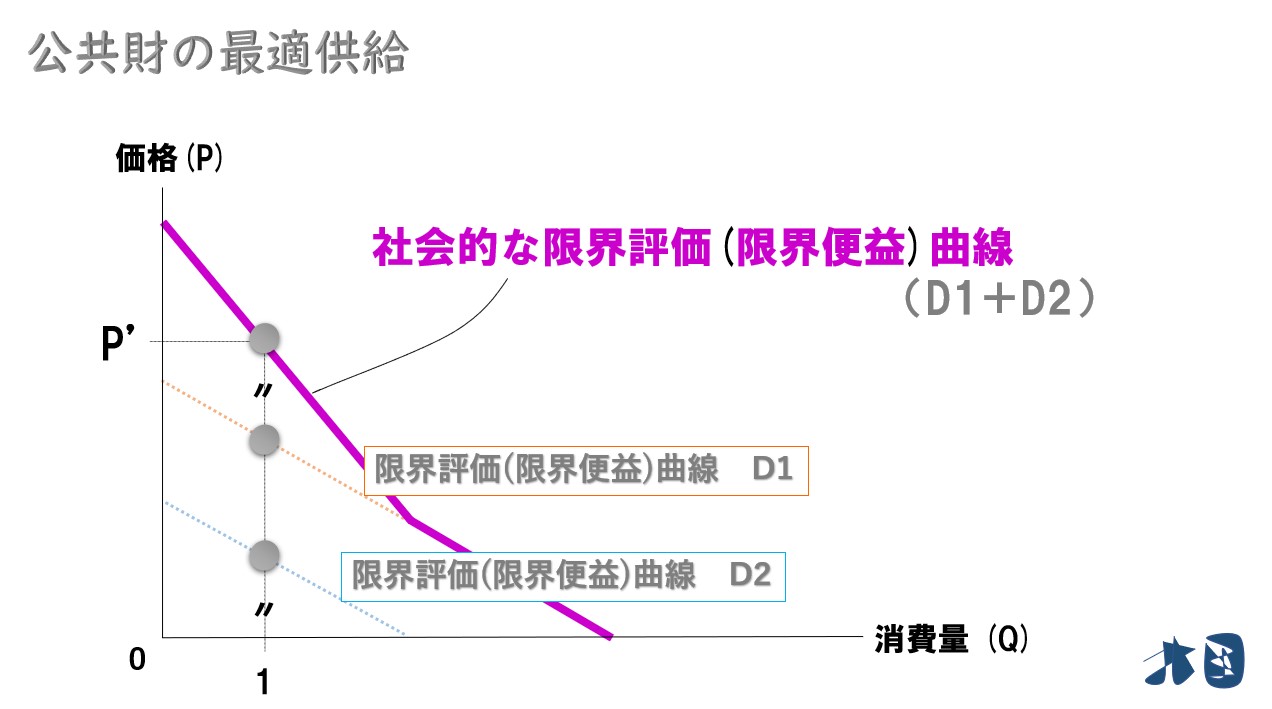
Aさん・Bさんの限界評価の合計は「100円+50円=150円」なので、この社会の「公共財の需要曲線(社会的な限界評価)」を次のように考える。
ポイント
社会にいる消費者の「限界評価の和=公共財の需要曲線(公共財の社会的な限界評価)」
公共財の供給曲線を考える
- ここまでは「公共財の需要曲線」について考えてきました。次に供給を考えます。
(例えば)公園を作るときに土地が必要になります。そのため、公園をたくさん作るほど公園に適した土地を確保するのが困難になるため、公園を作り続けるほど追加の生産コスト(限界費用)が高くなっていきます。これをグラフで見ると・・
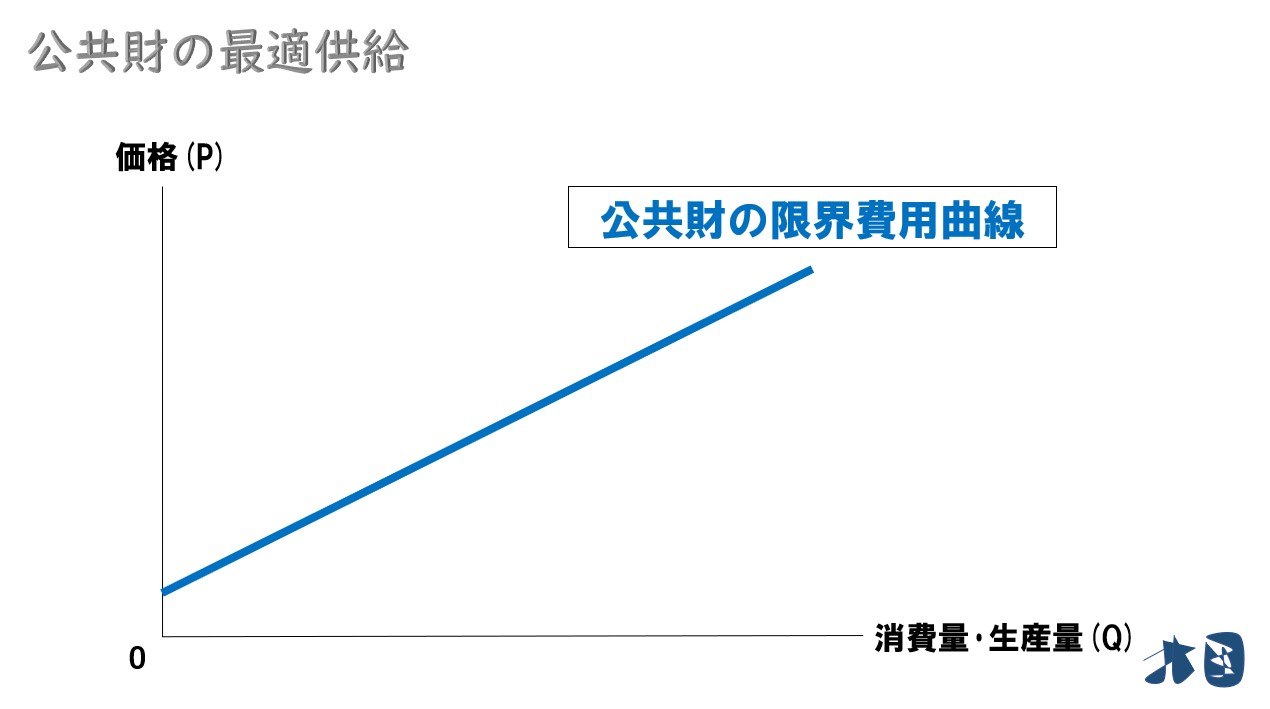

ふつうの限界費用曲線(MC)と同じだね。
うん。それでは次に進みます。

「公共財の需要曲線」と「公共財の限界費用(MC)曲線」が分かれば、あとは簡単です。
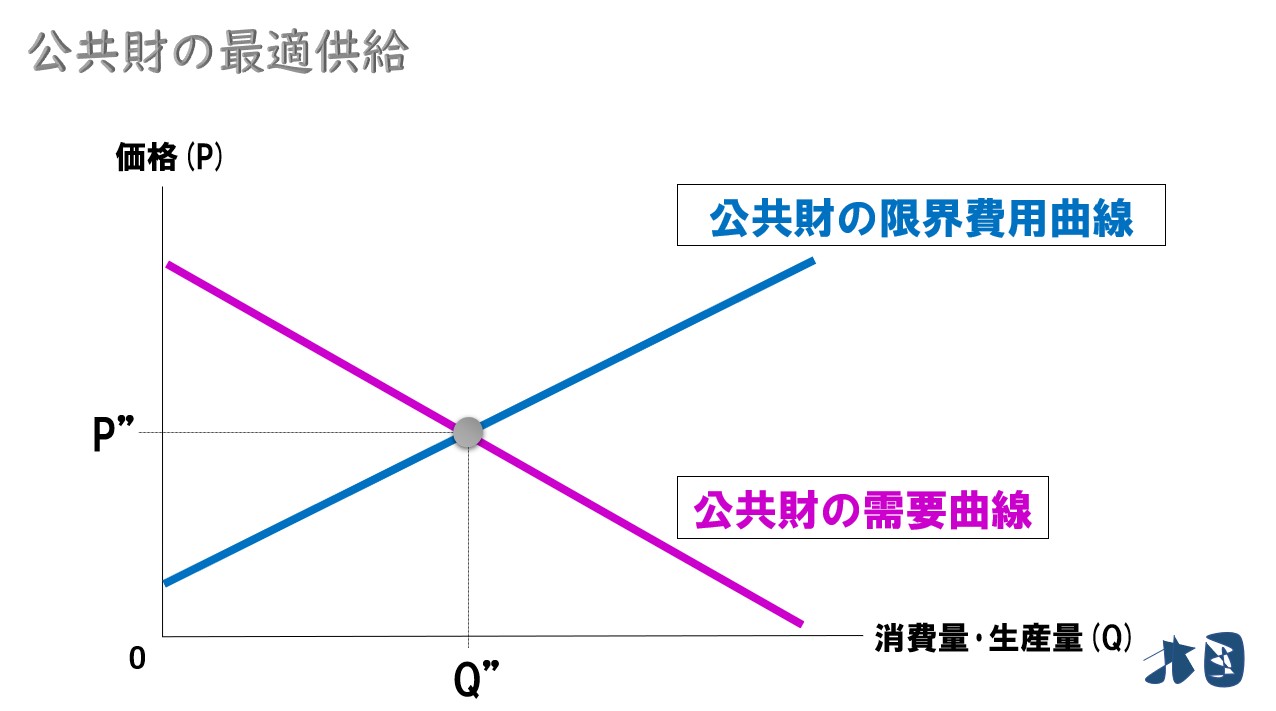
ふつうの「需要曲線」と「供給曲線」の交わるところで均衡になるのと同じです。2つの曲線の交点が「公共財の最適な供給量」となります。
ちなみに上記のような「需給のグラフで分析すること」を「部分均衡分析」と呼びます。※便宜上、需要曲線は右下がりの直線としています。

あっさり終わりました。。
そうだね、意外と簡単な話なんです。

限界評価を使って、グラフで最適な供給量を確認するのは簡単です。
問題になるのは、現実ではこのグラフのように最適な供給量が実現しない(市場が失敗する)ことです。そのあたりの話は「公共財の費用負担をどうするのか?」という問題と関わりがあるので、ここでは割愛します(詳細はリンダールメカニズムの話を参照してください)。
次は、少しレベルアップして生産可能性フロンティアという考え方を使って分析します。
PPFを使った分析(一般均衡分析)とサミュエルソン条件の導出
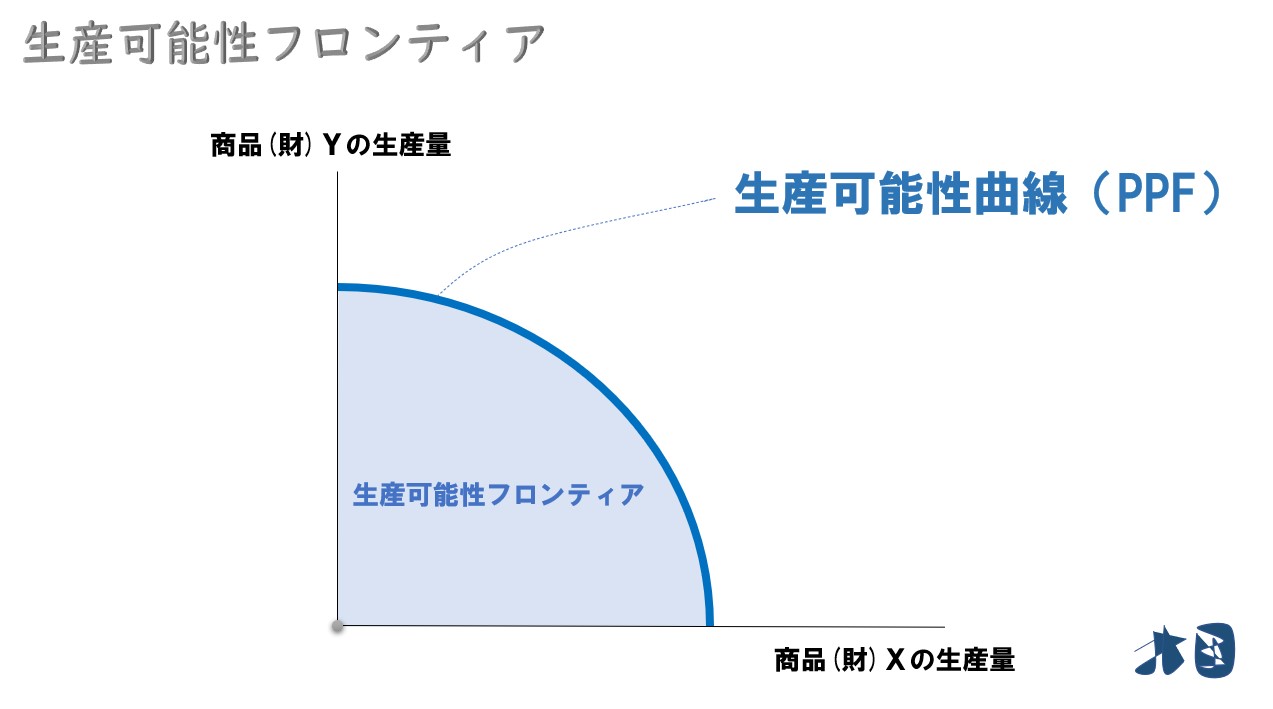
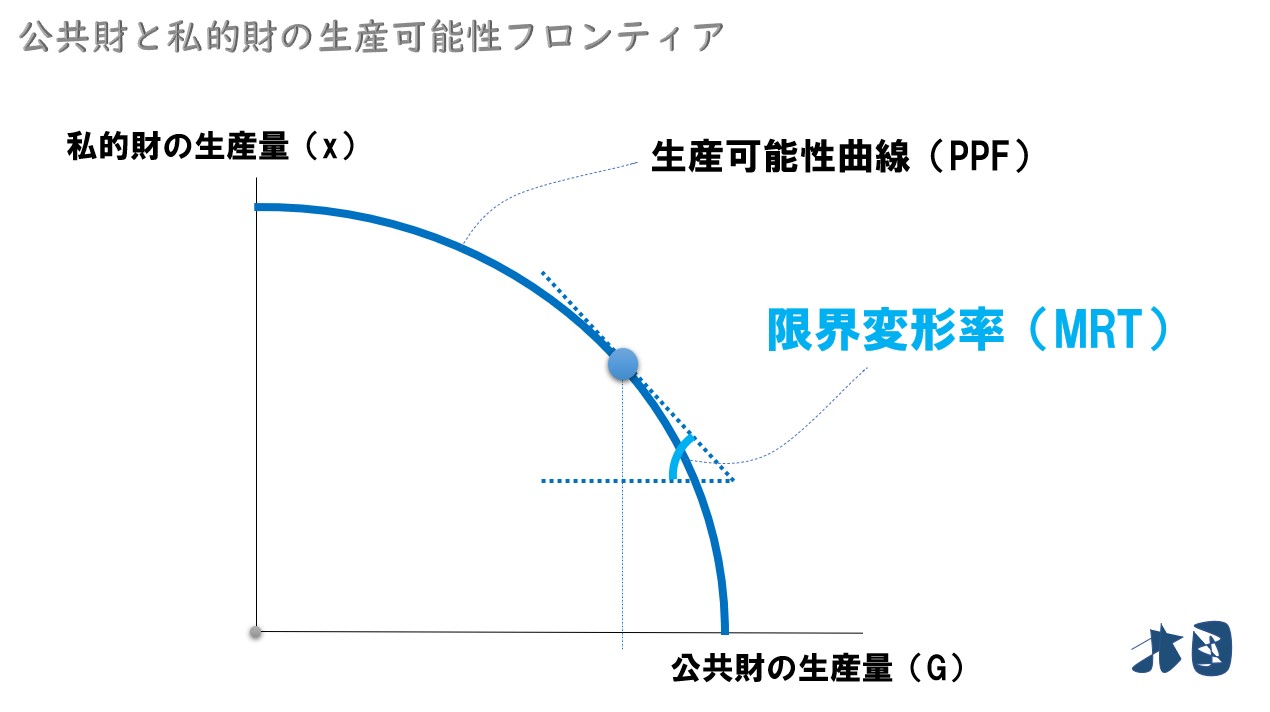
生産可能性フロンティアとは
ある経済主体が保有する資源・技術を用いて、効率的に生産を行ったときに得られる生産物(財)の組み合わせを表した曲線のこと。※Production Possibility Frontierの頭文字をとって通称PPFと略される。

。。。
別記事でまとめているから復習しましょう・・!

【生産可能性フロンティア・限界変形率】グラフを使って理解する
※生産可能性フロンティアは、公共財の分析以外にも「貿易」や「厚生経済学の基本定理の分析」などでも登場するので知っておきましょう。

復習してきました・・!
それでは本題です。

例えば
いま、Aさん・Bさんの2人がいる国を考える。
- この国では「公共財」と「私的財(ふつうの財)」の2財が生産消費されている
- ただし、公共財を生産するためには「私的財」が必要である
- 公共財はAさん・Bさんの2人に便益がある
このとき「公共財」と「私的財」の最適な供給バランスを考える。
現実的な話をすると、最近の新型ウイルスの医療体制(公共財)と自由という財(私的財)をイメージしてみてください。誰もが国家医療という便益を受けるためには、ある程度の自由を制限して感染拡大を抑える必要があります。このバランスをどうするのかを考えます。厳密にはちょっと違いますが、イメージはしやすいと思います。
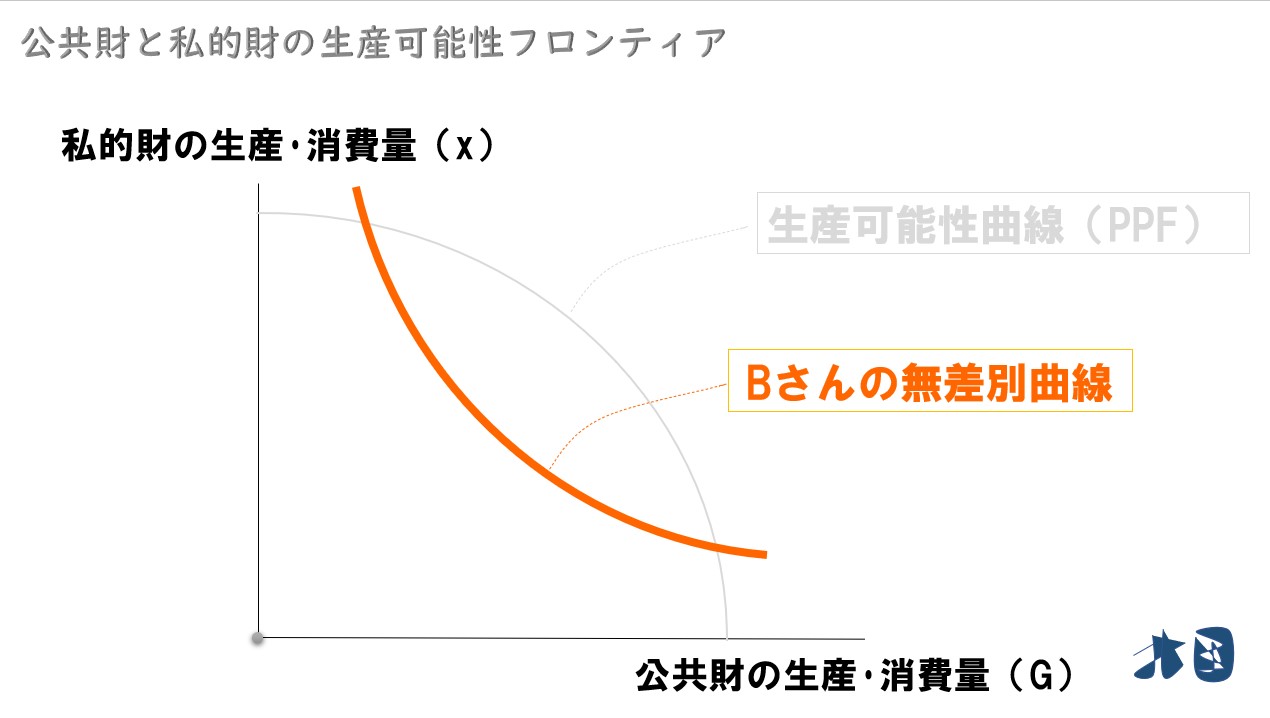
生産可能性フロンティアで考える
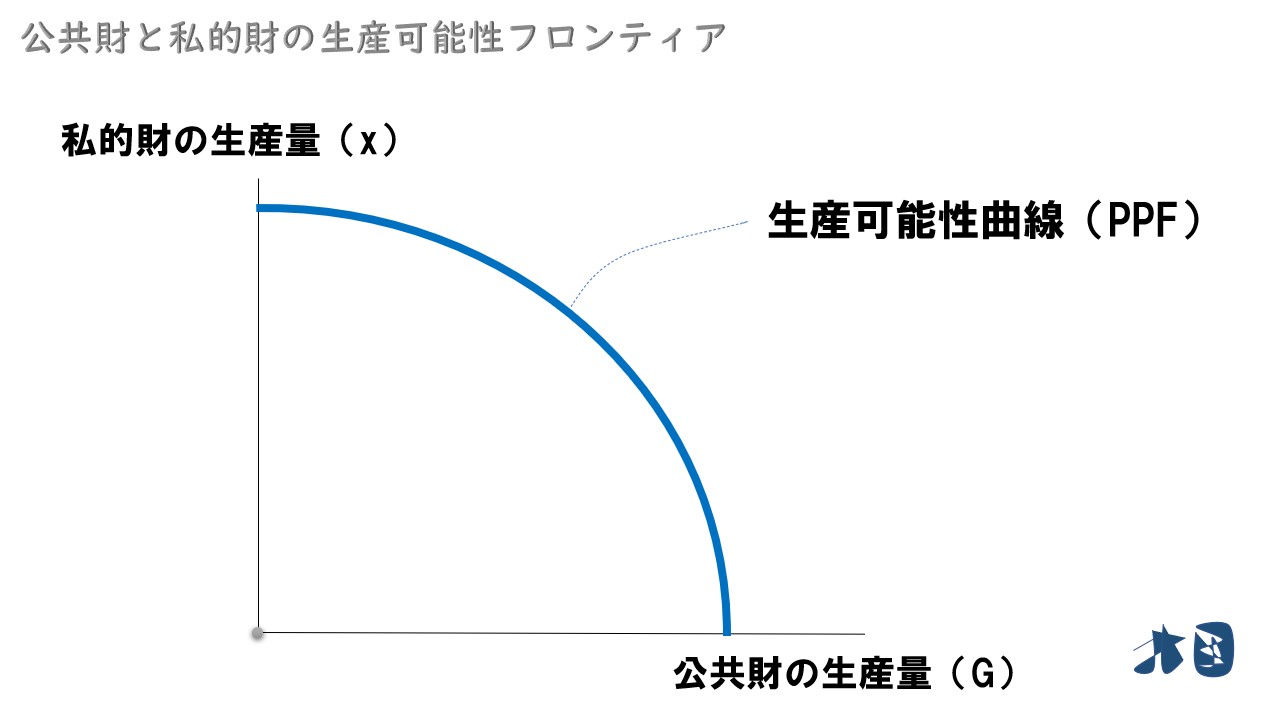
- 縦軸=私的財の消費量(x)
- 横軸=公共財の消費量(G)
縦軸に私的財の消費量を、横軸に公共財の消費量をとった一般的な生産可能性曲線(フロンティア)です。教科書では、公共財の消費量を「G」としているかと思いますが、これは「Public goods」のgoods(Pをとると私的財・private goodsと被る)か、政府が供給することを前提に「goverment」のgをとっている?と推察しています。私的財の消費量を「x」にするなら、公共財の消費量を「y」にすればいいんじゃないか?みたいに思うかもしれませんが、ここでの主役は公共財なので通常の財と区別するためにも「G」と置いています。
フロンティアの見方
念のため、生産可能性曲線(フロンティア)の見方を簡単に記載します。
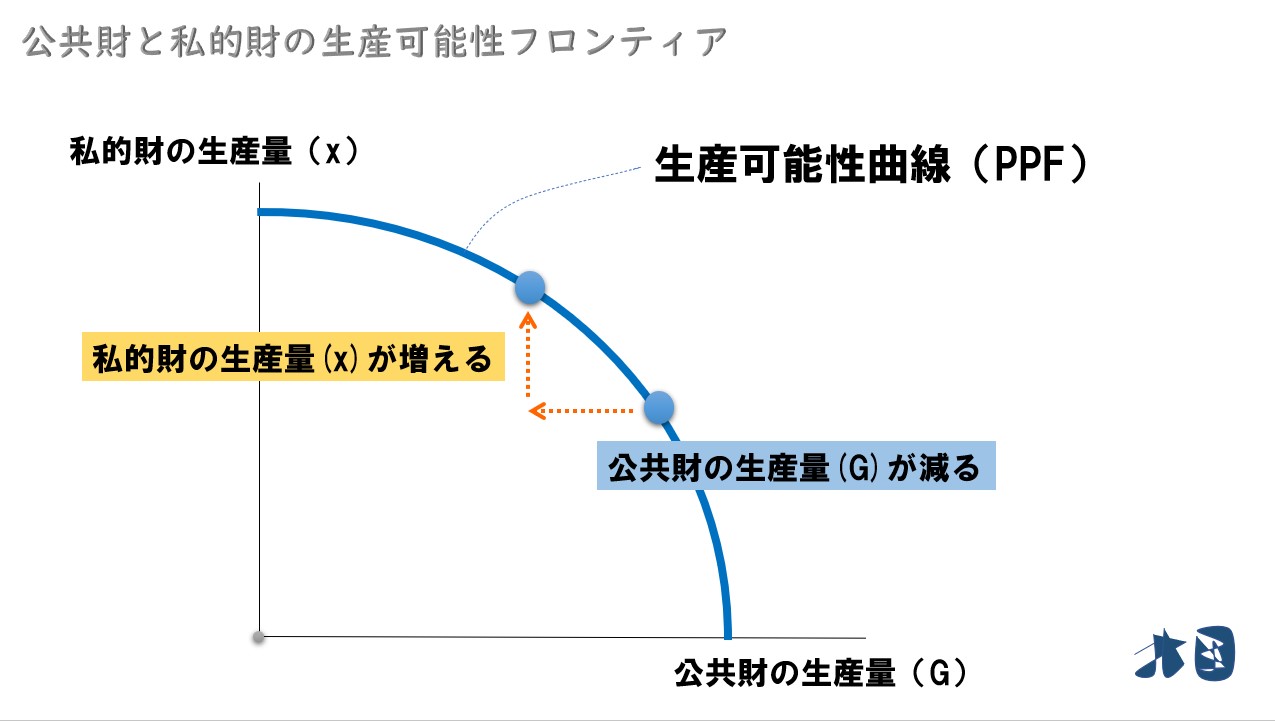
感染症の話を考えます。公共財(公共医療)を犠牲にする代わりに、私的財(マスクをしない、ワクチンを打たない、などの自由)を得られます。それを表しているのが上記のグラフ(生産可能性曲線・フロンティア)です。経済学でよく登場する「限界●●逓減(ていげん)の法則」のように、生産可能性曲線もカーブを描きます。いくら公共財(公共医療)を犠牲にしても、得られる私的財(自由)には限度があって逓減(ていげん)していく(=徐々に減っていく)と考えます。

ここまでは理解できました。
次に、Aさん・Bさんの効用を考えます。

社会全体の供給サイド(私的財・公共財の生産量)はグラフで可視化できました。
次に需要サイド(消費者側の行動)をグラフで考えます。
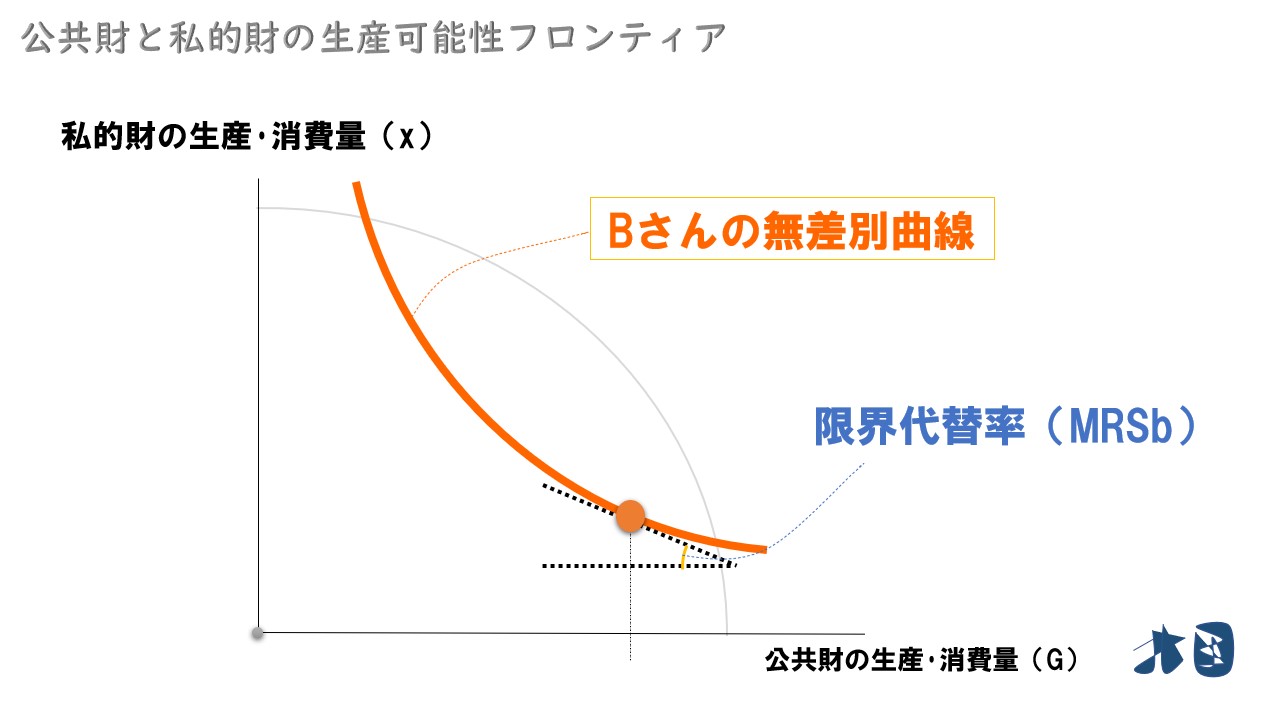
無差別曲線で考える
- 縦軸=私的財の消費量(x)
- 横軸=公共財の消費量(G)
- Bさんの無差別曲線が与えられている
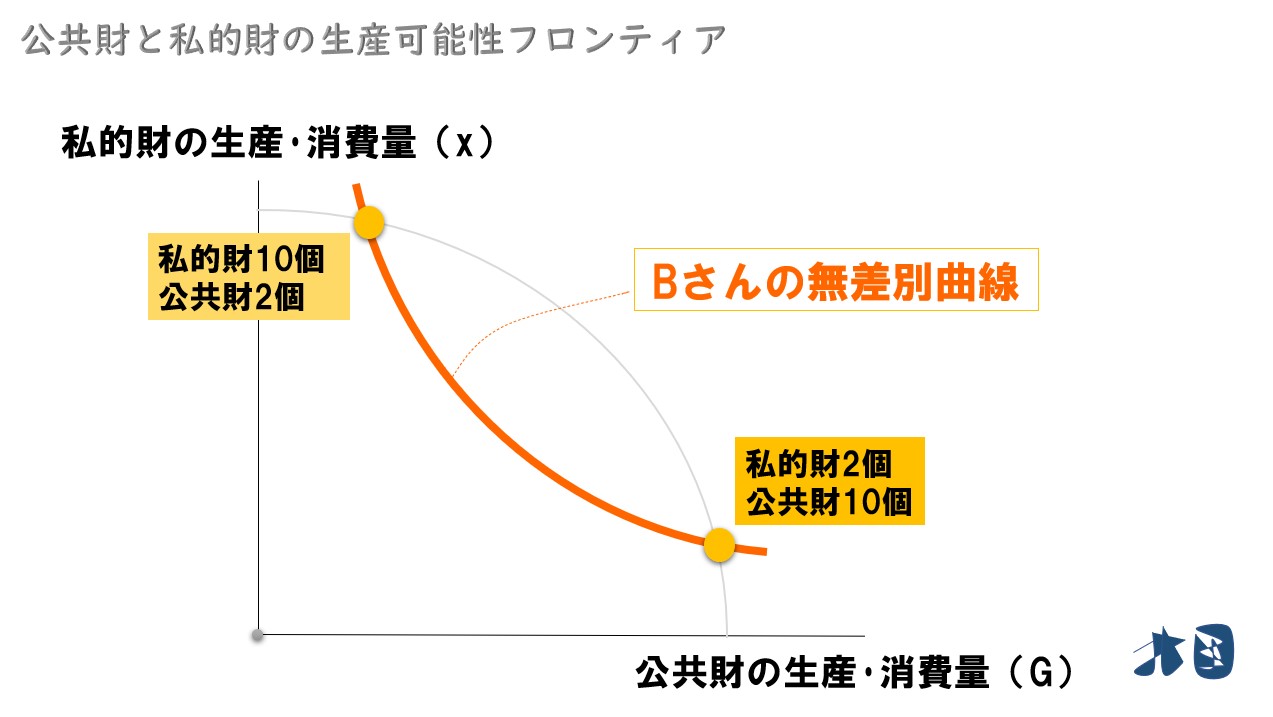
Bさんの無差別曲線の見方
Bさんの無差別曲線の見方を簡単に記載します。
Bさんのお財布状況などを考えて、上記のように無差別曲線が描けたとします。無差別曲線は、同じ曲線上では同じだけ効用を得られることを表しています。例えば、Bさんは「私的財10個・公共財2個」でも「私的財2個・公共財10個」でも同じ効用を得られるとき、上記のような無差別曲線が描けます。
ここで
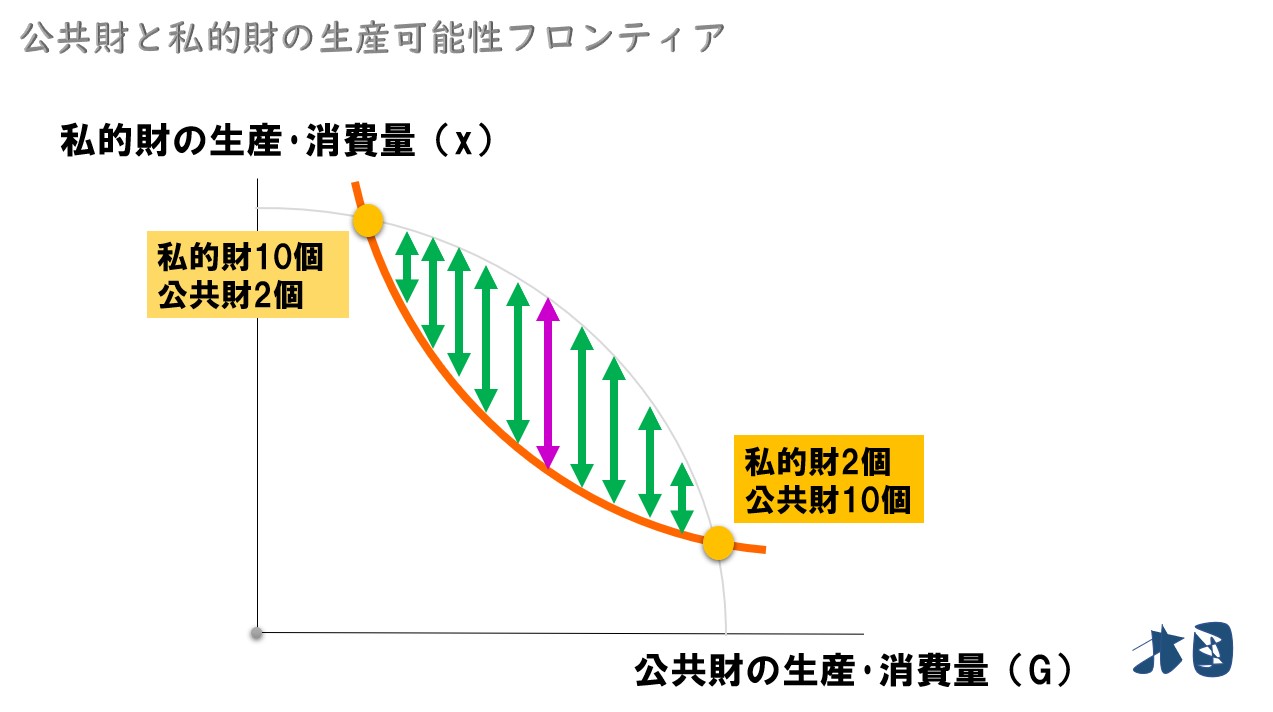
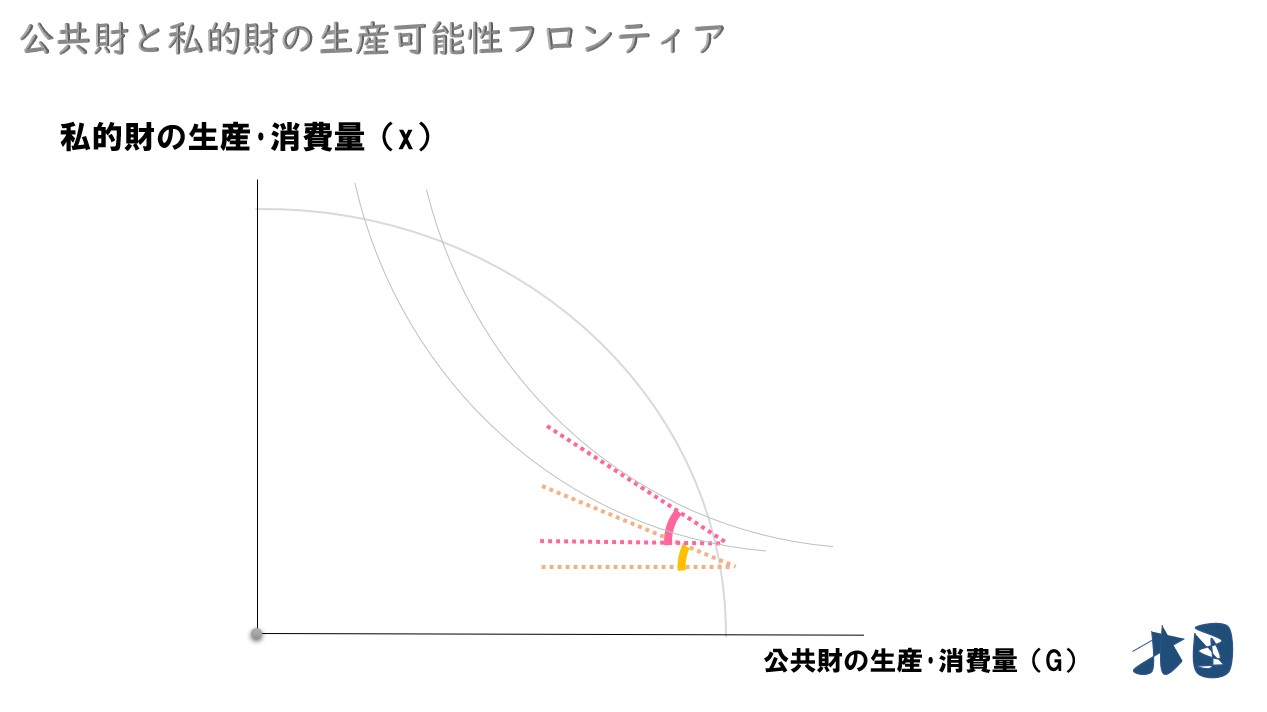
Aさん・Bさんがいる社会を想定していたので、次にAさんについて考えます。
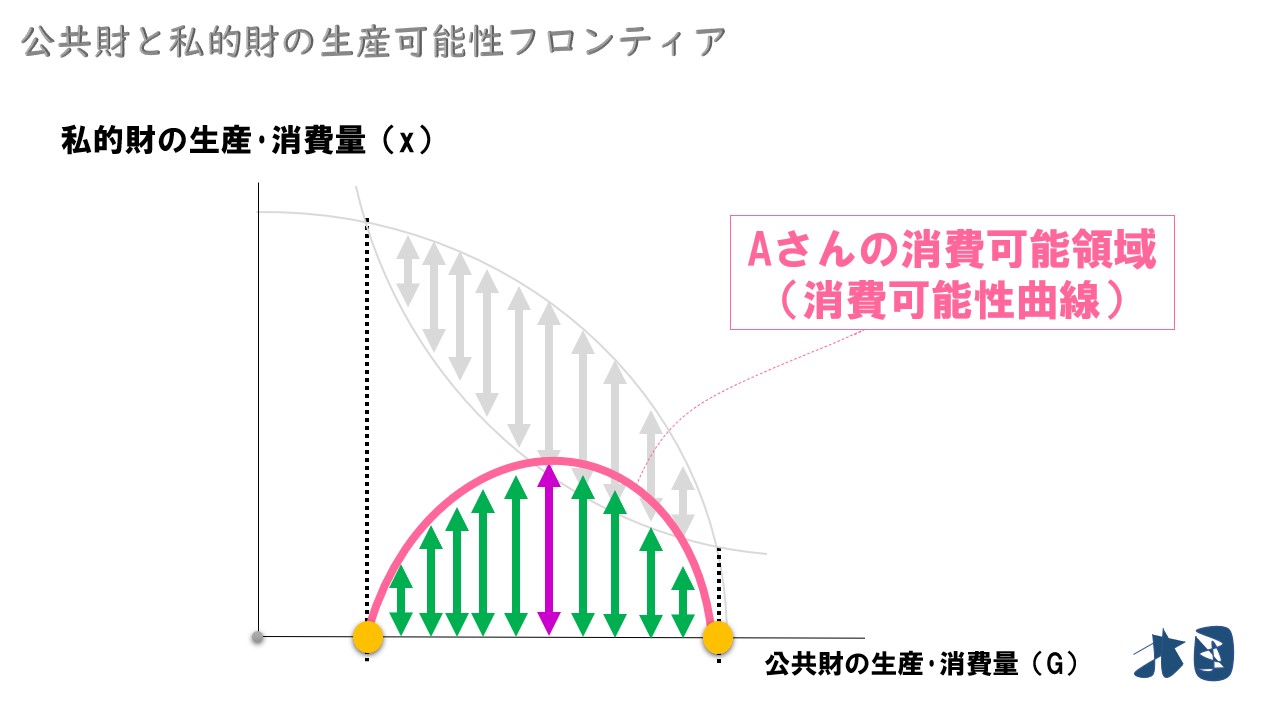
- 生産可能性曲線フロンティア
- Bさんの無差別曲線(Bさんが消費する可能性があるライン)
Aさんは「社会全体の生産量(生産可能性フロンティア)」から「Bさんが消費する分(Bさんの無差別曲線)」を差し引いた部分を消費することができる。
グラフで見ると・・・
Aさんは矢印部分(緑とピンク矢印部分)を消費できる。
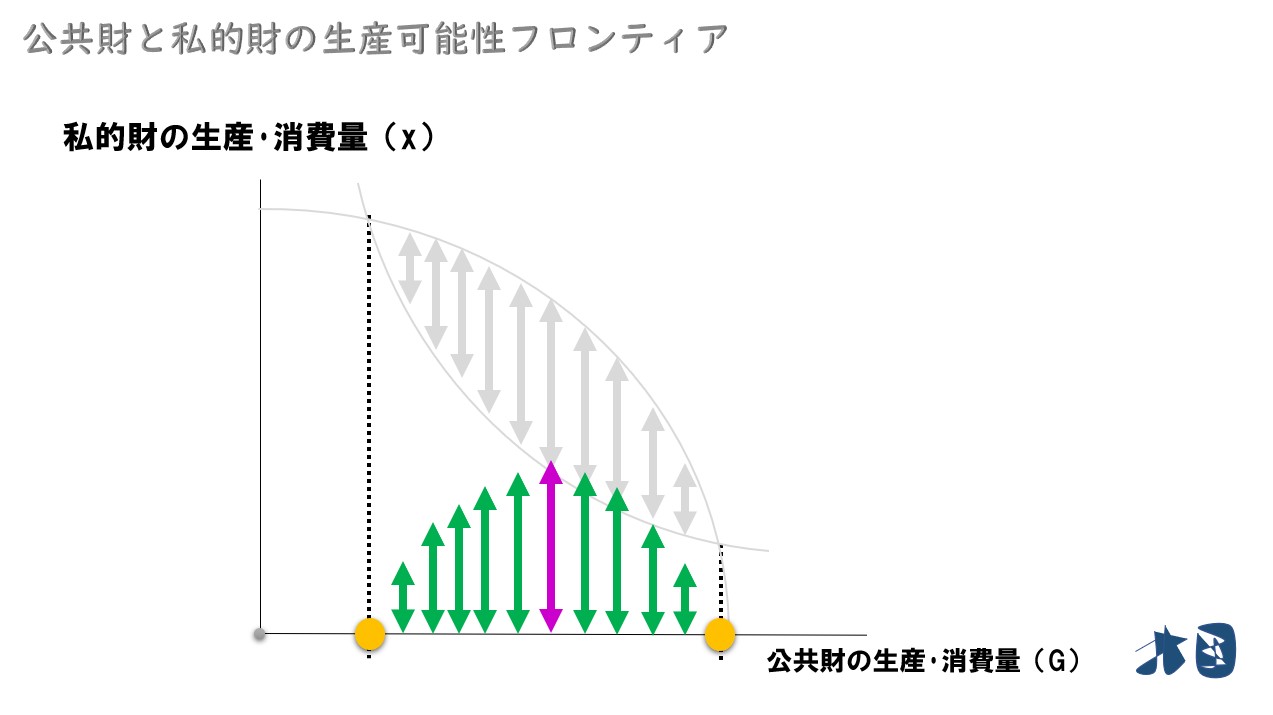
見やすくするために矢印を下へスライドする
Aさんの消費可能領域
Aさんが消費できる部分(矢印部分)を「消費可能領域」、領域を囲うラインを「消費可能性曲線」と呼びます。どちらも言葉の通りです!
ポイント
Aさんは、消費可能領域内で私的財・公共財を消費して、効用最大化を目指す。
ふつう、財をたくさん消費した方が効用を多く得られるはずです(はずと言いましたが、経済学ではこれを”単調性”と呼び、暗黙の前提としています)。
ここで
消費可能領域の横軸(公共財の消費量)に注目します。消費可能領域内では、私的財の消費量が同じでも、公共財の消費量が違うケースが考えられます。
途中で書きましたが、 ふつう、財をたくさん消費した方が効用を多く得られるので、私的財の消費量が同じなら、公共財を多く消費する方が効用がたくさん得られます。
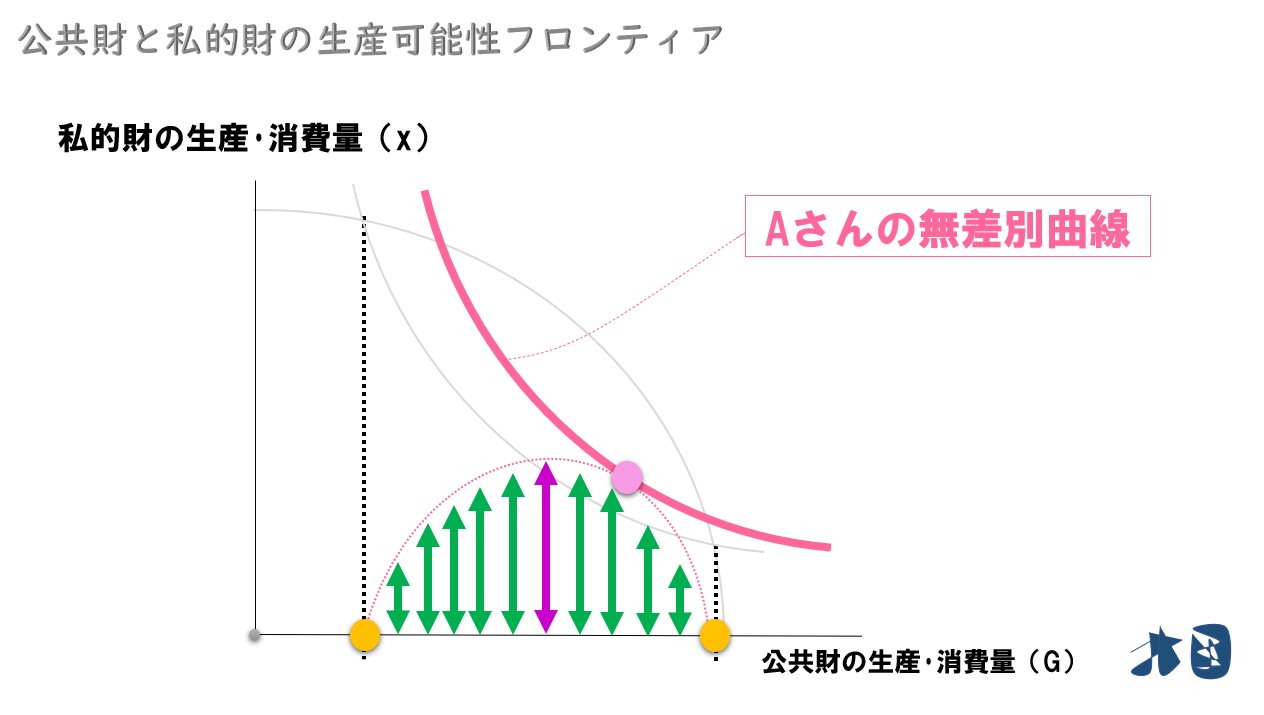
以上より、Aさんは消費可能領域の右側部分で消費の組み合わせを決めると考えます。
上記のグラフなら、消費可能領域のピンク太線上で消費の組み合わせを決める。
すべてを踏まえて
Aさんの無差別曲線は、例えばこのように描けます。

なんとなくの理解です。
最初は「ふーん」でいいので、ひとまず次を読み進めてね。次からが本題です・・!

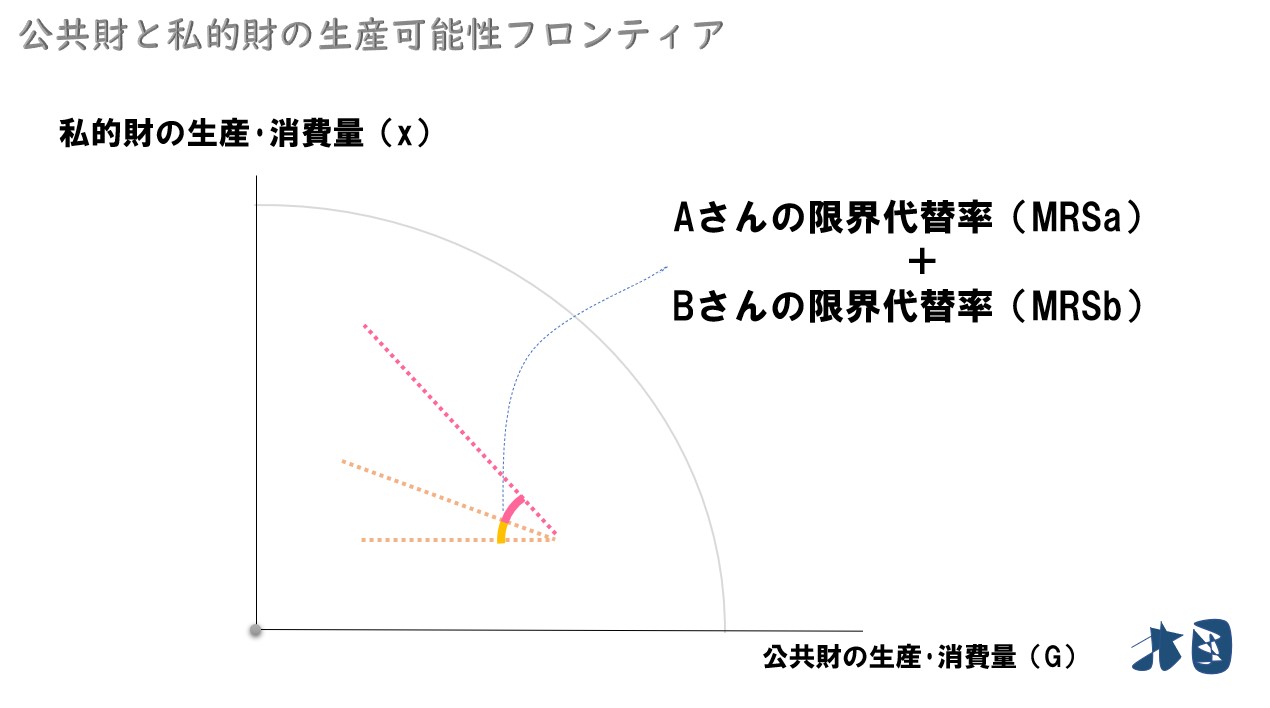
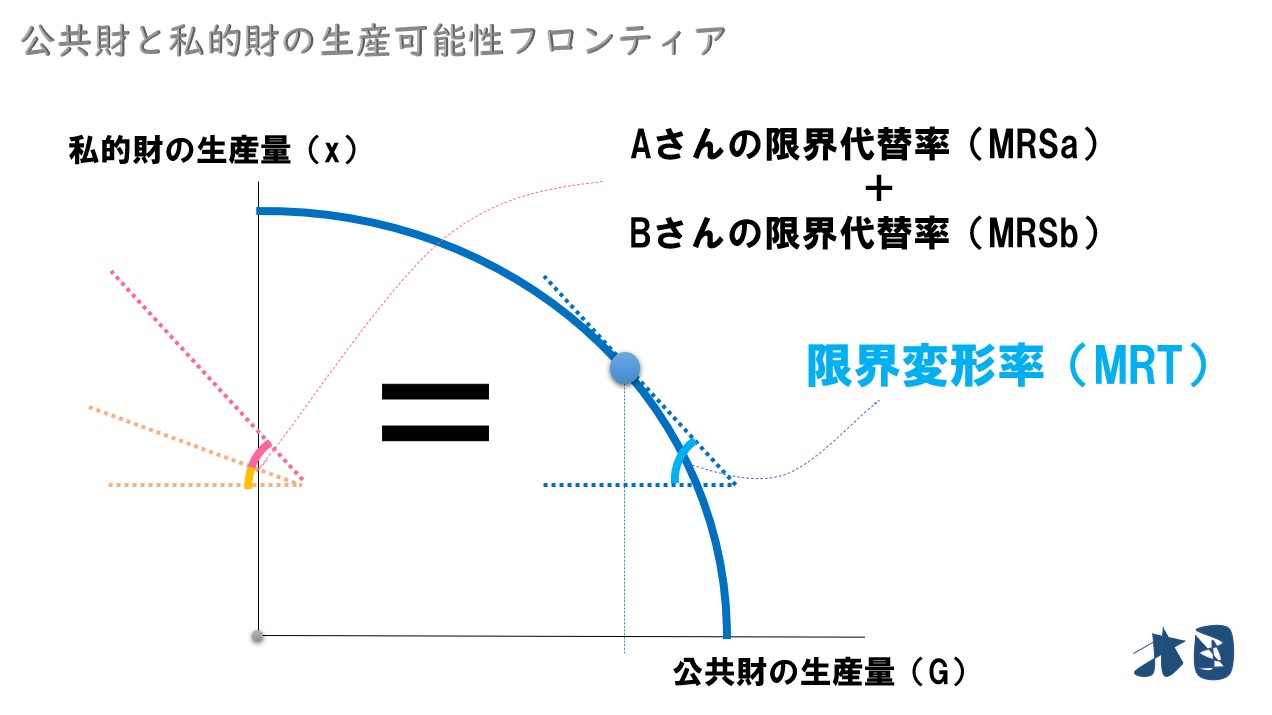
Aさん・Bさんの限界代替率を考える
ここまで、AさんとBさんの無差別曲線を導出しました。その無差別曲線より、2人の限界代替率(MRS)を考えます。
限界代替率(MRS)は、無差別曲線の傾きのことです。Aさん・Bさんが公共財を同じだけ消費したときの限界代替率をグラフで描いています。
限界代替率部分だけ抜き出します
2人の限界代替率を足し合わせる
教科書では、これを「MRSa+MRSb」や「MRS1 +MRS2」などと表記しています。AさんとBさんの限界代替率を足した「MRSa+MRSb」は、すごく重要なのでイメージをしっかりと持ちましょう。
生産可能性フロンティアの限界変形率を考える
次に、話を生産可能性フロンティアに戻します。生産可能性フロンティアの限界変形率を確認します。
生産可能性フロンティアの傾きを「限界変形率(MRT)」と呼びます。生産量がグラフのようになる時、限界変形率(MRT)は上記のように描けます。

牛さん、何を求めていたんだっけ?
次で終わりです!公共財の最適な供給量は・・

公共財の最適供給は・・
ポイント
- Aさん・Bさんの限界代替率を足し合わせたもの=「MRSa+MRSb」
- 生産可能性フロンティアの限界変形率=「MRT」
→「MRSa+MRSb=MRT」となるとき、 公共財の最適供給が実現する。※公共財の最適な供給量を実現するためには「MRSa+MRSb=MRT」を満たす必要があるが、これをサミュエルソン条件といいます。
※ちなみに「社会全体の限界便益(MB)=公共財の限界費用(MC)」という式もサミュエルソン条件と呼ばれることがありますが、上記の限界代替率の式を変形すると求められます(※省略)。
何故最適な供給量と分かるのか?と疑問に思う人もいるかと思いますが、次の例を考えれば分かるかと思います(下に続く)
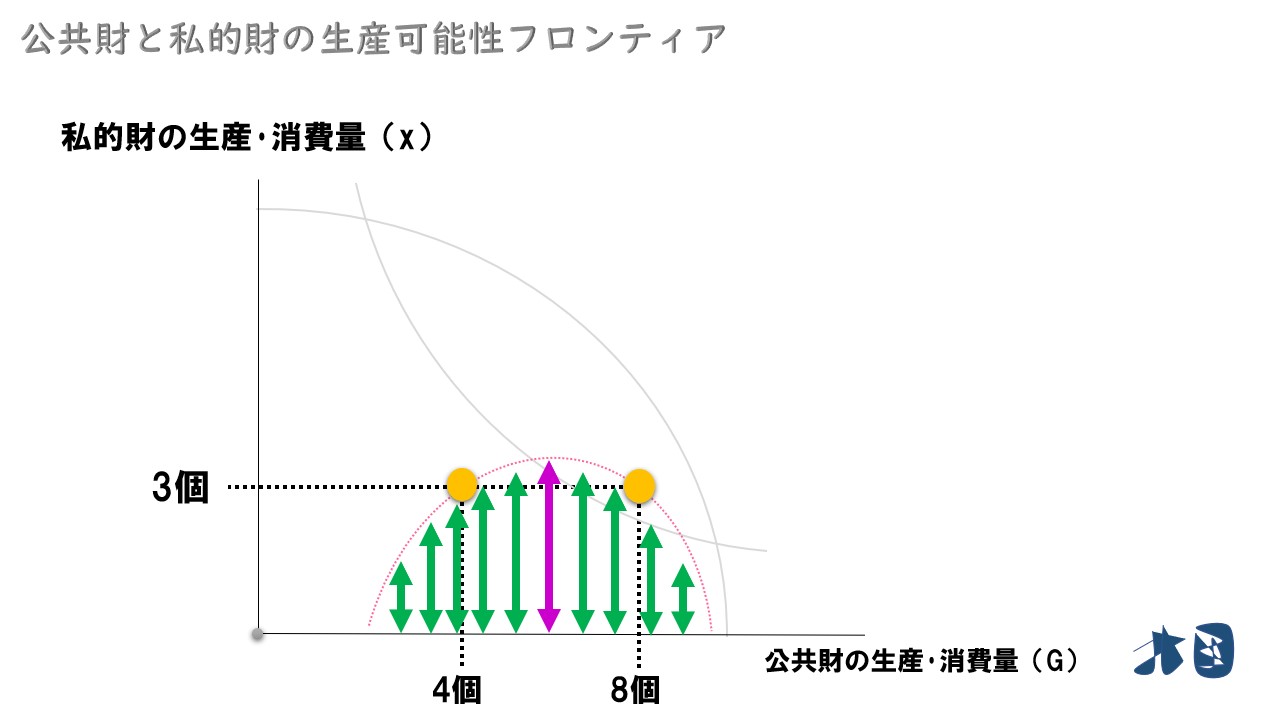
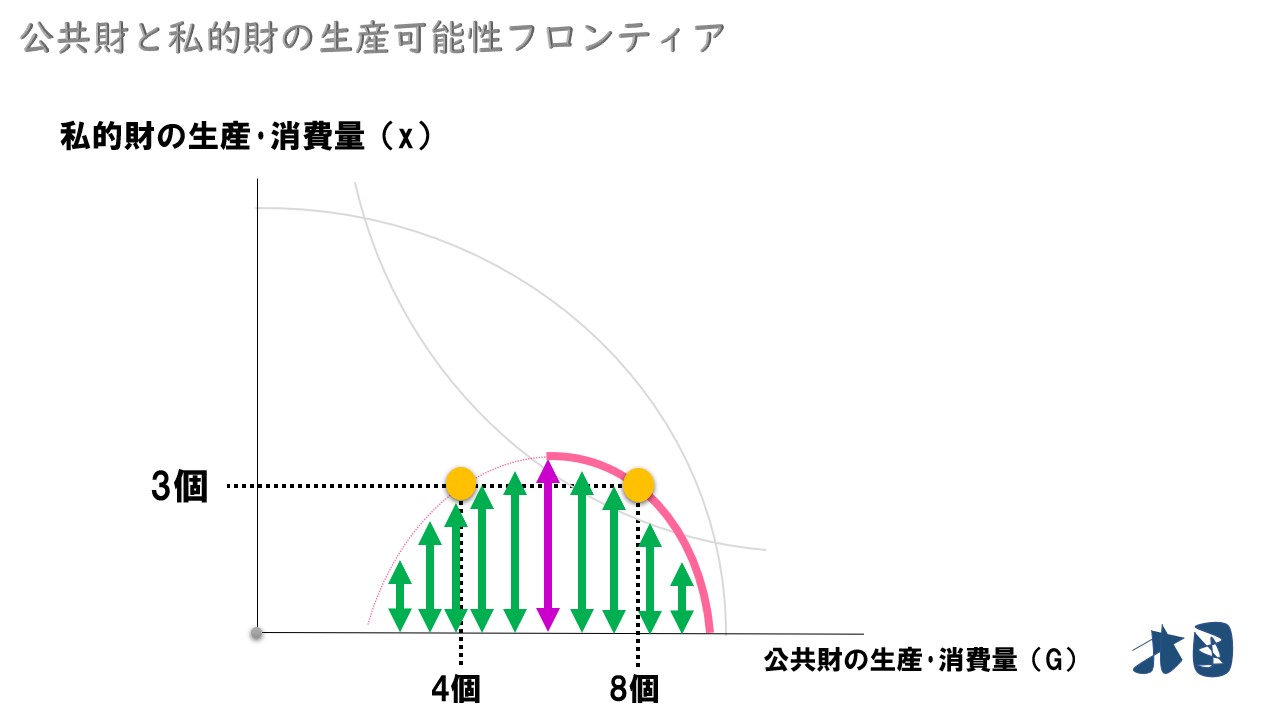
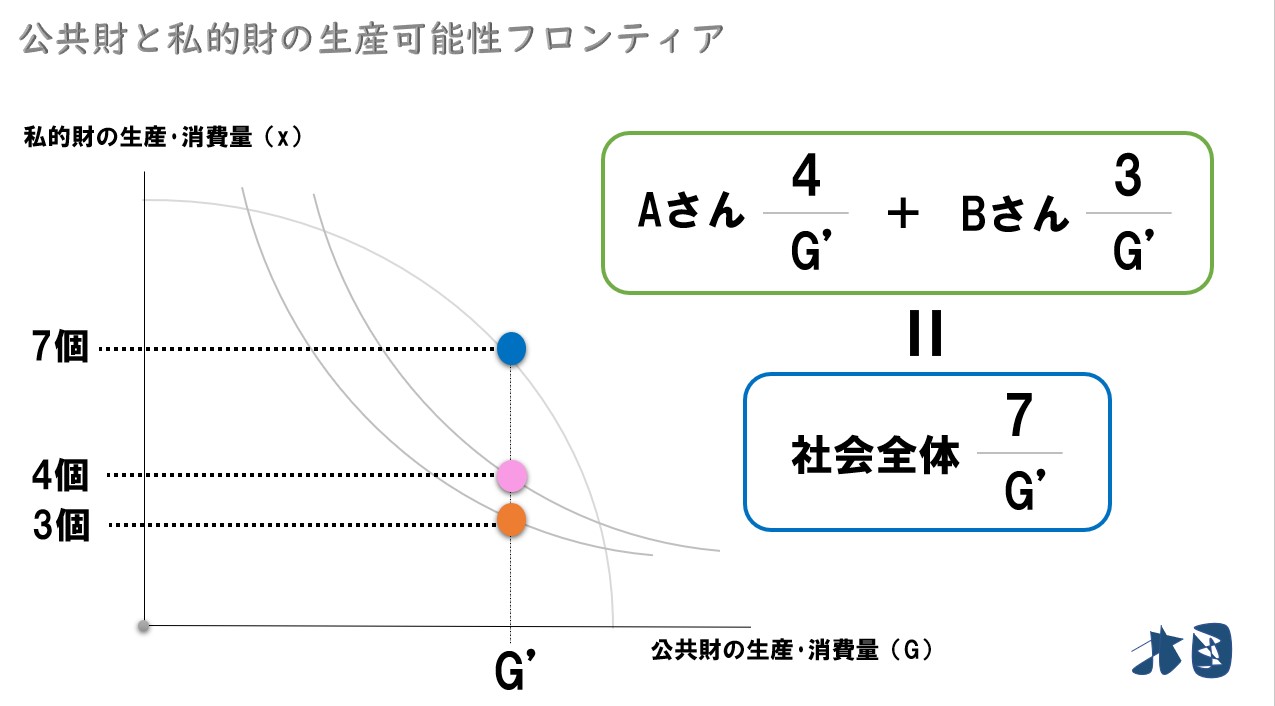
例えば
- 社会全体=私的財を7個・公共財をG’個
- Aさん=私的財を4個・公共財をG’個
- Bさん=私的財を3個・公共財をG’個
「限界代替率」や「限界変形率」は、言葉の違いはあれ「グラフの傾き」を求めているにすぎません。グラフの数値を使って傾きを求めてみます。
グラフの傾きは「縦軸/横軸」です。
私的財について「社会が7個生産」して「Aさん4個+Bさん3個消費」しています。公共財は、Aさん・Bさんも同時に消費できるため、供給されている量(G’)を2人が同じ量だけ消費できます。この「無駄なく、生産と消費が行われている社会」では、グラフの通り「AさんとBさんの傾きの合計」と「社会全体の傾き」が一致しています。※サミュエルソン条件の「限界代替率の合計+生産可能性フロンティアの限界変形率」が実現しています。
※ここでは公平性は考えていません。Aさんの方が私的財を多く消費していてズルいと思うかもしれませんが、途中で書いた通り、Bさんの無差別曲線を所与としたとき、結果的にAさんが多く私的財を多く消費することになっただけです。「公共財の最適供給」は、Aさんが社会で生産される私的財をほとんど消費して、Bさんが全く私的財を消費できなくても、社会全体で考えたときに効率性が実現していれば「最適な供給(パレート効率的)」となります。

イメージはできたので、細かいことはスルーします。
はじめは概要を理解できればOKだと思います。

サミュエルソン条件と市場の失敗
はてな
個人が自由に公共財を供給すると、公共財の最適な供給量(サミュエルソン条件)と比べて、公共財が過少供給になる。
公共財が過少供給になるのは有名な話で、色々な説明ができます。
例えば
公共財は、お金を支払わなくても利用できる性質(排除不可能)から、サービス提供者が負担を強いられる(料金を完全に徴収できないため)。その結果、本来よりも高い費用でサービスが提供されることになり、必要とされる量よりも過小供給となる。

お金を集められないから、コスト高になって供給量が制限されるって感じだね。
うん。公園とかをイメージすれば分かりやすいよ(利用料がないので税金を使わざるを得ないため、公園の供給量は必要最低限になってしまう)。

ここでは少しだけ専門的な話をします。
ポイント
公共財を市場に任せて供給することを「公共財の私的供給(公共財の自発的供給)」と呼ぶ。
現実では
公共財は、自治体や国が運営している。
公園・消防・警察など、基本的に国などの公共機関が運営しているものが大半です。これを「すべて民間企業に運営してもらう」というのが公共財の私的供給です。
先ほど説明した通り、これをすると「公共財は過少供給になり、市場が失敗します」。このとき、公共財の私的供給では下記の数式が成り立っています。
公共財の自発供給「MRSa=MRSb=MRT」
※AさんとBさんの2人がいて、私的財と公共財が生産供給されている社会を想定する。「MRSa=Aさんの限界代替率」「MRSb=Bさんの限界代替率」「MRT=限界変形率」を表す。
公共財の私的供給の説明や「MRSa=MRSb=MRT」の導出はこちら ⇒公共財の自発的供給(私的供給)と最適供給との比較
これは、公共財が通常の財(私的財)のように生産供給が行われるためです。通常の2財を生産供給する社会では「MRSa=MRSb=MRT」が実現します。ちなみに、これ1つで大きな項目となるため説明を割愛します⇒【消費と生産のパレート効率性】完全競争市場(市場均衡)がパレート最適となる理由をグラフ・数式で考える
一方で
公共財の最適な供給量表すサミュエルソン条件は「MRSa+MRSb=MRT」
ポイント
公共財を市場に任せて供給すると、サミュエルソン条件が満たされなくなるため、最適な供給量が実現していないことが分かる。
- 公共財の自発供給「MRSa=MRSb=MRT」
- サミュエルソン条件「MRSa+MRSb=MRT」

数式で見ても「公共財を市場に任せて供給すると市場が失敗する」っていうことだね。
うん。だから公共財は民間企業(市場原理)ではなく、国や政府などが供給するのが一般的なんだ。

公共財を国などが供給することは経済学的にも間違いではないことが分かれば、この分野はOKです。
他にも、反応曲線(反応関数)を使って公共財の私的供給が過少供給になることを説明することが出来ますが、教科書に載っているので省略します。反応曲線どころか、ふつうに計算して過少供給になることを説明した記事を書きました⇒こちら
サミュエルソン条件の数学的な導出(証明)

サミュエルソン条件を数学的に考えてみます(数式使って証明します)。
- Aさん・Bさんの2人がいる社会
- 「公共財」と「私的財(ふつうの財)」の2財が生産消費されている
- ただし、公共財を生産するためには「私的財」が必要である
- 公共財はAさん・Bさんの2人に便益がある
①それぞれ文字で置き換える
- 公共財の消費量=G ※1
- Aさんの私的財の消費量=xa
- Bさんの私的財の消費量=xb
- Aさんの初期保有・予算=wa ※2
- Bさんの初期保有・予算=wb ※2
※1 公共財はA・Bさんも同じ量消費できるので1文字
※2 Wealth(富)から「w」としている。
- 公共財の生産コスト=C(G)
「AさんとBさんの初期保有」=「公共財の生産コスト+私的財の消費量」
wa+wb = C(G)+xa+xb
AさんとBさんの初期保有が社会全体の資源制約と考える(AさんとBさんの初期保有以上に社会に資源がなく、2人が持っている資源と同じだけしか財を消費できない)。
②効用関数を考える
Aさんの効用関数(Ua)を考える。Aさんは「公共財(G)」と「私的財 (xa) 」を消費することで効用を得られる。
- Ua=〇G×〇xaとなる式(※)を想定する
- ※例えば「Ua=2G×3xa」のようになる。具体的な数値は不明。
これを「Ua(G,xa)」と表現する(具体的な値は分からないけど、上記のような式を想定する)
- Bさんも同様に「Ub(G,xb)」
Bさんの効用を一定と考える
ここで、Bさんが得られる効用を一定(所与=あらかじめ決めておく)とします。
Ub(G,xb)=Ub*
※通常はバーを引くことが多いですが、打てないのでアスタリスクにしています。
③条件をまとめる
まず、Aさんの効用を最大化させます
Ua(G,xb)を最大化・・(1)
次にBさんの効用は所与(一定)です
Ub(G,xb)=Ub*・・(2)
社会の資源制約を満たす必要があります
wa+wb = C(G)+xa+xb・・(3)
(1)~(3)をまとめて次のように表現します。
式を少し変形します。
①~③を元に「ラグランジュ関数(L)」を使って計算します。 これは「ラグランジュ未定乗数法」という「制約条件がある関数」の「極値」を求めることが出来る計算方法(数学的な手法)です。ここでは「②③を制約条件」「①の効用最大化」を極値を求めると考えます。
ラグランジュ未定乗数法の計算方法
はじめに「L=」として、制約条件にあたる部分に「μ(ミュー)※文字なら何でもよい。λ(ラムダ)とかも定番」をつける。
- 以上より「L=①+μ1②+μ2③」とします。※「=0」は無視

「L=①+μ1②+μ2③」の式を次の3つで微分して「=0」とします。
- Aさんの私的財の消費量(xa)
- Bさんの私的財の消費量(xb)
- 公共財の消費量(G)
ポイント
微分して「=0」と置くのが、この式の中でも重要なポイントです。
(微分する意味)初めはイメージで考えてほしいのですが、各消費量で微分することで「限界効用」を求めることができます。消費者理論の基本的な知識です。【限界効用・限界効用逓減の法則】求め方も含めて簡単にわかりやすく
(=0とする意味)微分すると限界効用になるとイメージ出来れば簡単です。追加的な効用(限界効用)が0ということは、もうこれ以上効用を増やすことができません~という状態です。つまり、これ以上は効用を増やすことができない状態=各財の消費によって得られる限界効用が最大化している=最適な状態と言えます。
以上より、微分して=0と置くことで「L=①+μ1②+μ2③」という式で、最適な状態(Aさんの効用最大化)を計算することができます。
諸条件がある中でAさんの効用最大化を実現させることで、公共財の最適な供給が実現していると捉える。
というわけで、初めにAさんの私的財の消費量(xa)で微分します。
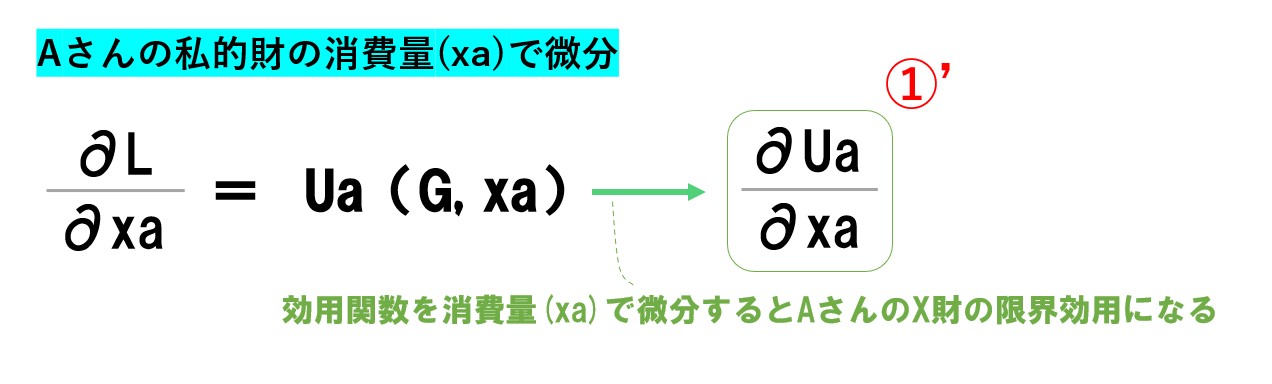
「∂」は微分していることを表します。デルやラウンドなどと呼びます。「L=①+μ1②+μ2③」の式を「xa」で微分したので「∂L/∂xa=~」と表現しています。
途中で書いた通り、効用関数(Ua)を消費量で微分すると限界効用(∂Ua/∂xa)になります。⇒【限界効用・限界効用逓減の法則】求め方も含めて簡単にわかりやすく
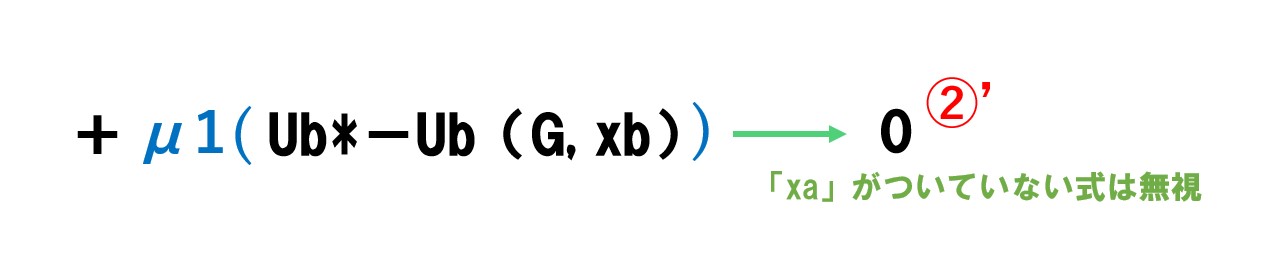
微分する時ですが、微分する文字「xa」がついてない部分は0となります。

効用関数を消費量で微分すると限界効用(∂Ua/∂xa)となるので、計算せずに文字式で表しました。そうではない部分は普通に計算します。
微分は、乗数を手前に持ってきて、乗数を1減らします。●乗と書いていなければ1乗です。1乗なので、手前に1を持ってきます。1乗から1を引くと0乗となります。0乗は1となります。

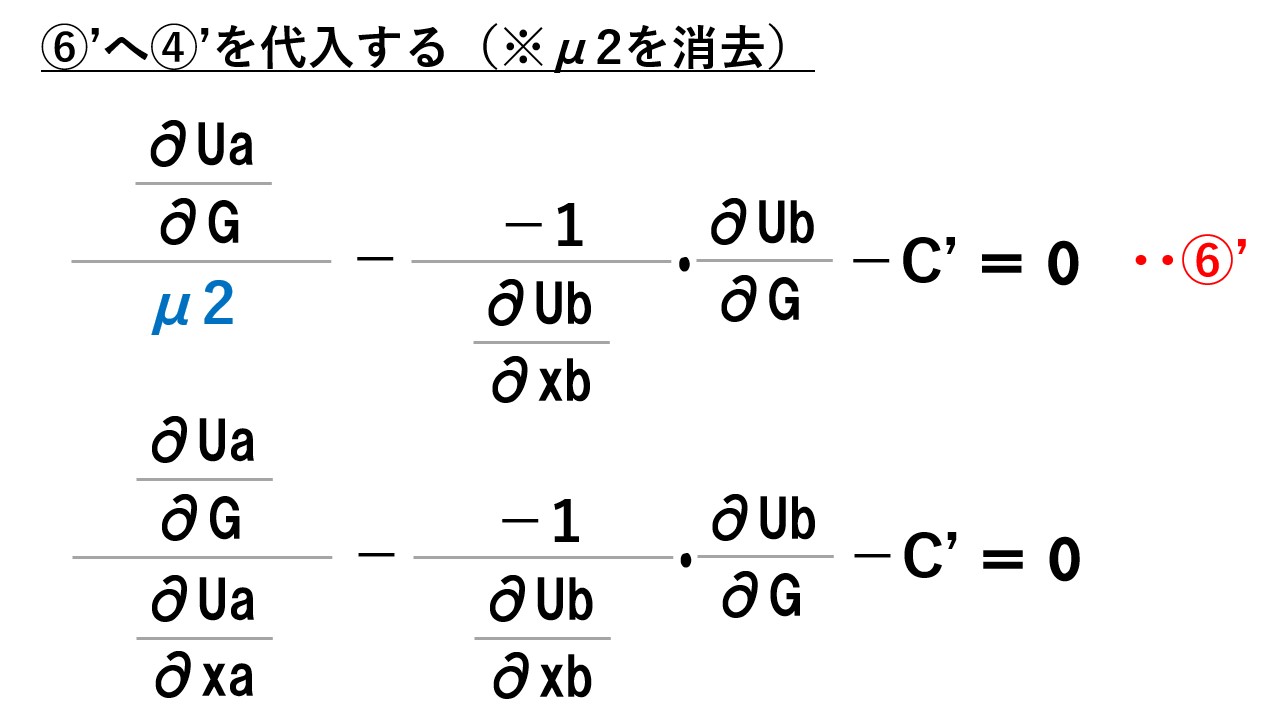
「L=①+μ1②+μ2③」の式を「Aさんの私的財の消費量(xa)で微分」して「=0」とすると「④」の式が得られます。これと同様に「xb」「G」でも微分して0とした式を求めます。

※Bさんの私的財の消費量(xb)で微分して「=0」とすると⑤の式が得られました。
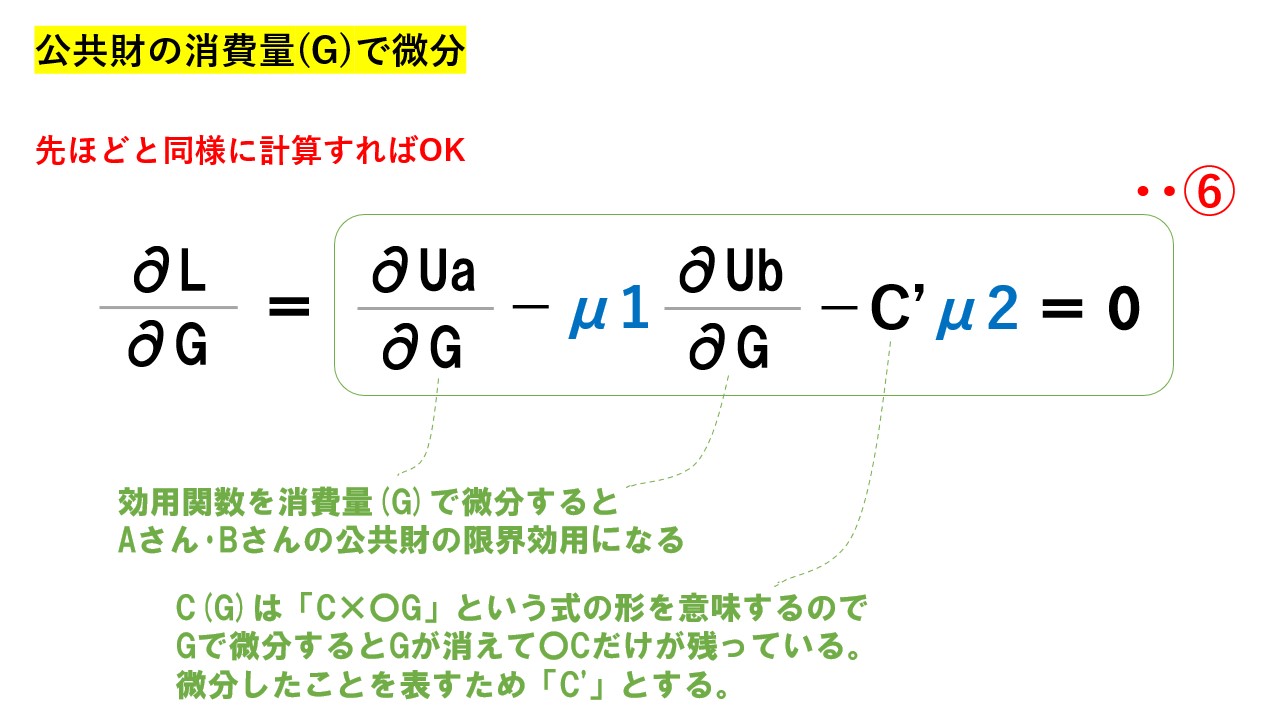
もう一度書きますが、微分は乗数を手前に持ってきて、乗数を1減らします。●乗と書いていなければ1乗です。1乗なので手前に1を持ってきます。1乗から1を引くと0乗となります。0乗は1となります。
効用関数を微分して限界効用が得られるように、費用関数を微分すると「限界費用(MC)」になります。ここでは「C’」と記載しています。限界費用とは?利益・平均費用との関係も分かりやすく簡単に解説
以上より

それぞれを文字で置いて「1階条件」として④⑤⑥の式を書ければ、大学の試験では部分点がもらえるはず、、
ポイント
「1階条件」というのは「社会の資源制約とBさんの効用を一定としたとき、Aさんの効用最大化するためには、次の式を満たしている必要がありますよ」という条件のことです。
各条件や前提を文字で表して、ラグランジュ関数(L)を作りました。そのラグランジュ関数を「微分して=0と置く」ことで、Aさんの効用最大化を求めることができます。この時「微分して=0と置く」ことで得られる3つの式を「1階条件」と言います。
なぜ「1階条件」なのかという話ですが、それはもちろん「2階条件」と話が続くからです。数学的に考えると、これまでの計算方法では極値を求めることしかできません(効用が最大化 or 最小化しているかは判断できない)。この極値が「最大」か「最小」かを判断するための条件式を「2階条件」と呼びます。
- 1階条件→「極値」を求めるための条件式
- 2階条件→求めた極値が「最大」か「最小」かを判断するための条件式
学部レベルの経済学の問題では、多くの場合、暗黙の了解で2階条件を計算する必要がありません。ここでなら、1階条件を計算すると暗黙の了解で「Aさんの効用最大化(最小ではない)」が得られると考えています。そのため2階条件は省略します。
あとは計算するだけ!
とりあえず、邪魔な「μ」を消していきます(1階条件を整理する、ラグランジュ乗数を消去するとか言います)。
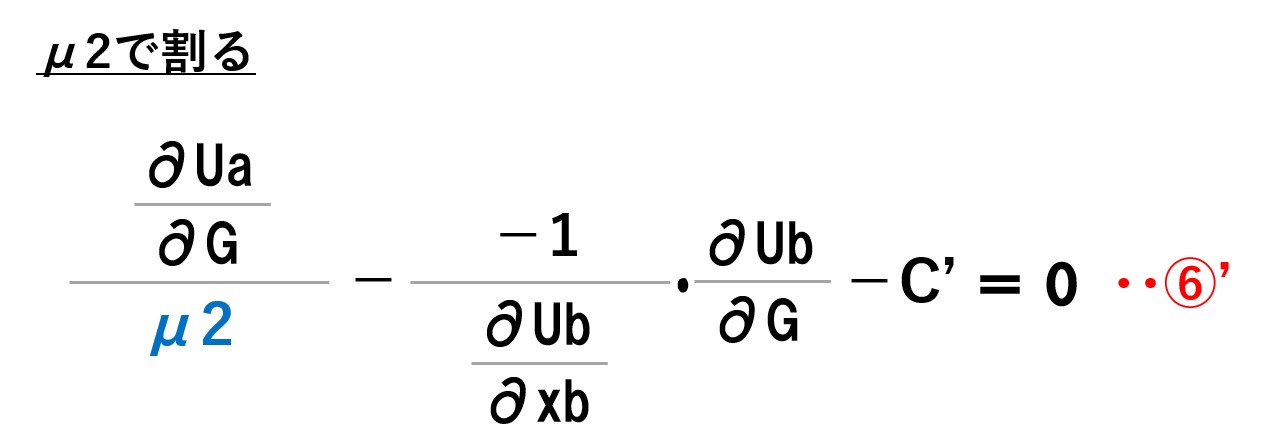
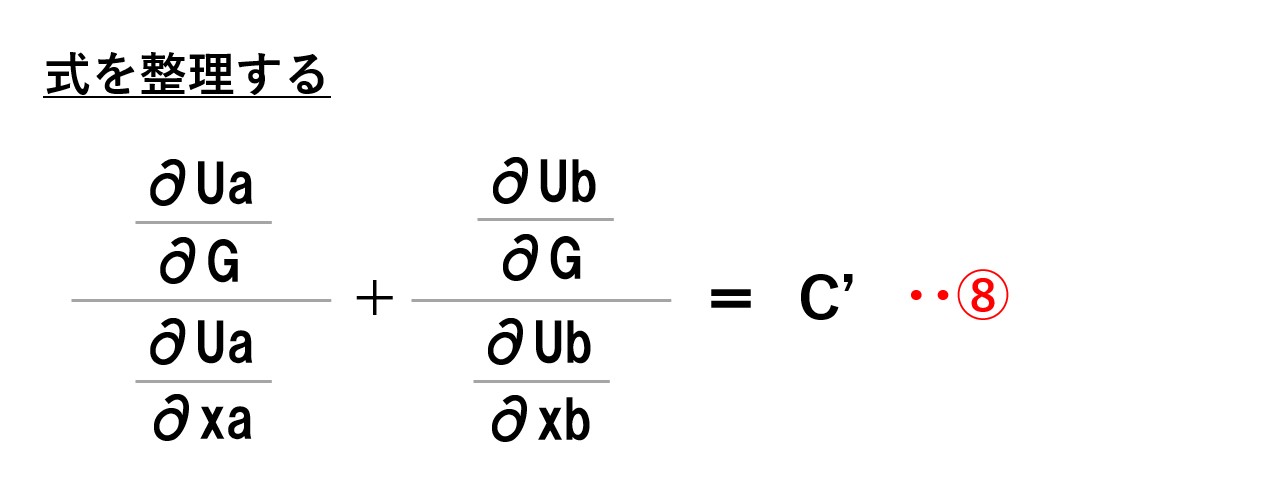
このとき、左辺と右辺がそれぞれ何を表しているかが重要です。
左辺
- 分子「∂U/∂G」⇒効用関数を公共財の消費量(G)で微分したもの=公共財の限界効用
- 分母「∂U/∂xa」⇒効用関数をAさんの私的財の消費量(xa)で微分したもの=Aさんの私的財の限界効用
※Bさんの分は省略
右辺
- 「C’」⇒公共財の生産コスト(費用関数)を微分したもの=公共財の限界費用
効用関数・費用関数を微分すると限界〇〇になるというのは、途中で説明した通りなので、理解できなければ最初の方から読み直してください。
左辺について
ポイント
また、消費者理論で登場する話で恐縮ですが「2財の限界効用の比(A財の限界効用/B財の限界効用)」というのは「限界代替率(MRS)」を表します。
つまり・・
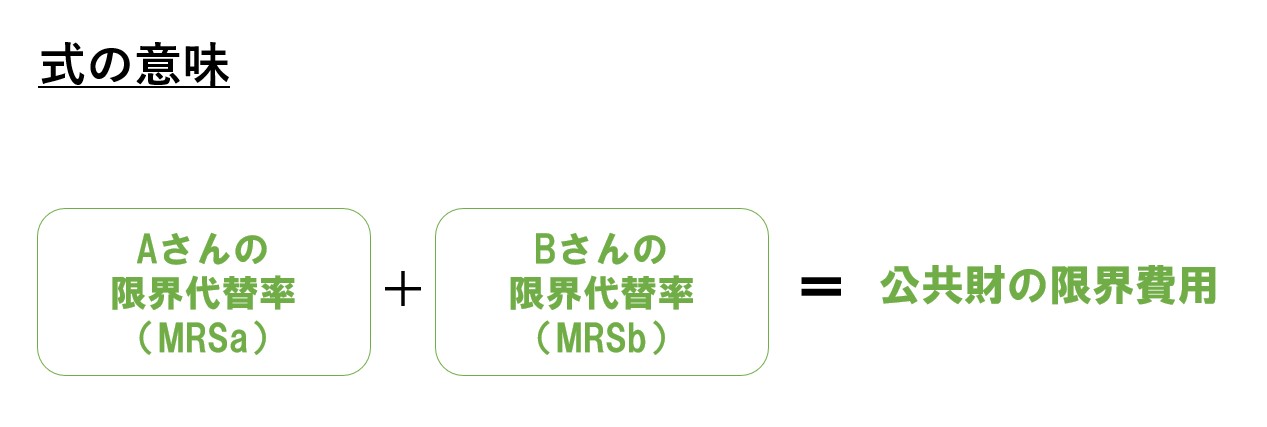
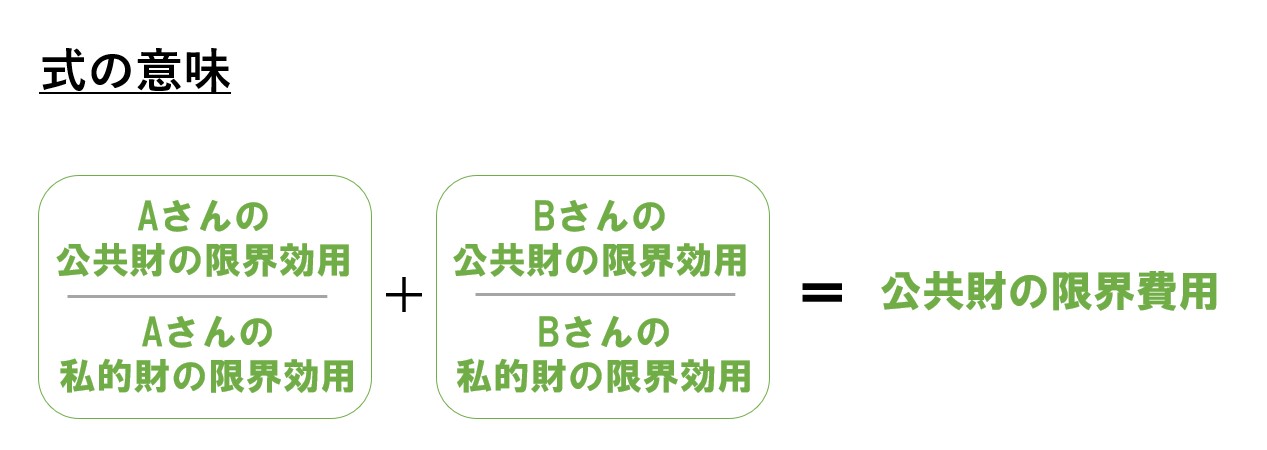
左辺は「Aさんの限界代替率+Bさんの限界代替率」を表します。
右辺について
ポイント
公共財を作るためには私的財が必要でした。つまり「公共財の限界費用(MC)=私的財の投入量」⇒ 公共財を1単位作るために、私的財が〇単位必要ということを意味します。
「ある財を作るために、もう片方の財をどれくらい諦めるか=限界変形率(MRT)」なので、「公共財の限界費用(MC)=公共財を1単位生産するために、私的財をどれくらい投入する必要があるか(私的財を投入する=失う=諦めると考える)」は同じことを言っていることになります。
以上より「公共財の限界費用(MC)=限界変形率(MRT)」となります。
最後
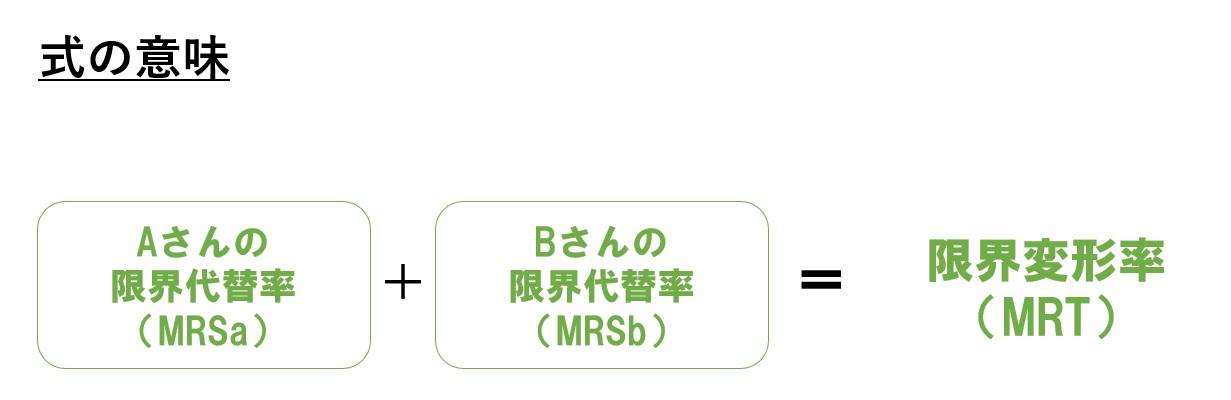
以上より、サミュエルソン条件が導出されていることが分かりました(終わり)。

この見出し初登場です。難しかった・・。
著者、自分で計算して導出したので間違っていたらすみませんとのことです。

計算問題の解き方(例題)

(1)公共財の最適供給量(パレート最適)と比較して、公共財を自発的に供給する(ナッシュ均衡)と公共財の供給量はどのように変化するか。
(2)次の条件のとき、公共財の最適供給量(最適水準)を求めよ。
- AさんとBさんの2人だけがいる社会を考える
- Aさんの公共財の消費量=Ga
- Bさんの公共財の消費量=Gb
- 公共財の価格=P
- Aさんの公共財の限界評価(限界便益)曲線(MB):Ga=-2P+12
- Bさんの公共財の限界評価(限界便益)曲線(MB):Gb=-3P+9
- 公共財の限界費用(MC)=6
(1)過少供給になる
政府に任せず、各個人が自由に公共財を生産供給する(各個人がベストな戦略を取っている=ナッシュ均衡)と、市場が失敗して、公共財の最適供給量(社会全体の便益が最大化=パレート最適)と比較して過少供給になる。
(2)2人の限界評価曲線を「P=~」の形にする
- Aさん「Ga=-2P+12」⇒「2P=12-Ga」⇒「P=6-(1.5/3)Ga」
- Bさん「Gb=-3P+9」⇒「3P=9-Gb」⇒「P=3-(1/3)Gb」
ここで公共財の特性(非排除性)より、AさんとBさんは同じ量の公共財を消費することになるので「Ga=Gb=G」となる。
- P=6-(1.5/3)G
- P=3-(1/3)G
社会全体の公共財の便益は、Aさん・Bさんの便益を足し合わせればよいので
「6-(1.5/3)G」+「3-(1/3)G」=「9-(2.5/3)G)」
「社会全体の公共財の便益=公共財の限界費用」で公共財の最適な供給量となるため
9-(2.5/3)G=6
(2.5/3)G=9-6=3
2.5G=9
G=3.6
以上より
公共財の最適供給量(最適水準)は「3.6」