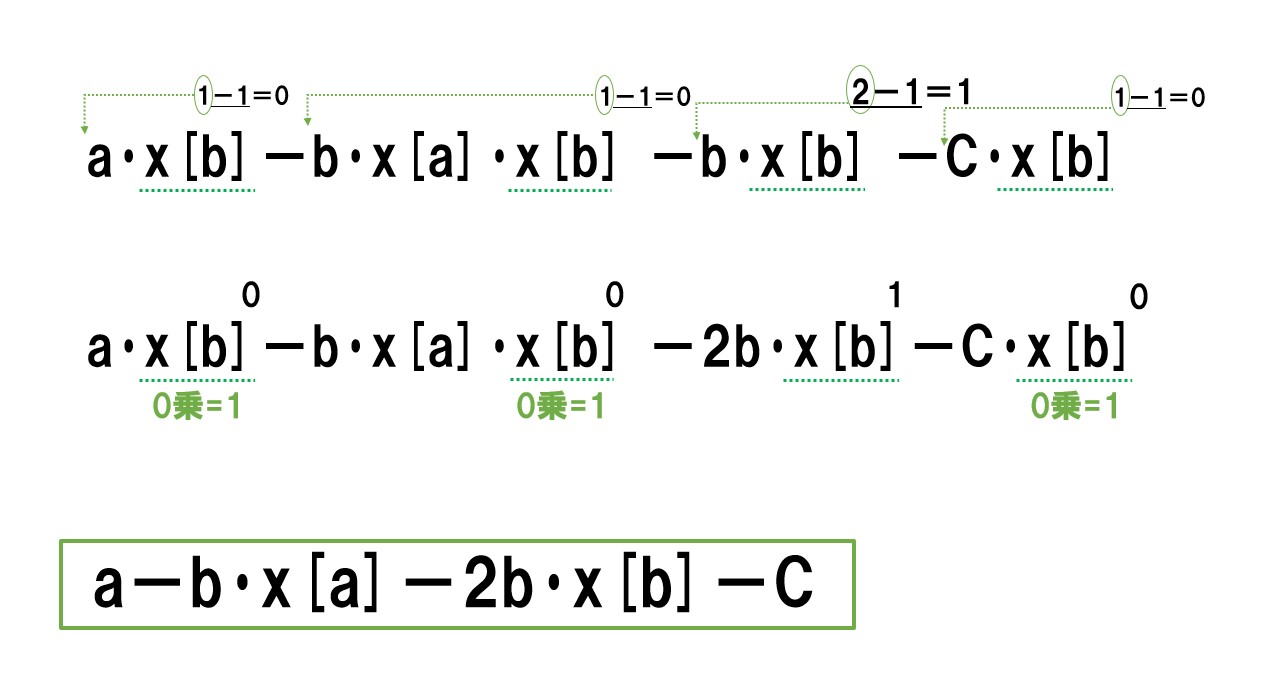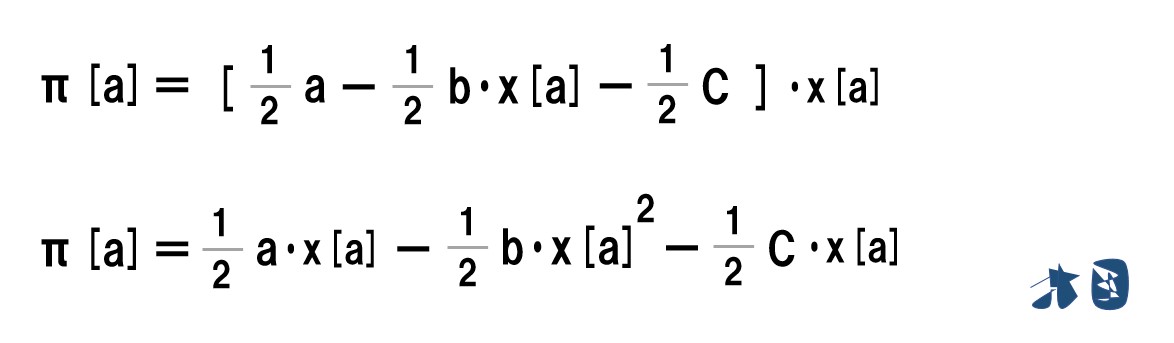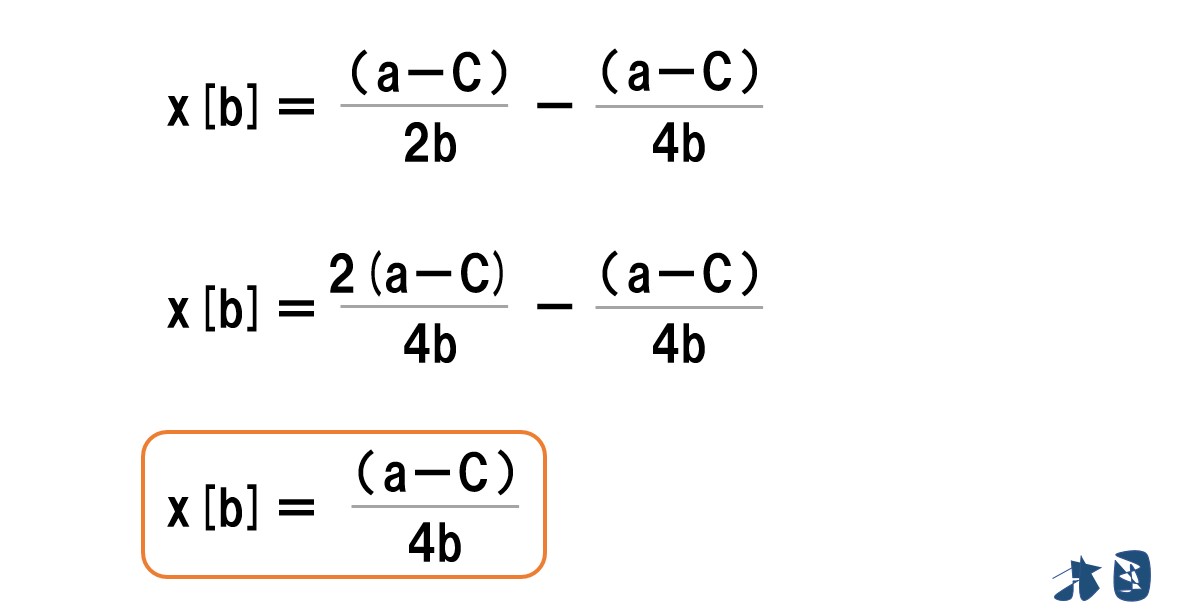ドイツの経済学者シュタッケルベルグが構築した「不完全競争市場における企業行動を分析したモデル」を1から簡単にまとめています。
- シュタッケルベルグの(先導者)モデル
- シュタッケルベルグ競争(例など)
- シュタッケルベルグ均衡
- 反応曲線
- シュタッケルベルグ均衡の意義
- 余剰分析
- 計算方法や求め方
この記事内では「シュタッケルベルグモデル」は、このモデルが経済学の中でどのような位置かを説明するために、「シュタッケルベルグ競争」はモデルの具体的な説明をするために段落を分けています。一般的には細かく分けません。
シュタッケルベルグ・モデル

(英語版Wikipediaより ハインリヒ・フライヘル・フォン・シュタッケルベルグ)
はてな
寡占市場(複占市場)の企業が、どのように生産量(価格)を決定するのかを分析したモデル。クールノーやベルトランモデルとは異なり、情報格差に注目している。
19世紀までの寡占市場のモデルでは「お互いが同時に生産量・価格を決定する」と考えていたが、シュタッケルベルク・モデルは「情報を持っている企業が先んじて行動に出る(先導者)」と考えている。このことから「シュタッケルベルグ先導者モデル」と呼ばれることもある。
その他「シュタッケルベルグ競争」「シュタッケルベルグ・ゲーム」など状況に応じて様々な呼称がある。
寡占市場の企業戦略には3つの有名なモデルがあります。
ここで扱うシュタッケルベルグ・モデルは20世紀前半※に登場したモデルです。19世紀に登場したクールノーやベルトランとは違い、「情報」と「順番(時間の経過)」という2つの要素が盛り込まれている点が大きな特徴です。
このモデルをゲーム理論で考えると「完全情報における展開型ゲーム」に当てはまる。「完全情報≒情報」「展開型ゲーム≒順番(時間の経過)」という要素を表している。
※1934年に発表した『Marktform und Gleichgewicht (Market Structure and Equilibrium)』という書籍で発表された。


シュタッケルベルグ競争
はてな
ある寡占市場において「情報優位にある企業が先導者(leader)となり生産量を決定する。その後、先導者の行動(生産量)を確認した企業が追随者(follower)となり自社の生産量を決定する」と考えるとき、寡占市場の企業が利潤最大化のために生産量をどのように決定するか(どのような競争が行われるのか)の過程・結果を分析する。
特定の企業が優位な情報を持っていたり、戦略決定に時間差が生まれるような状況のとき、シュタッケルベルグ競争になりやすい。
シュタッケルベルク競争は「寡占市場で情報優位にある企業が生産量(価格)を先に決定して(先導者)、それに追随する企業が生産量(価格)を決定する(追随者)」と考えているため、「先導者モデル」と呼ばれる理由になっている。
例えば

「QRコード決済サービス」
近年では「なんちゃらpay」というサービスが乱立しています。よく見ると、ソフトバンク系の「ペイペイ」、NTT系の「d払い」、KDDI系の「auPay」、楽天系の「楽天Pay」など、実質的に大手キャリアの寡占状態です。
その中でも「ペイペイ」は、いち早く市場を開拓しています。
QRコードサービスを「キャンペーンを行って(=生産して)、実際に使ってもらう(=消費してもらう)」と考えれば、シュタッケルベルク競争に近いことが起こっているのではないでしょうか。
特にpaypayは、当初「100億円あげちゃうよキャンペーン」などを実施していました。その後、ライバルA社は、追随して数十億円程度のキャンペーンで追随しています。
paypayがキャンペーンを実施すると聞けば、ライバル企業は、それよりも規模を落としてキャンペーンを実施します(paypayが最初のキャンペーンで大量のユーザーを囲い込んだので、全部を巻き返すのは無理だから)。

「某害虫ホイホイ」これはアース製薬が有名です。
同様のジャンルの商品を扱っている企業は「大日本除虫菊(キンチョール)」「小林製薬(ブラックキャップ)」などです。
アース製薬が「某害虫ホイホイ」を販売しようとした時に、社長が「今市場に出すと類似品が出回る」と言い、1年間、商品の改良を行ってからの販売になりました。
社長の狙い通り、作り込んだ商品で勝負したアース製薬は市場シェアを確立しました。追随したライバル他社は、この商品の残りの市場シェアを奪うにとどまります。「先導者が生産量を決定、追随者はその後に生産量を決定する」というシュタッケルベルク競争に近い流れになっています。
前提
- 寡占市場の企業は、利潤最大化のために生産量を操作する。
- どちらかの企業が先に生産量を決定する(逐次手番ゲーム)
- ライバルの生産量は順次変化する
逐次手番ゲームとは、ゲーム理論の考え方の1つ。(1)あるプレイヤーが先に戦略を決定して、(2)次に別のプレイヤーが戦略を決定する、という条件で繰り広げられる戦略的状況のこと。交互進行ゲームとも呼ばれる。
ゲームのモデル
- 独占的な企業が2社(A社・B社)存在する複占市場を考える‥①
- この2社は同質的な財を生産している‥②
①数社が独占的に市場を支配していると「寡占」になるが、その中で2社が独占的に支配しているケースを特別に「複占」と呼ぶ。②「同質的な財=似たような財」のこと。製品差別化がされるケースものちに紹介します。
いま
次の条件を考える
- x=生産量(需要量)
- P=価格
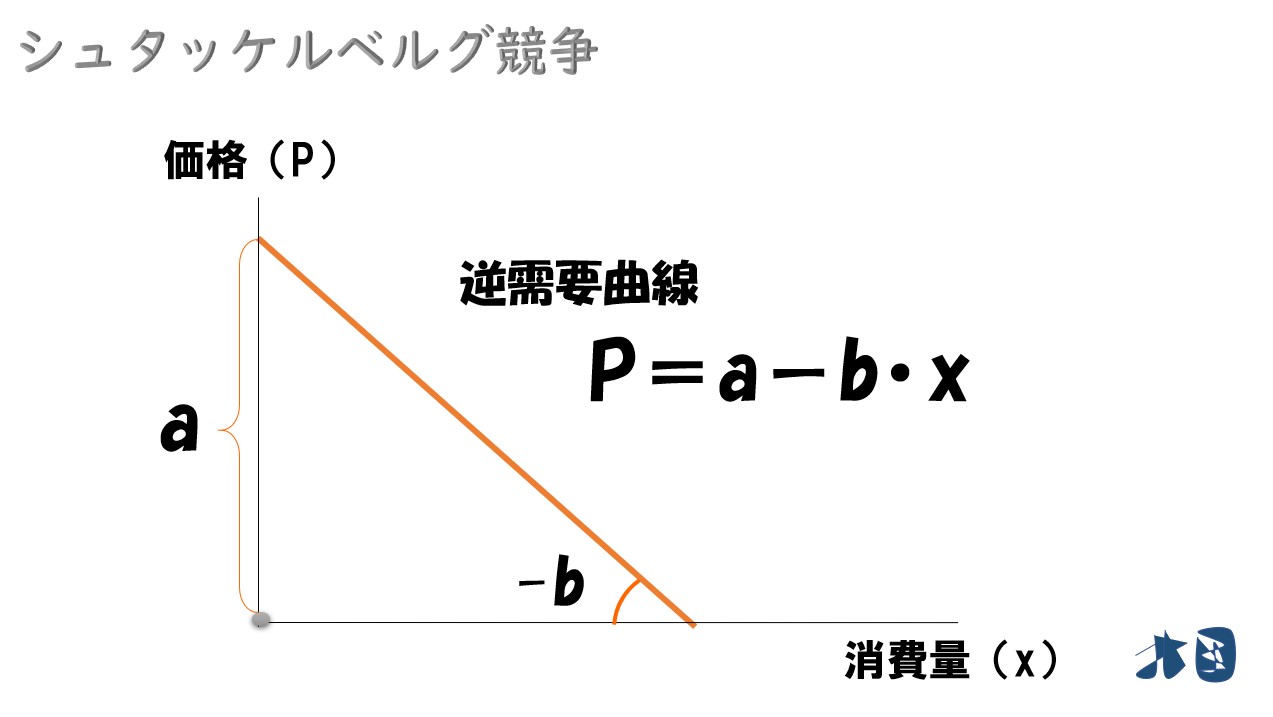
- 市場の逆需要関数(D)「P=a-b・x」‥①
- 2社の費用関数(C)「C・x」‥②
①逆需要関数というのは需要関数をP=の形にしたもの。②2社とも同質的な財を生産しているため、同じような費用関数になると考えています。
上記の条件のもとで、各社(今回のケースでは2社)が生産を行うと、最終的にどのような結果になるのかを考えます。①②はクールノー競争と同じです。
先に答えを書くと、最終的には「シュタッケルベルグ均衡」と呼ばれる状態にたどり着きます。
シュタッケルベルグ均衡
はてな
シュタッケルベルク競争の結果たどり着く状態を「シュタッケルベルグ均衡」と呼びます(もしくはシュタッケルベルグ解)と呼ぶこともあります。
※モデルの組み方によっては「クールノー・シュタッケルベルグ均衡」「ベルトラン・シュタッケルベルグ均衡」などと呼ばれることもあります。
※ゲーム理論ではシュタッケルベルグ均衡は「部分ゲーム完全均衡(サブゲーム完全均衡)」に分類される(シュタッケルベルグ競争は展開型ゲームに当てはまるため「バックワード・インダクション(後向きの帰納法)」によって均衡が得られる)。
ここからは均衡にたどり着く過程を説明します。競争(モデル)の前提条件などは前の段落で確認してください。
step
1企業Aの視点で考える
企業A
これからは電気自動車が主流になりそうなので、部品で使うモーターをたくさん生産しよう。⇒「xa」生産する。
※いい例が思いつかなかったので日本電産㈱を勝手にイメージしています。
step
2企業Bの視点で考える
企業B
A社が電気自動車向けので部品をたくさん作っているな。うちにも参入の余地がありそうだ。よし、生産開始だ!⇒「xb」生産する。
step
3ふたたび企業Aの視点
企業A
ライバル企業が市場に参入してきて生産開始したようだ。「xb」くらい生産しているから、うちもそれに合わせて生産量を変えていこう!⇒「⁇(ここがシュタッケルベルグ均衡になる)」


step
4数式で考える
はじめに企業Bの利潤を考える。
- (企業Bの利潤)=(価格)×(企業Bの生産量)-(企業Bの費用)
仮に2万個作って100円で売るとき「100円(P)×2万個(x)」です。
費用が1個当たり20円かかるなら「20円(C)×2万個(x)」です。
よって企業Bの利潤「π=100×2万-20×2万」
文字式に置き換えると
π[b]=P・x[b]-C・x[b]
教科書などでは添え字で「b」とか「1」など掛かれていますが、表現しきれないので[b]とつけて、π[b]やx[b]で企業Bの利潤や生産量を表しています。
次に「価格P」に注目する
初めに、市場の逆需要関数(D)「P=a-b・x」と表現したので「価格(P)」は「a-b・x」と表現できます。
グラフで見ると‥
生産量が多ければ価格や安くなるし、生産量が減れば価格は上昇する。ごく一般的な需要曲線を文字式を使って表しています。
ポイント①
更に「x」は、市場全体の生産量を表しています。
A社とB社しかいない複占市場を考えていたので、市場全体の生産量は「企業Aの生産量(x[a])+企業Bの生産量(x[b])」です。
つまり「x=x[a]+x[b]」となるため「P=a-b (x[a]+x[b])」
以上より
価格は「P=a-b (x[a]+x[b])」と表現できる。
上記の式を、企業Bの利潤を求める式「π[b]=P・x[b]-C・x[b]」に代入する。
⇒「π[b]=(a-b (x[a]+x[b])・x[b]-C・x[b]」
全体を「x[a]」でくくる
⇒「π[b]=(a-b (x[a]+x[b])-C)・x[b]」
カッコ内(-bの部分)を展開する
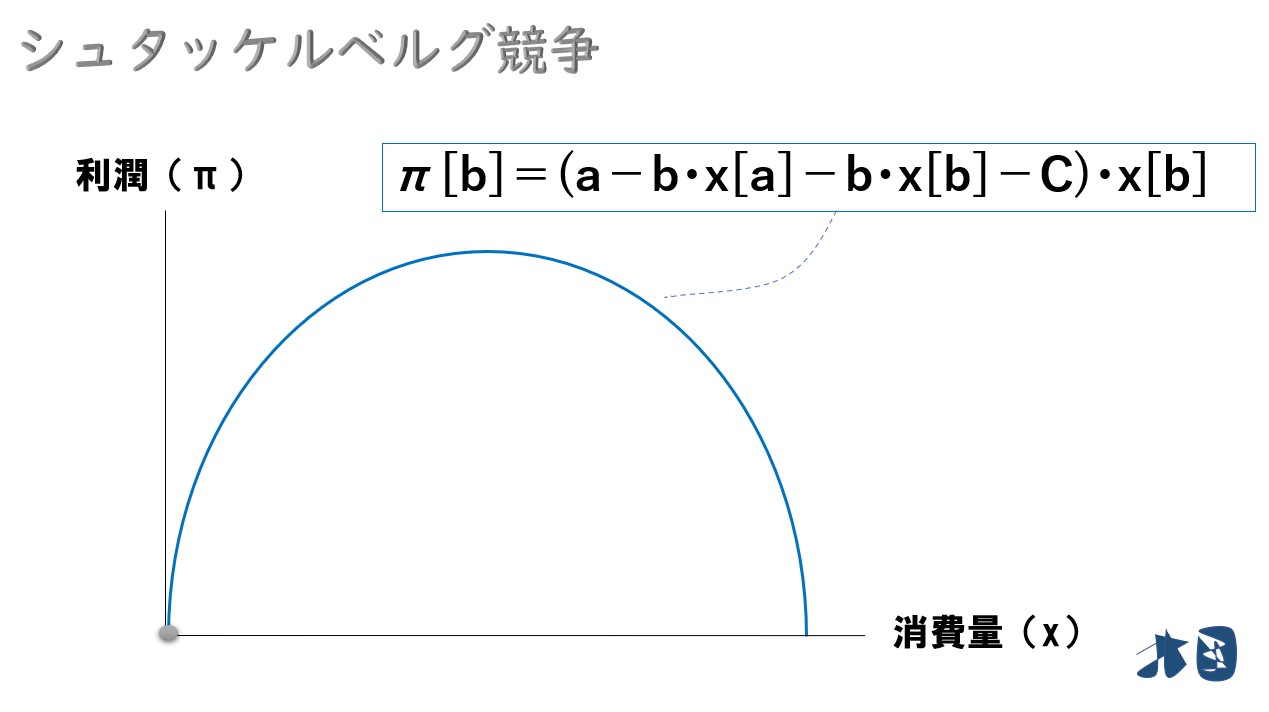
⇒「π[b]=(a-b・x[a]-b・x[b]-C)・x[b]」


step
5企業Bの利潤をグラフで考える
式を展開すると「-b・x[b]の2乗」が登場するため「π[a]=(a-b・x[a]-b・x[b]-C)・x[b]」は2次式です。中学校の数学を思い出してもらえればいいのですが、〇の2乗が登場する数式は放物線を描くようなグラフになります。
グラフの縦軸と横軸に注目
- 縦軸=企業Bの利潤の大きさ「π[b]」
- 横軸=企業Bの生産量「x[b]」
ポイント
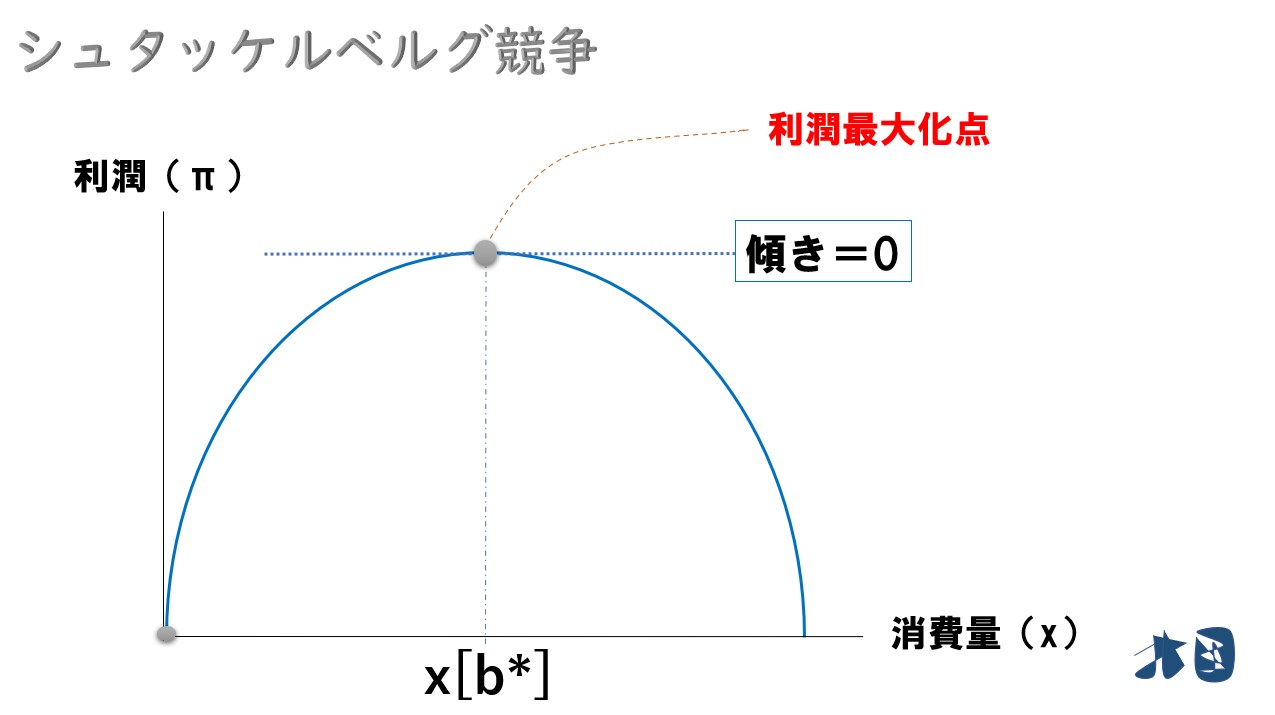
このグラフは、企業Bが生産量(xb)を増やすと利潤(π)がどのように変化するかを表している。グラフより、企業Bはグラフが頂点を描くときの生産量(x[b])にすれば利潤最大化を実現できることが分かる。
グラフの頂点では「傾きが0」になることにも注目する。
step
6企業Bの利潤最大化条件を計算する
先ほどのグラフより、グラフの傾きが0になるとき、企業Bの利潤が最大化します。
ポイント
- π[b]=(a-b・x[a]-b・x[b]-C)・x[b]
↑この式の傾きが0になる瞬間を求めれば利潤最大化点が分かる。


数学的には「微分して、イコール0」にすればOKです!
微分の意味が分からない人向けに簡単に補足です。微分は、グラフを細分化して、その小さな点の傾きがどれくらいなのかを計算できます。つまり、グラフの放物線の傾きが0になる⇒「微分した結果がイコール0になるはず」というわけです。
以上より
- 企業Bの生産量(x[b])で微分します。
「=0」で結びます。
最後に
企業Bの生産量(x[b])を求めます
企業Bの最適な生産量が求まりましたが、注意点があります。
この計算段階では、企業Aの生産量(xa)が文字として残っており、あくまで「企業Aの生産量(xa)に、この数式のように対応する」という戦略を表しています。
意味が分からなければ一旦飛ばしてOKです。
step
7再び企業Aの視点を数式で考える
- 企業Aは、企業Bの生産量「xb=(a-C)/2b-xa/2」を確認して、自社の生産量(xa)を調整します
企業Aの利潤の式「π[a]=(a-b・x[a]-b・x[b]-C)・x[a]」に企業Bの生産量を代入する。
企業Aの利潤式の求め方は、企業Bのときと同じなので省略します。


step
8企業Aの利潤が最大化する生産量を求める
企業Aの利潤式を微分して0と置きます。
企業Bの利潤最大化を求めたときに、利潤の式を「微分してイコール0」としたのと同じ考えです(説明は省略します)。
企業Aが最初に生産を開始して、それを見た企業Bも追随して生産を行います。企業Bが追随してきた状況を考慮して、最終的に企業Aは上記の生産量に落ち着きます。 ・x[a]=(a-C)/2b
最終的に
最終的に、企業Aと企業Bは上記の生産量(戦略)と取る。 シュタッケルベルグ競争の結果、たどり着いた2社の生産量(戦略)をシュタッケルベルグ均衡(部分ゲーム完全均衡)と呼ぶ。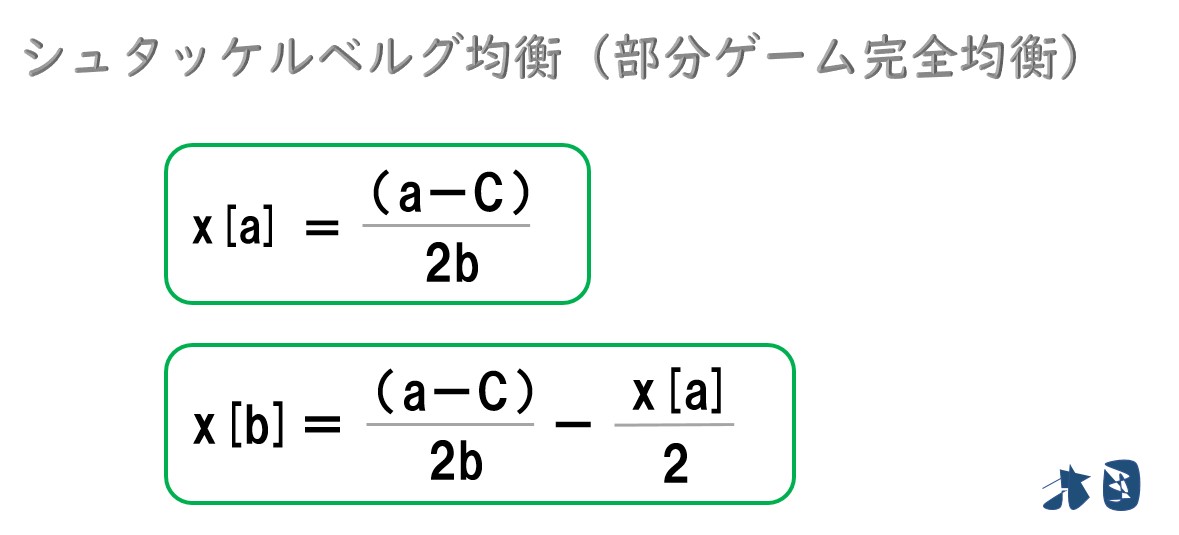
ちなみに
企業Bの生産量に「xa」という文字があるので、更に企業Aの生産量(xa)を代入することが出来ます。
以上より
シュタッケルベルグ均衡における2社の具体的な生産量は‥
シュタッケルベルグ均衡は「2社は、最終的にこの戦略(数式)で生産量を決めます」というものです。その均衡における具体的な生産量が上記となります。 違いが分からない人は、計算問題で「シュタッケルベルグ均衡を求めよ」と言われたら、先ほどの答えを計算する。 「シュタッケルベルグ均衡における生産量を求めよ」と言われたら、上記の具体的な生産量を計算する。 シュタッケルベルグ競争は、企業Aと企業Bが順番に生産量を考えていくモデルのため「具体的な生産量を均衡点とは考えない」で、「2社が生産量を決定するために取る戦略の組合せ」を均衡と考えている※。 ※「相手の行動を見ながら戦略を考える」というのは動的な(=たえず状況が変化する)状態なので「具体的な数字(生産量)がこうなる」と考えるよりも「お互いは、こういう戦略を取る」と考える方が応用が利く。この戦略の組合せ(「お互いは、こういう戦略を取る」)をゲーム理論では「部分ゲーム完全均衡」と呼び、シュタッケルベルグ均衡は「部分ゲーム完全均衡」に当てはまる。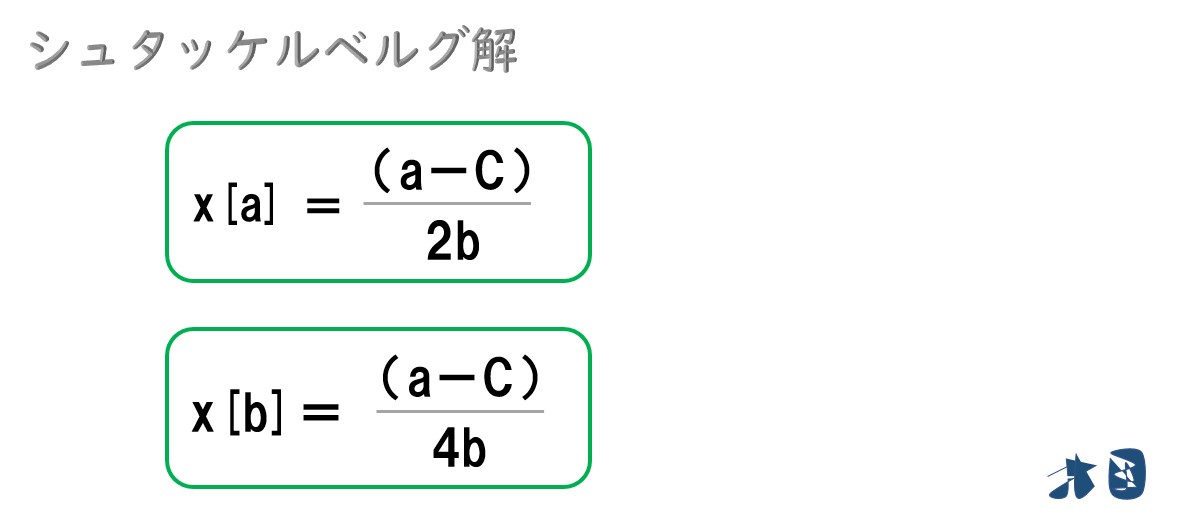


反応曲線
はてな
相手の生産量に応じて自社の生産量をどれくらいにしたらよいかを表した曲線(もしくは関数)。「反応曲線」「最適反応関数」とも呼ばれる。
ポイント
シュタッケルベルク競争の反応曲線は、クールノー競争のときと同じ反応曲線になるが均衡点が異なる。
はじめに
グラフを描く前に、最適反応を表す式を求めます。
シュタッケルベルク均衡を求めるときに登場した式を使います。どのような経緯でこの式が出てきたのか理解できない人は戻って確認してください。
この2つの式は、企業Aと企業Bの利潤式を「微分してイコール0」と置いたときの式です。シュタッケルベルク競争が行われているときの利潤最大化式を表す(1階条件)。
この式を「生産量(x)=~」の形にすれば最適反応曲線となります。
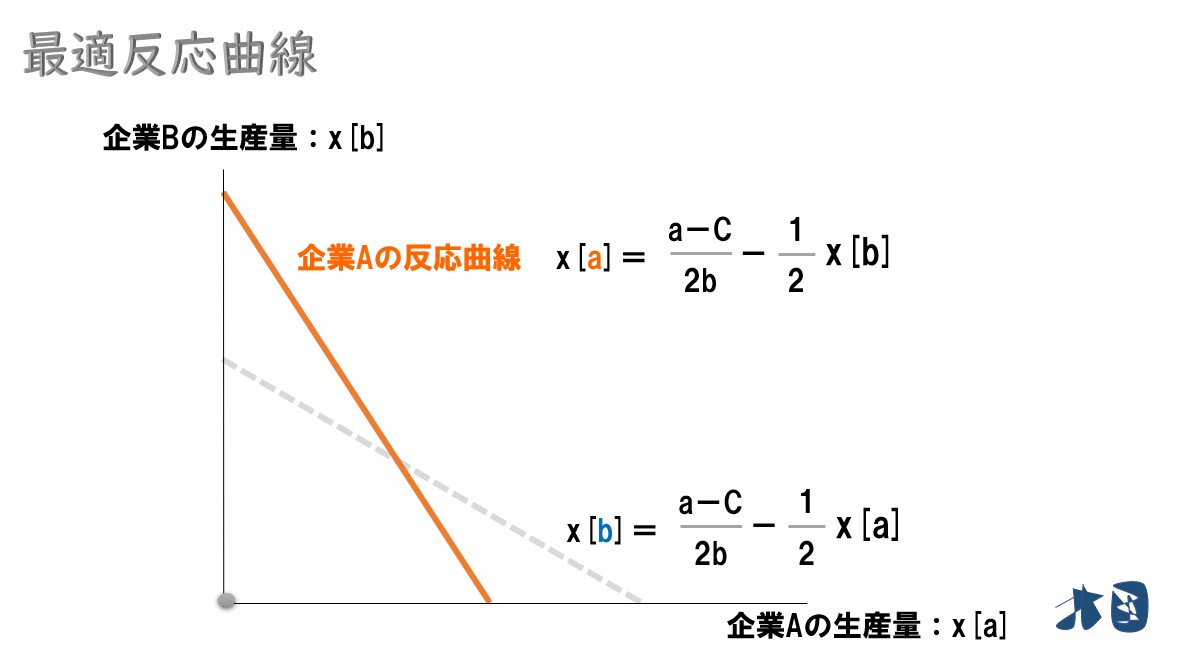
企業Bの式を変形してみる
ポイント
企業Bの最適反応関数=(a-c)/2b-1/2x[b]
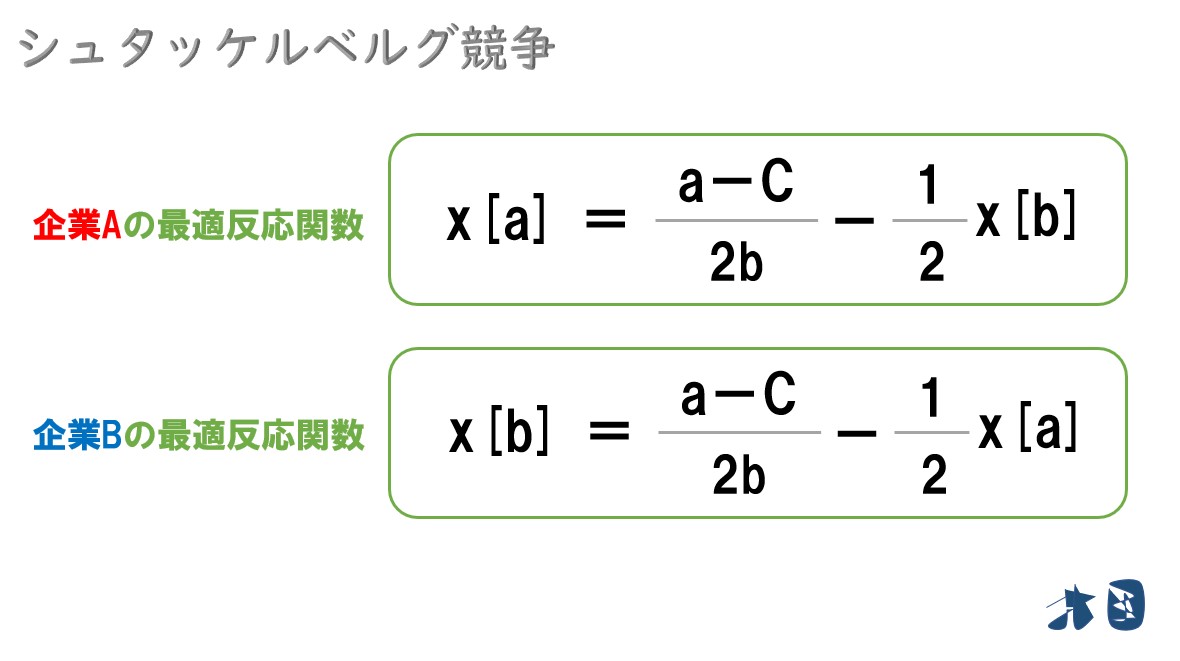
よって、A社・B社の最適反応関数は‥
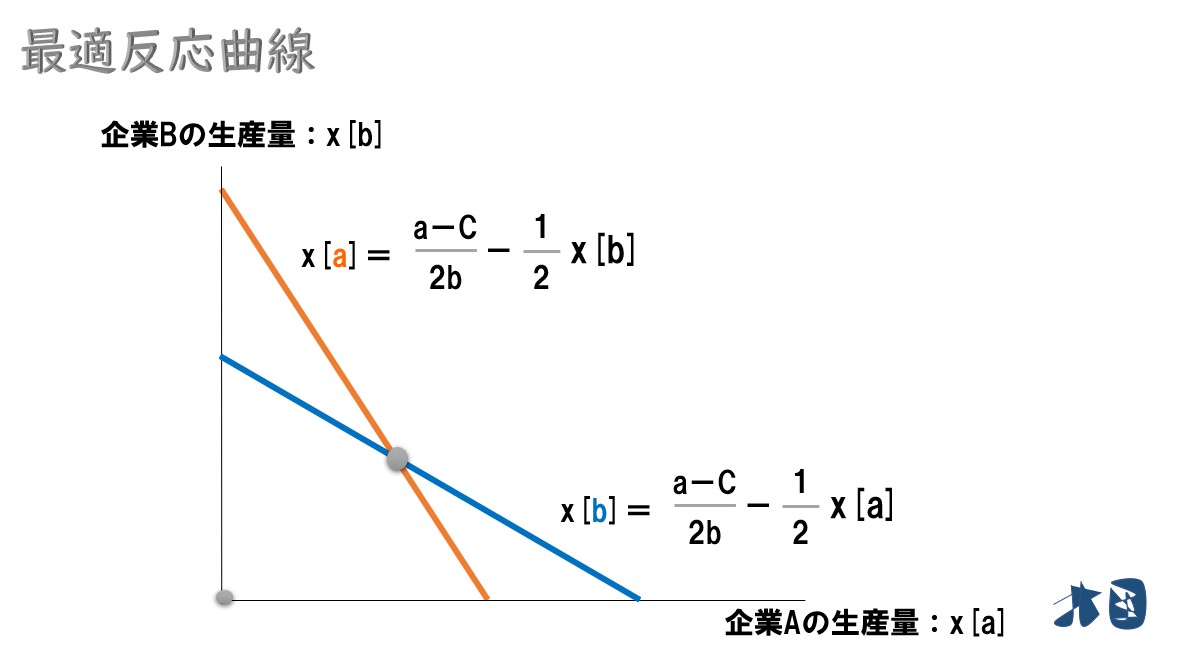
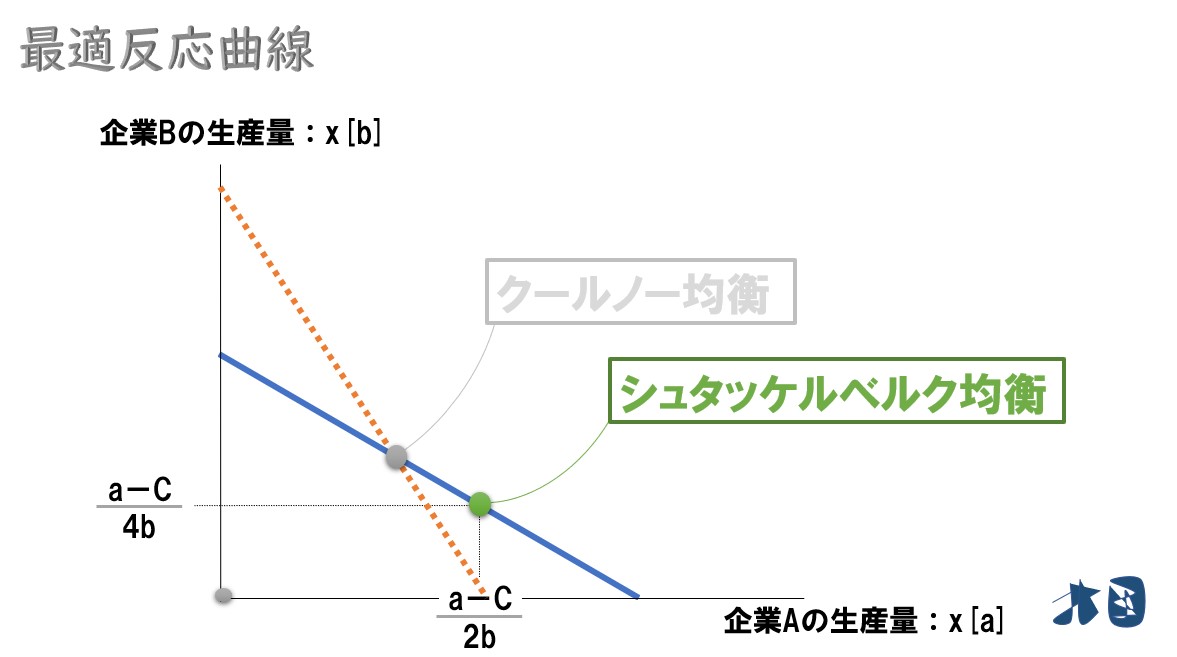
グラフにすると‥
初めて見る人は、グラフが少し分かりづらいかもしれません。ただ、2つの式が対照的でほとんど同じなので、グラフも似たような感じになっている程度でOKです。
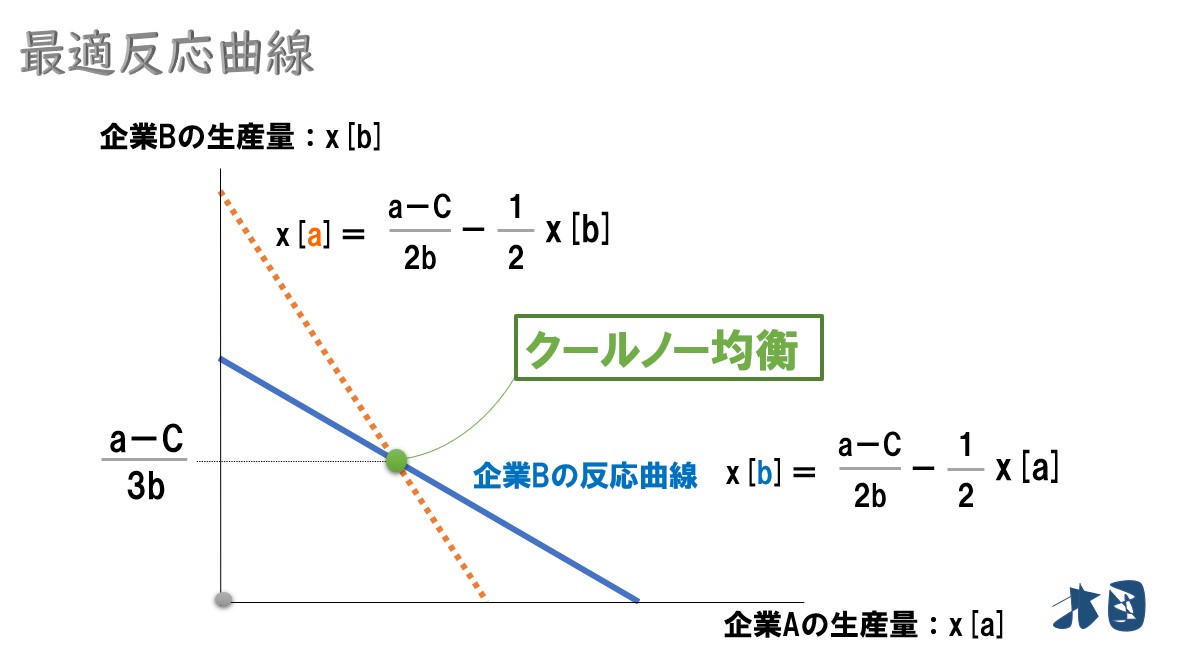
ちなみに2つの最適反応曲線が交わっている点はクールノー均衡です。


はじめに
シュタッケルベルク競争で「企業Aを先導者」「企業Bを追随者」と考えます。
企業Aは先に「xa」だけ生産しています。その後、企業Bは「企業Aは「xa」くらい生産している」と分かりました。イメージですが、企業Aの最適反応曲線が分かったような感じです。
なので
企業Bは「企業Aは「xa」くらい生産している」と分かったので、自社の最適反応曲線に沿って「クールノー均衡」の部分で生産量を決定します⇒「(a-C)/3b」
ここで
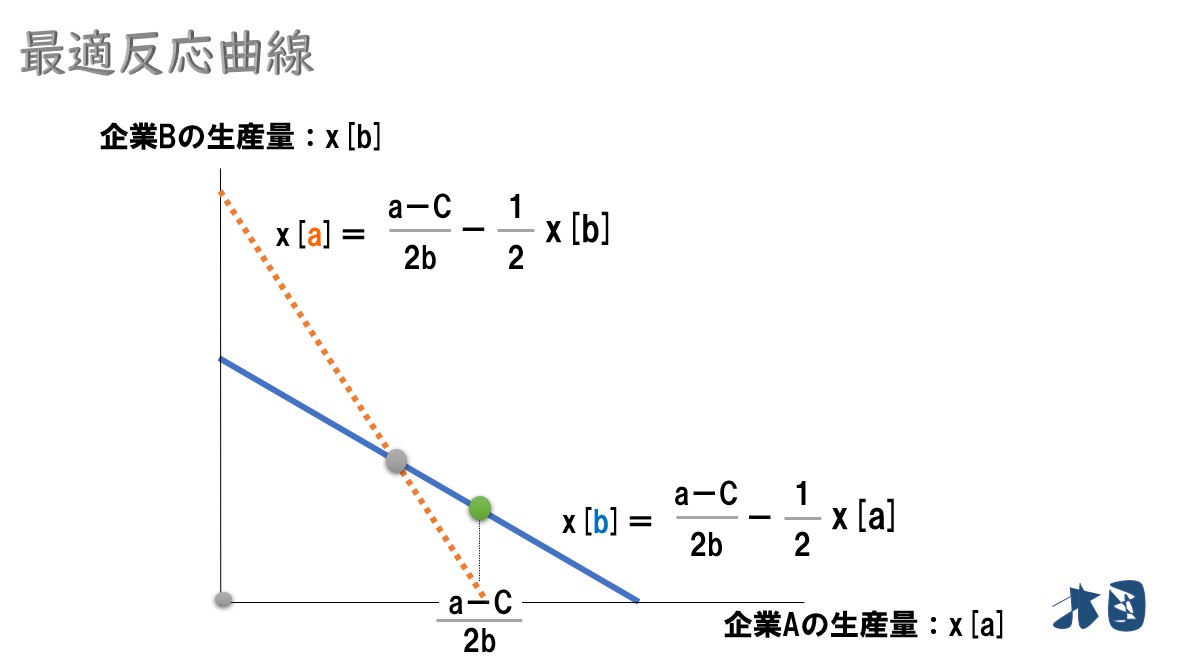
シュタッケルベルク競争では、企業Aは、企業Bの行動に合わせて自社の生産量を再調整します。
企業Aは、企業Bの行動を想定して自社の生産量を調整(増産)しました(企業Bの最適反応曲線上に生産量を動かせば、企業Bもさらに対応してくる)。
⇒「(a-C)/2b」
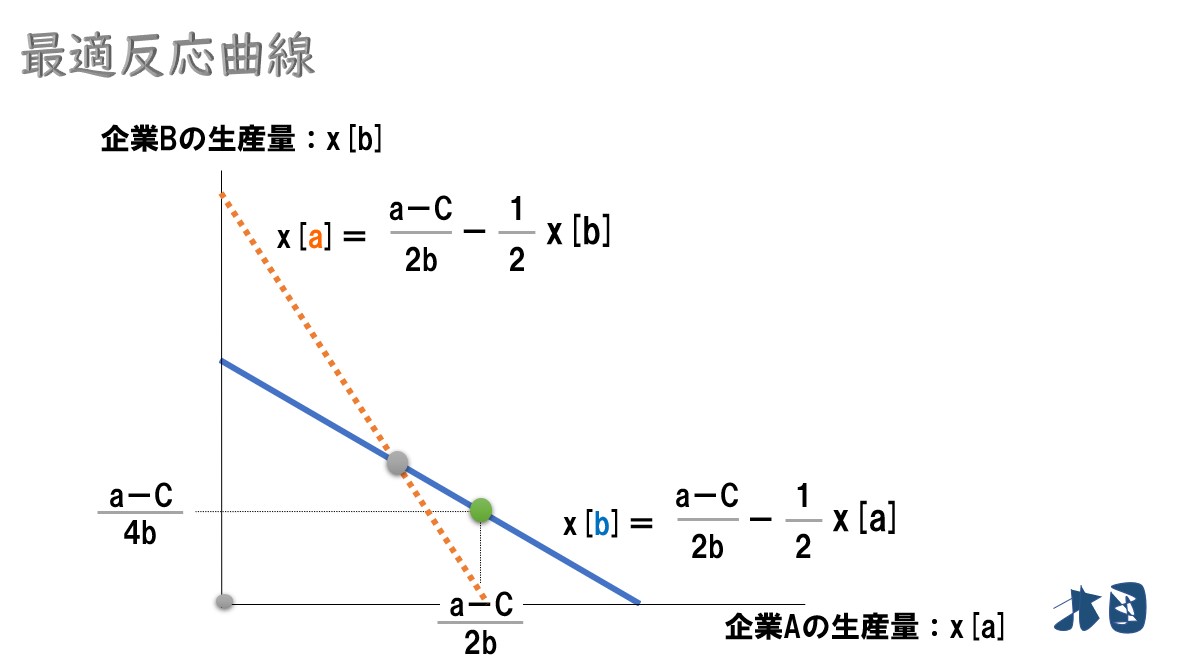
最後に
企業Bは、最終的に企業Aの行動に合わせて自社の生産量を調整(減産)します。
⇒「(a-C)/4b」
以上より


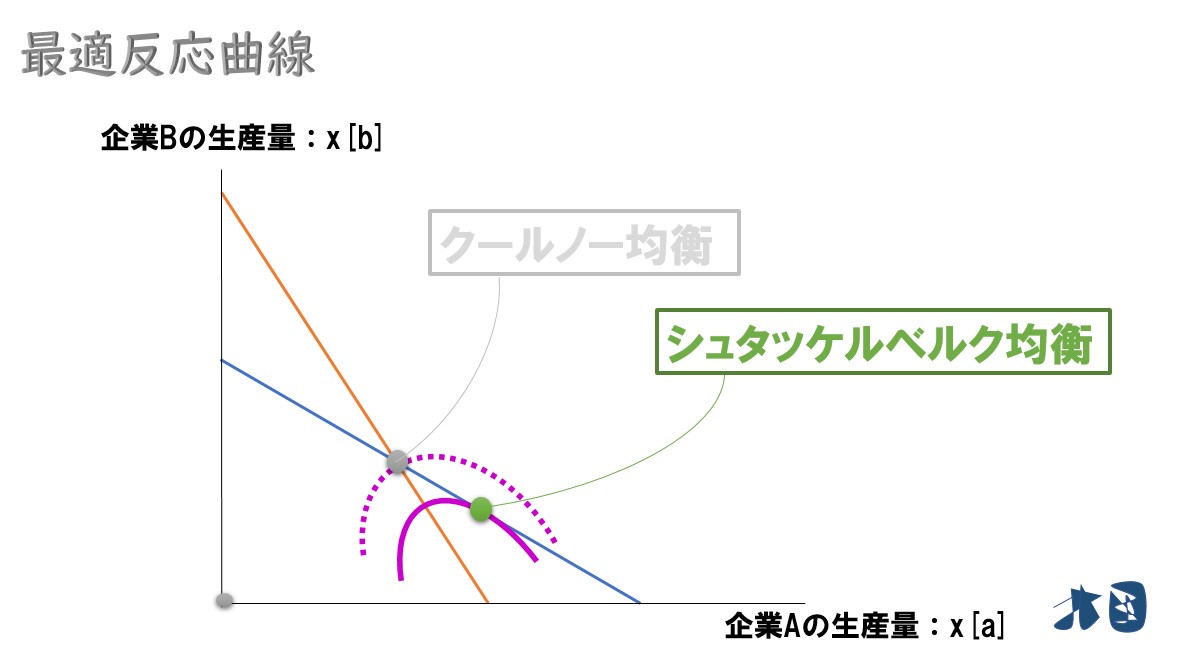
等利潤線
はてな
同じ利潤水準を表した曲線のこと。
シュタッケルベルグ均衡を求めるときに‥
企業Bの利潤式(π)を次のように求めました。
- π[b]=(a-b・x[a]-b・x[b]-C)・x[b]
シュタッケルベルク均衡を求めるときに登場した式を使います。どのような経緯でこの式が出てきたのか理解できない人は戻って確認してください。
企業Aも同様に考えて2社の利潤式は‥
2つの式から等利潤線をイメージします。
例えば「企業Aの利潤(πa)を100」と考えたとき2社の生産量の組合せが複数あります。
- 企業Aの生産量「xa」
- 企業Bの生産量「xb」
これを曲線で表したものが等利潤線です。
例えば
企業Aが100の利潤を実現しようとするとき、2社の生産量の組合せが複数あります。例えば次の2つです(実際にそうなるとかではなく、あくまでイメージです)。 このように、同じ利潤を実現させる生産量の組合せを結んでいくとピンク色の点線になります。これが等利潤線と呼ばれるものです。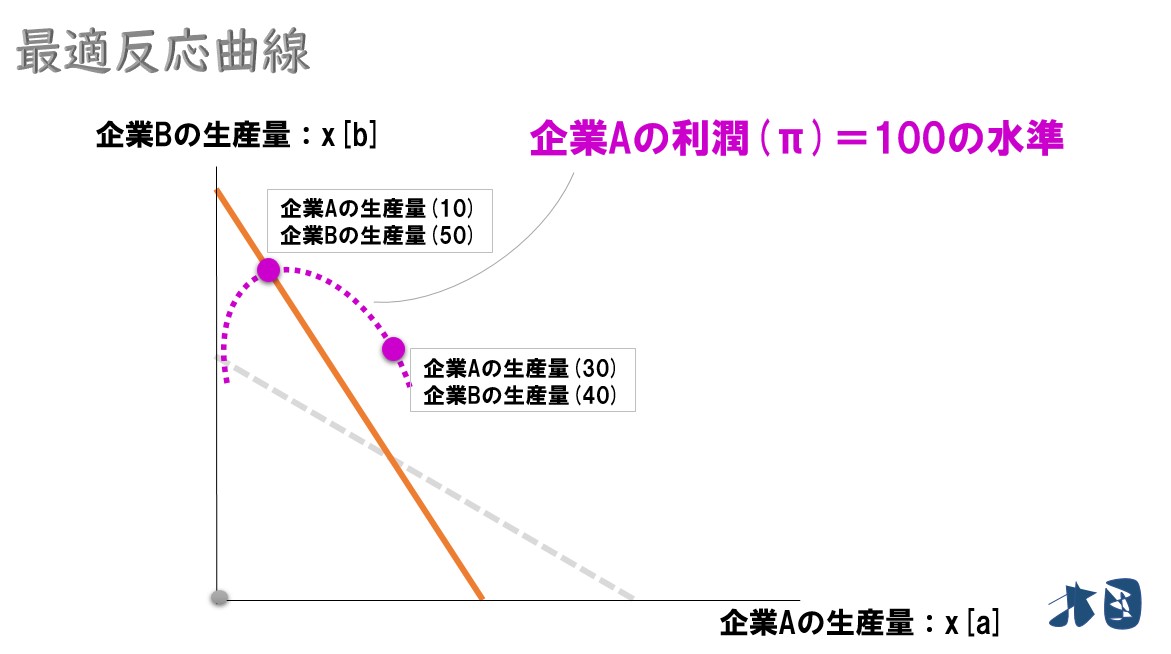
つまり
利潤が大きくなると等利潤線も下方向へ移動します。というのも、一般的に生産&販売量を増やすほど利潤が増えるはずです。 なので、企業Aが生産量を増やすほど利潤も大きくなる=等利潤線は右下方向へ移動します。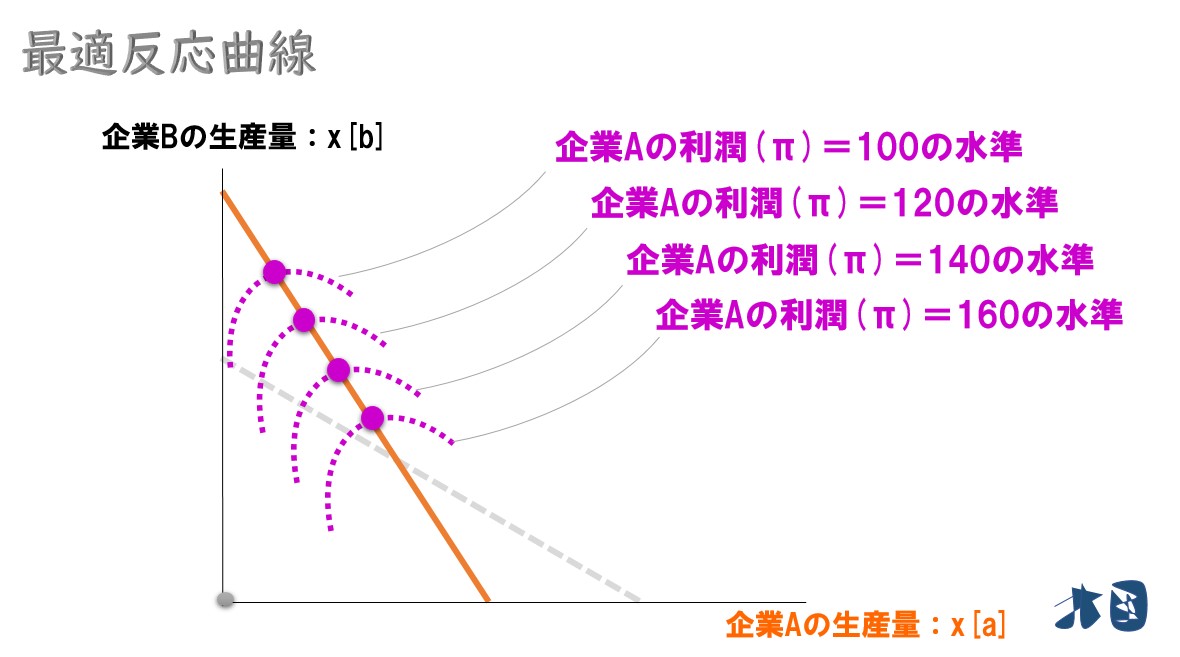
それで何が分かるのか
- 等利潤線についてイメージできたところで本題です
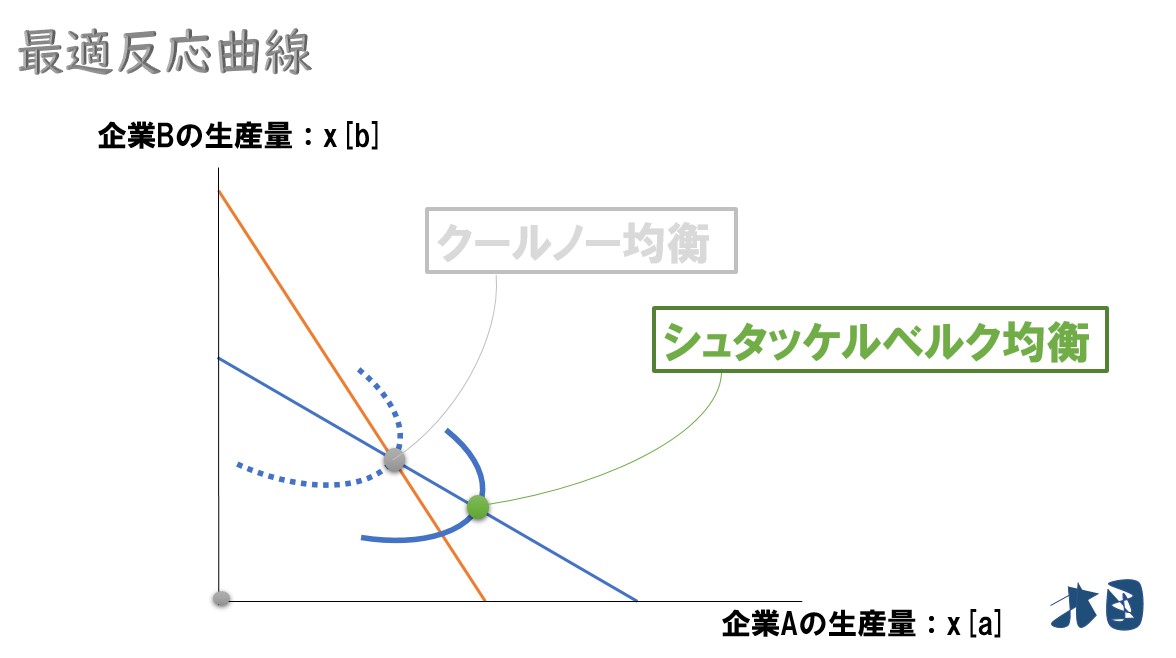
ここで、クールノー均衡とシュタッケルベルク均衡に接する等利潤線を考えます。
グラフより、クールノー均衡よりもシュタッケルベルグ均衡の方が右下にあります。
つまり「クールノー均衡に接する等利潤線」よりも「シュタッケルベルグ均衡に接する等利潤線」の方が右下に位置しています。
企業Aの視点で考えると、利潤が大きくなるほど等利潤線は右下へ移動するという話だったので、企業Aにとっては、シュタッケルベルグ均衡のときの方が利潤が大きくなることが分かります。
逆に企業Bの視点で考えると
企業Bの場合、等利潤線が左上に行くほど利潤が大きくなります(企業Aの生産量(xa)は横軸に取っていましたが、企業Bの生産量(xb)は縦軸に取っている影響)。
逆を言えば、企業Bは、右下に位置する等利潤線の方が利潤が小さいです。
つまり、企業Bにとっては、シュタッケルベルグ均衡のときの方が利潤が小さくなることが分かります。
クールノー競争(同時に生産量を決定するケース)とシュタッケルベルグ競争(先導者が先に生産量を決定するケース)を比べるとき
クールノー競争よりもシュタッケルベルグ競争によって
- 先導者となる企業(ここでは企業A)は利潤が大きくなる
- 追随者となる企業(ここでは企業B)は利潤が小さくなる
ポイント
以上より、生産量競争を行う場合、企業は(正しい情報のもとで)相手よりも先に行動することで利潤を大きくすることが出来る。逆に相手よりも行動が遅れた企業は利潤が小さくなる。


ゲーム理論的に考える(おまけ)

ここまで、数式をメインに考えてきましたが、もう少しゲーム理論的にシュタッケルベルグ競争を考えてみます。
シュタッケルベルグ均衡を「部分ゲーム完全均衡」と表現しましたが、ゲーム理論の展開図やバックワードインダクションを使ったときに登場する表現です。
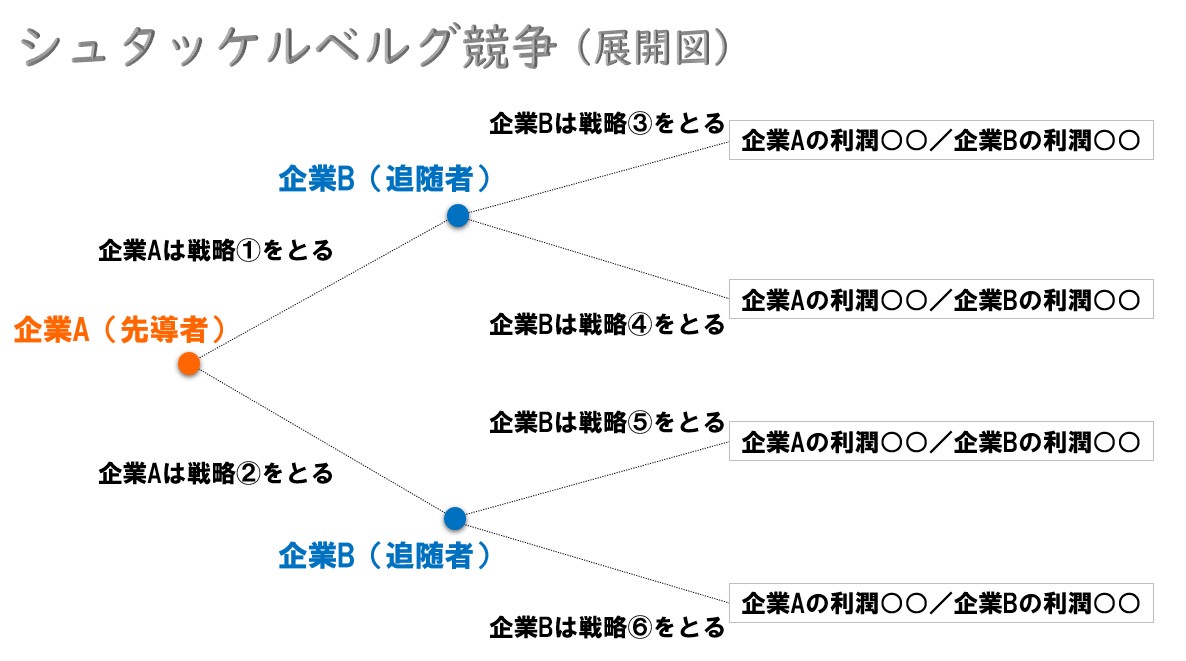
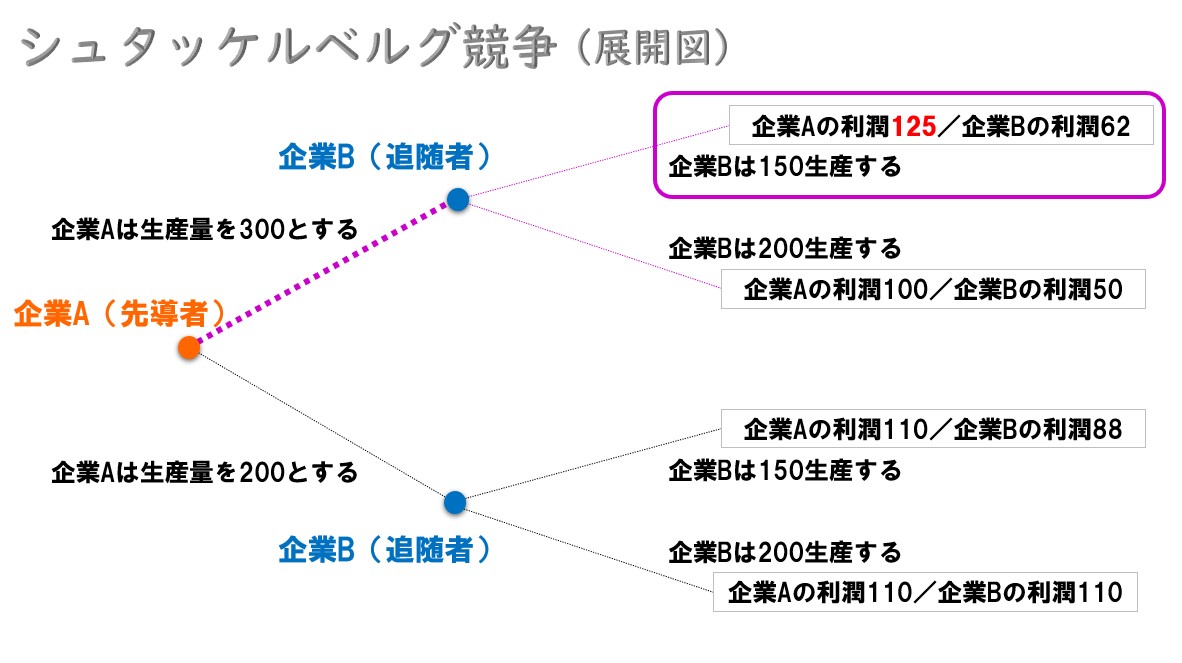
展開図(ゲームの樹)
先導者と追随者に分けるシュタッケルベルグ競争は、次のようなグラフで表現できます。
これをゲーム理論では「展開図(ゲームの木/ゲーム・ツリー)」と呼びます。
バックワード・インダクションと部分ゲーム
バックワードインダクションは「展開図の終わりの部分から、自分が一番得をする結果を得るにはどうすれば良いかを考える方法」です。後向き帰納法とも言う。
シュタッケルベルグ競争なら
いま、このような展開図(ゲームの木)があります。このとき、企業Aは次のような行動を取ります(数値は例です)。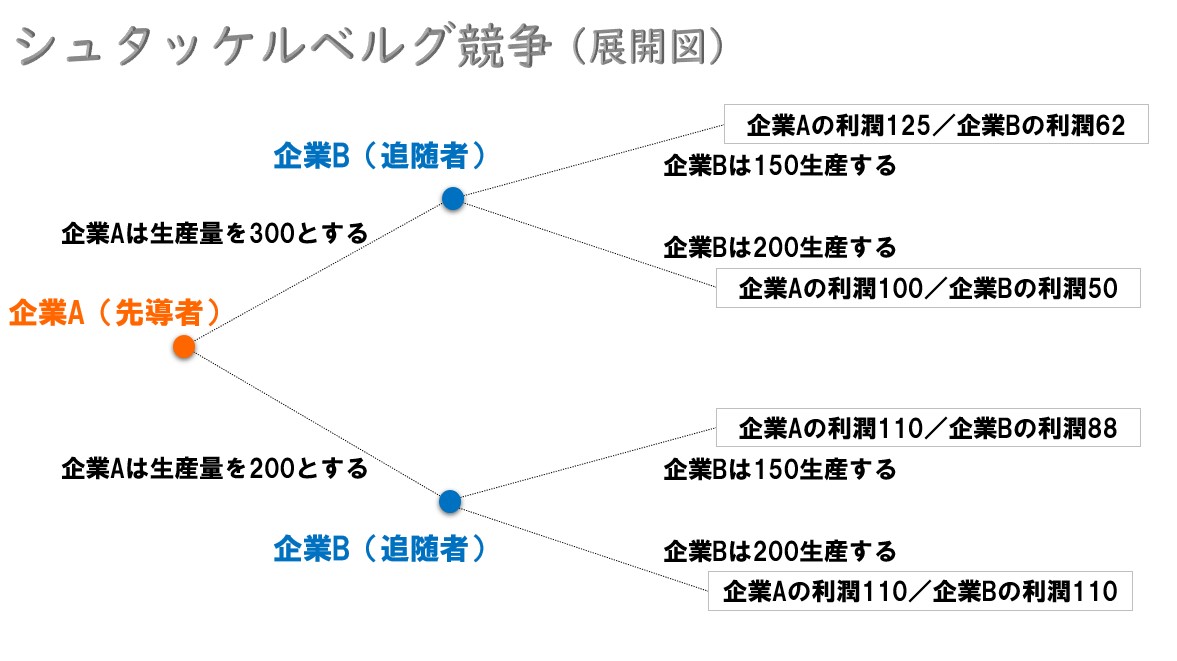
企業Aは、とりあえず一番大きな利潤を目指す


この時、企業Bはどのような行動を取るかを考える
《企業Aが300の生産量とするとき》 企業Bが150生産するか or 200生産するかを選択するとき「利潤62を得られるので150生産する方がよい(200を生産して利潤50を得るときと比べて)」 ⇒なので、企業Aは当初の狙い通り、300の生産量を実施すればよい。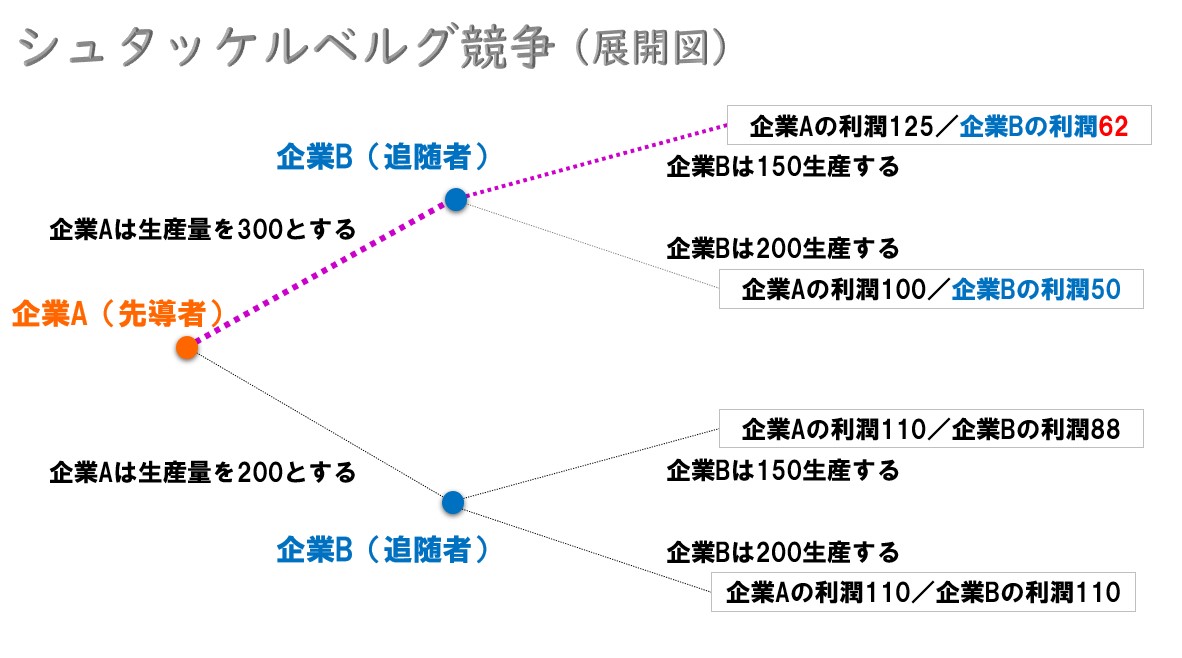
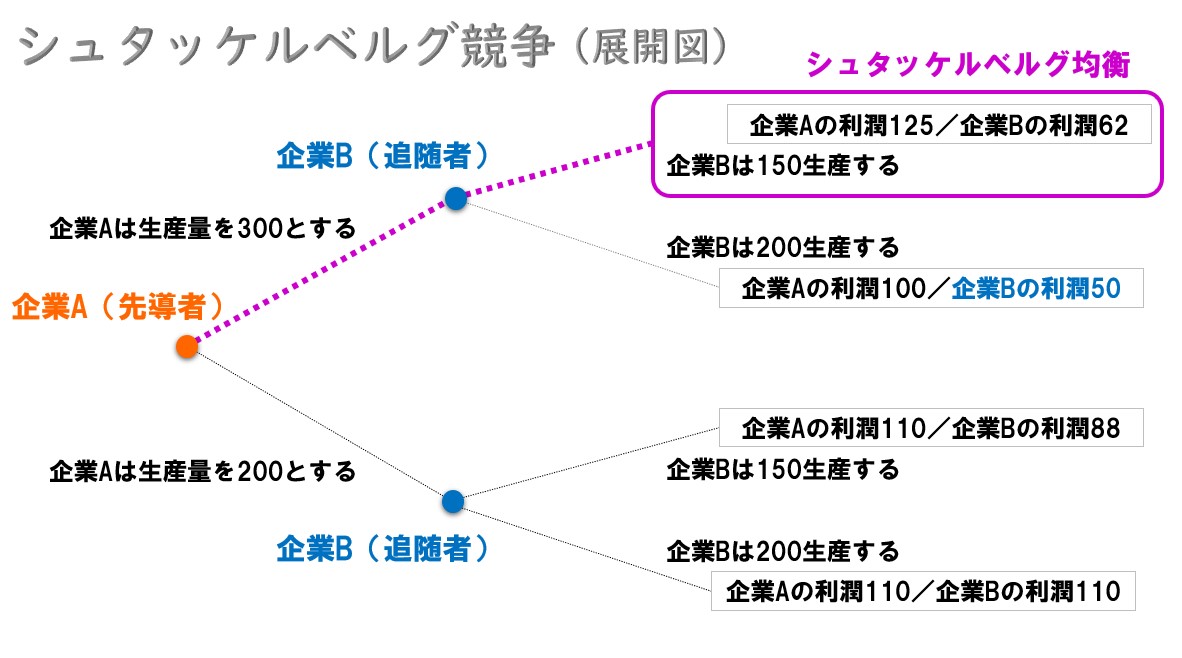
以上より
「企業Aが300」「企業Bが150」生産するというのがシュタッケルベルグ均衡となる。
部分ゲーム完全均衡
企業Aが300生産すると「企業Bは150生産するか or 200生産するかを選択する」ことになります。ゲーム理論ではこれを部分ゲームと呼びます(緑色の枠内)。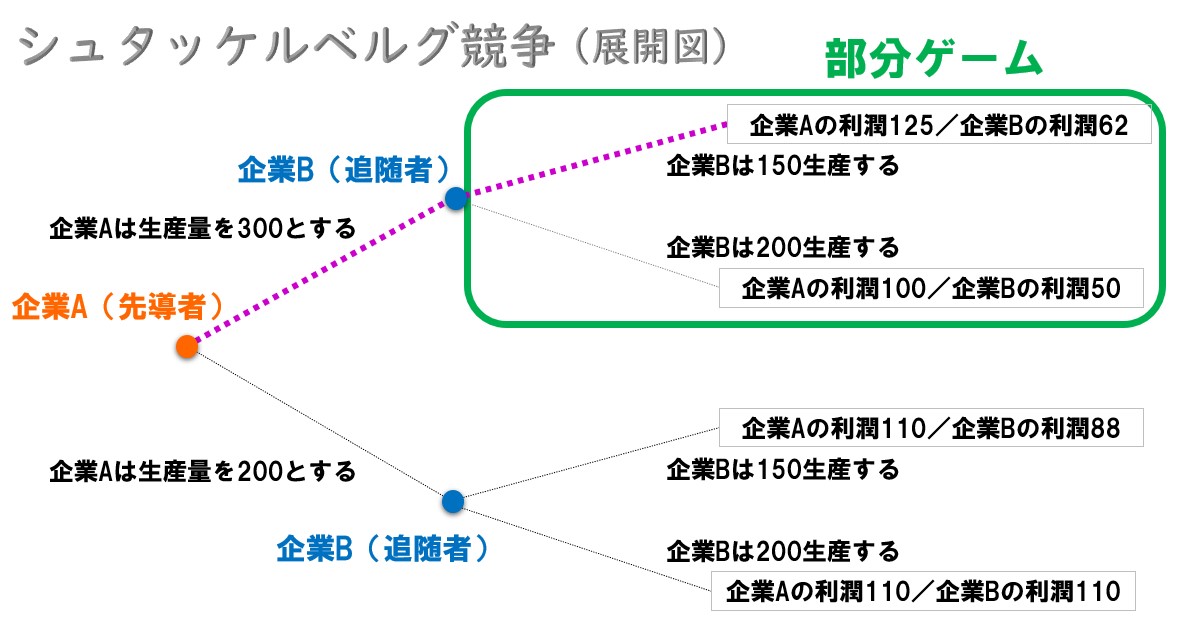
ポイント
部分ゲームで考えたとき、企業Bは「200を生産して利潤50を得る」よりも「150生産して利潤62を得る」ほうが得をするので、企業Bは150を生産するという行動を取る。
部分ゲームで考えると企業Bが合理的に行動するなら、選択肢が必然的に決まる。この必然的に決まった選択を「部分ゲーム完全均衡」と呼ぶ。
シュタッケルベルグ競争では、先導者となる企業Aが先に生産量を決める。その後、企業Bが生産量を考えるという部分ゲームに突入する。その結果、選択肢(戦略)が必然的に決まる。
ここで決まった戦略がシュタッケルベルグ均衡になるが、展開図で考えれば部分ゲーム完全均衡になっている。つまり「シュタッケルベルグ均衡」は「部分ゲーム完全均衡」になっている。


計算問題

いま、企業Xと企業Yの2社が支配する複占市場を考える。2社は同質的な財を生産している。
- 需要関数:D=12-P
- X社の生産量=x
- Y社の生産量=y
- X社費用関数(Cx)=x
- Y社費用関数(Cy)=2y
このとき、企業Xを先導者・企業Yを追随者(企業Xの生産量を所与として利潤最大化を目指す)として、シュタッケルベルグ均衡における下記2つを求めよ。
- 価格
- 2社の利潤
はじめに
2社が生産したものが需要されるため
- 需要(D)=「X社の生産量+Y社の生産量」
よって「12-P=x+y」
先に企業Xの利潤を考える。
- X社の利潤=「価格×生産量-費用」
- よって「πx=P・x-Cx」
「12-P=x+y」より「P=-x-y+12」‥①
X社費用関数(Cx)=x‥②
①②を代入する
・πx=P・x-Cx
・(-x-y+12)・x-x
・-xの2乗-xy+12x-x
・-xの2乗-xy+11x
・-xの2乗+(11-y)x
同様に企業Yの利潤は
・πy=P・y-Cy
・(-x-y+12)・y-2y
・-yの2乗-xy+12x-2y
・-yの2乗-xy+10y
・-yの2乗+(10-x)y
ここで
追随者の企業Yは、上記の情報をもとに自社の利潤最大化を実現する生産量を決定します。
なので、企業Yの利潤の式を「微分して=0」とする。
「-yの2乗+(10-x)y」を「生産量=y」で微分する
「y」という文字がついている部分の乗数を減らして手前に持ってくる。また0乗になった部分は「1」となることに注意する。
Δπ/Δy=
・-2y+10-x=0
・2y=10-x
・y=5-0.5x
更に
先導者である企業Xは、企業Yが上記のような行動を取ることを見越して生産量を調整する。
なので、企業Xの利潤式に上記で求めた「y=5-0.5x」を代入する。
企業Xの利潤式:-xの2乗+(11-y)x
⇒-xの2乗+(11-5+0.5x)x
=-xの2乗+(6+0.5x)x
=-0.5xの2乗+6x
=-0.5(xの2乗-12x)
=-0.5(x^2-12x-36+36)
=-0.5(x-6x)^2+18
x=6のとき、最大値18を取ることが分かる。
企業Xは「生産量(x)=6」「利潤(πx)=18」となる。
計算結果を企業Yの利潤最大化式「y=5-0.5x」に代入する
企業Yの利潤最大化式(微分した方):y=5-0.5x
⇒y=5-0.5・6
=5-3
=2
XとYの生産量を企業Yの利潤式に代入する
企業Yの利潤式(微分する前):-yの2乗+(10-x)y
⇒-2の2乗+(10-6)2
=-4+(4)2
=-4+8
=4
企業Yは「生産量(y)=2」「利潤(πy)=4」となる。
以上より、シュタッケルベルグ均衡のときの生産量は(x,y)=(6,2)である。
途中で、需要(D)「12-P=x+y」と求めたので、この式へ代入する。
・12-P=x+y
・12-P=6+2
・12-P=8
・12-8=P
・P=12-8
・P=4
シュタッケルベルグ均衡のときの価格は4である。