ミクロ経済学の第1ステップの「効用関数」
- 効用関数とは?(定義)
- 効用関数のグラフ
- 効用関数と限界効用
- 効用関数と無差別曲線
- 効用関数の種類
- 効用関数と需要関数
効用関数で登場する基本的な情報をまとめています。
効用関数とは?(財が1つ)

効用関数の定義
効用を数値に置き換えて関数化したもので、効用の選好が①完備性 ②推移性を満たす関数のこと。価値関数とも言う。
経済学では、人は「効用 (満足度)」を最大化するように行動するという前提
「効用 (満足度)」という考え方を使って経済を分析する時に、数値化することで分析しやすくなります。そこで「効用 (満足度)」を数値化して効用関数として扱うのです。


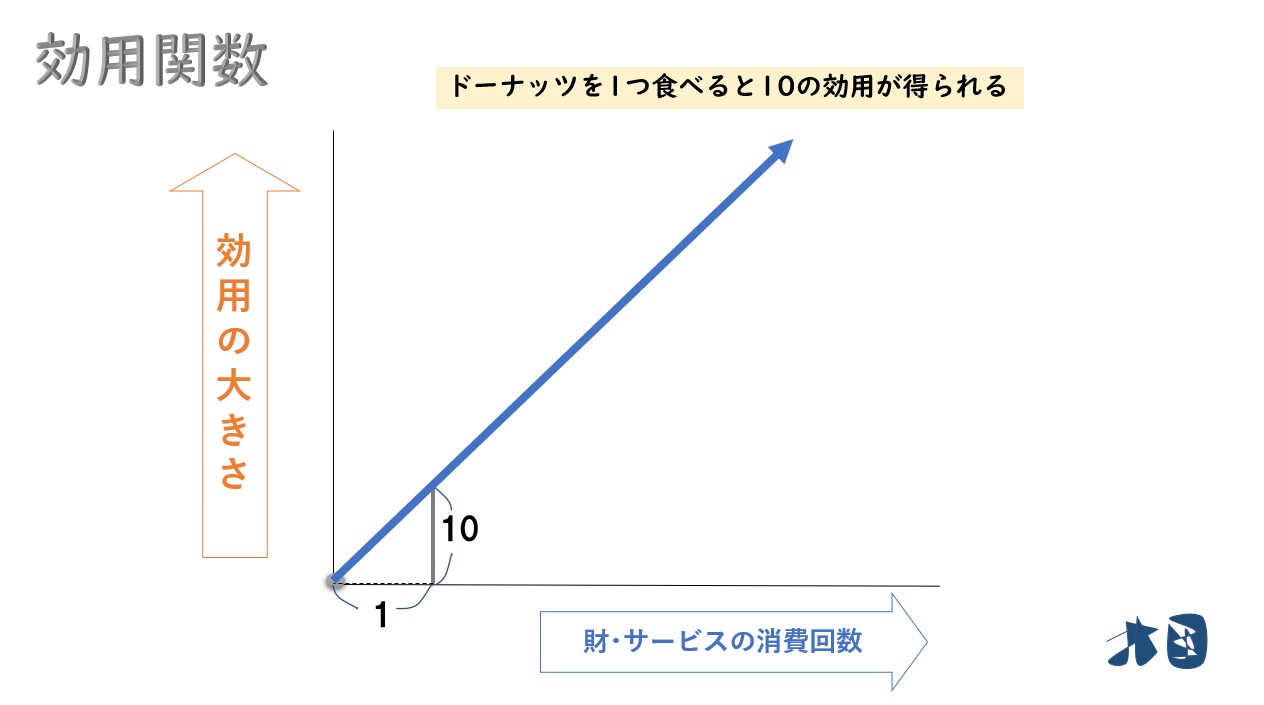
例えば
- ドーナッツを1つ食べて得られる効用(満足度)を10とします。
こんなグラフ(効用関数)になります。


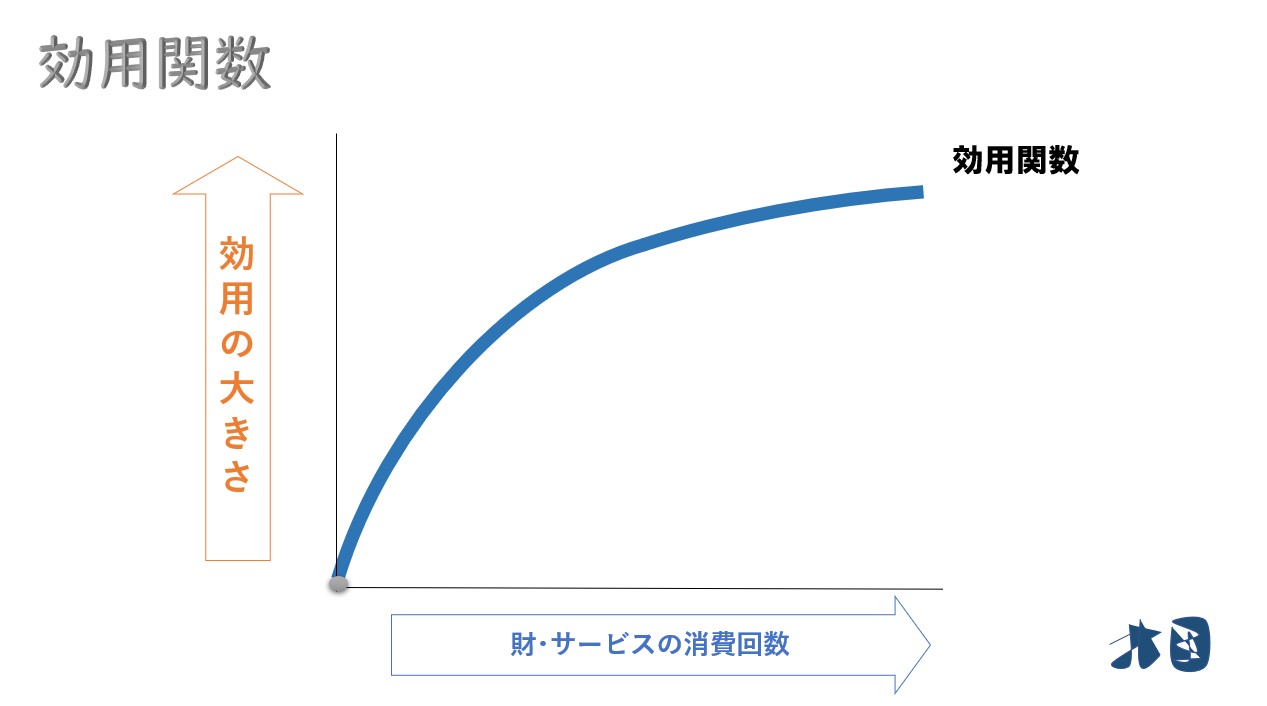
現実的な効用関数


続き
- ドーナッツを1つ食べて得られる効用(満足度)を10とします。
注意ポイント
しかし、ドーナッツを10個、20個と食べていくと、得られる満足度(効用)は小さくなっていきます。これはドーナッツに限った話ではありません。どんなものでも、最初が1番満足度が高まります。
ビールを飲むなら、最初の1口目が最高に美味しいのです。

2口目、3口目と飲み続けると、最初の感動からは少しづつ離れていきます。
曲線が緩やかになっているのは、次第に効用(満足度)が小さくなる様子を表現しています (限界効用逓減の法則)。
効用関数
財・サービスの消費量(X)と効用(U)の関係を表した効用関数は「U=U(X)」となる 。この時、U(X)はXの増加関数。また、消費出来なくなることは想定しない (非飽和性)。効用は英語で「Utilitiy」なので頭文字を取っている。
もちろん、色々な形の効用関数が考えられますが、経済学では一般的に上の形で登場します。
ちなみに
効用関数の定義にも記載しましたが、効用関数には2つの前提があります。
- 完備性(Completeness)を満たす
- 推移性(Transitivity)を満たす
A財・B財・C財があるとき、それぞれの効用の大小関係は
「完備性」必ずA≧B か B≧Aとなる。
「推移性」A>B, C>Aなら C>Bが成り立つ
これまでは消費する財・サービスを1つで考えてきましたが、2つ以上の場合もあります。その場合でも効用関数が存在しますが、必ず「完備性」「推移性」が満たされていることが効用関数の前提となっています。
さらに詳しく
・基数的効用と序数的効用
ここまで、効用関数を「効用を数値化して関数にしたもの」と記載しましたが「効用の数値」についての考え方が2つあります。
1つは、効用の数値には意味があるという考え方で、これを基数的効用と言います。例えば100円あれば100円の買い物ができます。つまり、100円という数値には意味があります。効用も同じで、効用=100ならば、その人は100の満足感を得ていると考えます。
もう1つは、効用の数値には意味がない(順序だけが重要)という考え方で、これを序数的効用と言います。例えば100円を持っているとき、100円という数字に意味はなく、お金を持っていることに意味があると考えるようなイメージです。効用で考えると、ジュースを飲むと100の効用が得られますが、その人が100の満足度を得ているかは分からない(重要ではない)と考えます。重要なのは比較することです。
ここで、紅茶を飲むと50の効用が得られるとき「ジュースの効用=100>紅茶の効用=50」なので、この人はジュースの方が高い満足度を得られると考えます。
ただし、それぞれ100の満足度・50の満足度を実際に得ているかは分からないけど、とにかくジュースの方が効用が高いこと(効用の順序)が分かればOKというのが、序数的効用です。
効用について「基数的」とか「序数的」という単語が飛び交うことがあるので、考え方を知っておくと混乱せずに済みます。
効用関数と限界効用の関係

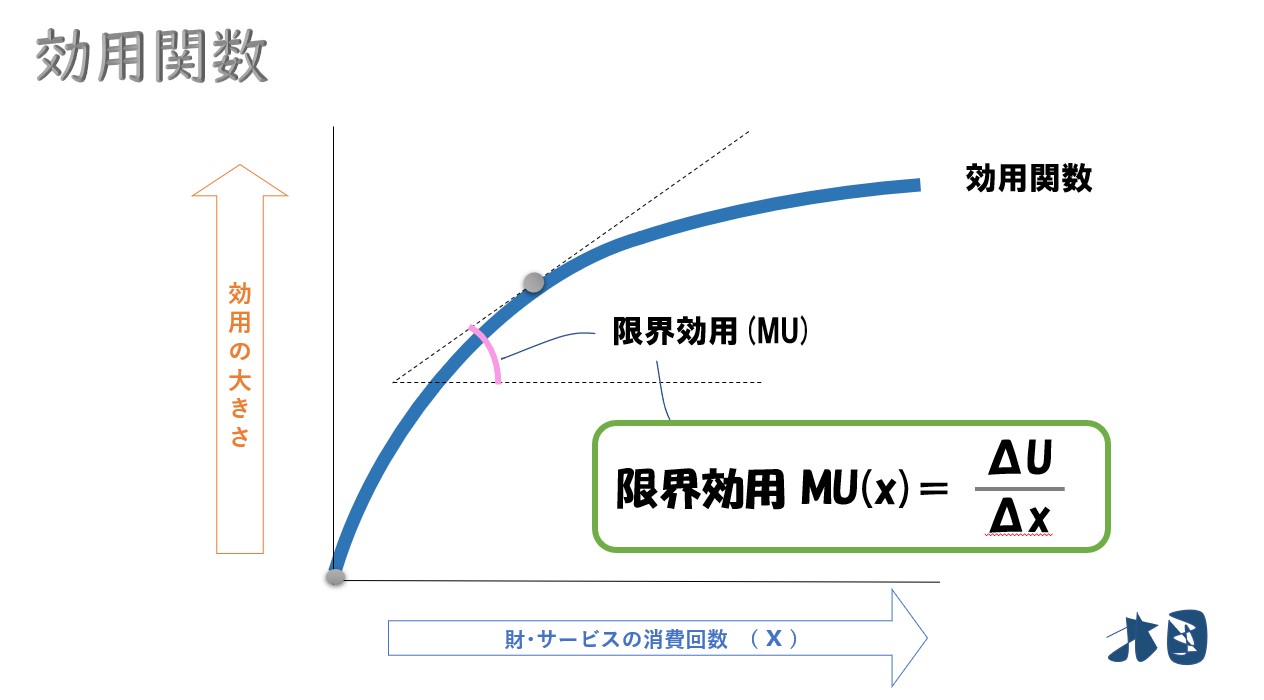
効用関数から限界効用を求めることが出来ます。
限界効用は、財を1単位追加的に消費した場合の効用の増加分のこと。
グラフで見ると
限界効用(Marginal Utilitiy)は、財を1単位追加的に消費した場合の効用の増加分のことなので、グラフの横軸が1メモリ移動した時の効用の増加分となります。
数学的に考えると
効用関数(U)を消費量(X)で微分すると限界効用(MU)になります。
微分で接線の傾きを求めることで、限界効用(MU)を求めることが出来ます。
分数の理由
例えば「Y=2x」という数式があったとき「2x」なので「傾きは2」です。
変化量を「Δ (デルタ)」とします。
- 消費量(x)が1増えたとき、変化量は「Δx=1」と書けます。
- 「Y=2x」なので、xが1増えれば「Yは2増えます (ΔY=2)」
まとめると「傾き2」=「2/1 = ΔY/Δx」となります。
効用関数で考えれば U=U(x) ⇒「ΔU/Δx」となります。


詳しい求め方はこちらで!
⇒@限界効用・限界効用逓減の法則とは?求め方も含めて簡単にわかりやすく
- 限界効用とは?・微分する理由・詳しい求め方についてまとめています ↑
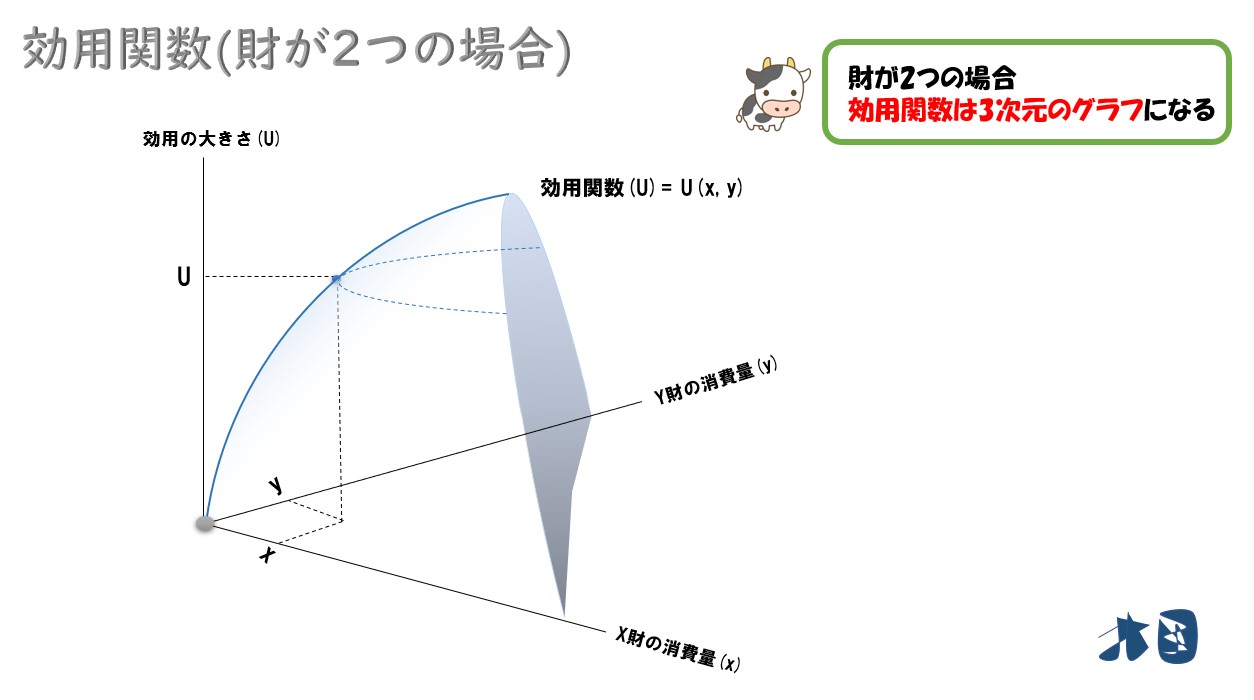
効用関数の種類(財が2つ)
先ほどは、財が1つの場合を考えました。
経済学では財が2つ以上の場合を考えることの方が多いので、ここからの話は重要です。


ポイント
財が2つの場合だと、グラフが3次元になります。
3次元グラフは使いづらいので、財が2つのときは、効用関数から得られる無差別曲線というのを使う場合が多いです。
ここでは
無差別曲線の話はせずに、効用関数の種類について話ていきます。
無差別曲線についてはこちらで確認する
財が2つある場合、効用関数は大きく2つの種類ある。
例えば
- チョコ1枚を食べると10の効用

「効用(U)=10X」とします。
※Xはチョコの消費量
- コーヒー1杯を飲むと10の効用

「効用(U)=10Y」とします。
※Yはコーヒーの消費量
この時、全体の効用(U)は、単純に「チョコの効用(=10X)」+「コーヒーの効用(=10Y)」と足し算をして求める場合もあります。
または
「チョコの効用(=10X)」×「コーヒーの効用(=10Y)」と掛け算をして求める場合もあります。(2財を消費したので相乗効果で効用が一気に高まっている。)
⇒この場合は「効用関数(U)=100XY」のようになります。
まとめると
- 効用関数(U)=「10x + 10y」
- 効用関数(U)=「10x × 10y」
効用関数は、足すパターンも掛けるパターンもあります。
消費量「x」と「y」を足し合わせる効用関数を「リニア型(線形)」と言います。
消費量「x」と「y」を掛ける効用関数を「コブ・ダグラス型」と言います。
そして
経済学の問題でよく登場するのは、2財の消費量を掛けあわせるケース「コブ・ダグラス型の効用関数」です。
- 効用関数(U)=「(x)×(y)」
- 効用関数(U)=「(√x) × (√y)」
実は、普通の経済学の問題で登場する足し算型は特殊ケースです。「U=x+y」などの足し算の効用関数「リニア型(線形)」は、2財が完全代替財の場合で登場します。
ここでは紹介しませんが、もう1つの有名な特殊ケースとして「U=min(x,y)」という効用関数があります。この形は「レオンチェフ型」と呼ばれ、2財が完全補完財のときに登場します。「min(x,y)」はxとyの小さい値を取るという意味です。
⇒特殊な無差別曲線の「右下がりの直線になる無差別曲線」「L字型になる無差別曲線」を参照
なので
簡単に「効用関数(U)=x・y」などとして、そこから無差別曲線の形状を出して答えるパターンの問題が多いです。
「x・y」の「・」は掛けるという意味です。
ちなみに
「効用関数(U)=x・y」だと限界効用逓減にならないので、消費量が増えるほど効用の増加が小さくなるように「効用関数(U)=√x・√y」や「効用関数(U)=(xの2分の1乗)×(yの2分の1乗)」などと出題されることが多い。「効用関数(U)=x・y」は簡単な例題として出されることが多いイメージ。
効用関数と需要曲線の求め方
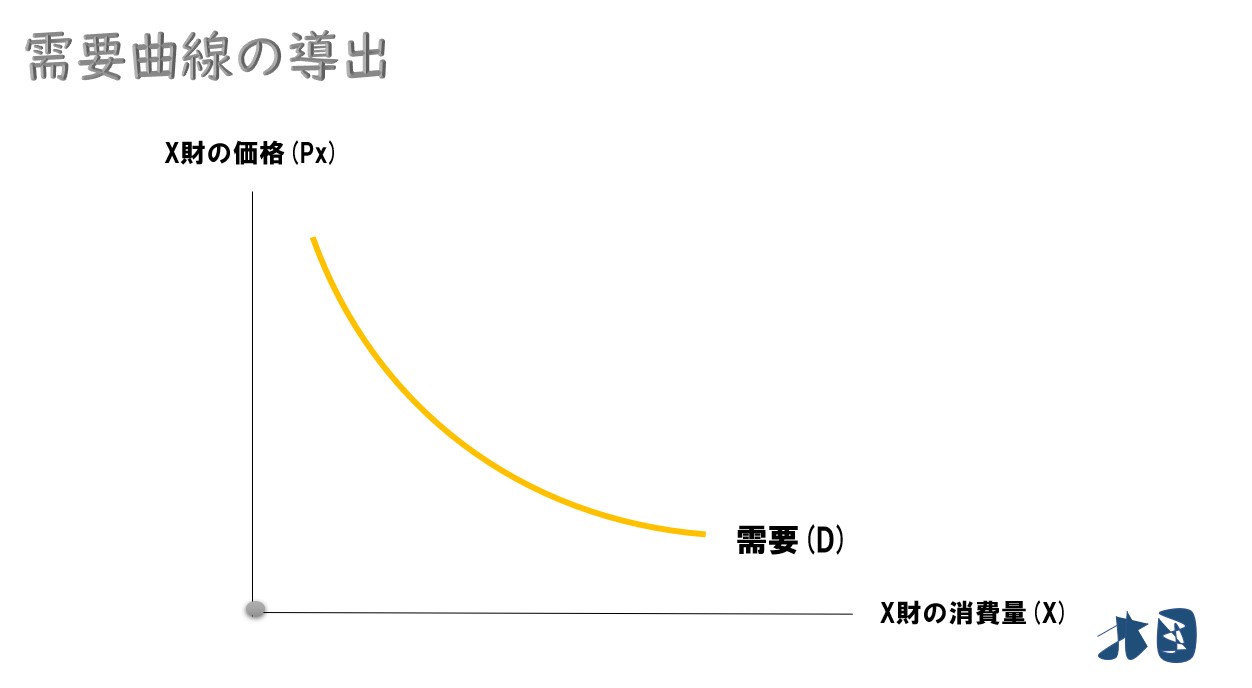
効用関数の話を発展させると「需要関数(D)・右下がりの需要曲線(D)」が求められます。
高校の政治経済でもおなじみの「需要と供給」の需要の方です。
前提
- 最適消費点の求め方を理解している
ここでは
需要関数(D)の計算方法を紹介します。右下がりの需要曲線を求める方法はこちらで確認してください⇒【需要曲線】右下がりの需要曲線を導出する方法


ここからは最適消費点の求め方を知っている前提で話を進めていきます。
例題
2財について、次の条件から需要関数(D)を求める
- 効用関数U(x, y)=xy
- X財の価格=Px
- Y財の価格=Py
- X財の消費量=x
- Y財の消費量=y
はじめに
予算制約線を求める
予算制約線(I)は「(X財の消費量×X財の価格)+(Y財の消費量×Y財の価格)」で決まるので「xPx + yPy」と置けます。
以上より「予算制約線(I)= xPx + yPy」です。
次に
与えられた条件から、最適消費点(効用最大化)を求めます。←ここが一番ポイント
最適消費点(効用最大化問題)の解き方は大きく4種類くらいあります。
ここでは、基本的な解き方である「予算制約線の傾き=限界代替率」を使います。他の解き方に興味がある人はこちらで確認できます。
それでは、この2つを使って最適消費点を求めます。
- 効用関数「U(x, y)=xy」
- 予算制約線「I=xPx + yPy」
(1)予算制約線の傾きを求める
I=xPx+yPyより
- I=xPx+yPy
- y=-(xPx/Py)+I/Py
- y=-(Px/Py)x+I/Py
(2)効用関数から限界代替率を求める
「U=xy」から「y=U/x」へ変形後に微分します。
- 「y=U/x」⇒「U/-xの2乗(=U・-xの-2乗)」
- 「U/-xの2乗」に「U=xy」を代入
- 「U(=xy)/-xの2乗」⇒「xy/-xの2乗」=「-(y/x)」
(3)予算制約線の傾き=限界代替率で効用最大化(最適消費点)を求める
「-(Px/Py)」=「-y/x」
このまま「x=~」にすると最適消費点でのX財の消費量が分かります。実は、これが需要関数となります。
- X財の需要関数「x=(Py/Px)y」
- Y財の需要関数「y=(Px/Py)x」
おまけ
さらに細かく書けば、需要関数(D)は「D=(X財価格(Px), Y財価格(Py), 所得(I))」と書く場合があります。
なので、X財の需要関数「x=(Px,Py,I)=(Py/Px)y」などと書くことがあります。


途中で分からなくなった人
需要関数を求めるのは、消費者理論の最後の方の項目です。自分が理解していない項目はどのあたりなのかを把握しましょう。
ちなみに
右下がりの需要曲線の導出方法はこちらでまとめています。