ミクロ経済学の消費者理論で登場する「双対性」
- 双対性(アプローチ)とは？
- 効用最大化と費用最小化の関係
- 双対性の全体図
双対性に関する項目を、分かりやすく簡単にまとめています。
双対性アプローチとは？
双対性アプローチ
消費者理論において、消費者の費用最小化問題から特定の値を求めること。効用最大化問題を主題と考えた場合に、費用最小化問題を双対的な問題と捉えることが出来る。
「効用最大化問題」と「費用(支出)最小化問題」の関係
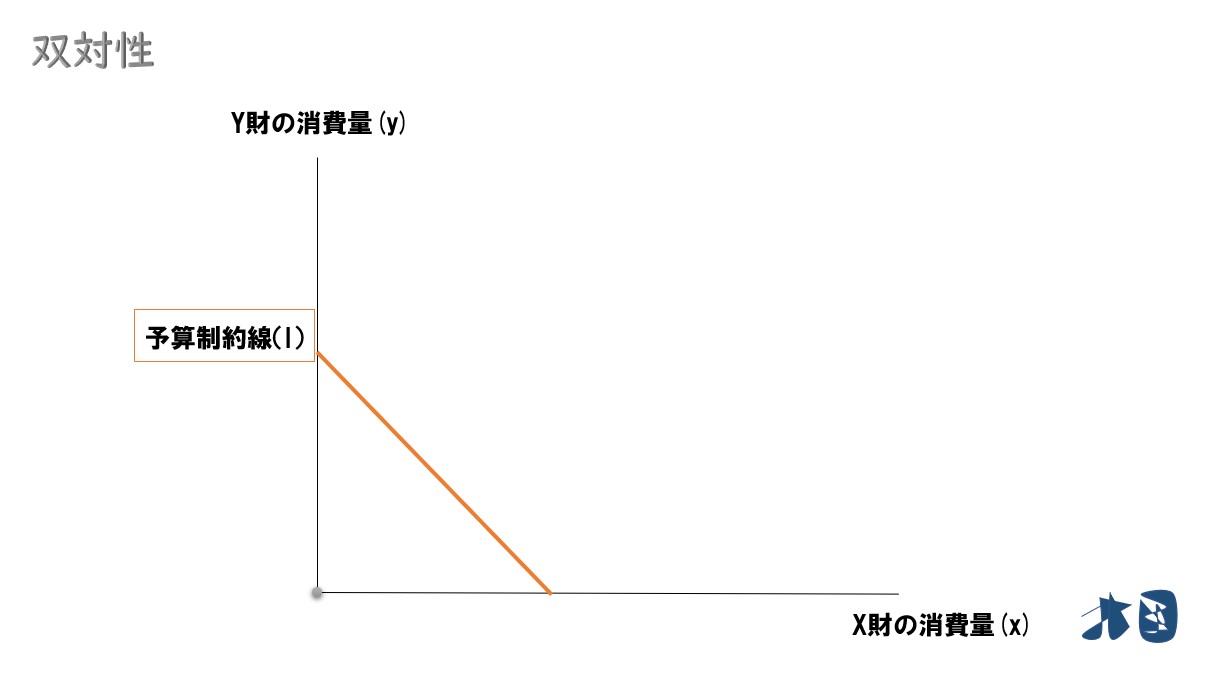
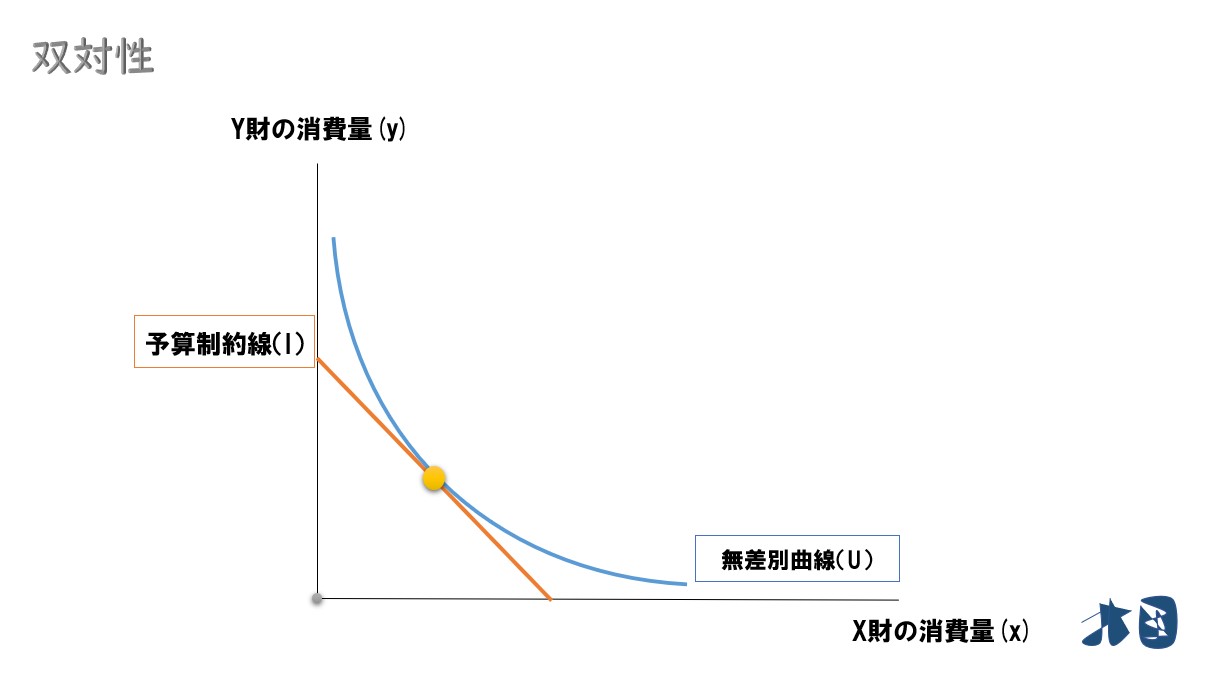
ふつうのミクロ経済学では、限界効用･無差別曲線･限界代替率･予算制約線などを使って、最適消費点(効用最大化)を求めます。
そのため、効用最大化問題を主題として学習している人が多いはずです。
一方で、この効用最大化問題は、別の視点からとらえることも出来ます。
例えば
- 最適消費が実現する効用水準を達成するのに100万円が必要な場合を考えます
100万円が必要なので、200万円でも300万円でも十分に足ります。しかし、ふつうの消費者は効率的に買い物をするため、100万円だけを使って最適消費の効用水準を達成しようとするでしょう。
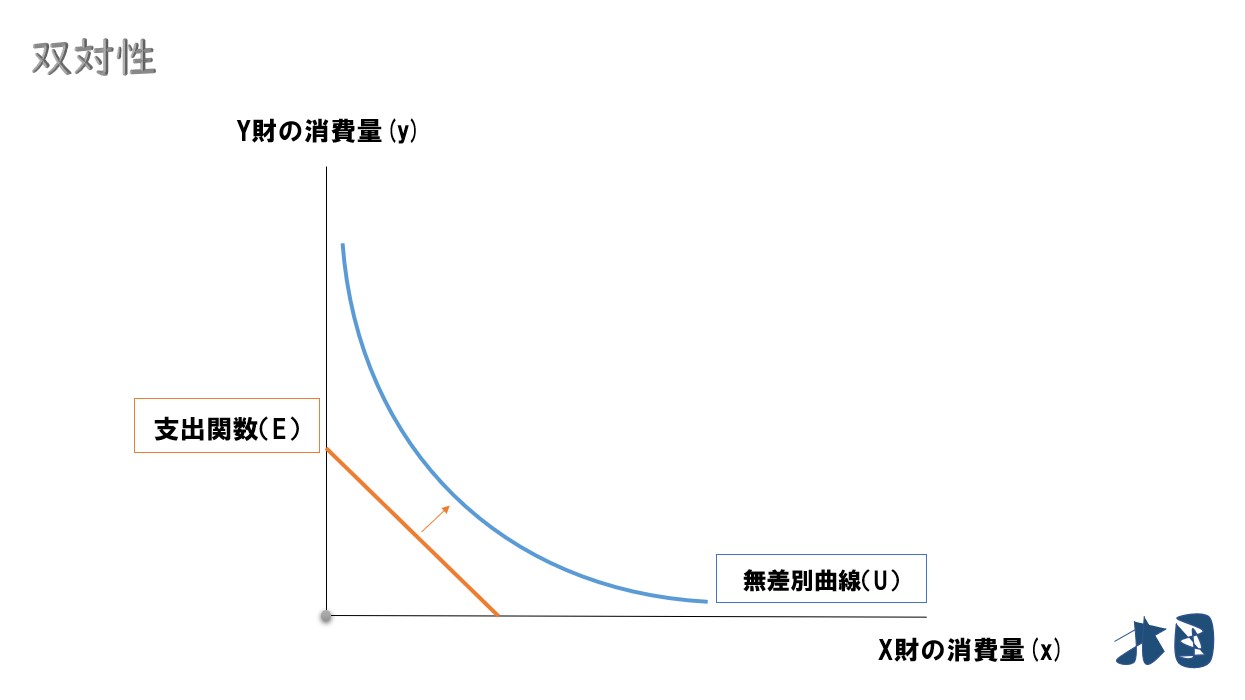
そのため、最適消費(効用最大化)が実現するとき、消費者の支出は必要最低限になるはずです。これを支出(費用)最小化と呼びます。
つまり
ふつうのミクロ経済学で学ぶ効用最大化問題（主問題）は、支出(費用)最小化問題（双対問題･Dual Problem）と考えることが出来ます。
双対問題とは、その問題を解くことで主問題の解も得られるものを言います。
このような両者の関係を、消費者理論における双対性と呼びます。
ミクロ経済学で双対性という場合、今回紹介する双対性と、生産者理論の双対性があります。2つを区別するため、ここでは消費者理論における双対性と呼びます。
「効用最大化問題」と「費用(支出)最小化問題」の違いを知る
「効用最大化問題」と「費用(支出)最小化問題」は、ともに最適消費点を求めることは出来ますが、途中の考え方が異なります。
効用最大化
①予算額が一定
②予算額を条件に効用水準が決まる
ある予算額のもとで、効用最大化させる効用水準はどれくらいか？を求めたことになる。
費用(支出)最小化
①効用水準が一定
②効用水準を条件に支出(費用)が決まる
ある効用水準を達成するために、いくら支出する必要があるのか？を求めたことになる。
「効用最大化問題」と「費用(支出)最小化問題」の全体図
縦(タテ)のつながり
効用最大化
費用(支出)最小化
効用関数(効用一定と仮定)
Min(最小化するもの)：P(x)※
s.t.(条件)：U(効用)=Ū(効用一定)
※支出は財の価格(P)と消費量(x)に依存
⇩
ヒックスの補償需要関数(D’)
h=h(P, Ū)
補償需要関数は価格P･効用Ūで決まる
⇩
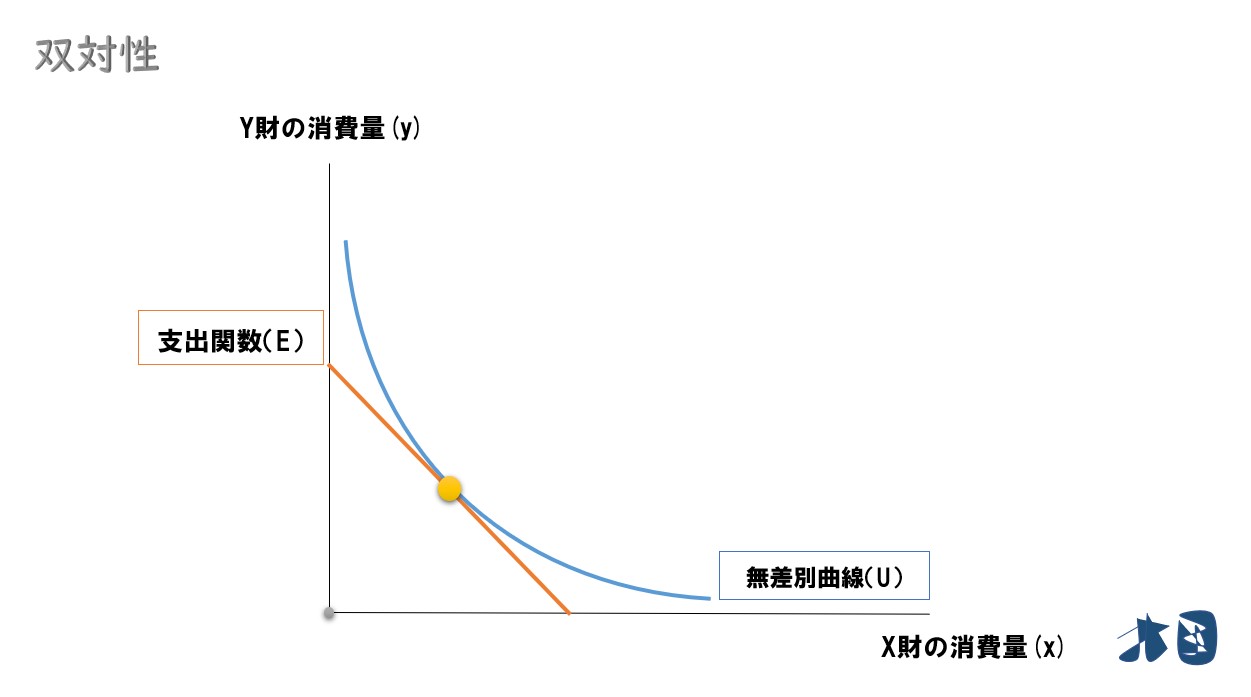
支出関数(E)
M=E(P, Ū)
補償需要関数を目的関数(Min):P(x)=Px･xに代入
横(ヨコ)のつながり
効用最大化
費用(支出)最小化
需要関数(D)
補償需要関数(D’)
⇔
【スルツキー分解】
需要関数から代替効果のみを抽出したものが補償需要関数
間接効用関数(V)
Ū=V(P, M)
支出関数(E)
M=E(P, Ū)
⇔
間接効用関数をMについて解く(M=)の形にすると支出関数になる
支出関数をŪについて解く(Ū=)の形にすると間接効用関数になる
「双対性」は中級以上の話なので、いきなり登場して混乱する人が多いです。そんな人に向けて、双対性についての簡単なイメージを掴めるようにまとめました。もっと深く勉強したい人は、数学的な話が中心になってくるので参考書を使う方が良いと思います。
とは？ 効用最大化と費用最小化の関係 双対性の全体図 ...){kind=link}