【リンダールメカニズム】リンダール均衡とサミュエルソン条件、問題点などを分かりやすく

公共財の供給方法として「リンダールメカニズム」があります。

• リンダールメカニズムとは
• リンダール均衡の式（グラフを見ながら確認）
• リンダール均衡とサミュエルソン条件
• リンダールメカニズムの問題点
• 簡単な計算問題

リンダールメカニズムに関する基本的な情報をまとめています。

リンダールメカニズムとは

公共財は市場を通して供給すると過少供給になることが分かっています（公共財の自発的供給）。

市場で供給すると、各消費者は誰かが供給する公共財にただ乗りしようとするため過少供給になります。

そこで

政府が税金を徴収して公共財を供給します（現実世界と同じ）。このとき、どのように「税金を徴収する」のが良いかが重要な問題点となります。

公共財を供給するにあたり「市場に任せる」か「政府が行うか」という選択肢がありますが、公共財の基本的な分析から「市場に任せると過少供給になる」ので、政府が公共財を供給するという結論になります。次のステップは、政府が公共財を供給するとき「税金をどのように徴収するのが好ましいか？」です。

2つの考え方

• 応益負担（受益者負担）
• 応能負担（所得に応じた負担）

⇒ リンダール･メカニズムは「応益負担（受益者負担）」の考え方に基づいた仕組みです。

リンダールメカニズムの概要

• 各個人に公共財を評価してもらい、自己申告してもらう
• 政府は、その自己申告に基づいて税金の負担額を割り振る

仕組みはシンプルです。この方法により、公共財を高く評価した人（便益をたくさん得る人）に、政府は高い税負担を要求するため「応益負担」が実現します。

リンダール均衡の導出

前提①

• 公共財の生産費用（税金）を政府が徴収する
• 政府は、各消費者に税率（費用負担率）を提示する
• その税率をもとに、消費者は、自身の公共財需要量を政府へ報告する
• 各消費者の公共財需要量が一致するまで2･3を繰り返す

前提②

• AさんとＢさんがいる社会を考える
• 政府は、AさんとBさんから公共財費用を徴収する
• Aさんの税負担率を「h」とする
• Bさんの税負担率を「1－h」とする
• Aさんの公共財の需要曲線を「Da」とする
• Aさんの公共財の需要曲線を「Db」とする
• 公共財の生産消費量を「G」とする

直感的に確認する

上記の前提をもとにグラフを見ながら話を進めます。数式を見るより、グラフを見ながらの方がイメージしやすいです。

グラフの見方

• 縦軸：Aさんの税負の負担割合（h）※通常の「需要と供給のグラフ」で財の価格(P)を縦軸に取るイメージ
• 横軸：公共財の供給量（G）

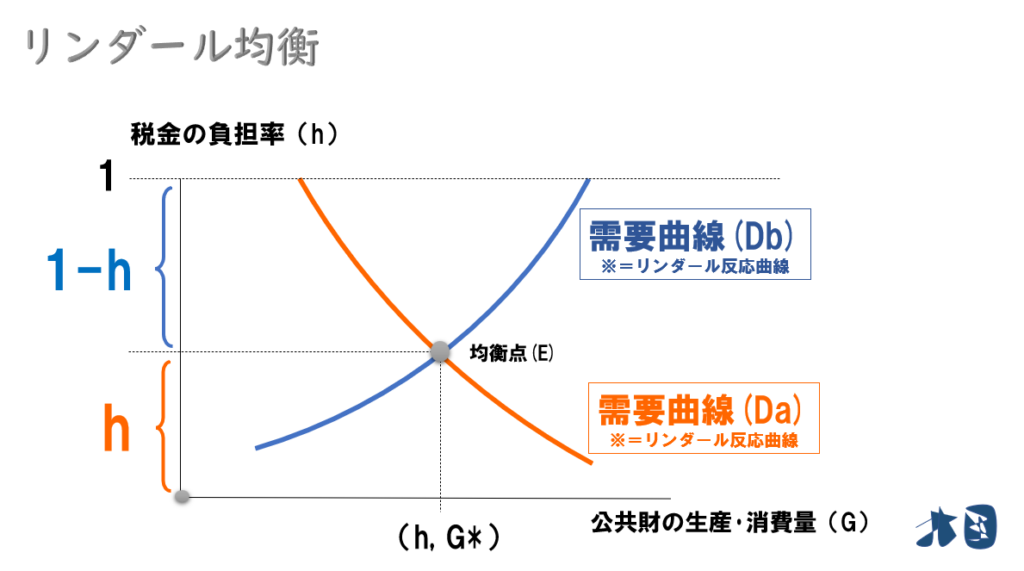
縦軸は「Aさんの負担率（h）」であることに注意しましょう。上にいくほどAさんの負担が増え（Bさんの負担は減る）、下にいくほどAさんの負担は減り（Bさんの負担は増える）ます。

Aさん（Da）の反応

自分の負担率（h）が下がれば（＝安くなれば）、公共財をもっと欲しいと思います。つまり、グラフの下に行けば行くほどAさんにとっては「安くなる」。（通常の需要曲線と同じ右下がりで「Aさんのリンダール反応曲線」などと呼びます。）

Bさん（Db）の反応

逆にBさんは、Aさんの税金の負担率（縦軸=h）が上がると「Bさんの負担率（1－h）は下がります」。つまり、グラフの上に行けば行くほどBさんにとっては「安くなる」ため、公共財をもっと欲しいと思います。（Aさんと逆で右上がり需要曲線（リンダール反応曲線）になる）

ここで

政府が登場して、税金の負担率（h）の調整を行います。

例えば

政府が提示した税金の負担が「Aさんは低すぎ」「Bさんは高すぎ」と感じたとします（Aさんの需要量 ＞ Bさんの需要量）。

Aさんが「もっと公共財を作ってくれ！」と主張して、Bさんが「そんなにいらない（高いから）」と思っている状態です。

この場合、政府はAさんの税金の負担率（h）を引き上げます。

• Aさんは税金の負担が増えるので、需要量を減らす（我慢する）
• Bさんは税金の負担が減る（1-hが下がる）ので、需要量を増やす
• 結果、2人の需要量が均衡に近づいていく

これを繰り返すことで、最終的に2人の需要量が一致する点（交点）に落ち着きます。

本来は市場が存在しない公共財に対して、政府が「疑似市場」を作り出して、参加者ごとに「税負担」を割り振ること（リンダール税を課すこと）で、需要と供給を一致させた状態です。

数式で確認する

つぎに、グラフで見た内容を簡単な数式で確認していきます（意外と簡単ですが、前段でイメージを固めてからの方が分かりやすいと思います）。

前提（最初に示したものと同じ）

• AさんとＢさんがいる社会を考える
• 政府は、AさんとBさんから公共財費用を徴収する
• Aさんの税負担率を「h」とする
• Bさんの税負担率を「1－h」とする
• Aさんの公共財の需要曲線を「MBa (=Da)」
• Aさんの公共財の需要曲線を「MBb (=Db)」
• 公共財の生産消費量を「G」とする
• 公共財の限界費用（コスト）を「MC」とする

グラフの時と違って、公共財の限界費用（コスト）「MC」というのが新しく追加されています。

具体的な例で考える

AさんとBさんは観光地に住んでいます。観光客が多すぎて（オーバーツーリズム）で道が狭いので、道路の拡張工事（道路10本）をしてほしいと考えています。

• 「200万円（MC）」あれば道路10本の工事ができる
• AさんもBさんも100万円支払ってもよいと考えている（負担率は0.5）

このとき

限界費用MC（200万円）を、AさんとBさんで折半すれば良い（負担率h=0.5）ので、Aさんの税金の負担は「200万円×0.5＝100万円」となります。Bさんも同様です。

つまり

• (限界便益)＝(公共財の限界費用)×(税金の負担率)が実現する

ここで

この2つの式（①と②）を足し合わせてみます（公共財の需要とコストは、2人の合算で決まるため足し合わす）

• MBa ＋ MBb ＝ h × MC ＋ (1－h) × MC
• MBa ＋ MBb ＝ (h ＋ 1－h) × MC
• MBa ＋ MBb ＝ 1 × MC
• MBa ＋ MBb ＝ MC

これがリンダール均衡が成立するときの基本式です。

グラフで見る

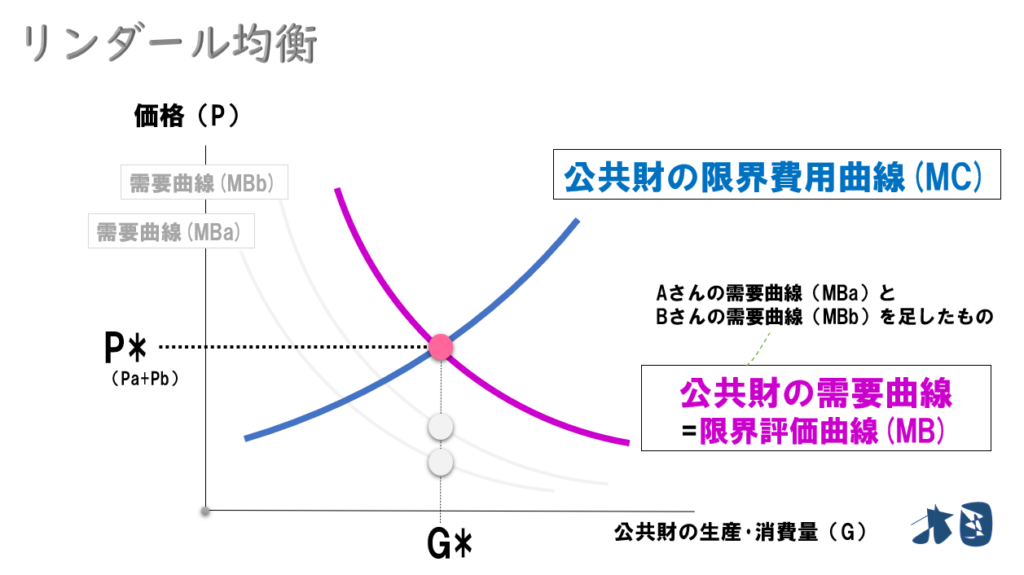
先ほどの例なら「G*＝道路10本」「P*＝20万円（単価20万円×10本で200万円となるので注意）」
※Aさん・Bさんの税負担＝Pa・Pbです。100万円ずつ支払うならPa＝Pb＝10万円です（グラフでは便宜上、AさんとBさんの需要曲線が異なるので、Pa=Pb=10万円にはなりません。

次に

「リンダール均衡」を求めましたが、次にこの均衡が経済学的に良いものなのか（効率的か）を確認する必要があります。それを確認するために、サミュエルソン条件（公共財の最適供給量）を満たすかを次に確認します。

サミュエルソン条件を満たす証明

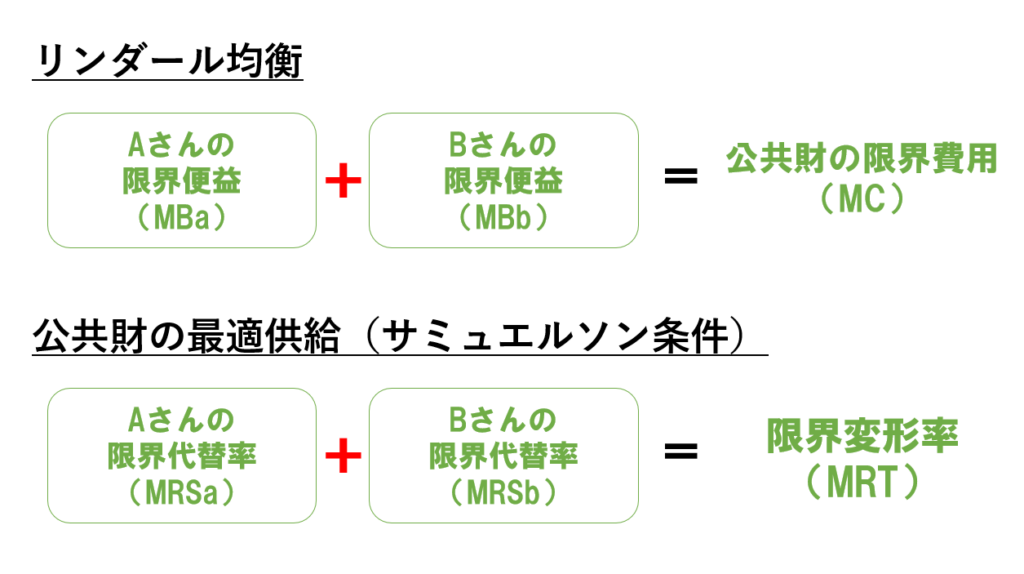
サミュエルソン条件

MRSa ＋ MRSb ＝ MRT（Aさんの限界代替率＋Bさんの限界代替率＝限界変形率）

サミュエルソン条件は、公共財の最適供給量（社会的に望ましい供給量）を実現するための条件です。なんだっけ？という人はこちらの記事で確認して下さい。

ポイント

• リンダール均衡：MBa ＋ MBb ＝ MC
• サミュエルソン条件：MRSa ＋ MRSb ＝ MRT

左辺

• リンダール均衡：MBa ＋ MBb（Aさんの限界便益＋Bさん〃）
• サミュエルソン条件：MRSa ＋ MRSb（Aさんの限界代替率＋Bさん〃）

限界便益（公共財から得られる便益）

お金をいくら支払っても良いか？と同義と考える。つまり「公共財から100万円の限界便益（MB）が得られるなら、100万円支払っても良いはず」です。

限界代替率（2財の交換比率）

公共財の話の中では「公共財」と「私的財（普通の商品）」の比率を表します。ここで、私的財を「お金」と考えます。つまり、サミュエルソン条件の限界代替率（MRS）は、公共財とお金の交換比率を表しています。

公共財とお金の交換比率なので「公共財にいくら支払って良いか」と同じです。

数式の左辺は、どちらも「公共財にいくら支払って良いか」を表しているので同じです。

右辺

• リンダール均衡：MC（公共財の限界費用）
• サミュエルソン条件：MRT（限界変形率）

限界変形率

限界変形率とは、「公共財の限界費用／私的財の限界費用」を表しています。便宜上、私的財の限界費用を「1」と考えれば、分子の公共財の限界費用(MC)が残ります。

数式の右辺も、どちらも「公共財の限界費用」を表しているので同じです。

なんで1円にするんだ、と思った人向けへ。経済学では、これを「ニュメレール（価値基準財）」と呼びます。先ほどと同様に私的財を「お金」と考えます。
お金の限界費用なので「お金の入手コスト」という意味になりますが、例えば1円を手に入れるのに1円以上のコストを支払うわけがないので「1円」となります。ここでは「私的財の限界費用」をお金1円と考えて、1円あたりの公共財の限界費用（分子）がいくらになるのかを考えます。
※左辺の限界代替率も同じです。「公共財」と「私的財（普通の商品）」の交換比率と書きましたが、こちらも1円と考えています。つまり、両辺の私的財を「お金1円」として式をまとめているのです。

まとめ

• リンダール均衡：MBa ＋ MBb ＝ MC
• サミュエルソン条件：MRSa ＋ MRSb ＝ MRT
  • MRS＝公共財の限界便益／私的財の限界便益
  • MRT＝公共財の限界費用／私的財の限界費用

このとき、私的財を「お金1円」と考える。※例えば、1円の限界便益（1円から得られる便益）も、1円の限界費用（1円を入手するためのコスト）も1円となる。つまり、私的財の限界便益も限界費用も1と考えることができる。

以上より

• MRS＝公共財の限界便益／1＝MB（限界便益）
• MRT＝公共財の限界費用／1＝MC（限界費用）

数式では効率的ですが、現実はそんなに簡単ではありません。ということで、つぎにリンダールメカニズムの問題点を見ていきます。

リンダールメカニズムの問題点

リンダール均衡（リンダールメカニズム）はサミュエルソン条件を満たすため、数式上では効率的です。しかし、現実ではうまく機能しない部分があり、問題点が複数あるので順番に見ていきます。

そもそも、政府が1人1人に税金をいくら負担するのか聞いて回るのは無理ですが、それ以外にも問題点があります。

1. 嘘をつく（フリーライダー問題）

リンダールメカニズムの大きな問題点は、「参加者が正直に自分の限界便益（支払ってもいい金額）を申告しない」可能性があることです（本当のことを申告するインセンティブがない）。

例えば

「私は公園なんて不要です」と嘘をついて、税金を支払わない。

リンダールメカニズムでは、正直に「私はこの公園に100万円の価値を感じています！」と申告すると、100万円の税金が課されます。逆に「私は公園なんて不要です」と嘘をつけば、税金の負担を逃れつつ、完成した公園をタダで利用できます（公園は誰でも利用できるので勝手に利用すればよい。）

合理的な消費者であれば、自身の負担を減らすために過少申告を行う戦略をとります（戦略的な虚偽申告）。

その結果

必要な公共財の供給が行われない（消費者は嘘をついて「公共財は要らない」と言った方が得なので、公共財は過少供給となる）。

2. 所得に依存する（初期保有の問題）

「お金持ちの意向」によって、公共財の最適な供給量が変わってしまうという問題点もあります。

例えば

多額の税金を支払える人（金持ち）がいたときに、その人が公園を欲しいといえば、公園がたくさん作られますし、公園はいらないと言えば、公園は作られません。

簡単な計算問題（例題）

AさんとBさんの2人だけがいる社会で、公共財（G）を供給することを考える。

• Aさんの限界便益（需要）曲線：MBa＝20－2G
• Bさんの限界便益（需要）曲線：MBb＝30－3G
• 公共財の限界費用：MC＝10

このとき、①公共財の最適供給量（G*）と、②リンダール均衡におけるそれぞれの負担額（リンダール価格：Pa, Pb）を求めなさい。

手順1：最適供給量を求める

まずは、サミュエルソン条件を使って社会全体での最適供給量を出します。

サミュエルソン条件を満「社会全体の限界便益（MBの合計）＝ 限界費用（MC）」

・(20－2G)＋(30－3G)＝10
・50－5G＝10
・5G＝40
・G*＝8

最適供給量は「8」となります。

手順2：リンダール価格を求める

先ほど求めた「G＝8」を、AさんとBさんの限界便益の式（需要曲線）に代入して、2人の税金負担額を求めましょう。

• Aさんの負担額（Pa）：20－2×8＝4
• Bさんの負担額（Pb）：30－3×8＝6

※なお、リンダール均衡では「AさんとBさんの限界便益（MB）＝費用の負担額（MC）」です。Aさんの負担「4」＋Bさんの負担「6」＝「10」となり、限界費用（MC=10）と一致します。