VCGの代表的な応用例であるクラークメカニズムについて
- クラークメカニズムとは
- クラークメカニズムとVCGメカニズムの関係
- クラーク税
- フリーライダー問題と耐戦略性
- クラークメカニズムの問題点
- 簡単な計算問題
混乱しやすい箇所を中心に、基本的な情報をまとめています。
クラーク・メカニズムとは(VCGメカニズムとの関係)
はてな
公共財の費用負担の仕組みの1つ。
公共財の自分の評価額を正直に申告させる(誘因両立的な)仕組み。リンダールメカニズムでは「参加者が嘘をつく」という欠点があるが、クラークメカニズムでは「参加者は正直に申告することが一番得する」ように設計されている。
クラークメカニズムの概要
- 全員に「公共財の評価額(どれくらい価値があるか)」を申告させる。
- 全員の評価額の合計が、公共財の生産コストを比較する
- 「全員の評価額合計>コスト」なら公共財を供給する(逆なら供給しない)
- 結果に影響を与えた人から税金を徴収する(クラーク税)
比較
リンダールメカニズムと比較すると下記のようになります。
| 特徴 | リンダール・メカニズム | クラーク・メカニズム |
|---|---|---|
| 考え方 | 応益負担(便益の分だけ支払う) | 社会的影響の補償(自分が決定を変えた分だけ支払う) |
| 負担額 | 公共財の「限界便益」の合計 | 自分が参加したことで他人に与えた「損」の合計 |
| 結果 | パレート最適(資源配分の効率性) | 誘因両立性(正直な申告の引き出し) |
| 欠点 | 参加者は嘘をつくのが合理的 | 予算が余る、共謀に弱い |
リンダールメカニズムだと「消費者が嘘をつくの合理的になってしまう」というフリーライダー問題がありました。クラークメカニズムでは「参加者の正直な申告を引き出すことができる」というのが一番の特徴です。
ちなみに
クラークメカニズムと似たものに「VCGメカニズム」というものがあります。
- Vickrey(ヴィックリー)
- Clarke(クラーク)
- Groves(グローブス)
この3人の名前をとってVCGメカニズムと呼ばれます。ヴィックリー (1961年)が「セカンドプライス・オークション」という考え方を生み出し、その10年後、1971年にクラークが、ヴィックリーの理論を公共財の供給に応用しました(論文:Multipart Pricing of Public Goods)。それを「クラークメカニズム」と呼びます。そして、1973年にグローブスがそれらを数学的にまとめて理論が確立しました。
一連の研究から「参加者に嘘をつかせない仕組みを設計して社会的余剰の最大化を目指す」ような仕組みをVCGメカニズムと呼びます。VCGメカニズムの中でも公共財の供給について応用されたものを「クラークメカニズム」と呼んでいます。そのため、クラークメカニズム≒VCGメカニズムと呼んでも差し支えないです。

なんとなく分かったけど、イメージはつかない・・。
次に、具体的な例を見ていこう!

クラーク税とピボットの決め方
具体例で考える
Aさん、Bさん、Cさんの3人で「橋(コスト300万円)」を架けるか決めます。
| 参加者 | 公共財の評価額(円) | 備考 |
|---|---|---|
| Aさん | + 200万 | 移動が楽になる |
| Bさん | + 200万 | 移動が楽にある |
| Cさん | - 150万 | 景観が悪くなる |
| 合計 | + 250万 | コスト300万に届かない |
「評価額の合計250万円< 公共財のコスト300万円」となったので「橋は作らない(公共財を供給しない)」となります。
ここで
- 結果に影響を与えた人物を確認します
「その人がいなかったら結果が変わっていたか?」を確認します。
判定方法
その人がいなかったと仮定して「残りのメンバーの評価合計-コスト」で結果を見る。
先ほどの例では、3人の評価額をもとに「公共財を供給しない」と決定しました。それを前提に確認を進めます。※「その人がもっと別の値を言っていたら」という仮定(タラレバ)は計算には含まれません。
① Aさん(Bさん)がいない場合
(200万円-150万円)-300万円= -250万円
- 結果:マイナス(評価額<コスト)なので公共財を供給しない
- 判定: Aさんがいなくても、結果は「供給しない」のまま
- 結論: Aさんは結果を変えていないのでクラーク税は0円
② Cさんがいない場合
(200万円+200万円)-300万円= +100万円
- 結果:プラス(評価額>コスト)なので公共財を供給する
- 判定: Cさんがいないと、結果は「供給する」になっていた
- 結論: Cさんは結果を変えたのでクラーク税が課される
ポイント
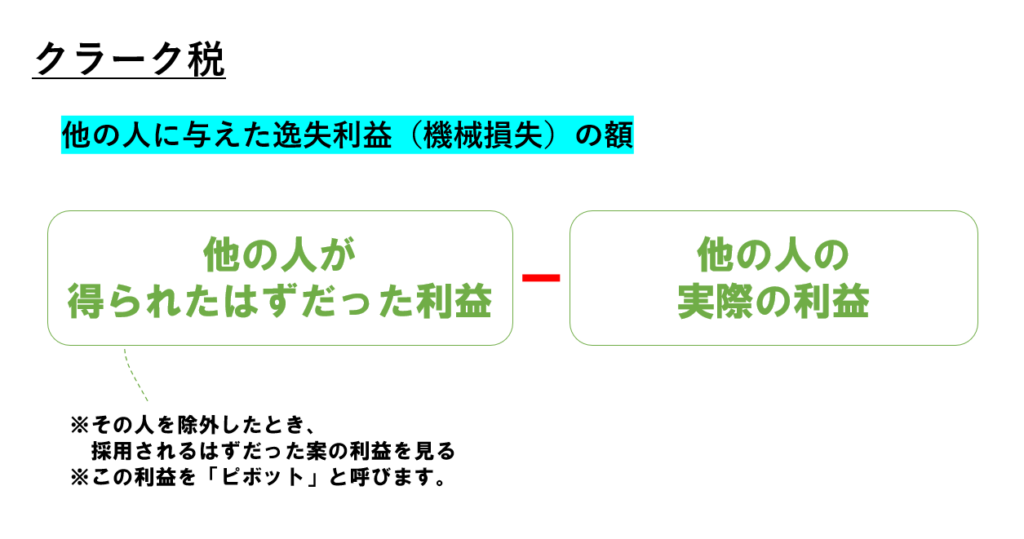
このとき、②のCさん以外が得られたはずの利益100万円(200万円+200万円-300万円)を罰金(クラーク税)としてCさんから徴収します。
※厳密には、実際に得られたCさん以外の利益を差し引いてクラーク税が決まります。ただし、今回のように公共財が供給されない場合、実際に得られた利益は0円になるので「100万円-0円=100万円」で計算を省略できます。
※ちなみに、この100万円(Cさん以外が得られたはずの利益)をピボット(基準値や定数項)と呼びます。覚えなくて良いです。

どうしてこれで正直な申告を引き出せるんだろう・・?
次は、この仕組みを数学的に見ていこう!

簡単な数式で見る(耐戦略性とフリーライダー問題)
ポイント
正直に申告することが一番得をする(支配戦略になる)ため、フリーライダー問題が発生しない。これを「耐戦略性」または「誘因両立性」と呼ぶ。
前提
- U: その人の満足度(Utility)
- P: その人が公共財から得られる利益(Profit)
- T: クラーク税(Tax)
- SW:社会全体の利益合計(Social Welfare)
Step1
まず、その人が実際に得られる満足度は「得られる利益」から「税金」を引いたものです。
① U(その人の満足度) = P(その人の利益)-T(クラーク税)
Step2【ここがポイント】
次に、クラーク税(T)を分解します。「嘘をついたことで、他の人に生じた逸失利益(機会損失)」がクラーク税になるので、下記のように整理できます。
- その人以外が得られたはずの利益を「本来の他人の利益」と表現する。
- クラーク税は「本来の他人の利益」から「実際に得られた他人の利益」を差し引くと計算できる。
- また、「本来の他人の利益」は、その人が嘘をついても変化しないので「定数」と表現できる。
先ほどの例で考えると、AさんとBさんが200万円ずつの評価と、300万円のコストが実現していたはずなので、本来の利益は100万円(400万円-300万円)となる。これは「本来の利益はこうだった」という計算なので、Cさんの嘘とは関係ないため「定数」と表現できる。
また、本来の利益から、実際に得られた利益を差し引いたものがクラーク税になる。先ほどの例なら、公共財が供給されなかったため、実際にAさんとBさんが得た利益は0円となり「100万円-0円=100万円」がクラーク税となる。
➂ T(クラーク税)= 本来の他人の利益(定数) ー 他人の利益
Step3
ステップ1の式に、ステップ2のクラーク税(T)の式を代入します。
➂ U(その人の満足度) = P(その人の利益)-(本来の他人の利益(定数) ー 他人の利益)
Step4
式を整理します。
④ U(その人の満足度)= P(その人の利益)+ 他人の利益- 本来の他人の利益(定数)
ポイント
P(その人の利益)+ 他人の利益
この部分に注目します。「(P)その人の利益」と「他人の利益」を足したものは、「社会全体の利益(SW)」と表現できます。
つまり
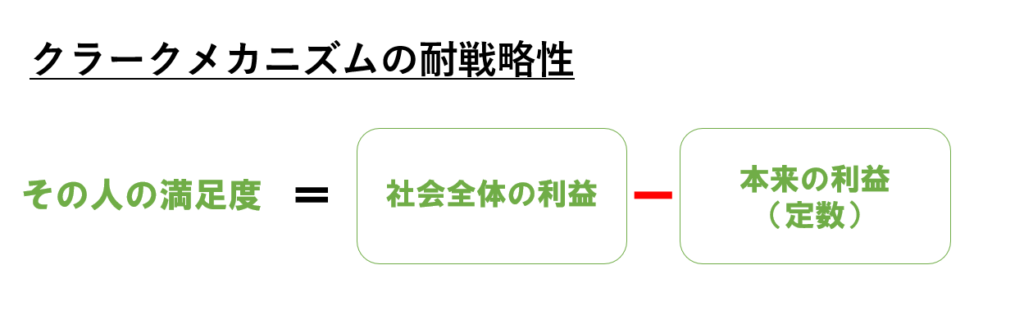
U(その人の満足度)= 社会全体の利益(SW)- 本来の他人の利益(定数)
※「本来の他人の利益(定数)」は、途中で説明した通り、あなたが嘘をつくかに関係なく決まるので、自分で操作することができない部分です。
以上より
その人の満足度を最大にするには、社会全体の利益(SW)を最大にすればよい。

正直に申告するのと嘘をつくのでは、どっちが社会全体の利益が大きくなるんだろう・・?
難しく考えず、簡単に考えてみよう!

ポイント
社会全体には自分も含まれている。つまり、嘘をついて結果をねじ曲げると、そのしわ寄せ(社会の損失)が自分にも返ってくる。
検証してみる(最初の例と同じ)
※最初と同じ例です。説明は省略します。
Aさん、Bさん、Cさんの3人で「橋(コスト300万円)」を架けるか決めます。
| 参加者 | 公共財の評価額(円) | 備考 |
|---|---|---|
| Aさん | + 200万 | 移動が楽になる |
| Bさん | + 200万 | 移動が楽にある |
| Cさん | - 150万 | 景観が悪くなる |
| 合計 | + 250万 | コスト300万に届かない |
「評価額の合計250万円< 公共財のコスト300万円」となったので「橋は作らない(公共財を供給しない)」となります。Cさんにクラーク税が100万円(=200万円+200万円-300万円)が課されます。
パターン①
Cさんが嘘をつく(マイナス額を過少申告する)
「-150万円」→「-90万円」と嘘をつき、評価額の合計を「310万円(=200+200-90)」とする。
公共財のコスト300万円を上回るので公共財が供給されます。Cさんにクラーク税が課されなくなりますが、そもそもCさんは公共財から得られる便益がマイナス150万円だったので、クラーク税を100万円課されていた方が良かったです。
パターン②
Cさんが嘘をつく(マイナス額を過大申告する)
「-150万円」→「-200万円」と嘘をつき、評価額の合計を「200万円(=200+200-200)」とする。
クラーク税の計算は、Cさん以外の本来得られた利益 100万円(200万円+200万円-300万円)が課されるので、虚偽申告する意味がない。

結局、Cさんは嘘をつかない方が得をするんだね。
正直者が得する世界

AさんとBさんの申告額を変えることができない以上、Cさんは嘘をつかずに正直に申告することで自分の利益(社会全体の利益)を最大化するのが合理的というわけです。
クラークメカニズムの問題点

クラークメカニズムは、フリーライダー問題を解決することは出来ますが、別の問題が生じます。
一人ひとりの評価額を聞いて回るのは当然無理なので、現実で運用できないという問題点は当然ありますが、それ以外に理論的な問題点があるので記載します。
色々と比較
- 効率性は「公共財の最適な供給量が実現するか(サミュエルソン条件を満たすか)」という意味
- 耐戦略性「嘘をつくメリットがあるか」という意味
- 予算均衡は「集めるお金と費用が一致するか」という意味
この3つに、個人合理性(そもそも参加するメリットがあるのか?)という項目がありますが、全部○になるので省略しています。
ちなみに、これらを同時に満たすメカニズムは作れません(フルヴィッツの不可能性定理)。①パレート効率性(サミュエルソン条件+予算均衡)・②耐戦略性・➂個人合理性の3つを同時に満たすメカニズムは存在しないというトリレンマです。
クラークメカニズムは「予算均衡しない」「結託に弱い」というデメリットがあるので、順番に見ていきます。
結託に弱いは、ここでいう耐戦略性とは関係ないです。あくまで「個人の耐戦略性」の話なので、結託のように集団的な耐戦略性は上の表の項目には入らないです。
1. 予算均衡しない(余剰の廃棄)

例えば
公共財を供給しないと決定して、誰かからクラーク税を徴収した場合、そのクラーク税をどうするか?という問題が生じます。
もし
徴収したクラーク税金を誰かに還元すると、還元目当てで嘘をつく動機が生まれてしまうので、誰かに還元することは出来ません。
そのため、集めたクラーク税は、社会から切り離す=捨てなければなりません(余剰の廃棄)。せっかく集めたお金をドブに捨てることになるので、パレート効率的ではありません。
今回の例では、公共財を作らないので徴収する税金は0円が好ましいのですが、そうなりません。つまり、公共財の供給に必要なコスト(予算)と、実際に徴収する税金に差額が生じてしまいます。これを予算が均衡しないと言ったりします。

なるほど、、もったいない。。
お金をどう使うかの方が難しい問題

2. 結託(共謀)に弱い

もし
参加者が口裏を合わせて嘘をつくと、クラークメカニズムは機能しません。
「みんなで評価額を高めに申告しよう」と結託されると、誰もクラーク税を払わずに、自分たちの望む結果に誘導することができます。

これは実際に起こりそうな問題だね。
経済学の仕組み、結託に弱い問題

簡単な計算問題(例題)

ある公共事業を行うかを3人(Aさん、Bさん、Cさん)で投票します。それぞれの純便益(便益-費用負担)は以下の通りです。
- Aさん:+10
- Bさん:+10
- Cさん:-25
このとき、①この事業は実施されるか また、②誰がいくらのクラーク税を支払うかを求めなさい。
解答
① この事業を実施するか
全員の純便益を足します。
- 10(Aさん)+10(Bさん)-25(Cさん)=-5
→合計がマイナスなので、この公共事業は実施されない(中止)。
② クラーク税の計算
それぞれの人が「いない場合」の結果を比較します。
- Aさんがいない場合:B(10)+C(-25)=-15(中止)※結果は変わらないので税は0。
- Bさんがいない場合:A(10)+C(-25)=-15(中止)※結果は変わらないので税は0。
- Cさんがいない場合:A(10)+B(10)=+20(実施)
Cさんが参加したことで「実施(+20)」が「中止」に変わったことが分かる。
3人全員の場合は、公共事業を実施しない(中止)という結果になりました。しかし、Cさんがいない場合のみ「実施する」という結論が得られたので、結果に影響を与えたのはCさんと判断する。
Cさんは、AさんとBさんが得るはずだった「20」の便益を消滅させたことになる。よって、Cさんは20のクラーク税を支払う。

