世界中で企業がカルテルを結ぶことは禁止されています。なぜそのような決まりがあるのか、カルテルを経済学の視点で考えていきます。
- カルテル(結託・共謀)とは
- カルテルを数式で考える
- 完全競争市場やクールノー競争との比較
- 計算問題の解き方
カルテルの安定性・カルテル破り(裏切り)・条件式の導出などは別記事で記載しています。
カルテル(結託・共謀)とは

はてな
複数の企業などが、互いに競争を避けて価格・販売数量を共同で取り決める行為のこと。カルテルは、独占禁止法3条により禁止される「不当な取引制限」の一つにあたる。
ちなみに「談合」との違いが分からなくなりますが、カルテルの一種に「談合(購入カルテル)※」があります。
※「談合(購入カルテル)」とは、工事などの受注のときに、各企業が入札競争を避けて高値で落札し合えるように話し合いを行うこと。
市場では、価格や生産量は市場競争によって決まります。
しかし、複数の企業がカルテルを行うと「価格が高止まり」したり、「生産量が調節される」などの弊害が生まれて、市場が非効率的になる。


ポイント
経済学では、カルテル(結託)が行われると「複数の企業が1つの企業グループとなり、独占企業のように行動する」と考える。
法律で「カルテル」が独占禁止法の範囲となっているのはこのため。カルテルは市場をゆがめる行為として、アメリカや中国をはじめ、世界各国で禁止されている。
通常、カルテルは同じ業種・産業内で行われるため、その産業内で単一の独占企業が誕生したような状態になる。


数式で考える

いま、企業2社がカルテルを結ぶことを考える。なお、市場はこの2社で寡占されている。カルテルを結ぶと市場価格や生産量がどのようになるのかを考える。
- 価格=P
- 企業Aの生産量=Ya
- 企業Aの費用=Ca
- 企業Bの生産量=Yb
- 企業Bの費用=Cb
2社の利潤関数(π)は「利潤(π)=(価格)×(生産量)-(費用)×(生産量)」なので
- (企業Aの利潤)πa=P・Ya-Ca・Ya
- (企業Bの利潤)πb=P・Yb-Cb・Yb
A社・B社は、カルテルを結び1つの企業グループのように行動するため、2社の利潤関数を合体する(足し合わせるだけ)。
式を合体させると
- (πa+πb)=P・Ya+P・Yb-Ca・Ya-Cb・Yb
YaとYbで括(くく)ります。
※(πa+πb)=πとする
- π=P・Ya+P・Yb-Ca・Ya-Cb・Yb
- π=(P-Ca)・Ya+P・Yb-Cb・Yb
- π=(P-Ca)・Ya+(P-Cb)・Yb
ここで、各企業は利潤最大化を目指して活動するので、企業Aと企業Bの利潤最大化を求めます。数学的には、企業の利潤最大化条件より「利潤関数を生産量で微分して=0」とする。
企業Aの利潤最大化を求める
- Yaで微分する
π=(P-Ca)・Ya+(P-Cb)・Yb
πa’=P-Ca=0
企業Aの生産量(Ya)で微分するとき、Yaがない部分は無視します。次に、Yaがついている部分は、Yaの乗数を手前に持ってくる&乗数を1減らせばOKです。
(P-Ca)・Yaは「Yaの1乗」なので、1乗を手前に持ってきて1×(P-Ca)・Yaの0乗となり、0乗=1なので(P-Ca)の部分だけが残っています。
企業Bの利潤最大化を求める
- Ybで微分する
π=(P-Ca)・Ya+(P-Cb)・Yb
πb’=P-Cb=0
企業Aのときと同じように微分します。
企業A・企業Bが利潤最大化を目指すとき、それぞれ下記の数式の状態になることが分かりました。
- πa’=P-Ca=0
- πb’=P-Cb=0
つまり「P-Ca=P-Cb」となります。
以上より
- P-Ca=P-Cb
- Ca=Cb です
ここでCaとCbは
- 企業Aの費用=Ca
- 企業Bの費用=Cb
を表していました。
ちなみに、CaとCbは生産1単位当たりの費用を表しています。ようは、商品1つ作るのにいくら費用が掛かるかを表している。つまり、商品1つ作るとき発生する追加的な費用なので「限界費用(MC)」のことを表しています。
※「Ca」「Cb」は総費用を表しているわけではありません。総費用は「Ca×(生産量)」という風に求めます。
ポイント
つまり「Ca=Cb」なので、カルテルを結んだ企業A・企業Bは、商品1つ作るのに発生する費用が同じになることを意味している。
→カルテルを結ぶと、費用面でどちらかが優位になる状態にはならないということ。
※上で書きましたが「総費用」が同じになるわけではなく「限界費用(MC)」が同じになることを意味しています。限界費用面では有意差がなくなる水準で生産量が決まることを意味している。
例えば
企業Aの方が商品1個当たりの費用が小さく済むようなら、企業Aの方がたくさん生産して、企業Bの生産量を小さくするように共謀するはずだ、ということを表しています。
企業B
うち、コスト面で不利だから、企業Aさんの方でたくさん生産してもらえますか?
企業A
確かにうちが生産量増やしたほうが効率的な気がするな。じゃあ、そうしよう。
数学的には、それが繰り返されていくと企業Aは過剰生産気味になるので、コストがひっ迫します。
すると、企業Aの費用的な優位性が無くなります。なので企業Aと企業Bの生産量はバランスよいところで落ち着くと考えているわけです。


でわ「Ca=Cb」と分かったところから続きです。
「Ca=Cb」なので、まとめて
- Ca=Cb=C とします。
以上より
2社の利潤関数を合体させた下の数式のうち「Ca」「Cb」を「C」に置き換えます。
- π=(P-Ca)・Ya+(P-Cb)・Yb
- π=(P-C)・Ya+(P-C)・Yb
- π=(P-C)(Ya+Yb)


次に「Ya+Yb」の部分を考える。
市場は企業Aと企業Bの2社で寡占しているので「2社の生産量が市場に供給されて、それがそのまま市場で需要」されます。
市場の総需要量を「x」と表すと‥
- x=Ya+Yb
したがって
- π=(P-C)(Ya+Yb)
- π=(P-C)(x)
- π=(P-C)・x
ここで
- 市場の逆需要関数(D)「P=a-b・x」と考える
逆需要関数というのは、需要関数(D)を「P=~」という形にしたもの。生産量が多ければ価格や安くなるし、生産量が減れば価格は上昇する。ごく一般的な需要曲線を文字式を使って表しているだけ。
先ほどの式に逆需要関数を代入します。
- π=(P-C)・x
- π=(a-b・x-C)・x


さきほどまでは、企業Aと企業Bの利潤最大化を考えてきました。
いつのまにか、式を変形したことにより「Ya」「Yb」などが消えて、市場全体を表す「x」などの文字式に置き換わっています。
ということで
利潤最大化条件より、市場全体の生産量・需要量である「x」で微分して「=0」とします。
- π=(a-b・x-C)・x
- π=a・x-b・x^2-C・x
- π’=a-2b・x-C=0
はじめに式を展開しています。微分は乗数を減らして手前に持ってくるだけです。各項の「x」の乗数を減らして手前に持ってきます。1a・x^0-2b・x^1-1C・x^0。0乗=1なので計算すると「a-2b・x-C」
「x」の値を求めます。
- a-2b・x-C=0
- a-C=2b・x
- (a-C)/2b=x
- x=(a-C)/2b
最後に市場価格を求めます。市場の逆需要関数(D)「P=a-b・x」と考えていたので、この式に上記の式を代入します。
- P=a-b・x
- P=a-b・(a-C)/2b
- P=a+(-a+C)/2
- P=(a+C)/2


企業A・企業Bが寡占している市場で、2社がカルテルを結んだとき、市場価格と生産量・需要量は下記の通りになる。
- P=(a+C)/2
- x=(a-C)/2b
グラフで見る
ポイント
この結果を、完全競争市場・独占市場・寡占市場と比較する。
他の市場との比較

ここから先は、カルテルが結ばれたときの市場の状態を「完全競争市場」「クールノー競争」「シュタッケルベルグ競争」「独占市場」と比較します。
(1)~(4)で少々細かく比較して、(5)でまとめに入ります。細かな話が嫌いな人は(5)から確認してください!
ベルトラン競争の場合、製品差別化が行われていないときは「完全競争市場」、製品差別化が完全に進めば「独占市場」と同じ状態になるため飛ばします。
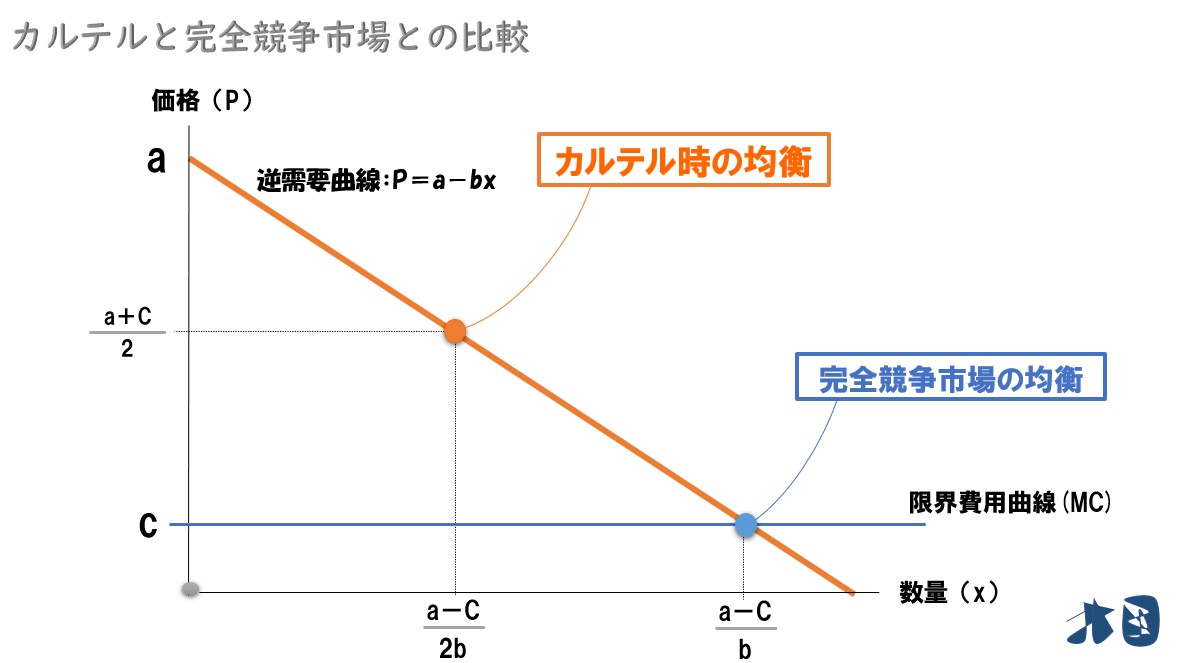
(1)完全競争市場との比較
下記条件で完全競争市場の生産量と価格を考えます。
- 市場の逆需要関数(D)「P=a-b・x」
- 費用関数(C)「C・x」
完全競争市場の利潤最大化条件「P(価格)=MC(限界費用)」より
- 「P=a-b・x=C」
限界費用(MC)は、費用関数を生産量(x)で微分すれば求められます。「C・x」をxで微分すると「C」になります。
市場全体の生産量(x)は‥
・a-b・x=C
・a-C=b・x
・x=(a-C)/b
カルテルを結んだときの生産量は「x=(a-C)/2b」だったので、完全競争市場と比較して、ちょうど半分しか市場では生産されなくなっています。
さらに
完全競争市場の価格は「P=C」となりますが、カルテル時は「P=(a+C)/2」となります。一応、完全競争市場よりも価格が高止まりするのですが、簡単に証明します。
- 完全競争:P=C
- カルテル:P=(a+C)/2
(どちらも2倍します)
- 完全競争:2C
- カルテル:a+C
ここで、2Cは「C+C」のことを指しています。つまり「C+C」と「a+C」の大きさを比較することになるため「a」「C」の大小を比較すればOKです。
より厳密な照明は専門書に譲り、ここでは簡易的にグラフで判断します(どういう風にやればいいか思いつきませんでした・・)。
通常、需要関数(D)と限界費用(MC)は次のような関係になる。
ふつうの市場では需要曲線は右下がりである。このときの切片を「a」と考えていた。通常、限界費用(MC)が切片「a」よりも下に位置するところで生産量が決まる。 もしも、需要曲線の切片「a」よりも高い位置に限界費用(MC)があると「市場で受け入れられる価格」よりも「企業が1つの商品を作るコスト」の方が高くなることを意味する。作れば作るほど赤字になるような商品を企業は生産しないため、そのようなところで生産量が決まる市場はふつう存在しない。 したがって「a >C」となる。
以上より、カルテル時の市場価格「P=(a+C)/2」は、完全競争市場の価格「P=C」よりも高くなる。
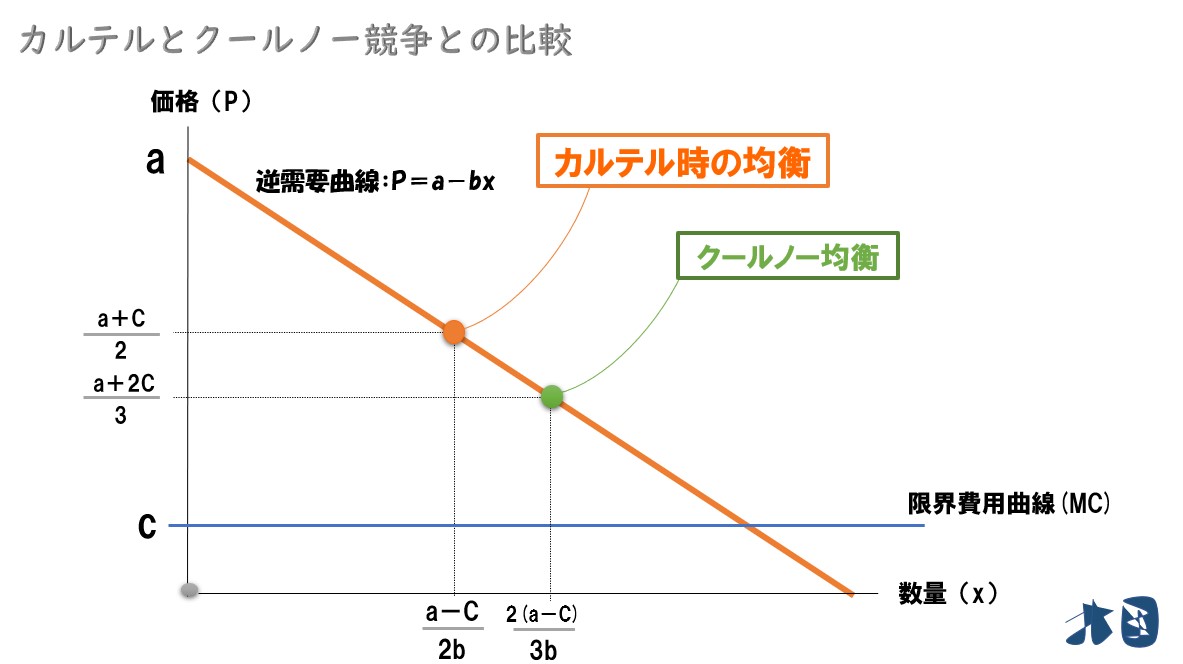
(2)クールノー競争との比較
下記条件で複占市場でクールノー競争が起こった場合の生産量と価格を考えます。
- 市場の逆需要関数(D)「P=a-b・x」
- 費用関数(C)「C・x」
計算すると次の通りになります(詳細は下記リンク参照)
- クールノー競争の生産量=2/3・(a-C)/b
- クールノー競争の価格=(a+2C)/3
カルテル時の生産量と比較します
カルテルを結んだときの生産量は「x=(a-C)/2b」でした。
- クールノー:2/3・(a-C)/b
- カルテル:(a-C)/2b=1/2・(a-C)/b
なので、クールノー競争時と比較して、カルテル時は1/6生産量が少なくなります。
カルテル時の価格と比較します
クールノー均衡の価格は「P=(a+2C)/3」となりますが、カルテル時は「P=(a+C)/2」となります。
- クールノー:(a+2C)/3
- カルテル:(a+C)/2
(両方とも6倍)
- クールノー:6(a+2C)/3=2a+4C
- カルテル:6(a+C)/2=3a+3C
ここで2つがどれくらい違っているのか考えるために差し引きします。
- (2a+4C)-(3a+3C)=-a+C
(クールノーの価格)-(カルテルの価格)=「-a+C」なので、クールノー価格の方が大きければ、この「-a+C」がプラスになる。カルテル価格の方が大きければ「-a+C」がマイナスになります。
ここからは、完全競争市場と同じ論法を使い、グラフで判断します(どういう風にやればいいか思いつきませんでした・・その2)。
ふつうの市場では需要曲線は右下がりである。このときの切片を「a」と考えていた。通常、限界費用(MC)が切片「a」よりも下に位置するところで生産量が決まる。 もしも、需要曲線の切片「a」よりも高い位置に限界費用(MC)があると「市場で受け入れられる価格」よりも「企業が1つの商品を作るコスト」の方が高くなることを意味する。作れば作るほど赤字になるような商品を企業は生産しないため、そのようなところで生産量が決まる市場はふつう存在しない。 したがって「a >C」となる。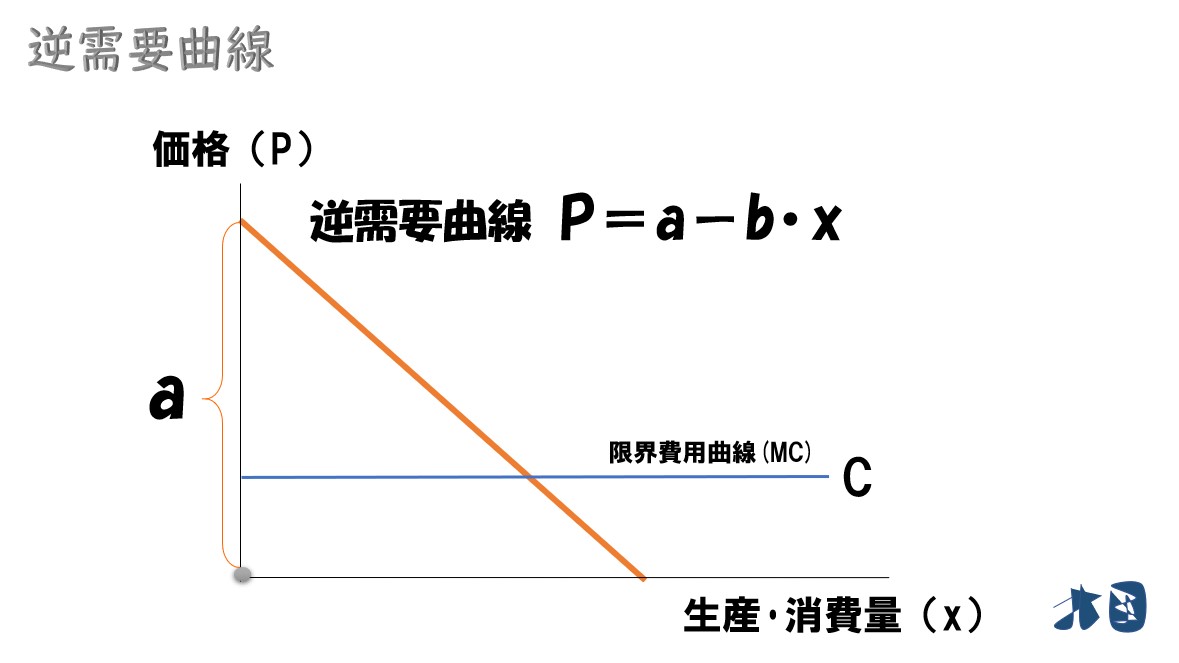
以上より
「-a+C」は「a」の方が大きくなるのでマイナスになる。
したがって、カルテル時の市場価格「P=(a+C)/2」は、クールノー競争の価格「P=(a+2c)/3」よりも高くなる。
(3)シュタッケルベルグ競争との比較
下記条件で複占市場でシュタッケルベルグ競争が起こった場合の生産量と価格を考えます。
- 市場の逆需要関数(D)「P=a-b・x」
- 費用関数(C)「C・x」
計算すると次の通りになります。
(シュタッケルベルグ競争の生産量)
- 企業A:(a-C)/2b
- 企業B:(a-C)/4b
⇒市場全体の生産量は2つを足せばよいので「(3a-3C)/4b」
(シュタッケルベルグ競争の価格)
逆需要関数「P=a-b・x」へ上記の生産量を代入する。
- P=a-b・x
- P=a-b・(3a-3C)/4b
- P=a-(3a-3C)/4
- P=(1/4)a+(3/4)C
カルテル時の生産量と比較します
カルテルを結んだときの生産量は「x=(a-C)/2b」でした。
- シュタッケルベルグ:(3a-3C)/4b=3・(a-C)/4b
- カルテル:(a-C)/2b=(2a-2C)/4b=2・(a-C)/4b
なので、シュタッケルベルグ競争時と比較して、カルテル時は1/4生産量が少なくなります。
カルテル時の価格と比較します
シュタッケルベルグ均衡の価格は「P=(1/4)a+(3/4)C」となりますが、カルテル時は「P=(a+C)/2」となります
- シュタッケルベルグ:(1/4)a+(3/4)C
- カルテル:(a+C)/2
(両方とも4倍)
- シュタッケル:4((1/4)a+(3/4)C)=a+3C
- カルテル:4((a+C)/2)=2a+2C
ここで2つがどれくらい違っているのか考えるために差し引きします。
- (a+3C)-(2a+2C)=-a+C
(シュタッケルベルグ価格)-(カルテル価格)=「-a+C」なので、シュタッケルベルグ価格の方が大きければ、この「-a+C」がプラスになる。カルテル価格の方が大きければ「-a+C」がマイナスになります。
ここからは、完全競争市場と同じ論法を使い、グラフで判断します(どういう風にやればいいか思いつきませんでした・・その3)。
ふつうの市場では需要曲線は右下がりである。このときの切片を「a」と考えていた。通常、限界費用(MC)が切片「a」よりも下に位置するところで生産量が決まる。 もしも、需要曲線の切片「a」よりも高い位置に限界費用(MC)があると「市場で受け入れられる価格」よりも「企業が1つの商品を作るコスト」の方が高くなることを意味する。作れば作るほど赤字になるような商品を企業は生産しないため、そのようなところで生産量が決まる市場はふつう存在しない。 したがって「a >C」となる。
以上より
「-a+C」は「a」の方が大きくなるのでマイナスになる。
したがって、カルテル時の市場価格「P=(a+C)/2」は、シュタッケルベルグ競争の価格「P=(1/4)a+(3/4)C」よりも高くなる。
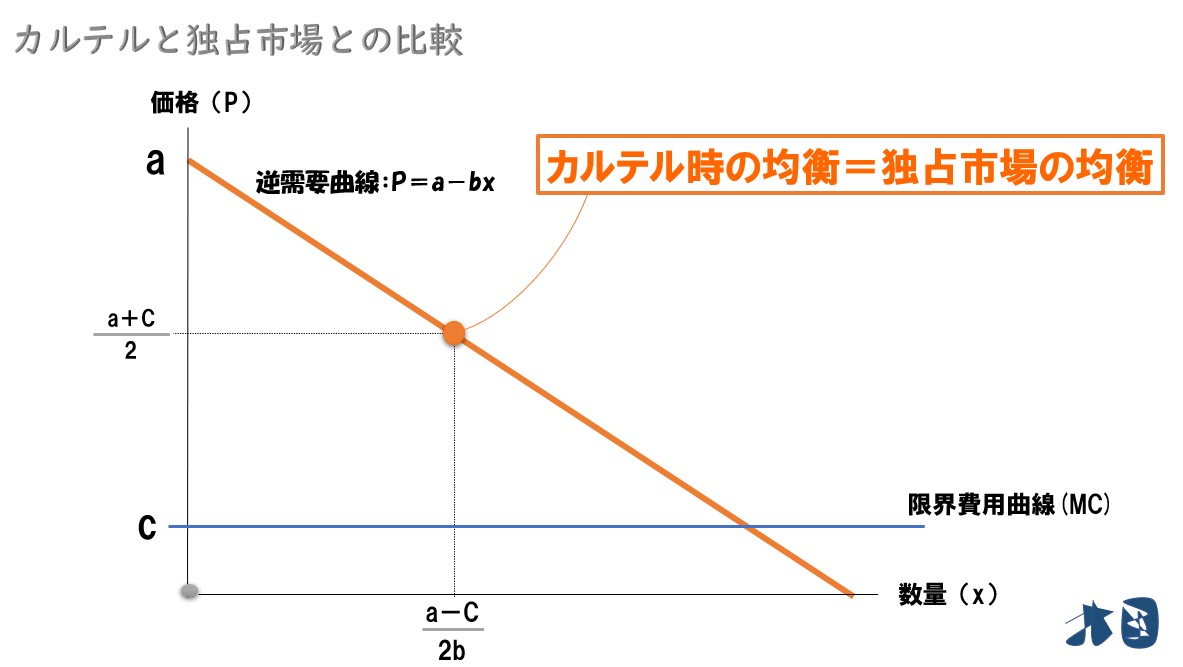
(4)独占市場との比較
下記条件で複占市場でクールノー競争が起こった場合の生産量と価格を考えます。
- 市場の逆需要関数(D)「P=a-b・x」
- 費用関数(C)「C・x」
独占市場の利潤最大化条件「MR(限界収入)=MC(限界費用)」より
- 「MR=a-2b・x」
- 「MC=C」
- 「a-2b・x=C」
独占市場の限界収入(MR)は、需要関数の傾きを2倍にすればOKです(独占市場の利潤最大化「限界費用=限界収入」と価格の決まり方)
限界費用(MC)は、費用関数を生産量(x)で微分すれば求められます。「C・x」をxで微分すると「C」になります。
市場全体の生産量(x)は‥
・a-2b・x=C
・a-C=2b・x
・x=(a-C)/2b
カルテルを結んだときの生産量は「x=(a-C)/2b」だったので、独占市場とカルテルが結ばれたときの生産量は同じになる。
さらに
独占市場の価格は、市場の逆需要関数(D)「P=a-b・x」に、先ほどの「x=(a-C)/2b」を代入すれば求まります。
- P=a-b・x
- P=a-b・(a-C)/2b
- P=a-(a-C)/2
- P=a+(-a+C)/2
- P=(a+C)/2
カルテル時の市場価格「P=(a+C)/2」だったので、独占市場の価格とカルテルが行われたときの価格は同じになる。
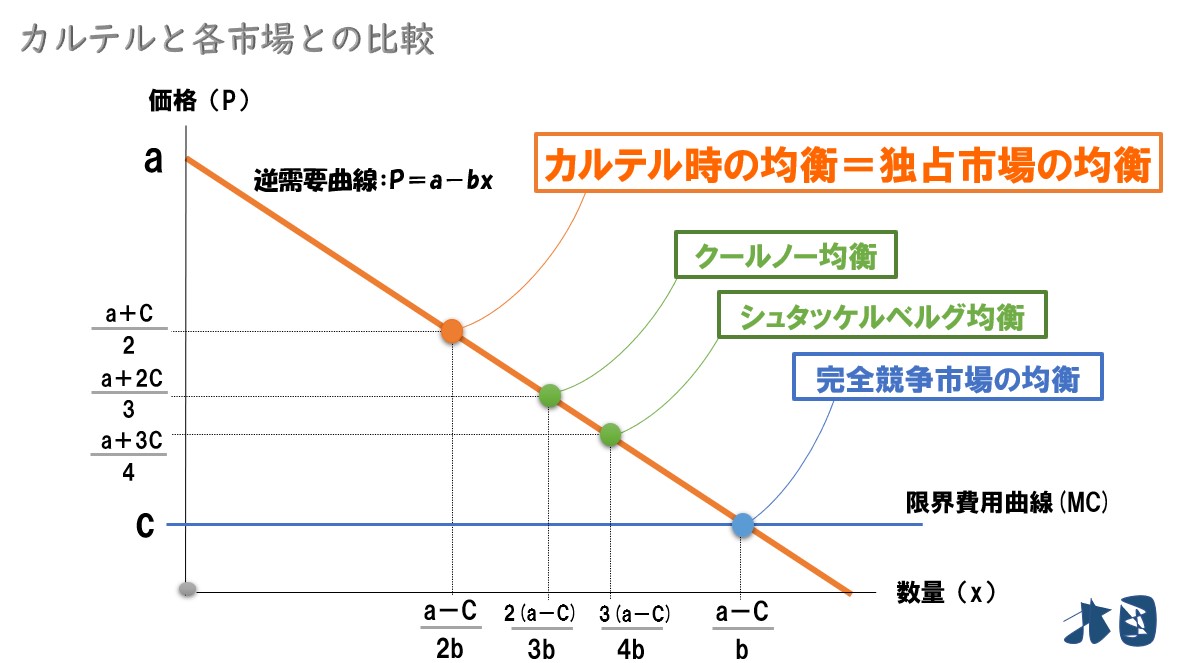
(5)まとめ(重要)
それぞれの市場では、均衡価格・生産量は下記の通りになる。
価格
- カルテル:P=(a+C)/2
- クールノー:P=(a+2C)/3
- シュタッケル:P=(a+3C)/4
- 完全競争:P=C
カルテル=独占市場 >クールノー競争 >シュタッケルベルグ競争 >完全競争市場
生産量
- 完全競争:x=(a-C)/b
- シュタッケル:x=3(a-C)/4b
- クールノー:x=2(a-C)/3b
- カルテル:x=(a-C)/2b
完全競争市場 >シュタッケルベルグ競争 >クールノー競争 >カルテル=独占市場
ポイント
カルテルが結ばれると、完全競争市場や寡占市場(クールノー競争やシュタッケルベルグ競争)よりも価格が高止まりして、生産量も少なくなるため、市場が非効率に陥っていることが分かる(独占市場と同じ状態になる)。


計算問題の解き方

いま、企業Xと企業Yの2社が支配する複占市場を考える。
- 需要関数:D=12-P
- X社の生産量=x
- Y社の生産量=y
- X社の費用関数(C)=2x
- Y社費用関数(Cy)=2y
※2社の費用関数は同一と考える。
両社がカルテルを結んだ(共謀・協調した)時の各社の利潤はいくらか。なお利潤は2社で半分ずつ配分する。
はじめに
複占市場なので2社が生産したものが需要される
- 需要(D)=「X社の生産量+Y社の生産量」
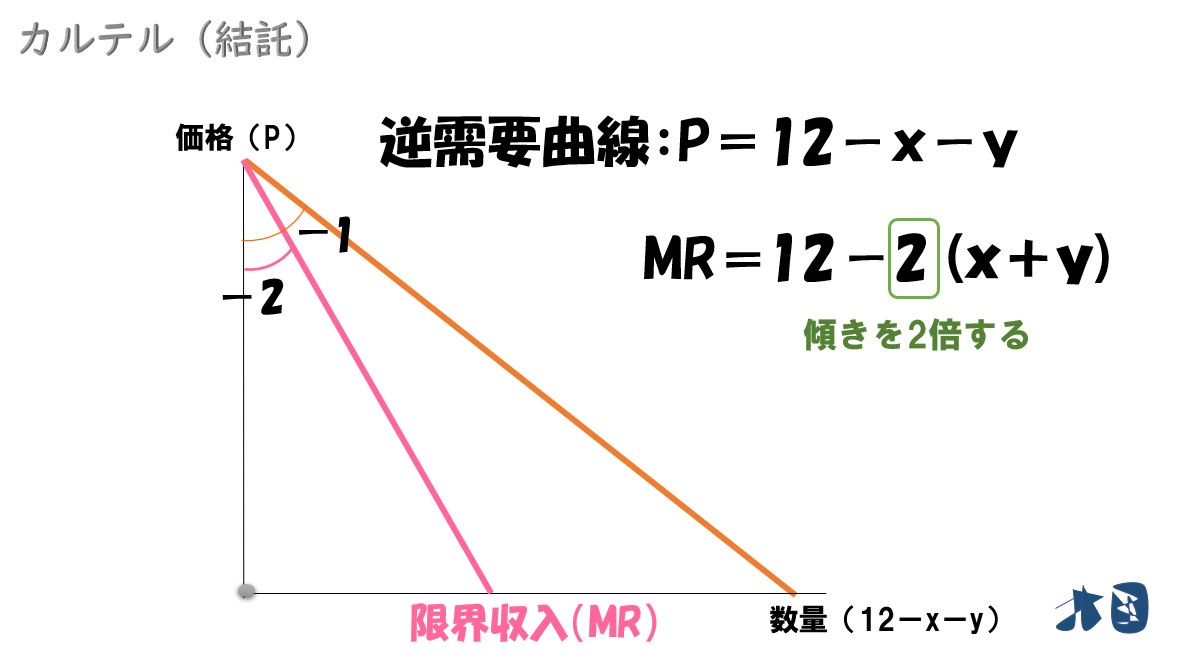
よって「(D=)12-P=x+y」⇒「P=12-x-y」となる
ポイント
カルテル(結託・共謀)は、独占市場と同じ状態になるため、独占市場の利潤最大化条件(MR=MC)を使って計算をすればよい。
カルテルが独占市場と同じになるイメージは最初で説明したとおりです(戻って確認する)。
step
1限界収入(MR)を求める
独占市場では、逆需要曲線(P=~)の傾きを2倍すれば限界収入になります。
独占市場で傾き2倍の話はこちらで確認してください⇒独占市場の利潤最大化「限界費用=限界収入」と価格の決まり方
step
2限界費用(MC)を求める
- X社費用関数(Cx)=2x
- Y社費用関数(Cy)=2y
問題文に「2社の費用関数は同一と考える」とあったので・・
- 2x=2y ⇒「x=y」
⇒「xとy」を「z」として両社の費用関数を「2z」とします。
カルテルの問題は、基本的に2社の費用関数が同一となります。ただし、発展問題で同一じゃない費用関数のときがあります。その時は、クールノー競争などで利潤が大きくなる企業がすべての生産を担って(他の企業は生産量0)、その後2社なり3社で分配すると考えます。
費用関数「2z」を微分すれば限界費用になります。
・費用関数=2zを「z」で微分する
・MC=2
微分は乗数を1減らして手前に持ってくる。「z」は「zの1乗」なので「1×2×zの0乗」となる。「0乗=1」なので「1×2×1=2」
step
3MR=MCより
- MR=12-2(x+y)
- MC=2
「12-2(x+y)=2」⇒「2(x+y)=10」⇒「(x+y)=5」
step
4需要曲線に代入する
・「(D=)12-P=x+y」
・「12-P=5」
・「P=7」
step
5利潤を計算する
全体の利潤は「市場価格(P)×生産量-総費用(費用×生産量)」
- 市場価格(P)=7
- 生産量(x+y)=5
- 総費用(2z)=2×5=10
市場価格(7)×生産量(5)-総費用(10)=35-10=25
2社は利潤を半分ずつ配分するので
- x社の利潤(πx)=12.5
- y社の利潤(πy)=12.5
X社の利潤は「12.5」/Y社の利潤は「12.5」


-グラフ1.jpg)
-グラフ2.jpg)
-グラフ3.jpg)