「厚生経済学の基本定理」の意義や証明を簡単に知りたい人向けにまとめています。
- 厚生経済学の第一基本定理
- 厚生経済学の第二基本定理
- それぞれの意味や含意
- それぞれの証明について
厚生経済学の基本定理とは?
はてな
完全競争市場とパレート効率性の関係について述べた2つの定理を指す。それぞれ「厚生経済学の第一基本定理」と「厚生経済学の第二基本定理」と呼ばれる。
経済学では「自由経済」の重要性が説かれることが多いですが、その根拠となっているのが厚生経済学の基本定理です。
ポイント
厚生経済学の基本定理により次の2つが分かる。
- 経済活動は自由経済を前提に行うことが望ましい
- 格差問題は所得再分配を実施すれば経済の効率性を壊さない
自由経済を行うことが望ましい(第一基本定理)、その結果生まれた格差は、所得再分配により是正すれば効率性を損なわない(第二基本定理)。


厚生経済学の第一基本定理
簡単な解説
厚生経済学の第一基本定理は「自由経済は効率的!」ということを証明しているのですが、何故そのような結論になるのかを順番を追って見ていきましょう。
ポイント
第一基本定理を理解するときに重要となるのは次の3つです。
- 完全競争市場ならば
- 消費者の選好が条件を満たせば
- パレート効率的(パレート最適)を実現
他にも市場の普遍性(財の所有権が明確になっており、すべての財に市場が存在して市場を通じて交換・売買が行われる)などの条件を記載している教科書もあります。
完全競争市場とは
- 市場参加者がたくさんいる(誰も価格決定権がない=価格は市場で決まる状態)
- 完全情報(市場参加者はすべての情報を把握できる)
- 市場への参入と退出が自由(参入規制は存在しない)
- 財の同質性(同じ財なら、Aが作ってもBが作っても同品質)
消費者の選好
- 局所非飽和性を満たす
局所非飽和性は、消費量を細かく増減できれば、消費者はより高い効用水準を実現できる状態のことを言います。
例えば、友人とケーキを食べるとき「自分がショートケーキを1つ食べるよりも、ショートケーキとモンブランを友達と半分こ(0.5個×2)したい!」と考える人がケーキを半分ずつ食べることが出来れば、より満足度が高まります。
このように、消費量を柔軟に変化させることが出来れば、消費者はより満足度の高い選択をできるはずで、これを局所非飽和性と呼んでいます。
パレート効率的
ある集団内の誰かの効用を犠牲にしなければ、他の誰かの効用を高めることができない状態をパレート効率的(パレート最適)と言います。←逆に言えば、これ以上誰かの効用を高めることが出来ないほど、資源配分が効率的になっている状態。
前提となる知識が揃ったところで
完全競争市場(参加者の多様性・完全情報・参入退出の自由・財の同質性が満たされる市場)で、消費者が局所非飽和性を満たしているならば、パレート効率的(これ以上、誰かの効用水準を高めることが出来ないほど効率的)な資源配分になる。
簡単に言うと
- 政府とかが介入せずに自由な経済活動を行えば資源配分が効率的になるので、自由経済が好ましい


意義
ポイント
厚生経済学の第一基本定理より、基本的には自由経済を目指すことが好ましいが、①現実の経済活動では第一基本定理の前提となる条件を満たさないことが多い。また、②前提条件を満たしても経済が効率的にならないケースも存在することを理解する。
第一基本定理のポイントは大きく3つです。
- 基本的には自由経済が効率的
- 前提条件を満たすのが困難
- 経済的に非効率になる場合もある
完全競争市場では、パレート効率的な資源配分が実現するので「現実世界も自由経済が好ましい!」となるわけですが話はそう簡単ではありません。
よくメディアなどで
コメンテーター的な人
政府は加入せずに自由に経済活動をする方が良い!
という人がいますが、この根拠は厚生経済学の第一基本定理と言えます。
現実との違い
思い出してほしいのですが、第一基本定理は「完全競争市場」を前提にしています。このとき、1つの疑問が浮かびます。
現実世界で完全競争市場は存在するのか?
- 市場参加者がたくさんいる
- 完全情報
- 市場への参入と退出が自由
- 財の同質性
このうち、完全情報と財の同質性を満たすのは困難であることがイメージできます
なぜなら、全ての人が合理的に判断するための情報をすべて把握できるわけがありません。「生産者しか知らない情報」「消費者しか分からない好み」が存在します。
同じ財を生産しても作り手によって品質が異なるケースもありますし、世に出回っている財のほとんどは差別化されています。
ココがポイント
厚生経済学の第一基本定理により自由経済が効率的であることが分かるが、現実世界では完全競争市場の前提となる条件を満たしていないケースが多い。
現実世界の多くは不完全競争市場や独占的競争市場
これは次のステップで学習する内容です。完全競争市場では自由経済が効率的ですが、現実では完全競争市場の前提を満たさない市場構造がたくさんある。
さらに
仮に完全競争市場だったとしても、効率性を損なうケースも存在する
- 外部性
- 公共財
- 費用逓減産業
完全競争市場だったとしても市場機能が上手く働かないことを「(狭義の)市場の失敗」と呼びます。ちなみに、そもそも完全競争の条件を満たすことが出来ないなどの問題を含めると「(広義の)市場の失敗」となります。
ココがポイント
仮に厚生経済学の第一基本定理が前提とする完全競争市場だったとしても、自由経済が効率的に働かないケースも存在する。
まとめ
- 厚生経済学の第一基本定理は完全競争市場の効率性を示しており、自由経済を尊重する根拠となる。ただし、自由経済は万能ではないことに注意する。
例えば、現実世界では完全競争市場の前提となる条件を満たさないケースが多く、不完全競争市場や独占的競争市場が存在する。
また、仮に現実世界が完全競争市場だったとしても、効率性を実現できないケースがあり、外部性・公共財・費用逓減作業に代表される「市場の失敗」が存在する。
ポイント
以上より、厚生経済学の第一基本定理をもとに自由経済を求めることは重要だが、現実では効率性を損なう要因が存在する。
その要因を分析して、効率的な資源配分を実現するためにはどうすれば良いか?をよく考えることが重要です。
「厚生経済学の第一基本定理は机上の空論だ!」と批判するのも良いですが、理論通りにならない理由や、どうすれば効率性を実現できるか?など、第一基本定理をスタート地点に学習を進めると経済学の理解が進むかと思います。
この後は、独占市場(1社)・複占市場(少数)・独占的競争・外部性・公共財・費用逓減産業などのトピックに繋がります。


代数的な証明

ポイント
教科書では「完全競争市場における競争均衡(ワルラス均衡)がパレート効率的ではないと仮定すると矛盾が生じるため、完全競争市場の競争均衡はパレート効率的になる」という証明(←背理法「~なら矛盾が生じるため○○は正しい」)をしているので、その方法で証明をしてみます。
いま、交換経済を想定して、完全競争市場におけるワルラス均衡がパレート効率的ではないと仮定する(また、消費者は局所非飽和性を満たす)。
Aさん・BさんがX財・Y財をそれぞれ消費しているので、消費の組合せは次のように表す
- Aさんの消費の組合せ(xa,ya)
- Bさんの消費の組合せ(xb,yb)
xa=AさんのX財の消費量・ya=AさんのY財の消費量という意味。xb・ybも同様
消費の組合せ「(xa,ya),(xb,yb)」がワルラス均衡のときパレート効率的ではないと考える。
ここで「パレート効率的ではない=パレート改善できる」という意味なので、パレート改善した後の資源配分を(x’a,y’a),(x’b,y’b)とする。
パレート改善した場合、Aさん・Bさんの効用は大きくなる、もしくは少なくとも片方は大きくなるはずなので、次のような不等式で表せる。
- Ua(xa,ya)≦Ua(x’a,y’a)
- Ub(xb,yb)≦Ub(x’b,y’b)
「Ua=Aさんの効用」を意味しています。なので「Ua(xa,ya)」は消費の組合せ(xa,ya)から得られる効用の大きさ、「Ua(x’a,y’a)」はパレート改善した消費の組合せ(x’a,y’a)から得られる効用の大きさを表しています。Bさんも同様。
式の意味をもう少し言葉で表現すると
- ワルラス均衡のAさんの効用≦パレート改善時のAさんの効用
- ワルラス均衡のBさんの効用≦パレート改善時のBさんの効用
ここでは、パレート改善により「Aさんの効用が大きくなり、Bさんの効用は変わらない(もしくは大きくなった)」と考える。
つまり
- Ua(xa,ya)<Ua(x’a,y’a)
- Ub(xb,yb)≦Ub(x’b,y’b)
ここで
そもそもワルラス均衡ならば「各消費者は、自身の予算内で効用最大化を実現している」はずなので、「パレート改善した後の資源配分は予算内では実現できない」と考える。
2人の予算については次のように考えます。
まず
交換経済を想定していたので、2人の初期保有量を次のように表現すると
- AさんのX財の初期保有量=Xa
- AさんのY財の初期保有量=Ya
- BさんのX財の初期保有量=Xb
- BさんのY財の初期保有量=Yb
大文字のX・Yで初期保有量を表現しましたが、教科書では文字に「-(バー)」を引いていることが多い印象です。
「自分の初期保有量を交換に差し出すことが出来る=予算」となるので、ワルラス均衡が実現するときの2財の価格をPx・Pyとして
- Aさんの予算=Px・Xa+Py・Ya
- Bさんの予算=Px・Xb+Py・Yb
ここで、先ほどの話を思い出します。
ワルラス均衡ならば「各消費者は、自身の予算内で効用最大化を実現している」はずなので、「パレート改善した後の資源配分は予算内では実現できない」と考える。
パレート改善した後の資源配分は予算内では実現できないので「Aさんの予算<Aさんのパレート改善時の支払総額」となる
- Aさんの予算=Px・Xa+Py・Ya
- Aさんのパレート改善時※=Px・x’a+Py・y’a
※パレート改善時のAさんの消費の組合せ(x’a,y’a)に価格を掛けて支払総額を表す
以上より
- Px・Xa+Py・Ya<Px・x’a+Py・y’a
同様にBさんも
- Px・Xb+Py・Yb≦Px・x’b+Py・y’b
2つの式を合わせると
「Aさん・Bさんの予算<Aさん・Bさんのパレート改善時の支払総額」となるはず
- Px(Xa+Xb)+Py(Ya+Yb)<Px(x’a+x’b)+Py(y’a+y'b)
ここで
Aさん・Bさんのパレート改善時の消費の組み合わせは、Aさん・Bさんの初期保有量の合計と等しくなる(少なくとも超えることはあり得ない※)ので
※交換経済なので2人が持っている財の総量を超えて消費出来ない。
次の2つがイコールになる
- X財の初期保有量の合計(Xa+Xb)
- X財のパレート改善時の消費の組合せ(x’a+x’b)
(Xa+Xb)=(x’a+x’b)
同様に(Ya+Yb)=(y’a+y’b)
上記の等式を、先ほどの不等式へ代入する
Px(Xa+Xb)+Py(Ya+Yb)<Px(x’a+x’b)+Py(y’a+y'b)
⇒Px(x’a+x’b)+Py(y’a+y'b)<Px(x’a+x’b)+Py(y’a+y'b)
左辺と右辺は全く同じものを表しているのに「=」になっていないため矛盾が生じる。
以上より、完全競争市場における競争均衡(ワルラス均衡)がパレート効率的ではないと仮定すると矛盾が生じるため、競争均衡はパレート効率的になる。


厚生経済学の第二基本定理
簡単な解説
「どのようなパレート効率的な資源配分(市場均衡)であっても」が分かりづらいですが、簡単に言えば「現状のパレート効率的な資源配分から、別のパレート効率的な資源配分を目指したいとき、初期保有量を変えれば実現できる」という意味です。
なぜ別のパレート効率的な資源配分を目指したいのか
例えば「貧乏人」と「金持ち」がいたとき、現在のパレート効率的な資源配分では金持ちに有利なので、貧乏人がもう少し有利になるようにしたい(公平性の問題)→貧乏人が有利となるような別のパレート効率的な資源配分を目指したい
このように公平性を考えると、社会的に望ましいバランスの取れた資源配分を目指す理由になります。
厚生経済学の第二基本では「初期保有量を調整する※ことで、市場の効率性を損なわずに狙った資源配分(しかもパレート効率的)を目指せる」ことを証明しています。
※初期保有量を調整する手段として、所得の再分配などがあげられます。
前提
第一基本定理の前提(完全競争市場・消費者の選好が局所非飽和性を満たす)を満たしたうえで必要な条件があるので注意しましょう
- 消費者の選好が凸性を満たす
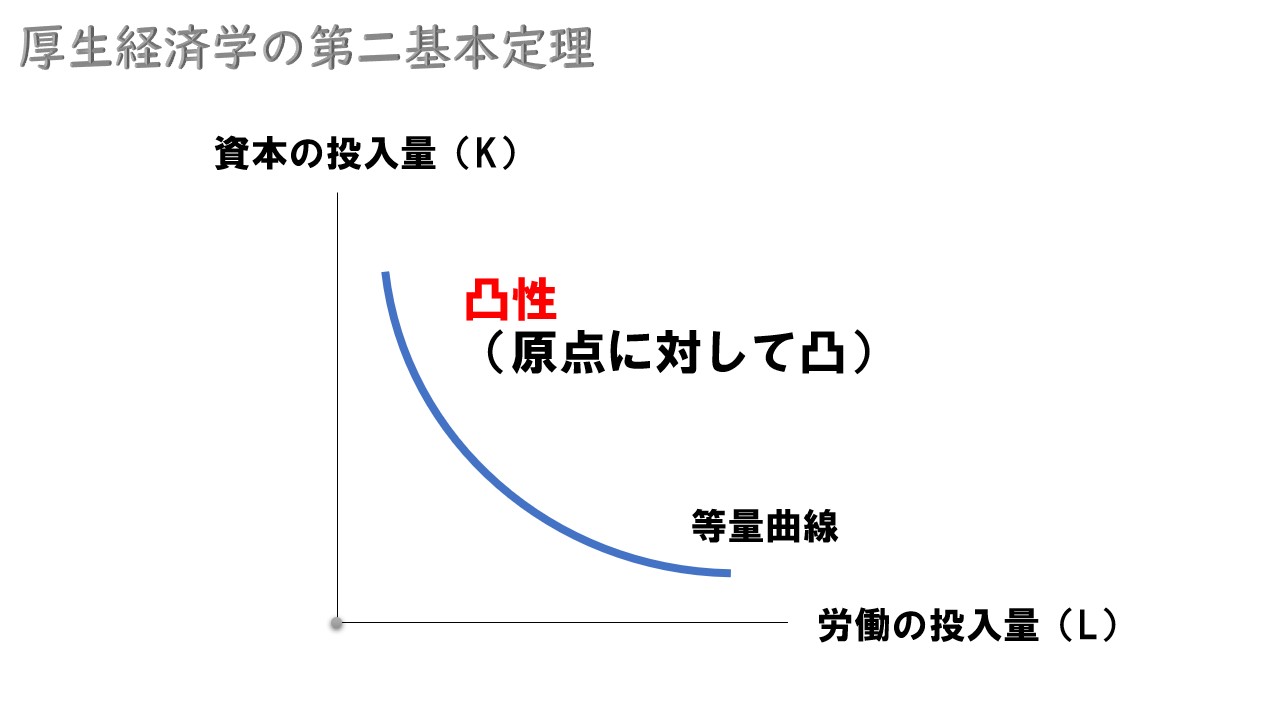
- 生産者の生産可能集合が凸性を満たす
凸性は、第二基本定理を証明するときに重要な条件となります。
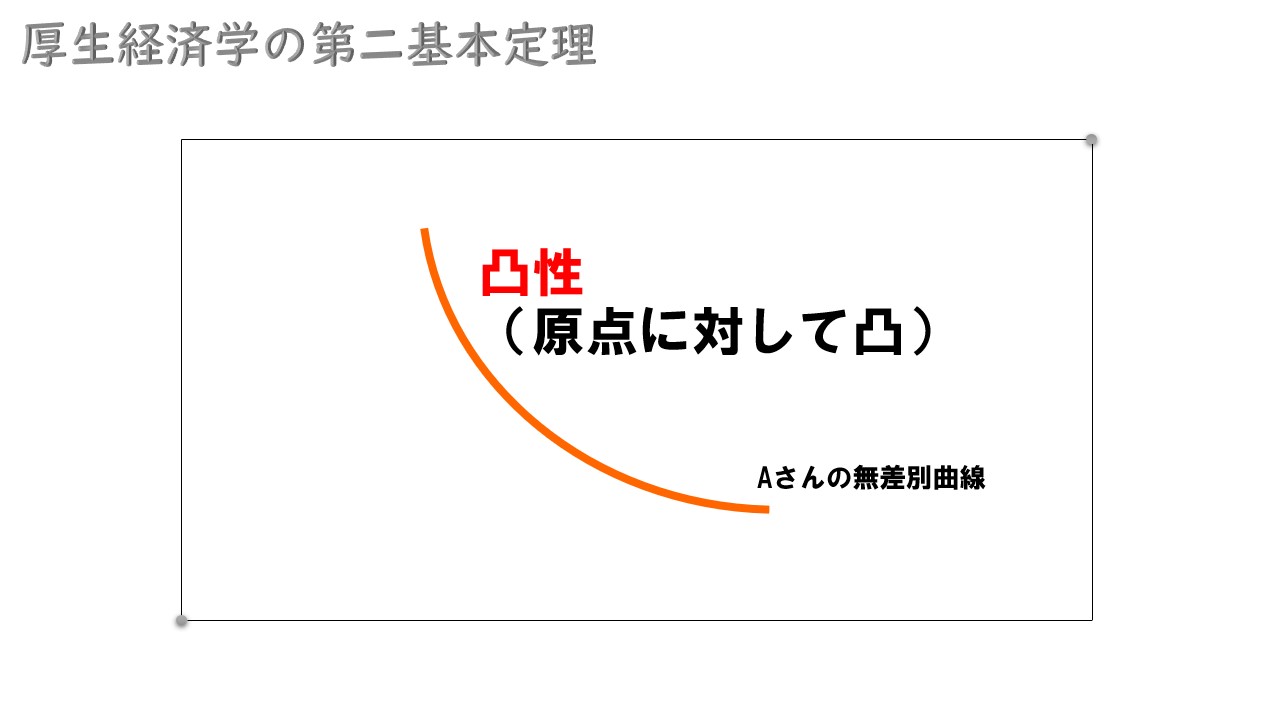
凸性とは
消費者の選好が凸性を満たすとは、無差別曲線が原点に対して凸になっていることを意味しています(ミクロ経済学で登場する一般的な無差別曲線の形状のこと)。
凸性を満たしていない例
無差別曲線が特殊な形状をしていると、消費者の選好は凸性を満たしていないと言えます。
意義
ポイント
厚生経済学の第二基本定理より、完全競争市場(自由経済)では効率性と公平性を同時に達成できることが分かるが、実現のためには所得再分配政策が重要である。ただし、公平性を実現するために再分配政策を実施するのは現実的に考えて困難である。
第二基本定理のポイントは大きく4つです。
- 市場は「資源配分」と「分配」を分けることが出来る
- 市場の効率性を損なわないために「分配」が重要
- 政府が消費者・生産者の初期保有を正確に把握するのが困難
- 何をもって”公平”とするのか
市場では「資源配分」と「分配」を分離して考えることが出来る
エッジワース・ボックスの分析から、初期保有量を前提に経済行動(交換)が行われて、最終的にパレート効率的な資源配分を実現することが分かります。
つまり
前提となる初期保有量を調整すれば、あとは市場に任せることで自然とパレート効率的な資源配分へたどり着きます(市場では「資源配分」と「分配(初期保有の調整)」を分けて考えることが出来ると言えます)。
重要なのは分配
よくある話ですが、生活が苦しい人を助けるための政策として
男性
食料品は安くなるようにした方が良い!(軽減税率)
女性
お年寄りはバス代を安く!
などがあります。
ここで重要なことは「市場の効率性を維持して公平性を実現するためには、分配が重要なのであって、価格を変えたり消費行動を歪める政策は(市場の効率性を維持するという観点からは)NG」です。
「貧しい人の生活を救うために食料品を安く買えるようにしたい」等は、気持ちとして理解は出来ますが市場の効率性を損ないます。
例えば
政府
パンは税金が掛からないようにします。
こんなことをすると、お米業界は不利になります。
政府
じゃあお米も税金なしで
- 業者が仕入れたときは?
- お金持ちも税金支払わなくていいの?
- お米使ってるし、餅も税金なし?
政府「・・・・。」
という風に、市場の資源配分の過程で政府が介入すると「非効率さ」が生まれます(市場の健全性が失われていく)。
なので、貧しい人を助けるなら「資源配分」に介入するのではなく「分配」に力を入れることが重要だ、ということを第二基本定理では示しています。
(ex)金持ちから金を集めて、貧乏人へ再配布する(所得再分配〉など
しかし
- 政府が「分配」することは可能か?
初期保有量を再分配するためには、各経済主体(消費者や生産者)の初期保有量を把握する必要があります。
もちろん各経済主体の「所得がいくらか」「利益をどれくらい出しているか」とかはある程度把握できます。だたし、経済活動の源泉となるのは所得だけではありません。
- どれくらい技能を持っているか
- どれくらい働けるか
- 病気の有無や生活環境
経済活動に関わるその人が潜在的に持ち合わせている初期保有量を政府が全て把握するのは、いくらなんでも現実離れしすぎです。
ココに注意
初期保有量を把握できなければ「誰にどれくらい再分配を行って、初期保有量をどれくらい調整すれば良いのか?」を判断するのは不可能です。仮に把握したとして、様々な利害が関わる政府が所得再分配政策を実行できるのか?も疑問が残ります。第二基本定理は、現実的には実現できないことを書いているので机上の空論的な批判を浴びることもあります。
何が公平なのか
- 公平をどうやって決めれば良いか
先ほどから「公平性が~」と書いてきましたが、そもそも何をもって公平となるのでしょうか?
- 所得が少ない人へ再分配すれば公平なのでしょうか?
- 美男美女は人生を得して生きているので対象から外すべきでしょうか?
- 医療従事者は人の命に関わる仕事をしているので優遇する?
- 若い人は働けるので年寄りを優遇する?
このように、どのような視点で考えるかで公平性は大きく変化します。第二基本定理では「分配」により、市場の効率性と公平性を実現すると示していますが、この公平性が何を意味しているのかは明確になっていません。
さらに詳しく
まとめ
- 厚生経済学の第二基本定理は完全競争市場の効率性を維持しつつ、公平性も実現できることを示しており、再分配政策(所得再分配など)の重要性が分かる。ただし、理論上は公平性を実現できるとなっているが、現実的には困難な側面があることに注意する。
例えば、現実世界では政府が各経済主体(消費者や生産者)の初期保有量を正確に把握することは困難で、初期保有量を把握できない以上、どのように分配を行えば良いのか判断できない。仮に政府が初期保有量を完ぺきに把握できたとしても、様々な利害調整を必要とする政府が所得再分配政策を実行するのは極めて困難である。
また、初期保有量を調整するときの公平性の基準(何をもって公平性が実現していると言えるのか?)は意見が分かれる。
ポイント
以上より、厚生経済学の第二基本定理から、市場の効率性と公平性が両立することが分かるため、自由経済と再分配政策の重要性が説かれる。しかし、現実で理想的な再分配政策を行うことは困難である。
第一基本定理でも書きましたが「机上の空論だ!」と批判するのも良いですが、どうすれば自由経済と公平性を両立できるか?を考えることが重要です。
ちなみに、厚生経済学の第二基本定理は「公平性」というものにスポットが当たっていますが、このような議論は経済厚生(経済的観点からみた人間の幸福や福祉)を扱った厚生経済学という分野で扱われます。基本的なミクロ経済学では第二基本定理くらいまでしか取り扱いません。


証明

ここでは、証明するときに重要となる考え方を簡単にまとめます。
ポイント
数学的に第二基本定理を証明するときに重要となるのは「凸性」です。
第二基本定理が成立するための条件として「消費者の選好が凸性を満たす(生産者の生産可能性集合も凸性を満たす)」というのがあります。この凸性を使うことで証明が出来るようになります。
例えば
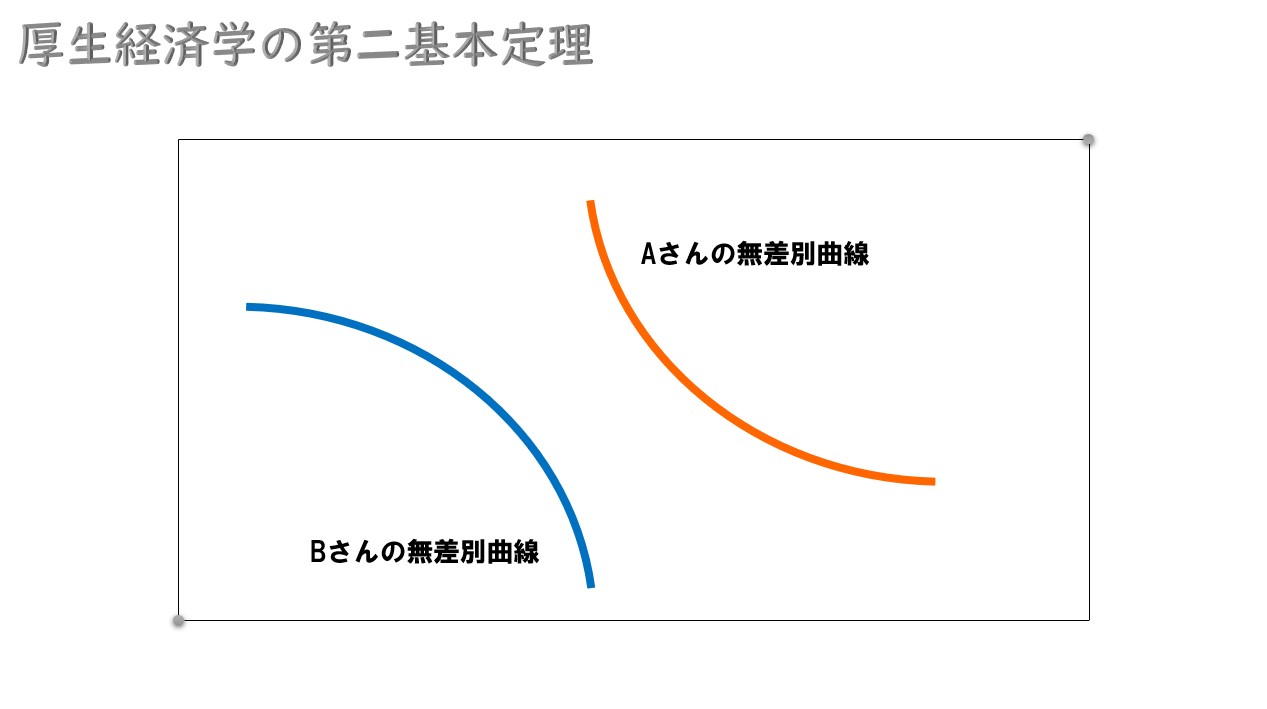
Aさん・Bさんの無差別曲線が凸性を満たすとき
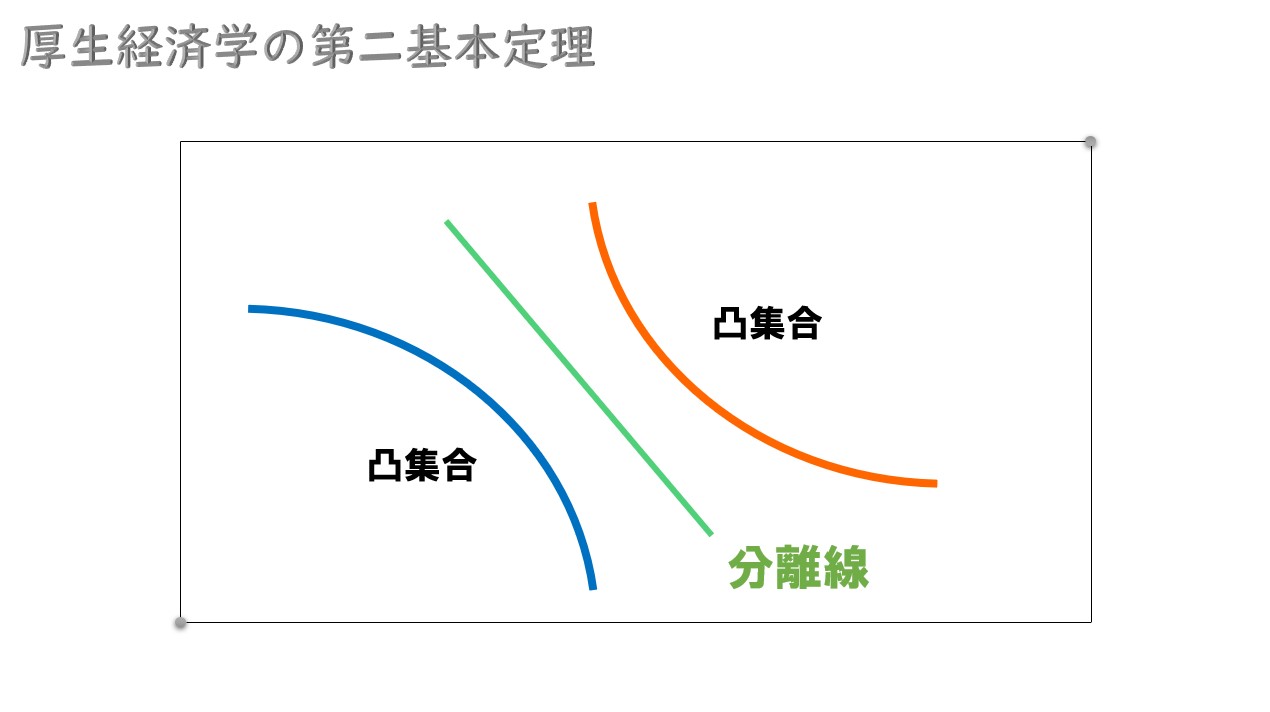
分離超平面定理
2つの凸集合より「分離超平面定理」が成立する
簡単に言えば、2つの凸集合を分離する線を引けるという定理。
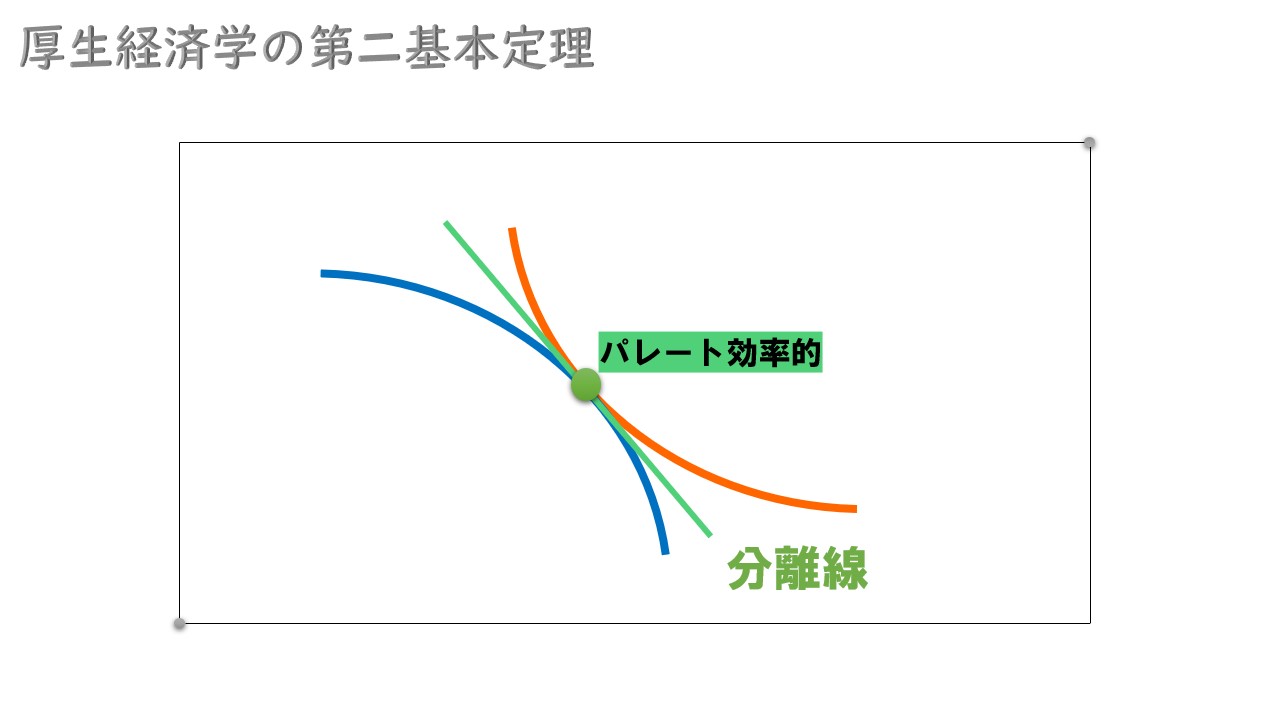
ここで
2人の無差別曲線が凸性を満たせば「分離超平面定理」が成立するので、どのパレート効率的な資源配分でも分離線が引けます。
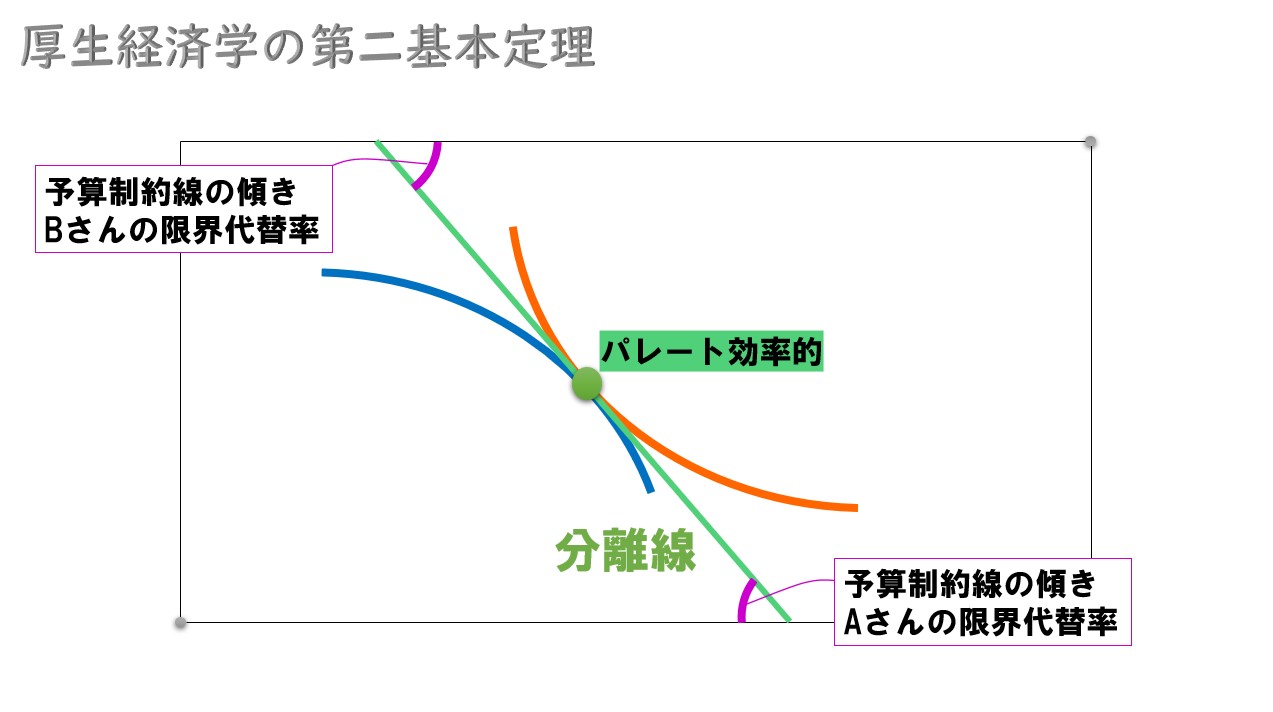
分離線=予算線の傾き(2人の限界代替率)
細かい話を置いておくと「分離線」は「予算制約線の傾き」とイコールになります。
つまり、どのパレート効率的な資源配分でも分離線が引けるということは、全てのパレート効率的な資源配分について予算制約線の傾きが存在することになります。
以上より
好きな分離線上(予算制約線の傾き)へ初期保有量を調整できれば、全てのパレート効率的な資源配分を実現できることになります。


第二基本定理の証明には、数学的な話をいろいろと解説しないといけないので、ここでは割愛しました。知りたい人は途中で紹介した『ミクロ経済学の力』などを参考にしてください。