ホテリングモデル（立地競争モデル）の基本をまとめたページです。
- ホテリングの立地競争モデル
- 均衡立地と最適立地（社会的最適解）
- 立地競争+価格競争
- 差別化最大原理
- ホテリングモデルの具体例
- 差別化最小原理
通常の教科書よりも少々細かい話をまとめています（ミクロ経済学の教科書よりも詳しく、産業組織論や経済地理の教科書よりはあっさり）
ホテリングの立地競争モデルとは
（英語版Wikipediaより・ハロルド･ホテリング）
はてな
お店の立地場所を製品差別化の一種と考えて、その立地場所をめぐる「立地競争」に注目した不完全競争市場のモデルの1つ。ホテリング・モデルとも呼ばれる。
企業は利潤最大化を目指して、より多くの消費者を獲得するために1次元空間（線形都市）で最適な立地場所を選択すると考える。
1929年エコノミック･ジャーナルに掲載された『競争での安定（Stability in Competition. Economic Journal, 39, 41-57）』の記事がはじまり。
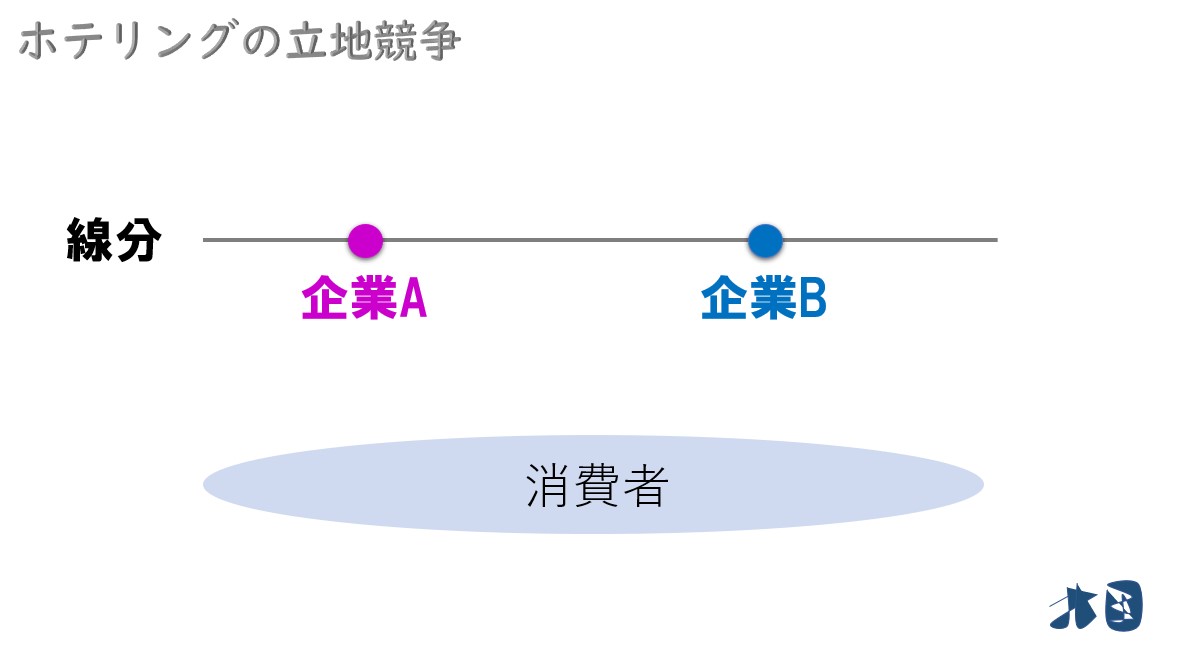
立地競争モデル（ホテリング･モデル）は、経済学に「空間」という概念を取り入れたことで有名です。
- 横線を都市（線形都市）と考える
- 横線に2つの企業が存在
- 消費者は横線上のどこかに分散して存在
ポイント
利潤最大化を目指す企業2社は、この横線（線形都市）のどの部分にお店を立地させるのか（＝立地競争）を考えます。
横線は1次元なので、この横線を1次元空間と呼ぶことがあります。
次に
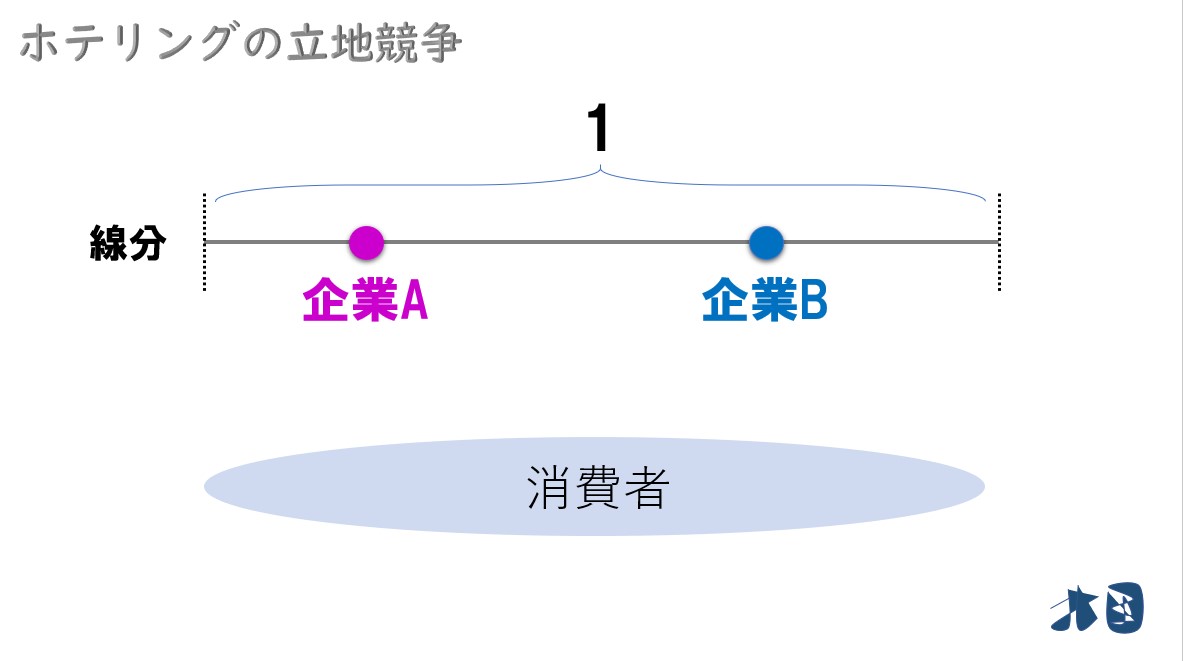
分かりやすくするために線の長さを「1」とします。
線の長さを1とするとき、この線分を区間［0,1］と書くことがあります。また、この区間に消費者がいることを消費者は区間［0,1］に一様に分布しているなどと言います。
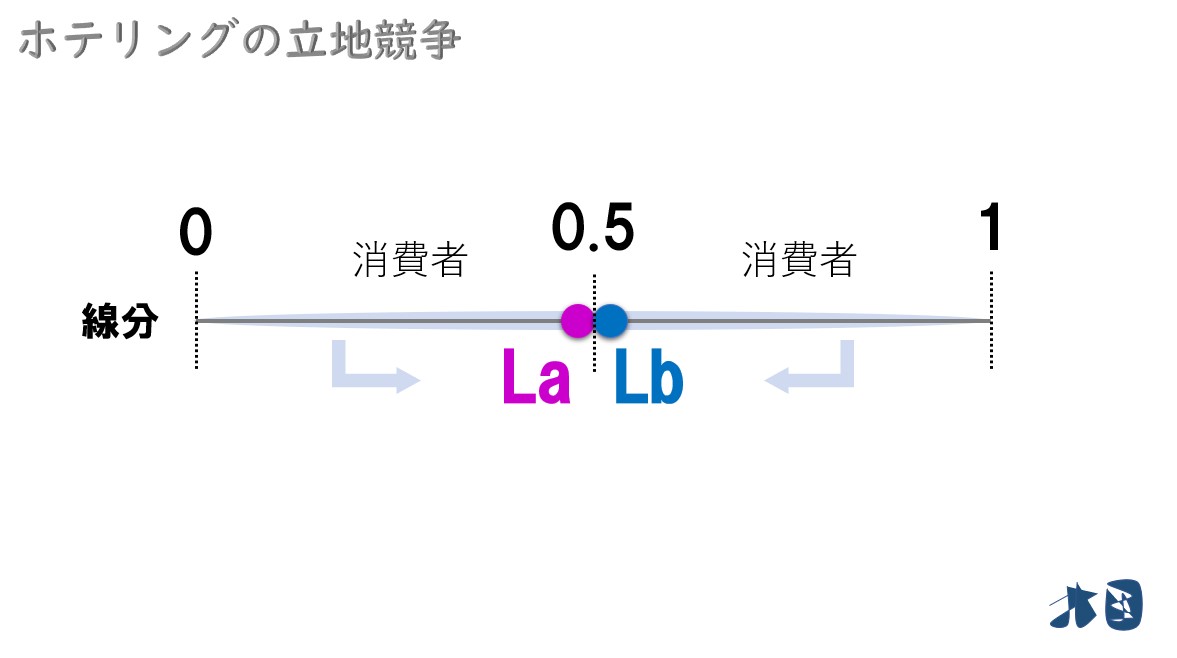
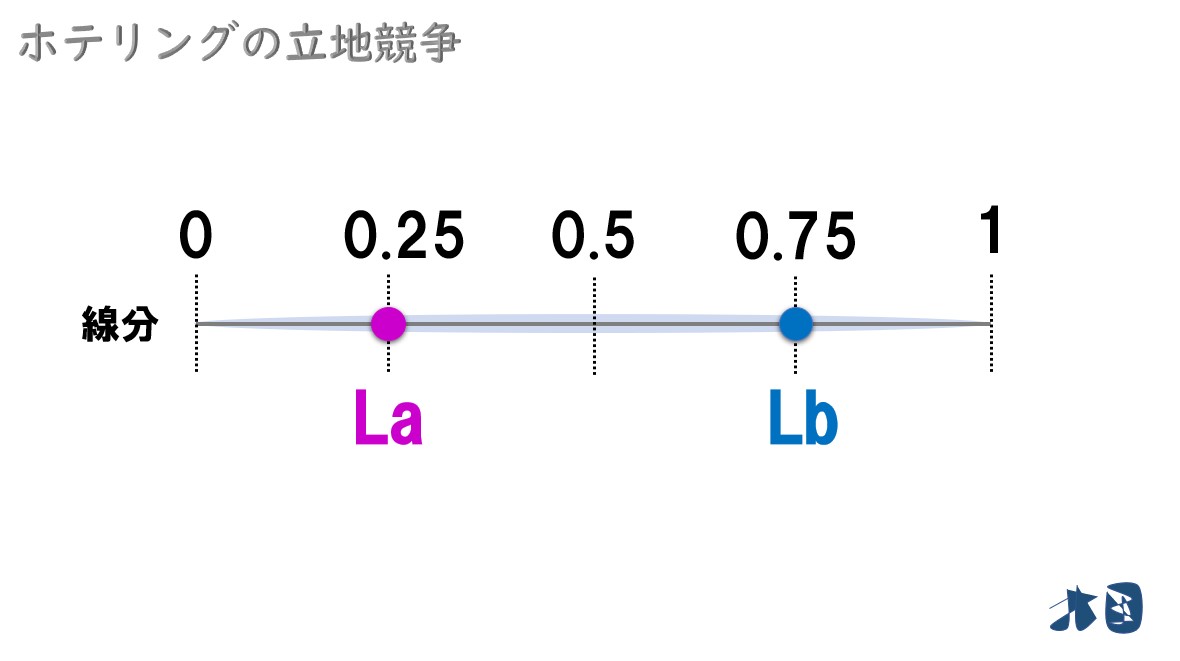
ここで
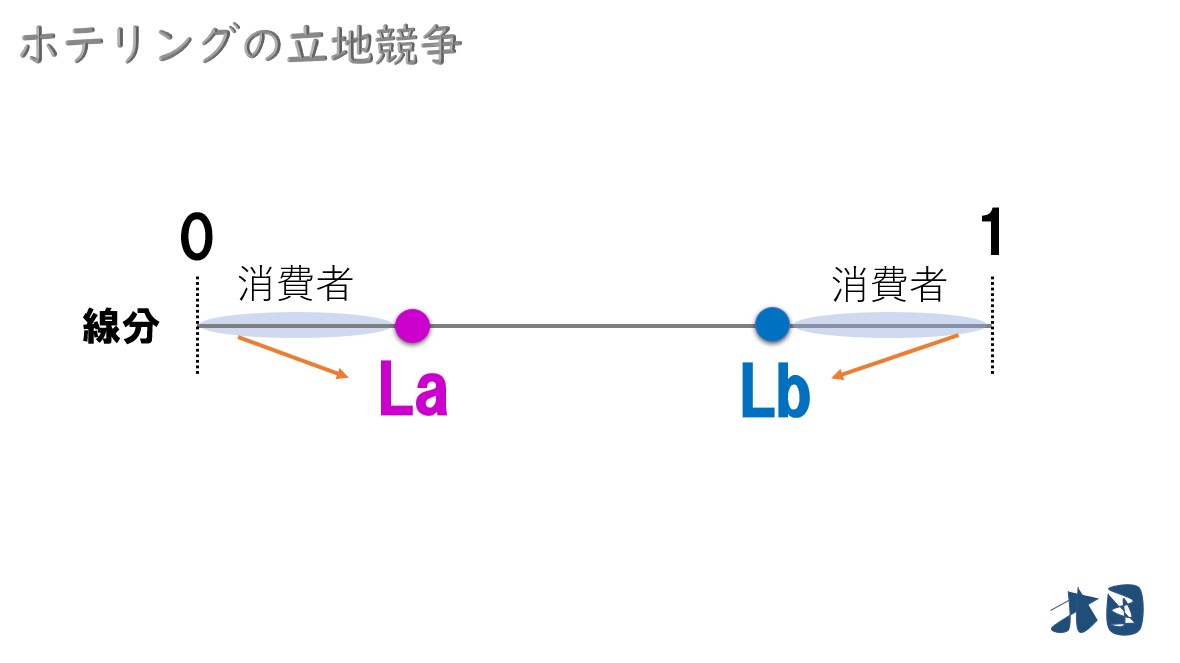
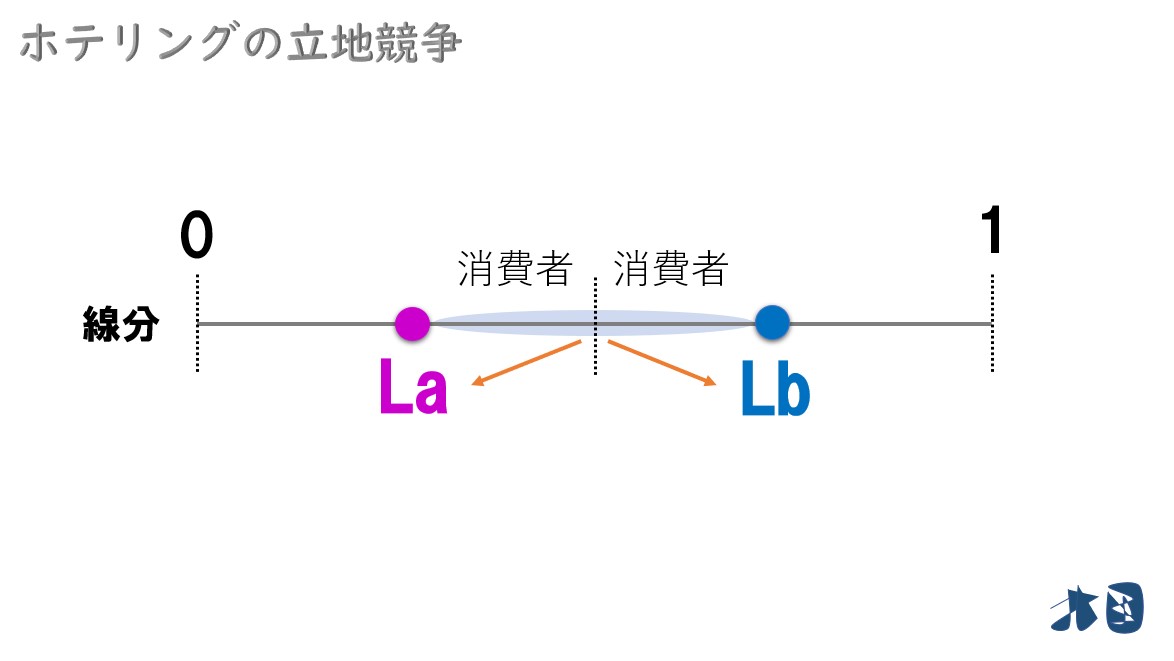
- 企業Aの立地場所を「La」
- 企業Bの立地場所を「Lb」
※英語の「Location(ロケーション)」の頭文字をとりました。
- 「La」より左にいる消費者→企業Aのお店
- 「Lb」より右にいる消費者→企業Bのお店
「同じ商品」で「同じ値段」なら、消費者は近場のお店に行きます。
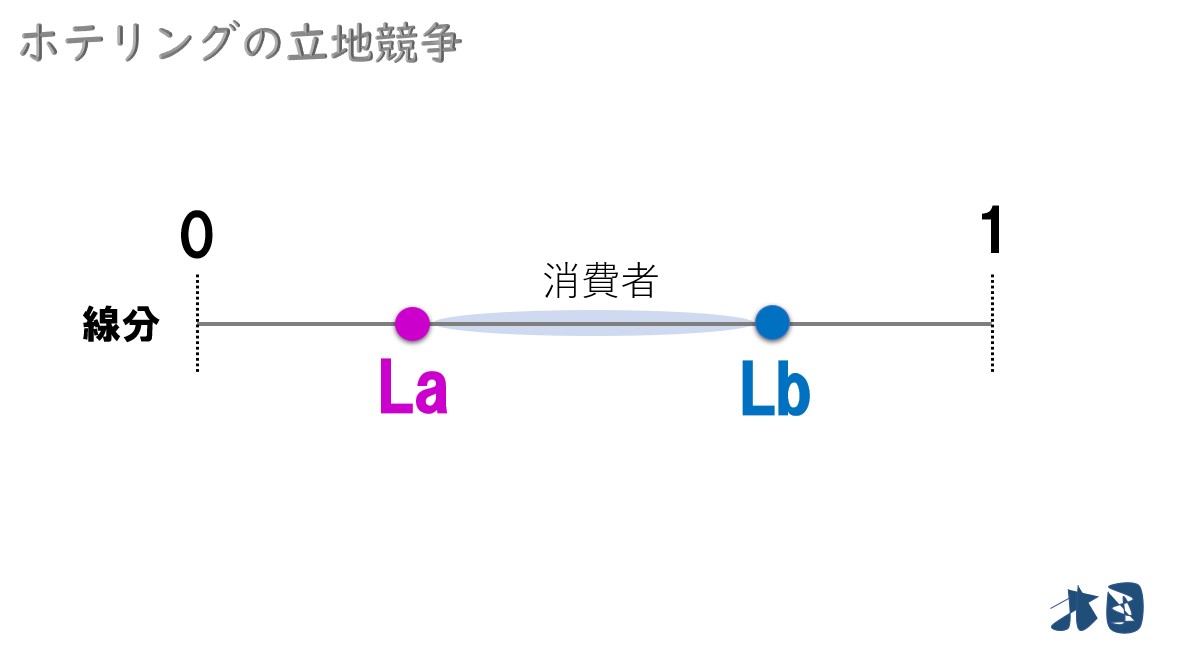
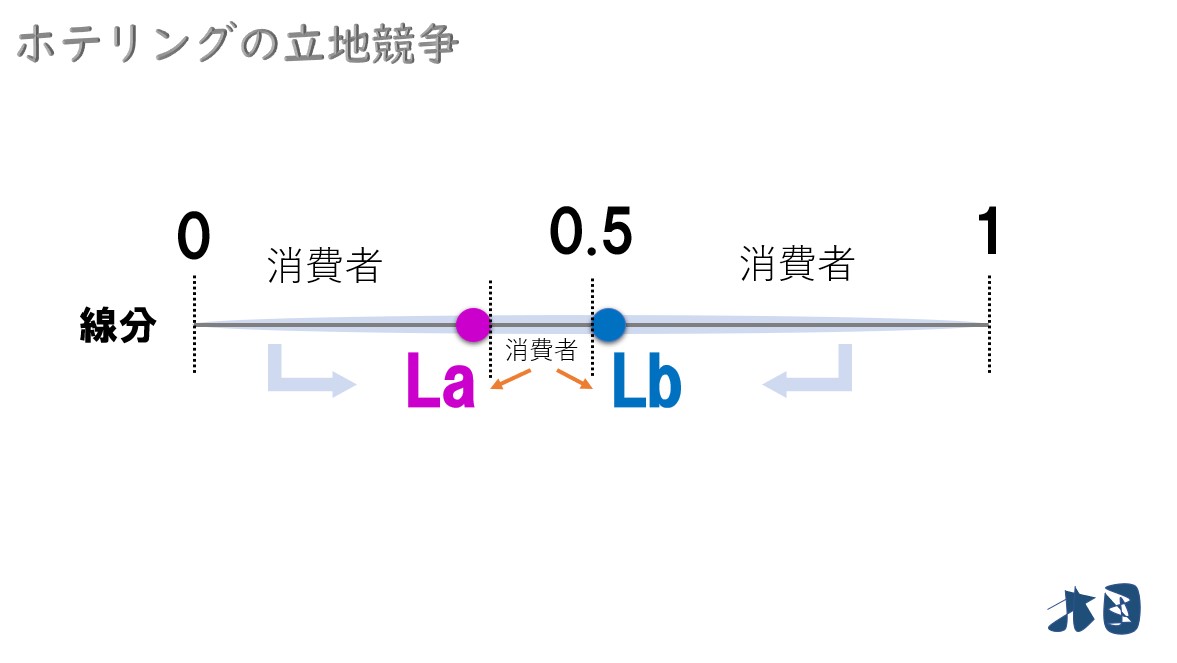
真ん中部分は
- 「La」と「Lb」の間にいる消費者を考える
ポイント
間にいる消費者も、より近いお店に行くはず。
イメージ
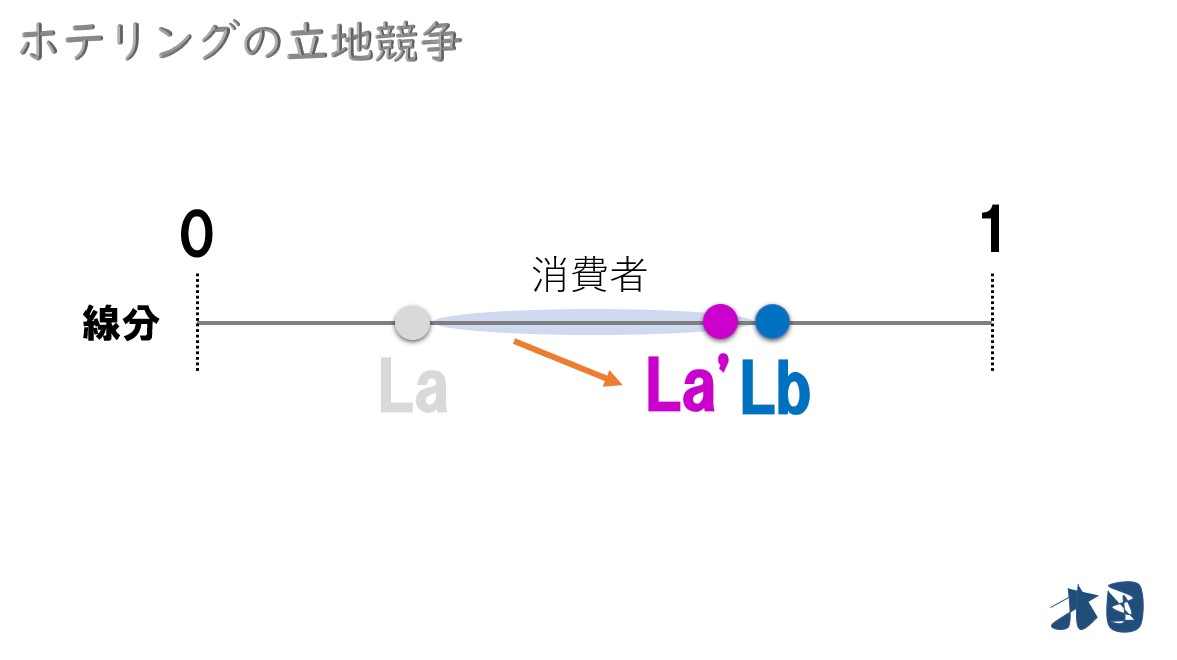
企業A
企業Bのお店に流れている消費者を奪うために、もっと右側に移動しよう。
企業Aが移動すると･･
企業Aと企業Bの間にいた消費者は、ほとんどが企業Aのお店が近くなります。そのため企業Bよりも企業Aのお店にいく消費者が増えます。
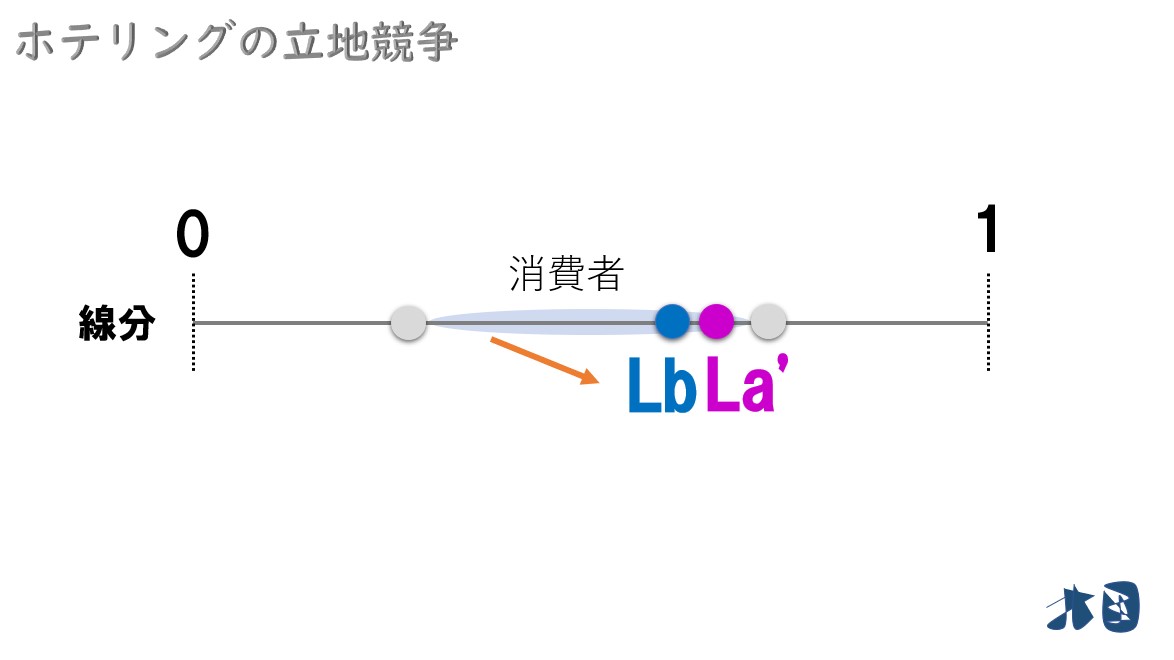
企業B
企業Aのお店に消費者が流れてしまった。企業Aの左側にお店を移動して消費者を奪い返そう！
企業Bが左側へ移動すると･･
企業Aと企業Bの間にいた消費者は、ほとんどが企業Bのお店が近くなります。そのため企業Aよりも企業Bのお店にいく消費者が増えます。
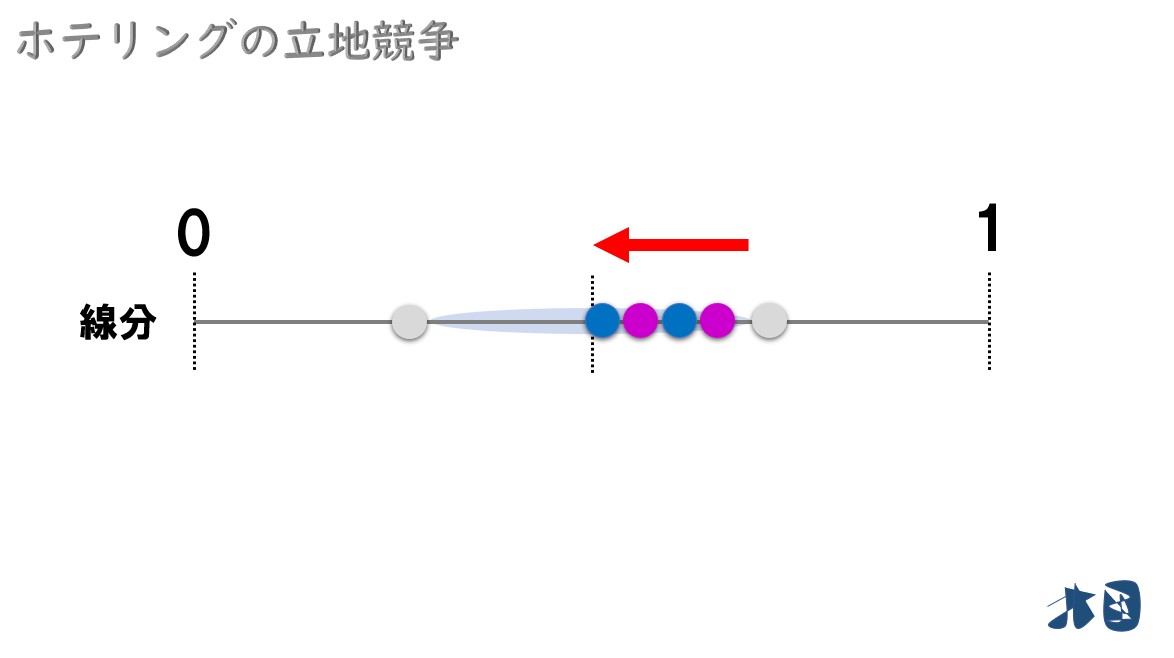
企業A･Bが移動を続けると･･
赤い矢印のように、企業2社が移動を繰り返すと中心へ近づいていきます。
最終的に
- 中心で落ち着く
「La＝Lb＝0.5」のとき、消費者を半分ずつ獲得して均衡に落ち着く。
もしも
これ以上動くと、自社の消費者を減らすことになる。
グラフの通り、中心から離れると消費者の一部がライバル企業へ流れてしまう。
ポイント
ホテリング･モデルで立地競争をするときの均衡(ナッシュ均衡)※は「La＝Lb＝0.5」となる。この均衡を「均衡立地」とよぶ。
※ここで言う均衡は「需要曲線と供給曲線が交わるところで均衡が決まる」という従来の考え方とは異なるので注意する。ホテリング･モデルはゲーム理論に分類されます。ナッシュ均衡は「互いに最適な戦略を取っている状態」をいいます。
均衡立地(ナッシュ均衡)と最適立地(社会的最適解)
ポイント
立地競争の結果、企業2社は最終的に線の中心にお店を立地させます。これを「均衡立地（ナッシュ均衡＝企業が互いに最適な戦略を取っている状態）」と呼びます。※前の段落で説明した通り。
しかし、これは企業の都合で決まった立地です。消費者にとって一番いい立地ではありません。消費者にとっても一番いい立地を「最適立地（社会的最適解）」と呼びます。
おさらい
- 立地競争の結果⇒中心で落ち着く
企業2社の立地場所は「La＝Lb＝0.5」となり、消費者を半分ずつ獲得して均衡となる。
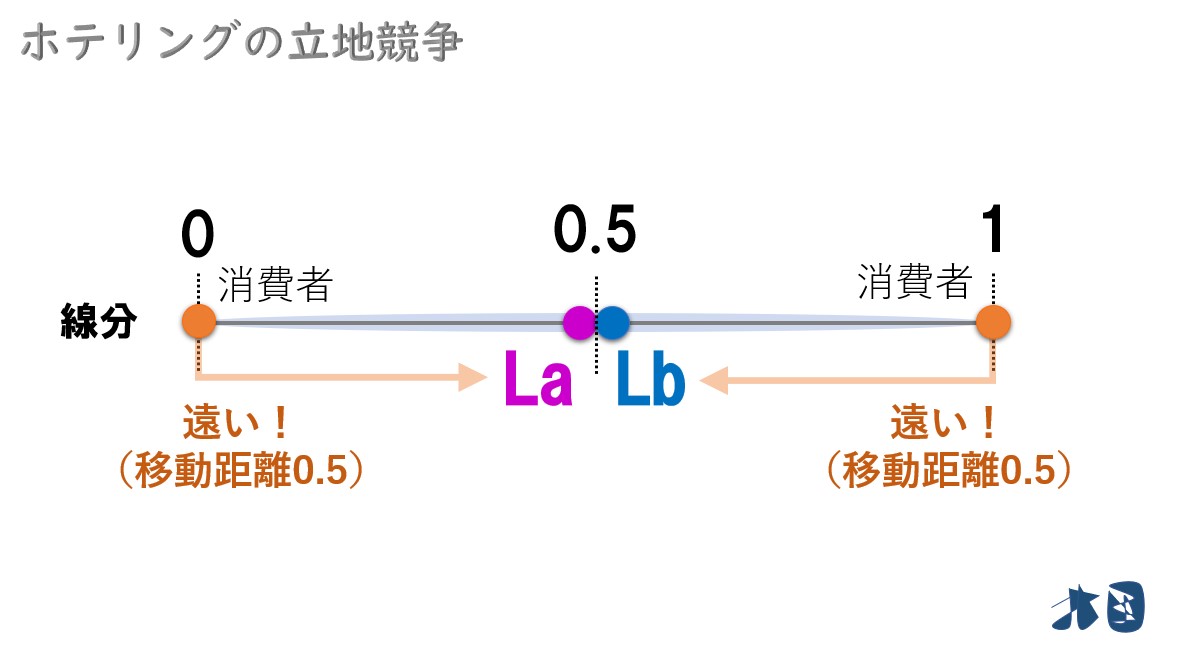
ここで
- 端にいる消費者は移動するのが手間
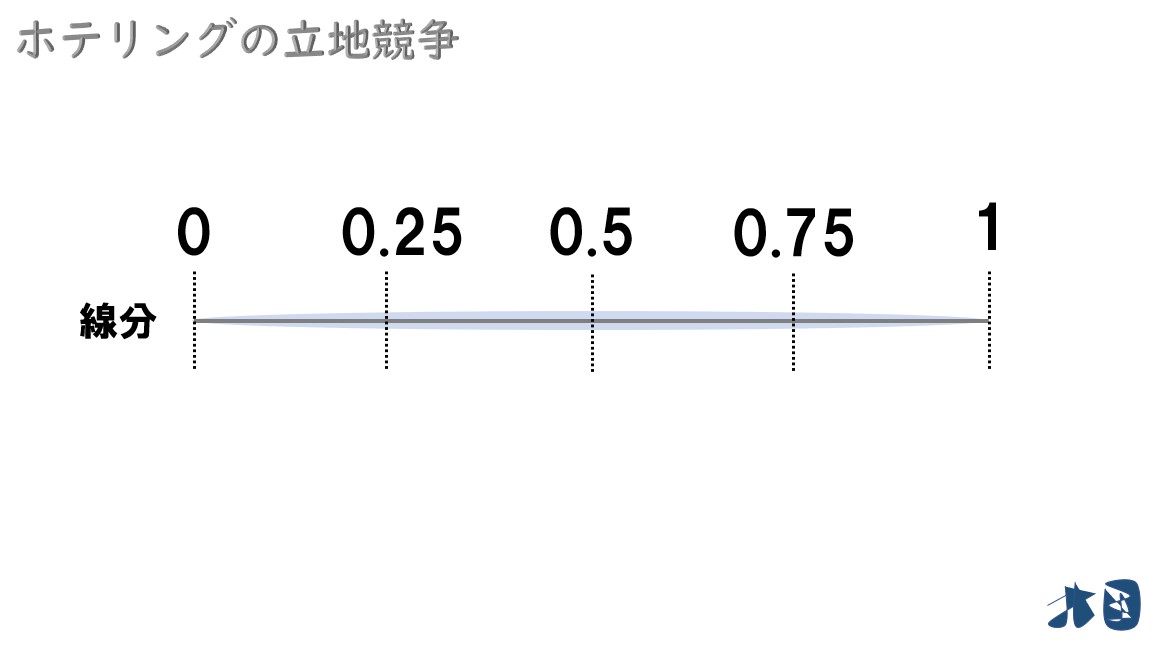
線を4等分する
均衡立地は、真ん中の「0.5（2/4）」でした。
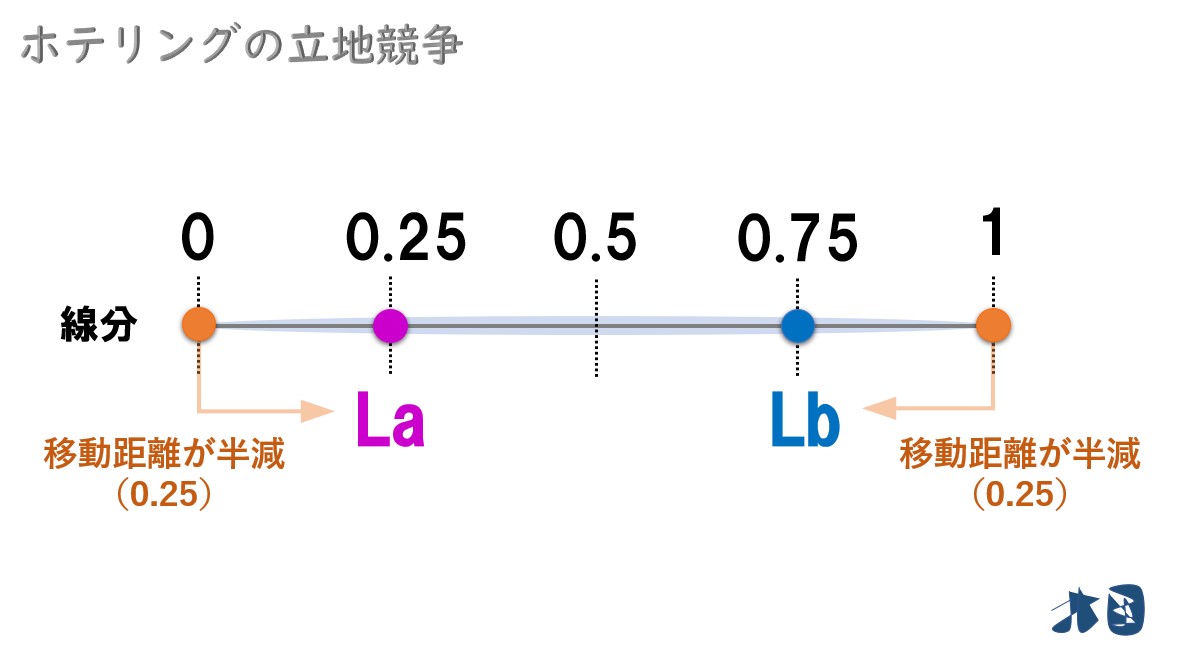
「0.25（1/4）」と「0.75（3/4）」に注目する
- 企業Aの立地場所を「La=0.25」
- 企業Bの立地場所を「Lb=0.75」
このとき
端にいた消費者の移動距離が半減する
さらに
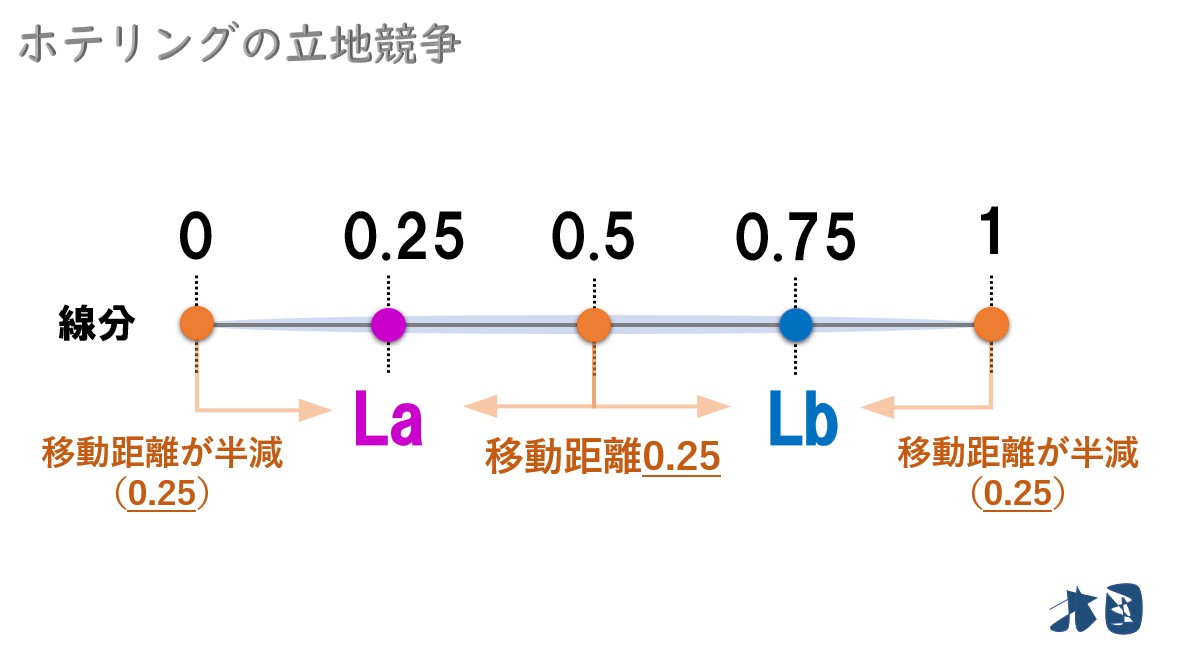
真ん中にいる消費者の移動距離は･･
- 端にいる消費者の移動距離＝0.25
- 真ん中にいる消費者の移動距離＝0.25
以上より、お店から最も離れている消費者の移動距離が0.25となる。企業が真ん中に立地するときは端にいる消費者が0.5移動する必要があったので半減している。
また、企業は消費者を半分ずつ獲得しているので、線の中心にお店を構えるのと同じ結果になる。
ポイント
このように、お店から最も離れている消費者の移動距離が小さくなるように、消費者全体で移動距離を負担しあうような立地場所を「最適立地（社会的最適解）」と呼ぶ。
注意ポイント
企業の自由競争に任せても、社会的･地域的な公正さを求めた「最適立地（社会的最適解）」は実現しない。
企業が自由競争すると、線の中心にお店を構えます
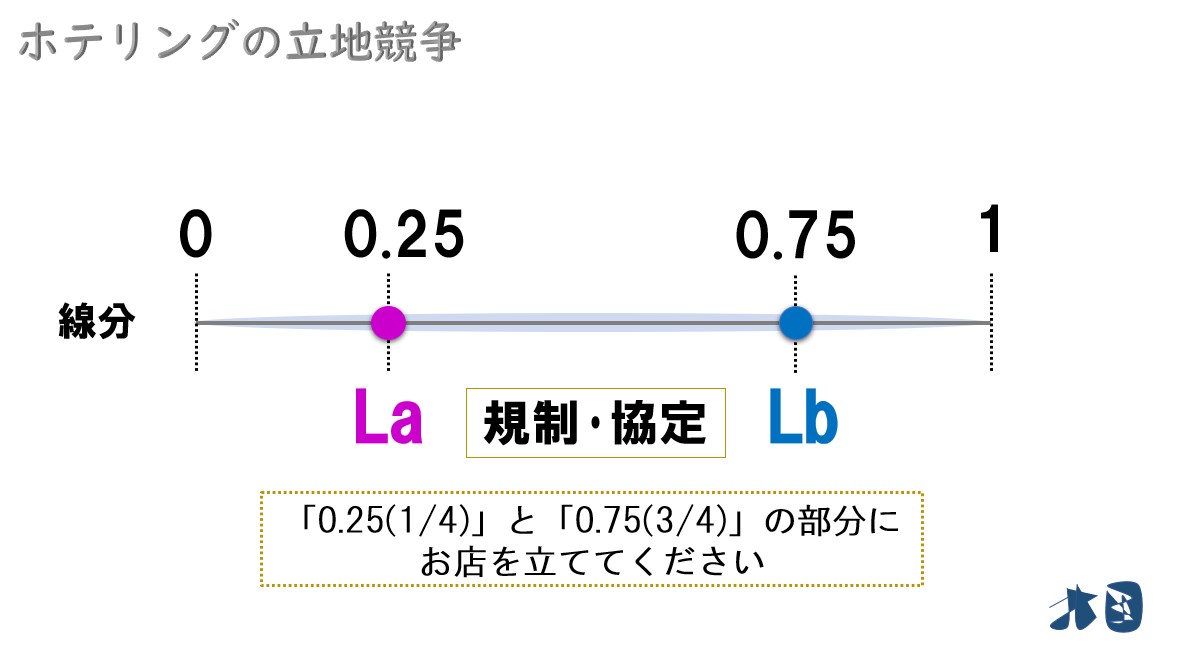
つまり最適立地を実現するには規制や協定が必要になる。
政府が規制したり、各企業で協定を結んで最適立地（社会的最適解）を実現させる必要がある。
さらに詳しく
こうした規制は現実には少ないですが、例えば「銭湯」は隣接して営業することが法律で禁止されています。
日本で自家風呂が普及する前の時代では、銭湯は公衆衛星のために必要なものと考えられていました。
しかし、同じ場所に銭湯が密集すると顧客を取り合って経営が安定しない可能性が出てきます。そこで、ある銭湯が立地している場所から距離制限を設けて営業許可を出しています。
立地･価格競争ゲームと最大差別化原理
ポイント
立地競争の結果、企業2社は最終的に線の中心にお店を立地させます。しかし、立地競争に価格競争を加えると結果が変わります。
立地競争に価格競争を加えたモデルを「立地･価格競争ゲーム（2段階ゲーム･2段階モデル）」などと呼びます。
数式で考えると分かりづらいので先にイメージから説明します。数式は後半にまとめます。
仮定
- 立地場所を決めた後、企業は価格を決める
- 消費者が移動するのにコストがかかる
- 移動コスト(輸送費)は「距離の2乗」で計算される
距離が離れるほど、指数関数的に移動が面倒になるので、移動コストが膨らむと考える。
このモデルは1979年に経済学の学術誌エコノメトリカに掲載された論文『On Hotelling's "Stability in Competition"』がもとになっています。この論文では従来のホテリングモデルは妥当ではないと指摘して、移動コストを考慮することでホテリングモデルの修正を図りました。
はじめに
価格競争をしない均衡立地のときを考える
企業2社の立地場所は「La＝Lb＝0.5」となり、消費者を半分ずつ獲得して均衡となる。
ここで
- 企業Aが値下げする
企業2社の立地場所は「La＝Lb＝0.5」だったので、消費者は値下げした企業Aのお店に流れる（同じ場所にお店があるなら安い方に行く）。
企業B
このままだと価格競争に巻き込まれて利益が出なくなるな。よし離れよう。
企業Bが離脱
- 同じ場所に立地していると価格競争になるので、企業Aから離れようとします
企業Bが値下げしなくても、移動コストが小さくなる消費者は企業Bのお店に行くことになる。
安いけど少し遠いスーパーよりも、値段が少し高いけど近くにあるコンビニで買い物を済ませるのと同じ。
ここで企業Aは困る
企業A
値下げしたままだと利益も少なくなるけど、値下げを止めると企業Bが戻ってくる。企業Bが戻ってくると結局は、値下げ競争になって利益が減る。そうだ、値下げは止めて中心から離れよう。
企業Aも離脱する
ポイント
お互いに近づくと価格競争に巻き込まれるので、それを嫌ってどんどん離れた場所に立地していく。また、離れた場所に立地しているときの方が高い価格で販売することができて、企業の利益もたくさん確保できる。
最終的に
2社が両端に立地して、価格も値下げなどが全くない状態（高止まり状態）が、立地･価格競争ゲームの均衡立地（ナッシュ均衡）となる。
この単純なモデルなら企業は両極端に位置するのが均衡ですが、モデルの設定次第で、均衡立地は異なります。ただし、どの設定でも価格競争があると各企業は同じ場所にお店を構えずに、散らばって立地します。
さらに詳しく
立地場所は企業の製品差別化の1種であることを考えると、企業2社の立地場所の距離は製品差別化の度合いを表しているといえる。
「立地競争と価格競争」では、その距離が最大限に広がったところで均衡となるため、製品差別化が最大限まで広がっていると解釈できます。
このように「立地競争と価格競争」が起こると製品差別化が最大限まで拡大することを「製品差別化の最大化原理（最大差別化原理）」と呼びます。
数式で考える
- 本当に両端に立地するのが均衡なのか？
と思った人向けに数学的に均衡立地を求めたいと思います。必要ない人は飛ばして大丈夫です。数学苦手な人は拒絶反応出るかも･･。
移動コストを考えたのはクロード･ダスプレモン･リンデン（Claude d'Aspremont Lynden）という経済学者です。この人のモデルの通りに計算を行ってみます。
はじめに
消費者が得られる効用を次の通りに考えます
- 商品を消費したときの満足感(U)－価格(P)＝U－P
消費したときの満足感から、支払うお金(価格)を差し引くことで、消費者が実際に得られる効用と考えます。
次に
線分の真ん中にいる消費者を考えます。
- 線分の真ん中までの距離を「X」
- 企業Aの立地場所までの距離を「a」
- 企業Bの立地場所までの距離を「b」
- 消費者の移動コストは距離の2乗で決まる
ここで真ん中にいる消費者を考える理由は、この後の数式を組むときにイコールと結ぶことができるからです。とりあえず続きを見てください。
消費者の移動に伴うコストは
- 企業Aに移動するとき「(X－a)^2」
- 企業Bに移動するとき「(b－X)^2」
ここですが、私は上記の通り計算したのですが、企業Bの方を「1－X－b」となるように設定（「b」を線の右側からの距離を表すことにする）した方がこの後の計算が楽かも。。。
以上より
- 企業Aを選択するときの効用は「U－P－(X－a)^2」
- 企業Bに選択するときの効用は「U－P－(b－X)^2」
線の真ん中にいる消費者は、企業A･企業Bの立地競争が均衡しているのなら、どちらのお店に行っても得られる効用は同じになると考える（直線上で2社が立地争いをしたら、左右対称になるような立地場所で均衡する）。
- 企業Aの価格＝Pa
- 企業Bの価格＝Pb
・U－Pa－(X－a)^2＝U－Pb－(b－X)^2
・－Pa－(X－a)^2＝－Pb－(b－X)^2
・Pa＋(X－a)^2＝Pb＋(b－X)^2
・Pa＋(X^2－2Xa＋a^2)＝Pb＋(X^2－2Xb＋b^2)
・Pa＋(－2Xa＋a^2)＝Pb＋(－2Xb＋b^2)
・Pa－2Xa＋a^2＝Pb－2Xb＋b^2
・2Xa－2Xb＝－Pa＋Pb－a^2＋b^2
・2X(a－b)＝－Pa＋Pb－a^2＋b^2
・X＝(－Pa＋Pb－a^2＋b^2)／2(a－b)
これで線の真ん中「X」にいる消費者の行動の情報が定まりました。
’
企業の利潤は･･
- (価格－費用)×(生産販売量)＝(P－C)･X です
ここで
線の真ん中にいる消費者がお店に来るかで生産販売量は異なってきます。消費者の行動が生産販売量(X)に直接影響を与えるため、上記で計算した数式を代入します。
企業Aの利潤＝(Pa－C)･(－Pa＋Pb－a^2＋b^2)／2(a－b)
企業Bの利潤＝(Pb－C)･(－Pa＋Pb－a^2＋b^2)／2(a－b)
’
ポイント
ここから、生産量は数式より所与なので、最適な価格を求めるために価格「Pa」「Pb」でそれぞれ微分して0とする（利潤最大化条件で計算するときと同じような考え）
その前に
企業Aの利潤を展開します･･。
(－Pa^2＋PaPb－Pa･a^2＋Pa･b^2＋C･Pa－C･Pb＋C･a^2－C･b^2)／2(a－b)
’
- 価格(P)で微分して「＝0」とする
Pa’＝(－2Pa’＋Pb’－a^2＋b^2＋C)／2(a－b) ＝0
企業Bも同様に
Pb’＝(－2Pb’＋Pa’－a^2＋b^2＋C)／2(a－b) ＝0
’
連立方程式で「Pa」「Pb」を求めます。
・－2Pa’＋Pb’－a^2＋b^2＋C)／2(a－b)
・－2Pb’＋Pa’－a^2＋b^2＋C)／2(a－b)
両方とも2(a－b)を消す
・－2Pa’＋Pb’－a^2＋b^2＋C
・－2Pb’＋Pa’－a^2＋b^2＋C
下の方を2倍する
・－2Pa’＋Pb’－a^2＋b^2＋C
・－4Pb’＋2Pa’－2a^2＋2b^2＋2C
足す（0どうしの式を足したので0となる）
・－3Pb’－3a^2＋3b^2＋3C＝0
展開する
3Pb’＝－3a^2＋3b^2＋3C
Pb’＝－a^2＋b^2＋C
同様に
Pa’＝a^2－b^2＋C
’
利潤最大化時の価格が分かったので、利潤の式に代入します。
企業Aの利潤＝(Pa－C)･(－Pa＋Pb－a^2＋b^2)／2(a－b)
- Pa’＝a^2－b^2＋C
- Pb’＝－a^2＋b^2＋C
⇒(a^2－b^2)･(－3･a^2－3･b^2)･0.5(a－b)
’
ここで
企業Aの最適な立地場所「a」を求めるためにaで微分します（利潤最大化条件で計算するときと同じ考え。通常は生産量で微分するという流れだけど、今回求めたいのは立地場所「a」なのでaで微分する）
’
積の微分公式より
2･(－3･a^2－3･b^2)･0.5(a－b)＋
(a^2－b^2)･(－6a)･0.5(a－b)＋
(a^2－b^2)･(－3･a^2－3･b^2)･0.5
積の微分公式が分からない人は検索してください。著者、計算が合っているのかよく分からず解説は飛ばします。
’
－3(a^2＋b^2)(a－b)＋
－3(a^2－b^2)･(a^2－b)＋
－1.5(a^2－b^2)･(a^2＋b^2)
－3(a^3－a^2･b^2＋a･b^2－b^3)＋
－3(a^4－a^2･b－a^2･b^2＋b^3)＋
－1.5(a^4－b^4)
－3(a^3)＋6(a^2･b^2)－3a･b^2＋3a^2･b－3a^4
－6a^4＋6b^4
－3(a^3)＋6(a^2･b^2)－3a･b^2＋3a^2･b－9a^4＋6b^4
ここで
係数にマイナスがついている項に注目します。
・－3(a^3)＋6(a^2･b^2)－3a･b^2＋3a^2･b－9a^4＋6b^4
この利潤の式の値を大きくしようと考えたとき、aの値がマイナスである必要があります。
例えば「－3(a^3)」と「－3a」の部分は「a=－1」なら「－3×－1＝3」となります。そして、ほかの項はすべて2乗と4乗なので「aがプラスでもマイナスでも」符号が変わることはありません。
’
まとめ
つまり、この利潤式を最大化させる立地場所「a」は0よりも小さい「a＜0」となります。ただし現実でマイナスの場所に立地できるわけはないので、企業Aは線の左端部分「0」に立地するとき、利潤が最大化すると考えます（企業Bも利潤式に代入&計算すると同様に考えることができます）。
ホテリングモデルの例と最小差別化原理
ホテリングモデルは身近な例からも理解できます。
例えば
- コンビニの立地が集中する
- 国道沿いにチェーン店が並ぶ
- ガソリンスタンドの立地が集中する
- 大学の立地が都心に集中（都心回帰）する
ホテリングモデルは、立地競争だけではなく通常の製品差別化競争を分析することができます。
例えば
- コーヒーの味
コンビニやチェーン店のコーヒーというのは、大体無難な味に落ち着いています。目隠しして利きコーヒーをしたら、ほとんど当てられないと思います。
ポイント
このように、ホテリングモデルを使って立地競争だけではなく、各社の製品の差別化度合いを分析することができる。
立地競争と同様に、製品差別化の度合いは中心に集中するため「製品差別化最小の原理（最小差別化）」と呼ばれる。
他にも
- 2大政党制で両党が似たような政策を打ち出す
- 食品メーカーが似たような商品を作る
- 平日の21～24時にニュース番組が集中する
- 車好き以外には自動車の見た目が大体同じに見える
- 家電メーカーが同じような製品を作る
