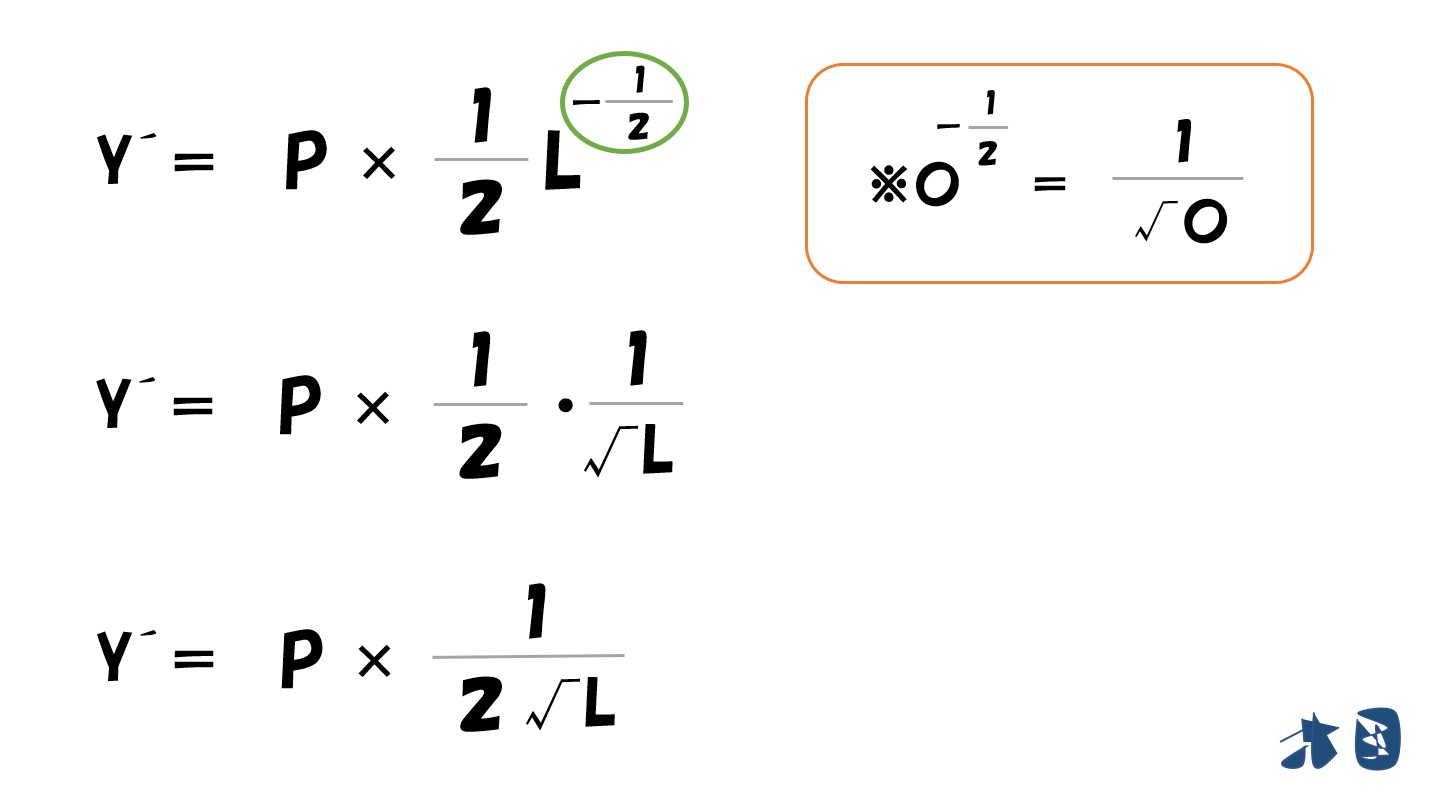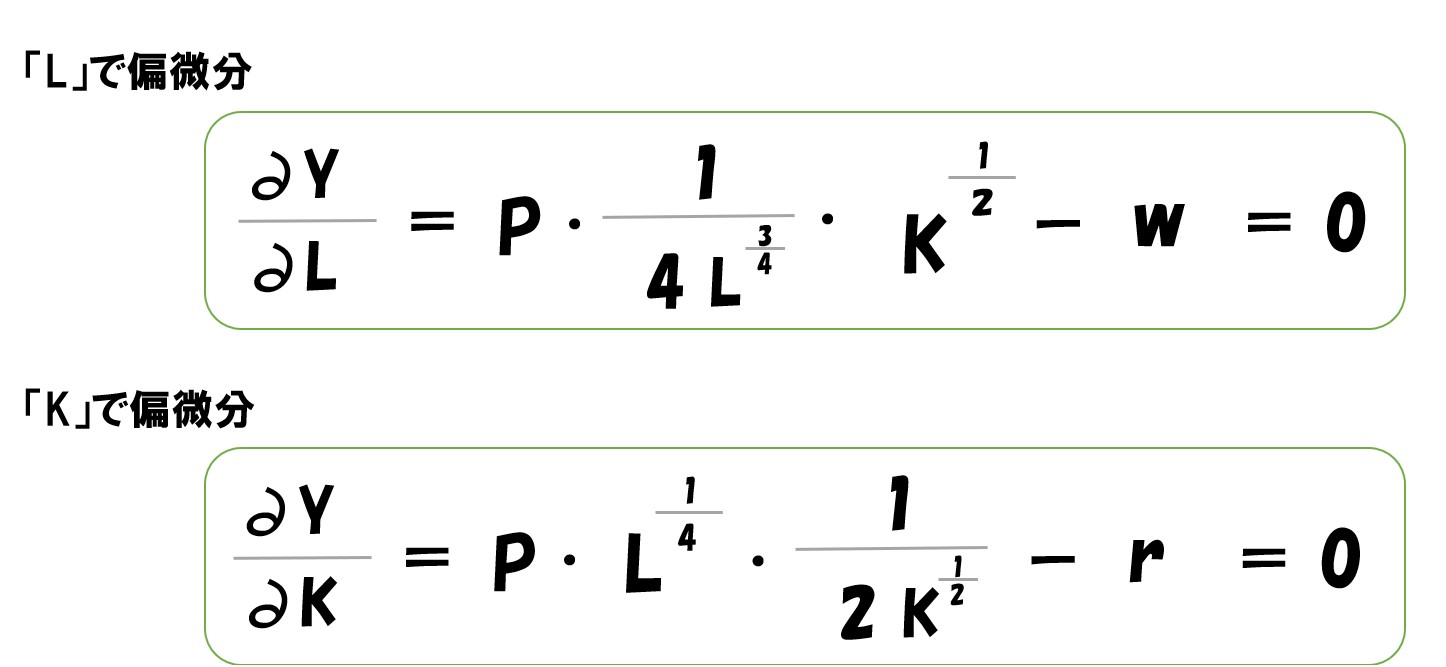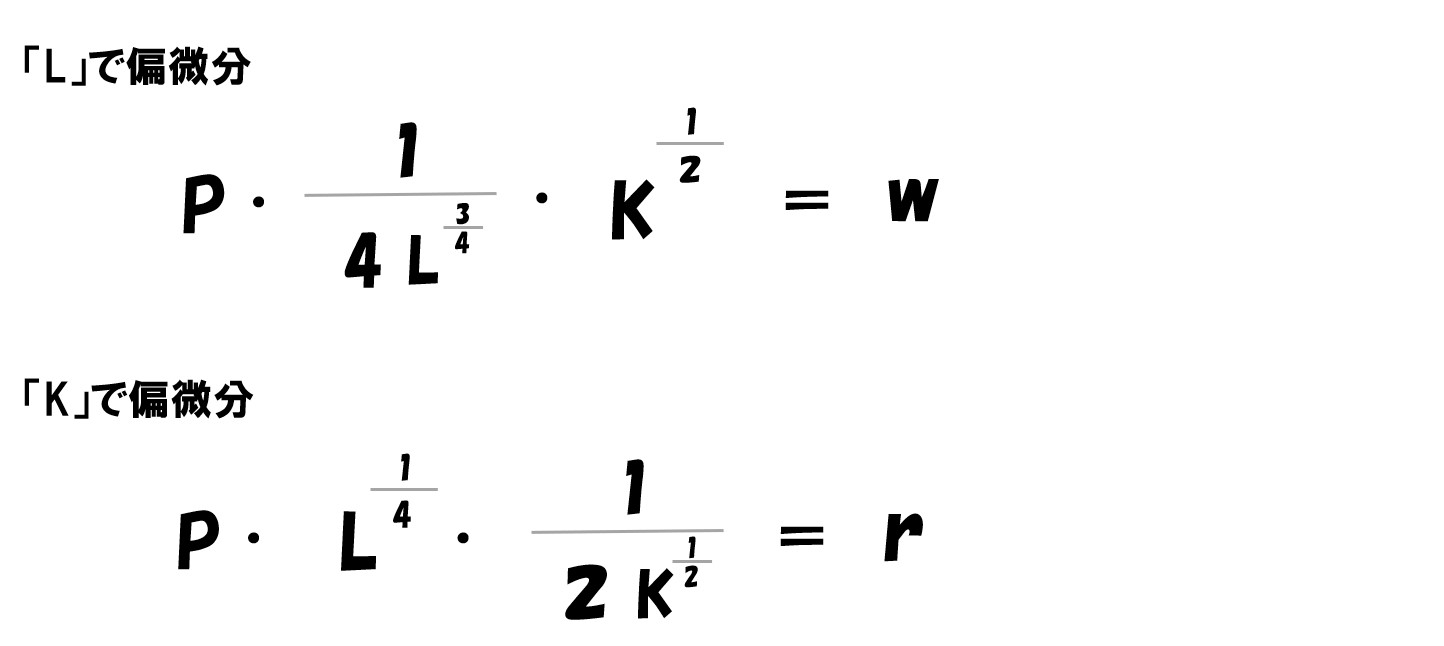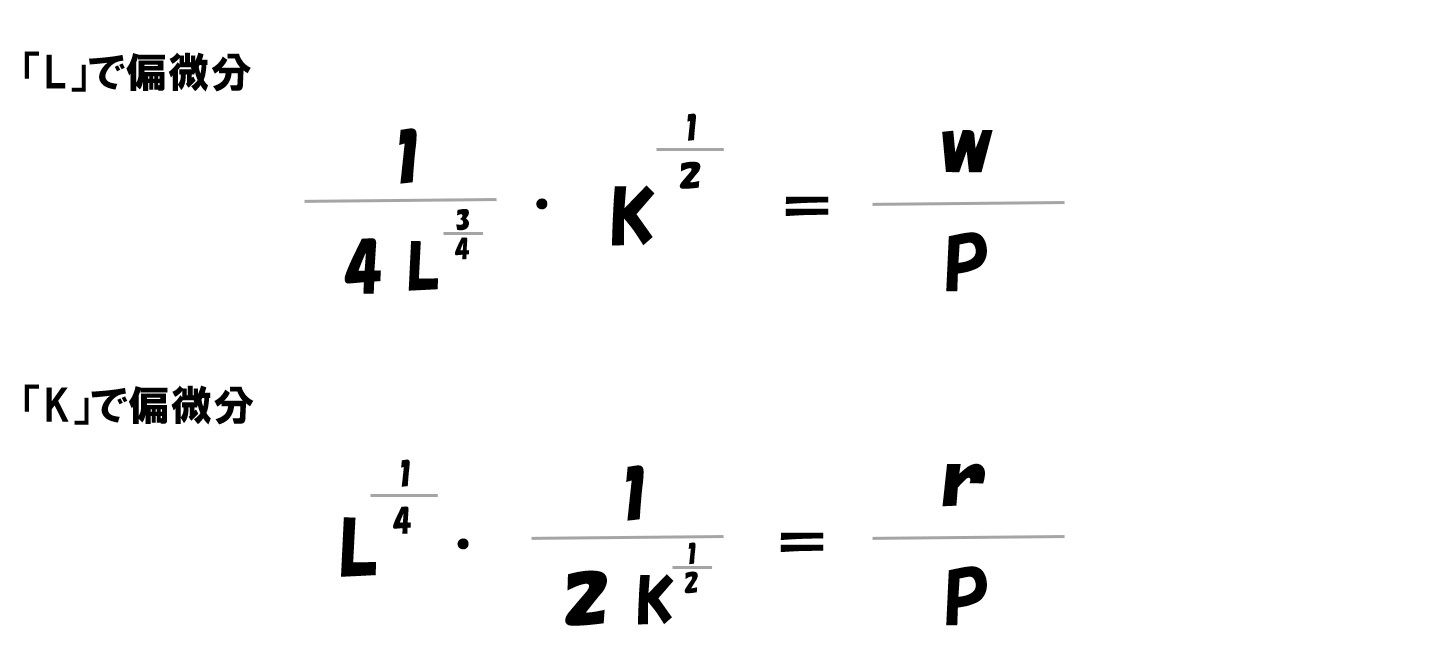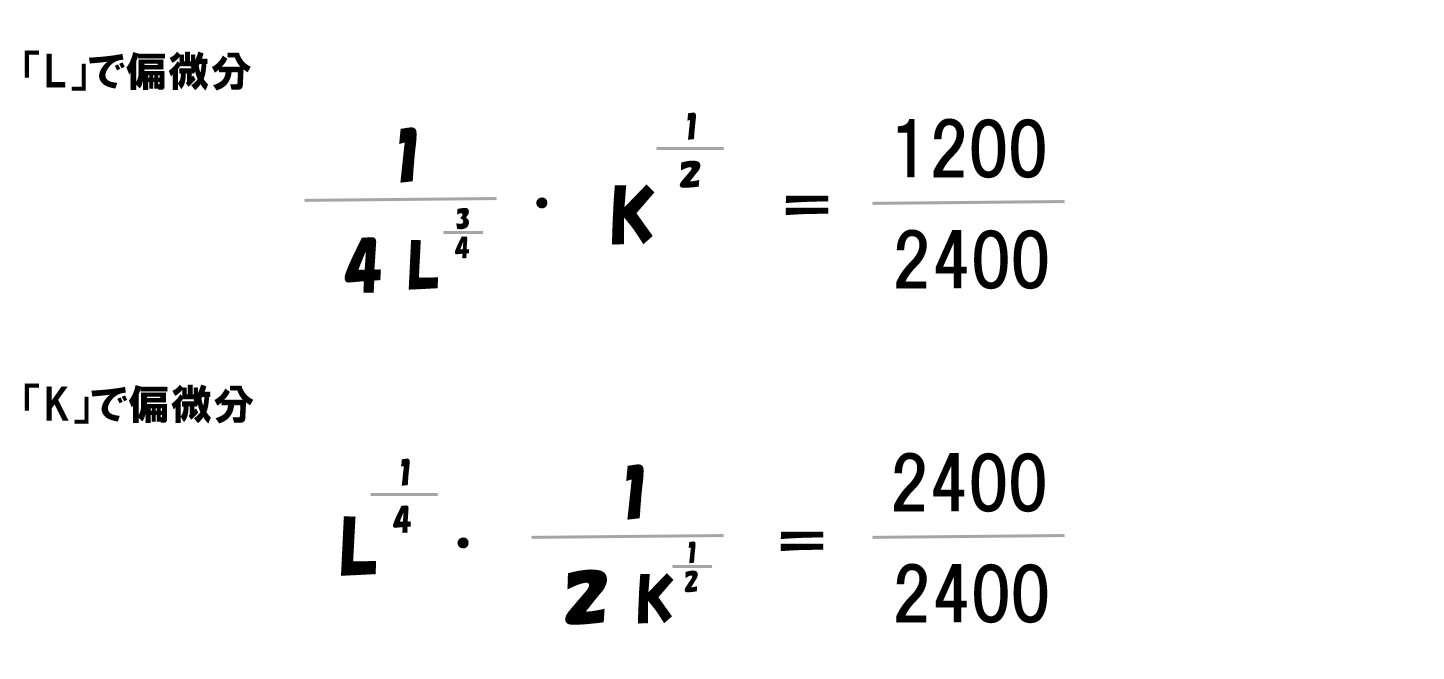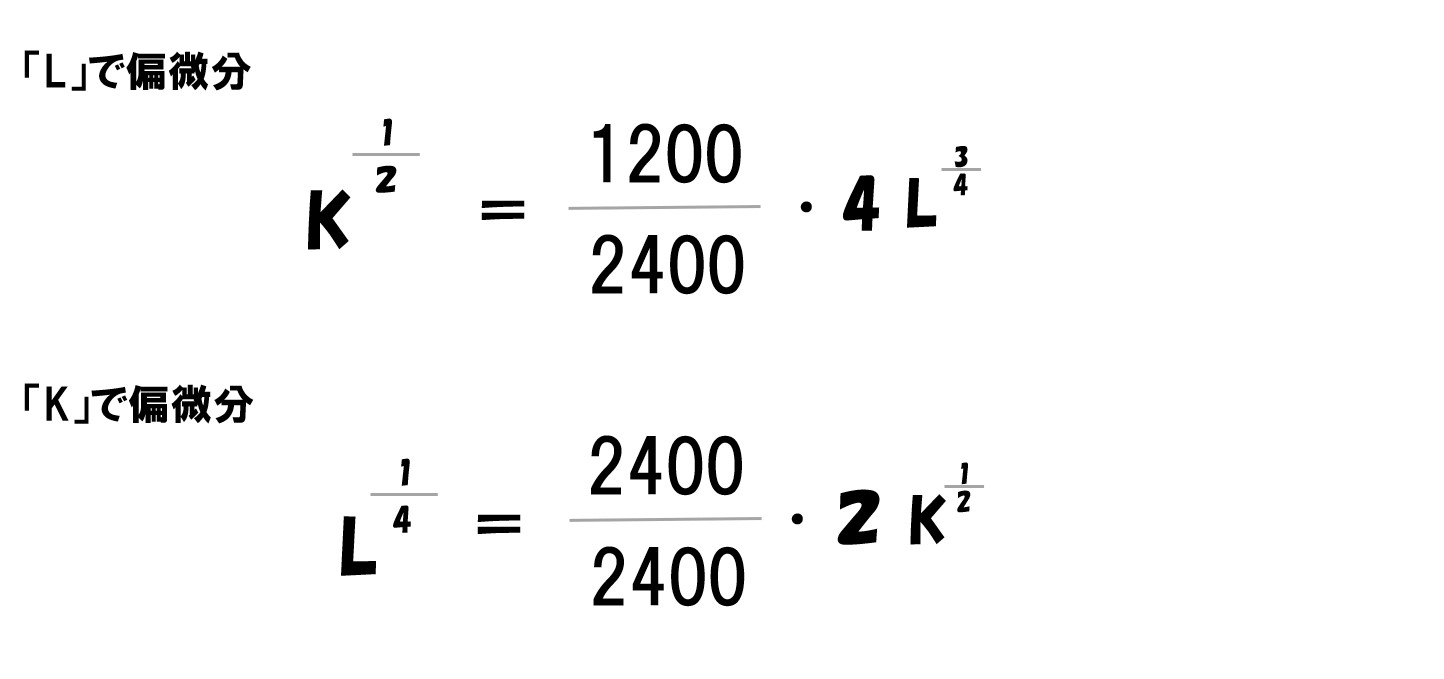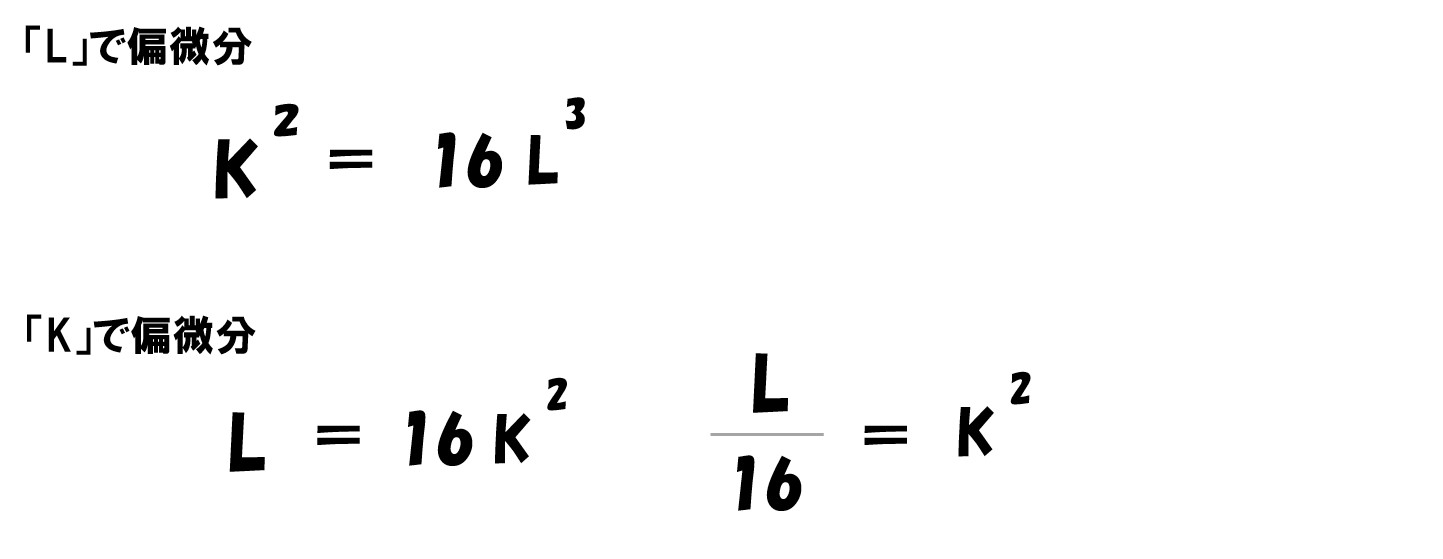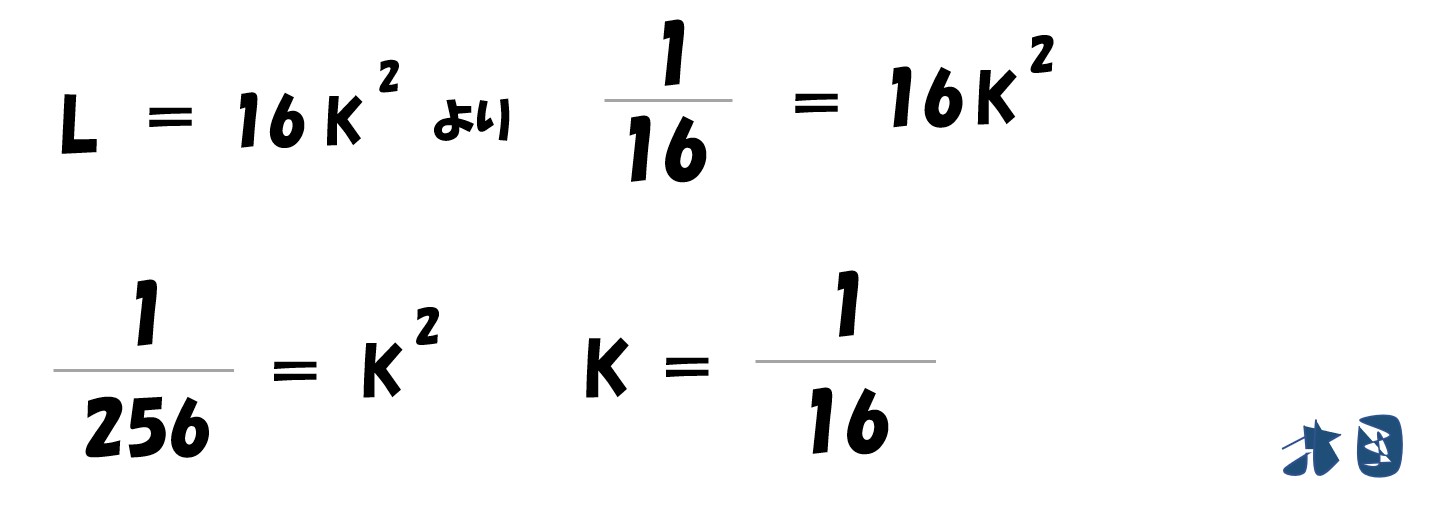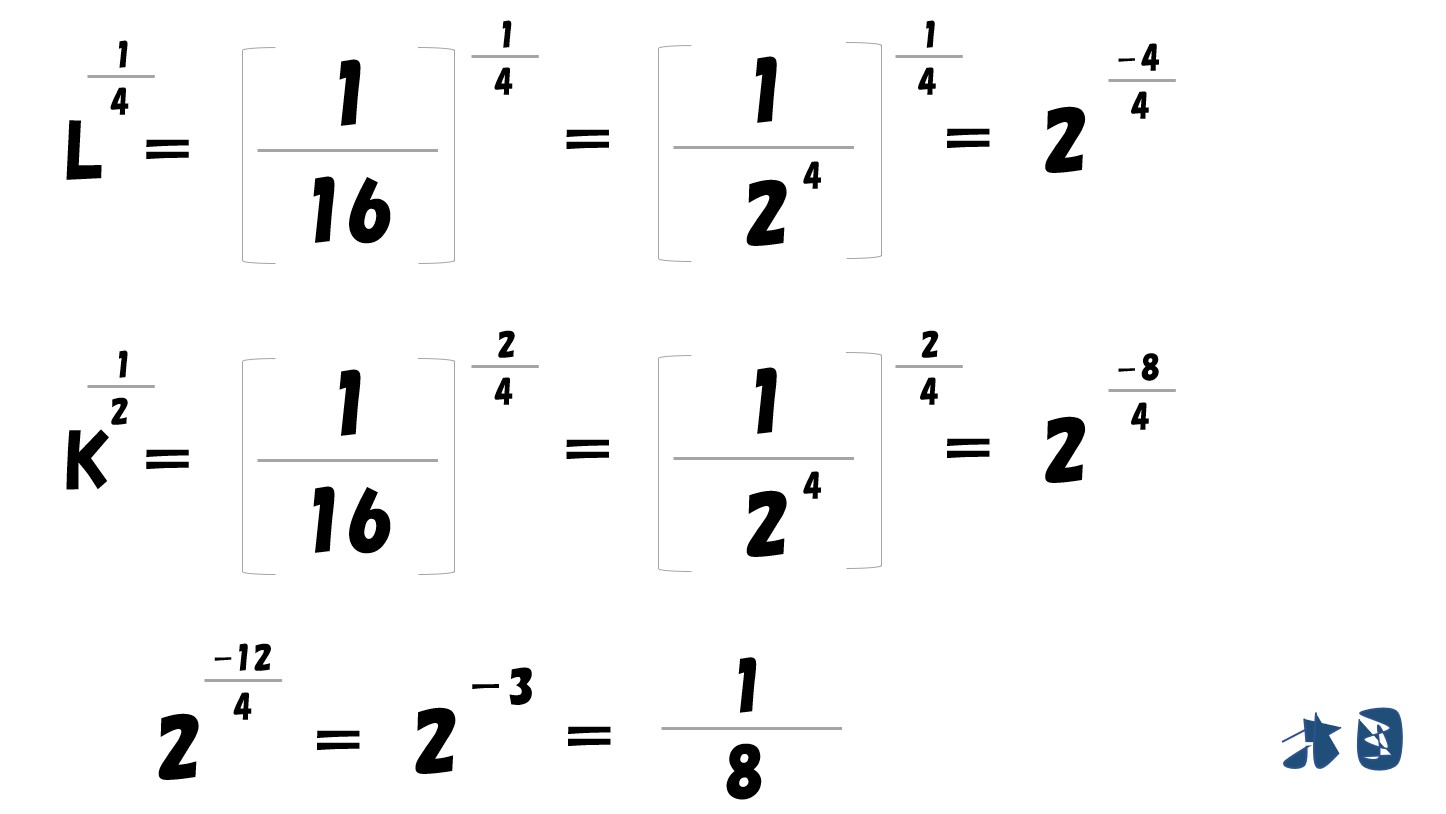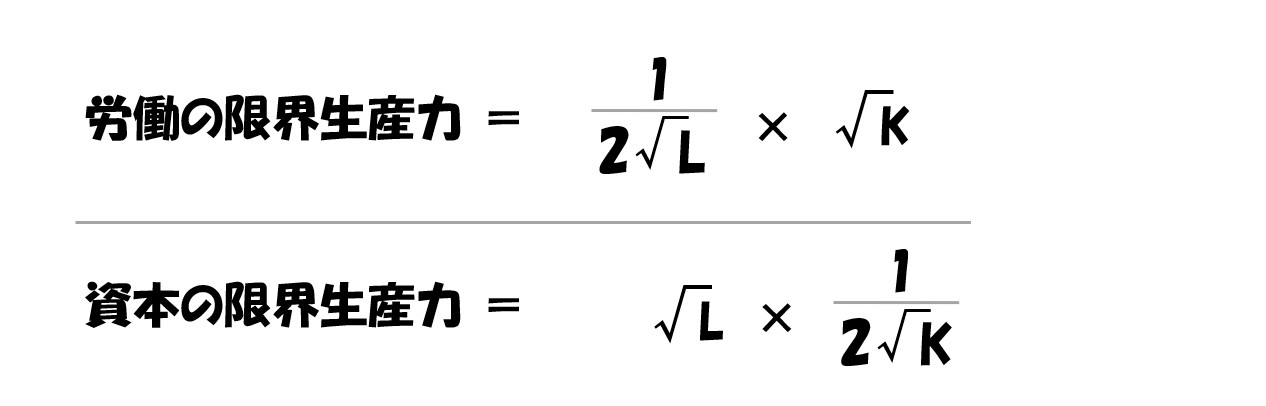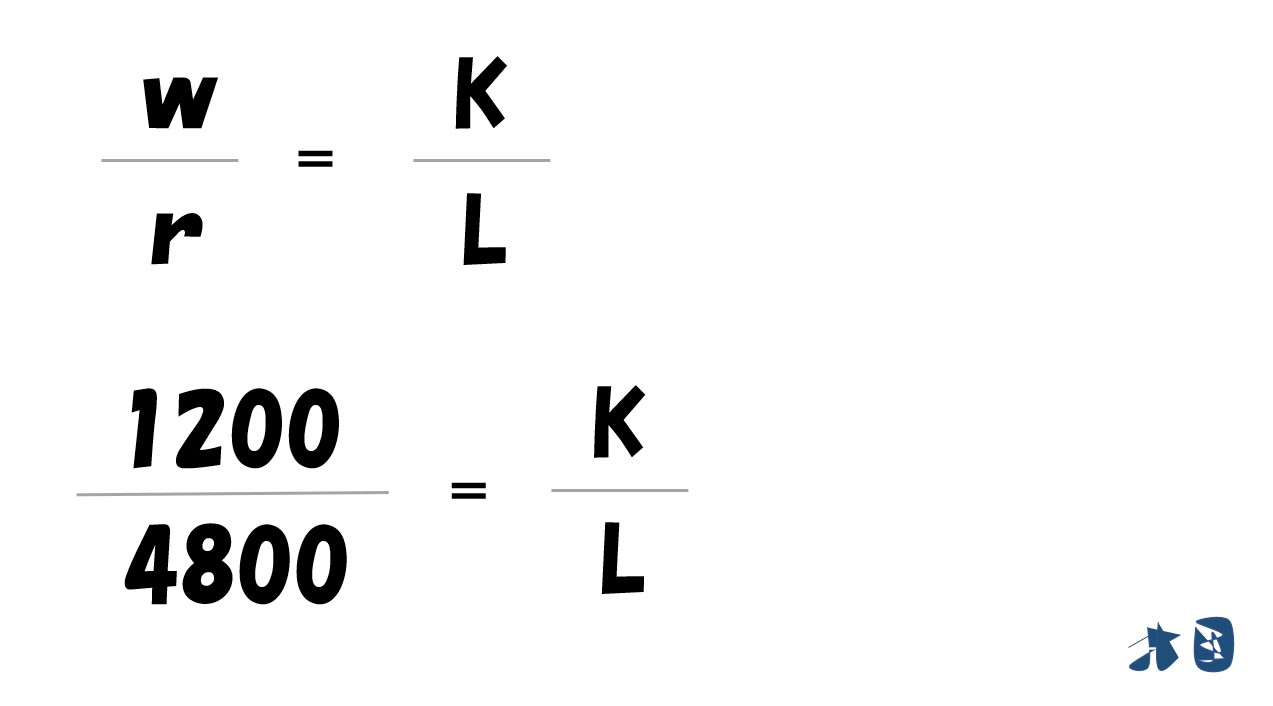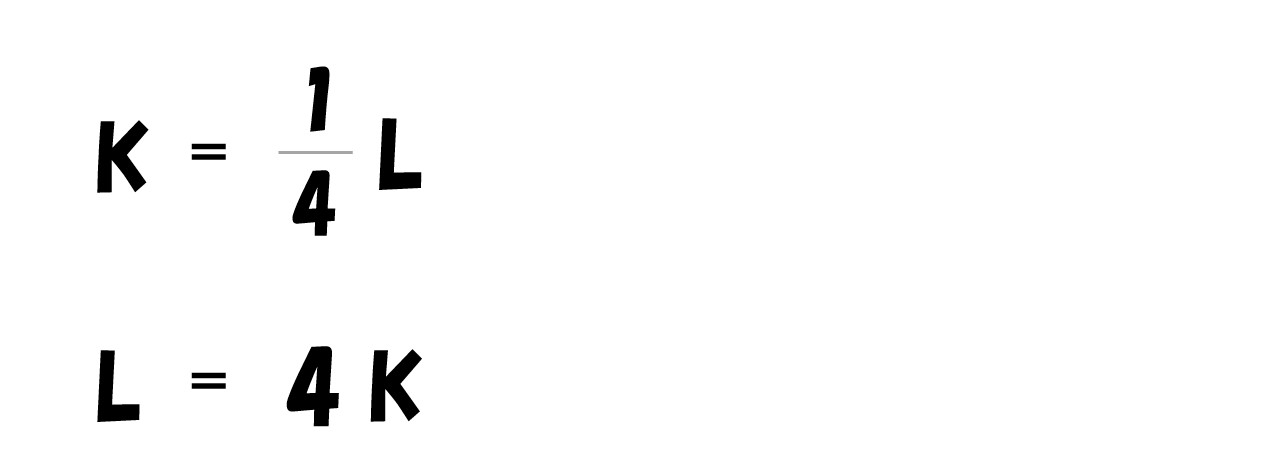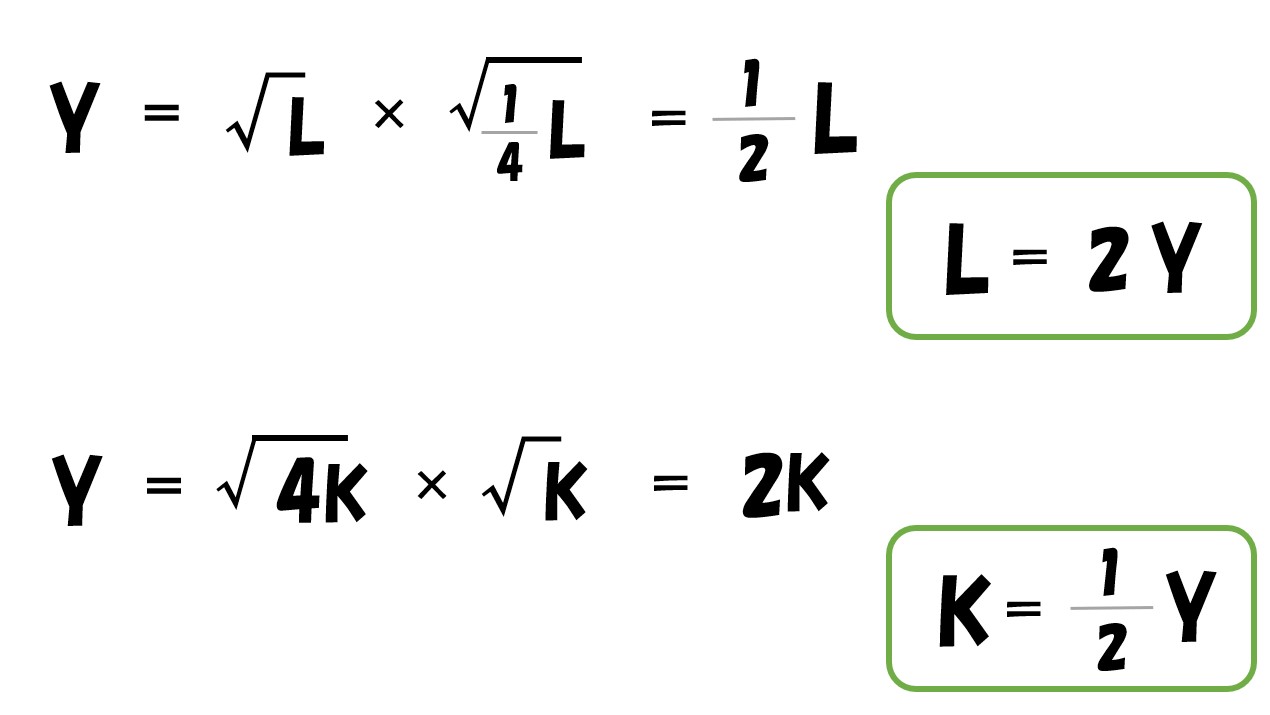「完全競争市場の利潤最大化」
- 利潤最大化の意味
- 利潤最大化の考え方
- 利潤最大化で微分が登場する理由
- 利潤最大化条件の計算方法
- 利潤最大化と限界生産力(MP)
- 費用関数から利潤最大化を求める
- 生産関数から利潤最大化を求める
生産者理論で重要な項目の1つである「利潤最大化」についての情報を、簡単に分かりやすくまとめました。
利潤最大化とは?
利潤最大化とは?
企業は、自社の利潤を最大化するために生産活動を行う。これを「利潤最大化(企業の利潤最大化行動)」と呼ぶ。また、その利潤最大化を求める問題・それに関連する問題を「利潤最大化問題」と呼ぶ。


利潤は「機会費用」を考慮している
機会費用
複数の選択肢のうち自分が選んでいない選択肢で得られたはずの利益のこと
例えば
企業が自社で保有している土地を
- 畑にする?
- 工場にする?
と迷っていた時を考えます。

結局100万円かけて工場を建設して商品を生産しました。しかし、商品は全く売れませんでした。
このとき「利益」を計算するには工場を建てる時に発生した「100万円」を使います。⇒「利益=-100万円」
一方で
「利潤」は、建設費「100万円」+「仮に、畑にして作物を作っていた時に得られていただろう利益」も考慮して計算します。
ポイント
畑にしていれば1,000万円の利益は確実に得られたなら「利益を逃した=費用」と考えます。工場の建設費100万円と合わせて「利潤=-1,100万円」と考えます。


ただし
- 利潤・利益の違いはそんなに気にしなくてよい
ミクロ経済学で登場する「利潤最大化問題」では「利潤=利益」と考えて差し支えないので、気にせずに計算を進めてOKです。
利潤最大化条件
完全競争市場における利潤最大化が理解出来ない人向けに
- そもそもの考え方
- 実際の文字式で考える
2つの段階に分けて説明をしていきます。
ここを理解すると、利潤最大化で微分する理由、計算過程で「=0」とする理由も分かります
①考え方を理解する

初めに
利潤を求めるには
⇒「全ての収入」から「全ての費用」を引けば利潤になる!
つまり「利潤(π)=総収入-総費用」となります。基本はこの式をもとに考えを進めていくので、しっかりと押さえましょう。
次は具体例をもとに話を進めていきます。
例えば
- ある企業が自動車の生産販売を行っています

この企業は、自動車の大量生産を実現しており、手ごろな価格で車を販売しています。
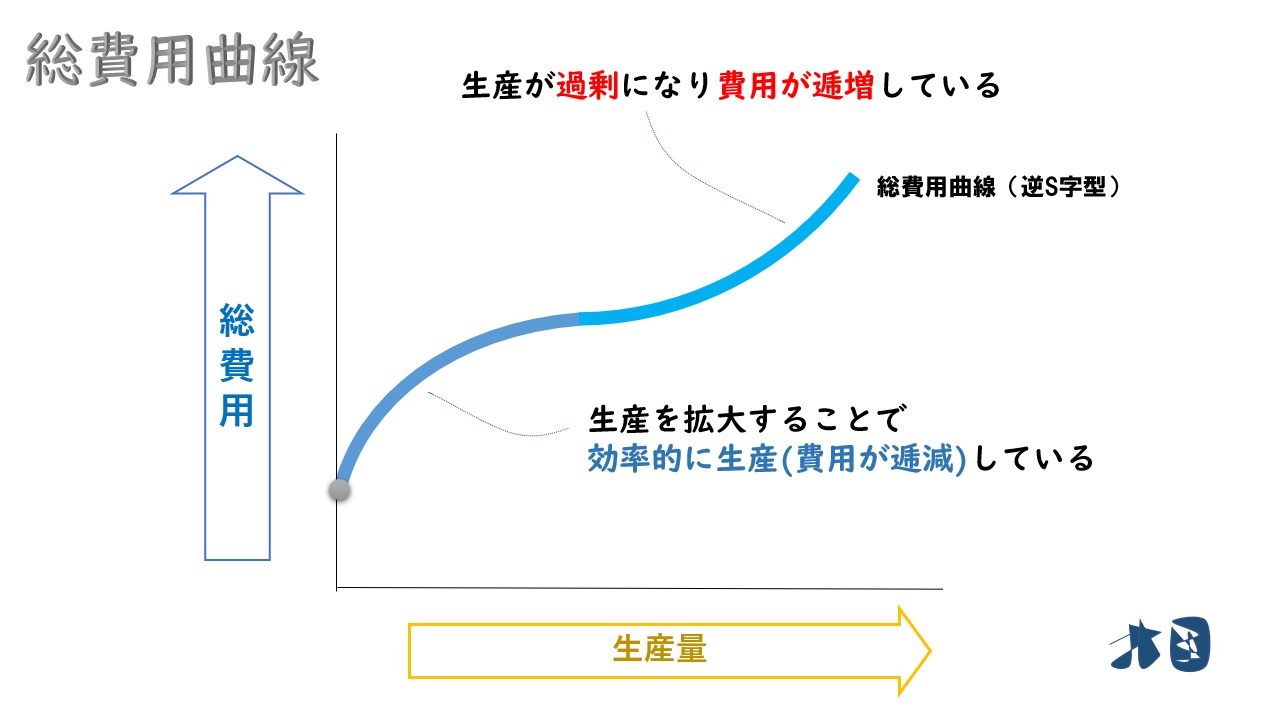
生産を拡大していけば、生産効率が上がるため費用を押さえて生産を行うことが出来ます。そのため、大量生産が実現すれば安く商品を提供できます。
- この時、企業は作って売れば売るほど利潤が発生します


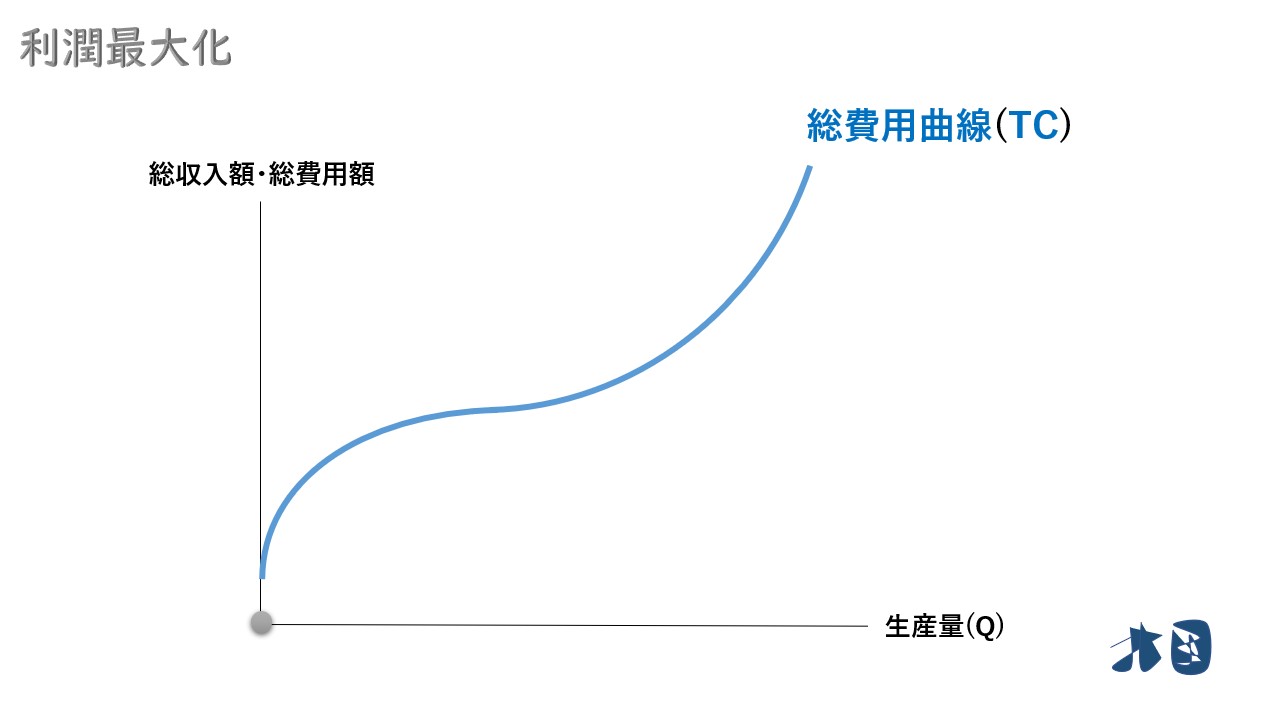
この企業は、無理に生産販売を続けた結果、生産効率が落ちていき費用が余計に掛かるようになりました。
このように、無理な生産拡大は費用の逓増をもたらします。
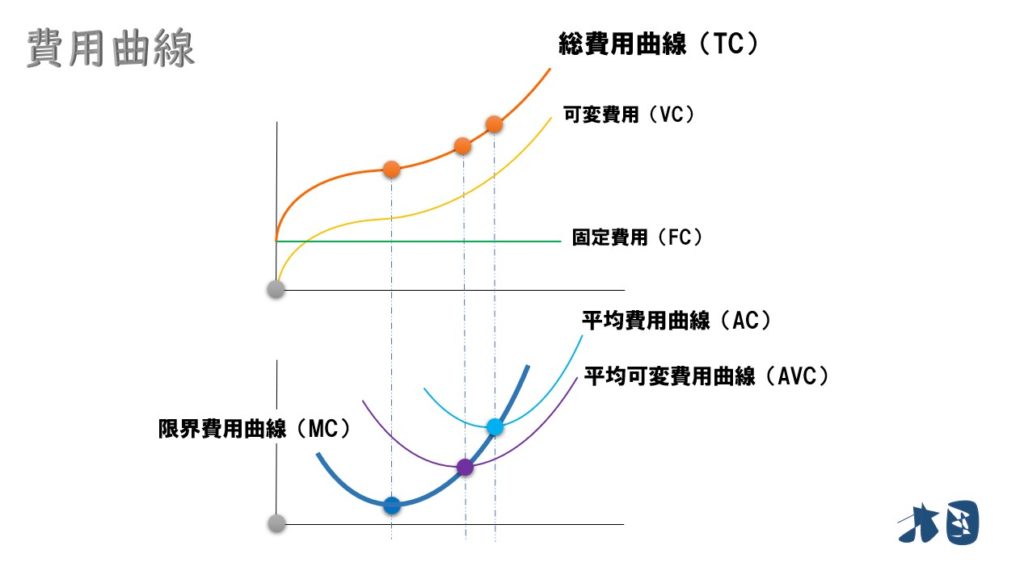
グラフで見ると
費用(総費用)については、こちらで確認できます⇒【費用曲線の要点を分かりやすく】総費用・固定・可変・平均可変・限界
一方で
- 完全競争市場ではライバル企業が多数いるため、安易に値上げ出来ません
市場の相場によって販売価格(P)が決まり、大きく変動することは基本はありません。企業はこの市場価格を受け入れるため、完全競争市場では企業はプライステイカー(価格受容者)と考えて、販売価格は一定だと仮定します。
すると
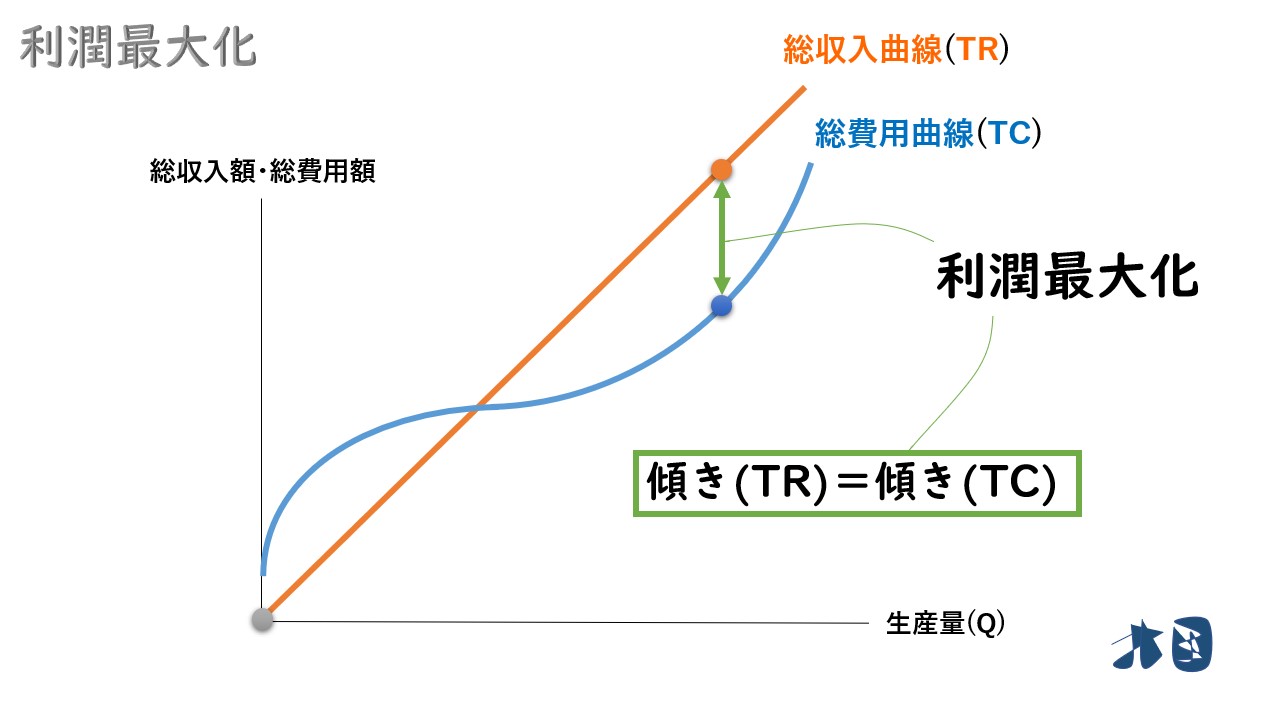
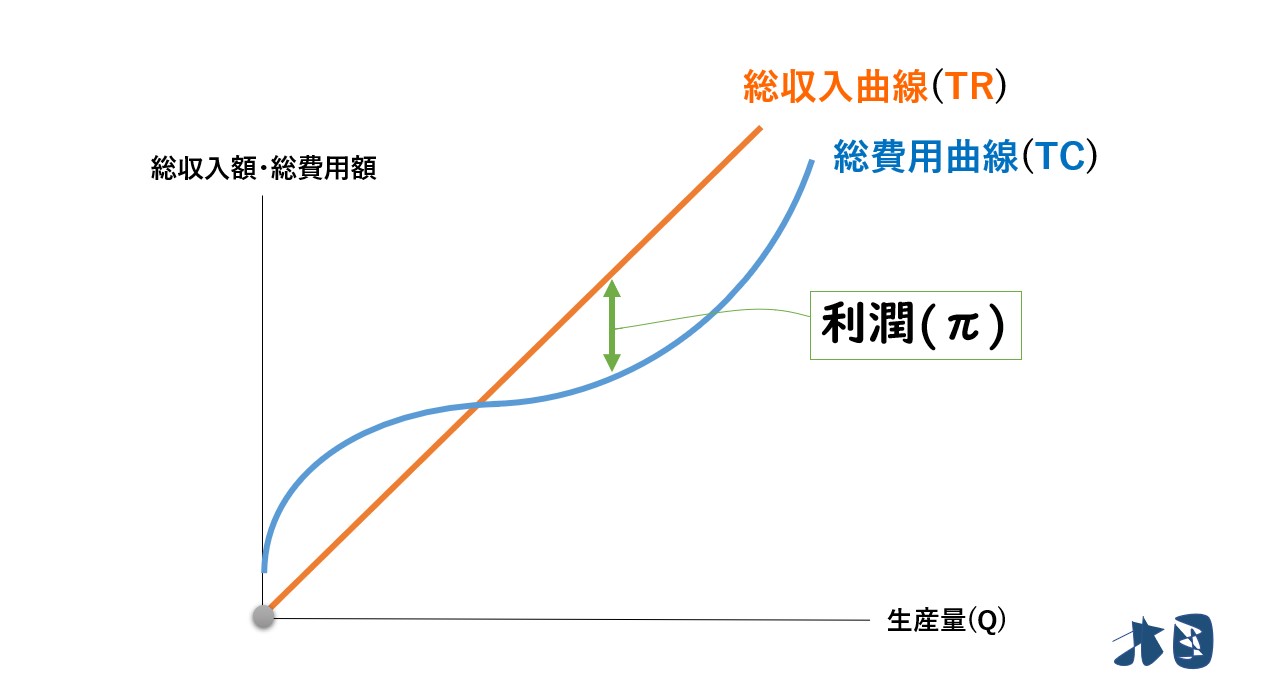
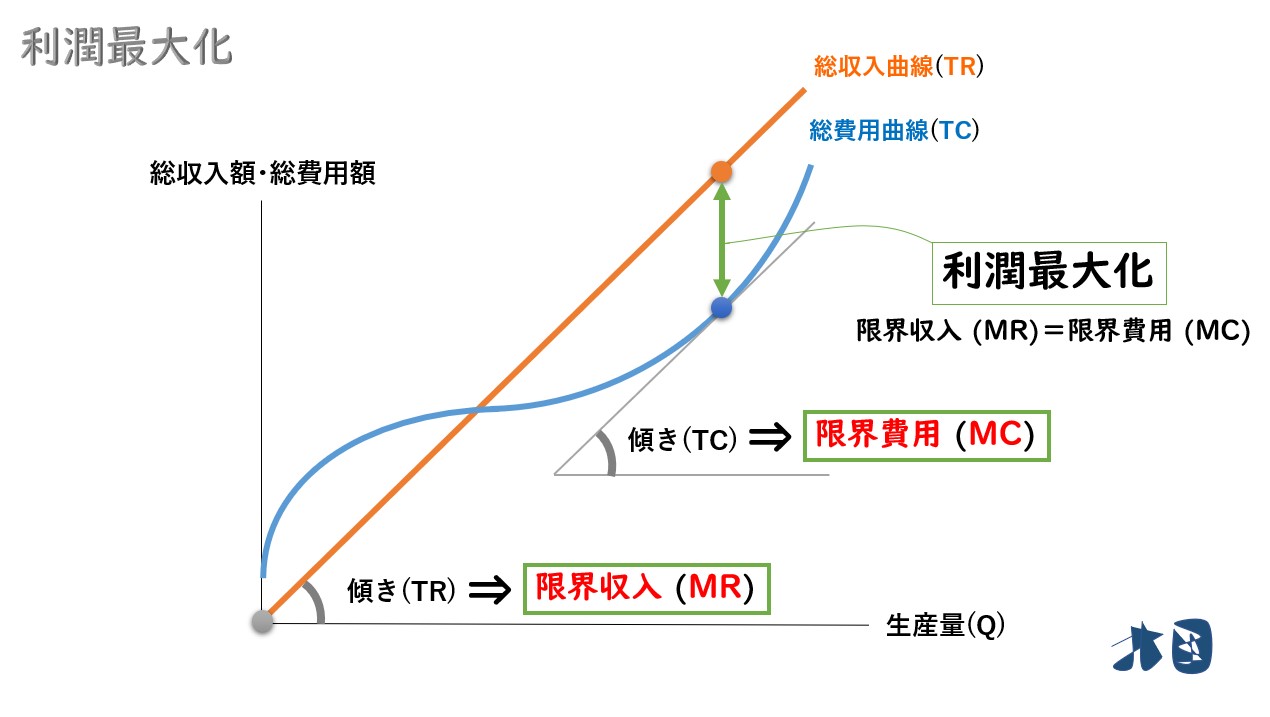
- 総収入と総費用の関係は次のようになります
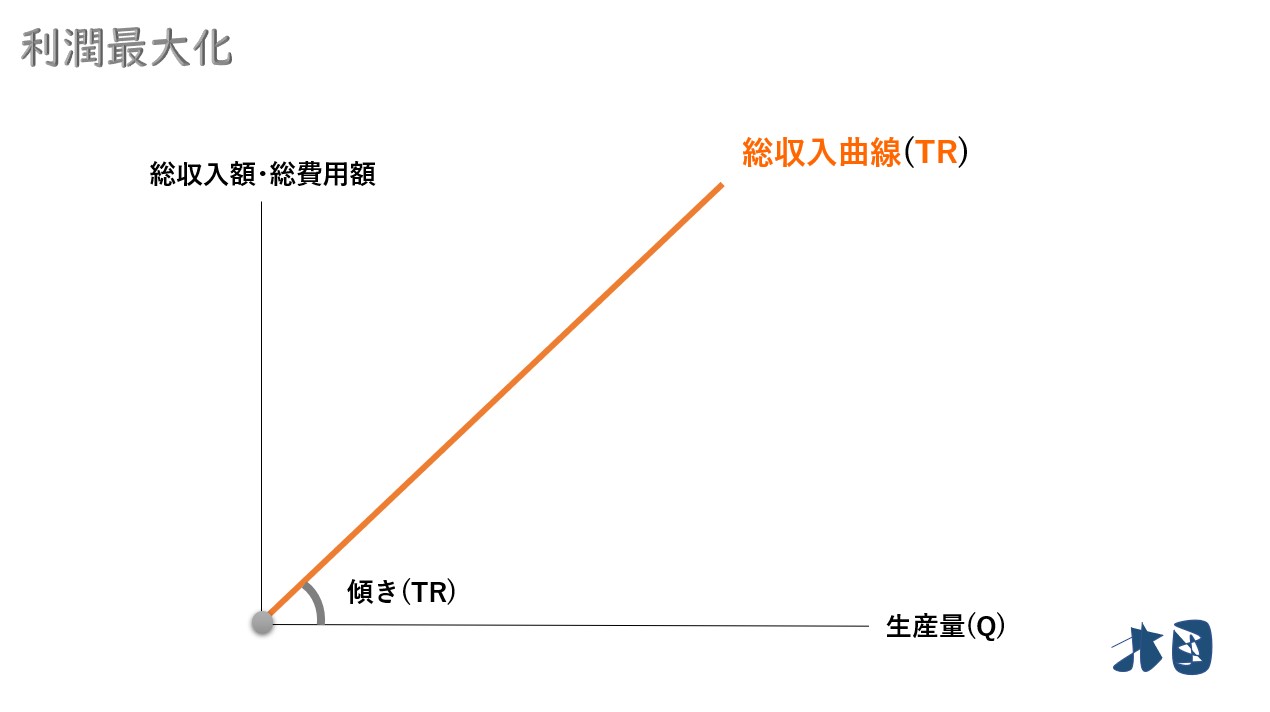
①販売価格(P)が一定なので、生産量(Q)を増やして販売すれば、常に一定の収入増となります。総収入曲線(TR)は右上がりの直線。
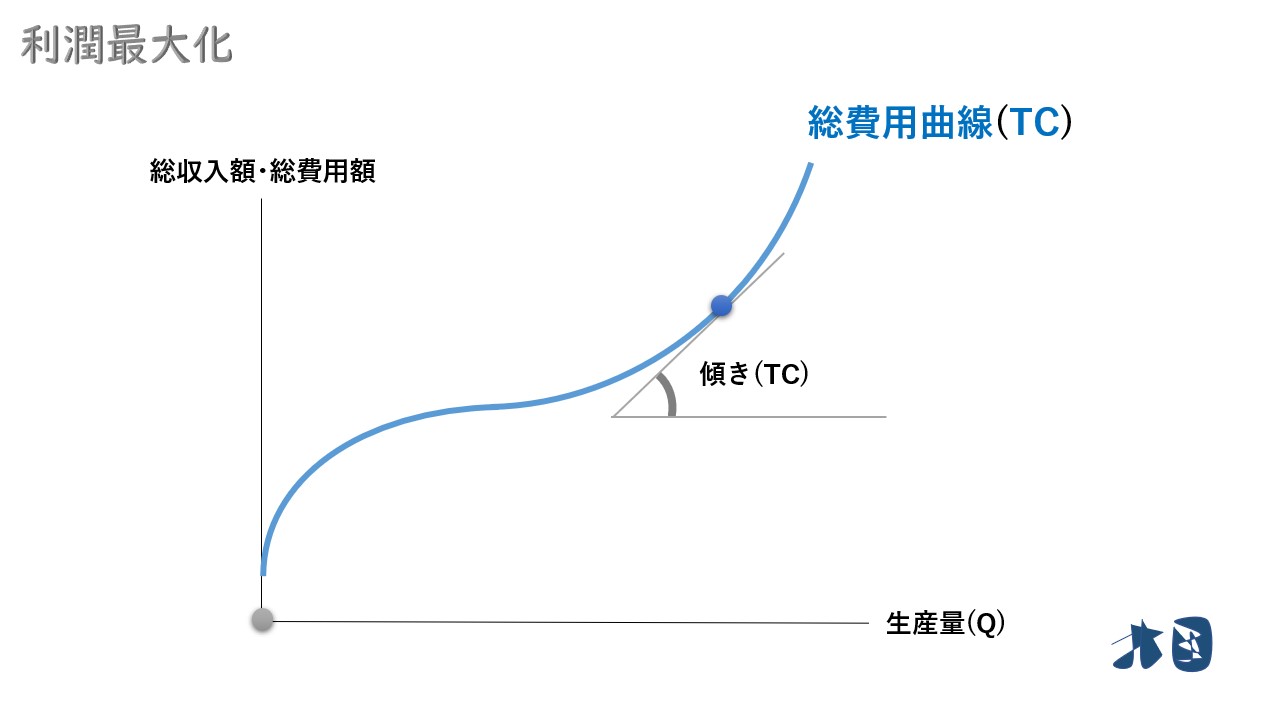
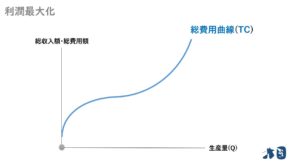
②規模を拡大しすぎると生産が非効率となるため、生産量(Q)を増やし過ぎたあたりから、急激に増加します。総費用曲線(TC)は右上がりの曲線。
③そして、利潤(π)は「総収入(TR)-総費用(TC)」なので、この2つのグラフの差の部分(黄緑色の矢印)が利潤だと分かります。


矢印を一番長くするためには?
- 限界収入(MR)と限界費用(MC)で考える
ここまでは、総収入(TR)と総費用(TC)で話を進めてきましたが、少し細かく見ていきます。ここを理解すると、利潤最大化問題で微分をする理由が分かります。
まずは、矢印が一番長くなる瞬間のグラフを見てみましょう。
総収入曲線(TR)と総費用曲線(TC)の傾きが同じになった瞬間に利潤最大化が実現します。
総収入曲線・総費用曲線の「傾き」がキーワードになります。「傾き」と限界収入(MR)と限界費用(MC)の関係について順番に見ていきましょう。
step
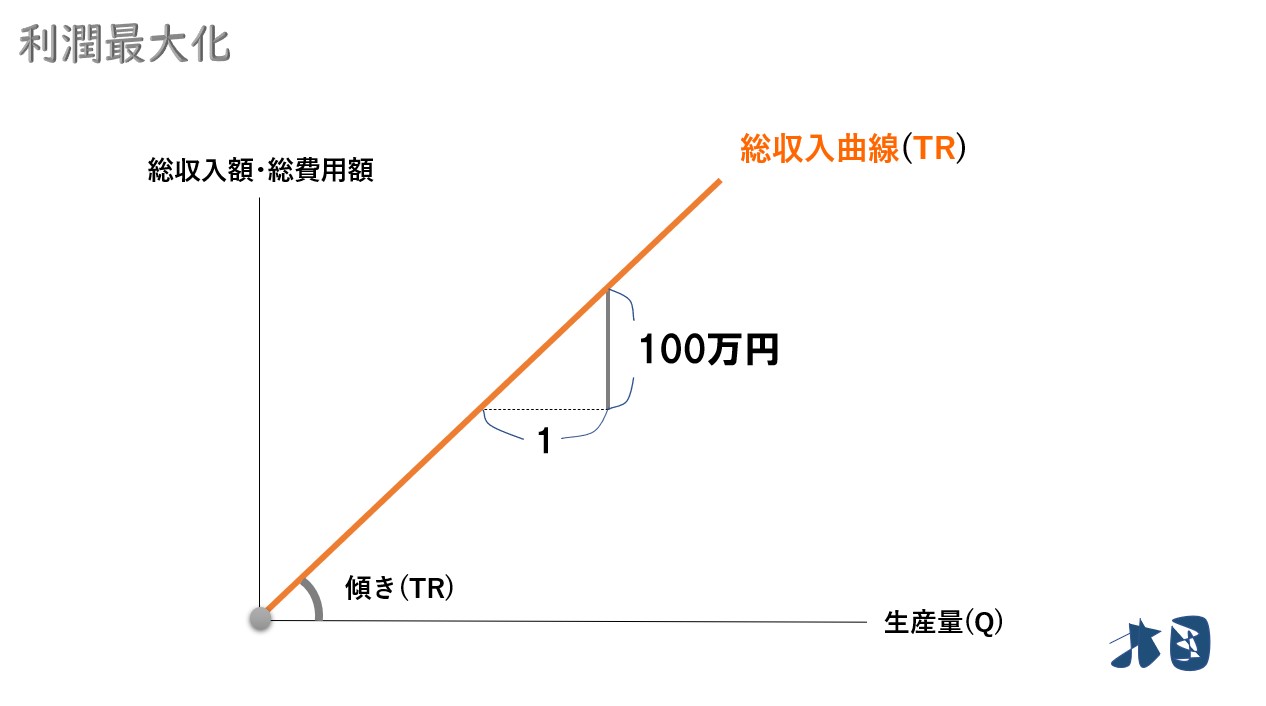
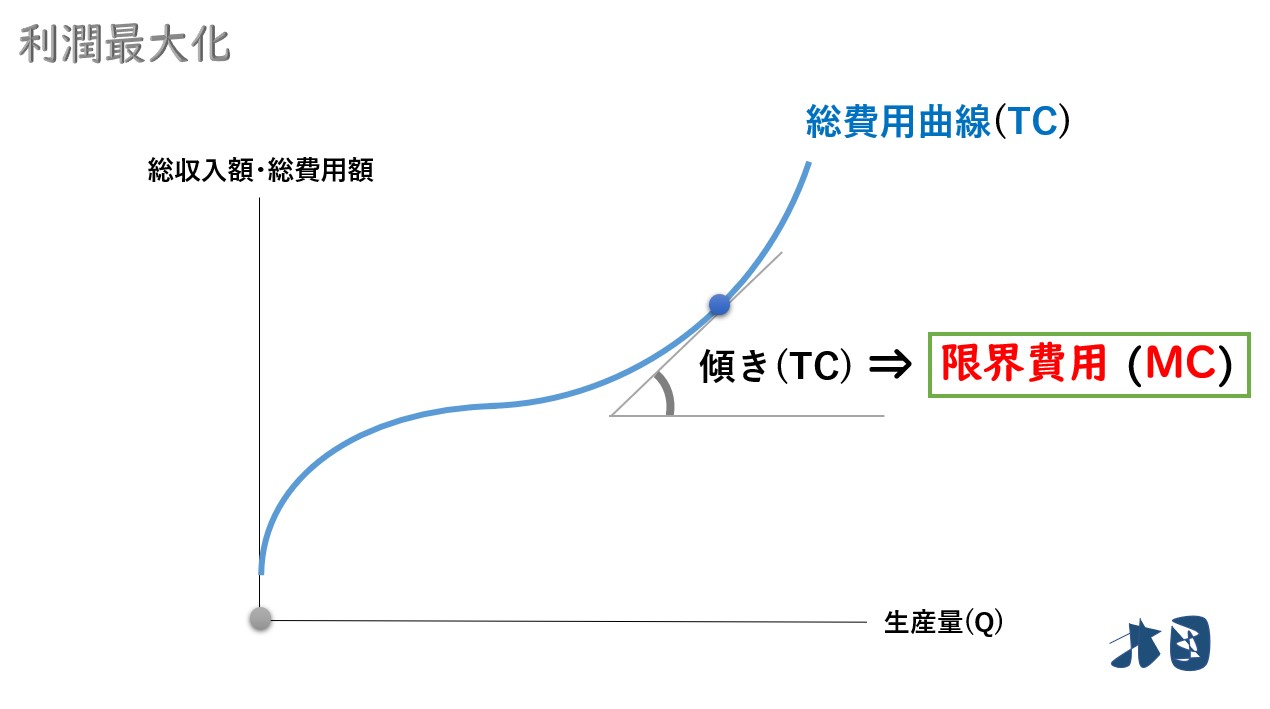
1「総収入曲線の傾き=限界収入」について
先ほど説明した通り、完全競争市場では販売価格(P)は一定なので、収入の増加は常に一定です。
例えば
- 1台100万円の車を販売する
すると、1台生産をして販売すれば100万円の収入増になります。
ここで2つ重要なことがあります。
まず
- 総収入曲線(TR)の傾きです
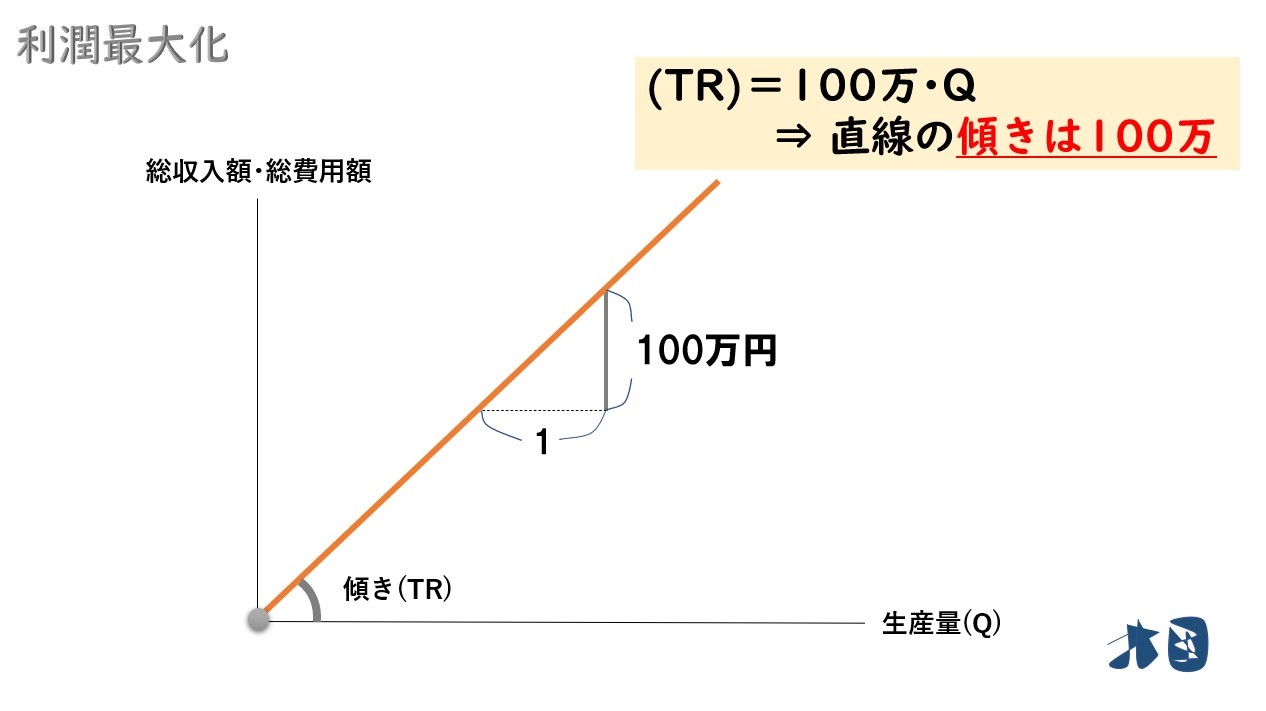
1台生産をして販売すれば100万円の収入増になるため、直線の式は次のようになります。
- 総収入曲線(TR)=100万円×生産量(Q)
この時、総収入曲線(TR)の「傾き=100万」となります。
※ちなみに、傾きの求め方は「(傾き)=縦軸÷横軸=100万÷1台=100万」


次に
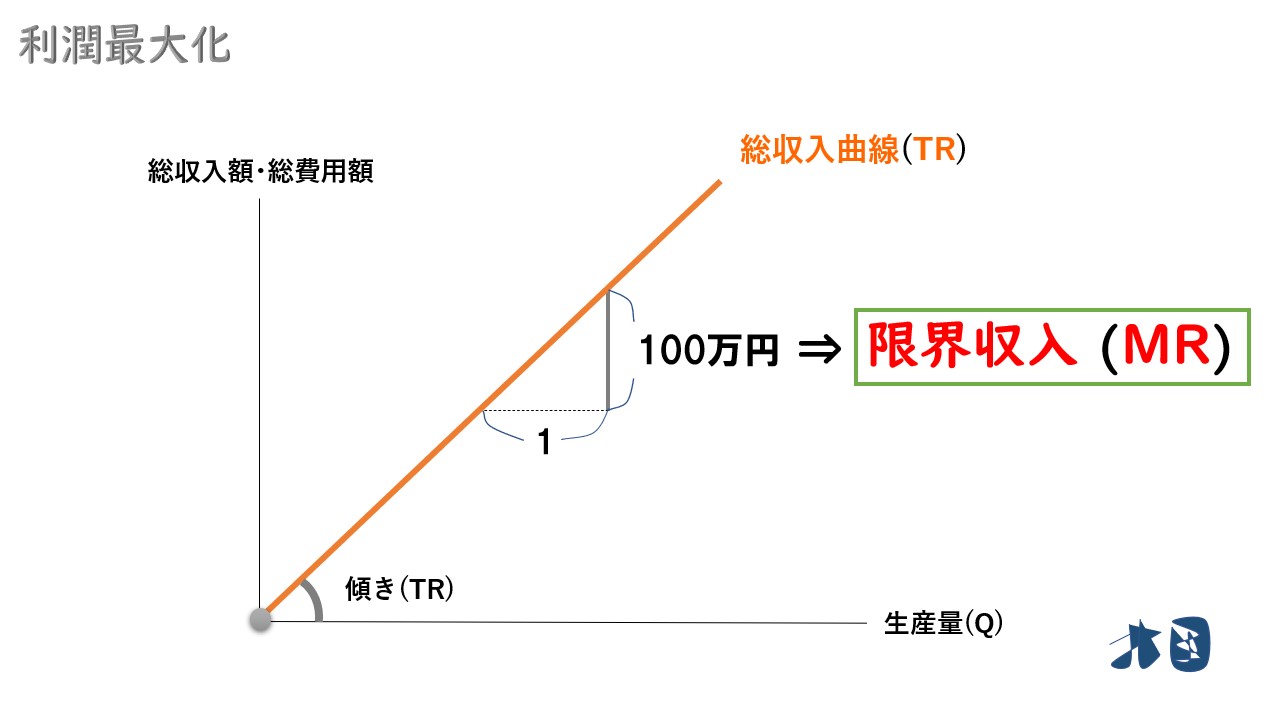
自動車を1台売ったときに発生する、売上の増加分のこと(生産物を1単位当たり売却した時に得られる収入の増加分)を限界収入(MR)と呼びます。
つまり、この100万は「傾き」であると同時に「限界収入(MR)」になります。
※限界収入(MR)の詳しい解説についてはこちら⇒限界収入とは?
ポイント
- 「総収入曲線(TR)の傾き」=「限界収入(MR)」
ちなみに、経済学で登場する「限界●●」は「傾き」と同じことを意味します。


step
2「総費用曲線の傾き=限界費用」について
先ほど説明した通り、総費用曲線(TC)は、生産の効率性によって増加具合が変化します。
つまり、生産が効率的か・過剰生産かによって費用が変化する


先ほどは、具体的に「1台生産したとき」と考えましたが、それでは傾きが分かりません。そこで「1台生産したとき」と考えず「1よりも小さい点」で考えます。
このように「ある点に対して接線を引いて、その傾き」を求めます。
ここで
先ほどと同じように「総費用曲線(TC)の接線の傾き=限界費用(MC)」となります。
ポイント
- 「総費用曲線(TC)の傾き」=「限界費用(MC)」
ちなみに
先ほどの例で考えれば自動車を1台生産したときに発生する、費用の増加分のこと(生産物を1単位当たり生産した時に発生する費用の増加分)を限界費用(MC)と呼びます。
限界費用(MC)の詳しい解説はこちら⇒限界費用とは?利益・平均費用との関係も分かりやすく簡単に解説
これではイメージしづらいと思いますので、先ほどの自動車の例で考えます。
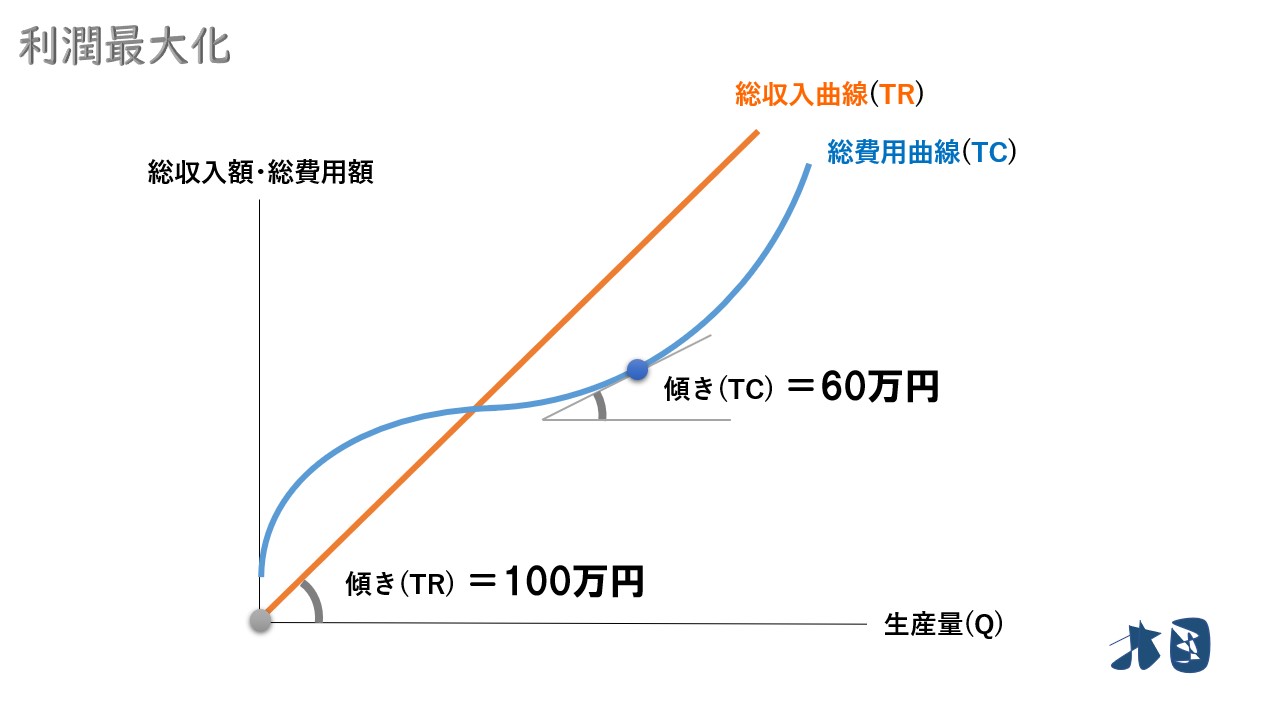
例えば①
- 1台100万円の車を販売する
- この1台の製造費は60万円
1台販売して、収入が100万円増加するため「限界収入(MR)=100万円」
1台生産して、費用が60万円増加するため「限界費用(MC)=60万円」
- この1台を販売したことで利潤(π)が「40万円」増加します
ポイント
ここで、限界収入(MR)が限界費用(MC)より大きければ利潤がプラスになるため、その1台を製造販売した方が利潤が増加することが分かる。
このとき
- 総収入曲線(TR)の傾き=限界収入(MR)=100万円
- 総費用曲線(TC)の傾き=限界費用(MC)=60万円
「総収入曲線(TR)の傾き>総費用曲線(TC)の傾き」となっていることが分かります。
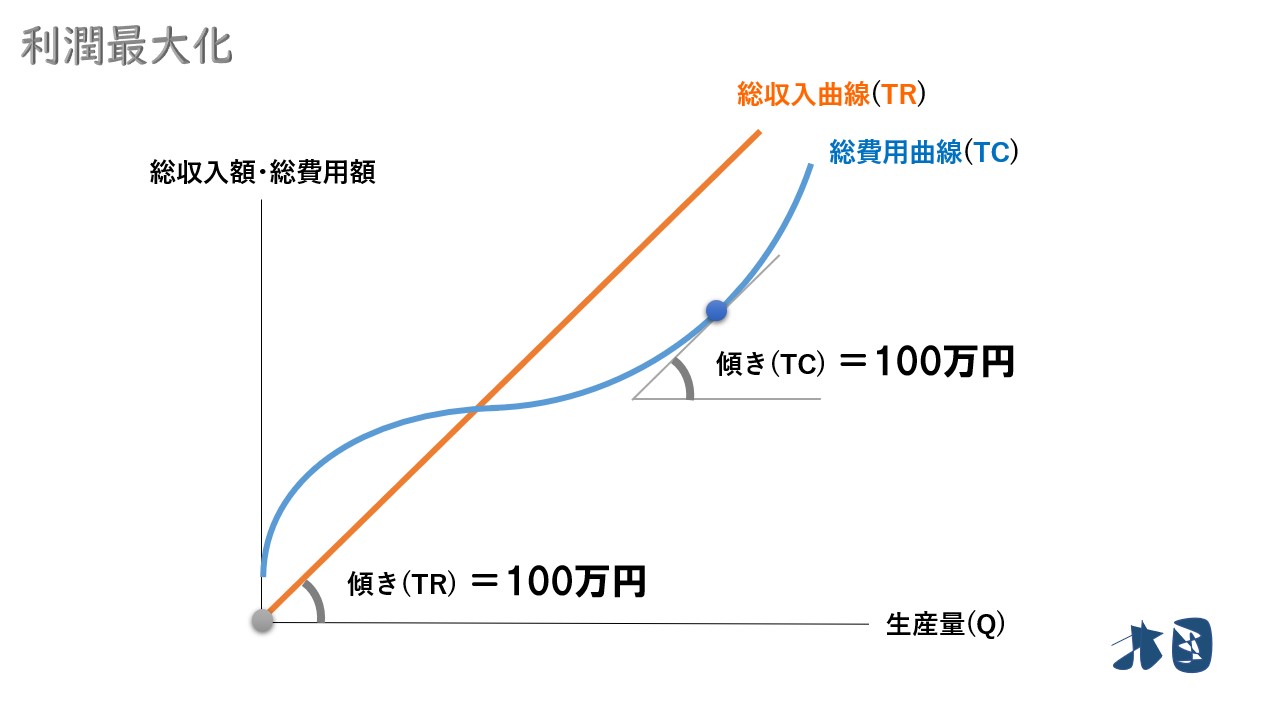
例えば②
- もう1台車を100万円で販売する
- この1台の製造費は100万円かかった
1台販売して、収入が100万円増加するため「限界収入(MR)=100万円」
1台生産して、費用が100万円増加するため「限界費用(MC)=100万円」
- この1台を販売しても利潤(π)は「0円」です
ポイント
限界収入(MR)と限界費用(MC)が同じ金額になるとき、利潤が発生しない。
このとき
- 総収入曲線(TR)の傾き=限界収入(MR)=100万円
- 総費用曲線(TC)の傾き=限界費用(MC)=100万円
「総収入曲線(TR)の傾き=総費用曲線(TC)の傾き」となっていることが分かります。
例えば③
- もう1台車を100万円で販売する
- この1台の製造費は150万円かかった
1台販売して、収入が100万円増加するため「限界収入(MR)=100万円」
1台生産して、費用が150万円増加するため「限界費用(MC)=150万円」
- この1台を販売しても利潤(π)は「-50万円」です
ポイント
ここで、限界収入(MR)より限界費用(MC)の金額が大きくなるとき利潤がマイナスになるため、その1台は製造販売しない方が良かったことが分かる。
このとき
- 総収入曲線(TR)の傾き=限界収入(MR)=100万円
- 総費用曲線(TC)の傾き=限界費用(MC)=150万円
「総収入曲線(TR)の傾き<総費用曲線(TC)の傾き」となっていることが分かります。
step
3「価格=限界収入=限界費用」について
まとめ
- 例①~③をまとめると‥
①「総収入曲線(TR)の傾き>総費用曲線(TC)の傾き」⇒追加の利潤がプラス
②「総収入曲線(TR)の傾き=総費用曲線(TC)の傾き」⇒追加の利潤が0円
③「総収入曲線(TR)の傾き<総費用曲線(TC)の傾き」⇒追加の利潤がマイナス
つまり
追加の利潤が0円になるまで製造販売を行えば、利潤を拡大することが出来る。別の言い方をすれば、利潤が0円になるまで製造販売をすれば、利潤が最大化する。
グラフで考えれば「総収入曲線(TR)の傾き=総費用曲線(TC)の傾き」になるまで製造販売すればOK。
更に…
- 総収入曲線(TR)の傾き=限界収入(MR)
- 総費用曲線(TC)の傾き=限界費用(MC)
となるため「限界収入(MR)=限界費用(MC)」で利潤が最大化するとも言えます。
重要
完全競争市場では、限界収入(MR)は販売価格(P)と同じです。
販売価格(P)=100円の商品を、追加で1つ売ったら収入が100円増加します(価格=限界収入=100円)。最初に説明した通り、完全競争市場ではライバル企業が多数いるため、安易に値上げが出来ません。市場の相場によって販売価格(P)が決まり、大きく変動することは基本ありません。そのため、完全競争市場では販売価格(P)は常に一定と考えました。販売価格(P)が常に一定なら、商品を何個売ろうが、増加する収入(限界収入)も一定になります。つまり「販売価格(P)=限界収入(MR)」です。
以上より
- 総収入曲線(TR)の傾き=限界収入(MR)=価格(P)
- 総費用曲線(TC)の傾き=限界費用(MC)
となるため「価格(P)=限界費用(MC)」で利潤が最大化するとも言えます。
利潤最大化条件
この「価格(P)=限界費用(MC)」を利潤最大化条件(1階条件)と言います。
つまり、利潤最大化が実現するとき「価格(P)=限界収入(MR)=限界費用(MC)」が実現することになります。この部分は重要なので、しっかりと理解しましょう。イメージが湧かない人はこちらでも確認できます⇒【価格=限界費用=限界収入】なぜ完全競争市場で「P=MC=MR」となるのか


step
4微分について
これまでの説明から、利潤最大化を求めるには「総収入曲線(TR)の傾き・総費用曲線(TC)の傾き」を求めれば良いことが分かったかと思います。
ここで、この傾きを求めるために「微分」が登場します。
この2つの傾きは微分をすれば求められる
通常、傾きは次の式で求められます。
- 傾き=(縦軸に移動した距離)÷(横軸に移動した距離)
ただし、総費用曲線(TC)がカーブを描いているため、上の計算方法では求めることが出来ません。そこで登場するのが微分です。
微分は、グラフを細かな点と考えて「その点の接線の傾き」を求めることが出来る計算方法です。
つまり
- 「利潤(π)=総収入(TR)-総費用(TC)」を微分すれば、それぞれの傾きが得られます
微分すると…「総収入曲線(TR)の傾き-総費用曲線(TC)の傾き」となります。
改めてですが、それぞれ限界収入・限界費用ともなります
・総収入曲線(TR)の傾き=限界収入(MR)
・総費用曲線(TC)の傾き=限界費用(MC)
ポイント
ここで、利潤最大化が実現するポイントでは「総収入曲線(TR)の傾き=総費用曲線(TC)の傾き」だったため「総収入曲線(TR)の傾き-総費用曲線(TC)の傾き=0」となります。
重要
まとめると、計算問題では「利潤(π)=総収入(TR)-総費用(MC)」を微分して「=0」とすれば、利潤(π)を最大化した状態になる。


利潤最大化問題を解けるように、次は、実際の文字式で考えられるようにしましょう。
②数式で考える
次は文字で考える
- 利潤=π
- 価格=P
- 生産量=Y
- 労働量=L
- 賃金=w
- 資本量=K
- レンタル料=r
ポイント
「利潤(π)=総収入ー総費用」なので
- 総収入=価格(P)×生産量(Y)
- 総費用=賃金(w)×労働量(L)+レンタル料(r)×資本量(K)
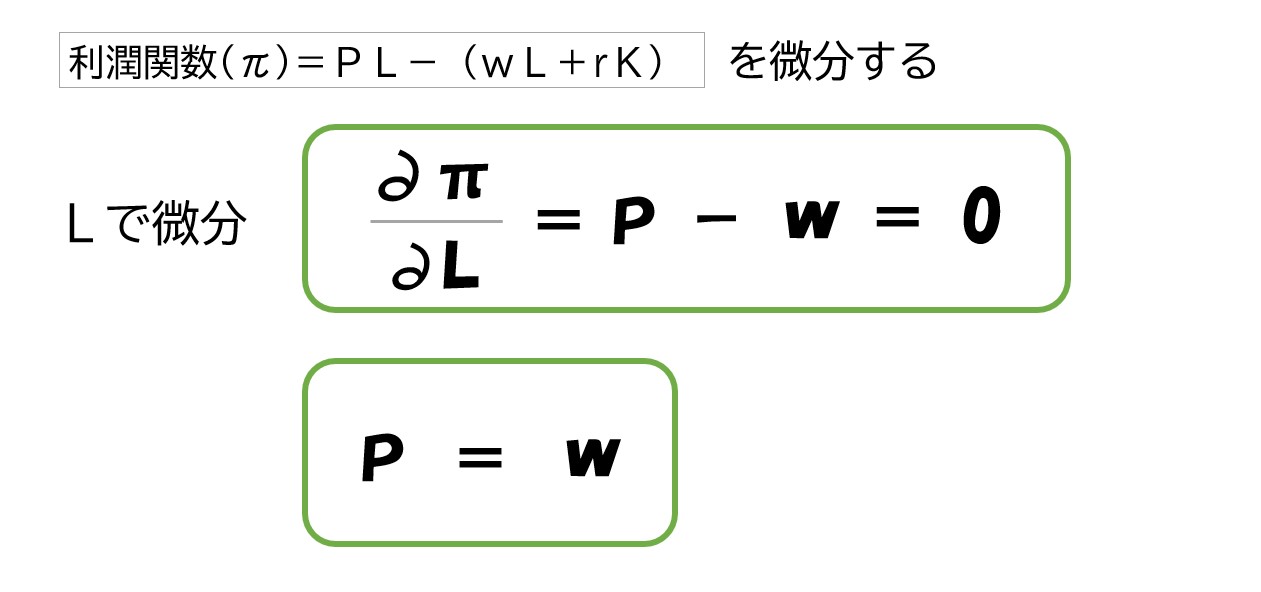
したがって「利潤(π)=(PY)-(wL+rK)」と考える。この数式を利潤関数(π)と呼ぶ。
※「価格(P)」は商品の販売価格(P)・「生産量(Y)」は作ったものを全部売ると考えて生産量=販売量と考えます。なので、販売量(Y)に販売価格(P)を掛けて収入額を計算していることになります。
ここで
- 「利潤(π)=(PY)-(wL+rK)」の利潤を最大化させるために微分して「=0」とする
微分して「=0」にすると利潤が最大化する理由を戻って確認する
なので
- 総収入=価格(P)×生産量(Y)
- 総費用=賃金(w)×労働量(L)+レンタル料(r)×資本量(K)
総収入(TR)と総費用(TC)にあたる点線部分を微分していきます。
このとき、重要なポイントが2つあります。
1つ目
- ここで注目するのは「労働量(L)・資本量(K)」です
総費用に関して、賃料・レンタル料は市場によって決められるので、企業は操作できません。そのため、商品・サービスの生産量に応じて変化するのは「労働量(L)・資本量(K)」だけになります(L・K=変数)。
ポイント
つまり、この労働量(L)・資本量(K)が変化すると「どれくらい費用が変わるか=総費用曲線(TC)の傾き」を計算することになります。
そこで、この2つの労働量(L)・資本量(K)のそれぞれで微分するわけです。
2つ目
- 生産量(Y)は、通常「労働量(L)・資本量(K)」によって決まる
「生産関数=Y(L,K)」のように、生産量(Y)は労働量(L)・資本量(K)で決まります。
完全競争市場では、販売価格(P)は市場によって決められるので、企業は操作できません。また、企業は「労働量(L)・資本量(K)」の投入量を変化させて、商品・サービスの生産量をコントロールするため、収入額に影響を与えるのは実質的に「労働量(L)・資本量(K)」です(L・K=変数)。
ポイント
つまり、労働量(L)・資本量(K)が変化すると「どれくらい生産量(収入)が変わるか=総収入曲線(TR)の傾き」を計算することになります
そこで、労働量(L)・資本量(K)をそれぞれで微分すれば、総収入曲線(TR)の傾きも求めることが出来ます。
さらに詳しく
本来ならば「利潤(π)=(PY)-(wL+rK)」を生産量(Y)で微分して「=0」とすることで、利潤最大化を求めることが出来ます。なぜなら、収入も費用も生産量に応じて変化するためです。例えば、生産量を1増やしたとき、収入がいくら増加したか・費用がいくら増加したかが、それぞれ「傾き」になります。
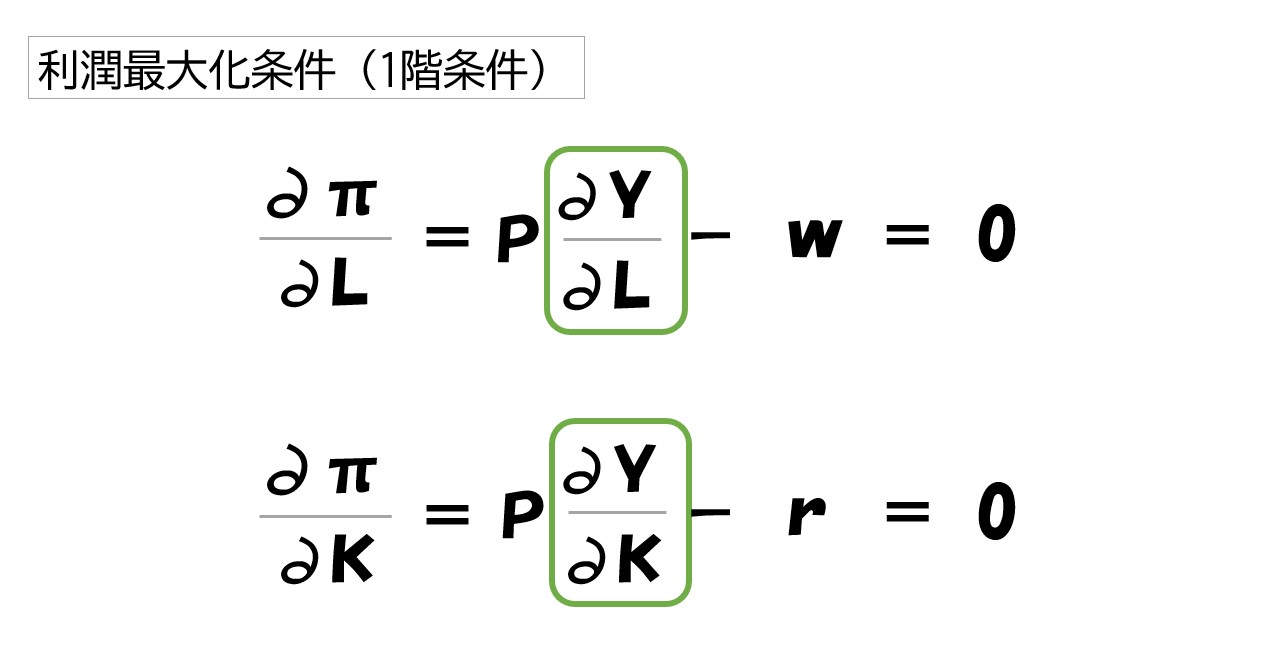
しかし「利潤(π)=(PY)-(wL+rK)」を微分する時は、一般的に労働量(L)・資本量(K)で偏微分して「=0」と出来ます。なぜなら、収入も費用も生産量に応じて変化しますが、この生産量(Y)は、労働量(L)・資本量(K)によって決まるからです。


実際に微分をしてみましょう!
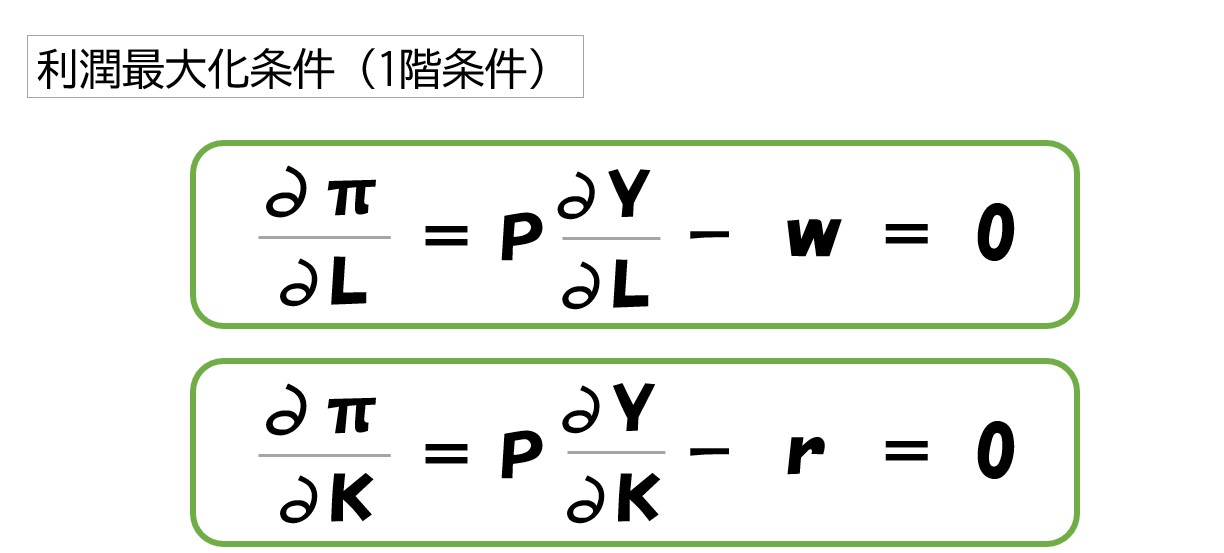
- 「∂π/∂L」「∂π/∂K」は、利潤関数(π)をL・Kで微分したことを表しています。
- 「∂Y/∂L」「∂Y/∂K」は、生産関数(Y)をL・Kで微分したことを表しています。
「利潤(π)」も「生産量(Y)」も、実際の数字が入っているわけではないので、このような表記で「微分をした」ということを表現しています。
また
(wL+rK)の部分は、この時点で実際に計算が可能なので、計算しています。
例えば「L」で偏微分すると‥


ちなみに
教科書や参考書によっては、生産量(Y)の部分を「小さなL」「小さなK」としている場合もあります。また、生産量をYではなく「F」「f」「f(L,K)」等としている場合もあります。
表記が違いますが、それぞれ同じことを書いているので混乱しないようにしましょう。
重要
この2つの式を「利潤最大化条件(1階条件)」と言います。


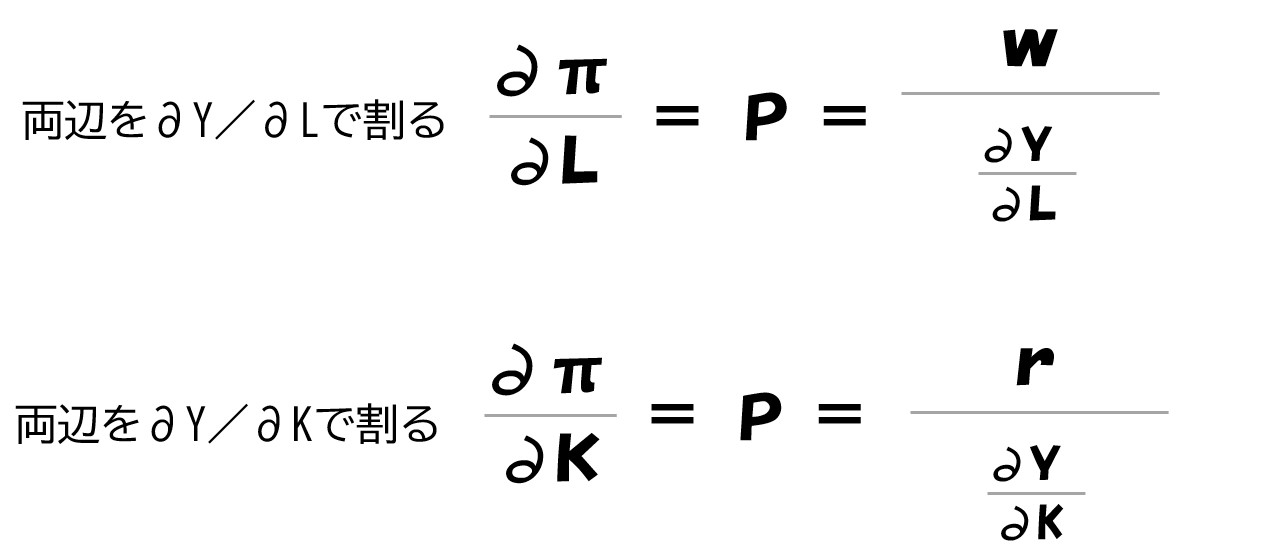
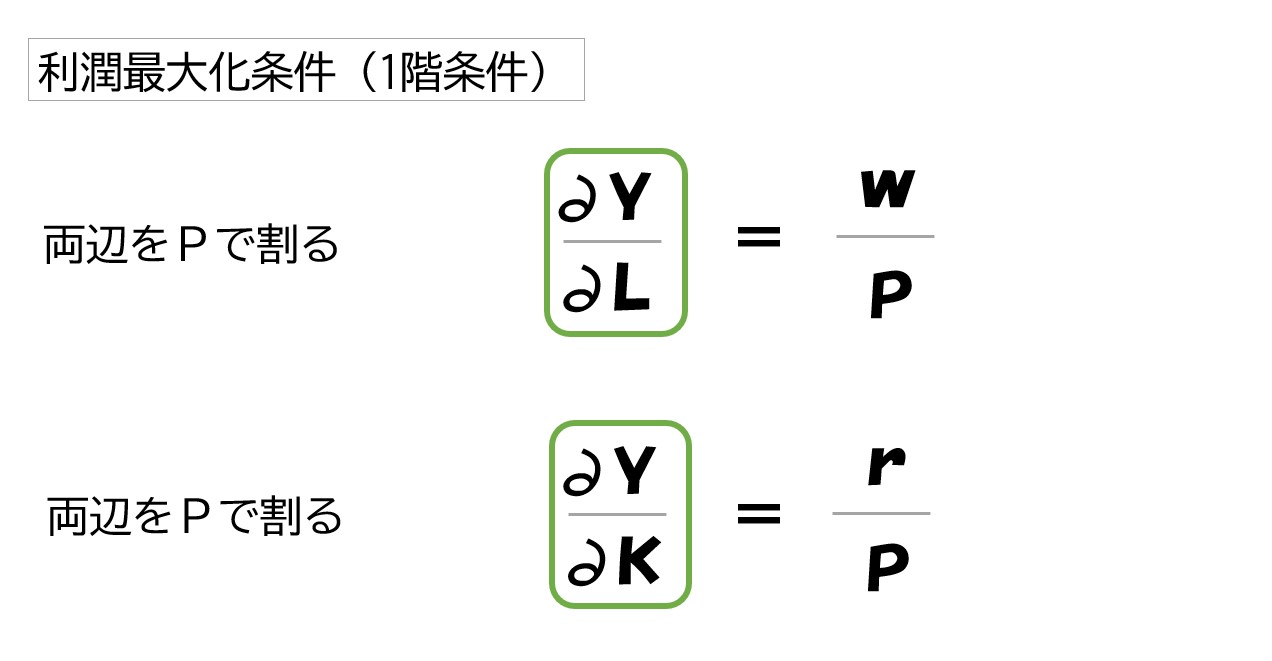
変形する
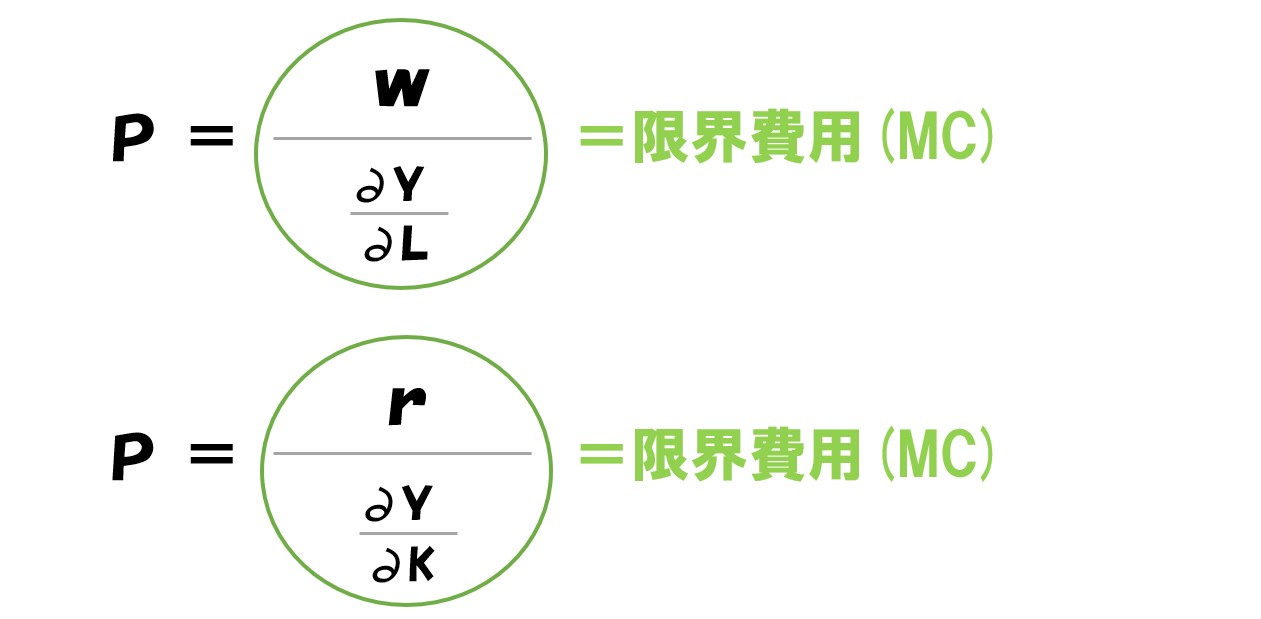
「w/∂Y/∂L」「r/∂Y/∂K」の部分が限界費用(MC)です
イメージが湧きづらいと思いますので「生産関数(Y)=L」の場合を考えます。
「生産関数(Y)=L」というのは、労働1単位で商品を1単位作れる状態です。
すると「利潤(π)=(PY)-(wL+rK)」は「利潤(π)=(PL)-(wL+rK)」となります。
ここで「賃金(w)」は労働1単位あたりの金額です。つまり、右辺は、労働を1単位増やした時の費用の増加分となり限界費用(MC)と同じです。
先ほど「w/∂Y/∂L」「r/∂Y/∂K」の部分が限界費用(MC)と言いましたが、実際に「生産関数(Y)=L」などの関数を使うとイメージできます。
以上より
この2つの式が利潤最大化条件(1階条件)となります。
また、完全競争市場の利潤最大化条件として有名な「価格(P)=限界費用(MC)」は、この数式を変形すると求められるものです。


ここまで理解出来れば、あとは実際の問題を解いていくことが重要です。
最後に大学でミクロ経済学を学習している人向けに「限界生産力(MP)」「生産要素価格」「限界生産物価値」との関係を紹介します。少し混乱するかもしれないので、不要な人は飛ばして大丈夫です。
限界生産力・要素価格との関係
生産関数(Y)をL・Kで微分した「∂Y/∂L」「∂Y/∂K」に注目します。
実はこの部分、限界生産力(MP)を表しています
なので、利潤最大化条件を次のように表記することがあります。
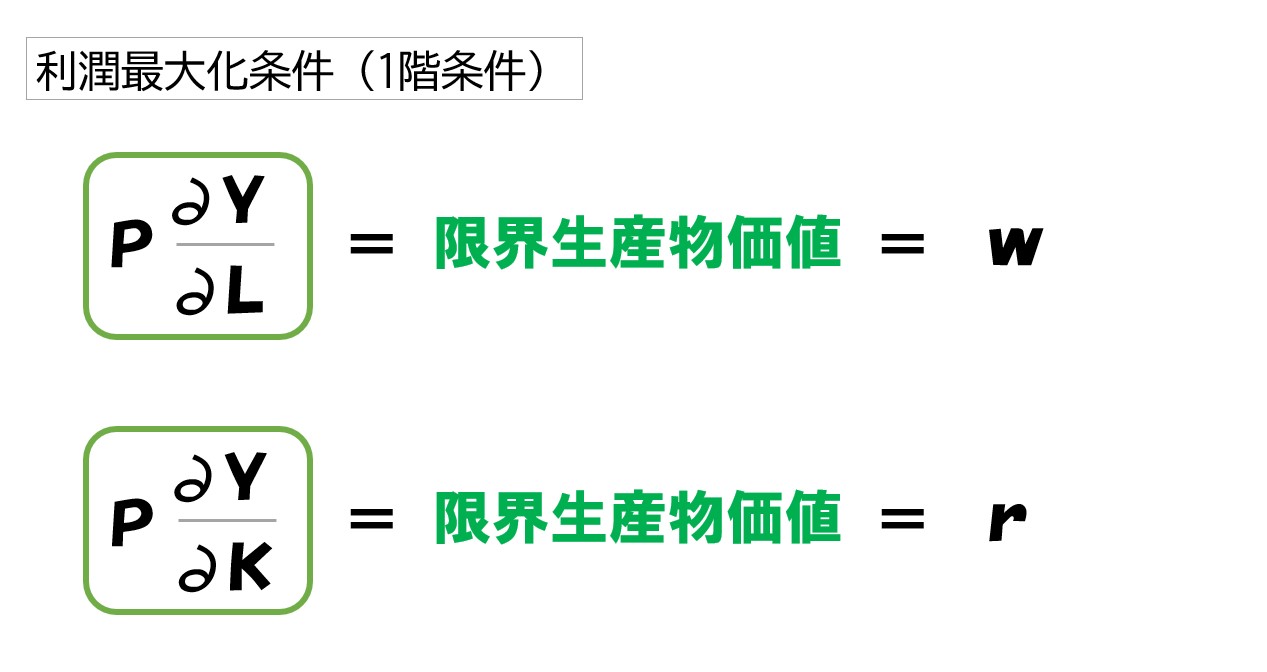
以上のように、利潤最大化条件(1階条件)を
- 労働の限界生産力(MPL)=w/P
- 資本の限界生産力(MPK)=r/P
と表記することもあります。


「限界生産物価値」と「要素価格」
限界生産物価値
限界生産力(MP)と価格(P)を掛けたものを「限界生産物価値」と言います。
なので、利潤最大化条件を次のように表記することがあります。
以上のように、利潤最大化条件(1階条件)を
- 労働の限界生産物価値=w
- 資本の限界生産物価値=r
と表記することもあります。
賃金(w)・資本のレンタル料(r)を要素価格と言います。そのため「限界生産物価値が要素価格と等しくなる時に、利潤が最大化する」と言葉で表現することもあります。
このように、数式を変形した形で利潤最大化条件(1階条件)とすることがあるので、頭の片隅にでも入れておきましょう。
求め方・計算方法

利潤最大化問題の形式は大きく2つあります。
- 費用関数(C)から求める
- 生産関数(Y)から求める
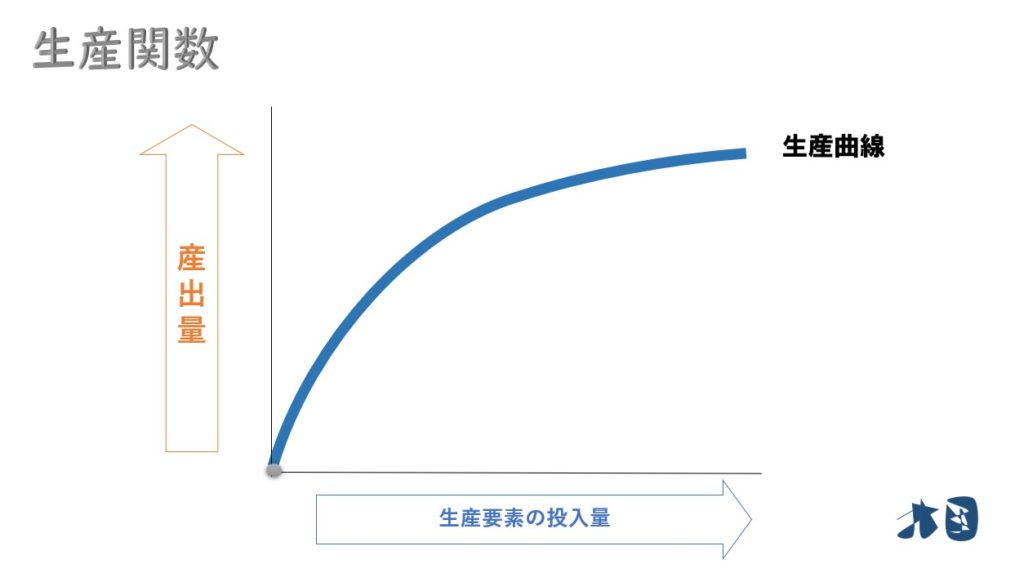
費用関数(C)は、総費用・平均費用・平均可変費用などから、利潤最大化を求めるものが多いです。
生産関数(Y)は、労働のみ(資本は固定・短期生産関数)・生産要素が2つ(長期生産関数)で考えるものがあります。
それぞれの例題を解いて、イメージを掴みましょう。
費用関数(C)から求める
総費用関数(TC)から求める
次の費用関数(C)と価格(P)が与えらえれているとき、完全競争市場において企業の利潤が最大化する最適生産量を求める。※Qは生産量を表す
- 価格(P)=21
ポイント
完全競争市場における利潤最大化条件「価格(P)=限界費用(MC)」を使う。
考え方
- 価格(P)=21と与えられているため、まずは限界費用(MC)を求める。
費用関数(C)を生産量(Q)で微分すれば限界費用になる
こちらの「限界費用曲線」の項目で総費用との関係性を知りましょう⇒【費用曲線の要点を分かりやすく】総費用・固定・可変・平均可変・限界 ※特に「接線の傾き」がポイント
を微分すると
次に
「価格(P)=限界費用(MC)」としてQを求める
・
① 左辺の21を右辺へ移行する
・
② 両辺を3で割る
・
③ 因数分解を行う
・0=(Q-3)(Q+1)
「Q=3,-1」となりますが、生産量はマイナスにならないので「利潤が最大化する生産量(Q)は3」が答えとなる。
平均可変費用関数(AVC)から求める

次の平均可変費用関数(AVC)と価格(P)が与えらえれているとき、完全競争市場において企業の利潤が最大化する最適生産量を求める。※Qは生産量を表す
- 価格(P)=21
ポイント
① 平均可変費用関数(AVC)から総費用関数(TC)を求める。
② 総費用関数(TC)から限界費用関数(MC)を求める。
③ 完全競争市場における利潤最大化条件「価格(P)=限界費用(MC)」を使う。
考え方
- まずは平均可変費用(AVC)から総費用(TC)を求める。
平均可変費用(AVC)は生産量(Q)を掛けて固定費用(FC)を足すと総費用になる
「AVC=(TC-FC)/Q」なので、Qを掛けてFCを足せば総費用を求められる。
にQを掛けると
最後に固定費用(FC)を足すと総費用になります
次に
- この総費用(TC)から限界費用(MC)を求める。
総費用関数(TC)を生産量(Q)で微分すれば限界費用になる
以下「C=~」として計算していきます。
こちらの「限界費用曲線」の項目で総費用との関係性を知りましょう⇒【費用曲線の要点を分かりやすく】総費用・固定・可変・平均可変・限界 ※特に「接線の傾き」がポイント
を微分すると
これで限界費用が求まりました。あとは完全競争市場における利潤最大化条件「価格(P)=限界費用(MC)」を使って、最適な生産量を求めます。
続き
「価格(P)=限界費用(MC)」としてQを求める
・
問題文から「価格(P)=21」となっていたことに注意
① 左辺の21を右辺へ移行する
・
② 両辺を3で割る
・
③ 因数分解を行う
・0=(Q-3)(Q+1)
「Q=3,-1」となりますが、生産量はマイナスにならないので「利潤が最大化する生産量(Q)は3」が答えとなる。
生産関数(Y)から求める
生産要素が1つ(労働のみ・短期生産関数)
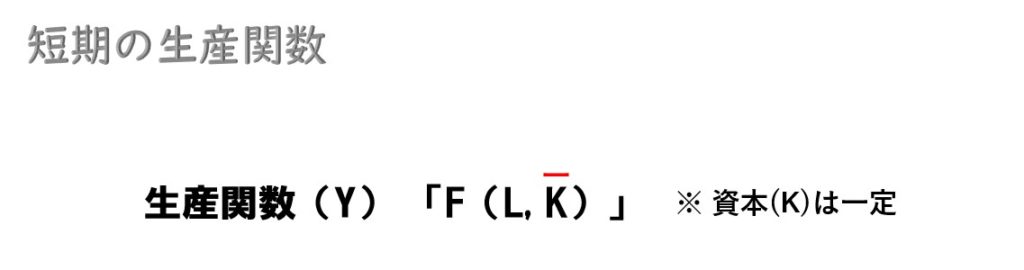
いま、ある企業の生産関数(短期生産関数)が「Y=√L」と与えられているとき、完全競争市場において、この企業が利潤最大化する生産量(Y)・労働の投入量(労働需要量・L)を求める。なお固定費用は考えないものとする。
- 価格(P)=4800
- 賃金(w)=1200
ポイント
「利潤(π)=総収入ー総費用」なので
- 総収入=価格(P)×生産量(Y)
- 総費用=賃金(w)×労働量(L)
したがって「利潤(π)=(PY)-(wL)」と考える。
※「価格(P)」は商品の販売価格(P)・「生産量(Y)」は作ったものを全部売ると考えて生産量=販売量と考えます。なので、販売量(Y)に販売価格(P)を掛けて収入額を計算していることになります。
初めに
- 字数を減らしたいので「利潤(π)=(PY)-(wL)」のY(もしくはL)を消す
ここではYを消す場合を考える
「Y=√L」より
- 利潤(π)=(PY)-(wL)
- 利潤(π)=(P√L)-(wL)
⇒「利潤(π)=(P√L)-(wL)」とする。
重要な考え方
- 「利潤(π)=(P√L)-(wL)」で利潤を最大化させるには?
上記の式を生産量で微分して「=0」とすれば、利潤が最大化したことになる。
理由が分からない人はこちらで確認!
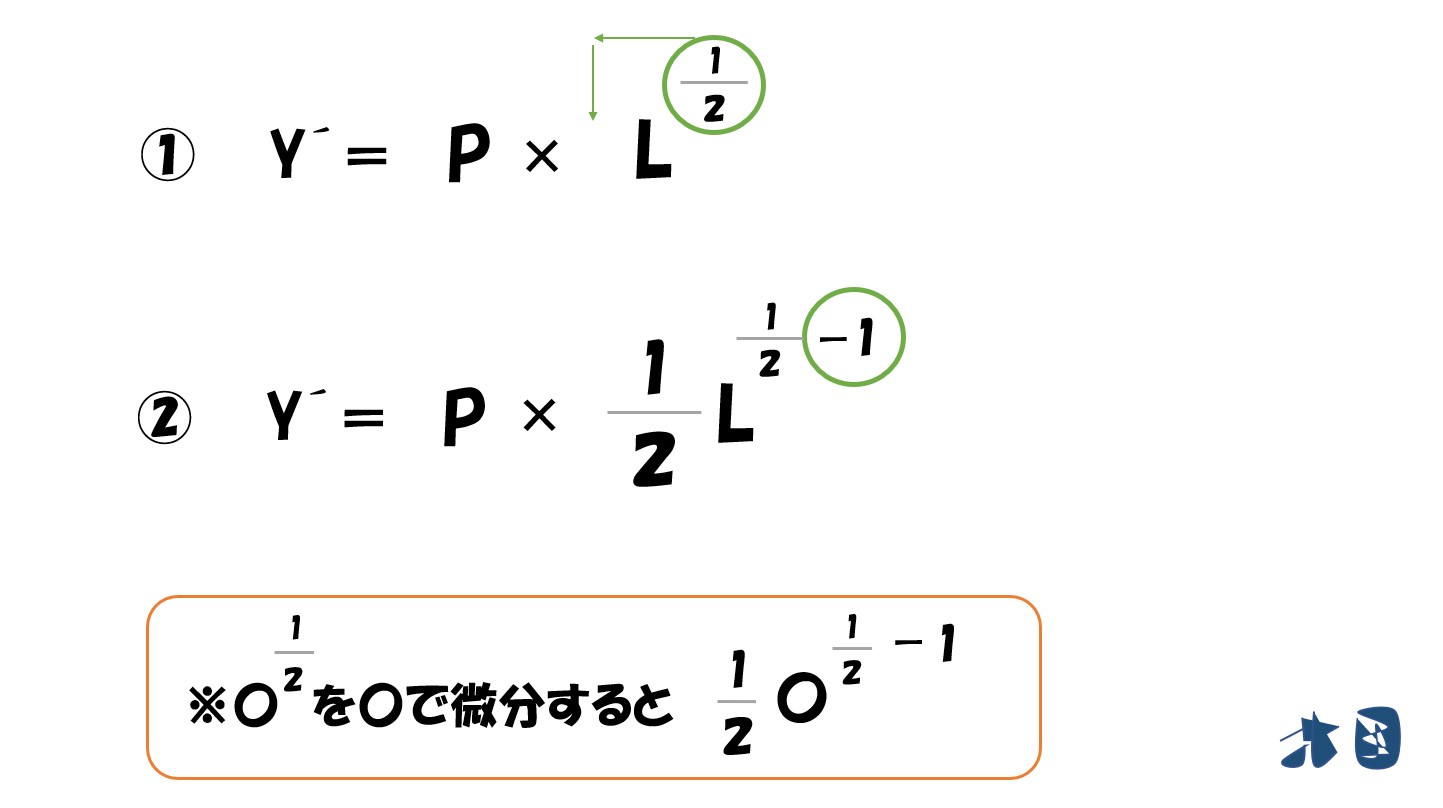
「利潤(π)=(P√L)-(wL)」を生産量で微分します。
ここで、当初の「生産量=Y」は「L」の文字を使って置き換えたので、「生産量(L)」として考えます。したがって「L」で微分して「=0」と置きます。
数式で考えると「Δπ/ΔL=0」←Δπ/ΔLは微分したことを表しています。
知っておく①
「√(ルート)」は「2分の1乗」
そのため「√L=Lの2分の1乗」となります。
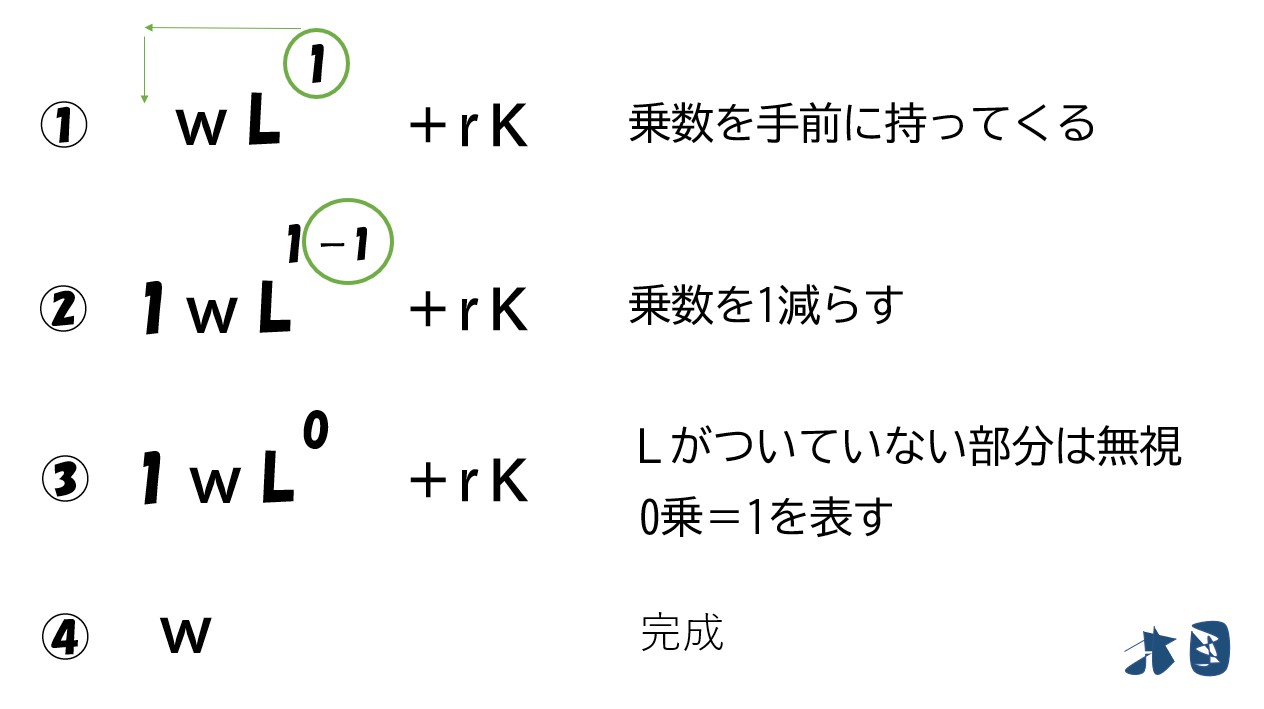
知っておく②
微分をするときは
- 乗数を手前に持ってくる
- 乗数を「1」マイナスする
知っておく③
「乗数がマイナス」のときは「分数になる」
というわけで
「利潤(π)=(P√L)-(wL)」を「L」で微分すると‥
- (P√L)は上で説明した通りで微分できます。
- (wL)は(Lの1乗)なので微分すると(1×Lの0乗)=1になります。よって「w×1=w」
最終的にコレ
生産量で微分して「=0」としているので、上記の式が利潤最大化が実現している状態となっている。
あとは問題で与えられた「P=4800」「w=1200」を代入して「L」の値を求めればOK!
このままでは計算しづらいので、値を代入する前に変形します。
- 「-w」を右辺へ移行する
- 両辺を「P」で割ります
ここで「P=4800・w=1200」を代入します。
- 両辺を2乗する
答え
利潤が最大化する生産量と労働投入量は‥
- 生産量(Y)=2
- 労働の投入量(L)=4
生産関数が「Y=√L」と与えられていたため「√L=2」を代入すれば生産量(Y)が得られる。
別解
- 完全競争市場における利潤最大化条件「価格(P)=限界費用(MC)」を使う
先ほどの説明を思い出す
「利潤(π)=総収入ー総費用」なので
- 総収入=価格(P)×生産量(Y)
- 総費用=賃金(w)×労働量(L)
したがって「利潤(π)=(PY)-(wL)」と考える。
⇒重要なのは「総費用=賃金(w)×労働量(L)」←コレ
ポイント
限界費用(MC)を求めるには、総費用(TC)を生産量で微分すれば求められる。
なので
- 「総費用=賃金(w)×労働量(L)」を生産量(Y)で微分すればOK
ここで、生産量(Y)で微分できるように、労働量(L)を”Y”を使って表す。生産関数「Y=√L」が問題文で与えられていたので、両辺を2乗して「Yの2乗=L」が得られる。
以上より
- 総費用=賃金(w)×(Yの2乗)となる。
これを生産量(Y)で微分すれば‥「限界費用(MC)=2wY」
最後に
利潤最大化条件の「P=MC」より「P=2wY」として計算します。
問題文から「P=4800」「w=1200」と与えられていたので
- 4800=2・1200・Y
- 4800=2400Y
- Y=2
また、生産関数「Y=√L」より「2=√L」となるので「L=4」
答え
利潤最大化が実現する最適な生産量は「Y=2」で、労働投入量は「L=4」となる。
生産要素が2つ(通常・長期生産関数)

いま、ある企業の生産関数(長期生産関数)が
と与えられているとき、完全競争市場において、この企業が利潤最大化する生産量(Y)・各生産要素の最適な投入量(L・K)を求める。
- 価格(P)=2400
- 賃金(w)=1200
- 資本のレンタル料(r)=2400
ここで、与えられた生産関数の乗数が足して1にならないことを確認してください。「Lの0.5乗」「Kの0.5乗」などのように「0.5+0.5=1」となっていると規模に関する収穫が一定となり計算過程が異なります。最後の章を確認してください。
ポイント
「利潤(π)=総収入ー総費用」なので
- 総収入=価格(P)×生産量(Y)
- 総費用=賃金(w)×労働量(L)+レンタル料(r)×資本量(K)
したがって「利潤(π)=(PY)-(wL+rK)」と考える。
※「価格(P)」は商品の販売価格(P)・「生産量(Y)」は作ったものを全部売ると考えて生産量=販売量と考えます。なので、販売量(Y)に販売価格(P)を掛けて収入額を計算していることになります。
初めに
- 字数を減らしたいので「利潤(π)=(PY)-(wL+rK)」のY(もしくはL・K)を消す
ここではYを消す場合を考える
より
- 利潤(π)=(PY)-(wL+rK)
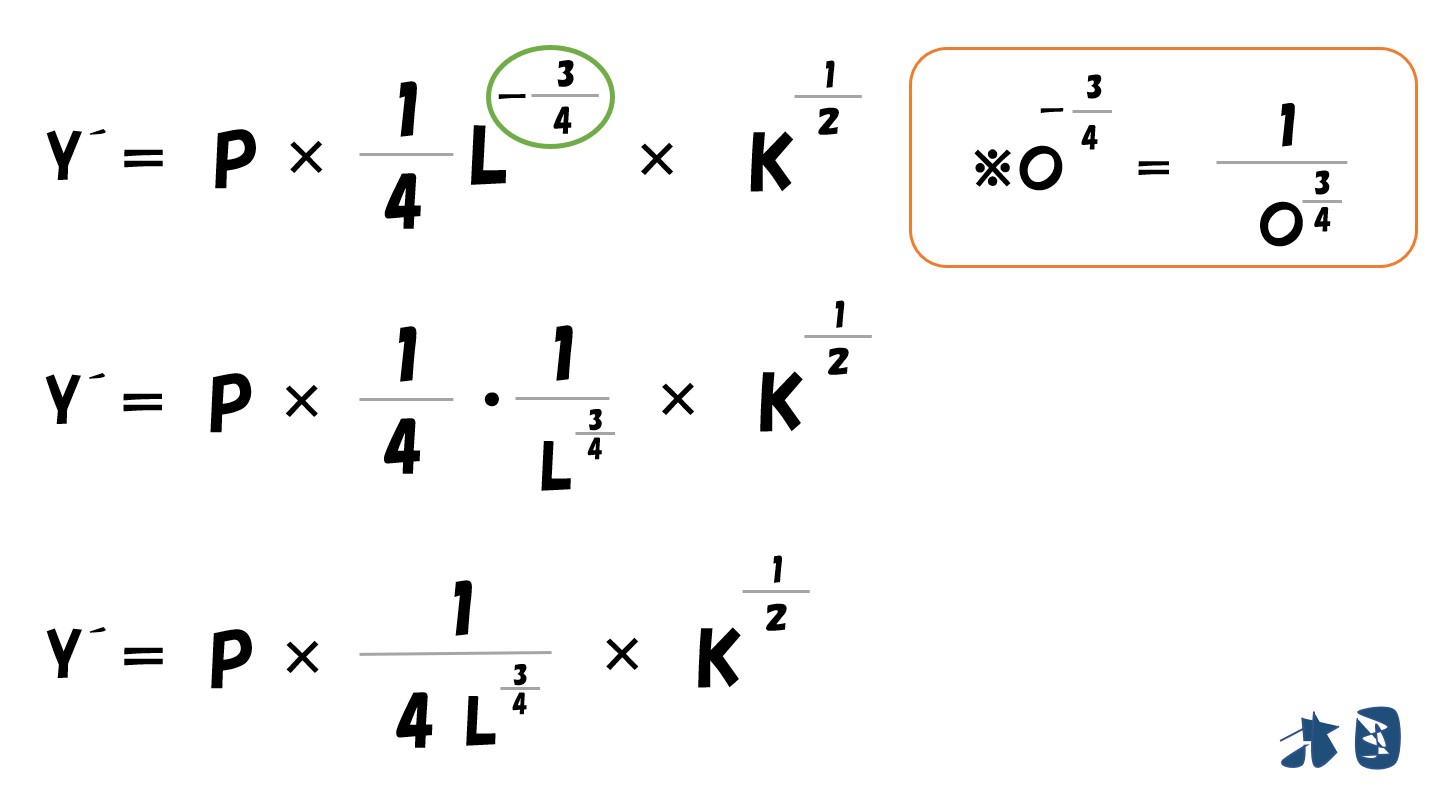
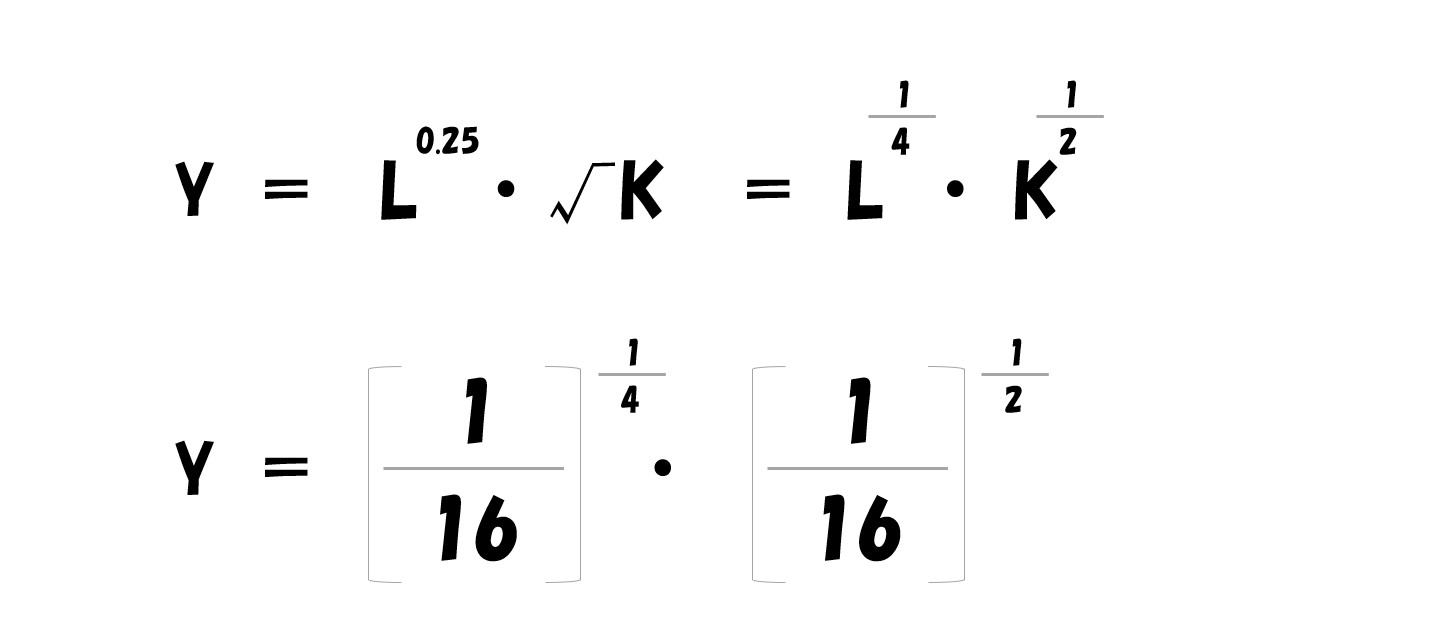
- 利潤(π)=(P・L^0.25・√K)-(wL+rK)
⇒「利潤(π)=(P・L^0.25・√K)-(wL+rK)」とする。
重要な考え方
- 「利潤(π)=(P・L^0.25・√K)-(wL+rK)」で利潤を最大化させるには?
上記の式を生産量で微分して「=0」とすれば、利潤が最大化したことになる。
理由が分からない人はこちらで確認!
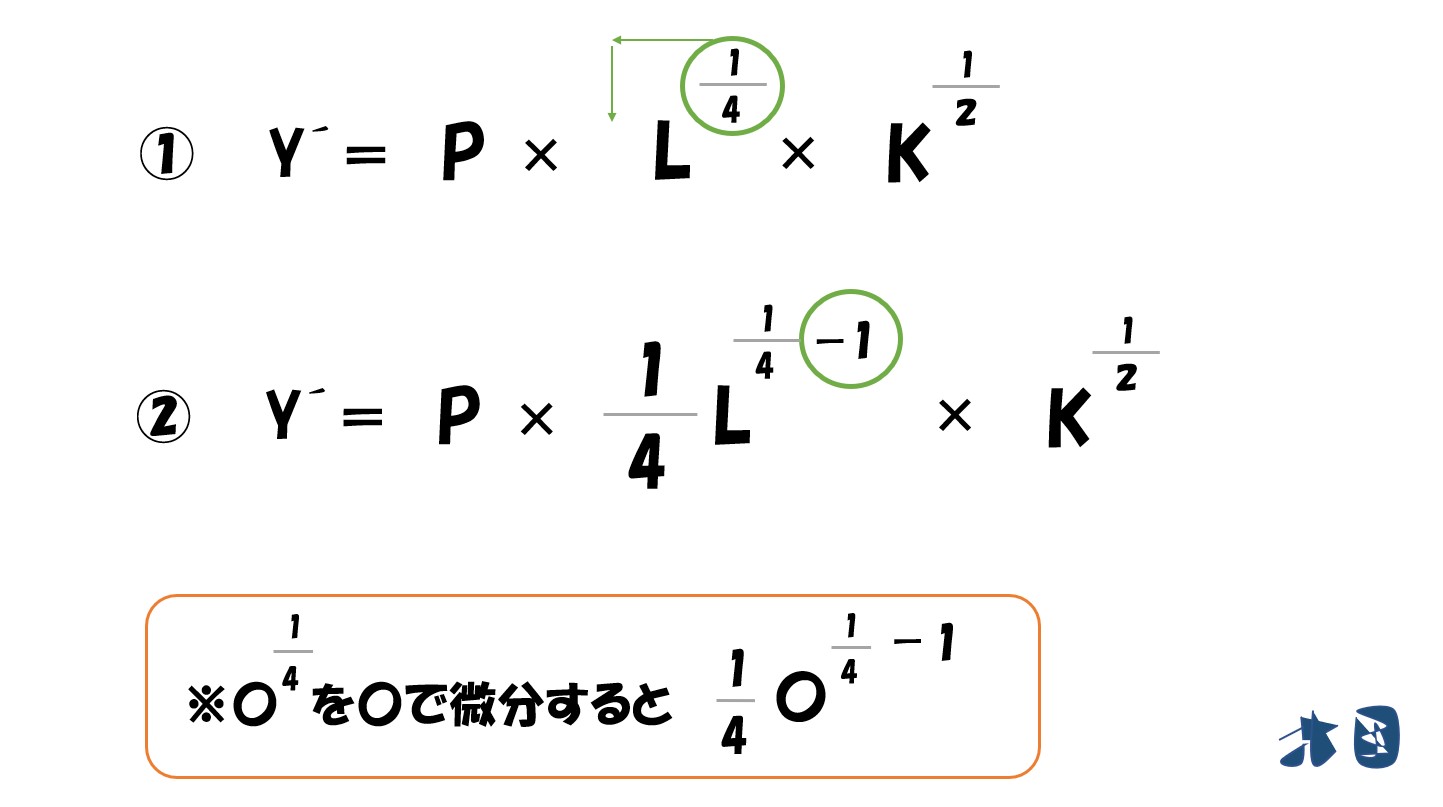
「利潤(π)=(P・L^0.25・√K)-(wL+rK)」を生産量で微分します。
ここで、当初の「生産量=Y」は「L・K」の文字を使って置き換えたので、「生産量(L・K)」として考えます。したがって「L」「K」で偏微分して「=0」と置きます。
数式だと「∂π/∂L=0,∂π/∂K=0」←∂π/∂L・∂π/∂Kは偏微分したことを表しています。
知っておく①
「√(ルート)」は「2分の1乗」
そのため「√K=Kの2分の1乗」となります。以下「√K=Kの2分の1乗(0.5乗)」と表記します。
知っておく②
偏微分をするときは
- 乗数を手前に持ってくる
- 乗数を「1」マイナスする
※0.25=1/4
知っておく②
「乗数がマイナス」のときは「分数になる」
というわけで
「利潤(π)=(P・L^0.25・K^0.5)-(wL+rK)」を「L」で偏微分すると‥
- (P・L^0.25・K^0.5)は上で説明した通りで微分できます。
- (wL+rK)は(Lの1乗)なので微分すると(1×Lの0乗)=1になります。よって「w×1=w」
「L」で偏微分するなら「L」という文字がついていない部分は無視されます。※あくまで微分は変化量(Lという数量が変化したら式の答えがどう変化するか?)を見るため。
最終的にL・Kで偏微分すると
生産量で微分して「=0」としているので、上記の2つの式が利潤最大化が実現している状態となっている。
あとは問題で与えられた「P=2400・w=1200・K=2400」を代入して「L・K」の値を求めればOK!
このままでは計算しづらいので、値を代入する前に変形します。
- 「-w」「-r」を右辺へ移行する
- 両辺を「P」で割ります
ここで「P=2400・w=1200・r=2400」を代入します。
計算していく
両辺を4乗する
「16Lの3乗」と「L/16」がイコール
L=1/16
計算途中で登場した「L=16Kの2乗」へ代入
K=1/16
生産関数「Y=L^0.25・√K」へ答えを代入
計算していく
答え
- 利潤が最大化する生産量(Y)は「1/8」
- 最適な労働の投入量(L)は「1/16」
- 最適な資本の投入量(K)は「1/16」
生産要素が2つ(収穫一定・長期生産関数)

いま、ある企業の生産関数(長期生産関数)が
- Y=√L・√K
と与えられているとき、完全競争市場において、この企業が利潤最大化する生産量(Y)・各生産要素の最適な投入量(L・K)を求める。
- 価格(P)=2400
- 賃金(w)=1200
- 資本のレンタル料(r)=4800
ここで、与えられた生産関数の乗数が足して1になるため収穫が一定となります。※「√L=Lの0.5乗」「√K=Kの0.5乗」⇒「0.5+0.5=1」となっている
ポイント
収穫が一定の場合は、費用最小化を求める。利潤最大化するときは、最も効率的な生産が実現しているはずなので、費用が最小化していると考える。
※収穫が一定の場合は特殊な答えになるため利潤最大化条件を使って計算することが出来ません。
費用最小化
- 「(w/r)」=「MPL/MPK」が成立
「生産要素の価格比(要素価格比)=2つの限界生産力の比」
費用最小化についてはこちら⇒【費用最小化】考え方・条件式・求め方について分かりやすく解説
というわけで、まず「労働の限界生産力(MPL)」「資本の限界生産力(MPK)」を求めます
限界生産力(MP)を求める時は微分をしますが、微分する理由が分からない人は「限界生産力・限界生産力逓減の法則」で確認してください。
計算する
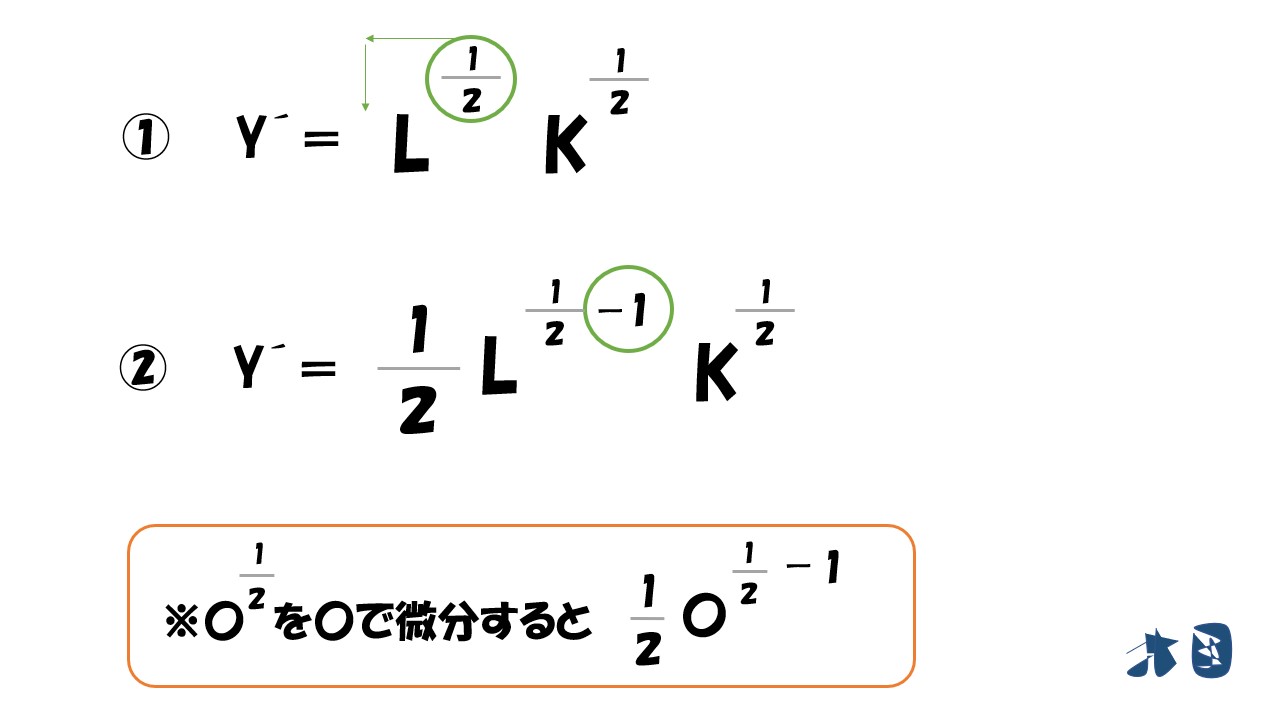
- 「Y=√L・√K」を「L・K」で微分します
※「√L=Lの0.5乗(1/2乗)」「√K=Kの0.5乗(1/2乗)」
労働(L)で微分する
資本(K)で微分する
ここで、費用最小化が実現するとき、下記の式が成り立つ
- 「(w/r)」=「MPL/MPK」が成立
「生産要素の価格比(要素価格比)=2つの限界生産力の比」
費用最小化についてはこちら⇒【費用最小化】考え方・条件式・求め方について分かりやすく解説
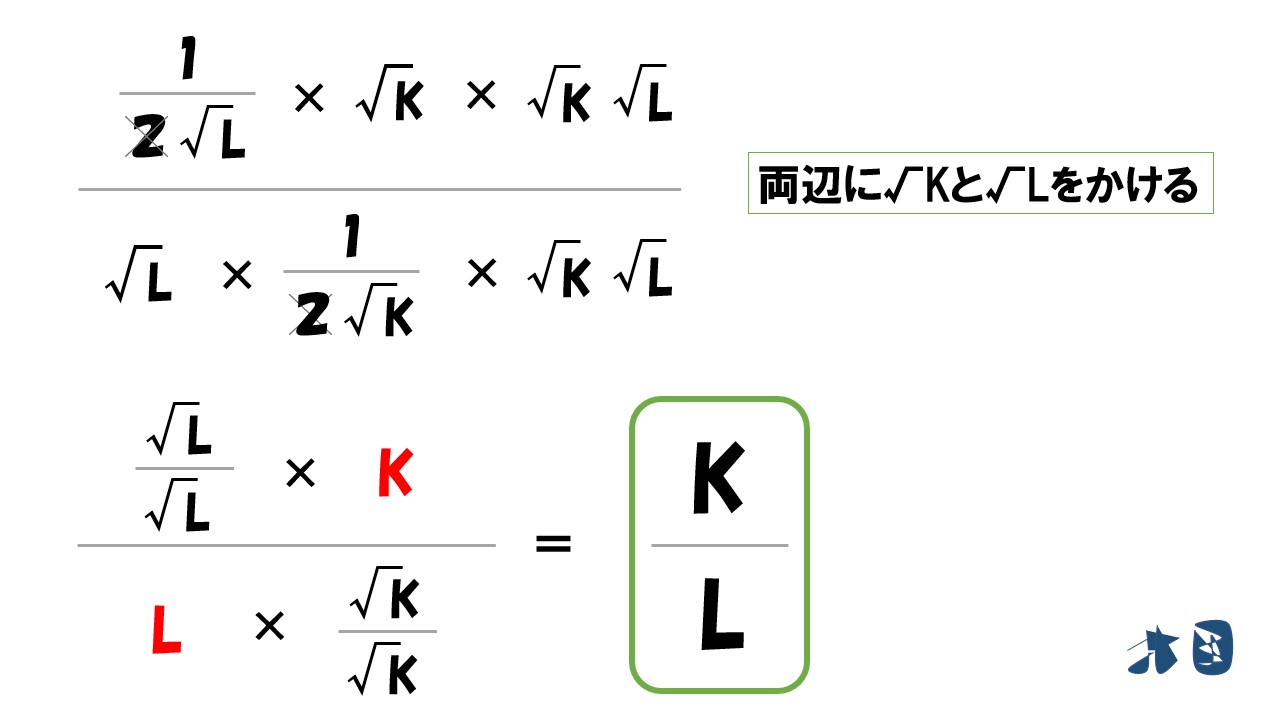
先に
- 「MPL/MPK」を求める
- 「(w/r)」=「MPL/MPK」より
生産関数(Y)に代入
- Y=√L・√K へ代入
ここで
- 費用(C)=wL+rK
「L=2Y」「K=(1/2)Y」を費用関数(C)へ代入する
C=w2Y+r(1/2)Y
C=1200・2Y+4800・(1/2)Y
C=2400Y+2400Y
C=4800Y
この「4800Y」に注目します。
この部分は生産量(Y)を1増やすと、費用が4800かかることを表しています。つまり、費用が4800で一定のため、販売価格(P)の大きさ次第で利潤が出るかが変わります。
- 販売価格(P)が4800より大きい場合(P>4800)
収穫が一定のため、無限に利潤を生み出すことが出来ます。つまり、利潤が最大化する生産量は定まらない(=無限)になります。
- 販売価格(P)が4800より小さい場合(P<4800)
商品を売るたびに赤字になります。そのため、利潤が最大化する生産量は0(=生産しない)になります。
答え
問題文で「価格(P)=2400」とあったので、利潤が最大化する生産量は0となります。