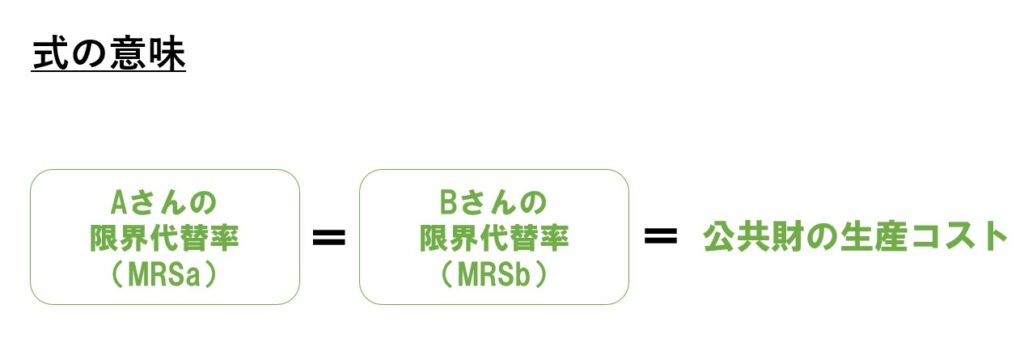
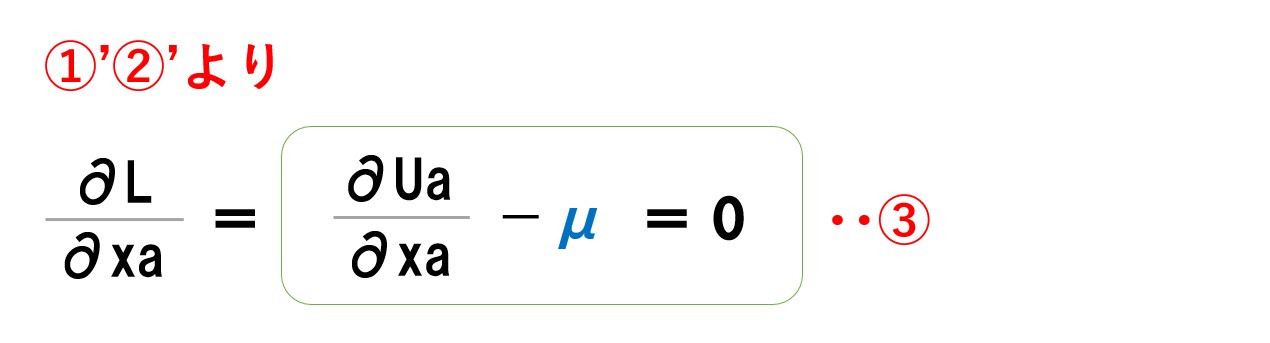公共財を市場原理に任せて供給するとき(自発的供給)の論点をまとめています。
- 公共財の自発的供給(私的供給)
- MRSa=MRSb=MRTの証明
- 自発的供給と最適供給の比較(市場の失敗)
- 過少供給になる証明
公共財の自発的供給(私的供給)とは
はてな
公共財を市場原理に任せて供給することを「公共財の自発的供給(私的供給)」と呼ぶ。
公共財は通常、政府や地方自治体などの行政がサービス提供しています。
例えば
- 警察
- 消防
- 国防
- 公園 など

行政じゃなくて、ふつうの会社が警察とかを運営するのが「公共財の自発的供給」っていうイメージだね。
その通りです!ア〇ソック!

ふつうは行政が運営する公共財を、市場に任せて個人・企業が運営するとどうなるかを考えていきます。
ポイント
公共財を自発的供給(私的供給)にすると「MRSa=MRSb=MRT」が実現する。
さて、この結果を求めるためには残念ながら計算が必要となります。というわけで、サミュエルソン条件を求めた時と同じように計算したいと思います。
前提
- Aさん・Bさんの2人がいる社会
- 「公共財」と「私的財(ふつうの財)」の2財が生産消費されている
- ただし、公共財を生産するためには「私的財」が必要である
- 公共財はAさん・Bさんの2人に便益がある
このとき、公共財を市場に任せて供給するとどうなるかを数学的に考えてみます(数式使って証明します)。
①それぞれ文字で置き換える
- Aさんの公共財の消費量=Ga
- Bさんの公共財の消費量=Gb
- 社会全体の公共財の消費量:G=Ga+Gb ※1
- Aさんの私的財の消費量=xa
- Bさんの私的財の消費量=xb
- Aさんの初期保有・予算=wa ※2
- Bさんの初期保有・予算=wb ※2
※1 A・Bさんが生産消費したいと考えた公共財の総量(G)を全員が消費できる(排除不可能性による)
※2 Wealth(富)から「w」としている。予算式は「I」を使うことが多いが数字の「1」と見分けづらいので「w」で表記
- 公共財の生産コスト=C(G)=G=1とする
- これは「公共財を1つ生産するために、私的財が1つ必要」という意味。
ここで
「Aさんの予算制約」=「公共財の生産コスト+私的財の消費量」
wa = Ga +xa
AさんとBさんの初期保有以上に社会に資源がなく、2人が持っている資源と同じだけしか財を消費できないと想定している。そのため「Aさんの予算制約=公共財の生産のために投入される私的財の消費量+通常の私的財の消費量」となる。
②効用関数を考える
Aさんの効用関数(Ua)を考える。Aさんは「公共財(G)」と「私的財 (xa) 」を消費することで効用を得られる。
- Ua=〇G×〇xaとなる式(※)を想定する
- ※例えば「Ua=2G×3xa」のようになる。具体的な数値は不明。
これを「Ua(G,xa)」と表現する(具体的な値は分からないけど、上記のような式を想定する)
- Bさんも同様に「Ub(G,xb)」
③条件をまとめる
公共財の自発的供給=市場に任せるということなので、Aさん・Bさんが自身の効用最大化に従って行動して公共財を供給すると考えます。
まず、Aさんは効用最大化を目指します
Ua(G,xb)を最大化・・(1)
Aさんは予算制約を満たす必要があります
wa = Ga + xa・・(2)
※Bさんも同様なので省略します。
気づいたかもしれませんが、公共財の自発的供給は、ふつうの効用最大化問題と同じように考えます。
(1)と(2)をまとめて次のように表現します。
式を少し変形します。
①~②を元に「ラグランジュ関数(L)」を使って計算します。 これは「ラグランジュ未定乗数法」という「制約条件がある関数」の「極値」を求めることが出来る計算方法(数学的な手法)です。ここでは「②を制約条件」「①の効用最大化」を極値を求めると考えます。
ラグランジュ未定乗数法の計算方法
はじめに「L=」として、制約条件にあたる部分に「μ(ミュー)※文字なら何でもよい。λ(ラムダ)とかも定番」をつける。
- 以上より「L=①+μ②」とします。※「=0」は無視
「L=①+μ②」の式を次の2つで微分して「=0」とします。
- Aさんの私的財の消費量(xa)
- 公共財の消費量(G)
- ※本来ではあれば「μ」でも微分する必要がありますが、ここでは影響ないので省略します。
ポイント
微分して「=0」と置くのが、この式の中でも重要なポイントです。
(微分する意味)初めはイメージで考えてほしいのですが、各消費量で微分することで「限界効用」を求めることができます。消費者理論の基本的な知識です。【限界効用・限界効用逓減の法則】求め方も含めて簡単にわかりやすく
(=0とする意味)微分すると限界効用になるとイメージ出来れば簡単です。追加的な効用(限界効用)が0ということは、もうこれ以上効用を増やすことができません~という状態です。つまり、これ以上は効用を増やすことができない状態=各財の消費によって得られる限界効用が最大化している=最適な状態と言えます。
以上より、微分して=0と置くことで「L=①+μ②」という式で、Aさんの効用最大化を計算することができます。
「公共財の自発的供給を行う」を「Aさんは予算内で効用最大化を目指して行動する」と考えています。つまり、ふつうに効用最大化問題を解きます。
というわけで、初めにAさんの私的財の消費量(xa)で微分します。
「∂」は微分していることを表します。デルやラウンドなどと呼びます。「L=①+μ②」の式を「xa」で微分したので「∂L/∂xa=~」と表現しています。
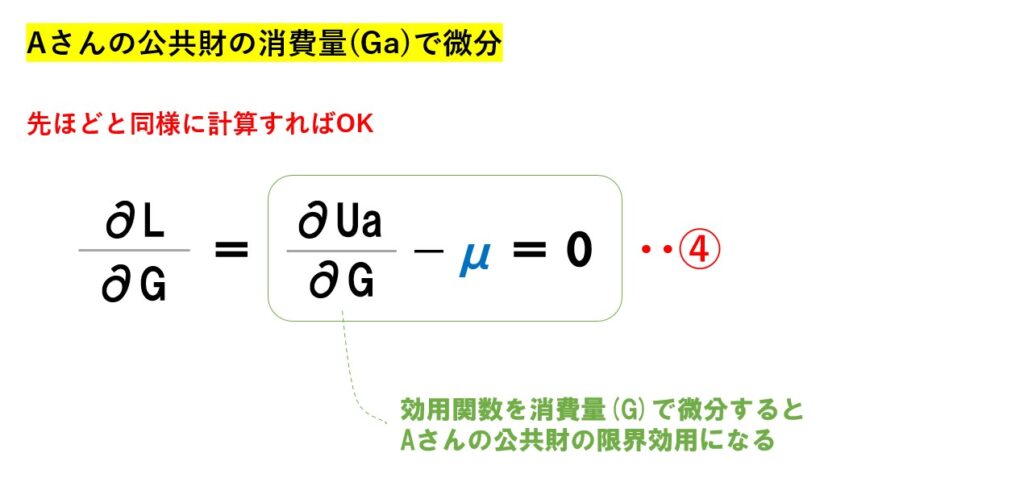
途中で書いた通り、効用関数(Ua)を消費量で微分すると限界効用(∂Ua/∂xa)になります。⇒【限界効用・限界効用逓減の法則】求め方も含めて簡単にわかりやすく
効用関数を消費量で微分すると限界効用(∂Ua/∂xa)となるので、計算せずに文字式で表しました。そうではない部分は普通に計算します。
微分は、乗数を手前に持ってきて、乗数を1減らします。●乗と書いていなければ1乗です。1乗なので、手前に1を持ってきます。1乗から1を引くと0乗となります。0乗は1となります。
「L=①+μ②」の式を「Aさんの私的財の消費量(xa)で微分」して「=0」とすると「③」の式が得られます。 これと同様に「Ga」でも微分して0とした式を求めます。
以上より
ポイント
「1階条件」というのは「Aさんの予算内で、Aさんの効用最大化するためには、次の式を満たしている必要がありますよ」という条件のことです。
各条件や前提を文字で表して、ラグランジュ関数(L)を作りました。そのラグランジュ関数を「微分して=0と置く」ことで、Aさんの効用最大化を求めることができます。この時「微分して=0と置く」ことで得られる3つの式を「1階条件」と言います。
なぜ「1階条件」なのかという話ですが、それはもちろん「2階条件」と話が続くからです。数学的に考えると、これまでの計算方法では極値を求めることしかできません(効用が最大化 or 最小化しているかは判断できない)。この極値が「最大」か「最小」かを判断するための条件式を「2階条件」と呼びます。
- 1階条件→「極値」を求めるための条件式
- 2階条件→求めた極値が「最大」か「最小」かを判断するための条件式
学部レベルの経済学の問題では、多くの場合、暗黙の了解で2階条件を計算する必要がありません。ここでなら、1階条件を計算すると暗黙の了解で「Aさんの効用最大化(最小ではない)」が得られると考えています。そのため2階条件は省略します。
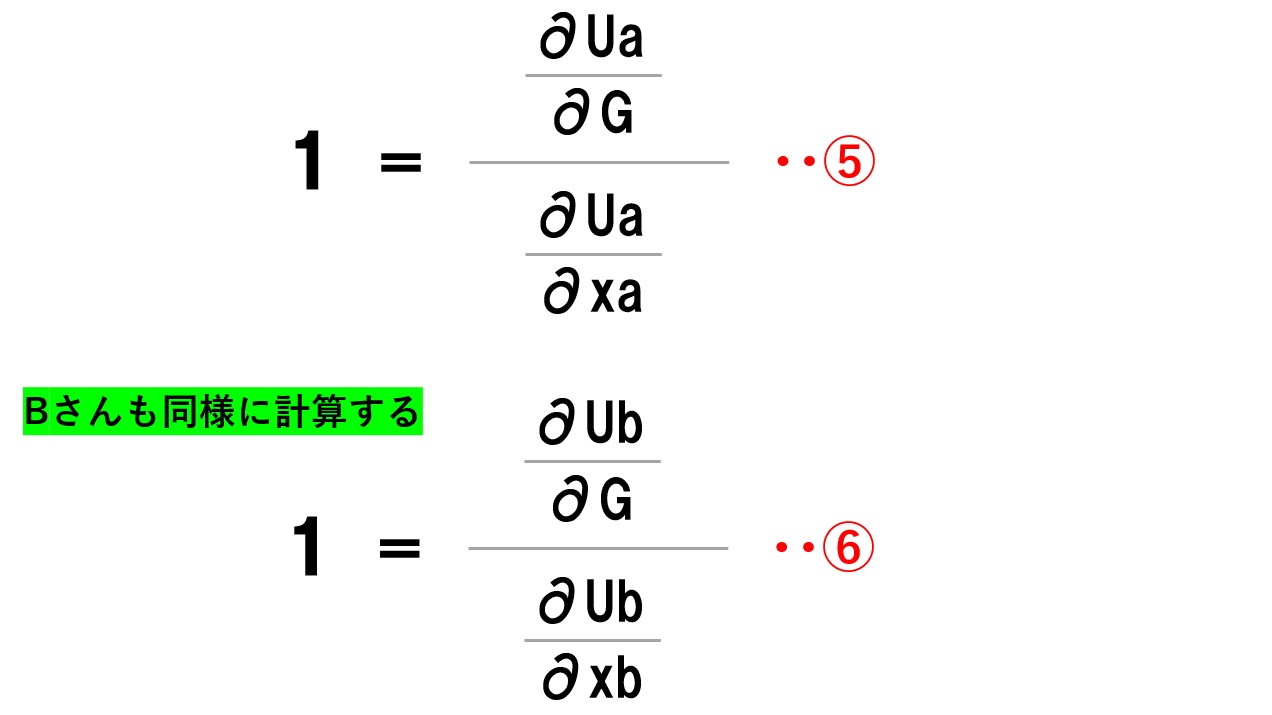
あとは計算するだけ!
Aさんについて計算してきましたが、Bさんも同様に計算できるので、Aさんと同様の⑥式が得られます。
この式が何を表しているかが重要です。
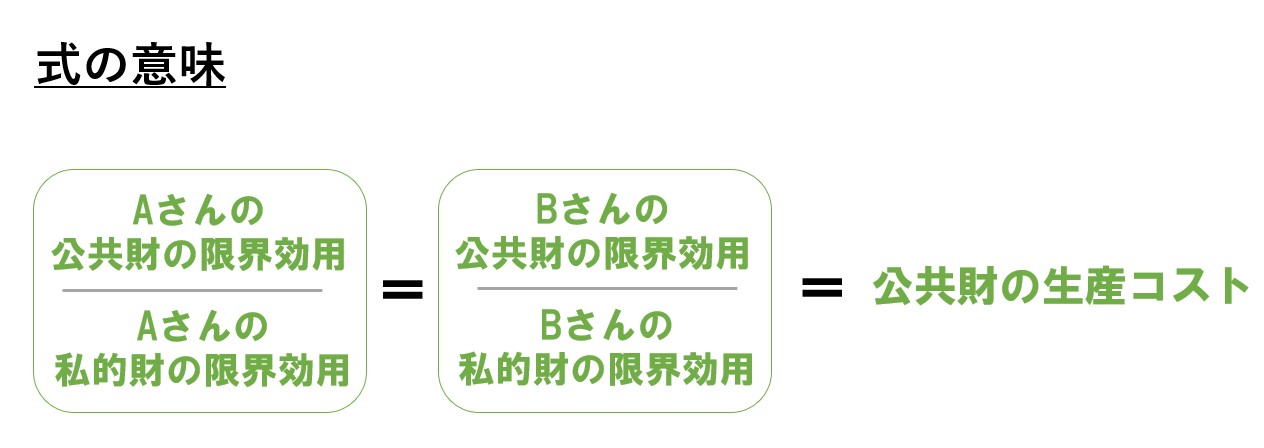
左辺
- 分子「∂U/∂G」⇒効用関数を公共財の消費量(G)で微分したもの=Aさんの公共財の限界効用
- 分母「∂U/∂xa」⇒効用関数をAさんの私的財の消費量(xa)で微分したもの=Aさんの私的財の限界効用
※Bさんの分は省略
右辺
- 「1」⇒公共財の生産コスト
冒頭でそれぞれを文字へ置き換えるときに「公共財の生産コスト=C(G)=G=1」としていたので、公共財の生産コストを表しています。「公共財を1つ生産するために、私的財が1つ必要」という意味。
効用関数・費用関数を微分すると限界〇〇になるというのは、途中で説明した通りなので、理解できなければ最初の方から読み直してください。
左辺について
ポイント
また、消費者理論で登場する話で恐縮ですが「2財の限界効用の比(A財の限界効用/B財の限界効用)」というのは「限界代替率(MRS)」を表します。
つまり・・
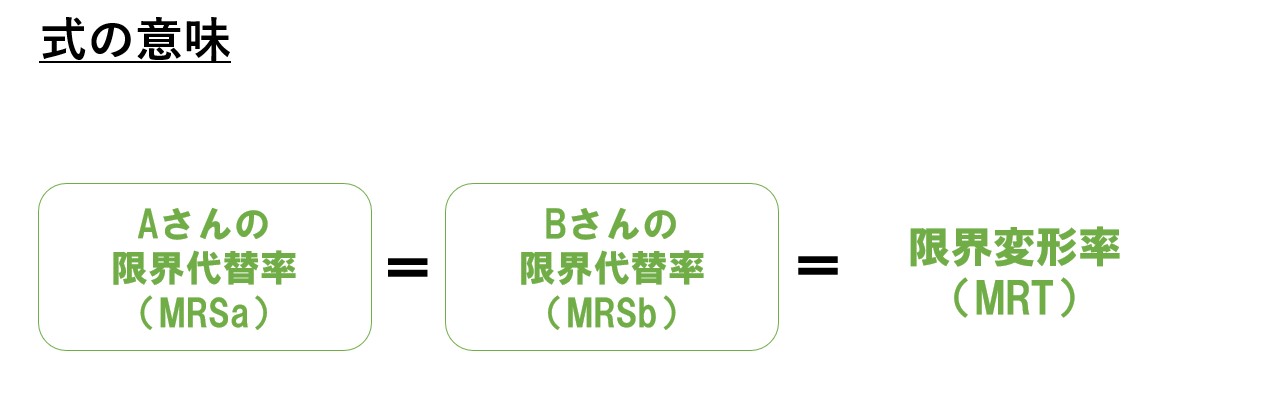
左辺は「Aさんの限界代替率=Bさんの限界代替率」を表します。
右辺について
ポイント
公共財を作るためには私的財が必要でした。つまり「公共財の生産コスト=私的財の投入量」⇒ 公共財を1単位作るために、私的財が〇単位必要ということを意味します。ここでは「1」と考えていました。
「ある財を作るために、もう片方の財をどれくらい諦めるか=限界変形率(MRT)」なので、「公共財の限界費用(MC)=公共財を1単位生産するために、私的財をどれくらい投入する必要があるか(私的財を投入する=失う=諦めると考える)」は同じことを言っていることになります。
以上より「公共財の生産コスト=限界変形率(MRT)=1」となります。
最後
以上より、公共財の自発的供給を行うと上記の結果になることが分かりました(終わり)。

サミュエルソン条件と計算結果が似ている気がする。
うん。実はほとんど同じです。でも、決定的に違うところがあるよ(後段に続く)。

自発的供給(市場原理)と最適供給(サミュエルソン条件)
はてな
公共財を市場原理に任せて供給すると、経済学が考える「公共財の最適な供給量(サミュエルソン条件)」が実現しないことが分かっている。「市場の失敗」の1つとして扱われる。
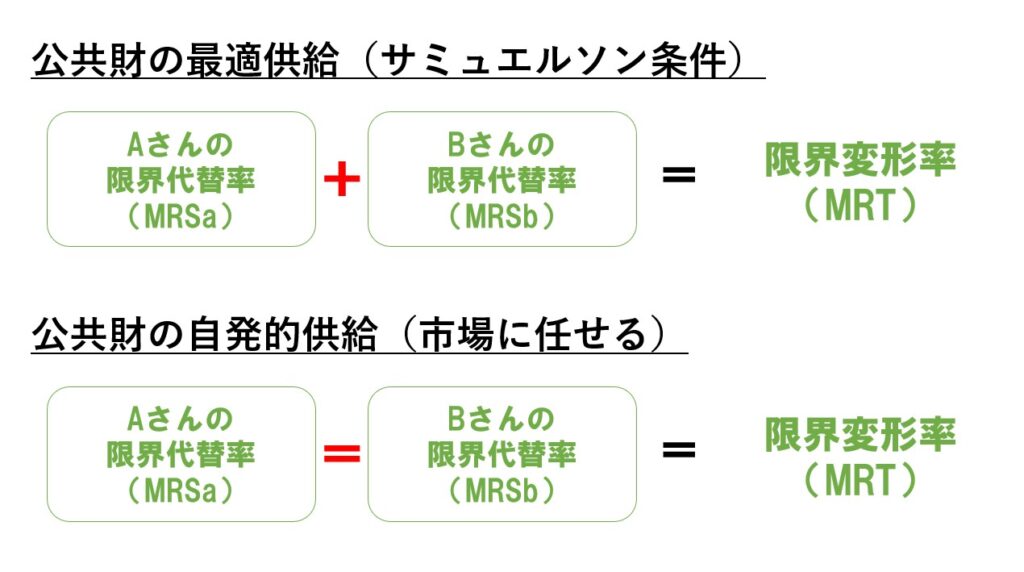
公共財の
- 最適供給(サミュエルソン条件)
- 自発的な供給(市場に任せる)
この2つは、それぞれ違う計算結果になります。
比較の通り、左辺が「+」と「=」で違うため、公共財を市場に任せて供給(自発的供給)しても、公共財の最適供給(サミュエルソン条件)は実現していないことが分かります。
公共財の自発的供給は前段で確認できます。サミュエルソン条件はこちらで確認してください。

この違いは何を意味しているのかな?
比較するために、具体的な数字を使って計算してみよう!

というわけで「自発的供給」と「最適供給」をそれぞれ、具体的な数字を使って計算して、計算結果を比較してみます。
以下、計算にあたり、こちらの資料を参考にさせていただきました。
公共財の私的供給を行う場合(ナッシュ均衡)
前提
- Aさん・Bさんの2人がいる社会
- 「公共財」と「私的財(ふつうの財)」の2財が生産消費されている
- ただし、公共財を生産するためには「私的財」が必要である
- 公共財はAさん・Bさんの2人に便益がある
このとき、公共財を市場に任せて供給するとどうなるかを数学的に考えてみます(数式使って証明します)。
①それぞれ文字で置き換える
- Aさんの公共財の消費量=Ga
- Bさんの公共財の消費量=Gb
- 社会全体の公共財の消費量:G=Ga+Gb ※1
- Aさんの私的財の消費量=xa
- Aさんの初期保有・予算=wa ※2
※1 A・Bさんが生産消費したいと考えた公共財の総量(G)を全員が消費できる(排除不可能性による)
※2 Wealth(富)から「w」としている。予算式は「I」を使うことが多いが数字の「1」と見分けづらいので「w」で表記
②効用関数と予算制約を考える
- Aさんの効用関数(Ua)を「U=xa・G」とする
- Aさんの予算制約(wa)を「wa = Ga +xa」※とする
AさんとBさんの初期保有以上に社会に資源がなく、2人が持っている資源と同じだけしか財を消費できないと想定している。そのため「Aさんの予算制約=公共財の生産のために投入される私的財の消費量+通常の私的財の消費量」となる。
④条件をまとめる
公共財の自発的供給=市場に任せるということなので、Aさん・Bさんが自身の効用最大化に従って行動して公共財を供給すると考えます。
まず、Aさんは効用最大化を目指します
「U=xa・G」を最大化・・(1)
Aさんは予算制約を満たす必要があります
wa = Ga + xa・・(2)
ここで予算制約を少し厳密に考えて、公共財を1つ生産消費するために、私的財が「P個」必要だと想定します。例えば、公共財を1つ作るのに、私的財を2個投入する必要があれば「P=2」となる。
wa = Ga・P + xa・・(2)’
公共財の消費量「G=Ga+Gb」を変形して「Ga=G-Gb」・・(3)
(3)を(2)'へ代入する
・wa = Ga・P+ xa
・wa =(G-Gb)・P + xa
・wa =G・P-Gb・P + xa
・(wa+Gb・P) =G・P + xa ・・(4)
ここで
効用最大化条件の1つ「2財の限界代替率=2財の価格比」より「xa/G=P ・・(5)」
「xa/G」=Aさんの「x財の消費量(xa)」と「公共財の消費量(G)」の比率(限界代替率)
「P」=公共財を1つ生産消費するために私的財が「P個」必要だと想定していました。公共財1個=私的財P個分の価値(価格)と捉えて、これを価格比で考えると「P/1」となります。1省略して「P」です(2財の価格比)
個人が効用最大化を実現するとき「2財の限界代替」と「2財の価格比」が一致する。これは消費者理論のはなしです⇒【最適消費・効用最大化】求め方をグラフを使って分かりやすく
(5)を(4)へ代入する
・(wa+Gb・P) =G・P + xa
・(wa+Gb・P) =G(xa/G)+ xa
・(wa+Gb・P) =xa+xa=2xa
・1/2(wa+Gb・P) =xa
・xa = 1/2(wa+Gb・P) ・・(6)
もう一度、(5)式を使います。
・xa/G=P
・xa=P・G ・・(5)’
(5)’を(4)へ代入する
・(wa+Gb・P)=G・P+ xa
・(wa+Gb・P)=G・P+P・G =2P・G
・wa/P+ (Gb・P)/P=2G
・wa/P+ Gb=2G
※G=Ga+Gbだったので
・wa/P+ Gb=2G=2Ga+2Gb
・wa/P-Gb=2Ga
・1/2( (wa/P)-Gb)=Ga
・Ga=1/2( (wa/P)-Gb) ・・(7)
ポイント
- xa = 1/2(wa+Gb・P) ・・(6)
- Ga = 1/2( (wa/P)-Gb) ・・(7)
(7)式は、Aさんの公共財の消費量(Ga)を決める数式となっています(反応関数)。Bさんの公共財の消費量(Gb)の大きさによって、Aさんの公共財の消費量(Ga)が変化することが分かります。
(6)式は、Aさんの私的財の消費量(xa)を決める数式となっています(需要関数)。※(6)式は使わないので、飛ばしてよいです。一応細かく書いておきます。この式にBさんの公共財の消費量(Gb)が混じっていることがポイントです。Bさんが公共財を消費するほど、Aさんの私的財の消費量が増えることが分かります。
- Bさん「公共財をたくさん消費したい」⇒Bさんは公共財の生産のために、私的財をたくさん投入してくれるはず
- Aさん「生産された公共財にただ乗りすればよい」※公共財には非排除性(誰でも利用できる)という性質があるのを思い出そう
- Bさんが公共財を生産するほど、Aさんは自身の私的財を公共財の生産に回す必要がなくなる⇒Aさんは、Bさんの公共財生産量が増えるほど、Bさんが作った公共財にただ乗りして自由に私的財を消費できるようになる(まるで所得が増えたような錯覚)※(6)式の需要関数は所得効果を表したような式になっている。
Bさんも同様の式が得らえる
- xb = 1/2(wb+Ga・P) ・・(8)
- Gb = 1/2( (wb/P)-Ga) ・・(9)
ポイント
Aさん・Bさんは、相手の公共財の生産消費量(Ga・Gb)を考慮して行動する。最終的に、2人の反応曲線が一致するところで均衡(ナッシュ均衡)となる。
※2人は反応曲線に従って自身の公共財の消費量を決める。そのため、お互いの反応曲線がぶつかるところが均衡になる。
(9)を(7)へ代入する
・Ga = 1/2( (wa/P)-Gb)
・Ga = 1/2( (wa/P)-1/2((wb/P)-Ga))
・Ga= 1/2(wa/P)-1/4(wb/P)+1/4(Ga)
・3/4(Ga)=1/2(wa/P)-1/4(wb/P)
・3Ga= 2(wa/P)-(wb/P)
・Ga= 2/3(wa/P)-1/3(wb/P)
同様に(7)を(9)へ代入すると
・Gb= 2/3(wb/P)-1/3(wa/P)
「G=Ga+Gb」より
・G=2/3(wa/P)-1/3(wb/P)+2/3(wb/P)-1/3(wa/P)
・G= 1/3(wa/P)+1/3(wb/P) ←ナッシュ均衡(Ga,Gb)が得られた
補足すると、AさんとBさんが互いの公共財の生産消費量を考慮しながら、自身の効用最大化を目指したとき、上記のように社会全体の公共財の生産消費量が決定された。市場でお互いが最適な行動(戦略)を取った結果として得られた均衡(=ナッシュ均衡)なので、これが公共財の自発的供給量ということになる。

長かった・・(ブルブル)
ところがどっこい、まだ折り返しです。。

反応曲線をグラフで見た方が分かりやすいですが、後でまとめてみることにします。ここでは計算結果のみ。ちなみに、途中で需要関数を求めましたが特に使わないです。
公共財の最適供給を行う場合(パレート最適)
公共財の最適供給が実現するとき「サミュエルソン条件」が成立していますが、サミュエルソン条件の証明についてはリンク先の記事で確認ください。以下、私的供給を行う場合(ナッシュ均衡)と同じ前提で話を進めていきます。
①それぞれ文字で置き換える
- Aさんの公共財の消費量=Ga
- Bさんの公共財の消費量=Gb
- 社会全体の公共財の消費量:G=Ga+Gb ※1
- Aさんの私的財の消費量=xa
- Aさんの初期保有・予算=wa ※2
※1 A・Bさんが生産消費したいと考えた公共財の総量(G)を全員が消費できる(排除不可能性による)
※2 Wealth(富)から「w」としている。予算式は「I」を使うことが多いが数字の「1」と見分けづらいので「w」で表記
②効用関数と予算制約を考える
- Aさんの効用関数(Ua)を「Ua=xa・G」とする
- Aさんの予算制約(wa)を「wa = Ga・P +xa」※とする
AさんとBさんの初期保有以上に社会に資源がなく、2人が持っている資源と同じだけしか財を消費できないと想定している。そのため「Aさんの予算制約=公共財の生産のために投入される私的財の消費量+通常の私的財の消費量」となる。※公共財を1つ生産消費するために、私的財が「P個」必要だと想定
- Aさんの効用関数「Ua=xa・G」①
- Aさんの予算制約「wa = Ga・P +xa」
- 「wa = Ga +xa」⇒「xa=wa-Ga・P」とする②
- 社会全体の公共財の消費量「G=Ga+Gb」③
②③を①へ代入する
・Ua=xa・G
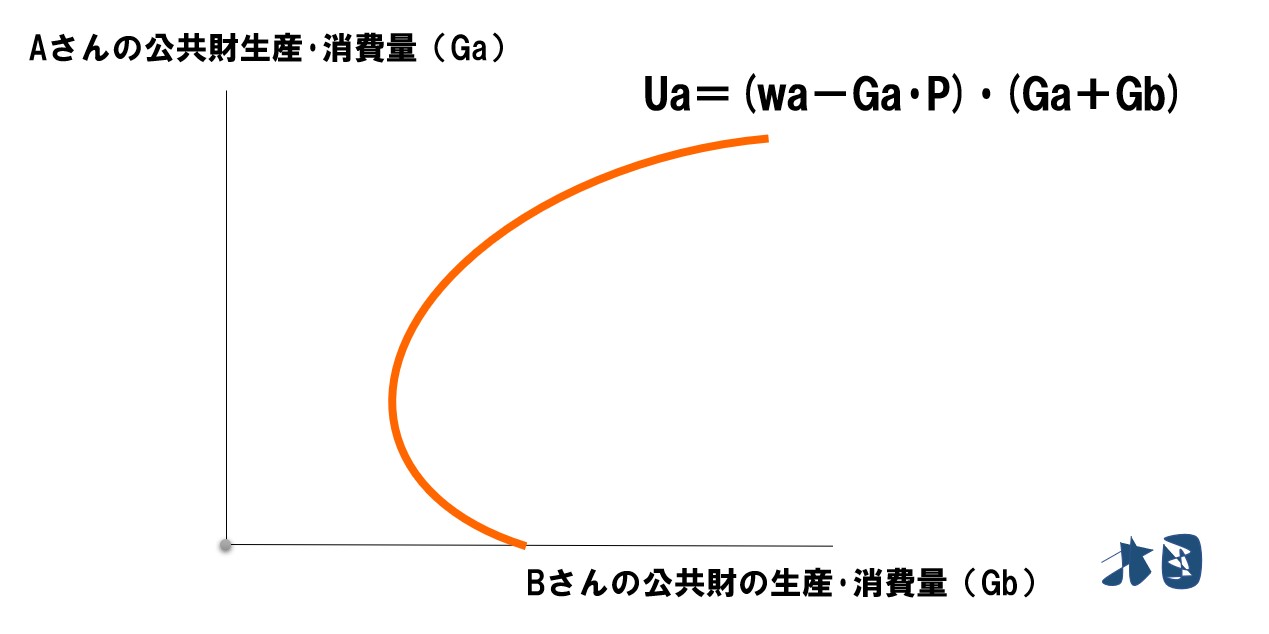
・Ua=(wa-Ga・P)(Ga+Gb)
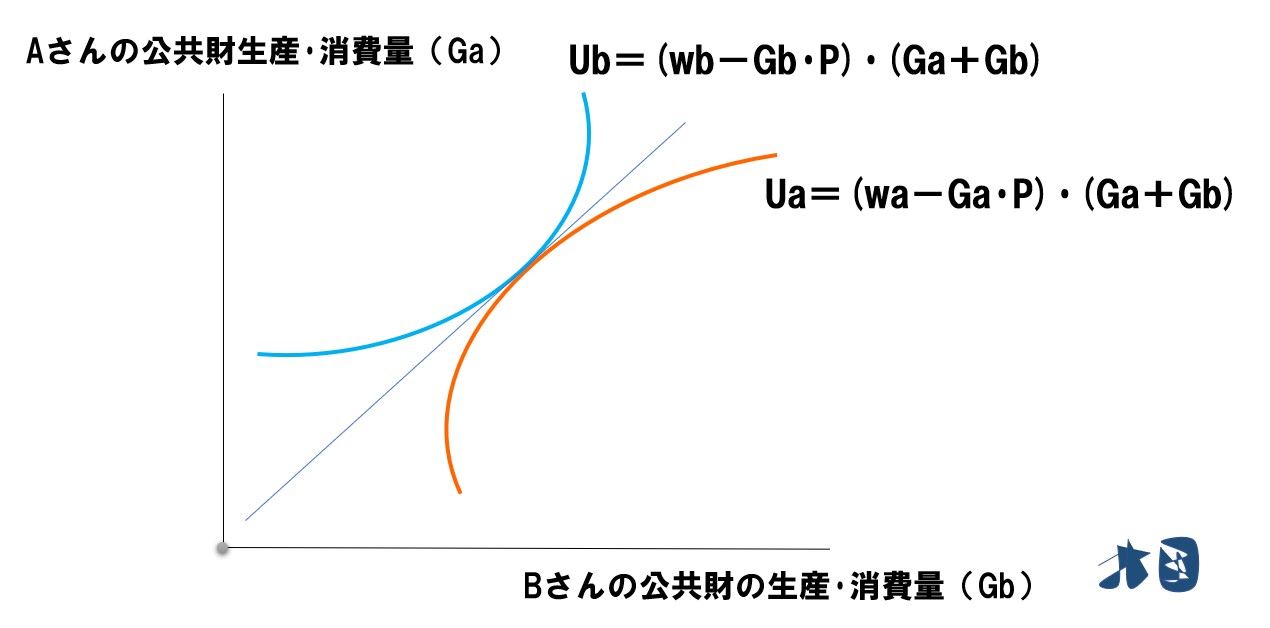
この式をグラフで見ると
効用関数(U)を2次元に落とし込んでいるので、これは無差別曲線となります。ふつうなら、Aさんの「私的財の消費量」「公共財の消費量」を使って無差別曲線を描きますが、私的財の消費量は「Aさんの公共財の生産・消費量(Ga)」と「Bさんの公共財の生産・消費量(Gb)」次第で変わるため、GaとGbを使って無差別曲線を描いていると考えてください。
Bさんも同様に無差別曲線を描けるとして、2人の効用が最大化しているとき
Aさんの無差別曲線は、右下へ行くほど効用が大きくなっている。Bさんの無差別曲線は、左上に行くほど大きくなっていく(エッジワースボックスと同じような考え方)。そのため、2人の無差別曲線が上記のグラフのようになるとき、2人の効用最大化が実現している。見ての通り、このとき、お互いの傾き(限界代替率)は一致している。
傾き(限界代替率)を求めるにあたり「X財の限界効用/Y財の限界効用=限界代替率(MRS)」という、消費者理論の話を使う。ここでは「Aさんの公共財の消費量(Ga)の限界効用」「Bさんの公共財の消費量(Gb)の限界効用 」で考える。
「Ua=(wa-Ga・P)(Ga+Gb)」を「Ga」と「Gb」で微分して分母分子へもっていく。
限界効用を求めるときに、微分する理由はこちらで参照(限界効用の求め方)
(wa-Ga・P)(Ga+Gb)を展開してみましょう。「Gbで微分する」=Gbがついていない項は無視。Gbがついてる項は乗数を1減らして手前に持ってきます。 乗数を1減らして、乗数が0になれば「=1」となり文字(Gb)が消えます。「Gaで微分する」ときも同様のやり方です。
(∂Ua/∂Gb)/(∂Ua/∂Ga)
=(wa-Ga・P)/(wa-2Ga・P-Gb・P) ・・(1)
「∂Ua/∂Gb」は式を「Gb」で微分したことを表しています。同様に「∂Ua/∂Ga」は「Ga」で微分したことを表す。先ほどの「X財の限界効用/Y財の限界効用=限界代替率」という式を使いたいので「(∂Ua/∂Gb)/(∂Ua/∂Ga)」としている。計算の結果、限界代替率=(1)と分かった。
Bさんの効用関数から、同様に下記が求められる。
(∂Ub/∂Gb)/(∂Ub/∂Ga)
=(wb-2Gb・P-Ga・P)/(wb-Gb・P) ・・(2)
(1)(2)より
先ほど記載した通り「お互いの傾き(限界代替率)」は一致している。したがって「(1)=(2)」となる。
(wa-Ga・P)/(wa-2Ga・P-Gb・P)
=(wb-2Gb・P-Ga・P)/(wb-Gb・P)
G=1/2(wa/P)+1/2(wb/P) ←パレート最適(Ga,Gb)が得られた
AさんとBさんを効用最大化させる公共財の生産消費量(G)が得られました(最適供給量=パレート最適)。私的供給のときは、AさんとBさんは自身の効用最大化を目指していたが、目指していただけで、実現しているわけではない。最適供給では「効用最大化が実現している前提」で公共財の供給量を求めている。

途中の計算は苦難の道でした・・(ブルブル)
筆者、効率的な求め方が分からず愚直に計算しています。

最後に、私的供給と最適供給の差を比較していきましょう!
私的供給と最適供給の比較(過少供給)
ポイント
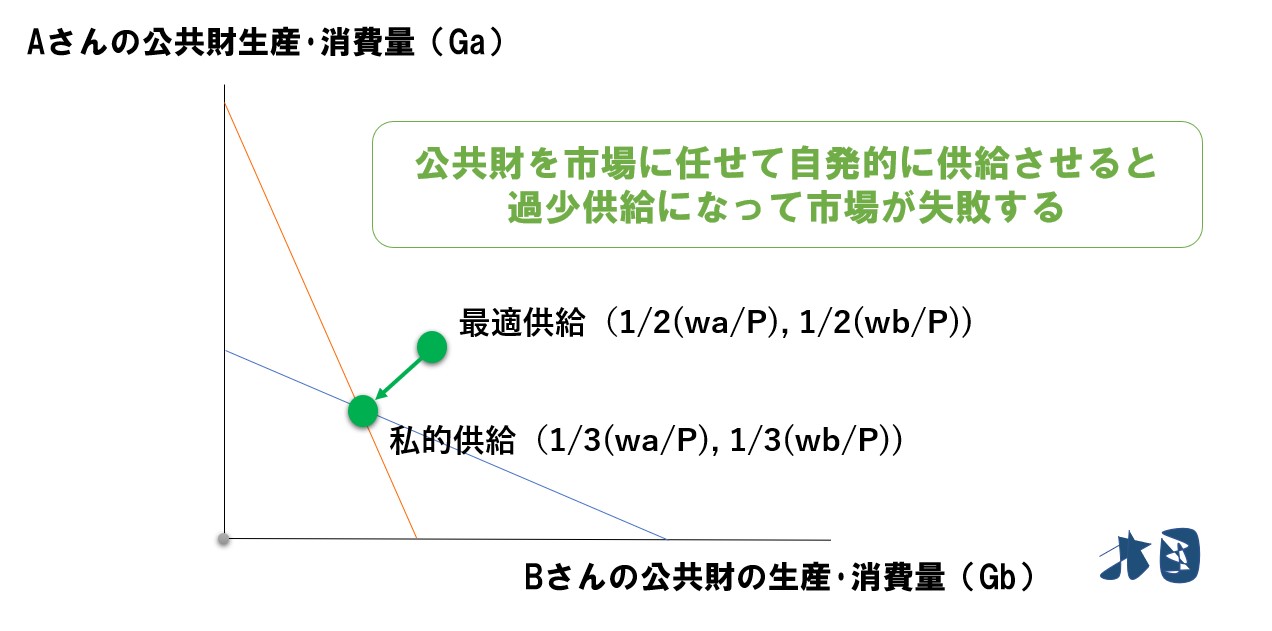
公共財を私的供給すると、効率的な供給量(公共財の最適供給)が実現せずに過少供給となる。
比較する
【私的供給】G=1/3(wa/P)+1/3(wb/P)
【最適供給】G=1/2(wa/P)+1/2(wb/P)
※具体的な計算過程は、前段落で確認してください。「私的供給を行う場合」と「最適供給を行う場合」でそれぞれ、公共財の生産消費量(G)がどのようになるか計算しています。計算の結果、上記の2つが得られています。
「1/3」と「1/2」なら、「1/3」の方が小さいです。つまり、私的供給のほうが公共財の生産消費量(G)が少なくなっている(過少供給となっている)ことが分かります。

おお!すぐに比較できました!
途中の計算は無駄ではなかった・・。

(おまけ)反応曲線で見てみる
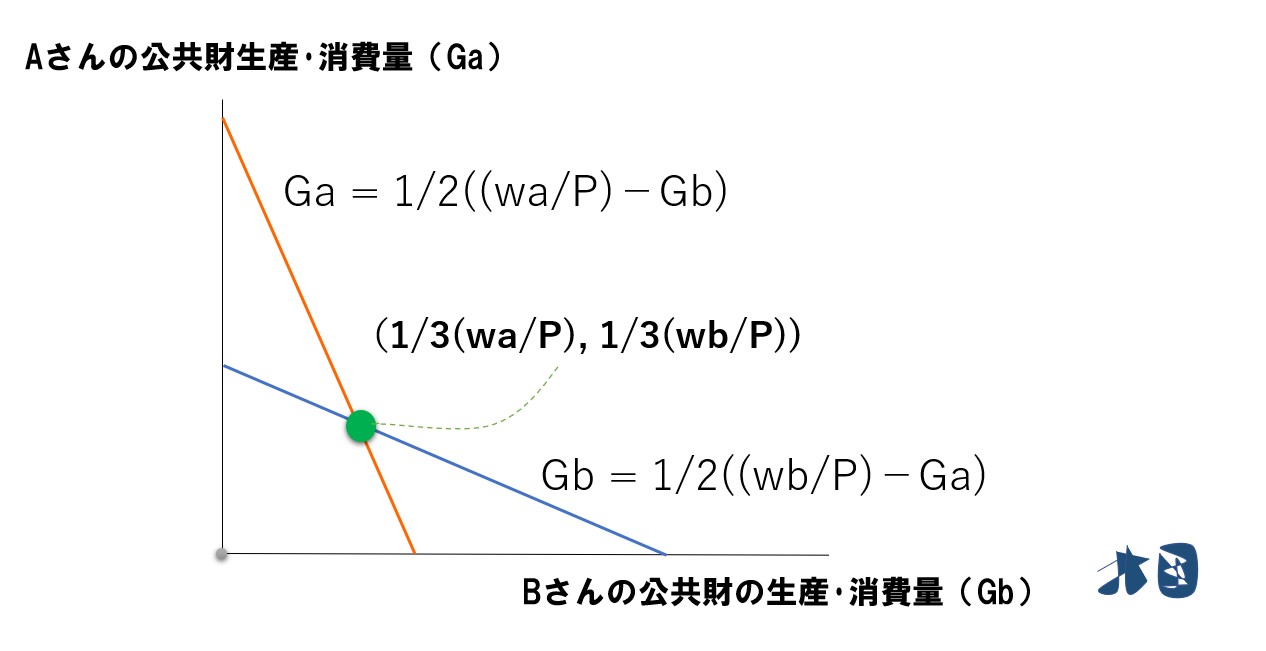
私的供給を求める過程で次の式が得られました。
Ga = 1/2( (wa/P)-Gb) ・・(7)
Gb = 1/2( (wb/P)-Ga) ・・(9)
これをグラフで見ます。
緑の丸点が私的供給により実現する均衡点(ナッシュ均衡)
最適供給量を求めるときに登場したAさんの無差別曲線「Ua=(wa-Ga・P)(Ga+Gb)」とBさんの無差別曲線(省略)を使って、最適供給量をグラフで見ると・・
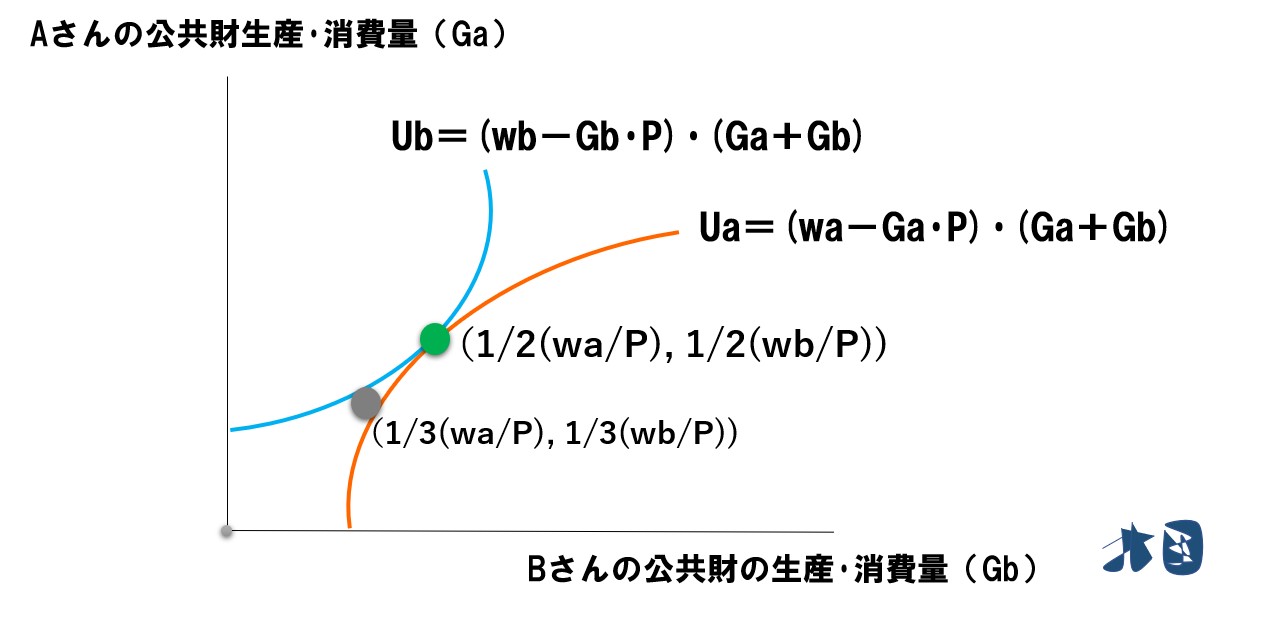
緑の丸点が最適供給量(パレート最適)
最後に見比べると

公共財は、費用を徴収しきれないから過少供給になるって話になるけど、ちゃんと計算しても過少供給になることが分かりました。
とりあえず過少供給になることが分かればOKです~